2. 武汉理工大学 交通学院,湖北 武汉 430063
2. School of Transportation, Wuhan University of Technology, Wuhan 430063, China
动力定位系统是一种闭环的控制系统,其基本工作原理是利用布置在船舶上的推进器产生的推力来抵抗作用在船舶上的风、浪、流等环境载荷,使船舶尽可能保持其预定位置与首向[1]。该系统包括数据处理与融合、环境力估算、状态估计、控制算法和推力优化分配算法等。
状态估计是船舶动力定位系统中一个重要组成部分,其主要功能是为动力定位系统的控制系统提供当前船舶的位置和外界环境的信息。对于动力定位船舶的状态估计,船舶所处的海洋环境和状态估计中所采用的滤波算法是2个关键的因素。目前已经有很多的滤波算法应用于状态估计中,应用最为广泛的是基于卡尔曼滤波的方法,包括扩展卡尔曼滤波、无迹尔卡尔曼滤波等,其次是无源滤波、自适应滤波算法等。这些滤波器对于船舶首向的滤波效果都不甚理想[2]。
本文将广泛用于机动目标跟踪领域的alpha-beta滤波器[3]用于对动力定位船舶首向的滤波。alpha-beta滤波是一种不基于模型的稳定常增益滤波器,主要适用于对没有精确数学模型的状态进行精确估计。由于在动力定位系统中船舶首向的变化主要是角度的变化,这个过程不能用精确的数学模型来描述。
为此,本文设计了一种混合滤波器,采用alpha-beta滤波器对船舶首向单独进行滤波,采用扩展卡尔曼滤波器对船舶横向和纵向进行滤波。首先介绍扩展卡尔曼滤波的算法原理,然后介绍alpha-beta滤波的算法原理,最后通过船模实验仿真验证了alpha-beta滤波器可改善船舶首向的滤波效果。
1 扩展卡尔曼滤波算法目前动力定位船舶3个方向均采用同一种滤波器进行滤波,但是无论是基于卡尔曼滤波的算法还是其他滤波算法,对于船舶首向的滤波效果相比较于另外2个方向,均是最差的。本文采用alpha-beta滤波算法对船舶首向单独进行滤波,而另外2个方向采用扩展卡尔曼滤波算法进行滤波。
扩展卡尔曼滤波状态方程和观测方程为:
| $\begin{aligned}&\mathit{\boldsymbol{X}}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{f}}[\mathit{\boldsymbol{x}}(t - 1),\mathit{\boldsymbol{u}}(t - 1)] + \mathit{\boldsymbol{Ew}}{\rm{(}}t{\rm{ - 1)}}\text{,}\\& \mathit{\boldsymbol{Z}}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{g}}[\mathit{\boldsymbol{x}}(t),\mathit{\boldsymbol{u}}(t)] + \mathit{\boldsymbol{v}}{\rm{(}}t{\rm{)}}\text{。}\end{aligned}$ | (1) |
利用一阶泰勒展开对扩展卡尔曼滤波进行线性化,可得到如下状态方程和观测方程:
| $\begin{aligned}&\mathit{\boldsymbol{X}}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{\Phi }} \cdot \mathit{\boldsymbol{X}}{\rm{(}}t{\rm{ - 1)}} + \mathit{\boldsymbol{G}} \cdot \mathit{\boldsymbol{w}}{\rm{(}}t{\rm{ - 1)}}\text{,}\\&\mathit{\boldsymbol{Z}}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{H}} \cdot \mathit{\boldsymbol{X}}{\rm{(}}t{\rm{)}} + \mathit{\boldsymbol{v}}{\rm{(}}t{\rm{)}}\text{。}\end{aligned}$ | (2) |
其中:
其滤波过程如下:
1)时间更新
| $\begin{aligned}& \bar{X}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{f}}[\mathit{\boldsymbol{x}}(t - 1),\mathit{\boldsymbol{u}}(t - 1)]\text{,}\\& \bar{P}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{\Phi }} \cdot \mathit{\boldsymbol{P}}{\rm{(}}t{\rm{ - 1)}} \cdot {\mathit{\boldsymbol{\Phi }}^{\rm T}} + \mathit{\boldsymbol{G}} \cdot \mathit{\boldsymbol{Q}} \cdot {\mathit{\boldsymbol{G}}^{\bf{T}}}\text{。}\end{aligned}$ | (3) |
2)状态更新
| $\begin{aligned}& \mathit{\boldsymbol{X}}{\rm{(}}t{\rm{)}} = \bar{X}{\rm{(}}t{\rm{)}} + \mathit{\boldsymbol{K}}{\rm{(}}t{\rm{)}}[\mathit{\boldsymbol{Z}}{\rm{(}}t{\rm{)}} - \mathit{\boldsymbol{H}} \cdot \bar{X}{\rm{(}}t{\rm{)}}]\text{,}\\&\mathit{\boldsymbol{P}}{\rm{(}}t{\rm{)}} \!=\! (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}{\rm{(}}t{\rm{)}} \cdot \mathit{\boldsymbol{H}})\bar{P}{\rm{(}}t{\rm{)}}{(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}{\rm{(}}t{\rm{)}} \cdot \mathit{\boldsymbol{H}})^{\rm T}} \!\!+\!\! \mathit{\boldsymbol{K}}{\rm{(}}t{\rm{)}} \cdot \mathit{\boldsymbol{R}} \cdot \mathit{\boldsymbol{K}}{\rm{(}}t{\rm{)}}\text{,}\!\!\!\!\\&\mathit{\boldsymbol{K}}{\rm{(}}t{\rm{)}} = \bar{P}{\rm{(}}t{\rm{)}} \cdot {\mathit{\boldsymbol{H}}^{\rm T}}{(\mathit{\boldsymbol{H}} \cdot \bar{P}{\rm{(}}t{\rm{)}} \cdot {\mathit{\boldsymbol{H}}^{\rm T}} + \mathit{\boldsymbol{R}})^{ - 1}}\text{。}\end{aligned}$ | (4) |
其中:
alpha-beta滤波可用如下状态方程和观测方程进行描述[4]:
| $\begin{split}& \mathit{\boldsymbol{S}}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{A}} \cdot \mathit{\boldsymbol{S}}{\rm{(}}t{\rm{ - 1)}} + \mathit{\boldsymbol{G}} \cdot \mathit{\boldsymbol{w}}{\rm{(}}t{\rm{)}}\text{,}\\& \mathit{\boldsymbol{Z}}{\rm{(}}t{\rm{)}}{\bf{ = }}\mathit{\boldsymbol{H}} \cdot \mathit{\boldsymbol{S}}{\rm{(}}t{\rm{)}}{\bf{ + }}\mathit{\boldsymbol{v}}{\rm{(}}t{\rm{)}}\text{。}\end{split}$ | (5) |
其中:
alpha-beta滤波进行状态估计过程与Kalman滤波类似,主要分为以下2个部分:
1)时间更新
| $\bar{S}{\rm{(}}t{\rm{)}} = \mathit{\boldsymbol{A}} \cdot \mathit{\boldsymbol{S}}{\rm{(}}t{\rm{ - 1)}}\text{,}$ | (6) |
2)状态更新
| $\mathit{\boldsymbol{S}}{\rm{(}}t{\rm{)}} = \bar{S}{\rm{(}}t{\rm{)}} + \mathit{\boldsymbol{K}}[\mathit{\boldsymbol{Z}}{\rm{(}}t{\rm{)}} - \mathit{\boldsymbol{H}} \cdot \bar{S}{\rm{(}}t{\rm{)}}]\text{。}$ | (7) |
其中:
alpha-beta滤波是一种二阶的常增益跟踪滤波器[5],从式(5)可以看出,它可以不基于精确的数学模型。其次,其滤波过程与扩展卡尔曼滤波相似,可以看作是一种扩展卡尔曼滤波的简化方案[6]。其相对于扩展卡尔曼滤波,最大的优点在于增益矩阵可以离线计算[7],从而可以大大降低计算的复杂度,实时性较好。
alpha-beta滤波的精度主要取决于增益系数的选取,目前增益系数选取主要有以下几种方法[8]:
1)常系数法
| $\alpha = 0.5,\beta = 0.3\text{。}$ | (8) |
2)稳态卡尔曼增益选择法[9]
| $\beta = 2(2 - \alpha ) - 4\sqrt {1 - \alpha }\text{。} $ | (9) |
3)自适应跟踪法
| $\alpha (k) = \frac{{2(2k - 1)}}{{k(k + 1)}},\beta (k) = \frac{6}{{k(k + 1)}}\text{。}$ | (10) |
以上各式计算增益系数的方法不同,滤波的效果也会不同,所以寻找合适的增益系数,是alpha-beta滤波算法的重点和难点。
3 实验仿真为了比较本文提出的混合滤波器和扩展卡尔曼滤波器的性能,进行实验仿真。仿真中,将滤波器与经典PID控制构成一个闭环系统,PID控制的横向和纵向输入值取自扩展卡尔曼滤波的结果,首向输入值取自alpha-beta滤波的结果。
实验仿真以1艘按1 : 20比例建造的平台供应船船模为仿真对象,船模相关参数如表1所示。
|
|
表 1 船模参数 Tab.1 Ship model parameters |
无因次化后的附加质量矩阵、水动力阻尼系数矩阵如下:
| $\mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}}{0.754}\!\!\!\!\!\!\!\!\!&0&\!\!\!\!\!\!\!\!\!0\\0\!\!\!\!\!\!\!\!\!&{1.199}&\!\!\!\!\!\!\!\!\!{0.211}\\0\!\!\!&{0.029}\!\!\!&{0.524}\end{array}} \right]\text{,}\mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}}{0.014}\!\!\!\!\!\!\!\!\!&0&\!\!\!\!\!\!\!\!\!0\\0\!\!\!\!\!\!\!\!\!&{0.102}&\!\!\!\!\!\!\!{ - 0.024}\\0&{0.192}&\!\!\!\!{0.095}\end{array}} \right]\text{。}$ |
仿真的控制周期为0.2 s,仿真时间为500个控制周期,船舶初始位置为
首先采用扩展卡尔曼滤波对船舶3个自由度方向进行滤波,其结果如图1~图3所示。由图1~图3可知,扩展卡尔曼滤波在纵向和横向2个方向低频估算位置曲线波动幅度很小,比较平滑,滤波效果较好,而在首向的低频估算曲线波动幅度很大,滤波效果不好。
为了提高动力定位船舶首向的滤波效果,本文采用混合滤波器,即在扩展卡尔曼滤波的基础上,采用alpha-beta滤波算法对首向进行单独滤波。对于alpha-beta滤波算法,最重要的是对于增益系数的选取,结合上文中提到的方法,共仿真3种方法。方法1:增益系数选取采用稳态卡尔曼增益选择法;方法2:增益系数选取采用自适应跟踪法;方法3:增益系数选取采用稳态卡尔曼增益选择法与自适应跟踪法结合的方式。
针对方法1,在本文的实验仿真中取
针对方法2,在本文的实验仿真中取
针对方法3,因为方法1与方法2在前100个周期均出现较大超调,所以增益系数在前100个周期取
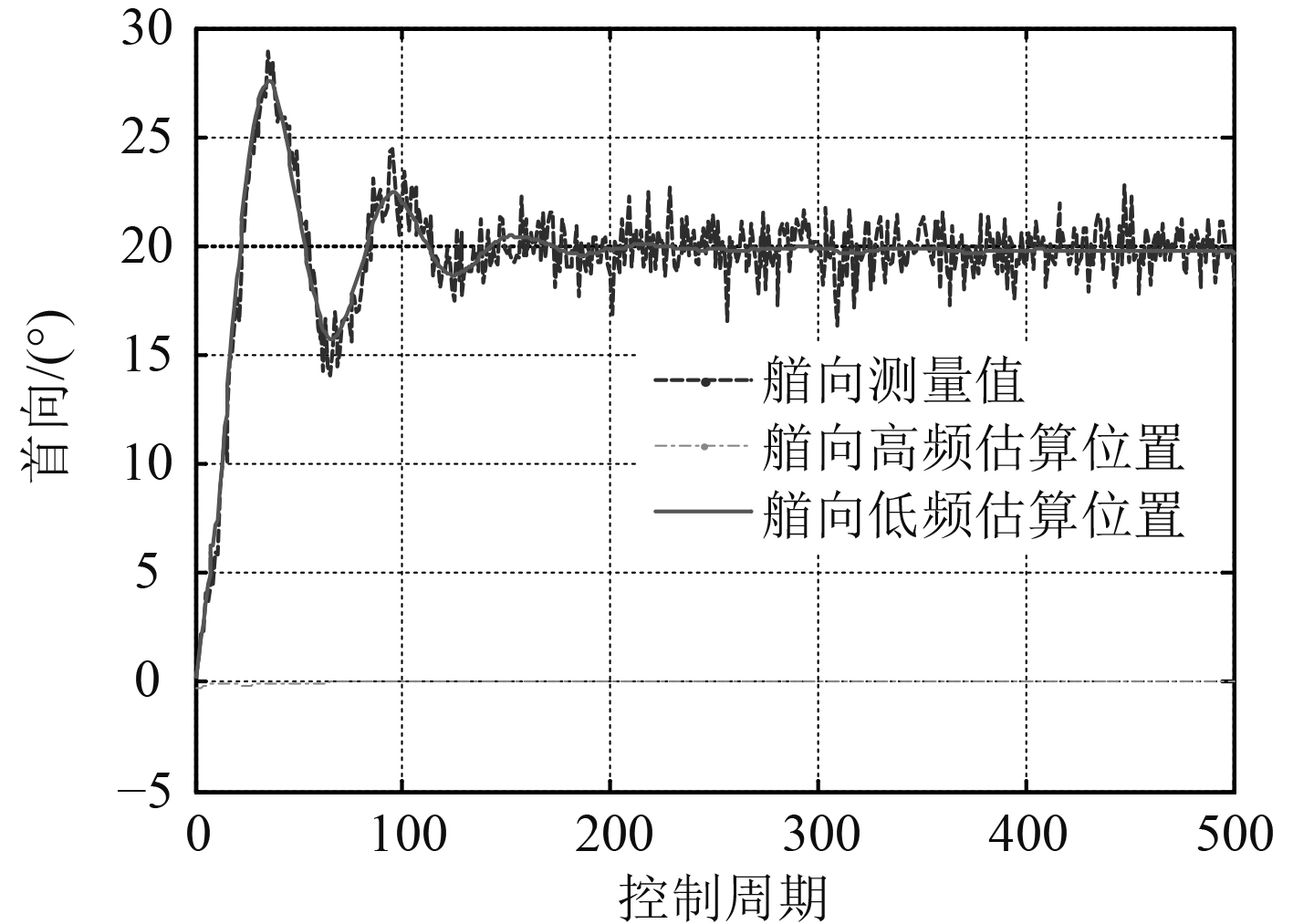
由图4可知,第1种方法首向低频估算位置曲线在前100个周期与首向测量值偏差较大,在100个周期之后曲线较扩展卡尔曼滤波效果有所改善,但是仍有一定波动,不够平滑,滤波效果不太理想;由图5可知,第2种方法首向低频估算位置曲线在前100个周期波动很大,且相对于目标位置有较大超调,100个周期之后曲线波动很小,十分平滑,整体滤波效果不太理想;由图6可知,第3种方法解决了第2种方法在前100个周期超调较大的问题,其首向低频估算位置曲线在全部500个周期内波动较小,且从100个周期之后曲线趋于平滑,可以起到较好的滤波效果。
为综合不同因素对滤波精度的影响,本文采用首向低频估计值的均方根误差作为滤波器滤波精度的评价标准,具体计算公式如下:
| $RMSE = {\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\hat x}_i} - {x_i}} \right)}^2}} } \right]^{1/2}}\text{。}$ | (11) |
其中,
|
|
表 2 不同滤波方法艏向滤波精度 Tab.2 Heading filtering precision of different method |
由表2可知,方法1由于前100个周期超调过大,均方根误差大于扩展卡尔曼滤波,方法2和方法3均方根误差均远小于扩展卡尔曼滤波,滤波精度较高。综上所述,方法3对船舶首向滤波效果最好。
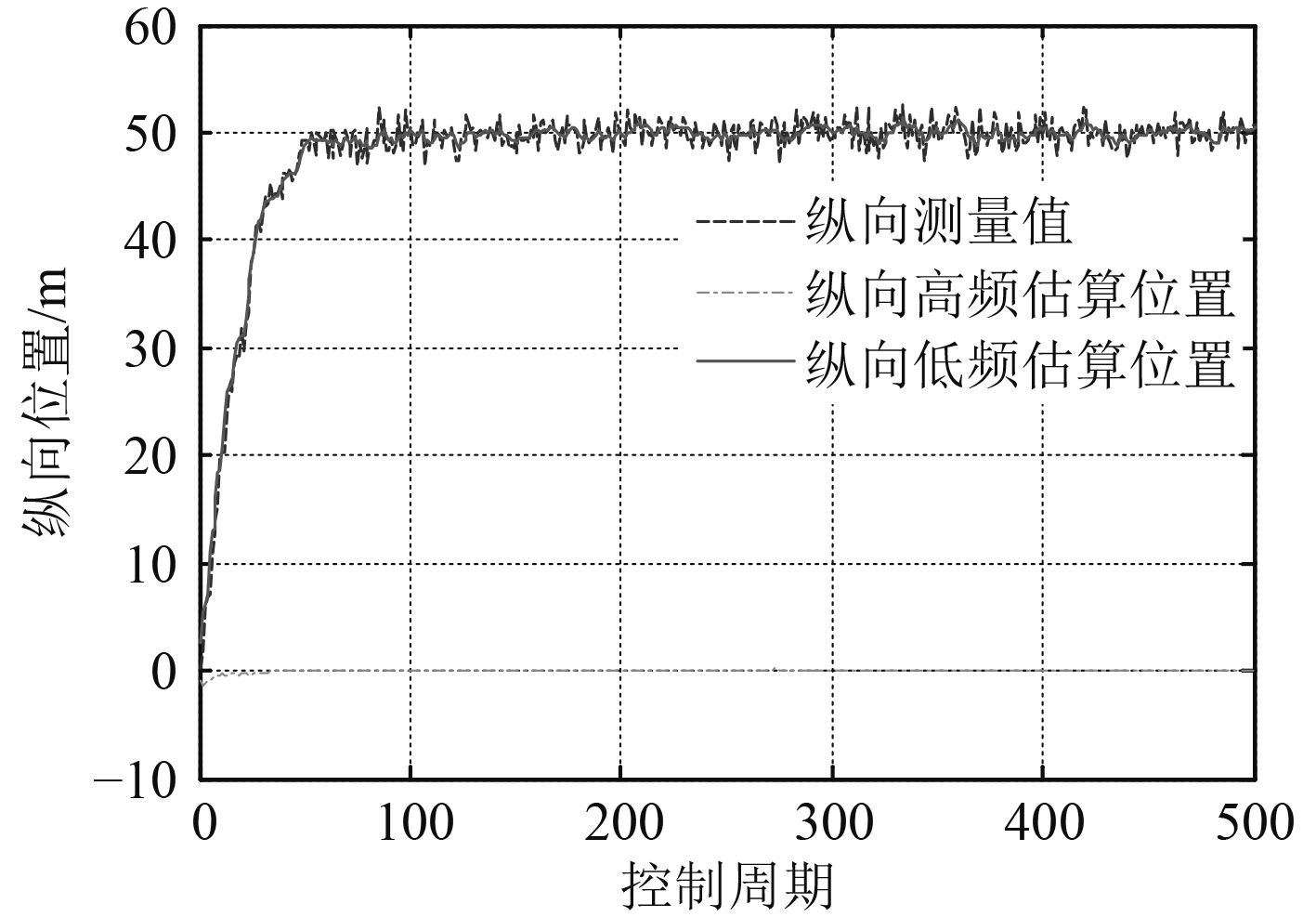
|
图 1 扩展卡尔曼滤波纵向位置滤波结果 Fig. 1 Surge position of extend Kalman filter |
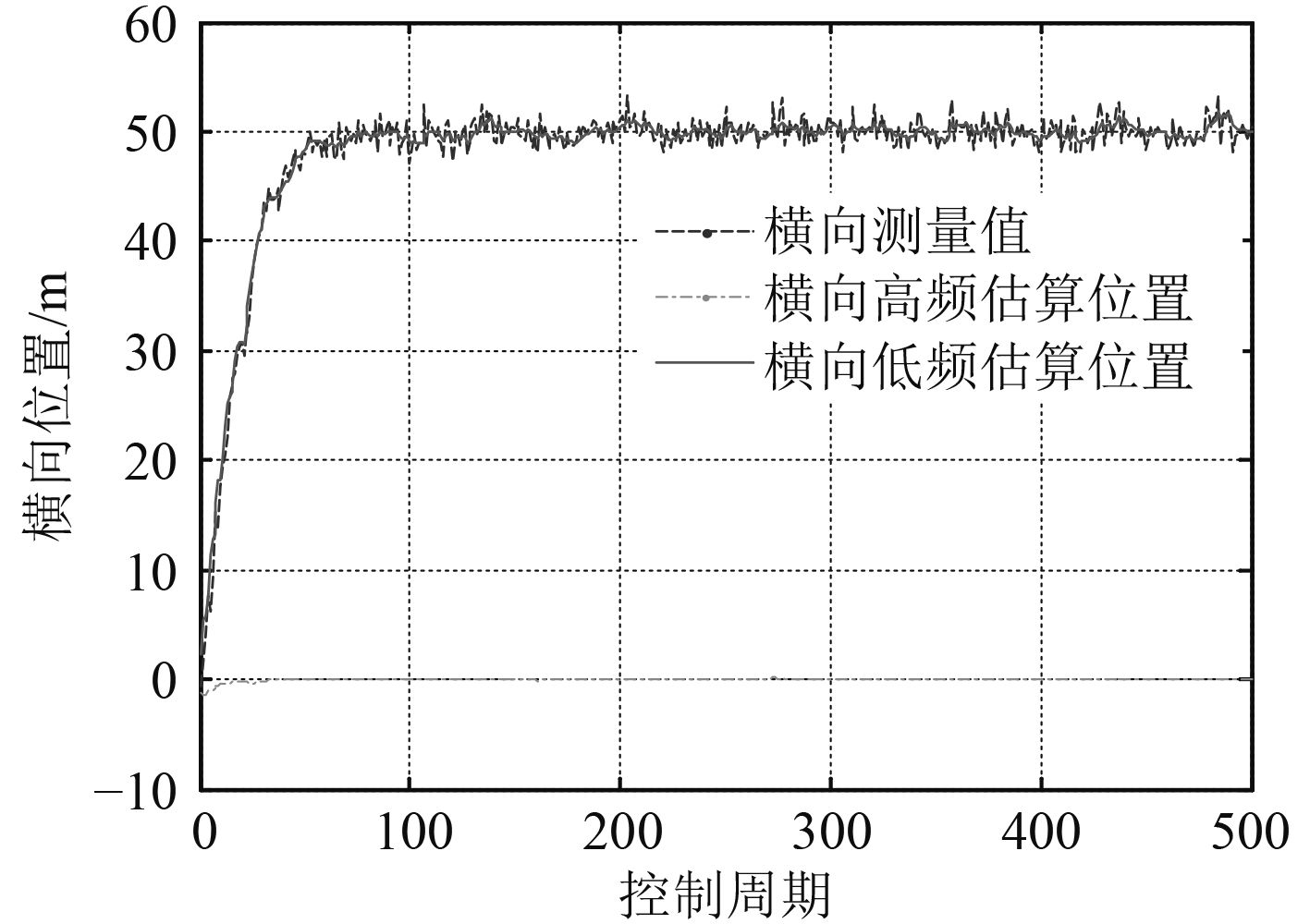
|
图 2 扩展卡尔曼滤波横向位置滤波结果 Fig. 2 Sway position of extend Kalman filter |
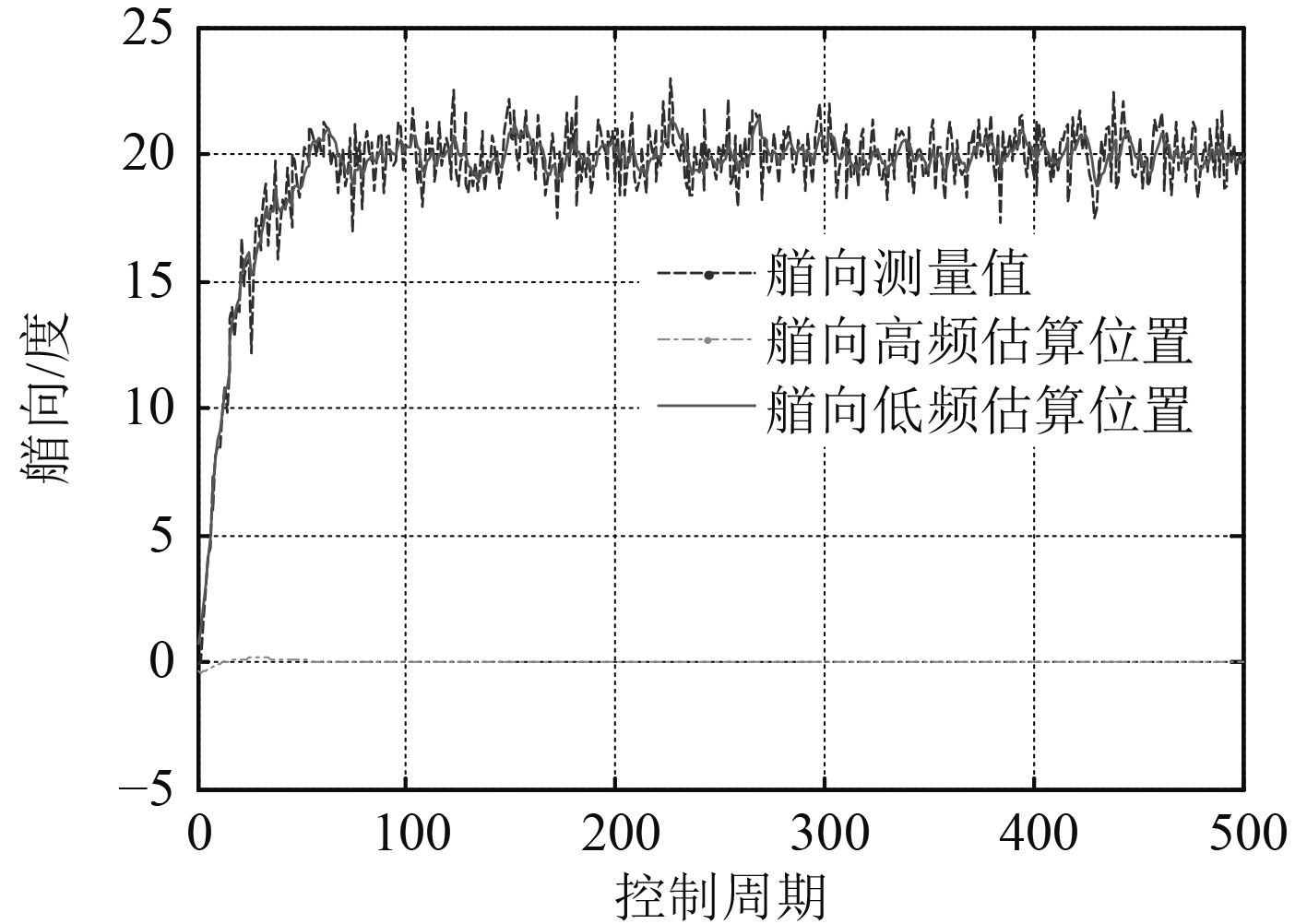
|
图 3 扩展卡尔曼滤波艏向滤波结果 Fig. 3 Yaw position of extend Kalman filter |
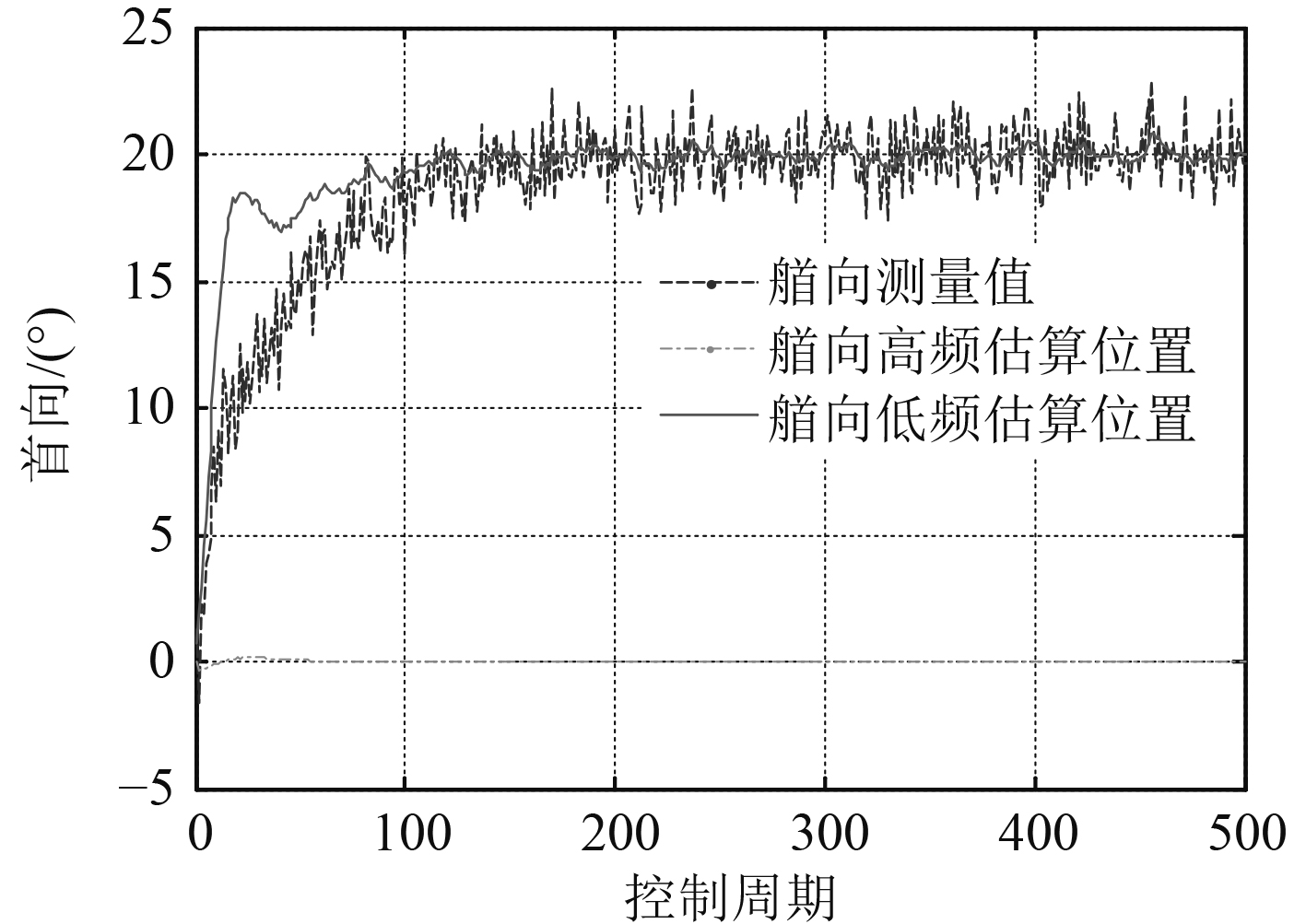
|
图 4 方法1首向滤波结果 Fig. 4 Yaw position of method one |
|
图 5 方法2首向滤波结果 Fig. 5 Yaw position of method two |

|
图 6 方法3首向滤波结果 Fig. 6 Yaw position of method three |
本文在扩展卡尔曼滤波的基础上,提出了利用alpha-beta滤波算法对动力定位船舶首向单独进行滤波,对alpha-beta滤波算法的增益系数选取采用固定增益和自适应增益结合的方法,经过对比仿真实验,验证了该方法可以取得较好的首向滤波效果,相较于扩展卡尔曼滤波,可以很好地改善首向滤波效果。该算法计算量小,易于实现,并且实时性好,在工程应用中有较强实用性。
| [1] | 边信黔, 付明玉, 王元慧, 等.船舶动力定位[M]. 北京: 科学出版社, 2011: 25–29. |
| [2] | FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. 2011: 2–4. |
| [3] | 潘显俊. α-β滤波器在相控阵雷达机动目标跟踪中的应用[J]. 装备指挥技术学院学报, 2005, 16 (2): 96–100. |
| [4] | 戴文舒. 自适应Alpha-beta修正的线谱检测后置处理方法[J]. 电子与信息学报, 2014, 36 (10): 24–30. |
| [5] | 朱齐丹. 自动着舰系统α-β滤波器研究[J]. 计算机仿真, 2014, 31 (2): 121–125. |
| [6] | 贺利文. 一种改进的α-β滤波算法[J]. 现代电子技术, 2012, 35 (21): 28–31. DOI: 10.3969/j.issn.1004-373X.2012.21.009 |
| [7] | 朱薇. 一种改进的α-β目标跟踪滤波算法[J]. 计算机应用, 2007, 27 (8): 45–49. |
| [8] | 王红亮. 一种机动目标跟踪的自适应α-β滤波算法[J]. 雷达科学与技术, 2007, 5 (4): 278–282. |
| [9] | Kalata P R. The Tracking Index: A Generalized Parameter for and α-β-γ Target Trackers [J]. IEEE Transactions on Aerospace & Electronic Systems, 1984, AES-20 (2): 174–182. |
 2018, Vol. 40
2018, Vol. 40
