2. 上海交通大学海洋水下工程科学研究院有限公司,上海 200231;
3. 上海振华重工(集团)股份有限公司,上海 200125
2. Shanghai Jiaotong University Underwater Engineering Institute Co., Ltd., Shanghai 200231, China;
3. Shanghai Zhenhua Heavy Industry Co., Ltd. (EPMC), Shanghai 200125, China
J型铺管法非常适合于深海、超深海海底管道铺设,管道几乎以垂直的位置离开船舶,并且具有J型的管道形状。由于其作业水深一般较大,锚泊定位不再适用,要求船舶配备动力定位系统,能够凭借自身推进器推力抵抗外界环境载荷以及作业载荷,以保持船舶位置与首向。拥有动力定位系统的铺管船无需长时间的起、抛锚过程,到达地点即可开始进行铺管作业。在铺管船动力系统的设计论证阶段,需要考虑管线对船舶的作用,以确保船舶在进行管道铺设也能够满足动力定位要求。
国外对动力定位铺管船的研究开展较早。Brink A和Jin C[1]对动力定位辅助的采矿船进行了铺管作业的可行性研究。E.A. Tannuri和C.P.Pesce[2]研究了在已有的铺管驳船上加装动力定位系统,并进行了模型试验。Cédric Brun等[3]研究了铺管船在进行铺管作业时对静态定位能力的影响。国内对铺管船的研究开展较晚,目前尚未有自主设计的J型铺管船,但已有不少学者开展了研究。王川等[4]开发了铺管船动力定位能力评估系统,并对极端海况下提出了优化辅助方案。谢文博等[5]建立了J型半潜式起重铺管船的非线性船舶运动数学模型以及环境模型,对铺管船定位作业的过程进行建模及分析。施小成等[6]利用被动非线性观测器来滤波,采用终端滑模控制器进行航迹追踪,建立了水平面动力定位船舶运动模型,海洋干扰力模型以及J型铺管模型。
本文以J型铺管船为研究对象,对船舶动力定位能力进行分析,在此基础上对铺管作业对船舶动力定位能力影响进行研究,得到了J型铺管船的静态定位能力(风速包络线与推力使用率包络线),确定了在不同方向下铺管船能够抵抗的极限载荷,以及在作业工况下不同方向上的推力使用率。在时域中对动力定位控制的J型铺管船的真实运动进行实时模拟,获得了定位精度等信息。研究了不同铺管角度下进行管道铺设时对推力使用率包络线的影响,并在时域中对进行铺管作业船舶的动力定位精度进行研究与比较。
1 环境载荷 1.1 主尺度、计算坐标系与环境条件目标船舶垂线间长为127.85 m,型宽为29 m,型深为12.8 m,吃水为8.5 m,排水量为46 235 t。取随船坐标系,坐标系原点位于重心在水线面的投影,采用右手坐标系,X轴向船首为正,Y轴向右舷为正,Z轴向上为正。计算坐标系如图1所示。
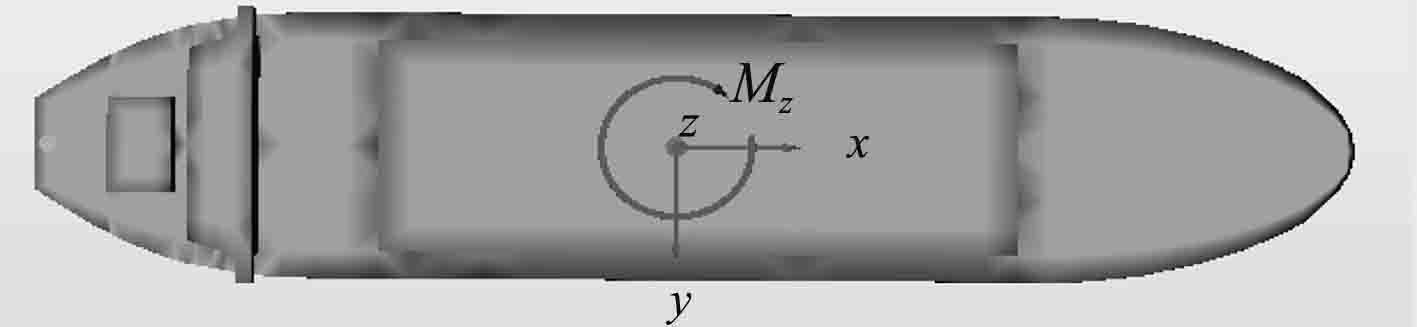
|
图 1 计算坐标系 Fig. 1 Coordinate system |
计算环境条件见表1。
|
|
表 1 计算环境条件 Tab.1 Environment Condition |
采用API风谱估算作用在船体上的风载荷:
| ${{\rm{S}}_{API}}\left( f \right) = s_v^2/{f_p} \cdot {\left( {1 + \frac{{1.5}}{2} \cdot \left( {\frac{f}{{{f_p}}}} \right)} \right)^{\left( { - \frac{5}{3}} \right)}}{\text{。}}$ |
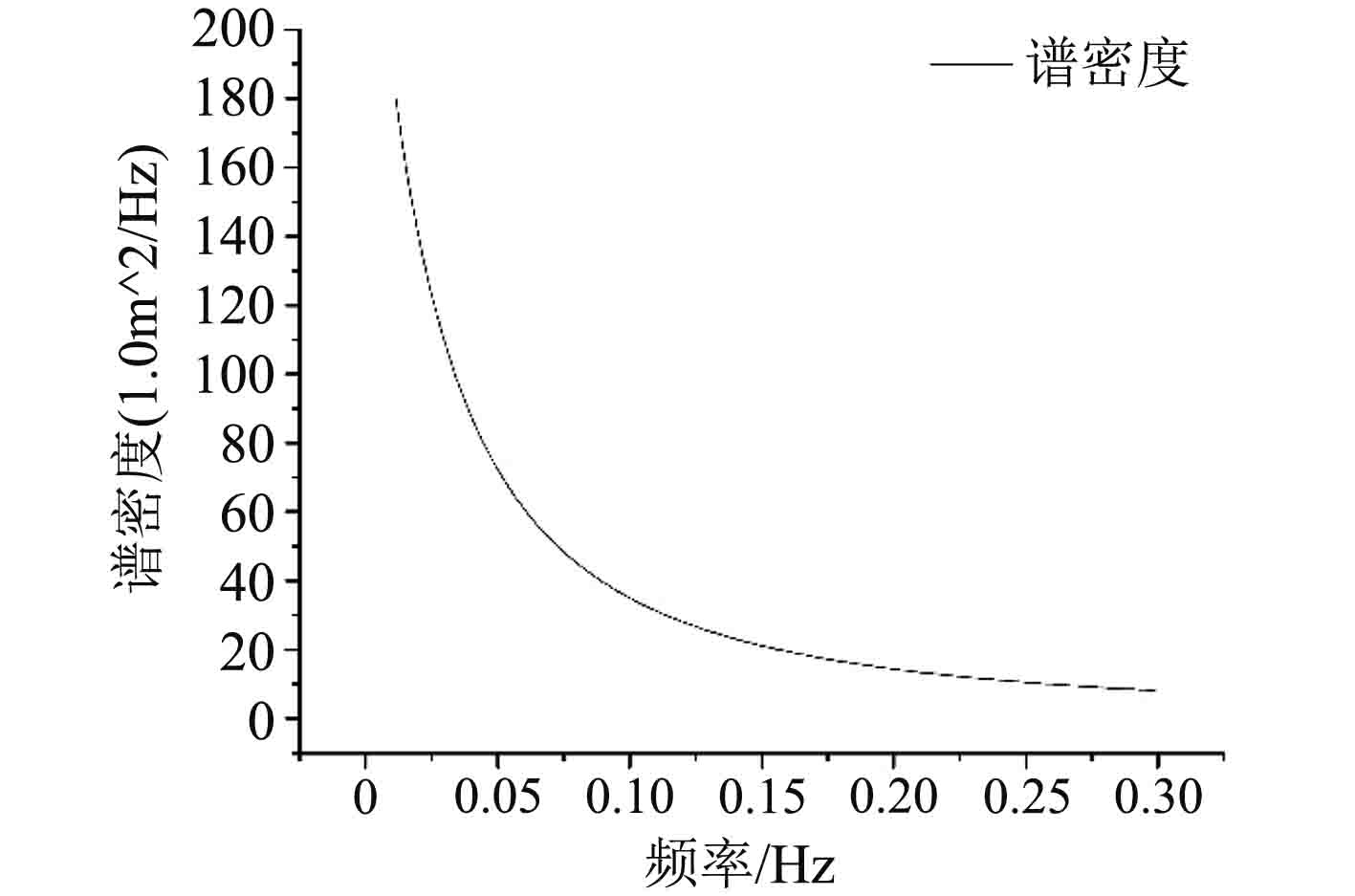
式中:f为风载荷频率,Hz;SAPI为能力谱密度,m2/s;VW10为海平面以上10 m处的每小时平均风,m/s;fp为平均频率(默认为0.002 5 VW10);sv为脉动密度,在推荐高度10 m处sv=0.164 VW10。谱密度可见图2。
|
图 2 API谱密度 Fig. 2 Spectral density of API |
对于主船体采用三维势流理论计算波浪载荷,求解满足流场控制方程的格林函数获得速度势,在频域中求解运动方程以确定附加质量系数、阻尼系数、运动响应和波浪力。利用水动力系数求解铺管船的时域运动方程以确定船舶运动与受力。船舶湿表面模型如图3所示。

|
图 3 船舶湿表面模型 Fig. 3 Ship wet surface model |
采用Pierson-Moskowitz谱计算作用在船体上的波浪载荷。P-M谱表达式为:
| $S\left( \omega \right) = 4{\pi ^3}\frac{{H_S^2}}{{T_Z^4}}\frac{1}{{{\omega ^5}}}\exp \left( { - \frac{{16{\pi ^3}}}{{T_Z^4}}\frac{1}{{{\omega ^4}}}} \right){\text{。}}$ |
式中:
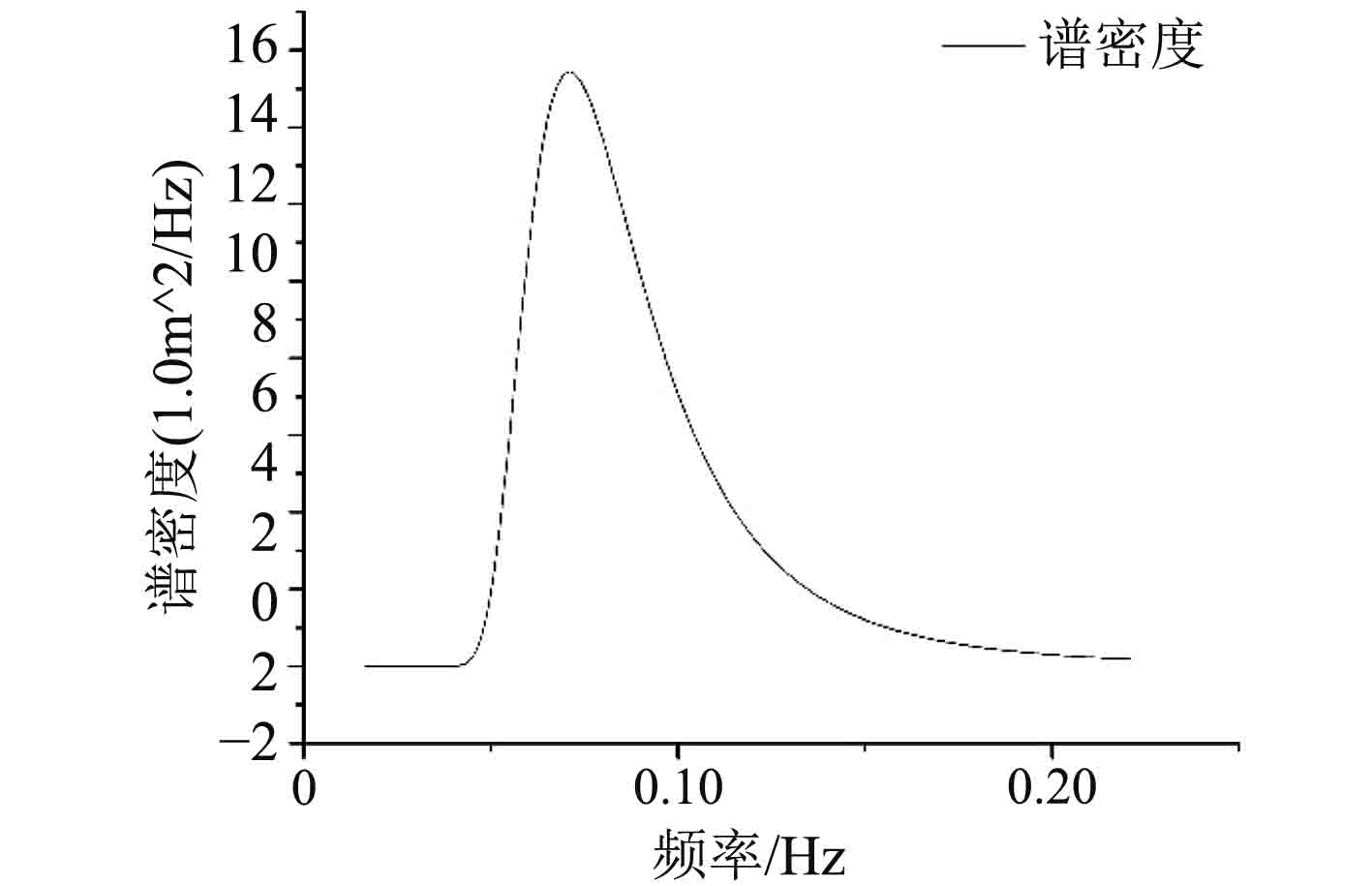
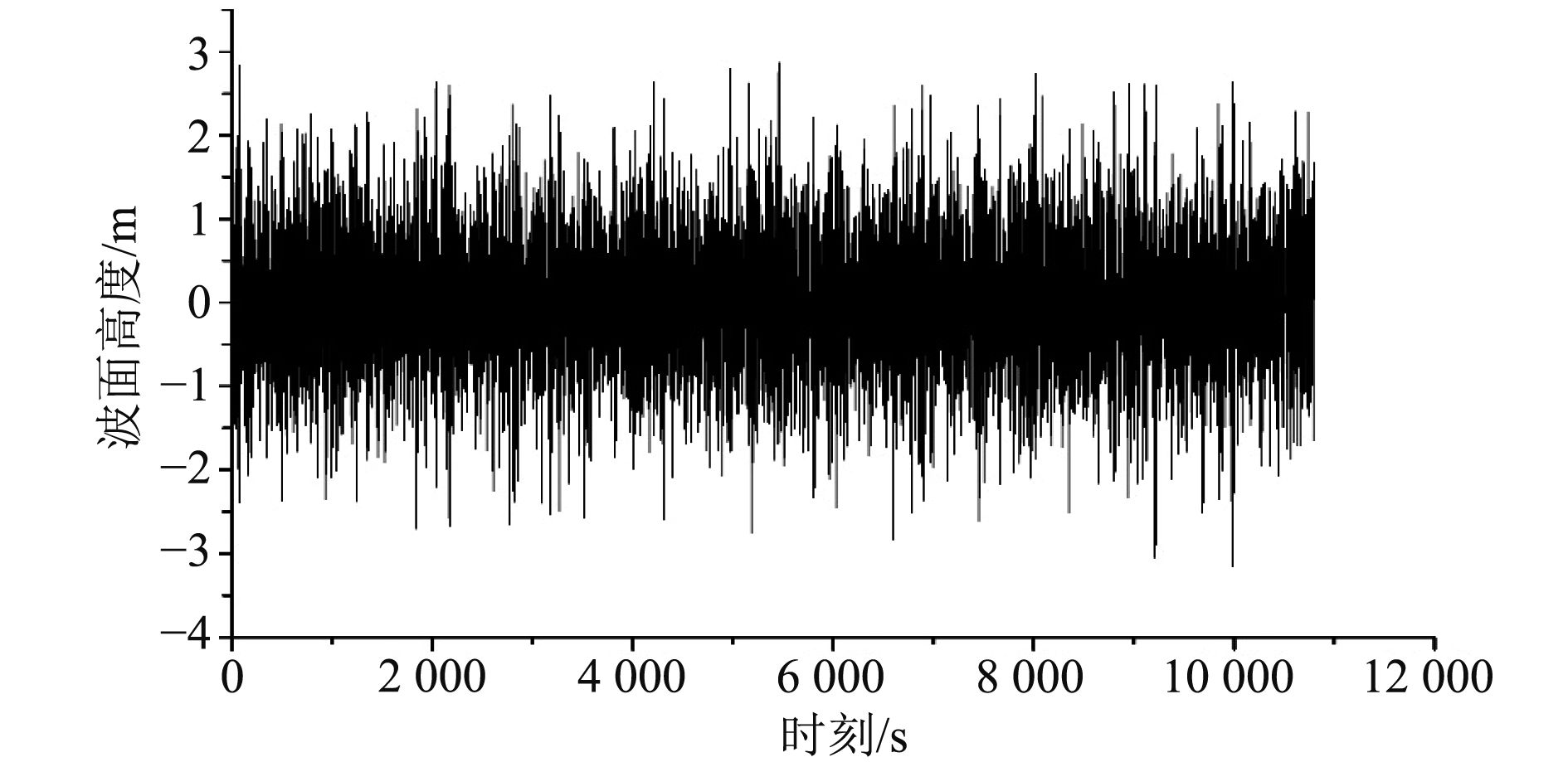
P-M波浪谱密度如图4所示,P-M谱波浪时历曲线如图5所示。
|
图 4 P-M波浪谱密度 Fig. 4 P-M wave spectrum density |
|
图 5 P-M谱波面时历曲线 Fig. 5 Wave surface time history for P-M Spectrum |
一阶波浪力引起的船体在平衡点附近做往复运动,动力定位系统不可能也无需抵消一阶波浪力。因此,动力定位中只平衡波浪二阶漂移力、风载荷、流载荷。对于波浪载荷主要关注二阶波浪慢漂力,根据纽曼近似来计算:
| $\begin{align}{l}&{F_D}\left( t \right) = \left[ {\mathop \sum \limits_{j = 1}^{{N_{wave}}} QTF\left( {{\alpha _{wave}},{\omega _j},{\omega _j}} \right){\alpha _j} \cos\left( {{\omega _j}t + {\varphi _j} - {k_j}x} \right)} \right]\times \\ & \left[ {\mathop \sum \limits_{j = 1}^{{N_{wave}}} {\alpha _j} \cos\left( {{\omega _j}t + {\varphi _j} - {k_j}x} \right)} \right] + \\ &\left[ {\mathop \sum \limits_{j = 1}^{{N_{wave}}} QTF\left( {{\alpha _{wave}},{\omega _j},{\omega _j}} \right){\alpha _j} \sin\left( {{\omega _j}t + {\varphi _j} - {k_j}x} \right)} \right] \times \\ &\left[ {\mathop \sum \limits_{j = 1}^{{N_{wave}}} {\alpha _j} \sin\left( {{\omega _j}t + {\varphi _j} - {k_j}x} \right)} \right]{\text{。}}\end{align}$ |
其中:
流载荷根据OCIMF估算:
| $\begin{split}{l}{F_{Cx}} = \frac{1}{2}{\rho _{water}}{L_{pp}}{T_d}{C_{Cx}}\left( {{\alpha _{current}}} \right)U_C^2, \\{F_{Cy}} = \frac{1}{2}{\rho _{water}}{L_{pp}}{T_d}{C_{Cy}}\left( {{\alpha _{current}}} \right)U_C^2, \\{M_{Cz}} = \frac{1}{2}{\rho _{water}}{L_{pp}}^2{T_d}{C_{Cz}}\left( {{\alpha _{current}}} \right)U_C^2{\text{。}}\end{split}$ |
其中:
动力定位模型由Kalman滤波器、PID控制器以及推力分配算法组成。Kalman滤波器估计低频载荷值大小,联合已知的风载荷来决定铺管船的低频速度与位置分量,由此过滤掉波频分量。将预估位置与设定位置比较,将此差值与低频速度、PID增益值输入控制器,以决定为了维持船位与首向所需的推力大小和方向。将推力指令输入推力分配算法,以确定每个推进器在每个时刻所要发出的推力大小与方向。
2.1 控制系统J型铺管船在外力作用下的水平面低频运动方程为:
| $\left( { {M} + {{{M} _{aT}}} } \right)\left\{ {{{\ddot X}_{LF}}\left( t \right)} \right\} + {B} \left\{ {{{\dot X}_{LF}}\left( t \right)} \right\} = \mathop \sum \nolimits \left( {\left\{ {{F_{LF}}\left( t \right)} \right\}} \right){\text{。}}$ |
其中:M为船舶质量矩阵;
PID控制器根据船位与设定位置的差值以及风前馈信息来决定推力大小:
| $\begin{array}{l}{X_{{\rm{req}}}} = - \overline {{X_e}} + {c_{tx}}\Delta x + {b_{tx}}\Delta \dot x + {a_{tx}}\int {\Delta x{\rm d}t} + {F_{wx}},\\{Y_{{\rm{req}}}} = {c_{ty}}\Delta y + {b_{ty}}\Delta \dot y + {a_{ty}}\int {\Delta y{\rm d}t} + {F_{wy}},\\{M_{{\rm{req}}}} = {c_{tz}}\Delta z + {b_{tz}}\Delta \dot z + {a_{tz}}\int {\Delta z{\rm d}t} + {M_{wz}}{\text{。}}\end{array}$ |
其中:
J型铺管船的动力定位系统由3个全回转推进器和2个侧推器组成,推进器编号、命名、类型和位置如表2所示,推进器布置如图6所示。

|
图 6 推进器布置 Fig. 6 Thruster arrangement |
|
|
表 2 推进系统概况 Tab.2 General information of thrust system |
采用基于Lagrange乘数法的优化推力分配算法[7],拉格朗日函数不仅代表所有推进器提供的总推力,也限制了推力饱和值和全回转推进器的禁止角。推力分配算法的目标是使得推进器消耗的功率最优,及寻找各个推进器状态分量
横向力、纵向力和首摇力矩满足要求:
| $\begin{array}{l}{R_x}\left( {\vec F} \right) \equiv {F_{x,req}} - {F_{x,tot}} = 0,\\{R_y}\left( {\vec F} \right) \equiv {F_{y,req}} - {F_{y,tot}} = 0,\\{R_z}\left( {\vec F} \right) \equiv {M_{z,req}} - {M_{z,tot}} = 0{\text{。}}\end{array}$ |
推力受到最大推力限制:
| ${M_i}\left( {\vec F} \right) \equiv T_{max,i}^2 - ({F_{x,i}}^2 + {F_{y,i}}^2) \geqslant 0,\;\;\;i = 1,2, \ldots ,N{\text{。}}$ |
Langrange函数为:
为了达到最优必须满足:
| ${\nabla _{\vec F}}{\Lambda ^{\left( 2 \right)}} = \vec 0,\;\;\;{\nabla _{\vec \rho }}{\Lambda ^{\left( 2 \right)}} = \vec 0,\;\;\;{\nabla _{\vec \mu }}{\Lambda ^{\left( 2 \right)}} = \vec 0{\text{。}}$ |
其中:
可应用牛顿迭代法进行求解。如果方向角
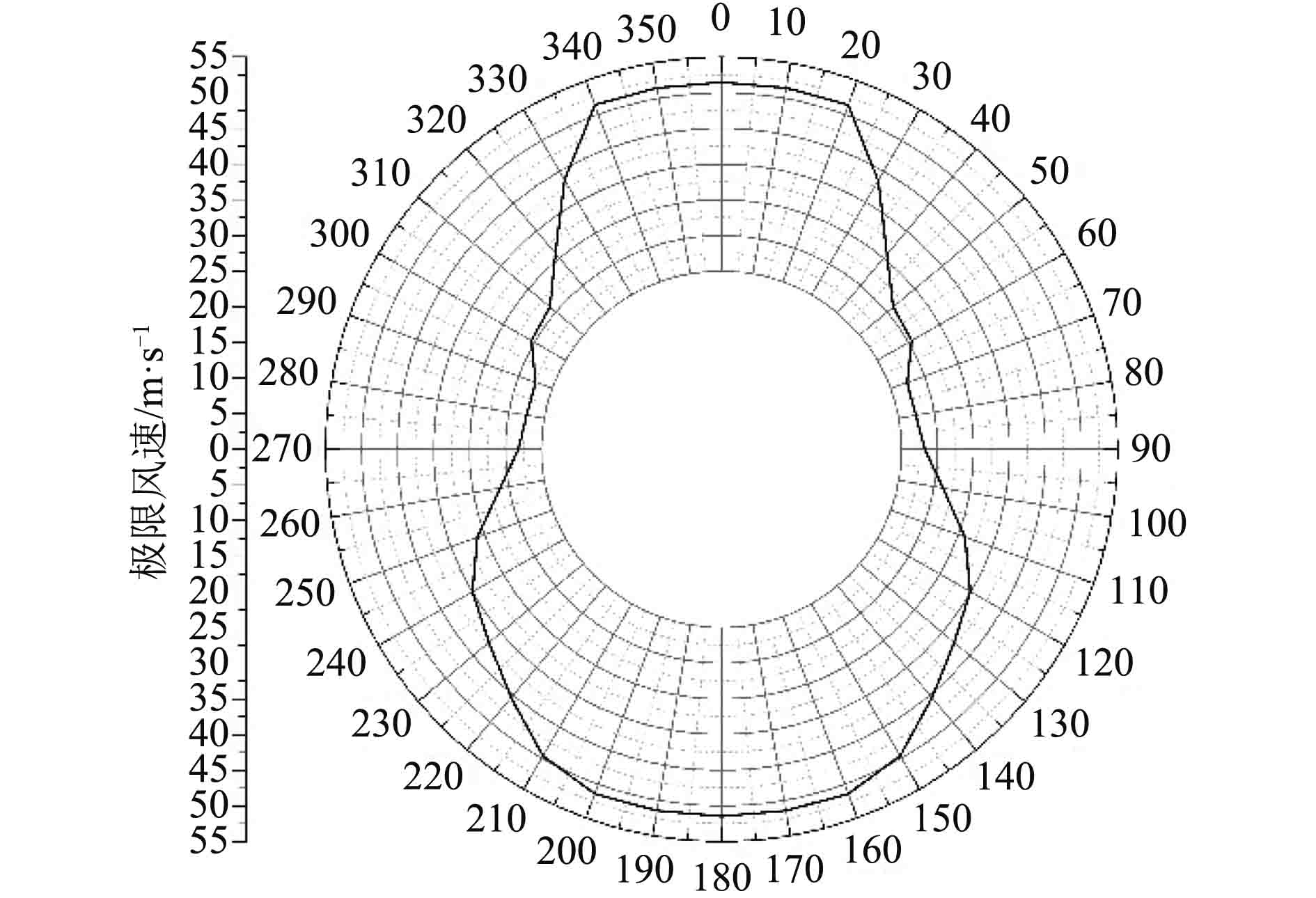
动力定位系统的定位能力通常用风速包络线以及推力使用率包络线来表示。风速包络线表示在风、浪、流共同作用下可以满足定位要求即船位与首向的极限环境条件。计算中风、流、浪设定为同向,给定流速,计算初始风速与波浪参数下对应的推进器推力,不断增大风速直到推进器达到满负荷情况。通过改变环境载荷方向,可以得到各个风向上的风速极值,由此得到风速包络线。
风速包络线如图7所示。由图可知,当推力系统完好,推进器正常工作时,定位能力为可抵抗27.41 m/s的风速,定位能力最差的方向为70°与80°。不同风向上的定位能力差距较大,迎浪以及随浪方向附近定位能力好,横浪方向附近定位能力相对较差。
|
图 7 风速包络线图 Fig. 7 Wind limit |
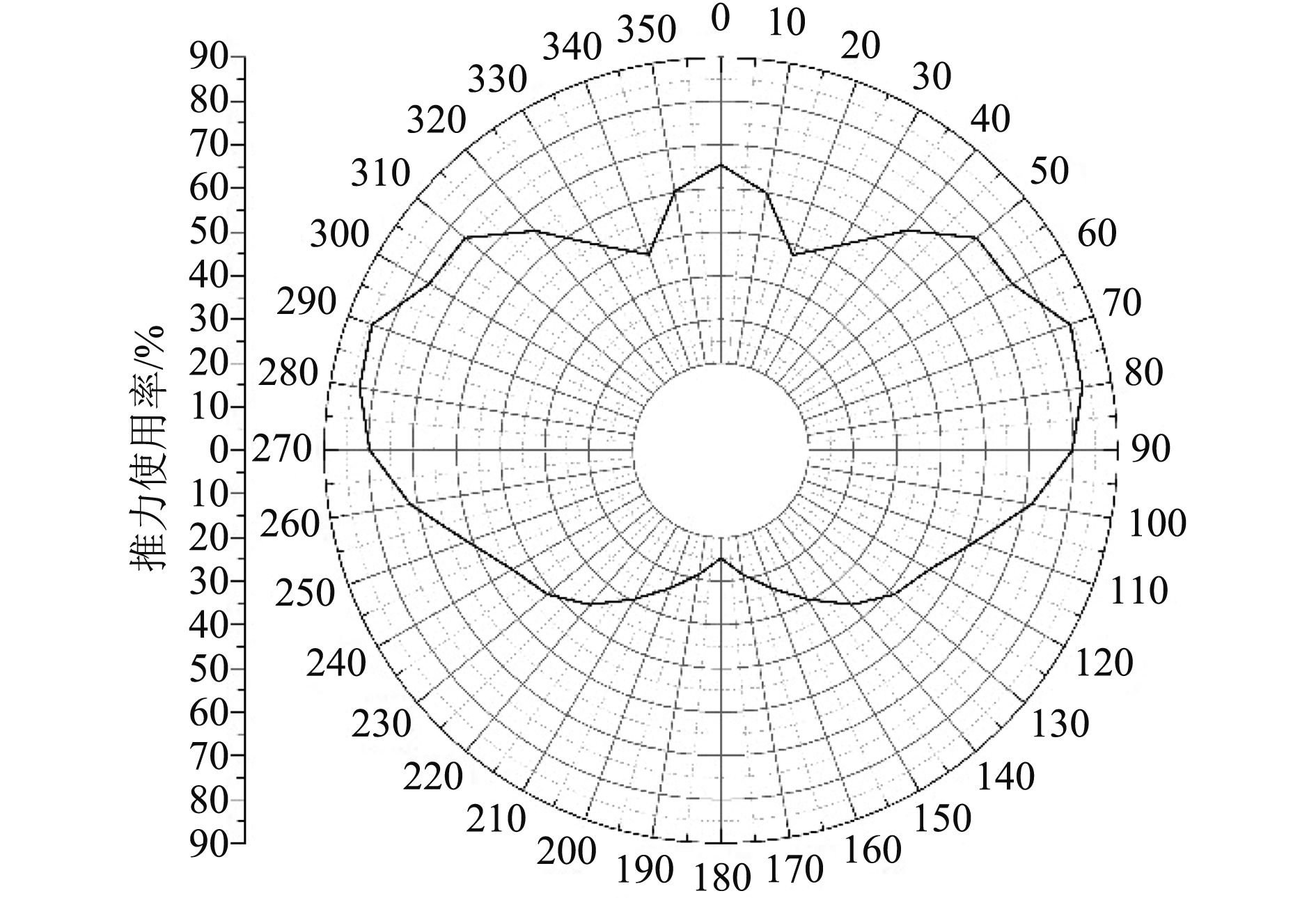
推力使用率包络线表示在确定的风、浪、流环境条件下保持定位要求时推进器的推力使用率。计算中风、浪、流设定为同向,对每一个方向,根据设定的环境条件,即规定的流速、平均风速、对应波谱计算出为了保持船位以及船舶首向所需的推力数据,计算推进器与其最大推力的比值,获得该风向的推力利用率。改变环境载荷方向,得到各个方向上的推力利用率,由此得到推力利用率包络线。当每个方向上所有推进器的推力利用率均小于等于100%,船舶才可以在这个环境条件下保持船位和首向稳定。
推力使用率包络线曲线如图8所示。由图可知,在每个环境载荷方向上,推力使用率皆小于100%,在该环境条件下可以达到定位要求。不同的环境载荷方向上,推进器使用率相差较大,70°的定位能力相对最差,推力使用率最高为84.33%;180°的定位能力相对最好,推力使用率最低为24.78%。
|
图 8 推力使用率包络线 Fig. 8 Thrust utilization |
动力定位动态模拟是对动力定位控制的J型铺管船的真实运动进行实时模拟。与动力定位能力曲线相比,时域模拟动力定位控制下的J型铺管船可以考虑更多限制条件与相关因素, 获得动力定位精度等信息。
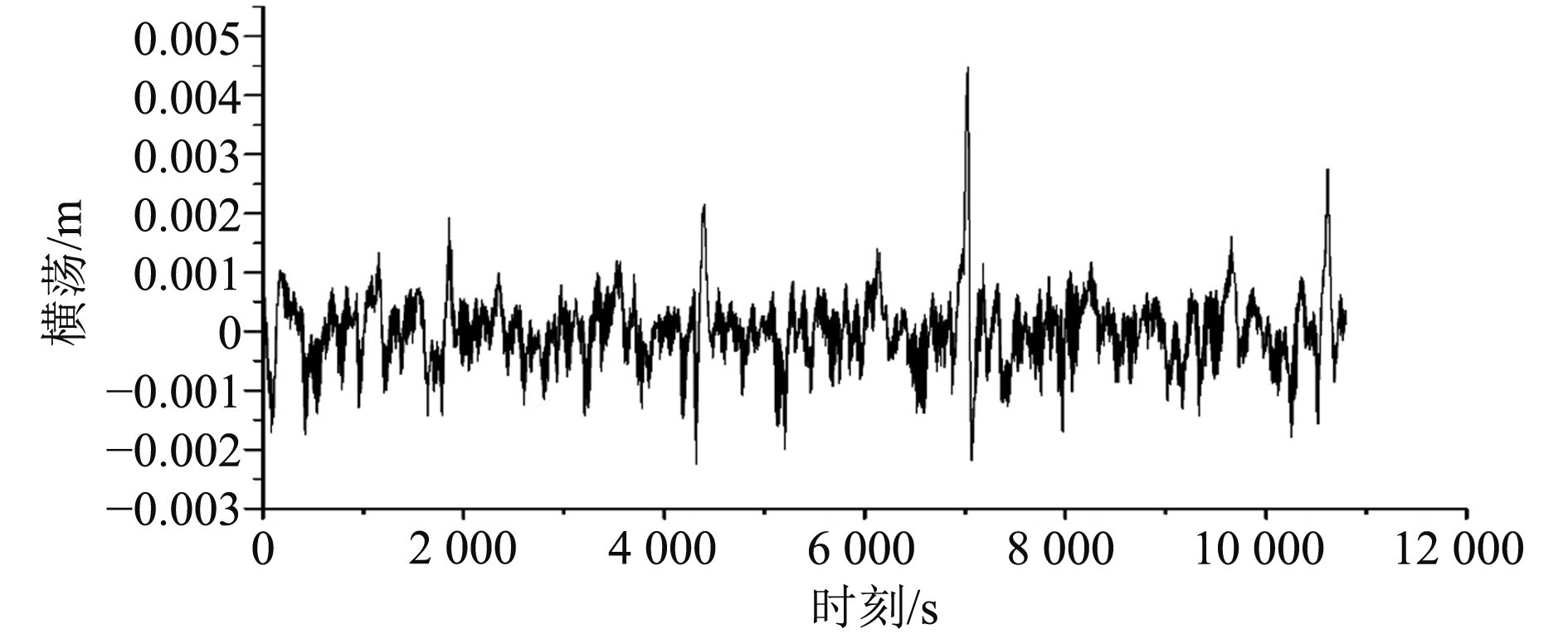
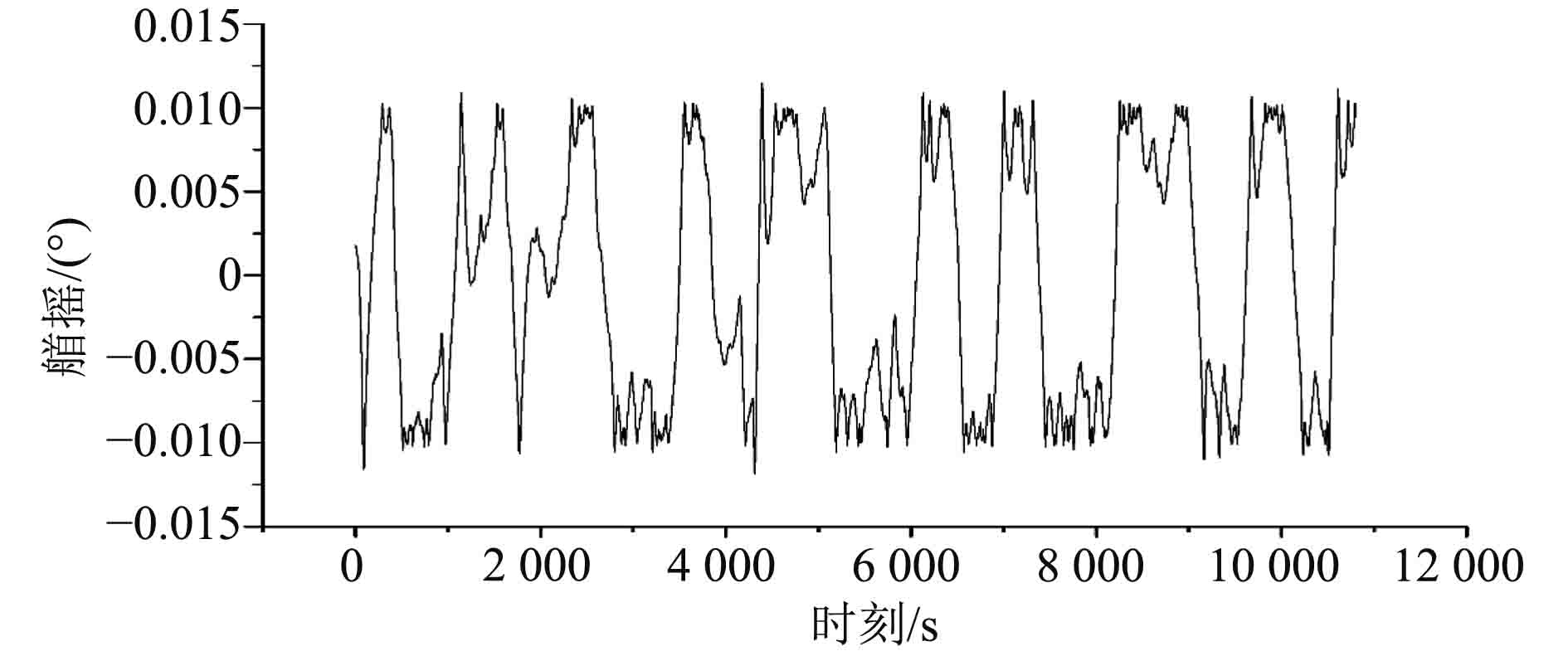
以浪向0°为例,给出J型铺管船动态时域模拟结果。横荡、纵荡、首摇的时历曲线分别如图9、图10和图11所示。综合各个浪向情况,J型铺管船在动力定位系统作用下,横荡、纵荡范围都在3 m以内,定位精度可达3‰水深,远低于常规2%~3%水深要求,首摇可控制在3°以内。设计定位系统在设定的环境条件下可达较高的定位精度。
|
图 9 横荡时历曲线 Fig. 9 Time series of sway |

|
图 10 纵荡时历曲线 Fig. 10 Time series of surge |
|
图 11 首摇时历曲线 Fig. 11 Time series of yaw |
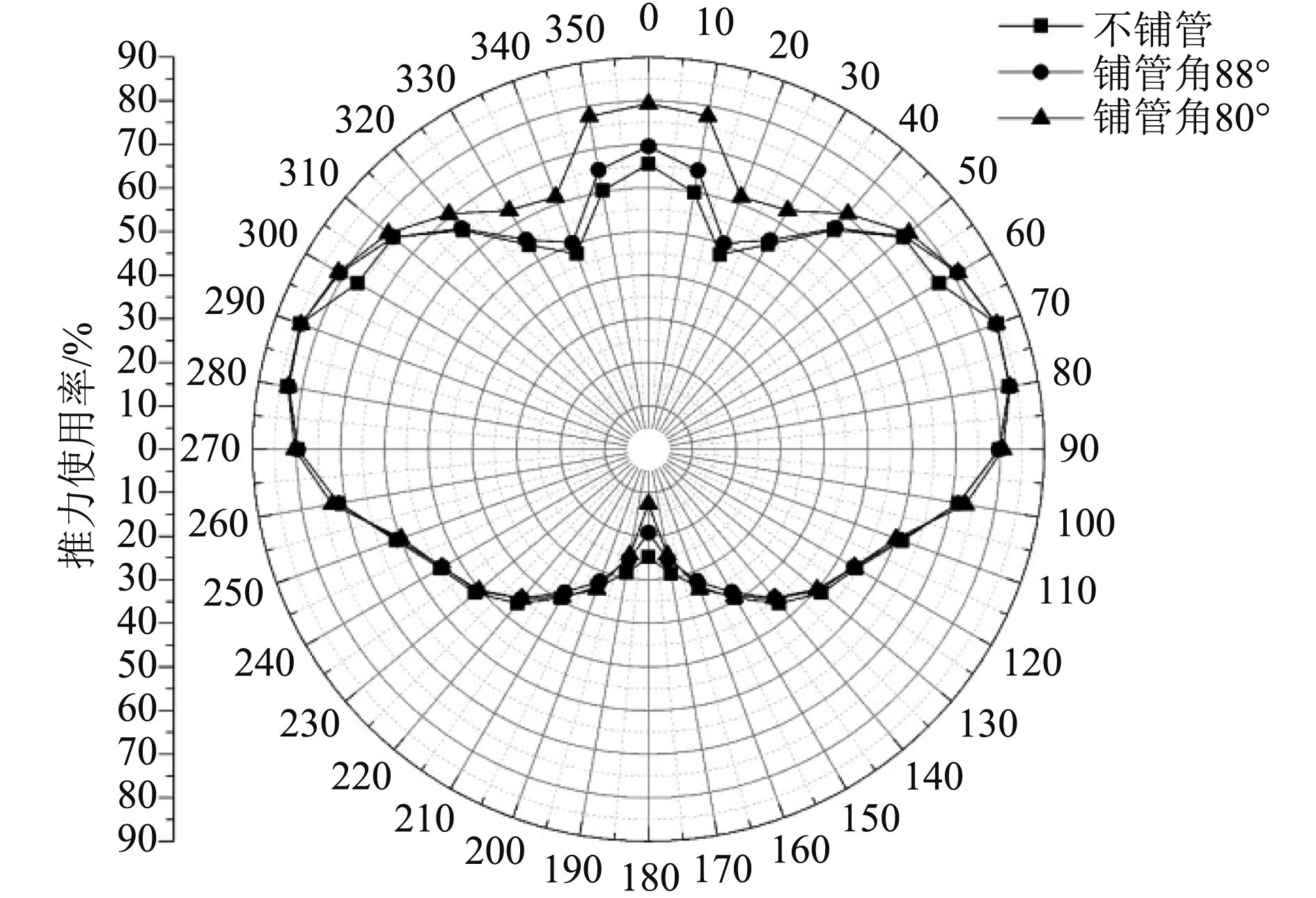
动力定位主要考虑水平内船舶运动,即横荡、纵荡、首摇,而对其他3个自由度的运动关注度较小。因此在考虑J型铺管船进行铺管作业时对动力定位能力的影响时,主要考虑张紧器上的水平张紧力。管线预张力假定为一个恒定的纵向作用力。这个载荷与铺管角度有关,铺管角度越大,纵向张紧力越小。计算分别以80°,88°进行铺管时的推力使用率,并与不铺管时的推力使用率作比较,如图12所示。
由图可知,考虑风、浪、流的动力定位能力——推力使用率显著受到铺管作业的影响。铺管作业力处于纵荡方向,因此当船舶处于迎浪、随浪中时,推力使用率受到铺管作业的影响最大。迎浪中,铺管作业力与环境载荷同向,当铺管船进行铺管作业时,推力使用率显著增大即动力定位性能显著变差,且铺管作业角度越小,推力使用率越大。随浪中,铺管作业力与环境载荷反向,因此当铺管船进行铺管作业时,铺设的管线相当于锚链,可以抵消环境载荷的作用,故推力使用率显著减小即动力定位性能变好,且铺管作业角度越小,推力使用率越小。当船舶处于横浪附近时,推力使用率受铺管作业影响不大。可见,以80°,88°进行铺管时,推力使用率皆小于等于100%,可以满足定位要求。
|
图 12 铺管作业对推力使用率影响 Fig. 12 Influence of pipe-laying on thrust utilization |
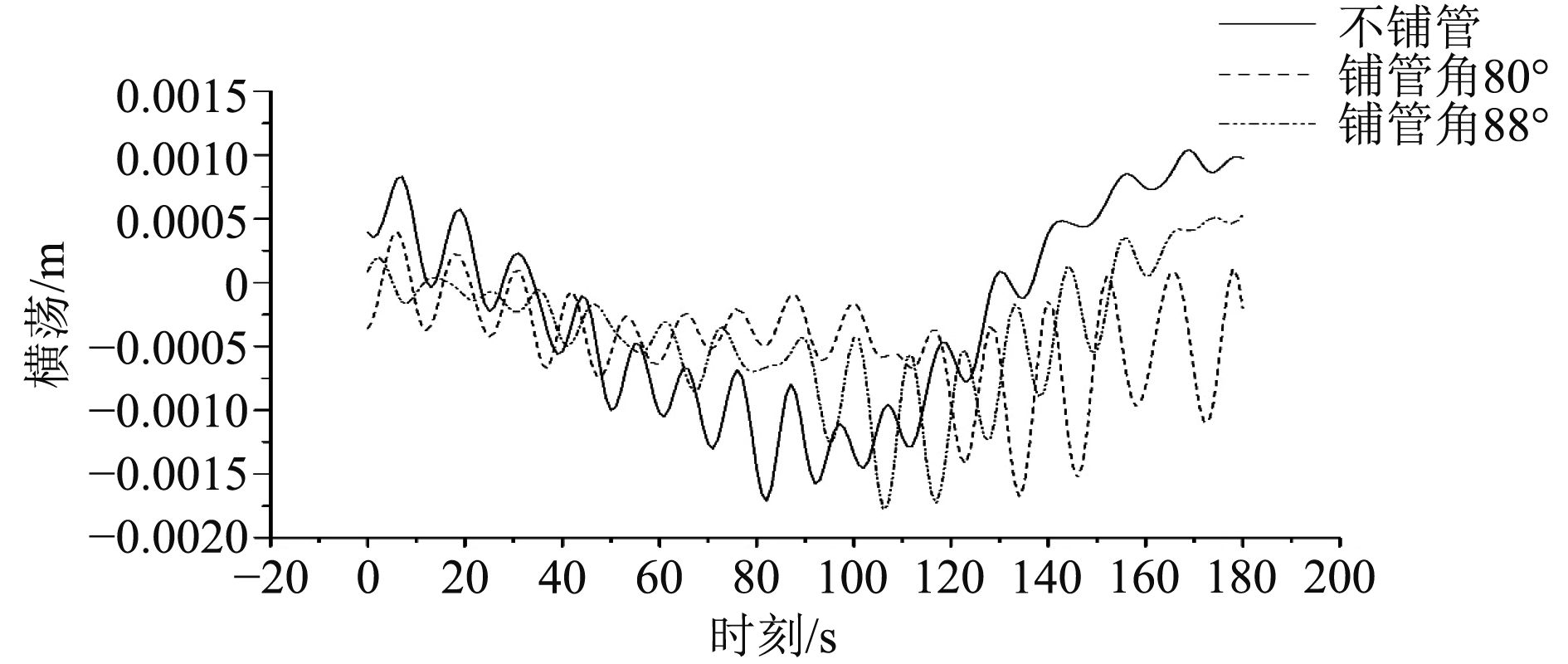
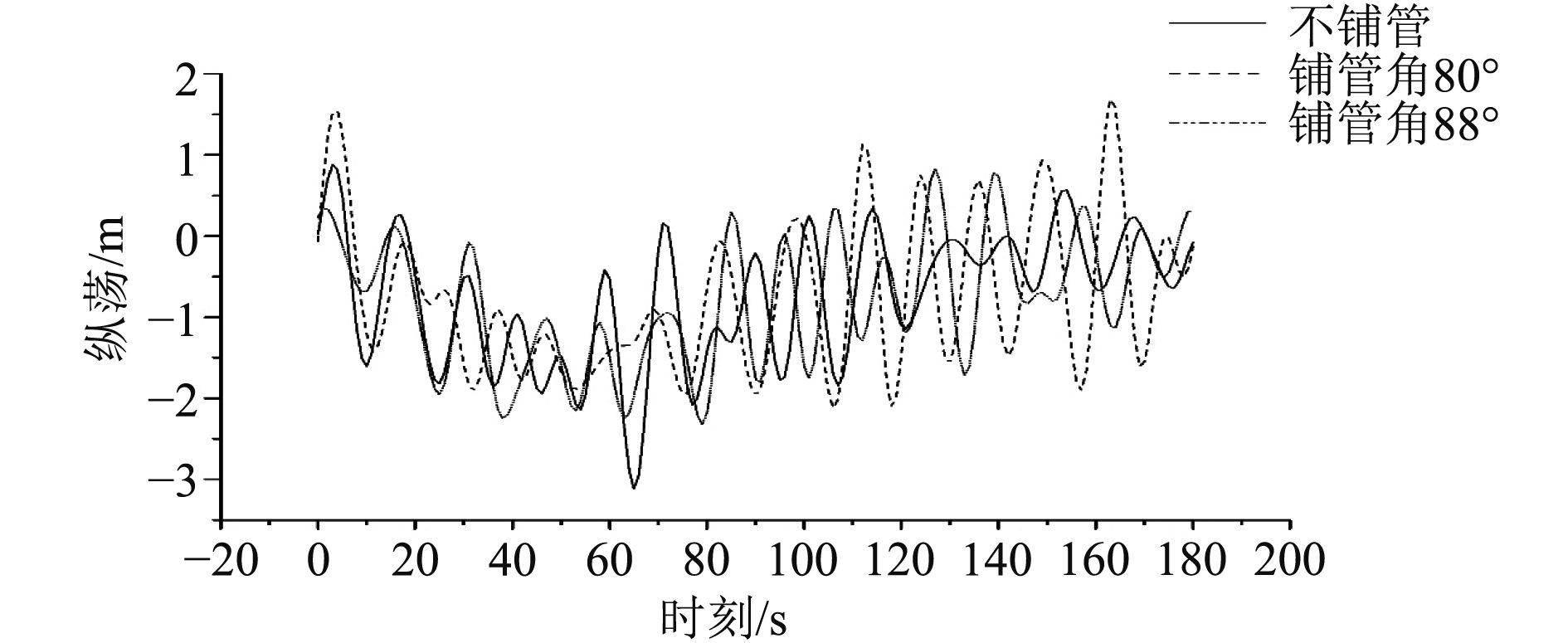
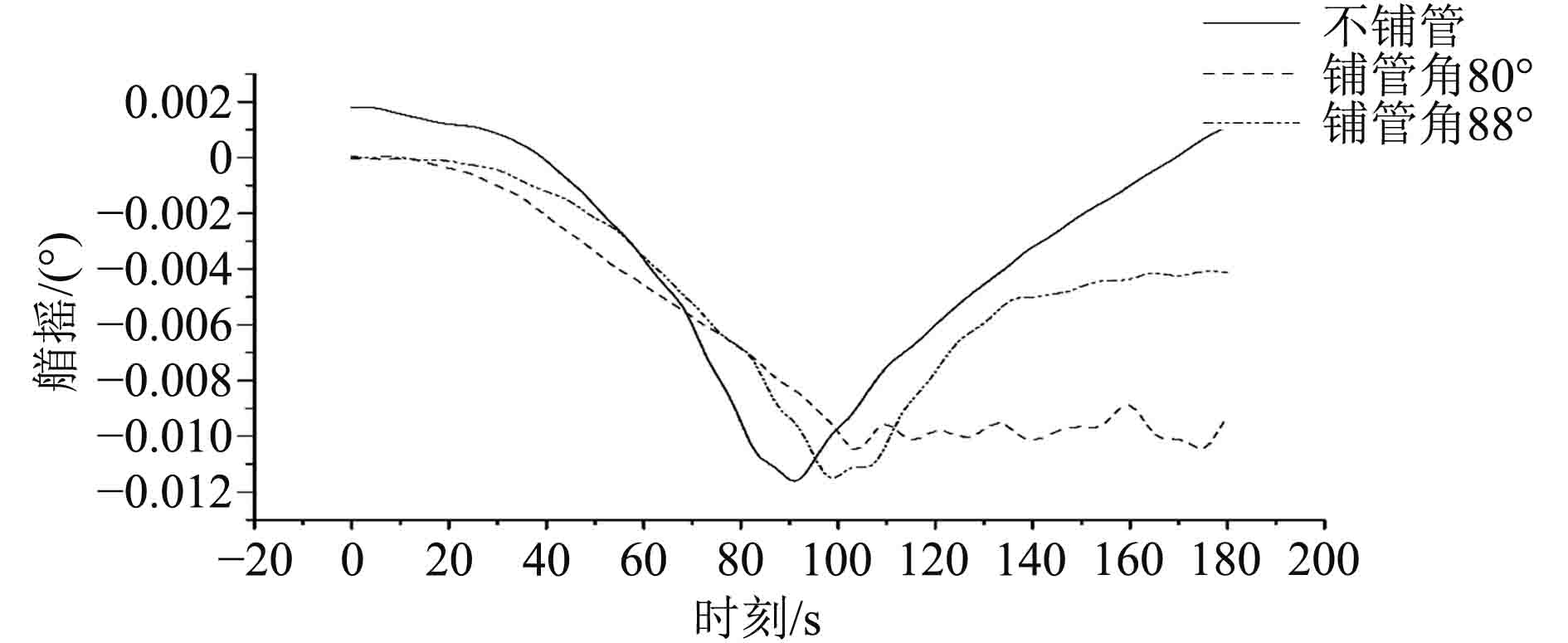
在时域中,对J型铺管船的铺管作业进行模拟,分别得到以80°,88°进行铺管时的横荡、纵荡、首摇时历曲线,并与不铺管时进行对比,分别给出前180 s结果对比如图13、图14和图15所示,并对运动的最值、平均值、标准差进行统计(见表3)。由图可知,在不同的铺管情况下,横荡、纵荡、首摇时历曲线略有不同,但整体趋势相同。由表3可知,在不同的铺管情况下,运动的最大值、最小值、平均值、标准差都相近,基本处于同一数量级。由铺管作业对动力定位的静态定位能力可知,在铺管作业下也能满足定位要求,故在时域模拟中,能够达到对船位、首向的控制要求,因此时历曲线差别不大。
|
图 13 铺管作业对横荡时历曲线的影响 Fig. 13 Influence of pipe-laying on sway time series |
|
图 14 铺管作业对纵荡时历曲线的影响 Fig. 14 Influence of pipe-laying on surge time series |
|
图 15 铺管作业对首摇时历曲线的影响 Fig. 15 Influence of pipe-laying on yaw time series |
|
|
表 3 铺管作业对运动时历曲线的影响 Tab.3 Influence of pipe-laying on ship motion time series |
本文对J型铺管船的静态定位能力进行研究,获得了风速包络线以及推力使用率包络线,确定了在不同载荷方向下能够抵抗的极限载荷,以及在给定环境条件下不同环境载荷方向上的推力使用率。在时域中对J型铺管船的实际运动进行了模拟,横荡、纵荡运动范围都在3 m以内,定位精度可达3‰水深,首摇可控制在3°以内。对进行铺管作业时对动力定位性能的影响进行了研究,研究了不同铺管角度下对推力使用率包络线的影响,并在时域中对进行铺管作业的船舶的动力定位精度进行了研究。在迎浪中作业时动力定位性能显著变差,在随浪中铺管作业时动力定位性能显著变好,且变化程度受铺管角度影响。进行铺管作业时能够满足动力定位要求,铺管作业在时域模拟中对横荡、纵荡、首摇运动值影响不大,仍能保持动力定位精度。
| [1] | BRINK A, JIN C. Automatic position control of a30, 000 tons ship during ocean mining operations[C]//Offshore Technology Conference. Offshore Technology Conference, 1981. |
| [2] | TANNURI E A, PESCE C P, ALVES G S, et al. Dynamic positioning of a pipeline launching barge[C]//The Twelfth International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2002. |
| [3] | BRUN C, COACHE D, GIORGIUTTI Y, et al. Influences on dynamic positioning system capability[C]//The Twenty-fifth International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2015. |
| [4] | 王川, 李辉, 任慧龙, 等. 深水铺管船的动力定位能力评估系统[J]. 华中科技大学学报(自然科学版), 2015 (2): 61–65. |
| [5] | 谢文博, 付明玉, 陈翠和, 等. 铺管船定位作业时的建模与分析[J]. 中国造船, 2011, 52 (3): 101–108. |
| [6] | SHI X, XIE W, FU M, et al. Terminal sliding mode tracking control for dynamic positioning J-lay vessel[J]. 2011: 293–298. |
| [7] | VAN E P G D, COZIJN J L, LOUSSOUARN G, et al. A generic optimization algorithm for the allocation of DP actuators[J]. 2011. |
 2018, Vol. 40
2018, Vol. 40
