空腔是广泛存在于船舶系统和管道运输的储液系统中的结构形式,尤其在船舶系统中,一些有特殊用途的船体开口,都可以看作有流体流经的空腔结构[1]。以舰船通海口为例,空腔的非定常流动会对舰船造成严重危害,所以有必要深入了解空腔流的速度场和压力脉动。因此,空腔流的研究具有重要的实际意义。20世纪50年代起,国外开始对空腔流的压力振荡和声辐射进行了大量的实验研究和数值计算研究[2–7],国内空腔流的研究起步较晚,且多集中在超声速和跨声速空腔流方面。例如Rossiter等[7]从实验研究出发,提出空腔振荡的流声共振反馈模型,并给出预估振荡的半经验公式。目前空腔的研究主要集中于可压缩流动方面,对极低马赫数或不可压缩空腔流关注较少,极低马赫数范围或者不可压缩空腔流条件下,空腔流可分为剪切层模式和尾流模式[8]。剪切层模式的空腔流与自由剪切层流动极为类似,腔内涡的基本形态比较稳定,腔内流体与腔外主流之间的质量交换不明显。而空腔流的尾流模式,腔内的流体不稳定,在腔的前缘处会形成一个旋涡,此旋涡不断变大直到脱离前缘,在主流的作用下向腔后缘运动,最后从尾缘抛射向腔外,自由流周期性进出空腔,腔外流体受腔内流体的影响极为明显。根据声速附近可压缩空腔流的机理,空腔跨度对振荡频率有明显影响,而深度几乎不影响振荡频率,可压缩流空腔振荡机理是否可以推广至不可压缩流中有待研究,所以本文针对不可压缩空腔流,研究尾流模式振荡频率的影响因素。
大多数研究者通过求解非定常可压缩N-S方程模拟空腔流,对于湍流项的处理,最初研究者采用B-L代数湍流模型[9],后来也有人采用一方程和二方程湍流模型,但是结果并不理想。之后大涡模拟(LES)、直接数值模拟(DNS)也被运用到空腔流的数值模拟中,但这2种方法需要占用巨大的计算机内存。而DES对壁面边界层完全采用RANS湍流模型模拟,利用RANS可以有效处理壁面边界层流动的优点,不需要耗费很大的计算机资源;在远离壁面的分离区域内,对小尺度涡采用亚格子模型模拟,对大尺度涡进行直接模拟,利用LES可以比较有效地模拟分离流动的优点。通过结合RANS和LES各自的优点,DES可以比较快速而有效的模拟空腔流。
综上所述,以DES为代表的RANS/LES混合方法在空腔流中具有一定的优势,因此,采用基于k-ω-SST模型的IDDES方法模拟空腔的振荡特性。首先根据肥皂膜水洞实验结果,数值模拟同一工况的空腔流,将仿真结果与实验结果进行对比,验证数值计算方法的准确性。在此基础上对目标模型进行研究,得到空腔流一个周期内涡的演化过程,着重分析了空腔的跨度和深度对振荡频率的影响。
1 数值方法及几何模型基于有限体积法求解RANS方程组,湍流模型采用基于两方程k-ω-SST的IDDES[10], 以降低分离区域湍流粘性,解析流动小尺度结构。以k-ω-SST模型构造IDDES方法仅需要在湍动能输运方程引入混合长度尺度lIDDES,如下式所示:
| $\frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho {u_j}k)}}{{\partial {x_j}}} = {\tau _{ij}} - \frac{{\rho {k^{3/2}}}}{{{l_{{\mathop{\rm IDDES}\nolimits} }}}} + \left[ {\left( {\nu + \frac{{{\nu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial (\rho k)}}{{\partial {x_j}}}} \right]\text{。}$ | (1) |
其中,混合长度尺度lIDDES定义为
本文计算5类不同类型的空腔,空腔的具体参数如表1所示,其中模型4跨度为
|
|
表 1 空腔模型参数 Tab.1 Parameters of the cavity model |
为考察IDDES数值计算方法的准确性,对跨度为80 mm,深度为15 mm的空腔进行数值模拟,模型的外轮廓采用翼型曲线进行改进,来流速度为1.5 m/s,流体为肥皂液,粘性为2×10–5 m2/s。
图1(a)给出了基于肥皂膜水洞装置的实验结果,图1(b)为数值模拟的瞬时涡量图。图1(a)中明显可以观察到腔口位置的自由剪切层,起始阶段自由剪切层扰动不明显,自由剪切层与腔口位置基本重合,图1(b)中自由剪切层起始阶段与实验结果一致,自由剪切层位置与腔口基本重合;图1(a)在腔口中间靠后位置自由剪切层明显向腔外突出,腔内靠近后壁位置出现明显的涡结构,图1(b)数值仿真结果靠近腔后壁位置也出现了相同的涡结构,导致腔口自由剪切层向腔外突出。数值计算与实验结果吻合良好,验证了IDDES模型在计算空腔流方面的准确性,为下一步使用IDDES模型开展空腔流数值模拟研究打下了坚实的基础。

|
图 1 空腔流场结构 Fig. 1 Flow field structure of cavity |
图2给出了模型1(80:20)一个周期内不同时刻的涡量云图,流速v=1.5 m/s。来流到达腔口位置失稳产生涡结构(本文将此涡命名为腔口涡),受前一周期涡挤压,腔口涡紧贴空腔前壁发展,如图2(a);腔口涡尺度逐渐增长,与空腔深度相当时,受腔底限制,腔口涡转而横向发展并变得扁平,如图2(b);腔口涡与空腔前壁底角组成一个封闭区域,此封闭区域内出现另一小涡(本文将此涡命名为腔角涡),如图2(c);腔角涡不断增长并挤压腔口涡,如图2(d);直至腔口涡脱离空腔导边,之后腔角涡跟随腔口涡向空腔后壁运动,如图2(e);最终腔口涡撞击空腔后壁,和腔角涡一起被甩至腔外,如图2(f)。

|
图 2 空腔涡量云图(80:20,v=1.5 m/s) Fig. 2 Vorticity contours of cavity(80:20,v=1.5 m/s) |
根据一个周期内涡发展规律,发现空腔流尾流模式振荡主要是由腔口涡导致。当来流到达空腔开口时,在导边处发生流动分离,产生自由剪切层,剪切层下侧腔内流速较低,上侧流速接近于来流速度。由于存在较大速度梯度,剪切层卷起形成腔口涡,腔口涡增长并脱离空腔前缘,最终撞击至后缘角被甩出腔外,产生流激振荡。
图3给出了模型1(80:20)在5T/6和T时刻的速度矢量图,来流流速v=1.5 m/s。图3(a)腔口涡影响范围超过空腔深度,腔内流体不稳定,腔外流体回流至腔内;图3(b)腔口涡从尾缘抛射向腔外,腔外流体受腔内流体的影响极其明显,腔内流体与腔外流体有明显的质量交换,这是典型的尾流模式特征。

|
图 3 空腔速度矢量图(80:20,v=1.5 m/s) Fig. 3 Velocity vector of cavity (80:20,v=1.5 m/s) |
图4给出了不同跨度空腔模型在T/2时刻的涡量云图,来流流速v=1.5 m/s。图4(a)为模型1(80:20)的涡量云图,图4(b)为模型2(100:20)的涡量云图,图4(c)为模型3(120:20)的涡量云图,图4(d)为模型4(step flow)的涡量云图。涡量云图显示不同跨度空腔结构在T/2时刻流动特征相似,都存在腔口涡和腔角涡,腔口涡的尺度大于腔角涡,腔角涡位于腔口涡与空腔前壁底角构成的封闭空间内。图5给出了不同深度空腔模型在T/2时刻的涡量云图,来流流速v=1.5 m/s。图5(a)为模型1(80:20)的涡量云图,图5(b)为模型5(80:15)的涡量云图,涡量云图显示不同深度空腔结构在T/2时刻流动特征基本一致,也出现腔口涡和腔角涡,且出现位置和相对尺度基本一致,可见不同跨度和深度空腔尾流模式流场结构及涡发展规律基本一致。

|
图 4 不同跨度空腔涡量云图(T/2) Fig. 4 Vorticity contours of different length cavities(T/2) |

|
图 5 不同深度空腔涡量云图(T/2) Fig. 5 Vorticity contours of different depth cavities(T/2) |
Rossiter给出空腔振荡频率预测半经验公式:
| $St = \frac{{fL}}{U} = \frac{{n - \alpha }}{{Ma + 1/\kappa }}\text{。}$ | (2) |
式中:St为斯特劳哈尔数;f为振荡频率;κ为涡迁移速度与自由流速度之比;α为涡通过与产生压之间的时间延迟因子;n为模态阶数。α=0.25,κ=0.66是常数[11]。
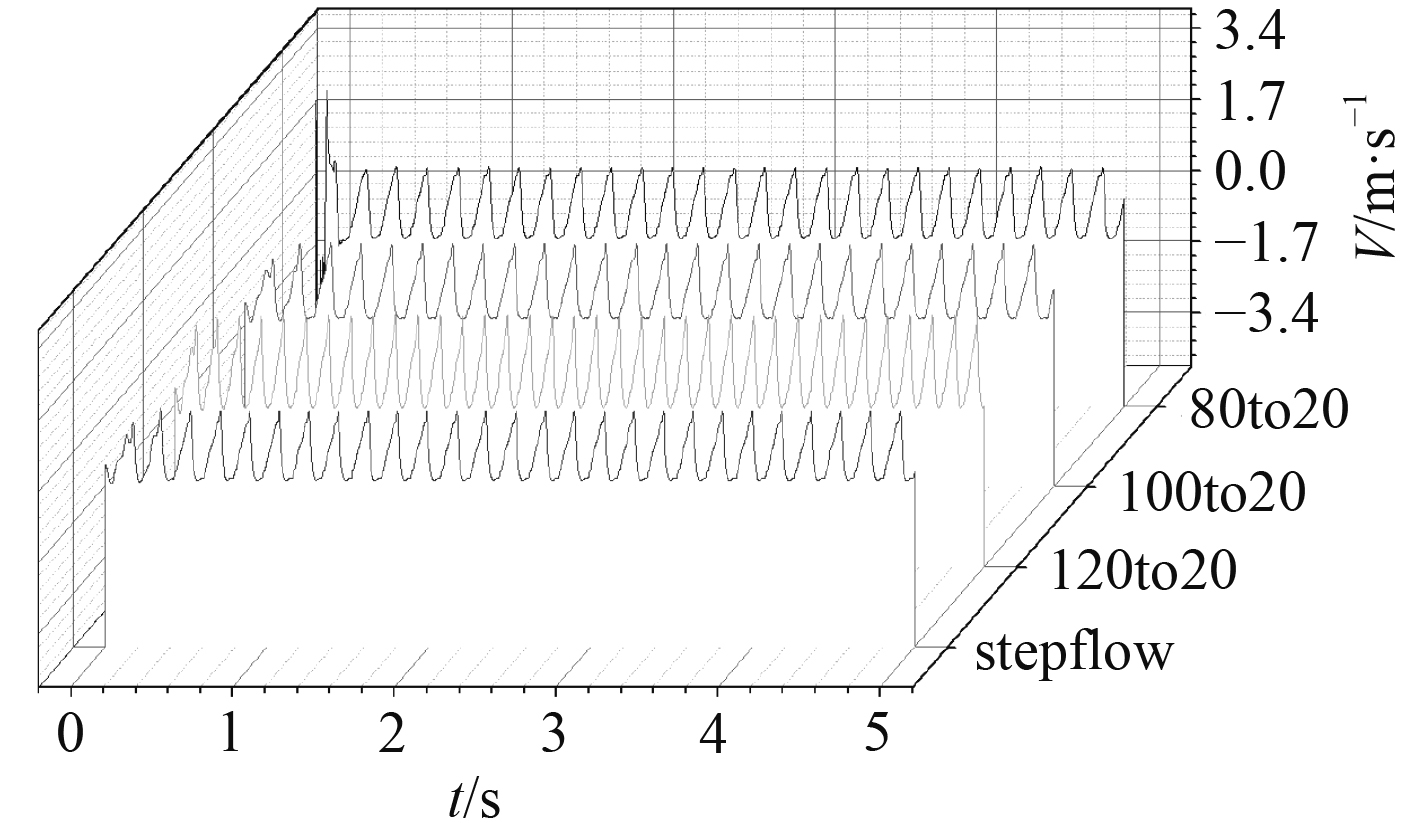
图6给出了v=1.5 m/s条件下,模型1(80:20)、模型2(100:20)、模型3(120:20)及模型4(step flow)监测点法向速度。从前文流场结构可发现,空腔振荡由前缘涡脱落导致,则腔口监测点位置频率即空腔前缘脱涡频率,也是空腔振荡频率。图中可以观察到4种不同空腔法向速度周期性均较为明显,仅起始阶段周期性较差,为确保计算准确性,选择空腔振荡稳定后的法向速度,即2~5 s的法向速度,进行傅里叶变换得到腔口法向速度频谱。
|
图 6 监测点法向速度(v=1.5 m/s) Fig. 6 Normal velocity of monitoring point (v=1.5 m/s) |
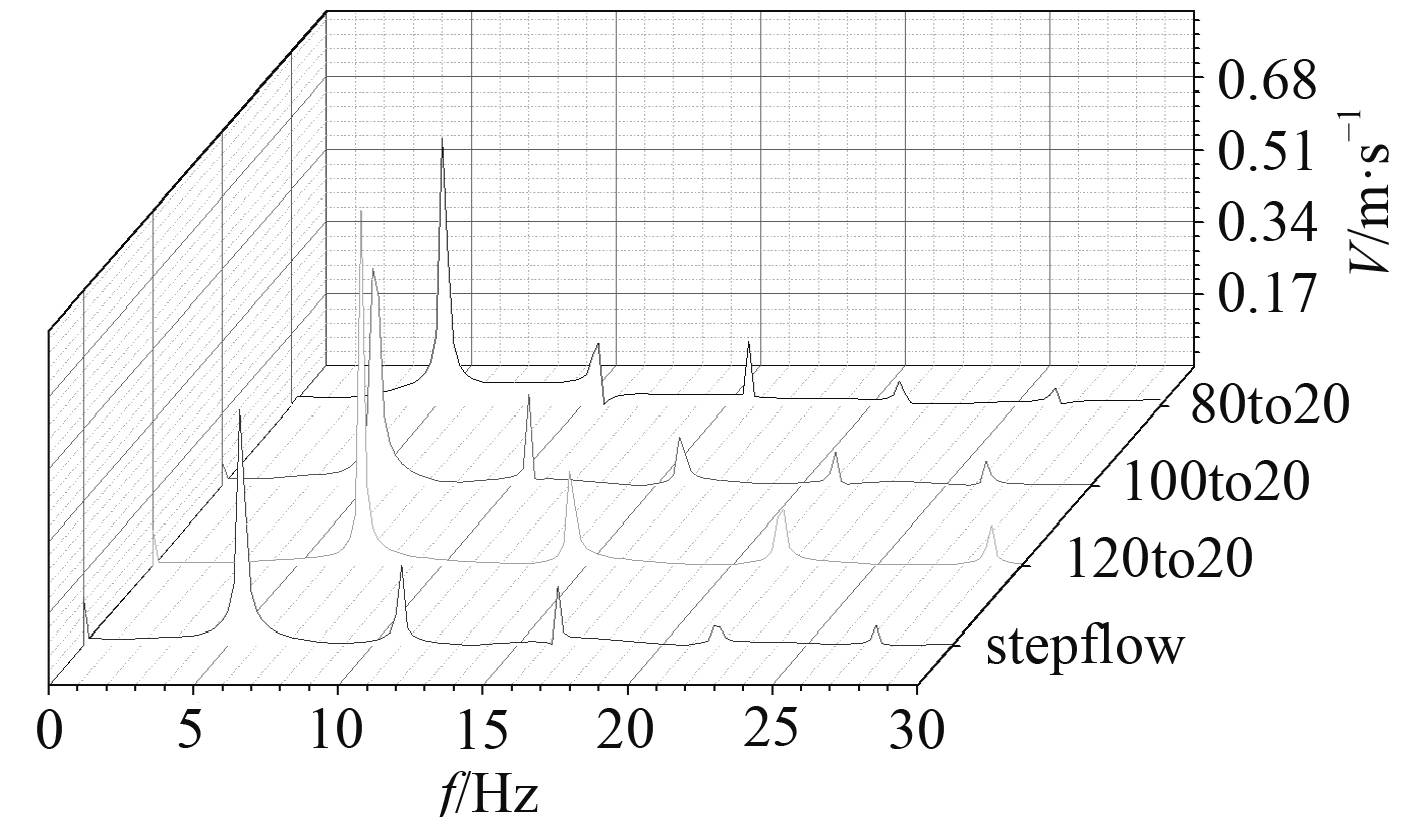
图7给出了v=1.5 m/s条件下,模型1(80:20)、模型2(100:20)、模型3(120:20)及模型4(step flow)腔口法向速度频谱。图中可以明显观察到空腔振荡存在多阶频率,阶数越高,振荡幅值越低,其中1阶频率幅值最强,高阶频率幅值依次递减。监测点法向速度频谱各阶频率,即空腔振荡各阶频率。
|
图 7 监测点速度频谱(v=1.5 m/s) Fig. 7 Power spectrum of monitoring point (v=1.5 m/s) |
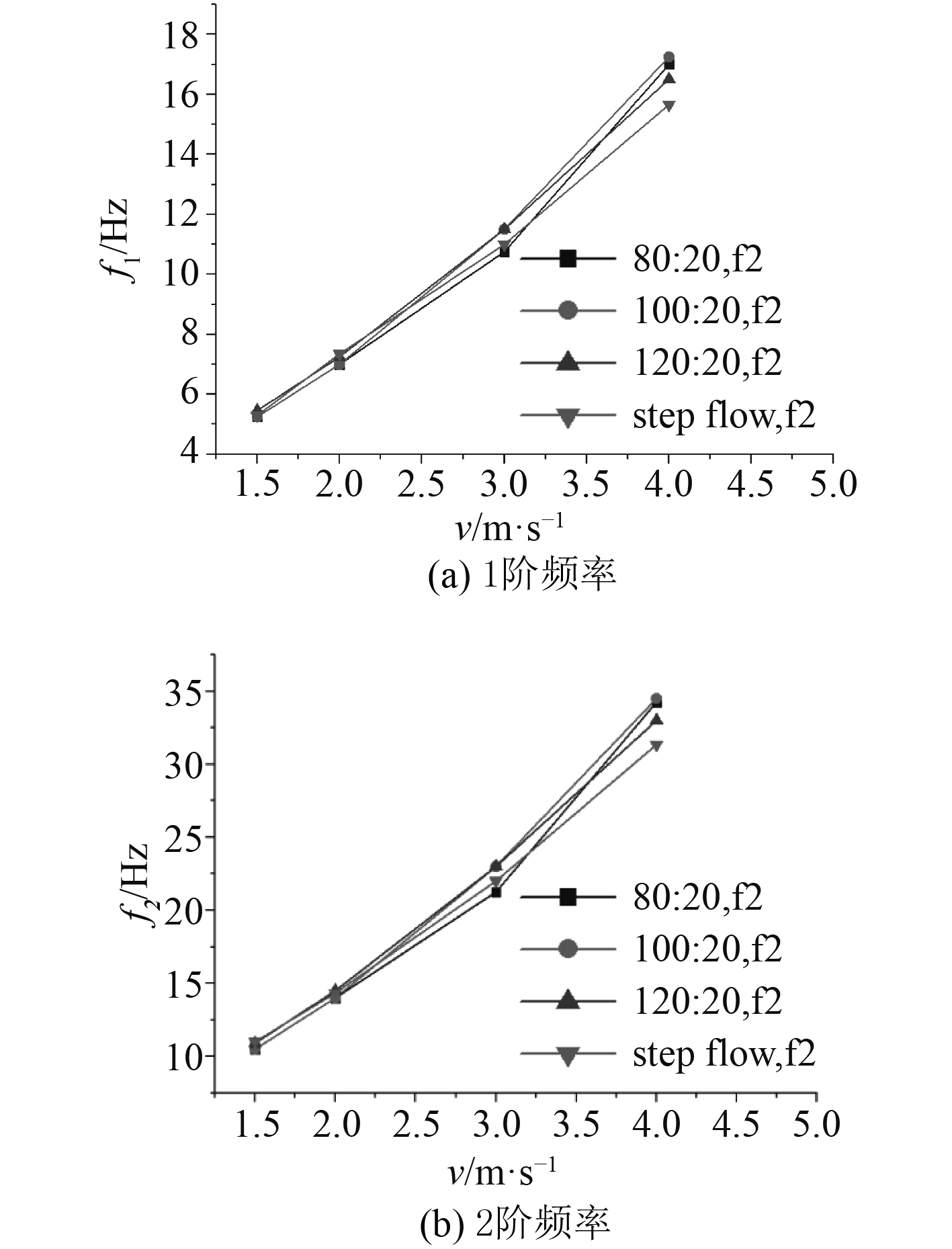
图8给出了模型1(80:20)、模型2(100:20)、模型3(120:20)及模型4(step flow)不同来流条件下1阶和2阶振荡频率。图8(a)为1阶振荡频率,图中可发现深度相同、跨度不同的空腔,振荡频率随流速增加而增加,但空腔跨度的改变几乎不影响振荡频率,4种不同跨度空腔的振荡频率大小和变化趋势基本一致;图8(b)为2阶振荡频率,可发现深度相同、跨度不同的空腔结构,其2阶振荡频率大小和变化趋势也基本一致。说明尾流模式振荡频率与空腔跨度几乎无关,而Rossiter公式中空腔振荡频率与空腔跨度直接相关。
|
图 8 空腔振荡频率 Fig. 8 Frequency of the oscillation cavity |
由于腔口自由剪切层由一系列涡组成,这些涡从空腔前缘处脱落,并跟随主流向下游运动,撞击后缘角产生压力脉冲,压力脉冲以当地声速向上游传播,到达上游反馈至导边又会激起新涡产生。在亚声速和超声速可压缩流中,来流运动速度和反射压力脉冲速度量级相当,所以反射压力脉冲对空腔前缘的脱涡频率有明显影响,即空腔振荡频率与跨度相关;而不可压缩流中,反射压力脉冲速度远远大于流体运动速度,空腔跨度改变对反射压力脉冲到达前缘的影响可忽略不计,所以反射压力脉冲对空腔前缘的脱涡频率影响不明显,即空腔振荡频率与跨度几乎不相关。
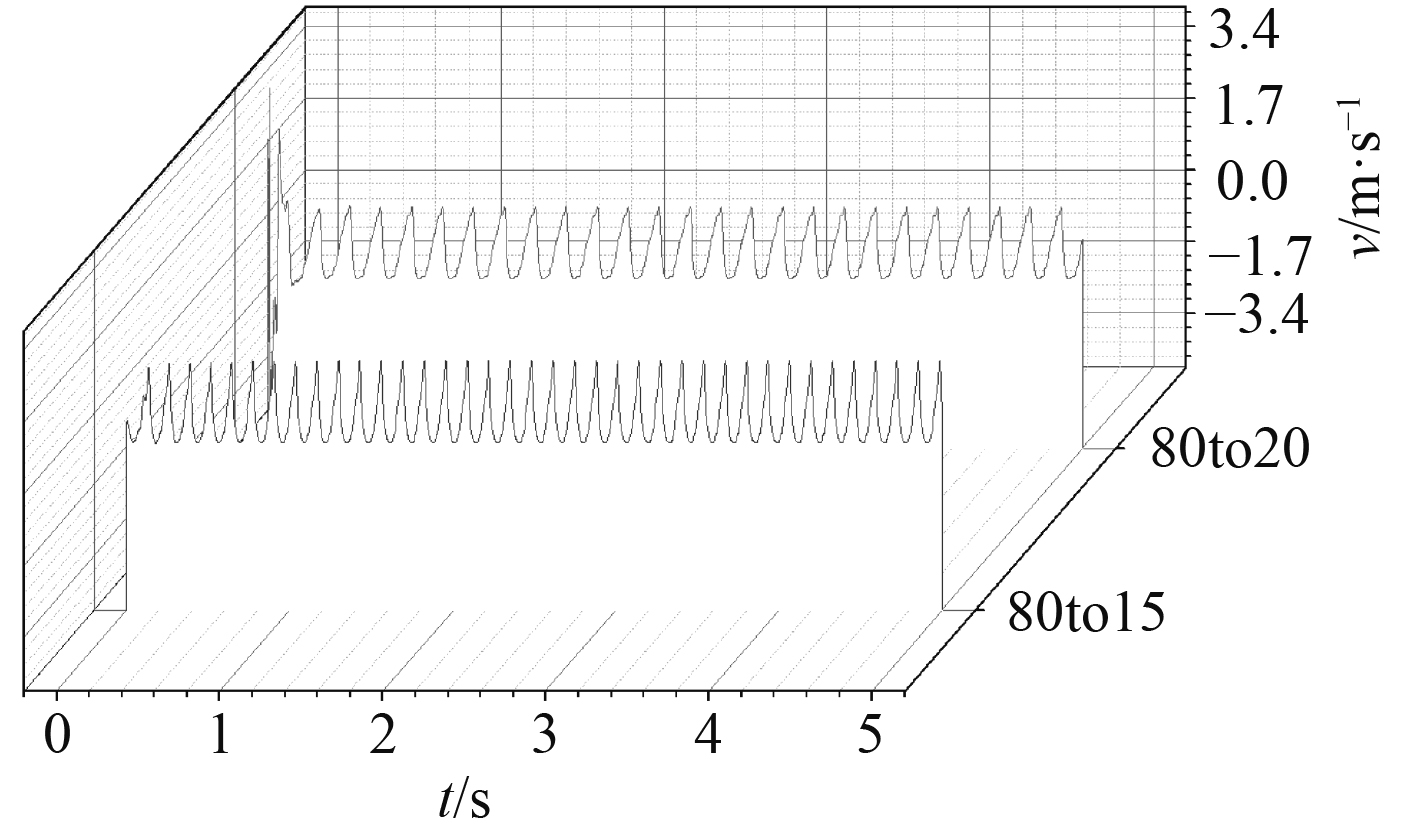
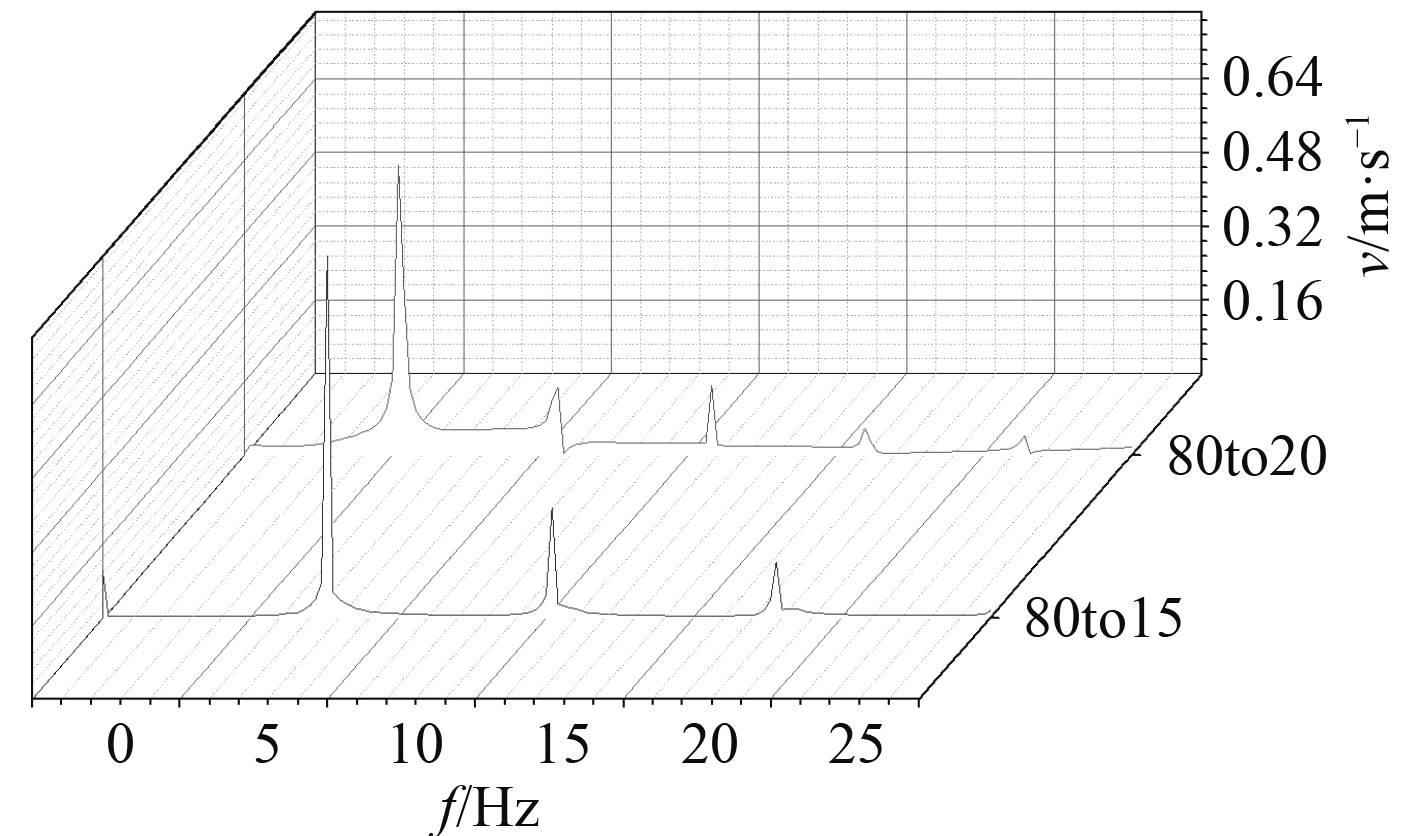
3.2.2 空腔深度对振荡频率的影响图9给出了v=1.5 m/s条件下,模型1(80:20)和模型5(80:15)腔口监测点法向速度。图中可发现腔口法向速度有很强的周期性,为保证计算准确,选取2~5 s的法向速度进行傅里叶变换得到法向速度频谱。图10给出了v=1.5 m/s条件下,模型1(80:20)和模型5(80:15)腔口法向速度频谱。可发现不同深度的空腔,尾流模式也存在多阶频率,阶数越高,振荡幅值越低。
|
图 9 监测点法向速度(v=1.5 m/s) Fig. 9 Normal velocity of monitoring point (v=1.5 m/s) |
|
图 10 监测点速度频谱(80:15, v=1.5 m/s) Fig. 10 Power spectrum of monitoring point (80:15, v=1.5 m/s) |
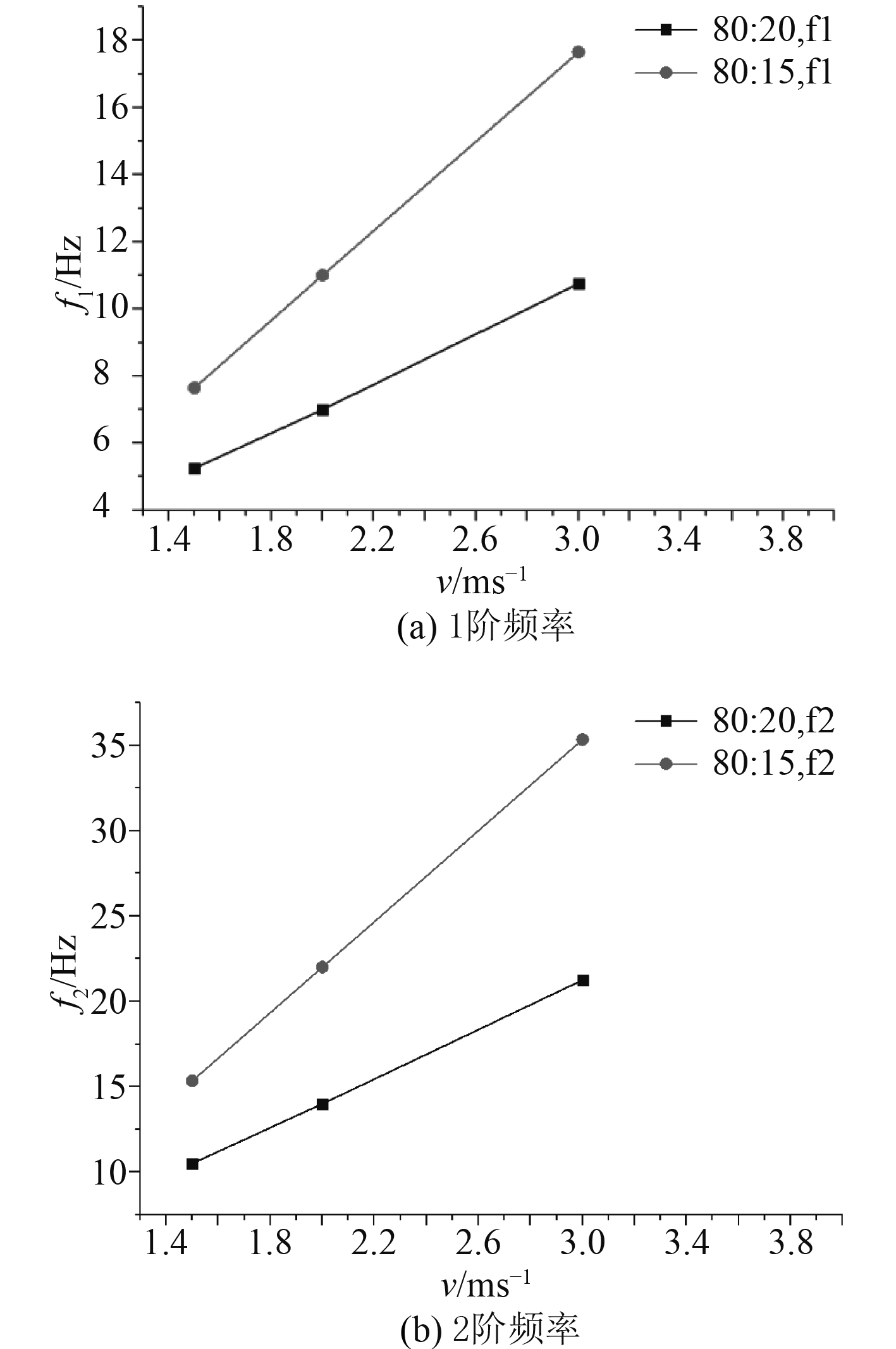
图11给出了模型1(80:20)和模型5(80:15)不同来流条件下1阶和2阶振荡频率,其中模型5(80:15)4 m/s来流条件时,空腔振荡的周期性较差,没有明显的主频,此工况振荡频率不作对比。图8(a)为1阶振荡频率,图中可发现相同跨度、不同深度的空腔结构,其1阶振荡频率出现了明显差别,同一工况下模型5(80:15)的振荡频率高于模型1(80:20);图8(b)为2阶振荡频率,图中可发现相同跨度、不同深度的空腔结构,其2阶振荡频率也出现明显差别,同一工况模型5(80:15)的振荡频率高于模型1(80:20)的振荡频率。可见空腔深度对尾流模式振荡频率有明显影响,而Rossiter公式中空腔振荡频率与空腔的深度不相关。
|
图 11 空腔振荡频率 Fig. 11 Frequency of the oscillation cavity |
前文图2给出尾流模式一个周期内的涡量云图,空腔前缘腔口涡在增长过程中尺度接近深度时,受到腔底限制转而横向发展并变得扁平,直至腔口涡脱离导边。此过程中腔底限制腔口涡发展是导致腔口涡脱落的关键因素,模型1空腔深度为20 mm,模型5空腔深度为15 mm,模型1深度大于模型5的深度,所以同一工况,模型1腔口涡受腔底限制晚于模型5,导致模型1腔口涡脱离导边晚于模型5,腔口涡脱离导边后的发展两者几乎一致,所以模型1一个周期持续的时间长于模型5,即模型1的振荡频率小于模型5的振荡频率。
4 结 语本文采用基于两方程k-ω-SST模型的IDDES方法,对5类空腔流进行数值模拟,主要对空腔流场结构及振荡频率进行了详细分析,得到以下结论:
1)IDDES方法可有效模拟尾流模式不可压缩空腔流,捕捉空腔流的涡结构,反映空腔流的流场特征;
2)5类空腔尾流模式流场结构及涡发展规律基本一致,都存在腔口涡和腔角涡,腔口涡由空腔自由剪切层卷起在腔口位置产生,腔角涡出现在腔口涡与空腔前壁底角构成的封闭区域。剪切层卷起形成腔口涡,腔口涡增长并脱离空腔前缘,最终撞击至后缘角被甩出腔外,腔口涡是产生流激振荡的主要原因。
3)空腔跨度几乎不影响振荡频率,而深度对振荡频率有显著影响,振荡频率随空腔深度的增长而降低,与可压缩空腔流Rossiter给出的半经验公式有明显区别。不同跨度的空腔,不可压缩流中来自下游的反射压力脉动速度远远高于来流流速,空腔跨度改变对反射压力脉冲到达前缘的影响可忽略不计,所以反射压力脉冲对空腔前缘脱涡频率影响不明显,即空腔振荡频率与跨度几乎不相关。不同深度的空腔,腔底对腔口涡限制是腔口涡脱离导边的关键因素,空腔深度越大,腔口涡增长尺度越大,一个周期持续时间也越长,导致振荡频率越低。
| [1] | 尹立中, 王本利, 邹经湘. 航天器液体晃动与液固耦合动力学研究概述[J]. 哈尔滨工业大学学报, 1999, 31 (2): 118–122. |
| [2] | SUPONITSKY V, AVITAL E, GASTER M. On three-dimensionality and control of incompressible cavity flow[J]. Physics of Fluids, 2005, 17 : 104–130. |
| [3] | DE ROECK W, RUBIO G, BAELMANS R, et al. Toward accurate hybrid prediction techniques for cavity flow noise applications[J]. Int J Numer Meth Fluids, 2009, 61 : 1363–1387. DOI: 10.1002/fld.v61:12 |
| [4] | HAIGERMOSER C, VESELY L, NOVARA M, et al. A time-resoved particle image velocimetry investigation of a cavity flow with a thick incoming turbulent boundary layer[J]. Submitted to Physics of Fluids, 2008. |
| [5] | GRACE SM, DEWAR WG, WROBLEWSKI DE. Experimental investigation of the flow characteristics within a shallow wall cavity for both laminar and turbulent upstream boundary layers[J]. Experiments in Fluids, 2004 (36): 791–804. |
| [6] | AHUJA KK, MENDOZA J. Effects of cavity dimensions, boundary layer, and temperature on cavity noise with emphasis on benchmark data to validate computational aeroacoustic codes[J]. NASA contractor report: Final report contract NAS1-19061, task 13. |
| [7] | ROSSITER J E. Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[J]. Royal Aircraft Establishment Technical Report, 1964, 3438 : 8–12. |
| [8] | GHARIB M. The effect of flow oscillations on cavity drag[J]. Fluid Mech, 1987, 177 : 501–530. DOI: 10.1017/S002211208700106X |
| [9] | RIZZETTA D P. Numerical simulation of supersonic flow over a three-dimensional Cavity[J]. AIAA Journal, 1988, 26 (7): 799–807. DOI: 10.2514/3.9972 |
| [10] | SHUR M L, SPALART P R, STRELETS M, TRAVIN A. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29 (6): 1638–1649. DOI: 10.1016/j.ijheatfluidflow.2008.07.001 |
| [11] | 程艳伟. 二维非定常可压缩湍流的大涡数值模拟[D]. 长沙: 国防科学技术大学, 2002. |
 2018, Vol. 40
2018, Vol. 40
