2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
采用超空泡减阻技术的水下航行体,其减阻率可达95%以上,因此该项技术获得广泛应用研究[1]。为了描述自然空化过程中汽-液之间的相变过程,目前发展出了多种空化模型,这其中包括基于Rayleigh-Plesset气泡动力学方程的Singhal模型[2]、Zwart模型[3],基于经验的Kunz模型[4]、Hosangadi模型[5]等。不同的空化模型基本都包含可人工调节的相变系数,对于不同的空化模型、不同类型的空化问题,相变系数对数值计算结果影响很大。
研究人员针对半球头圆柱研究了Singhal空化模型中不同相变系数对计算结果的影响,指出不同空化数下相变系数的设置规范[6 – 7]。Liu等[8]在研究水泵叶轮的空化问题后认为,Zwart空化模型中的蒸发系数和冷凝系数的取值对叶轮上的空泡形态和尺度有重要影响。事实上,不同头型(平头、球头、锥头等)会导致周围流场产生不同的脉动特性和漩涡特性,致使初生空泡形态和空化产生的难易程度不尽相同[9]。因此在利用空化模型模拟不同头型的空化现象时,相变系数也不是一成不变的。
本文采用基于CFD的数值计算方法,研究利用Zwart空化模型模拟不同头型的空化现象时相变系数对数值计算结果的影响,为进一步提高空化问题的数值计算精度提供指导性依据。
1 数值计算理论 1.1 N-S方程针对汽-液两相流,混合介质的N-S方程可以表示为:
| $\begin{array}{l}\displaystyle\frac{{\partial {\rho _m}}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_j}} \right)}}{{\partial {x_j}}} = 0\text{,}\\\displaystyle\frac{{\partial \left( {{\rho _m}{u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_i}{u_j}} \right)}}{{\partial {x_j}}} = \\ \displaystyle- \frac{{\partial p}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left( {\left( {\mu + {\mu _t}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}\frac{{\partial {u_i}}}{{\partial {x_j}}}{\delta _{ij}}} \right)} \right)\text{。}\end{array}$ | (1) |
式中:小标i和j分别为坐标方向;
计算中,湍流模型选择应用广泛的
| $\frac{{\partial \rho k}}{{\partial t}} + \nabla \cdot (\rho \bar Uk) = \nabla \cdot [(\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}})\nabla k] + {P_k} - \rho \varepsilon\text{,} $ | (2) |
耗散率ε方程为:
| $\begin{split}&\displaystyle\frac{{\partial \rho \varepsilon }}{{\partial t}} + \nabla \cdot (\rho \bar U\varepsilon ) = \\& \displaystyle\nabla \cdot [(\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}})\nabla \varepsilon ] + \frac{\varepsilon }{k}({C_{\varepsilon 1}}{P_k} - {C_{\varepsilon 2}}\rho \varepsilon )\text{,}\end{split}$ | (3) |
式(2)与式(3)中:
| ${P_k} = {\mu _{\rm{t}}}\nabla \bar U \cdot (\nabla \bar U + \nabla {\bar U^{\rm{T}}}) - \frac{2}{3}\nabla \cdot \bar U(3{\mu _{\rm{t}}}\nabla \cdot \bar U + \rho k)\text{。}$ | (4) |
在
|
|
表 1 |
有研究人员认为
| ${\mu _t} = f\left( \rho \right){C_\mu }\frac{{{k^2}}}{\varepsilon }\text{,}$ | (5) |
式中:
| $f\left( \rho \right){\rm{ = }}{\rho _v} + \frac{{{{\left( {{\rho _m} - {\rho _v}} \right)}^n}}}{{{{\left( {{\rho _l} - {\rho _v}} \right)}^{n - 1}}}},n \gg 1\text{。}$ |
式中:n一般取值范围为7~15,本文中n=10。
1.3 空化模型Zwart空化模型是在Kubota[12]空化模型的基础上做了一定的修正,其描述液-汽质量传递率的表达式如下:
| ${\dot m^{\rm{ - }}} = {F_{{\rm{vap}}}}\frac{{3{\alpha _{nuc}}\left( {1 - {\alpha _v}} \right){\rho _v}}}{{{R_{nuc}}}}\sqrt {\frac{2}{3}\frac{{\left| {{p_v} - p} \right|}}{{{\rho _l}}}}\text{,} $ | (6) |
| ${\dot m^{\rm{ + }}} = {F_{{\rm{cond}}}}\frac{{3{\alpha _v}{\rho _v}}}{{{R_{nuc}}}}\sqrt {\frac{2}{3}\frac{{\left| {{p_v} - p} \right|}}{{{\rho _l}}}}\text{,} $ | (7) |
式中:
Fvap和Fcond为有关相变的经验系数(相变系数),分别代表蒸发系数和冷凝系数,默认的经验值为50, 0.01[3, 13]。本文主要研究对于不同头型空化问题,这2个经验系数的设置规范。
另外,研究表明湍动能对空化也有重要影响,目前普遍采用以下方式对汽化压强修正[2]:
| ${p_{turb}} = 0.39\rho k\text{,}$ | (8) |
汽化压强:
| ${p_v} = \left( {{p_{sat}} + \frac{{{p_{turb}}}}{2}} \right)\text{。}$ | (9) |
式中:
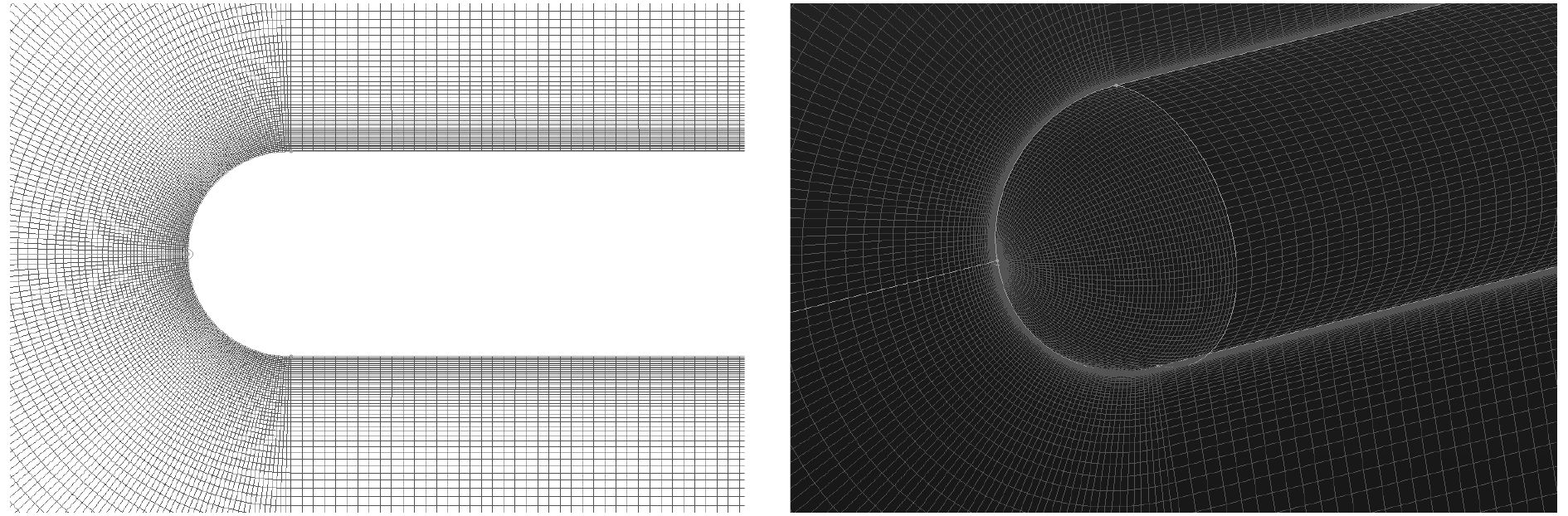
采用三维结构网格划分不同头型的圆柱模型所在流场,以半球头圆柱为例,其网格模型如图1所示。其中,边界层首层厚度保证y+=50左右。计算中采用速度入口,流速U=10 m/s;压力出口,相对压力0 Pa。
|
图 1 半球头圆柱网格模型 Fig. 1 Grid model of hemispherical cylinder |
流场中无穷远处的参考压力根据流速和不同空化数确定。空化数计算公式为:
| $\displaystyle\sigma = \frac{{{p_\infty } - {p_{sat}}}}{{\frac{1}{2}{\rho _l}{U^2}}}\text{。}$ | (10) |
表面压力系数计算方法为:
| $\displaystyle{p_{coe}} = \frac{{p - {p_\infty }}}{{\frac{1}{2}{\rho _l}{U^2}}}\text{。}$ | (11) |
Hunter等[14]采用试验方法研究了不同头型在不同空化数条件下模型的表面压力系数分布情况,这类头型可以分为两类:流线型和非流线型。流线型头型的圆柱表面光顺,流场不易产生分离涡,如半球头圆柱、尖顶圆角圆柱等。非流线型头型会使流场产生强烈的脉动和流动分离,如平头圆柱、不同锥角的锥头圆柱等。本文研究了不同相变系数对这两类头型空化计算结果的影响。
3.1 流线型头型的空化计算采用不同的相变系数计算空化数
当发生空化时,空泡内压力为饱和蒸汽压psat,因此空化区内的压力系数与空化数互为相反数,也是半球头圆柱体表面的最低压力系数。图2(a)中未显示出空泡表面,说明流场内部气相体积分数都在0.5以下,蒸发速率较慢。从表面压力系数分布看,最低压力低于饱和蒸汽压,也说明蒸发速率不够。主要原因是半球头圆柱表面光顺,周围流场相对稳定,脉动和涡特性不明显,不易产生空化现象。因此需要提高蒸发速率,使头部周围在低压环境下快速形成空化区,目标是使压力提高到饱和蒸汽压。保持Fcond不变,增大Fvap,计算了如图2(b)~图2(f)所示的算例。
从图2(b)~图2(f)中可以看出,当蒸发系数Fvap达到5 000时,表面压力系数最小值达到空化区内饱和蒸汽压产生的压力系数值,半球头圆柱头部圆周出现稳定空泡。然而圆柱表面压力达到最低值后呈缓慢趋势增加至零压,未出现正压力的尖峰突变。这种现象可以理解为冷凝速率较低,回射流不及时,空泡呈较慢的速度溃灭消失。因此需提高冷凝系数,验证冷凝系数对空化现象的影响,计算图2(g)~图2(k)所示的算例。

|
图 2 $\sigma {\rm{ = }}0.4$时半球头圆柱不同相变系数空化计算结果 Fig. 2 Numerical results of hemispherical cylinder under different phase-change coefficients when $\sigma {\rm{ = }}0.4$ |
从图2(g)~图2(k)可以看出,当冷凝系数Fcond达到0.4后,表面压力系数分布已经很接近试验值,出现正压力峰值,圆柱头部有一个主空泡,主空泡后出现次生空泡脱落现象,与局部空化的试验现象相符。当冷凝系数Fcond达到0.7~1时,表面压力系数与试验值基本吻合。因此,对于半球头圆柱,当空化数
|
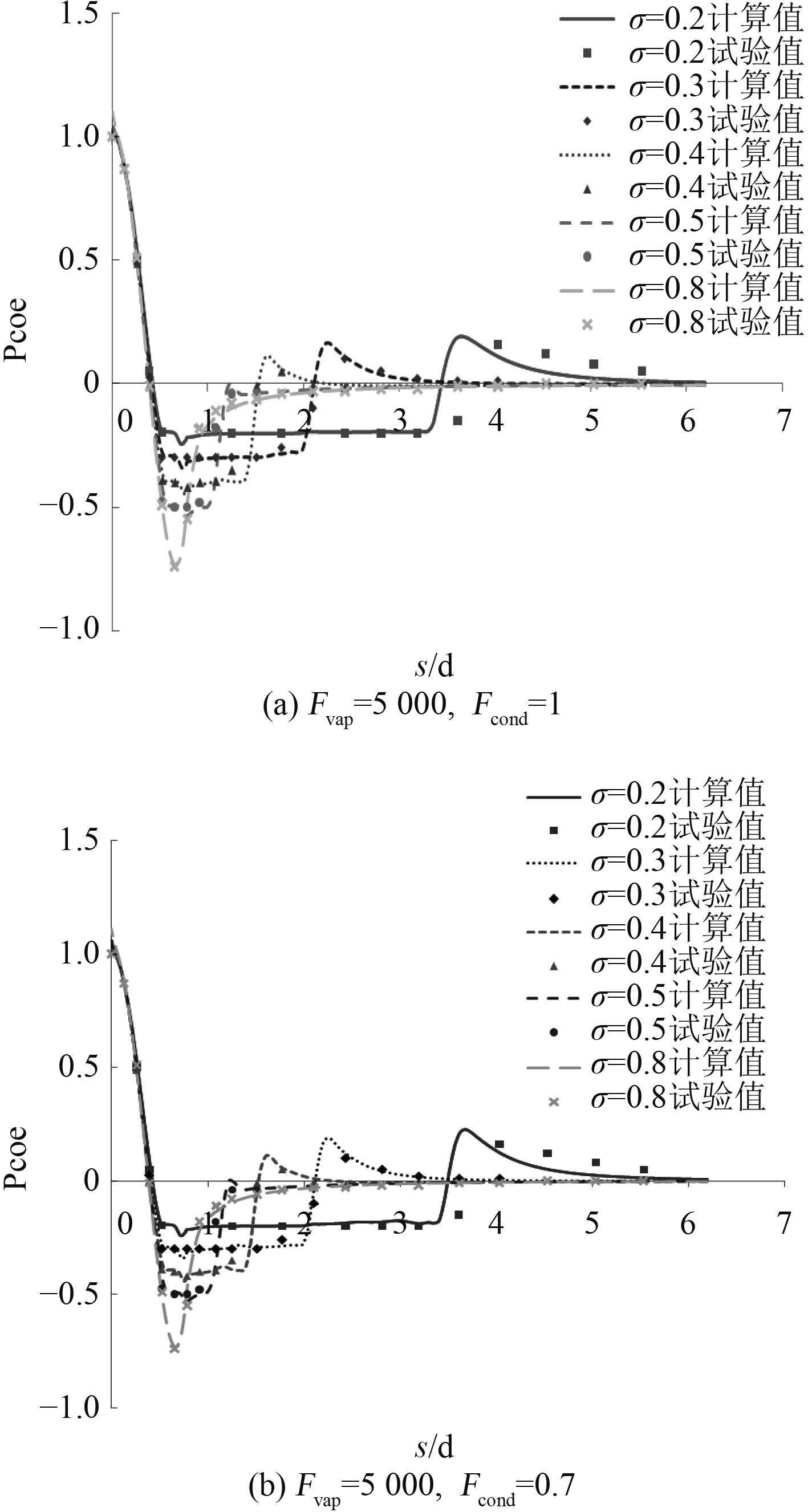
图 3 半球头圆柱不同空化数下表面压力系数分布 Fig. 3 Surface pressure coefficient distribution of hemispherical cylinder under different cavitation numbers |
在一定空化数下,计算得到的表面压力系数出现一段较平稳的最低值,这个压力系数值与空化数互为相反数,代表这段区域压强为饱和蒸汽压,即出现了空泡,这段压力系数最低值的长度范围在一定程度上表明了空泡的长度尺度。由图3可以看出,将蒸发系数设定为5 000,冷凝系数设定为0.7,1时,不同空化数下表面压力系数的分布与试验值吻合的很好,间接地验证了数值计算得到的空泡尺度与试验结果一致,只有当空化数为0.2时,在空泡溃灭区压力分布与试验值相比有些异常,但总体来看压力变化趋势与试验值吻合,这样的对比结果验证了计算半球头圆柱空化问题时相变系数设置的合理性。
为了验证以上结论对其他流线型头型的空化问题是否适用,基于以上设置规范计算了尖顶圆角圆柱在不同空化数小的压力系数分布和空泡形态如图4和图5所示。
|
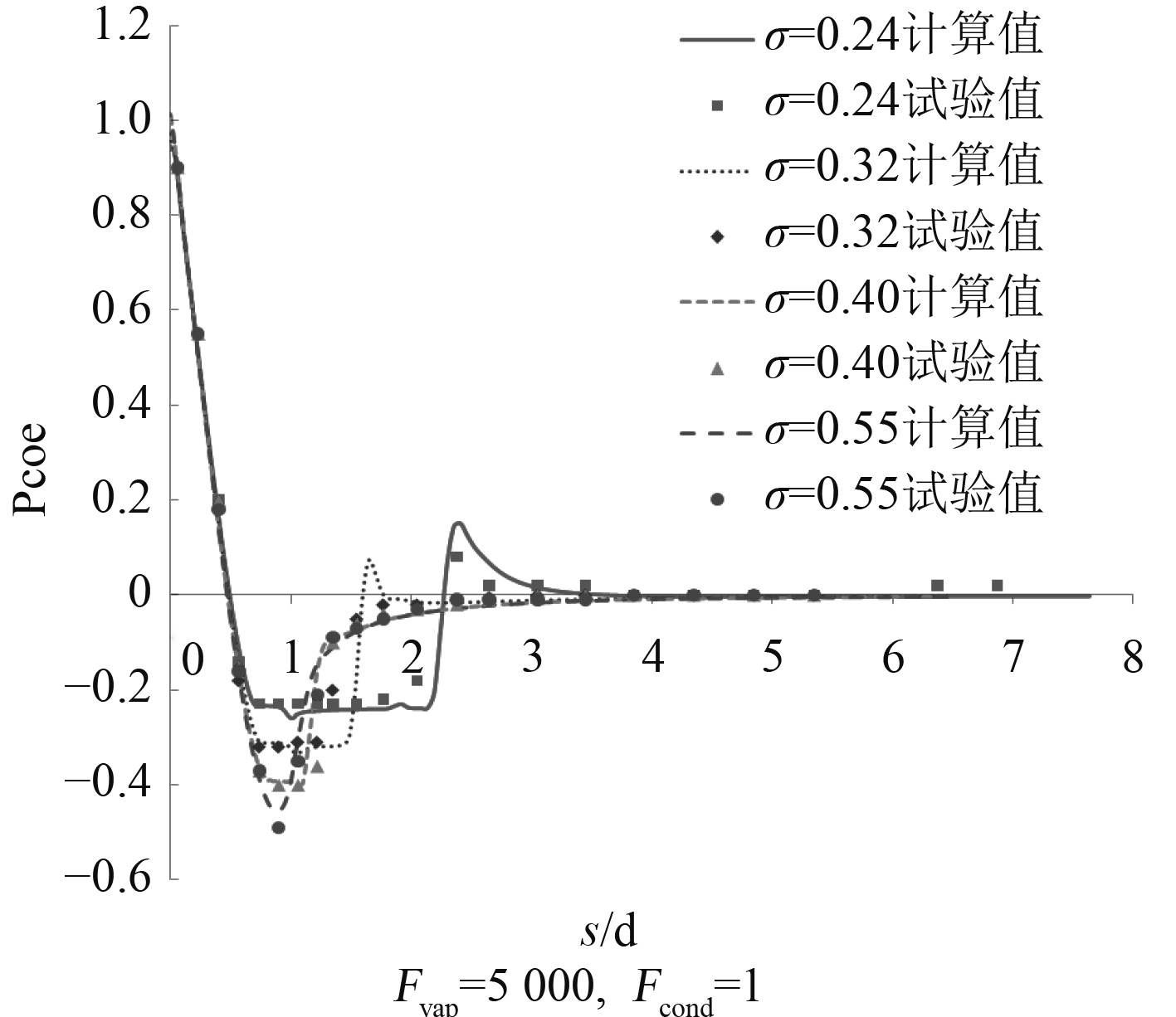
图 4 尖顶圆角圆柱不同空化数下表面压力系数分布 Fig. 4 The surface pressure coefficient distribution of ogival rounded cylinder under different cavitation numbers |
|
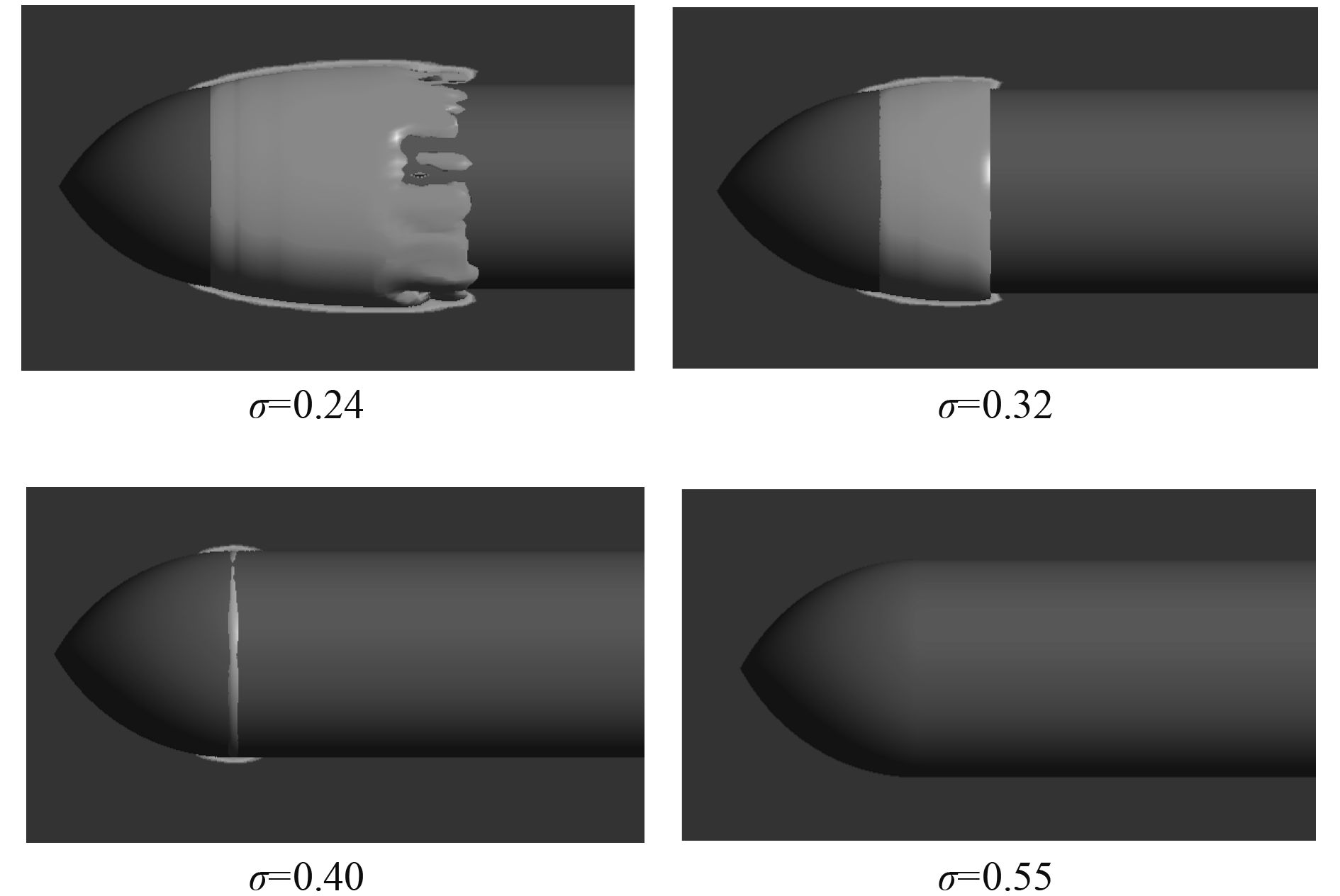
图 5 尖顶圆角圆柱在不同空化数下空泡形态 Fig. 5 The cavity shapes of ogival rounded cylinder under different cavitation numbers |
图4中不同空化数下,数值计算得到的表面压力系数与试验值变化趋势吻合,证明计算方法的准确性和相变系数设置的合理性。图5为不同空化数下空泡的形态变化。空化数为0.4时空泡初生,当空化数达到0.24时,空泡特征为一个主空泡后夹杂即将脱落的次生空泡。
以上计算结果表明,对于流线头型的空化问题,这样的相变系数设定原则合理。
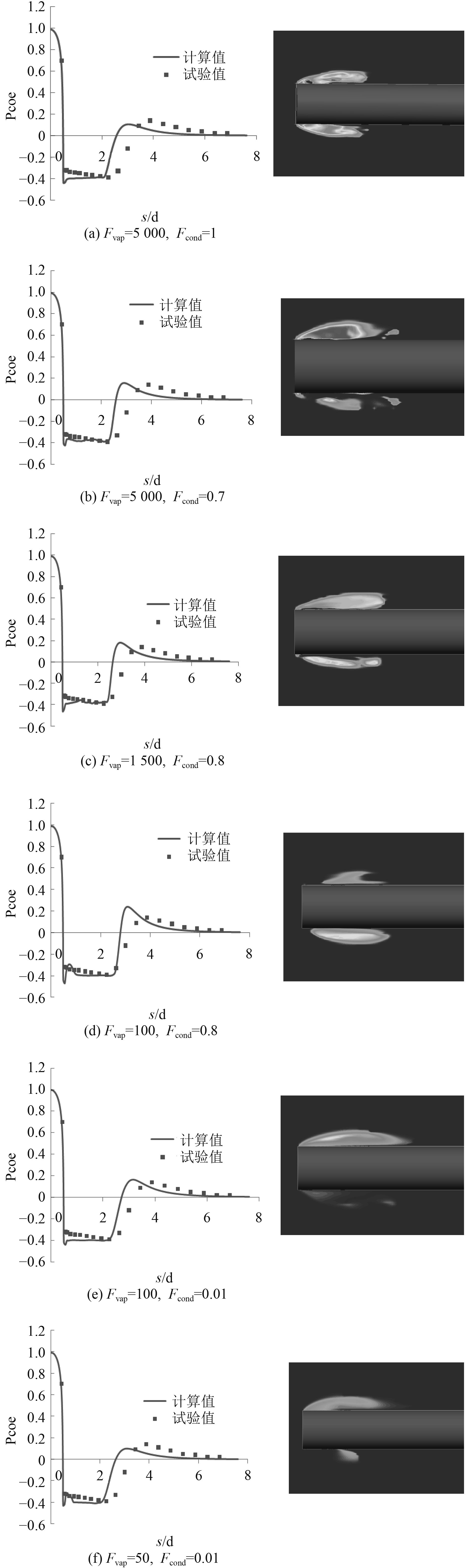
3.2 非流线型圆柱的空化计算以平头圆柱作为计算对象,计算其在空化数为0.4时不同相变系数下的压力分布情况和纵剖面蒸汽体积分数分布云图,如图6所示。
|
图 6 $\sigma {\rm{ = }}0.4$时平头圆柱不同相变系数下空化计算结果 Fig. 6 Numerical results of of blunt cylindrical under different phase-change coefficients when $\sigma {\rm{ = }}0.4$ |
从图6可以看出,相变系数的改变对于平头圆柱表面压力系数分布影响不大。蒸发系数和冷凝系数的取值影响了流域内蒸汽体积分数的分布,并且流域内的蒸汽体积分数在平头圆柱周围的分布不均匀,具有强烈的不规则性。由于在获得表面压力系数分布曲线时是取纵剖面与圆柱表面交线的其中一侧,因此空化的不规则性在一定程度上会影响表面压力系数的分布情况。但是综合来看,不同相变系数下计算的压力分布结果与试验值变化趋势基本一致。
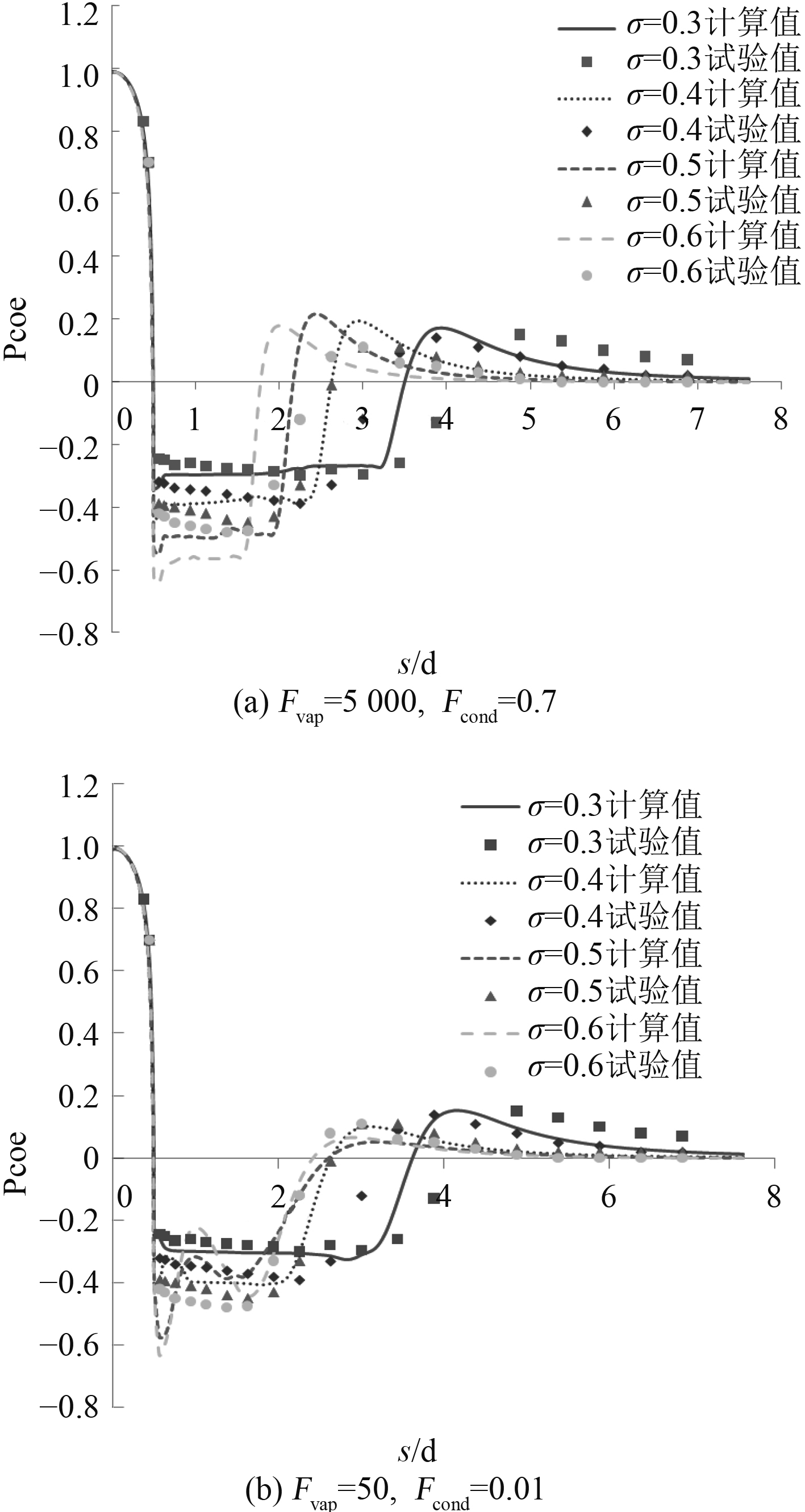
取Fvap=5000 ,Fcond=0.7(流线头型空化计算建议值)和Fvap=50,Fcond=0.01(空化模型默认值)2组相变系数计算平头圆柱在不同空化数下的表面压力分布如图7所示。
|
图 7 平头圆柱不同空化数表面压力系数分布 Fig. 7 Surface pressure coefficient distribution of blunt cylinder under different cavitation numbers |
图中显示,不同相变系数下计算得到的表面压力系数变化趋势符合试验现象,但是与试验值存在一定的偏差,在空泡溃灭区压力上升段,计算值相对试验值有提前的现象。尤其当空化数较大时,试验中平头圆柱头部周围未达到空化压力却已经出现空化,这主要是由于平头圆柱头部周围产生严重的流动分离导致过早的出现空化现象,当空化数较小时(
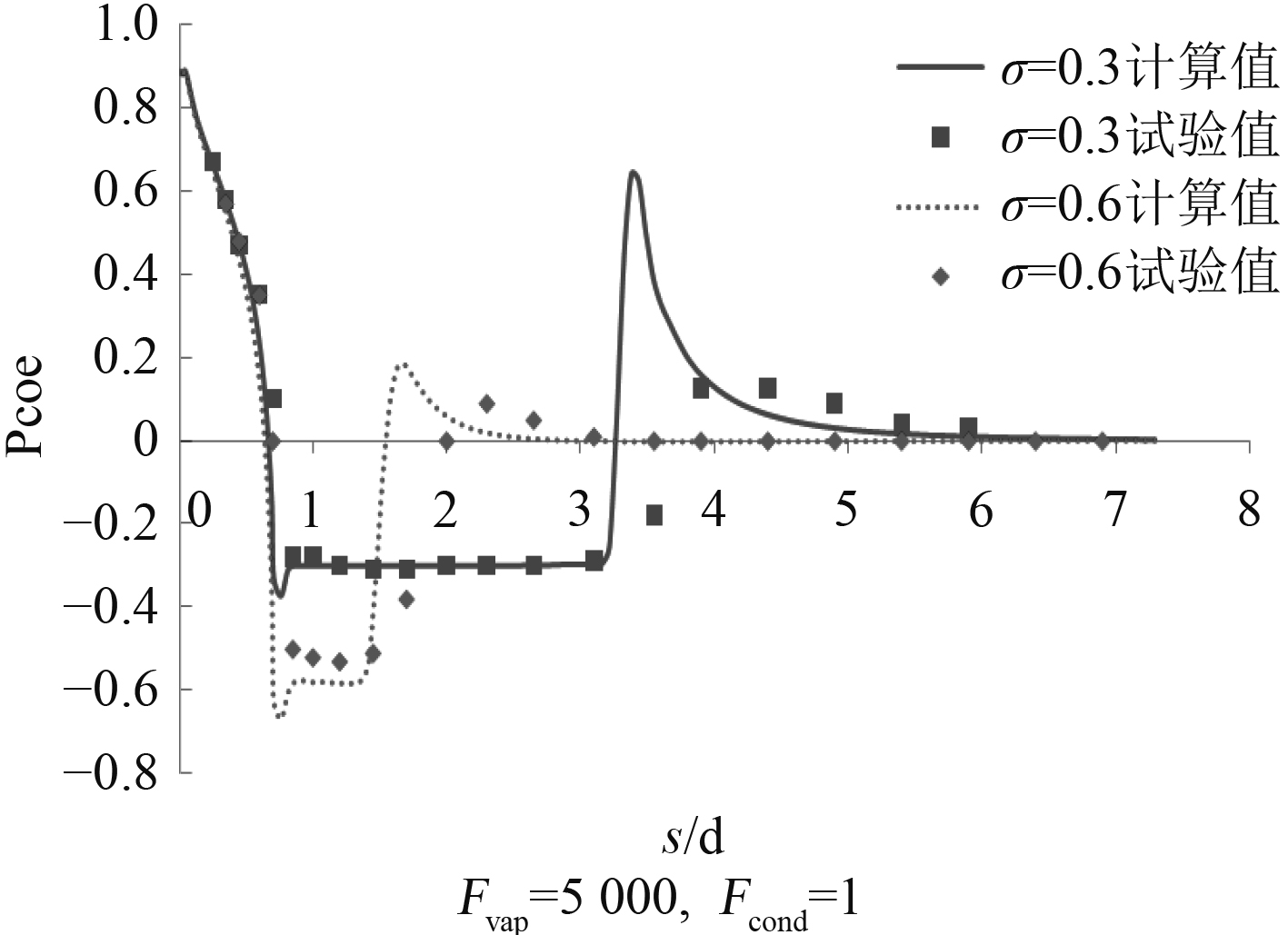
以上计算说明,对于非流线型圆柱的局部空化计算,只有当空化数小于0.3时,数值计算结果才能更接近试验结果。令Fvap=5 000,Fcond=1计算90°锥头圆柱在不同空化数条件下的空化现象,如图8所示。当空化数
|
图 8 90°锥头圆柱表面压力系数分布 Fig. 8 Surface pressure coefficient distribution of 90° conical cylinder |
采用基于CFD的数值计算方法结合Zwart空化模型求解不同头型圆柱在不同空化数条件下的表面压力系数,并与试验数据对比,可以得到以下结论:
1)流线型头型周围流场稳定,不易产生空化,增大相变系数才能保证计算结果接近试验结果,建议值为Fvap=5 000,Fcond=0.7~1.
2)非流线型头型周围流场流动分离和脉动强烈,在计算空化问题时对相变系数的变化不敏感,当空化数较小(
3)对于非流线型头型,当空化数较大时(
后续工作将基于现有空化模型结构,考虑流场内流动分离强度因素,对汽化压强再次修正,使其能够适应非流线头型在较大空化数条件下空化问题的求解。
| [1] |
易文俊, 熊天红. 高速航行体的自然超空泡流阻力特性研究[J]. 舰船科学技术, 2009, 31 (1): 38–42.
YI Wen-jun, XIONG Tian-hong. Research on drag characteristics of natural supercavitation profile for high speed bodies[J]. Ship Science and Technology, 2009, 31 (1): 38–42. |
| [2] | SINGHAL A K, ATHAVALE M M, LI Hui-ying, et al. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering, 2002, 124 (3): 617–624. DOI: 10.1115/1.1486223 |
| [3] | ZWART P J, GERBER A G, BELAMRI T. A two-phase flow model for predicting cavitation dynamics[C]// 5th International Conference on Multiphase Flow, Yokohama Japan: ICMF, 2004. |
| [4] | KUNZ R F, BOGER D A, STINEBRING D R, et al. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J]. Computers & Fluids, 2000, 29 (8): 849–875. |
| [5] | MERKLE C L, FENG J, BUELOW P E O. Computational modeling of the dynamics of sheet cavitation[C]//Proceedings of Third International Symposium on Cavitation. Grenoble: [s. n.], 1998: 307–313. |
| [6] |
王柏秋, 王聪, 黄海龙, 等. 空化模型中的相变系数影响研究[J]. 工程力学, 2012, 29 (8): 378–384.
WANG Bai-qiu, WANG Cong, HUANG Hai-long, et al. Study of the influence of phase-chage coefficient in the cavitation model[J]. Engineering Mechanics, 2012, 29 (8): 378–384. DOI: 10.6052/j.issn.1000-4750.2011.09.0592 |
| [7] | WANG Bai-qiu, WANG Cong, HUANG Hai-long, et al. Study of the phase-change coefficients of the cavitation model in cavitation flow fields generated from cone cavitator[J]. Journal of Harbin Institute of Technology, 2012, 19 (4): 1–8. |
| [8] | LIU Hou-lin, WANG Jian, WANG Yong, et al. Influence of the empirical coefficients of cavitation model on predicting cavitating flow in the centrifugal pump[J]. Int. J. Nav. Archit. Ocean Eng, 2014, 6 : 119–131. DOI: 10.2478/IJNAOE-2013-0167 |
| [9] |
黄彪, 王国玉, 胡常莉, 等. 绕回转体初生空化流场特性的实验及数值研究[J]. 工程力学, 2012, 29 (6): 320–325.
HUANG Biao, WANG Guo-yu, HU Chang-li, et al. Experimental study on fluctuating hydrodynamics around axisymmetric bodies[J]. Engineering Mechanics, 2012, 29 (6): 320–325. DOI: 10.6052/j.issn.1000-4750.2010.09.0654 |
| [10] | DULAR M, BACHERT R, STOFFEL B, et al. Experimental evaluation of numerical simulation of cavitating flow around hydrofoil[J]. European Journal of Mechanics-B/Fluids, 2005, 24 (4): 522–538. DOI: 10.1016/j.euromechflu.2004.10.004 |
| [11] | COUTIER-DELGOSHA O, FORTES-PATELLA R, REBOUD J L. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation[J]. Journal of Fluids Engineering, 2003, 125 (1): 38–45. DOI: 10.1115/1.1524584 |
| [12] | KUBOTA A, KATO H. A new modeling of cavitation flows: a numerical study of unsteady cavitation on a hydrofoil section[J]. Journal of Fluid Mechanics, 1992, 240 (1): 59–96. |
| [13] |
王复峰, 王国玉, 黄彪, 等. 通气空化多项流动特性的实验与数值研究[J]. 工程力学, 2016, 33 (9): 220–226.
WANG Fu-feng, WANG Guo-yu, HUANG Biao, et al. Experimental and numerical study on characteristic of ventilated cavitation multiphase flow[J]. Engineering Mechanics, 2016, 33 (9): 220–226. |
| [14] | HUNTER R, JOHN S M. Cavitation and pressure distribution, head forms at zero angle of yaw[R]. State University of Iowa, Studies in Engineering, Bulletin 32. |
 2018, Vol. 40
2018, Vol. 40
