0 引　言

随着我国大力推进海洋经济发展战略的实施，海洋工程领域的作业范围从近海向深海不断拓展，作业环境更加复杂，由此引发的船撞事故的风险也大大增加。船舶与海洋平台的碰撞是一个复杂的非线性接触损伤过程，碰撞中平台的损伤程度由航速、撞击形式以及环境载荷等多种因素影响^[1]。Lenselink H和Thung K.G^[2]利用有限元法分析内部碰撞机理，同时考虑船体在碰撞过程中与水流的相互作用，得到结构变形和碰撞力时序的仿真结果；李润培^[3]将极限分析法与增量有限元法相结合，在极限条件下分析平台的结构变形，获得平台承载力；唐友刚^[4]以系泊游轮作为研究对象，采用频域与时域分析方法，模拟了系泊船舶在风、浪、流联合作用下与海上平台的碰撞，得到护舷刚度与碰撞力间的相互影响。

目前，对于船舶与海洋平台的碰撞研究着重于结构的破坏损伤等内部动力学方面，对于外部动力学问题的研究较少。因此本文在碰撞部分利用Ansys/LS-DYNA进行碰撞动力分析，在水动力部分利用AQWA对平台受碰撞前后进行运动响应及系泊缆顶端张力分析来研究外部动力学问题非常必要。

1 船舶碰撞时的动力学方程

对于船舶碰撞的外部动力学研究，20世纪中期Minorsky假设碰撞系统动量守恒，用非线性理论求解动能损耗^[5–6]。碰撞后船速由方程式（1）求出：

${m_1}{u_1}\sin \alpha = \left( {{m_1} + {m_2} + d{m_2}} \right)U\text{，}$

(1)

由能量守恒定理解得碰撞时的动能损耗：

$\Delta {E_k} = \frac{{{m_1}\left( {{m_2} + d{m_2}} \right)}}{{2\left( {{m_1} + {m_2} + d{m_2}} \right)}}{\left( {{u_1}\sin \alpha } \right)^2}\text{，}$

(2)

对于碰撞时的受力可用耗散简化理论进行分析，将碰撞系统简化为2个分别表示船和平台的质量系统。由力-刚度关系，平台的受力可表示为：

${F_\delta } = {K_{11}}{\delta _b} + {K_{12}}{\delta _p}\text{，}$

(3)

$F{}_p = {K_{21}}{\delta _b} + {K_{22}}{\delta _p} = - {M_p}{\delta _p}\text{，}$

(4)

式中： ${F_\delta }$ 为船体与平台间的碰撞力； ${\delta _b}$ 为平台碰撞点的位移；F_p为传递至平台顶部的作用力，其中平台质量为M_p； ${\delta _p}$ 为平台顶部的位移。

船体与海洋平台间的相互作用可表示为：

${F_\delta } = \left\{ \begin{array}{l}{K_S}\left( {{\delta _a} - {\delta _b}} \right)\text{，}\;\;\text{当}\mathop {{\delta _a}}\limits^ \cdot - \mathop {{\delta _b}}\limits^ \cdot \geqslant 0\text{，}\\0\text{，}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{当}\mathop {{\delta _a}}\limits^ \cdot - \mathop {{\delta _b}}\limits^ \cdot \leqslant 0\text{。}\end{array} \right.$

(5)

式中： ${\delta _a}$ 为船体碰撞点位移； ${{{K}}_{11}}{\text{，}}{{{K}}_{12}}{\text{，}}{{{K}}_{21}}{\text{，}}{{{K}}_{22}}$ 均为刚度系数。

若假设第1次碰撞后 $\mathop {{\delta _a}}\limits^ \cdot = \mathop {{\delta _b}}\limits^ \cdot $ ，平台顶部位移非常小，故有：

${F_p} = \frac{{{K_{21}}}}{{{K_{11}}}}{F_\delta }\text{。}$

(6)

2 船体与平台的尺寸及有限元模型 2.1 平台的尺寸及有限元模型

本文选取的研究对象是具有4个立柱和2个下浮体的半潜式海洋平台，平台主要尺寸如表1所示。

对于平台的有限元结构，立柱等被碰撞部分采用塑性动态材料，材料参数如表2所示，单元类型为Huges-Liu壳单元；非碰撞部分采用线弹性材料，单元类型为Belytsch-Tsay壳单元。由于碰撞损伤及水动力特性的研究集中于立柱和下浮体结构区域，因此对甲板及甲板以上的结构进行简化处理，用一层甲板来代替，其重量及重心利用LS-DYNA控制密度的方式进行调整。海洋平台的有限元模型如图1所示。

2.2 船尾的尺寸及有限元模型

船舶与海洋平台的碰撞形式主要有首碰、侧碰和尾碰。对于常规的补给船，尾碰占到70%，因此本文选择尾碰作为平台发生碰撞的研究形式。

本文主要研究海洋平台所受的碰撞力，且船尾刚度相对于平台立柱的刚度较大，故建立有限元模型时只需构建船尾部分，并将其简化为刚性模型。碰撞船主尺度如表3所示，船尾有限元模型如图2所示。

3 碰撞部分的数值仿真研究 3.1 碰撞场景的选取

船舶与海洋平台碰撞的因素很多，实际碰撞中碰撞参数具有多种复杂的组合情况^[7]，无法将全部情景考虑在内。因此本文选取最常见的碰撞参数组合对结构的碰撞性能进行研究。挪威船级社推荐的典型船舶碰撞速度为2 m/s且船舶正向撞击平台立柱时造成的损伤更大^[8]，因此本文选取船尾以2 m/s速度正碰平台立柱的碰撞场景进行研究。

3.2 碰撞仿真结果及分析

船尾与海洋平台碰撞时，假设船尾正向撞击于平台的左前侧立柱。碰撞过程中几个典型时刻的Mises等效应力云图如图3所示。

从应力分布云图中可以看出所受应力最大区域集中出现在受船尾碰撞的立柱上，且在碰撞发生的初始阶段，碰撞区的应力大于屈服应力，进入塑性阶段。在碰撞发生的过程中，立柱与上甲板以及与两浮体间横撑的连接处也均有较大的应力分布。因此从防撞层面上考虑，应该在最易受撞击的平台立柱上增加护舷、夹芯板等防护措施，并提高立柱与上甲板、立柱与横撑连接处的强度，从而减轻船撞事故对平台结构造成的损伤。

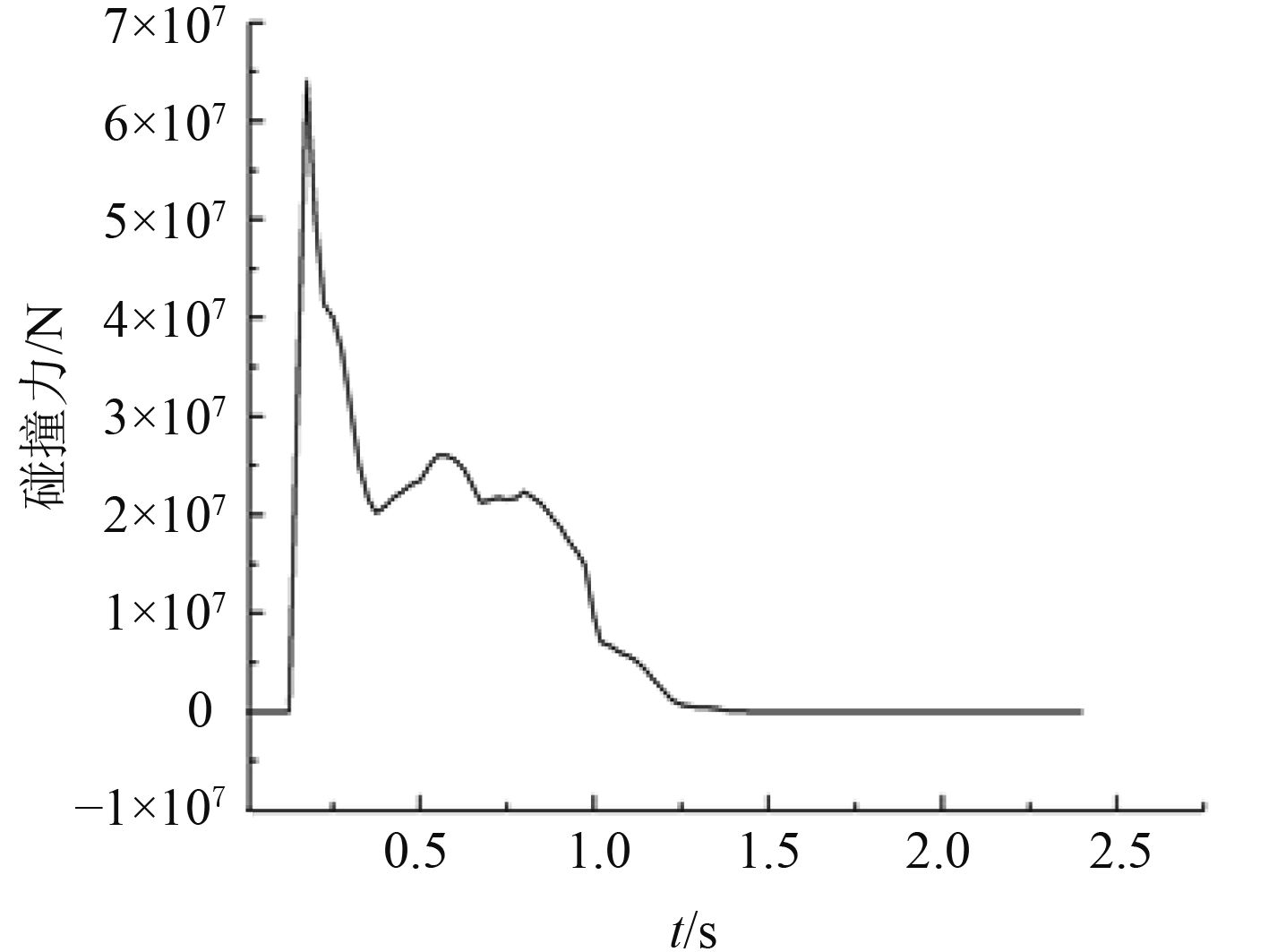
碰撞过程是一种复杂的非线性动态响应过程。本文由有限元软件Ansys/LS-DYNA计算得到的碰撞力时程曲线如图4所示。

碰撞力曲线总体呈现明显的非线性，在船尾与平台产生接触开始，0.15~0.175 s内碰撞力急剧增加，并在0.175 s达到最大值 $6.405 \times {10^7}{\rm{N}}$ ，最大值的出现是由于立柱表面及内部垂向板壁、横向框架等构件不断受力失效造成的，由此可知平台所受最大碰撞力发生在刚产生碰撞的极短时间内。此后碰撞力在0.175~0.375 s内迅速减小，这是由于船尾撞击平台一侧立柱，致使海洋平台绕z轴旋转的结果。随着碰撞过程中船速不断降低，动能下降，以及平台构件的损伤失效，碰撞力不断减小，直至碰撞结束。

4 水动力部分的数值仿真研究 4.1 水动力模型及系泊系统

本文利用AQWA对目标平台进行水动力研究时，将平台模型进行适当的简化，建立平台的浮式基础结构及相应的湿表面部分，平台的重量及重心位置可以通过对平台模型不同部位的密度设置来控制，以保证平台的有限元模型与实际平台的重量重心基本一致。

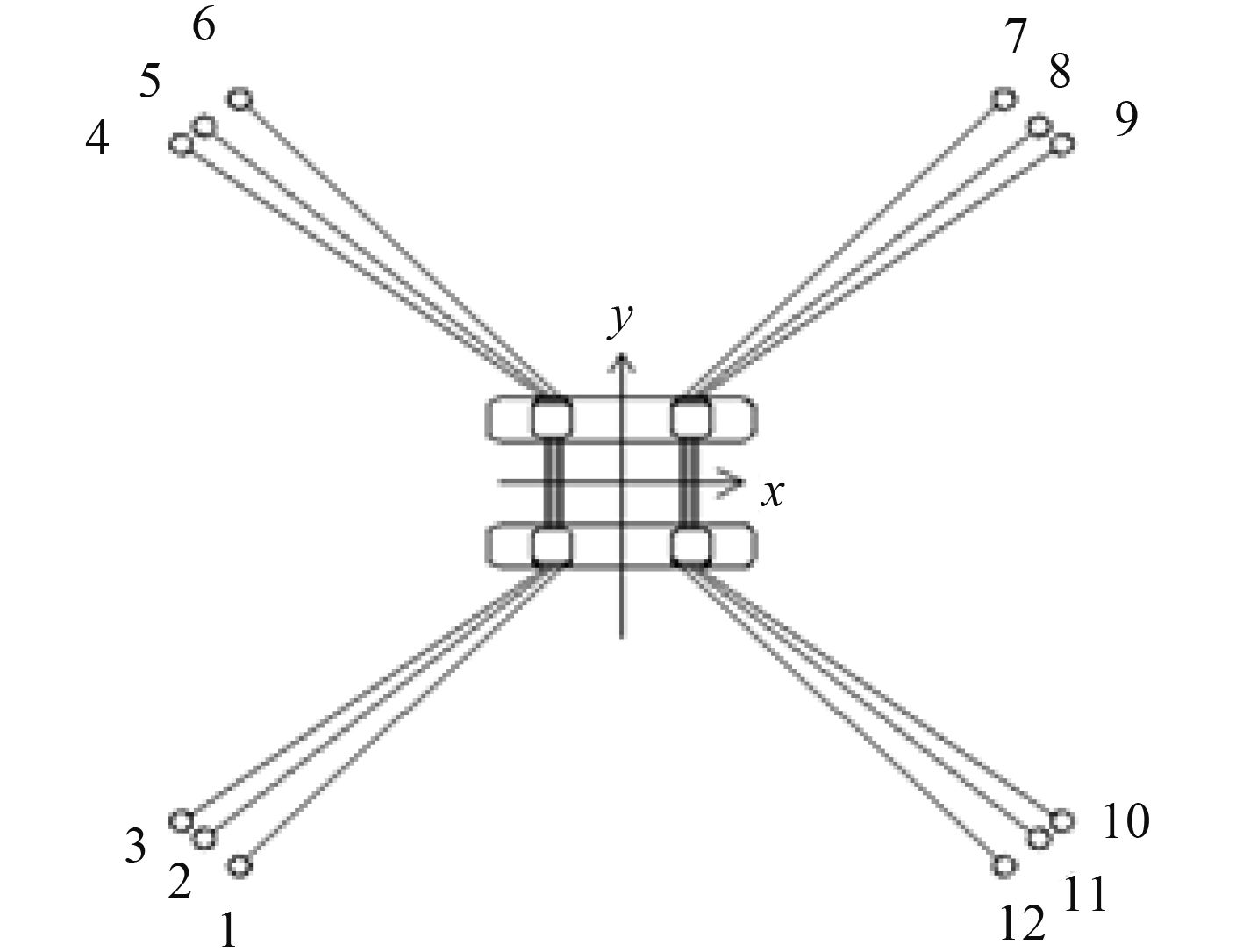
为使研究具有代表性，海洋平台系泊系统布置方案与传统张紧式系泊方案相同。系泊缆数量为12根，布置形式为缆绳与x轴方向夹角为37°/40°/45°对称分布，如图5所示。系泊缆主要参数如表4所示。

4.2 时域耦合结果及分析

当风、浪、流同向作用时，系泊缆产生最大拉力，因此本文进行水动力分析所选取的环境参数为风、浪、流同向从0°方向入射。波浪谱选择JONSWAP谱，有义波高6.0 m，周期11.2 s；海面流速为0.98 m/s；海上平均风速为22.5 m/s。

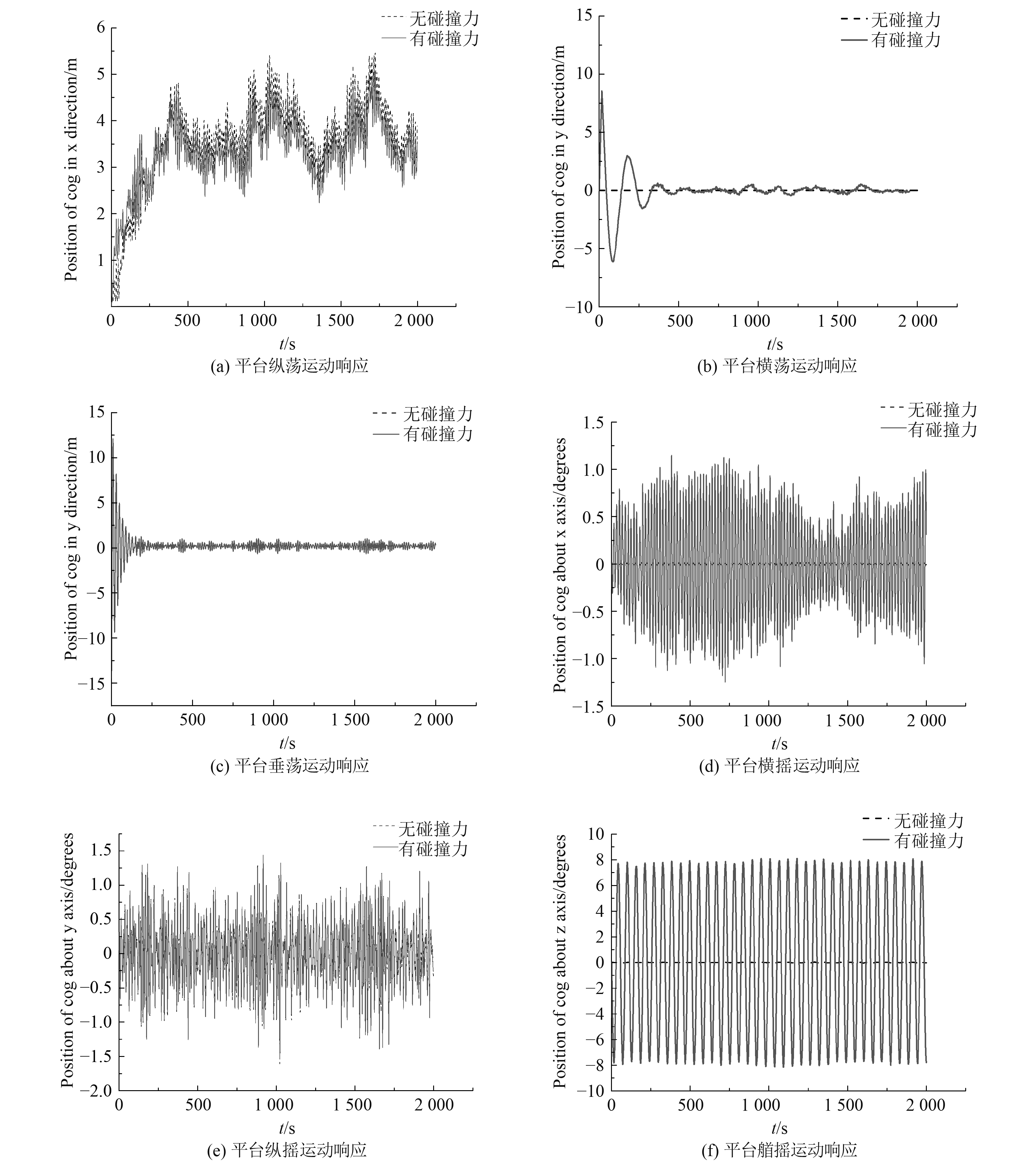
4.2.1 平台运动响应结果及分析

将碰撞部分得到的完整碰撞力时序导入AQWA，对平台在受碰撞力和外部环境共同影响下的时域运动响应进行模拟，并与自身未受船舶撞击时的运动响应进行对比。运动响应曲线如图6所示。

从图中运动响应曲线的对比可以看出，平台在受船尾撞击时，碰撞力对横荡、横摇以及首摇的影响较大，对纵荡、垂荡以及纵摇的影响很小。对于横荡运动，平台受到沿y轴负方向的碰撞力，因此在y方向会有较大位移，受碰撞前的位移很小，受碰撞后最大位移达到8.52 m。对于横摇运动和首摇运动，由于平台受碰撞部位为左前侧立柱，因此会使平台绕x轴和z轴产生一定的旋转，且相比于无碰撞力时运动响应的最大值有明显增加；碰撞后平台绕x轴旋转的最大响应值为1.149°，绕z轴旋转最大响应值为8.145°。对于受碰撞力影响较小的3种运动响应，纵荡比其他2种运动碰撞前后变化相对更明显，因为平台受到沿y轴负方向的碰撞力后绕z轴产生旋转，碰撞力出现在x方向上的分力，因此在x方向上的影响相对更大；而对于z轴方向上的平移和绕y轴方向上的旋转2种运动响应需要有沿z轴方向的力影响时才会有明显变化，而在本文的船舶与平台碰撞过程中并没有这种竖直方向的力，因此对垂荡和纵摇影响最小。

另外，由上图可以看出在1 000 m工作海域中，受碰撞后平台产生最大水平位移8.52 m，远小于水深的6%，因此符合规范，模拟结果符合实际情况。从防撞安全的层面上考虑，平台除了在关键结构处提高强度外，还应安装一定的吸能减摇装置，减小受撞击后平台的水平位移和绕轴旋转的角度。

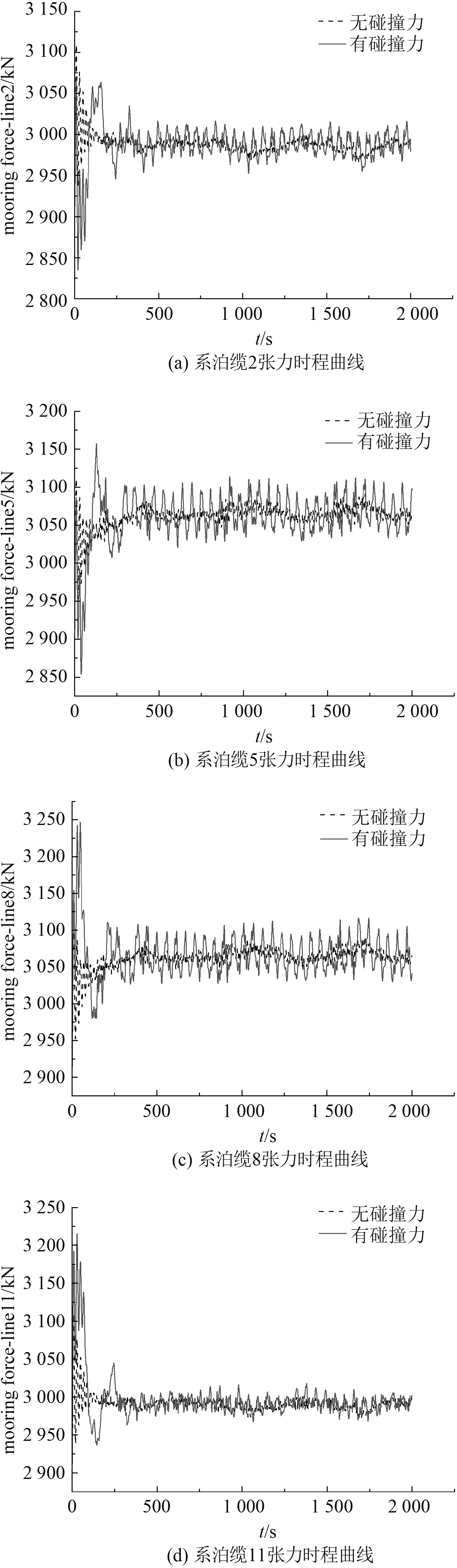
4.2.2 系泊缆顶端张力变化结果及分析

由于12根系泊缆呈对称分布，同一立柱上的3根缆绳在宏观上张力变化趋势相同，故本文仅选取4根不同立柱上相对位置相同的缆绳为例进行说明。因为缆绳2，5，8，11的顶端张力为所在立柱上各缆绳张力的均值，因此选取缆绳2，5，8，11的顶端张力时程曲线为例，如图7所示。

从总体上看，船体撞击平台会使系泊缆的张力产生较大幅度的变化，其中对系泊缆8和系泊缆5对应立柱上的缆绳张力影响较大，顶端张力变化幅值较大；对系泊缆2对应立柱上的缆绳张力影响次之；对系泊缆11对应立柱上的缆绳张力影响最小。这是由于平台的左前侧立柱受到y轴负方向的碰撞力以及0°方向入射的风、浪、流的联合作用力，导致平台在平动的同时产生旋转运动，直接受碰撞力和外环境影响的部分缆绳受影响最大，对其他部分缆绳产生的影响最小。

由表5对比12根系泊缆顶端张力可以看出，系泊缆最大张力出现在缆绳7中，最大值为3 255.47 kN，这是由于受碰撞力和风、浪、流联合作用力的结果；最小张力出现在缆绳3中，最小值为2 832.643 kN，这是因为缆绳3处不受碰撞力直接影响，最小值明显小于有碰撞力影响的缆绳。从防撞安全角度上考虑，系泊缆顶端张力会因为碰撞位置和方向不同而产生不同变化趋势，因此应充分考虑船体撞击海洋平台的各种形式，优化系泊系统或提升最易受碰撞部位附近缆绳的强度，防止因系泊缆顶端张力过大而引起的缆绳断裂等事故。

5 结　语

本文将完整的碰撞力载荷加载到平台结构上，利用完全时域耦合方法对半潜式海洋平台受船舶碰撞的动力响应进行求解分析，得到平台运动响应特性和系泊缆顶端张力变化情况，所得结论如下：

1）船舶撞击平台时，平台受到应力最大的区域为平台的立柱部分，并且碰撞力在碰撞发生的极短时间内会迅速增大到最大值；在碰撞过程中，立柱与上甲板、立柱与浮体横撑的连接处也有较大的应力分布。

2）平台的横荡、纵摇和首摇受碰撞力影响较大，纵荡、横摇和垂荡受碰撞力影响相对较小；平台立柱受船体撞击后会产生明显的首摇运动，碰撞力在此期间显著减小；在碰撞过程中平台产生的最大水平位移远小于水深的6%，故模拟结果符合规范要求。

3）系泊缆顶端张力最大值出现在平台直接受碰撞部位附近的缆绳中。

4）从防护安全的角度上考虑，海洋平台应对立柱、立柱与上甲板、立柱与横撑的连接处进行加固，尽量避免构件在碰撞中的损坏失效；在立柱上增加护舷等减震吸能装置，减小碰撞对平台造成的外部动力响应幅值；同时应优化系泊系统，以防止缆绳断裂事故的发生。