波浪能滑翔器(Wave Glider)是近年来出现的一种新型海洋观测平台。它由水面母船和水下牵引机两部分构成,能够利用其特殊的双体结构将波浪上下起伏的势能转化为其前进的动能[1]。因此它可以摆脱传统海洋观测手段对化石能源的依赖,具有观测周期长、成本低等优点,已逐渐成为国内外研究的热点。在这方面,美国的Liquid Robotics公司技术最为成熟,其研制的SV2、SV3型波浪能滑翔器已被应用于环境监测、海洋科学研究以及军事等多个领域[2]。在2012年12月,其布放的4个波浪能滑翔器完成了横渡太平洋的航行任务,总航程超过9 000 nmile,创下了自主航行器行驶路线最长的世界纪录。国内对其的研究主要还处在样机的仿制阶段。贾丽娟[3]应用Fluent软件对水翼的翼型、间距、摆角等做了分析研究。杜晓旭[4]基于Kane方程建立波浪能滑翔器动力学模型,对系统进行了二维运动仿真。李小涛[5]对波浪能滑翔器做了动力学建模仿真和航行性能的研究。然而,作为对阻力有关键影响的母船线型部分,相关的研究工作较少。一个良好的线型能有效降低阻力,从而提高波浪能滑翔器的航速,进而提升其经济效益。本文对波浪能滑翔器的母船线型做了优化设计,并通过数值仿真对优化结果进行验证。
1 Friendship参数化建模在母船方案设计和方案论证阶段,需要频繁修改船型设计方案或快速生成多种可选设计方案。为确保方案论证过程中能拥有更准确、更详尽的技术数据,需要在方案设计阶段就建立三维的船体几何模型。参数化技术正是通过约束关系,利用主要参数修改来快速进行方案修改的一种设计手段。
1.1 水面母船的初步设计由于波浪能滑翔器航速较低,产生的兴波可以忽略,总阻力主要由摩擦阻力和粘压阻力构成,摩擦阻力主要取决于船体的湿表面积,横剖面形状宜采用V形,这样可减少湿面积,从而减小摩擦阻力,同时它的水下部分较瘦,易于使水流沿纵剖线方向流动,可减少舭部产生的漩涡,对阻力性能有利。
参考相关文献,对水面母船进行初步设计,水面母船的总长取为3.6 m,宽度取为0.82 m,甲板高度取为0.38 m,吃水为0.28 m,排水量大约为450 kg。
1.2 特征参数在母船的全参数化建模中,特征参数决定了船型的纵向特征曲线、横剖面曲线,并最终决定船体外形,直接影响设计的质量。
对于该船,可以将特征参数[6]分成3类,一类是表征船型主要特征的参数,如主尺度、方形系数等;一类是构建纵向特征曲线需要用到的参数,如尾封板位置、设计水线丰满度等;第3类是生成横剖面曲线所需的特征参数,如舭部半径、水线外飘角等。设计人员可以根据已有经验,确定合理的特征参数的值。
1.3 纵向特征曲线纵向特征曲线是沿船长方向生成横剖面曲线以及船体面所需要的光顺曲线,它们对船体曲面的光顺性和流体性能具有重要影响,因此纵向曲线的设计是该船参数化设计的重要环节。也可以将纵向特征曲线分成为纵向位置曲线、纵向积分曲线和纵向微分曲线3类。其中平边线(FOS)、平底线(FOB)、设计水线(DWL)等都属于纵向位置曲线,而对水动力性能影响非常大的横剖面面积曲线(SAC),很显然属于纵向积分曲线,而角度分布就属于纵向微分曲线,图1给出了本文用到的部分纵向特征曲线。

|
图 1 纵向特征曲线 Fig. 1 Longitudinal characteristic curves |
在建立横剖面曲线时,需要借助Friendship的Curve Engine功能。Curve Engine组合了一个定义的“模板”曲线和该曲线的连续分布。该“模板”曲线通过Feature[7]定义,并包含数个生成该曲线所需要的参数,Curve Engine获取该定义并建立与参数的函数分布间的联系。对于任意给定的横坐标,“模板”曲线可以从函数关系得到需要的参数值生成某一曲线。为保证生成面的UV度一致,通常按照从中纵剖面轮廓线到甲板边线的顺序生成横剖面曲线。
1.5 生成船体曲面FRIENDSHIP的Meta Surface功能是基于任意的复杂的曲线描述的参数化曲面,通过Curve Engine功能可以方便的对几何面进行修改变换。由于船体曲面的复杂性,常常需要根据不同的位置,定义不同的曲线模板(即Curve Engine),从而船体曲面通常由几个光顺连接的曲面构成。图2给出了运用Friendship软件生成的船体曲面,它由6个面组成的,但从图中可以发现,该船体曲面非常光顺。

|
图 2 船体曲面 Fig. 2 The ship surface |
在获得参数化模型后,需要对该船进行优化设计。Friendship软件的设计引擎功能可以实现线型的优化计算,它包含嵌入的变量和最优化策略。嵌入的变量包含设计变量和设计参数,通过设置设计变量的范围,采用Friendship软件集成的优化方法,就可以进行单目标或者多目标的优化计算。在该船的优化中,我们主要使用Ensemble Investigation方法确定设计参数的变换范围,用Sobol方法进行以总阻力最小为目标的优化计算。优化的基本流程为:首先对初步线型进行计算,选择总阻力最小为目标,而排水量作为约束条件,根据经验选择设计参数,并确定设计参数的合理范围,采用Sobol方法进行多轮优化计算,最后对结果进行验证分析。
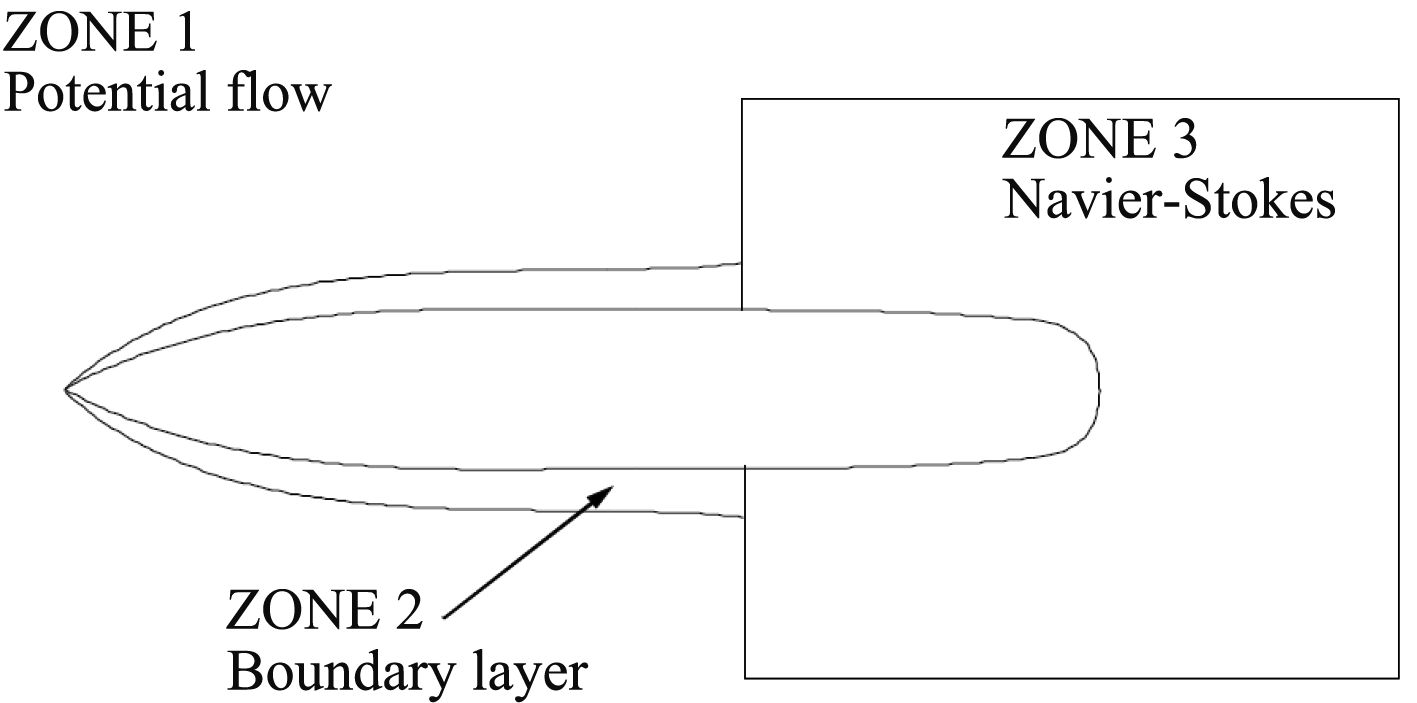
2.2 优化采用的CFD软件Friendship软件可以与Shipflow软件进行自动连接,构成完整的研发平台,实现项目的协同作业。由于该船主要针对粘性阻力进行优化,需要考虑CFD软件的计算效率。Shipflow软件采用自动网格划分和分区计算模式(见图3),具有极高的计算效率,非常适合多方案选优的趋势计算。
|
图 3 船体周围流场划分 Fig. 3 The flow field around the ship |
图4给出了部分设计参数与总阻力间的变化关系。从图中可以看到,在选择的6个参数中,图4(a)、图4(b)、图4(c)和图4(e)参数的改变对总阻力的影响不显著,相关性不强。而图4(d)随着该参数的增大,总阻力逐步减小,在对母船进行设计时,该参数取值应较大些更合适。而对于图4(f)总阻力随该参数增大先减小而后增大,在设计取值时,应选择该参数在中间附近的值。考虑到各个参数间的交互效应,需要对这些重要参数进行多轮优化,从而找到最佳的设计方案。

|
图 4 部分设计参数与总阻力变化关系 Fig. 4 The changing relationship between the total Drag and part of the design parameters |
选取优化得到的最佳方案,通过Star-ccm+进行数值仿真验证。计算域取船前1.5倍船长,船后2.5倍船长。同时,在水面和开尔文波处进行加密,壁面y+值控制在60左右,生成的网格如图5所示,网格量为150万。采用SST k-ω模型,时间步长取0.001 s,对几个设计航速下的总阻力进行非稳态数值仿真。

|
图 5 母船计算域与网格 Fig. 5 The fluid and mesh of the ship |
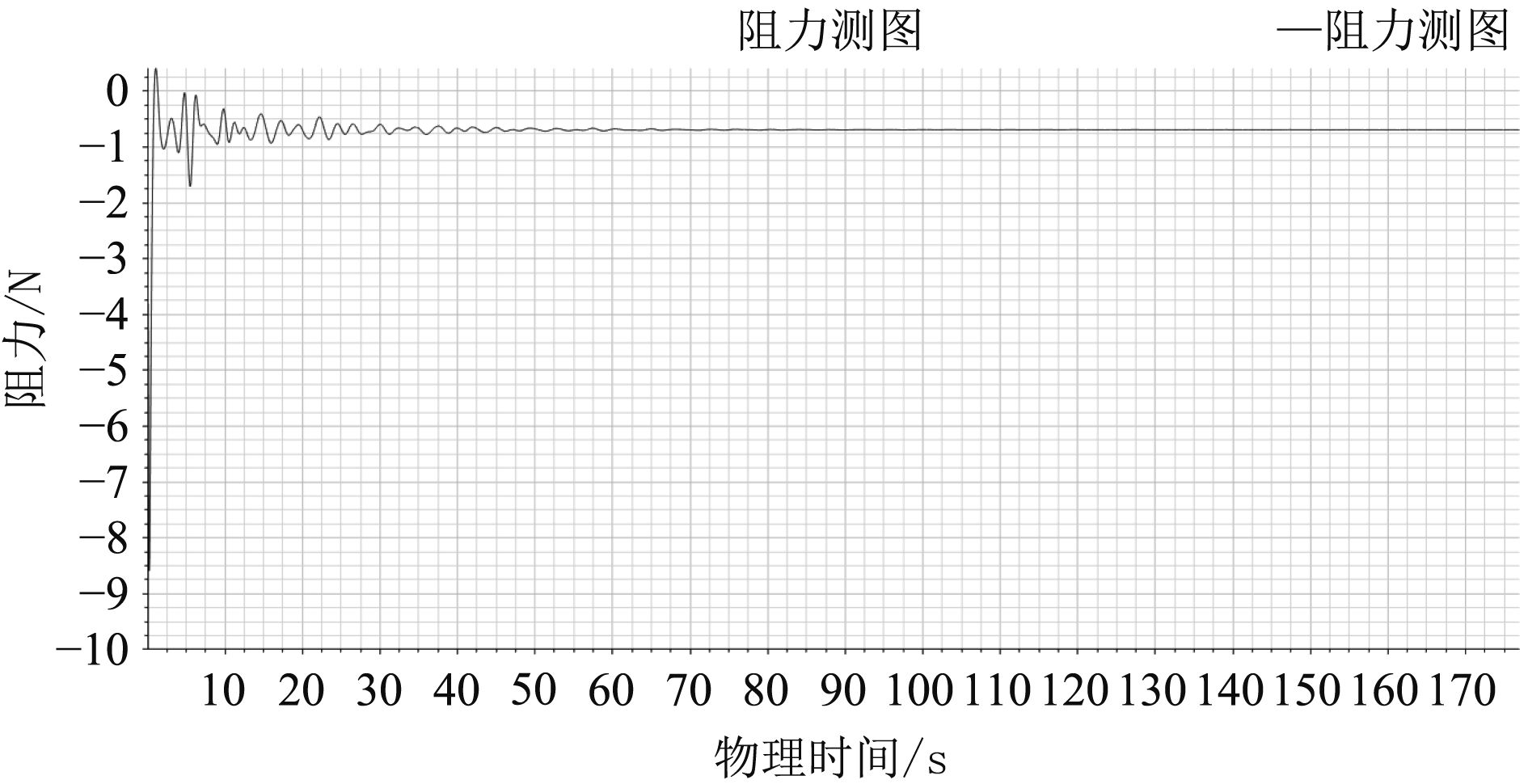
经过计算,得到给定航速下母船总阻力随时间变化的曲线图(见图6)。由图得计算结果在80 s后趋于稳定。取100~150 s内力的平均值作为仿真的结果。
|
图 6 母船总阻力随时间变化曲线图 Fig. 6 The curve of total ship resistance changing with time |
分别计算几组不同航速下的总阻力值,与初始线型的比较结果见表1。
|
|
表 1 母船总阻力优化结果 Tab.1 Results of the optimized total ship resistance |
波浪能滑翔器母船不同于普通船,其前中部还将受到绳缆拉力的影响。因此需要确定合理的重心和绳缆挂点位置来提高母船航行时的稳定性。
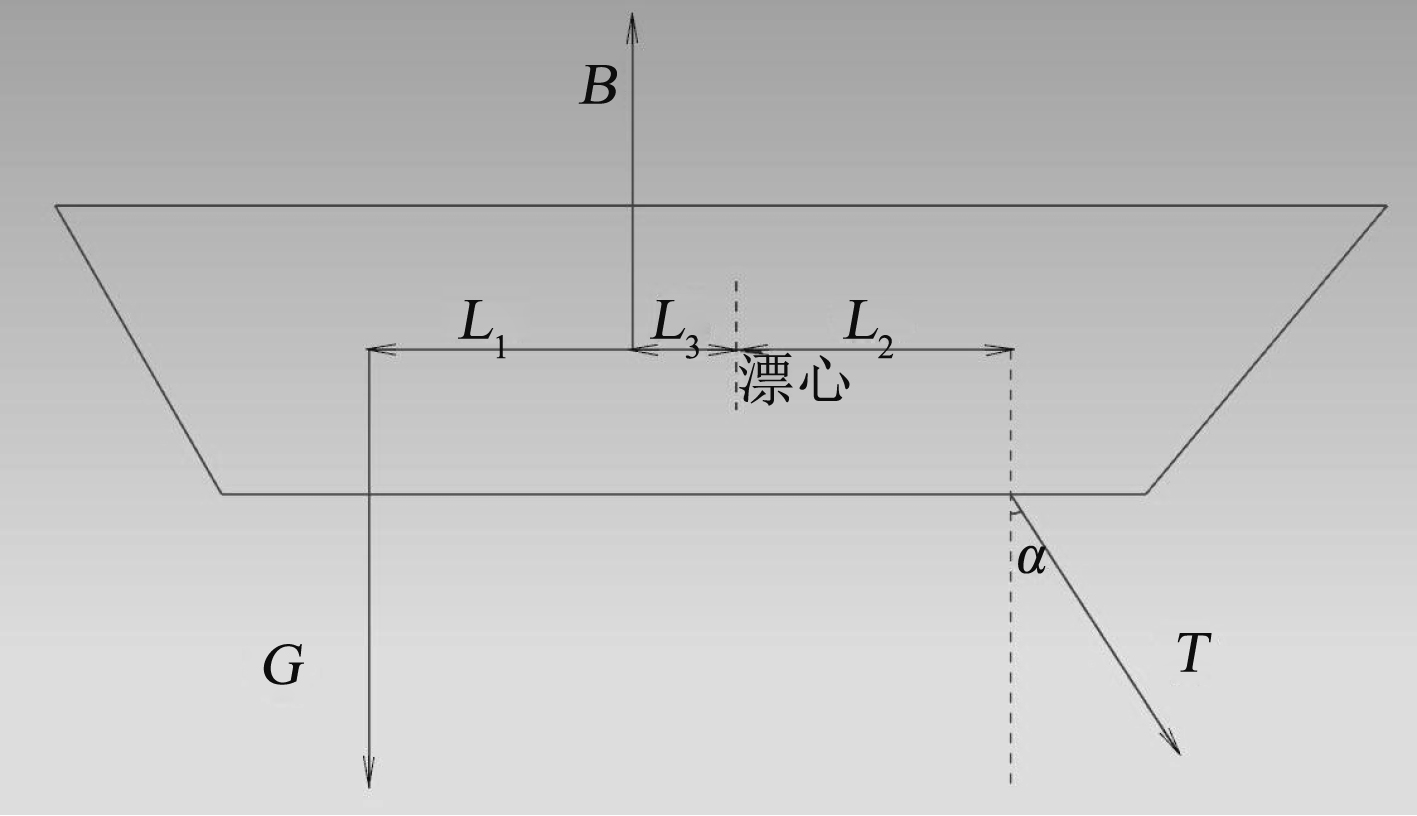
如图7,母船受重力G,浮力B以及拉力T。由于纵倾过程中排水体积变化较小,认为漂心位置保持不变,并以此作为系统参考点。重心纵向位置距漂心L1,挂点纵向位置距漂心L2,正浮浮心纵向位置距漂心L3,拉力与铅垂线的夹角为α。

|
图 7 船体受力示意图 Fig. 7 The hull’s free-body diagram |
则系统对漂心的力矩平衡方程为:
| $G{L_{\rm{1}}} = B{L_{\rm{3}}} + T{\rm{cos}}\alpha {L_2}\text{。}$ | (1) |
同时,为了使船在航行过程中阻力和稳性达到最优,对其提出以下几个要求:
1)绳子松弛时出现尾倾,要求上甲板不没入水中;
2)绳子张紧至最大拉力时发生首倾,要求上甲板不没入水中;
3)绳子的平均拉力满足式(1)。
对于(1)(见图8),若此时船不受拉力,只受重力和浮力,则船在这种状态下保持平衡的条件是重心和浮心在同一铅垂线上,因此可以确定船重心的最小纵向坐标与此时浮心纵向坐标相同为XG1,即可得到L1最大值。
|
图 8 尾倾极限状态 Fig. 8 The limiting condition of aft trim |
对于(2)(见图9),假定此时船在只受重力和浮力的作用下处于平衡状态,此时重心的纵向坐标为XG2,设正浮状态下浮心纵向坐标为Xb0。

|
图 9 首倾极限状态 Fig. 9 The limiting condition of forward trim |
则在正浮状态下船所能承受的最大纵倾力矩M为:
| $M = G({X_G}_{\rm{2}} - {X_{b{\rm{0}}}})\text{,}$ | (2) |
从而系统对漂心的力矩需满足:
| $T\cos \alpha {L_2} + B{L_3} - G{L_1} \leqslant M\text{。}$ | (3) |
同时,假设在最大纵倾力矩下船处于这种首倾的极限状态,则T和L2均达到最大值,当T或L2继续增大船首将没入水中,应当避免。在此条件下L2最大值取为
| $G{L_{\rm{1}}} = B{L_{\rm{3}}} + {T_{\rm{1}}}\cos \alpha {L_2}\text{,}$ | (4) |
再由首倾极限状态下静力平衡得:
| ${B_{\rm{1}}} = G + {T_{\rm{2}}}\cos \alpha\text{,} $ | (5) |
其中:T1,T2为T的两个同向分量;B1为该状态下的浮力。则L1,L2满足关系:
| $G{L_1} = B{L_{\rm{3}}} + (T{\rm{cos}}\alpha - {B_1} + G){L_{\rm{2}}}\text{。}$ | (6) |
根据初步仿真得到的绳子拉力值T和夹角α及当前的L2最大值可以求得L1的最小值。
再由不等式(3),得
| ${L_{\rm{2}}} \leqslant \frac{{M + G{L_{\rm{1}}} - B{L_3}}}{{T\cos \alpha }}\text{。}$ | (7) |
L1取最小值,
再将仿真得到的平均拉力T、平均夹角α及L1的取值区间代入式(1),可求得L2的取值范围,结合不等式(7)得到修正的L2取值区间。最终,以尾封板处为原点,得到重心的纵向坐标范围为1.27~1.65 m,挂点位置的纵向坐标范围为1.90~2.24 m。
5 结 语本文通过应用Friendship的Feature二次开发功能,结合Sobol优化算法,对波浪能滑翔器母船的优化设计做了研究。同时,应用CFD软件Star-ccm+对优化结果进行了验证。最后对影响母船稳性的重心及挂点位置做了初步的分析。结论如下:
1)参数化建模的方法有效且可靠,能极大地缩短母船体的设计周期。
2)优化后总阻力较初始线型减小8%左右,优化结果比较理想。
3)重心位置和挂点位置的初步分析对于后续的设计有很大的参考价值。
本文仅从阻力方面对波浪能滑翔器的母船线型进行了设计,在今后的研究中还将考虑母船的结构强度、舱室布置等问题。同时,优化的结果仅靠数值仿真验证是不够的,还需要进行实验来进一步验证。
| [1] | HINE R, S WILLCOX, G HINE, et al. The wave glider: A wave-powered autonomous marine vehicle[C]// IEEE OCEANS. 2009: 1–6. |
| [2] | MANLEY J, WILLCOX S. The Wave Glider: A new concept for deploying ocean instrumentation[J]. IEEE Instrumentation & Measurement Magazine, 2010 (12): 8–13. |
| [3] |
贾丽娟. 波浪动力滑翔机双体结构工作机理与动力学行为研究[D]. 天津: 国家海洋技术中心, 2014.
JIA Li-juan. Study of operation principle of two-part architecture and dynamic behavior of wave glider[D]. Tianjin: National Marine Technology Center, 2014. |
| [4] |
杜晓旭, 崔航, 向祯晖. 基于Kane方法的波浪驱动水下航行器动力学模型建立[J]. 兵工学报, 2016, 37 (7): 1236–1244.
DU Xiao-xu, CUI Hang, XIANG Zhen-hui. The multi-body system dynamics modeling of wave-driven underwater vehicle based on kane method[J]. Acta Armamentarii, 2016, 37 (7): 1236–1244. |
| [5] |
李小涛. 波浪滑翔器动力学建模及其仿真研究[D]. 北京: 中国舰船研究院, 2014.
LI Xiao-tao. Dynamic model and simulation study based on the wave glider[D]. Beijing: China Ship Research Institute, 2014. |
| [6] | M BRENNER, C ABT, S HARRIES, et al. The Feature modeling technique and simulation design helping speed the design process and the design of green product[J]. Ship Engineering, 2011, 33 (2). |
| [7] |
张萍. 船型参数化设计[D]. 无锡: 江南大学, 2009.
ZHANG Ping. The parametric design to hull form[D]. Wuxi: Jiangnan University, 2009. |
 2018, Vol. 40
2018, Vol. 40
