随着船舶制造和运输行业的持续发展,单一的海洋浮式结构物已无法满足开发生产的实际需求,全世界将面临更多有关于多浮式结构协同作业的问题。相比于单一作业的浮式结构,多浮式结构系统间的强非线性、强耦合以及耦合共振问题极其明显和复杂。如浮式生产储油装置(FPSO)、浮式液化天然气系统(Floating Liquefied Natural Gas System,FLNG)、超大型浮体(Very Large Floating Structures,VLFS)等,这些皆称为海洋浮式结构。当这些海洋浮式结构在海上输运/驳运作业时,运输驳船与其组成了相对复杂的多浮式结构系统。在某些海况下,多浮式结构之间会出现严重影响海上作业安全性和稳定性的强耦合作用情况,如何有效预报和评估海洋浮式结构在海上作业时的水动力性能与结构可靠性,是最近几年船舶与海洋工程领域相关学者关注的热点问题。
旁靠系泊由于窄缝距离小、管路易于布置等优点,有着广泛的应用。但两浮式结构之间狭小的距离使旁靠系统对海况的敏感度很大:每个单一浮式结构对波浪的作用也可能会对其他浮式结构产生影响;某些局部波浪会产生放大或遮掩效应。尤其是窄缝间流场发生流体共振时,流场的强非线性会变得极其明显,这使得预报和评估多浮式结构之间的相对运动、流场分布以及受到的水动力变得相当困难。
目前主要通过理论分析、数值模拟和模型试验3个方面来研究多浮式结构间的流场分布以及水动力耦合问题。本文在入射波浪为线性规则波,浮体近场的波浪运动为完全非线性,暂不考虑结构变形和液舱晃荡影响的前提下,对波浪作用下两固定浮式结构窄缝间流场(旁靠问题)的水动力相互作用开展数值模拟方面的研究,对比探究不同波浪周期(波浪频率)、不同窄缝间距对窄缝间流场的影响,其次对不同模型参数的模拟结果进行对比探究。最终通过对比分析不同工况下窄缝间流场的波面升高,对两固定浮式结构窄缝间流场的水动力共振现象作出初步预测。
1 数值模拟基本理论 1.1 流体运动基本方程假设流体为粘性且不可压缩,同时满足质量守恒的连续方程和动量守恒的运动方程。
1)连续方程(质量守恒方程)
Euler型连续性方程的微分表达式如下:
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho v} \right) = 0\text{,}$ | (1) |
如流动定常,则
| $\nabla \cdot \left( {\rho v} \right) = 0\text{,}$ | (2) |
若流体不可压缩,则
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0{\text{。}}$ | (3) |
2)动量守恒方程(N-S方程)
动量守恒方程是所有流体运动都必须满足的方程。最早由Navier于1827年提出,当时只考虑流体不可压缩。而后进过多年的不断发展,在1831年Possion提出了可压流体的运动方程。随后在1843年和1845年,Saint-Venant和Stokes分别提出将粘性系数看作常数的运动方程。
| $\frac{{Dv}}{{Dt}} = f - \frac{1}{\rho }\nabla p + \nu {\nabla ^2}v + \frac{\upsilon }{3}\nabla \left( {\nabla \cdot v} \right)\text{,}$ | (4) |
对不可压流体,由于
| $\frac{{Dv}}{{Dt}} = f - \frac{1}{\rho }\nabla p + v{\nabla ^2}v\text{。}$ | (5) |
在FINE/Marine软件计算过程中引入湍流模型(如k-ε模型,k-w模型等)即可求解粘性流体的湍流流动相关问题。
1.2 数值离散方法对于实际工程问题,计算之前需要对计算区域进行离散,离散方法分为有限元法、有限差分法以及有限体积法。有限体积法,作为CFD领域使用最为广泛的离散方法之一,可视作有限元法和有限差分法的中间产物。
对于动量方程和湍流方程的离散方法,FINE/Marine软件中的离散格式有:GDS、UPWIND、HYBRID、CENTERED、AVLSMART和BLENDED等。对于动量方程和湍流方程,本文在FINE/Marine里运用基于有限体积法的AVLSMART离散格式对计算区域进行离散处理海洋平台运动问题。在FINE/Marine中有压力、速度分量、速度通量、矫正量、湍流频率、湍动能以及气水质量的欠松弛因子可用于求解器加速收敛的参数。
1.3 自由液面捕捉法在船舶与海洋工程的计算流体力学(CFD)技术发展过程中,对自由液面计算的研究一直是个难题。
早期的自由液面数值计算,主要采用势流理论方法,但无法准确地预报尾部流动,随后在基于RANS方法求解时采用欧拉模型中的MAC法和VOF法,VOF方法是通过流体占据网格单元体积比例以追踪自由液面的方法。较于MAC方法,VOF法具有计算时间短、存储量小、边界条件易处理、便于编制计算程序等优点。
VOF方法的基本原理如下:
假设第q种流体在单元中体积分数是αq,因此存在3种可能:
1)αq=0表示在单元中第q种流体的含量为0;
2)αq=1表示在单元中充满了第q种流体;
3)0<αq<1表示在单元中存在着不同流体交界面。
流体之间的交界面可以利用体积分数的连续性方程来确定,对第q种流体有:
| $\frac{{\partial {\alpha _q}}}{{\partial t}} + {u_i}\frac{{\partial {\alpha _q}}}{{\partial {x_i}}} = 0\text{,}$ | (6) |
各种流体的体积分数满足以下公式:
| $\sum\nolimits_{q = 1}^n {{\alpha _q}} = 1\text{,}$ | (7) |
自由表面处αq满足连续方程:
| $\frac{{\partial {\alpha _q}}}{{\partial t}} + \frac{{\partial \left( {u{\alpha _q}} \right)}}{{\partial x}} + \frac{{\partial \left( {v{\alpha _q}} \right)}}{{\partial y}} + \frac{{\partial \left( {w{\alpha _q}} \right)}}{{\partial z}} = 0,\;q = 1,\;2\text{。}$ | (8) |
式中:u为x方向速度分量;w为z方向速度分量。
需要注意的是,在每个单元中物理量都由单元中的所有分相的体积加权平均值决定,例如单元中流体的密度表示为:
| $\rho = \sum\limits_{i = 1}^2 {{\alpha _q}{\rho _q}} \text{,}$ | (9) |
其他流体特性(如粘性等)也可用类似方法计算得到。
VOF法追踪自由液面虽然取得了一定的进步,但是仍无法满足实际工程的需求,并不能很好地处理像波浪破碎这样复杂地自由液面变化特征,从而无法准确预报船舶与海洋结构物在风浪流中的运动特性和水动力特性。针对这些问题,在本次研究中对于波浪自由液面的处理方法,Fine/Marine软件采用基于全六面体非结构化网格技术求解粘性雷诺数平均方程的自由液面捕捉法。采用该自由液面捕捉法将空气和水作为单一流体同时计算,该单一流体的特性(密度ρ,粘性系数υ)在空间的变化取决于构成函数c。
通过求解以下运动方程来确定构成函数c:
| $\frac{\partial }{{\partial t}}\int\nolimits_V {c{\rm d}V} + \int\nolimits_S {c({\mathit{\boldsymbol{U}}} - {\mathit{\boldsymbol{U}}_d}) \cdot {\mathit{\boldsymbol{n}}}{\rm d}S} = 0\text{。}$ | (10) |
式中:V为控制体;S为围成控制体的面积;U为速度;Ud为S上n方向的速度。
与其他文献普遍采用的自由液面跟踪法相比,该自由液面捕捉法具有更好的灵活性与适应性,可较好地处理破碎波等复杂的自由液面。本文的自由液面捕捉采用BRICS离散格式,可压缩型离散格式BRICS可以减小自由液面附近构成函数的数值扩散,可以有效地减小自由液面模拟的数值耗散误差。
1.4 波浪理论水波问题的基本方程和边界条件如下:
| ${\nabla ^2}\varphi (x,y,z,t) = 0\text{,}\; {{\rm{Laplace}}\;{\text{方程}},{\text{基本方程}}} \text{,}$ | (11) |
| $\frac{{\partial \varphi }}{{\partial z}} = 0\text{,}\; {z = - d,\;{\text{底面条件}},\;{\text{底面是水深为}} d {\text{的水平面}}} \text{,}$ | (12) |
| $\begin{split}&\frac{{\partial \varphi }}{{\partial z}} = \frac{{\partial \eta }}{{\partial t}} + \frac{{\partial \eta }}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} + \frac{{\partial \eta }}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}}\text{,}\;\\ & {z = \eta ,\;{\text{自由面}}\left( {z = \eta (x,y,t)} \right){\text{运动学条件}}} \text{,}\end{split}$ | (13) |
| $\eta = - \frac{1}{g}[\frac{{\partial \varphi }}{{\partial t}} + \frac{1}{2}(\nabla \varphi \cdot \nabla \varphi )]\text{,}\; {z = \eta ,\;{\text{自由面动力学条件}}} ;$ | (14) |
| $\frac{{\partial \varphi b}}{{\partial n}} = 0\text{,}\; {{\text{物面条件}},\;n{\text{为固壁法向量}}} {\text{。}}$ | (15) |
其中,
研究选用2个相同的DTMB5415模型作为两固定浮式结构的几何模型。该船模为国际船模水动力数值计算会议的标模,模型的主要参数如表1所示。
|
|
表 1 浮式结构模型(DTMB5415船模)的主要参数 Tab.1 Main parameters of the floating structure model(DTMB5415 ship model) |
本次对比分析采用控制变量法,通过改变波浪参数以及数值模型之间距离的大小,对比探究不同参数对窄缝间流场的影响,并对窄缝间流场的水动力共振问题进行规律探索。
模型间距为0.06 m时,共3种工况:波浪周期分别为0.506 s,0.716 s以及1.012 s,对应的波长分别为0.4 m,0.8 m以及1.6 m;间距为0.12 m时,共4种工况:波浪周期分别为0.566 s,0.8 s,1.132 s以及1.389 s,对应波长分别为0.5 m,1 m,2 m以及3 m;间距为0.24 m时,共3种工况:波浪周期分别为0.62 s,0.877 s以及1.24 s,对应波长分别为0.6 m,1.2 m以及2.4 m。
2.2 模型间距为0.06 m,3种波浪周期下窄缝间流场的波面升高窄缝间距(0.06 m)、波高(0.02 m)以及水深(1.5 m)相同,选取波长为0.4 m,0.8 m以及1.6 m三种工况,分别对应波浪周期0.506 s,0.716 s以及1.012 s,对比分析各自窄缝间流场。选取典型时刻,以上3种工况对应的波面升高如图1~图3所示。

|
图 1 波浪周期为0.506 s,T=3.9 s~T=4.3 s内窄缝间流场的波面升高变化示意图 Fig. 1 A diagram of wave elevation changes in the flow field between 0.506 s and T=3.9 s T=4.3 s in the wave period |

|
图 2 波浪周期为0.716 s,T=6.3 s~T=6.7 s内窄缝间流场的波面升高变化示意图 Fig. 2 A diagram of wave elevation changes in the flow field between 0.716s and T=6.3 s T=6.7 s in the wave period |

|
图 3 波浪周期为1.012 s,T=4.0 s~T=4.4 s内窄缝间流场的波面升高变化示意图 Fig. 3 A diagram of wave elevation changes in the flow field between 1.012 s and T=4.0 s T=4.4 s in the wave period |
分析以上波面升高图,可以得出以下结论:
1)在波浪周期为0.506 s的工况下,当入射波波峰(波谷)传播到窄缝入口约1/10~1/9船长处时,波幅增大。当波浪在窄缝间继续传播至约1/6~1/5船长处时,波峰(波谷)的峰(谷)点高度达到极大值约为波幅的1.5~2.5倍。随后,窄缝内的波浪幅值持续减小直至波面平稳。由于波幅的减小幅度较为缓慢,加上选取的波长较短,窄缝间流场出现多个峰值点(见图1)。
2)在波浪周期为0.716 s的工况下,当入射波波峰传播到窄缝入口处时,窄缝内流场的波面升高十分明显。当波峰传播到模型首部约1/5~1/4船长处时,窄缝内流场的波面升高出现极大值(见图2):窄缝内波面升高的峰值点高度约为同一波峰其余流场(窄缝外流场)波面高度的1.5~2.5倍。随着波浪的继续传播,窄缝内波面升高的峰值以相对较缓的幅度持续减小:当入射波峰传播到船舯处时,窄缝内的波面升高值约为波浪幅值的0.5~1.5倍(见图2)。随后,该波峰处的窄缝内流场波面趋于平稳。
3)在波浪周期为1.012 s的工况下,入射波峰在窄缝入口处同样也存在着波面升高,但波面升高的峰值出现于船首部约1/10~1/8船长处。相比于波浪周期为0.716 s的工况,接下来窄缝内波浪幅值的减小更加迅速:波峰传播到船中附近时,窄缝间流场波面已趋于平稳。
2.3 模型间距为0.12 m,4种波浪周期下窄缝间流场的波面升高窄缝间距(0.12 m)、波高(0.02 m)以及水深(1.5 m)相同,选取波长为0.25倍、0.5倍、1倍以及1.5倍船长(LPP=2 m)4种工况,分别对应波浪周期0.566 s,0.8 s,1.132 s以及1.389 s,对比分析各自窄缝间流场。选取典型时刻,以上4种工况对应的波面升高如图4~图7所示。

|
图 4 波浪周期为0.566 s,T=4.9 s~T=5.2 s内窄缝间流场的波面升高变化示意图 Fig. 4 A diagram of wave elevation changes in the flow field between 0.566 s and T=4.9 s T=5.2 s in the wave period |

|
图 5 波浪周期为0.8 s,T=4.6 s~T=5.0 s内窄缝间流场的波面升高变化示意图 Fig. 5 A diagram of wave elevation changes in the flow field between 0.8 s and T=4.6 s T=5.0 s in the wave period |

|
图 6 波浪周期为1.132 s,T=6.0 s~T=6.3 s内窄缝间流场的波面升高变化示意图 Fig. 6 A diagram of wave elevation changes in the flow field between 1.132 s and T=6.0 s T=6.3 s in the wave period |

|
图 7 波浪周期为1.389 s,T=3.6 s~T=3.9 s内窄缝间流场的波面升高变化示意图 Fig. 7 A diagram of wave elevation changes in the flow field between 1.389 s and T=3.6 s T=3.9 s in the wave period |
分析以上波面升高图,可以得出以下结论:
1)在波浪周期为0.566 s(波长为0.25倍船长)的工况下,当入射波波峰(波谷)传播到窄缝入口约1/10~1/9船长处时,波幅增大。当波浪在窄缝间继续传播至约1/6船长处时,波峰(波谷)的峰(谷)点高度约为波幅的1.5~2.5倍。随后,窄缝内的波浪幅值持续减小直至波面平稳。由于波幅的持续减小较为缓慢,加上波长较短,窄缝间流场出现多个峰值点(见图4)。
2)在波浪周期为0.8 s(波长为0.5倍船长)的工况下,当入射波波峰传播到窄缝入口处时,窄缝内流场的波面升高十分明显。当波峰传播到模型首部约1/4~1/3船长处时,窄缝内流场的波面升高出现极大值(见图5):窄缝内波面升高的峰值点高度约为同一波峰其余流场(窄缝外流场)波面高度的1.5~3倍。随着波浪的继续传播,窄缝内波面升高的峰值以相对较缓的幅度持续减小:当入射波峰传播到船中处时,窄缝内的波面升高值约为波浪幅值的0.5~1.5倍(见图5)。随后,该波峰处的窄缝内流场波面趋于平稳。
3)在波浪周期为1.132 s以及1.389 s的工况下,入射波峰在窄缝入口处同样也存在着波面升高,但波面升高的峰值出现于船首部约1/10~1/8船长处。相比于波浪周期为0.8 s的工况,接下来窄缝内波浪幅值的减小更加迅速:当波峰传播到船中附近时,窄缝间流场波面已趋于平稳。
2.4 模型间距为0.24 m,3种波浪周期下窄缝间流场的波面升高窄缝间距(0.24 m)、波高(0.02 m)以及水深(1.5 m)相同,选取波长为0.6 m,1.2 m以及2.4 m三种工况,分别对应波浪周期0.62 s,0.877 s以及1.24 s,对比分析各自窄缝间流场。选取典型时刻,以上3种工况对应的波面升高如图8~图10所示。

|
图 8 波浪周期为0.62 s,T=8.6 s~T=9.0 s内窄缝间流场的波面升高变化示意图 Fig. 8 A diagram of wave elevation changes in the flow field between 0.62 s and T=8.6 s T=9.0 s in the wave period |

|
图 9 波浪周期为0.877 s,T=7.3 s~T=7.7 s内窄缝间流场的波面升高变化示意图 Fig. 9 A diagram of wave elevation changes in the flow field between 0.877 s and T=7.3 s T=7.7 s in the wave period |

|
图 10 波浪周期为1.24 s,T=7.3 s~T=7.7 s内窄缝间流场的波面升高变化示意图 Fig. 10 A diagram of wave elevation changes in the flow field between 1.24 s and T=7.3 s T=7.7 s in the wave period |
分析以上波面升高图,可以得出以下结论:
1)在波浪周期为0.62 s的工况下,当入射波波峰进行到窄缝入口约1/9~1/8船长处时,波幅增大。当波浪在窄缝间继续进行至约1/6~1/5船长处时,波峰的峰值点高度达到极大值,约为波幅的1~2倍。随后,窄缝内的波浪幅值持续减小直至波面平稳。由于波幅的减小幅度较为缓慢,加上选取的波长较短,窄缝间流场出现多个峰值点(见图8,T=9.0 s时刻的流场波面升高示意图)。
2)在波浪周期为0.877 s的工况下,当入射波波峰传播到窄缝入口处时,窄缝内流场的波面升高十分明显。当波峰传播到模型艏部约1/4~1/3船长处时,窄缝间流场的波面升高出现极大值(见图9):窄缝内波面升高的峰值点高度约为同一波峰其余流场(窄缝外流场)波面高度的1.5~2.5倍。随着波浪的继续传播,窄缝内波面升高的峰值以相对较缓的幅度持续减小:当入射波峰传播到船中处时,窄缝内的波面升高值约为波浪幅值的0.5~1.5倍(见图9)。随后,该波峰处的窄缝内流场波面趋于平稳。
3)在波浪周期为1.24 s的工况下,入射波峰在窄缝入口处同样也存在着波面升高,但波面升高的峰值出现于船艏部约1/10~1/9船长处。相比于波浪周期为0.877 s的工况,接下来窄缝内波浪幅值的减小更加迅速:当波峰传播到模型中后部时,窄缝间流场波面已趋于平稳。
2.5 小结通过对以上3种模型间距及其典型波浪周期的波面升高结果进行分析比较,本次研究得到如下规律以及可能的解释:
1)在波浪周期较大即波浪较长时,入射波浪无法进入两固定浮式结构间的窄缝,波浪直接绕过两浮式结构继续传播,窄缝内流场受遮蔽效应而幅值很小,波浪升高的峰值点出现在船体迎浪处的前端。
2)随着波浪周期与入射波波长的减小,一部分波浪从模型首部的间隔处进入窄缝间的狭长间隔,并在模型两侧的不断反射与叠加作用以及船底水体的流动作用下,到达共振周期,窄缝间流场出现了十分显著的波浪放大。
3)而当入射波周期进一步减小时,窄缝间流场的内部作用更为复杂,加上入射波长较短,导致了多个峰值点的出现。
2.6 窄缝间流场水动力共振问题的规律探索根据之前的数值计算结果,现通过对比分析对两固定浮式结构窄缝间流场的水动力共振现象进行预测。研究主要通过观察由于间隙共振引起的波面升高,分析波浪周期、窄缝间距等参数与水动力共振现象的内在联系。
通过观察窄缝间流场的波浪放大现象,选取不同窄缝间距、不同波浪周期的多种工况进行多次数值模拟近似预测出对应于特定窄缝间距的共振周期。相应共振周期时两固定浮式结构周围的波面升高如图11~图13所示,图11(b)~图13(b)显示的是对应图11(a)~图13(a)中黑线位置处的波高历程图。

|
图 11 窄缝间距为0.06 m,波浪周期为0.716 s(近似达到共振周期),T=6.7 s时刻的流场波面升高示意图 Fig. 11 The spacing between the slit holes is 0.06 m, the wave period is 0.716 s (approximately to achieve the resonance period), and the elevation of the wave field at T=6.7 s time is shown. |
|
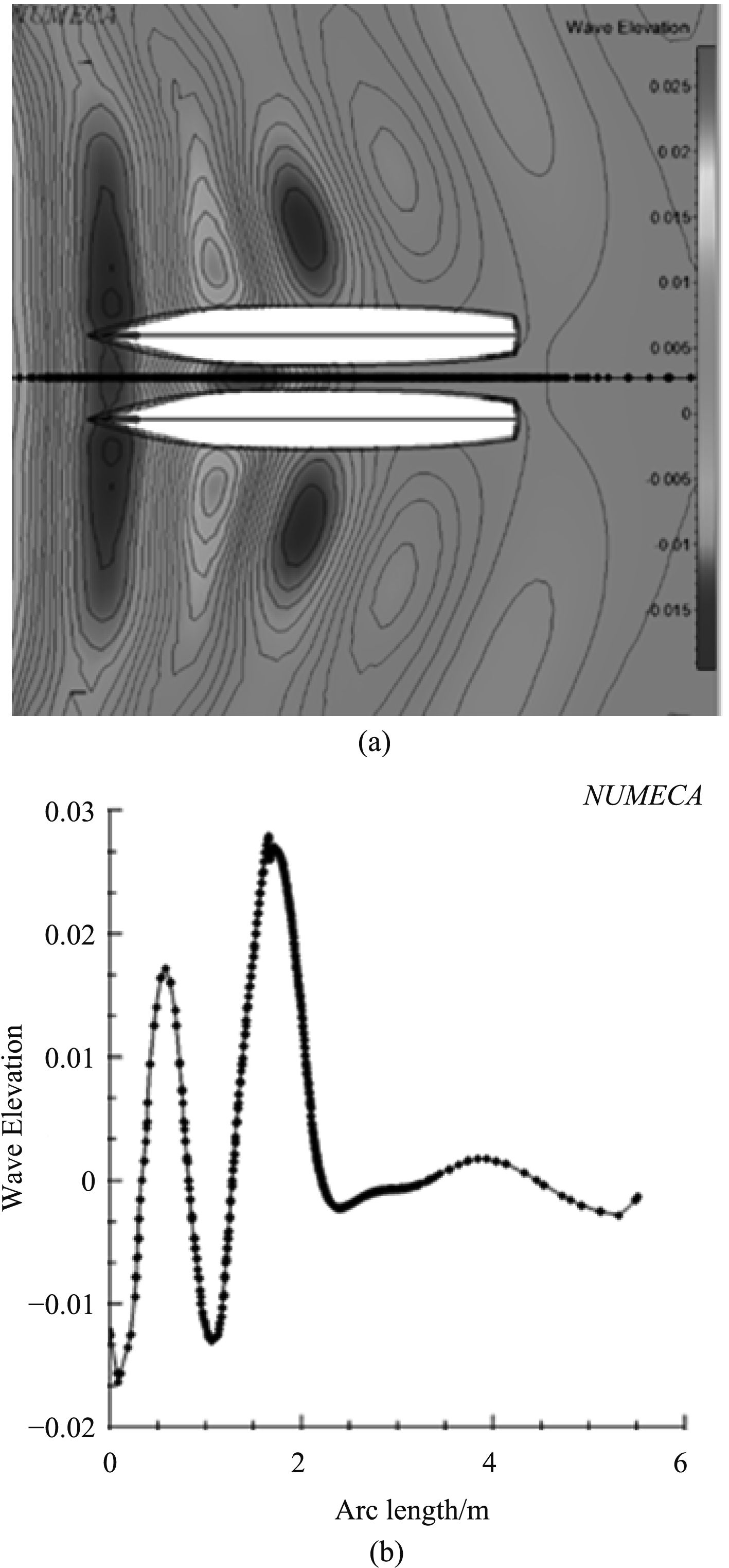
图 12 窄缝间距为0.12 m,波浪周期为0.8 s(近似达到共振周期),T=4.8 s时刻的流场波面升高示意图 Fig. 12 The spacing of the narrow gap is 0.12 M, the wave period is 0.8 s (approximate to the resonance period), and the wave surface elevation of the flow field in the T=4.8 s moment is shown. |
|
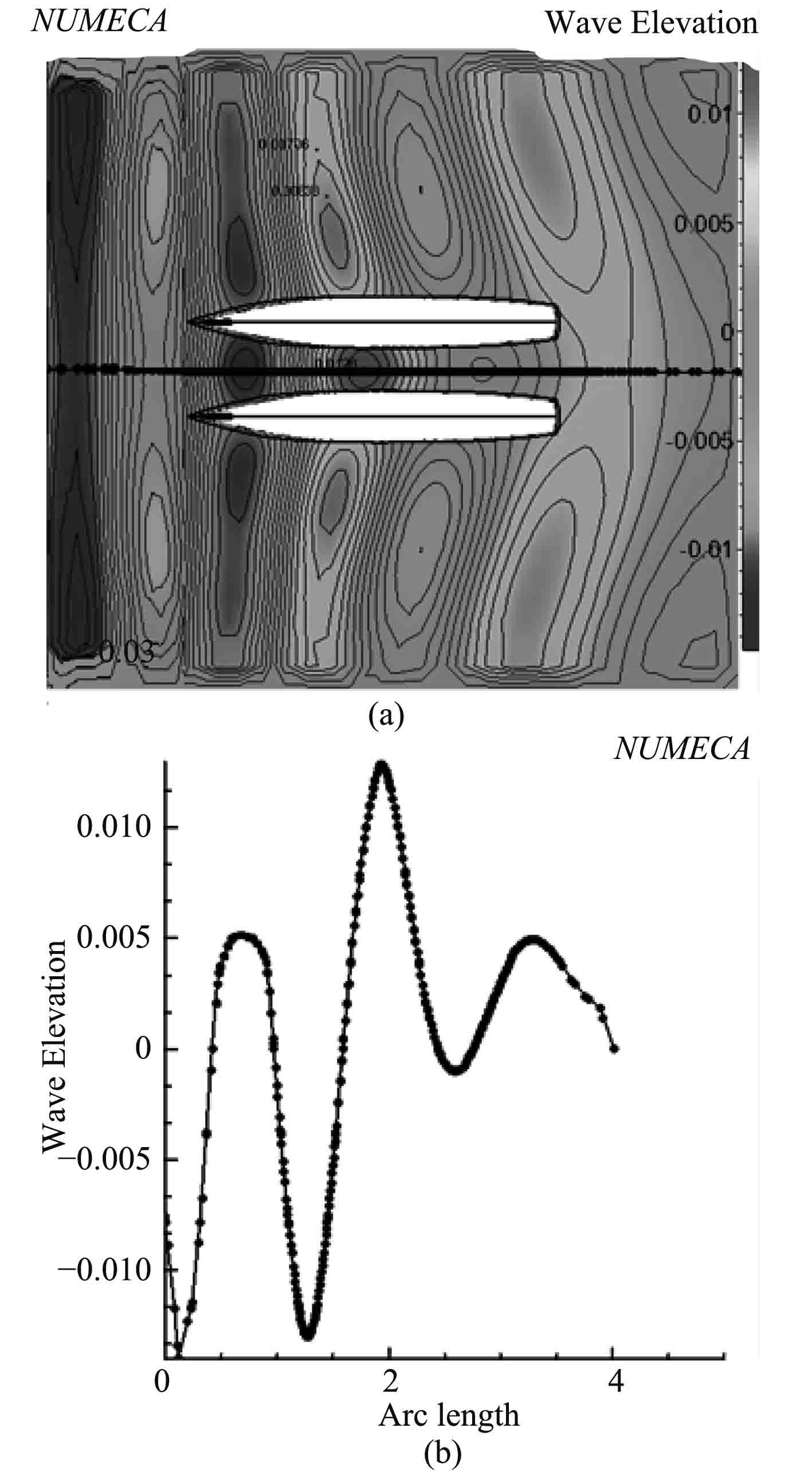
图 13 窄缝间距为0.24 m,波浪周期为0.877 s(近似达到共振周期),T=7.7 s时刻的流场波面升高示意图 Fig. 13 The spacing of the narrow gap is 0.12 M, the wave period is 0.8 s (approximate to the resonance period), and the wave surface elevation of the flow field in the T=4.8 s moment is shown. |
分析以上波面升高图,可以得出以下结论:
1)当两固定浮式结构在规则波的迎浪作用下到达共振周期时,窄缝间流场出现了十分显著的波浪放大现象,窄缝间流场有且只有一个波面升高的峰值点,其最大高度约为同一波峰其余流场(窄缝外流场)波面高度的1.5~3倍。
2)当两浮式结构间距增加时,窄缝间流场的水动力共振周期显著增大:间距为0.06 m时,共振周期在0.716 s附近;间距为0.12 m时,共振周期在0.8 s附近;间距为0.24 m时,共振周期在0.877 s附近。
3 不同浮体形状对窄缝间流场的影响 3.1 计算模型和计算工况选择窄缝间距0.24 m,入射波长1 m(0.5倍船长),入射波高0.036 m,在改变浮式结构外形尺寸的条件下进行多组数值模拟,并将计算结果与上一节的计算模拟结果进行对比分析。
对应上一节选取的垂线间长LPP为2 m的DTMB5415标准船模,现选取相同主尺度(2 m×0.28 m×0.14 m)建立方形驳船的几何模型。驳船模型的几何外形如图14所示。
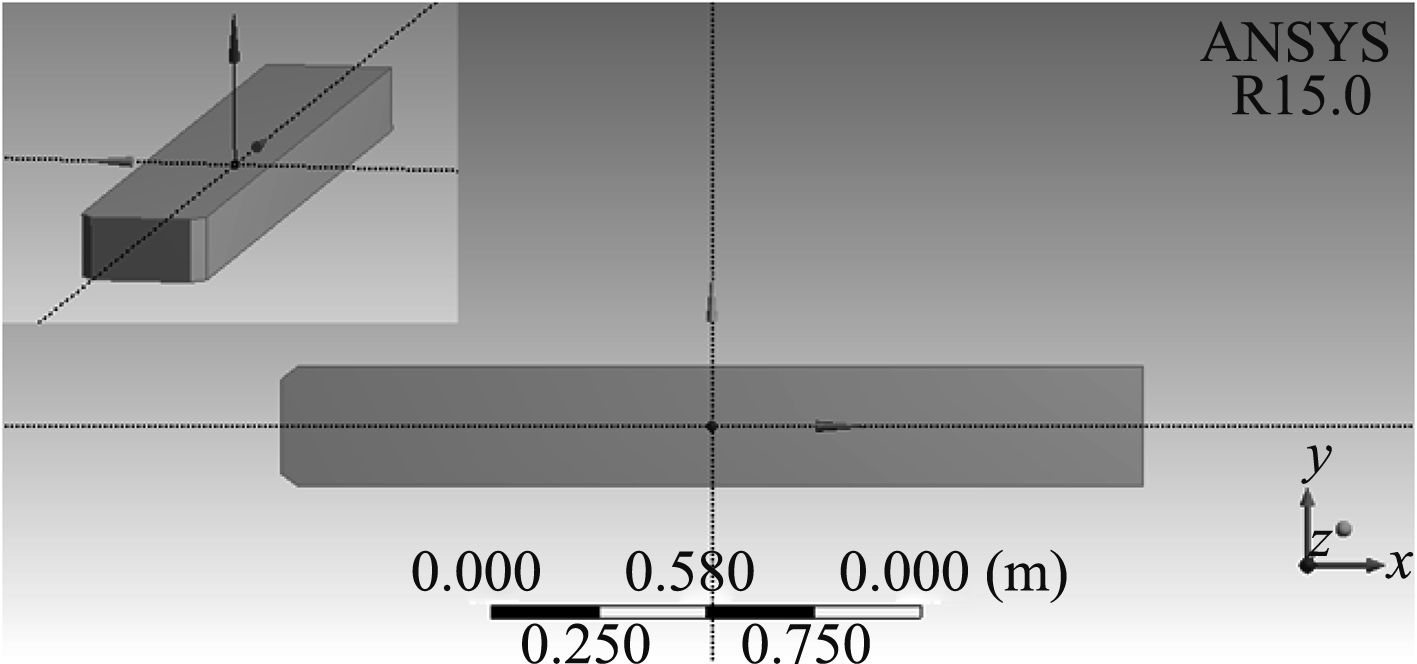
|
图 14 方形驳船外形图 Fig. 14 Shape of a square barge |
在T=7.0 s附近选取几个典型时刻,浮式结构周围及其窄缝间流场的波面升高如图15~图16所示。

|
图 15 T=6.6 s(左)、T=6.8 s(右)时刻的流场波面升高示意图 Fig. 15 A diagram of flow elevation of flow field at T=6.6 s (left) and T=6.8 s (right) time |

|
图 16 T=7.0 s(左)、T=7.2 s(右)时刻的流场波面升高示意图 Fig. 16 A diagram of flow elevation of flow field at T=7.0 s (left) and T=7.2 s (right) time |
选取典型时刻T=6.8 s以及T=7.0 s,浮式结构周围及其窄缝间流场的速度分布如图17~图18所示。

|
图 17 T=6.8 s时刻的流场速度矢量图 Fig. 17 Velocity vector diagram of flow field at T=6.8 s time |
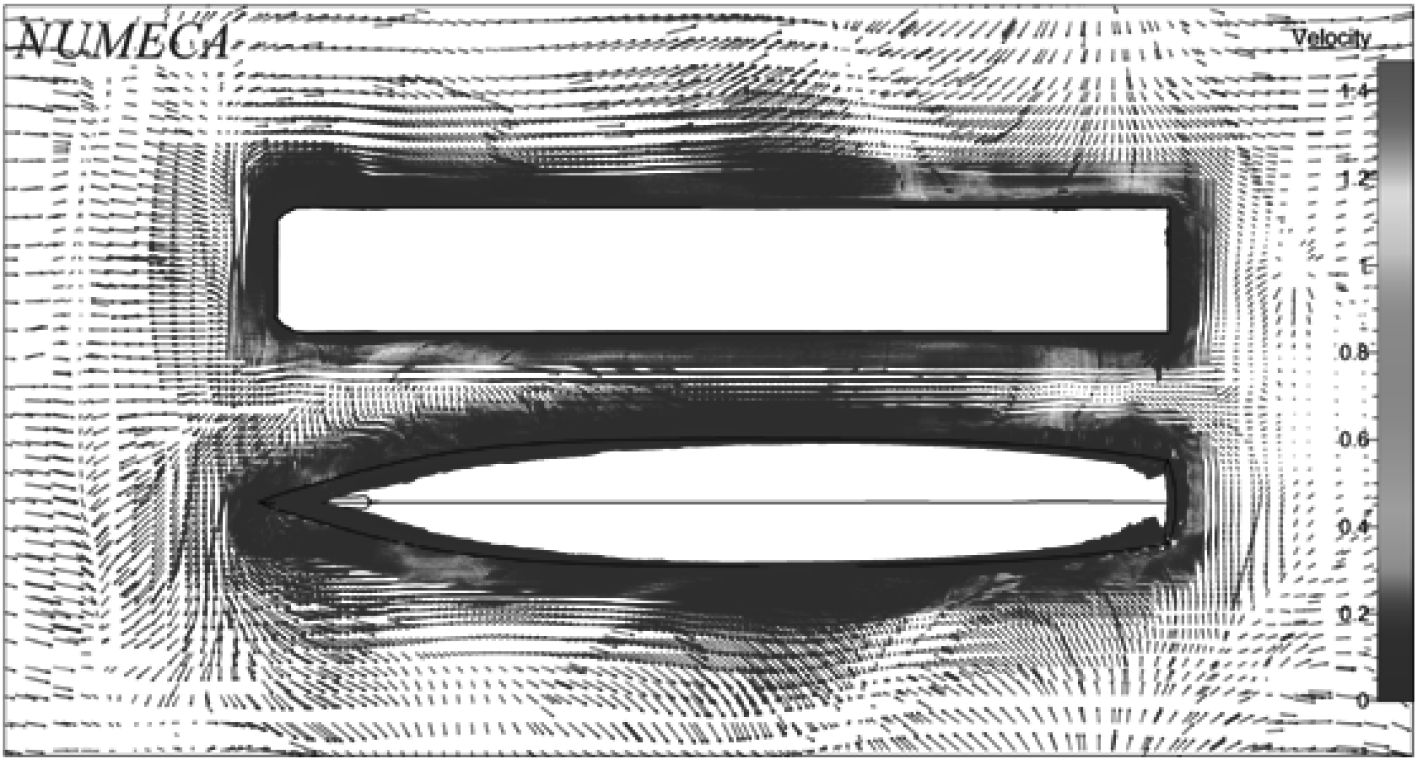
|
图 18 T=7.0 s时刻的流场速度矢量图 Fig. 18 velocity vector diagram of flow field at T=7.0 s time |
对比之前选取的典型时刻波面升高图,同样选取T=6.8 s、T=7.0 s两个典型时刻,作用于DTMB5415标准船模内表面(与窄缝内流体相接触一侧表面)的水动压力如图19~图20所示。

|
图 19 T=6.8 s时刻浮式结构内表面的水动压力云图 Fig. 19 Hydrodynamic pressure cloud on the inner surface of a floating structure at T=6.8 s time |

|
图 20 T=7.0 s时刻浮式结构内表面的水动压力云图 Fig. 20 Hydrodynamic pressure cloud on the inner surface of a floating structure at T=7.0 s time |
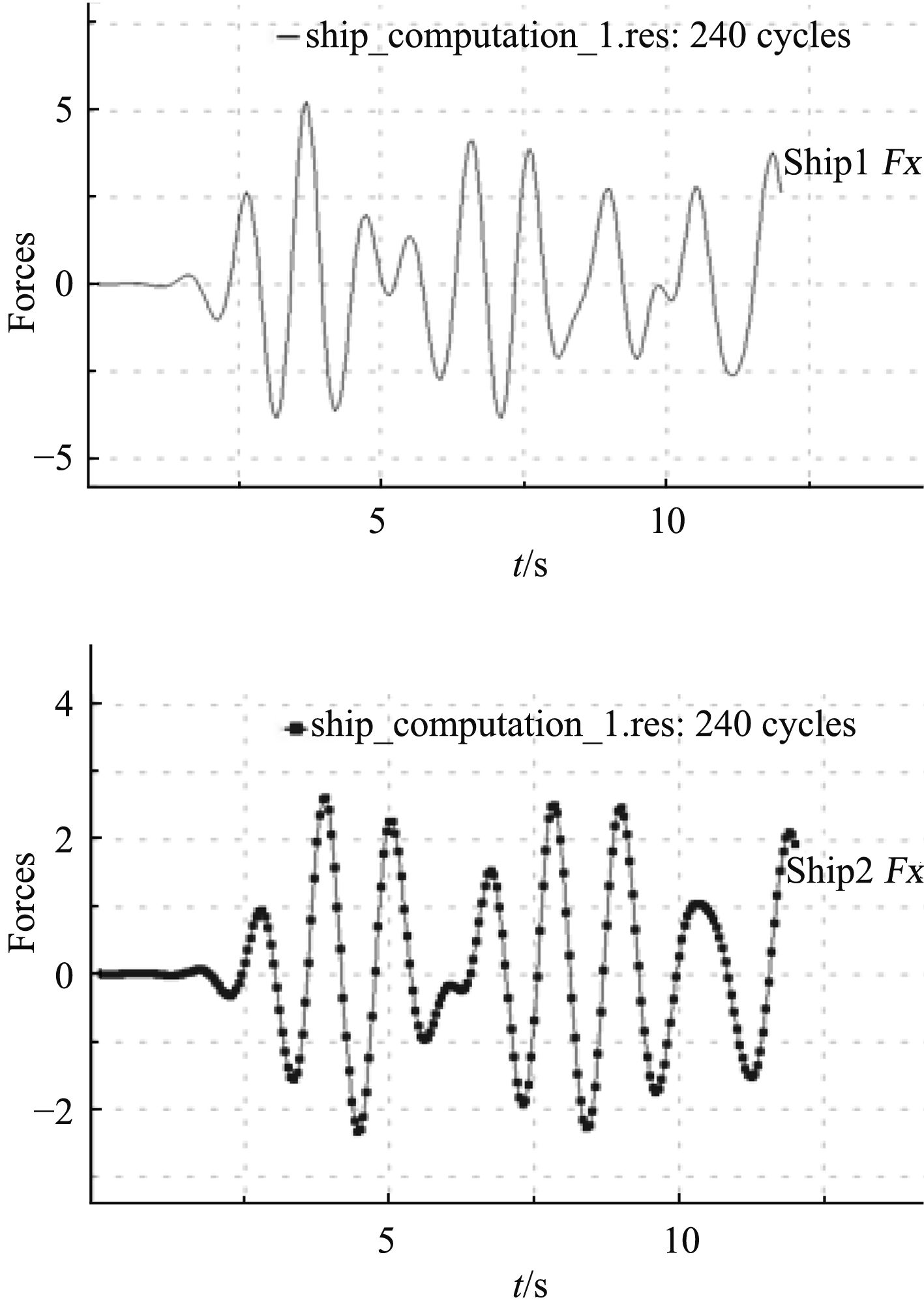
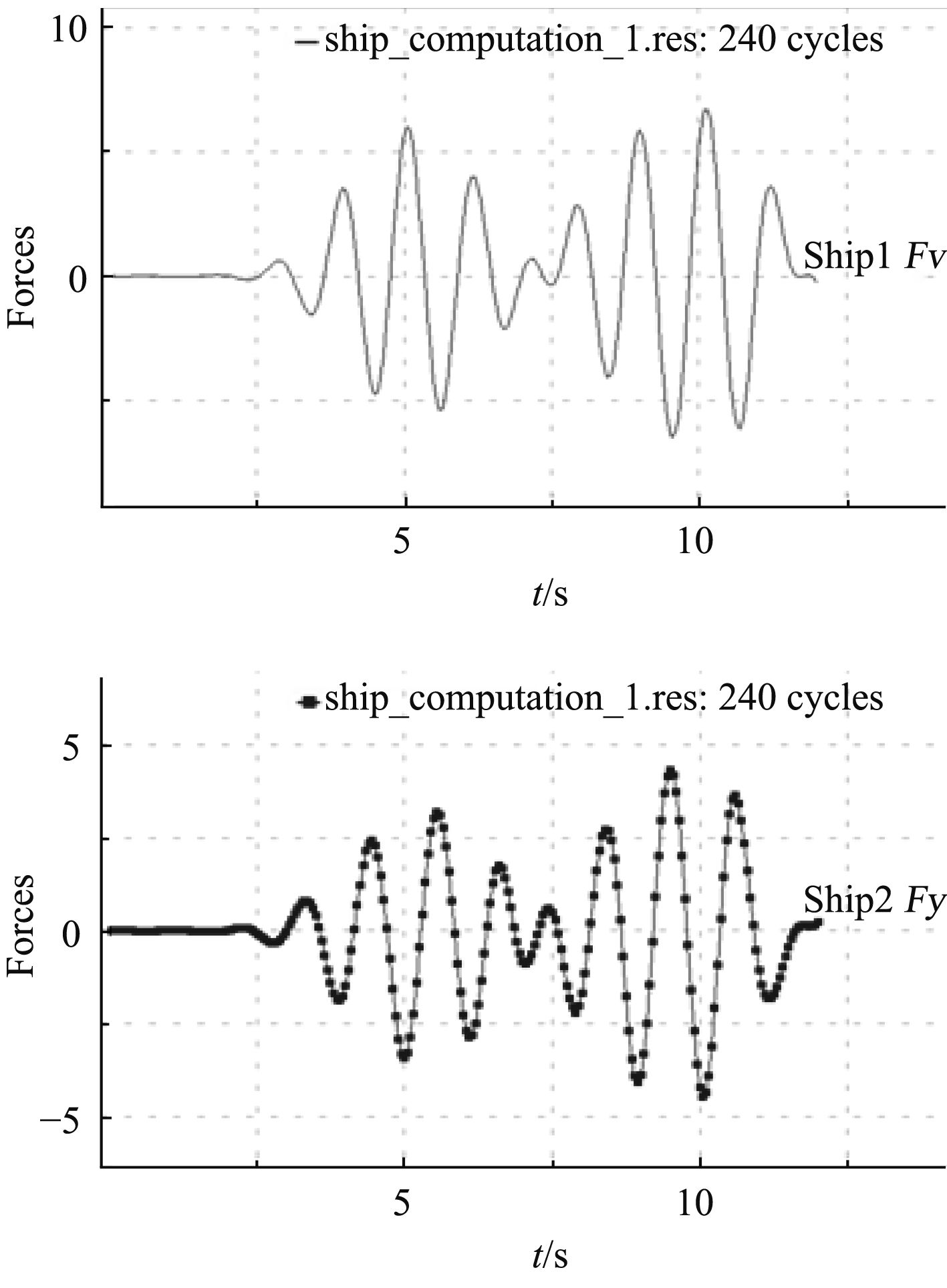
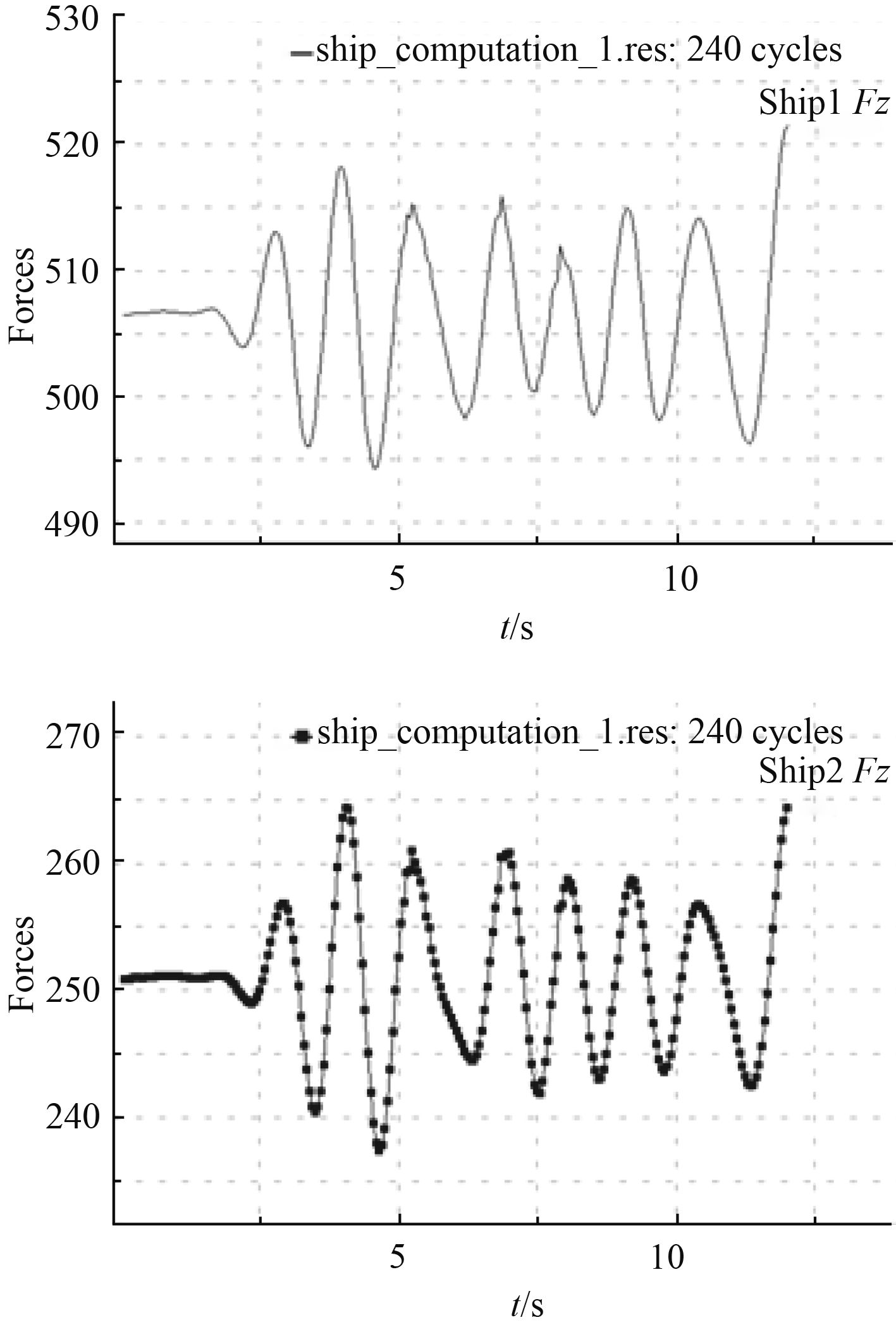
两固定浮式结构(DTMB5415标模Ship1、方形驳船模Ship2)受到的纵向、横向以及垂向波浪力的时历曲线如图21~图23所示。其中,垂向波浪力包括浮力。
|
图 21 纵向力的时历曲线 Fig. 21 The time history curve of the longitudinal force |
|
图 22 横向力的时历曲线 Fig. 22 The time history curve of transverse force |
|
图 23 垂向力(包括浮力)的时历曲线 Fig. 23 The time history curve of the vertical force (including buoyancy) |
分析以上波面升高图、流场速度矢量图、水动压力云图以及波浪力的时历曲线,可以得出如下结论:
1)在两浮式结构窄缝间的流场内,相比靠近DTMB5415模型一侧的流场,靠近方形驳船一侧的流场波面升高更加明显。由此可以推测:相对于拥有优良型线的船体,拥有规则几何外形的浮式结构更加易于引发流场的波面升高。
2)在窄缝间流场的波面升高处,作用于两固定浮式结构内表面的水动压力明显增大。由此可以推测:如果本次研究没有约束两浮式结构的横向自由度,窄缝间流场的波面升高会引发浮式结构强烈的运动响应。
3)以上波浪力的时历曲线呈现出更多的非线性。引发这种现象的可能原因:计算模型的非对称性会引发窄缝间流场强烈的水动力耦合作用。
3.3 方形驳船模/方形驳船模窄缝间流场的数值模拟结果 3.3.1 流场的波面升高在T=7.2 s附近选取几个典型时刻,浮式结构周围及其窄缝间流场的波面升高如图24所示。

|
图 24 T=7.1 s~T=7.3 s内窄缝间流场的波面升高变化示意图 Fig. 24 Diagram of wave elevation change in the flow field between narrow slots in T=7.1 s T=7.3 s |
选取典型时刻T=7.2 s,浮式结构周围及其窄缝间流场的速度分布如图25所示。

|
图 25 T=7.2 s时刻的流场速度矢量图 Fig. 25 Velocity vector diagram of flow field at T=7.2 s time |
对比之前选取的典型时刻波面升高图,同样选取典型时刻T=7.3 s,作用于方形驳船模型内表面(与窄缝内流体相接触一侧表面)的水动压力如图26所示。

|
图 26 T=7.3 s时刻浮式结构内表面的水动压力云图 Fig. 26 Hydrodynamic pressure cloud on the inner surface of a floating structure at T=7.3 s time |
分析以上波面升高图、流场速度矢量图以及水动压力云图,可以得出如下结论:
1)对于2个几何外形规则且相同的方形浮式结构,规则波作用下其窄缝间流场的波面升高十分明显,且流场的波面升高可以在窄缝内稳定传播,不发生波浪破碎。
2)两浮式结构周围及其窄缝间流体的速度矢量分布均匀,几乎不存在有旋运动以及速度的局部放大。
3)窄缝间流场对浮式结构的水动压力与波面的升高/降低相对应:波面升高,浮式结构在对应位置附近受到的水动压力增大;波面降低,浮式结构在对应位置附近受到的水动压力减小。另外,水动压力随水深的增加而减小。
4 结 语本文首先阐述了该研究课题的背景及意义,基于粘性流体力学理论以及计算流体力学(CFD)理论,利用较为成熟的计算流体力学软件FINE/Marine,对两固定浮式结构窄缝间的流场问题进行了数值模拟计算,通过观察窄缝间流场的波面升高,对比探究不同波浪周期(波浪频率)、不同窄缝间距对窄缝间流场的影响,同时还对不同波浪入射方向、不同模型参数的模拟结果进行了分析及对比探究。最后得到与参考文献相一致的结论:当入射规则波达到共振周期时,窄缝间流场会出现显著的波浪升高现象;随着窄缝间距的增大,窄缝间流场的共振周期也随之增大。
综上所述,利用本文所采用的研究分析方法,可以对两固定浮式结构窄缝间的流场问题进行有效模拟与分析,为后续多浮式结构窄缝间流场的分析研究奠定基础。
| [1] |
谢楠, 郜焕秋. 波浪中两个浮体水动力相互作用的数值计算[J]. 船舶力学, 1999, 3 (2): 7–15.
XIE Nan, GAO Huan-qiu. Numerical calculation of hydrodynamic interaction of two floating wave[J]. in Ship Mechanics, 1999, 3 (2): 7–15. |
| [2] | TEIGEN P. Numerical aspects of multiple body hydrodynamics[C]// Proceedings of the 10th International Offshore and Polar Engineering Conference, Seattle, 2000: 165–173. |
| [3] | C Xu-jun, C Wei-cheng, S Qing. New method for predicting the motion responses of a flexible joint multi-body floating system to irregular waves[J]. China Ocean Engineering, 2001, 15 (4): 491–498. |
| [4] |
朱仁传, 朱海荣, 缪国平. 具有小间隙的多浮体系统水动力共振现象[J]. 上海交通大学学报, 2008, 42 (8): 1238–1242.
ZHU Ren-chuan, ZHU Hai-rong, MIAO Guo-ping. With the small gap between multi body floating system hydrodynamic resonance[J]. Journal of Shanghai Jiao Tong University, 2008, 42 (8): 1238–1242. |
| [5] | 沈庆, 陈徐均, 江召兵. 浮体和浮式多体系统流固耦合动力分析[M]. 北京: 科学出版社, 2011. |
| [6] |
徐亮瑜, 杨建民, 李欣. 基于黏性流体的小间距多浮体水动力干扰研究[J]. 第十六届中国海洋(岸)工程学术讨论会论文集(上册), 2013.
XU Liang-yu, YANG Jian-min, LI Xin. The small spacing of viscous fluid floating multi-body hydrodynamic interference study of [J]. Sixteenth Chinese (bank) based on Marine Engineering Symposium (1), 2013 |
| [7] | 徐亮瑜. 多浮体水动力干扰研究[D]. 上海: 上海交通大学, 2014. |
| [8] | 郭飞. 波浪作用下多浮体系统的动力响应特性研究[D]. 上海: 上海交通大学, 2014. |
| [9] |
赵文华, 杨建民, 等. FLNG系统进行旁靠卸载作业时的水动力性能研究[J]. 船舶力学, 2012, 16 (11): 1248–1256.
Zhao Wen-hua, Yang Jian-min, et al. Study on hydrodynamic performance of FLNG system for side loading unloading[J]. Journal of Naval Mechanics, 2012, 16 (11): 1248–1256. |
 2018, Vol. 40
2018, Vol. 40
