2. 武汉理工大学 船舶动力系统运用技术交通行业重点实验室,湖北 武汉 430063
2. Key Laboratory of Marine Power Engineering and Technology, Ministry of Communications, Wuhan 430063, China
噪声源的定位是机械设备振动噪声控制工作中的关键部分,基于波束形成的噪声源定位技术属于非接触、中远距离阵列测量定位方法,可在不影响设备正常运行的情况下进行声源定位[1]。但当声源频率接近阵列上限截止频率时,波束形成技术不仅在真实声源位置输出具有一定宽度的“主瓣”,而且在非实际声源位置处会输出“旁瓣”,严重的旁瓣效应会引入虚假声源干扰[2–4]。
波叠加法最初应用于结构声辐射的计算[5],随着波叠加理论的不断改进和完善[6–9],其应用范围也得到扩展,结合波束形成和声全息等技术,波叠加法已在噪声源定位领域得到应用[10]。本文结合波叠加法的特点,提出了基于声压匹配波叠加法对波束形成的改进算法,以消除波束形成的旁瓣效应,排除虚假声源的干扰。通过仿真与消音室内的已知声源试验,验证了改进算法的有效性。
1 波束形成噪声源定位波束形成技术可使在真实声源位置处输出较大,而其他位置输出幅值较小,通过各个点处输出幅值的对比达到声源定位的目的。

|
图 1 波束形成示意图 Fig. 1 Diagram of beamforming |
由图1所示波束形成示意图可推导出,对于同一声信号,第m号阵元相对于参考阵元的时间延迟或提前可以表示为:
| ${\tau _m}(\mathit{\boldsymbol{s}}) = \frac{{\left| \mathit{\boldsymbol{s}} \right| - \left| {\mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{s}}_m}} \right|}}{{{c_{\rm{0}}}}},{\rm{ }}m = 1,{\rm{ }}2,{\rm{ }} \ldots ,{\rm{ }}M\text{。}$ | (1) |
式中:s为扫描点的位置向量;sm为第m号传声器阵元的位置向量;c0为声速。基于
| $B(\mathit{\boldsymbol{s}},t) = \frac{1}{M}\sum\limits_{m = 1}^M {{w_m}{p_m}(t - {\tau _m})} ,{\rm{ }}m = 1,{\rm{ }}2,{\rm{ }} \ldots ,{\rm{ }}M\text{,}$ | (2) |
式中:M为传声器阵列阵元数目;wm为m号传声器信号相位对齐后的加权系数,均取加权系数为1;pm(t)为第m号传声器时域声压。
通常在机械设备噪声源定位识别中,是分别对不同频率下噪声源进行定位识别,因此对式(2)进行FFT变换后可得频域波束形成为:
| $B(s,\omega ) = \frac{1}{M}\sum\limits_{m = 1}^M {{p_m}(\omega )} {w_m}{{\rm{e}}^{ - {\rm{i}}\omega {\tau _m}({\bf{r}})}},{\rm{ }}m = 1,{\rm{ }}2,{\rm{ }} \ldots ,{\rm{ }}M\text{。}$ | (3) |
式中:
改进算法是基于声压匹配波叠加法提出,通过计算每个峰值处等效源的强度,来判断此波峰是否为旁瓣,具体思路是:
1)用波束形成技术对噪声源的位置进行预估,预估结果中每一个波峰均表示该处可能存在噪声源,这些波峰位置则被作为等效源的布置位置。
2)提取波束形成定位结果中波峰坐标放置等效源,在已知等效源和传声器阵列阵元坐标的前提下,由声压匹配波叠加法和已知的传声器阵列声压反算出等效源强度。
3)以计算出的等效源相对强度替代波束形成输出结果中的波峰幅值,对声源强度进行表示,进而对主次声源进行判断,以消除波束形成输出结果中的旁瓣效应的干扰。
根据波叠加法基本思想,声场中任意一点处的声压均可由各等效源强度与格林函数计算得到:
| $p\left( r \right) = \sum\limits_{m = 1}^M {{{i}}\rho \omega q\left( {{r_m}} \right)} G\left( R \right)\text{。}$ | (4) |
式中:
| $G\left( R \right) = \frac{{\exp ( - {\rm{i}}kR)}}{{4{\rm{\pi }}R}}\text{。}$ | (5) |
式中:R为rm与r距离;R=|rm-m|;k为波数;
| ${{P = {\mathit{\boldsymbol{T}}}Q}}\text{,}$ | (6) |
式中:P为场点声压向量;Q为波叠加等效源强度向量;T为P与Q传递函数矩阵:
| ${\mathit{\boldsymbol{T}}} = \left[ {\begin{array}{*{20}{c}}{{\rm{i}}\rho \omega {G_{11}}\left( R \right)}&{{\rm{i}}\rho \omega {G_{12}}\left( R \right)}& \cdots &{{\rm{i}}\rho \omega {G_{1M}}\left( R \right)}\\{{\rm{i}}\rho \omega {G_{21}}\left( R \right)}&{{\rm{i}}\rho \omega {G_{22}}\left( R \right)}&{}& \vdots \\ \vdots &{}& \ddots & \vdots \\{{\rm{i}}\rho \omega {G_{N1}}\left( R \right)}& \cdots & \cdots &{{\rm{i}}\rho \omega {G_{NM}}\left( R \right)}\end{array}} \right]\text{。}\!\!\!\!\!\!\!\!\!\!$ | (7) |
式中:GNM(R)为第N个场点与第M个等效源间格林函数;R为第N个场点与第M个等效源间空间距离;当等效源个数及位置确定后,T可通过格林函数计算得到,之后通过测量获取场点声压P,由式(6)反算出等效源源强Q,再由所得源强再经式(6)计算出出重建面声压,进而对噪声源定位。
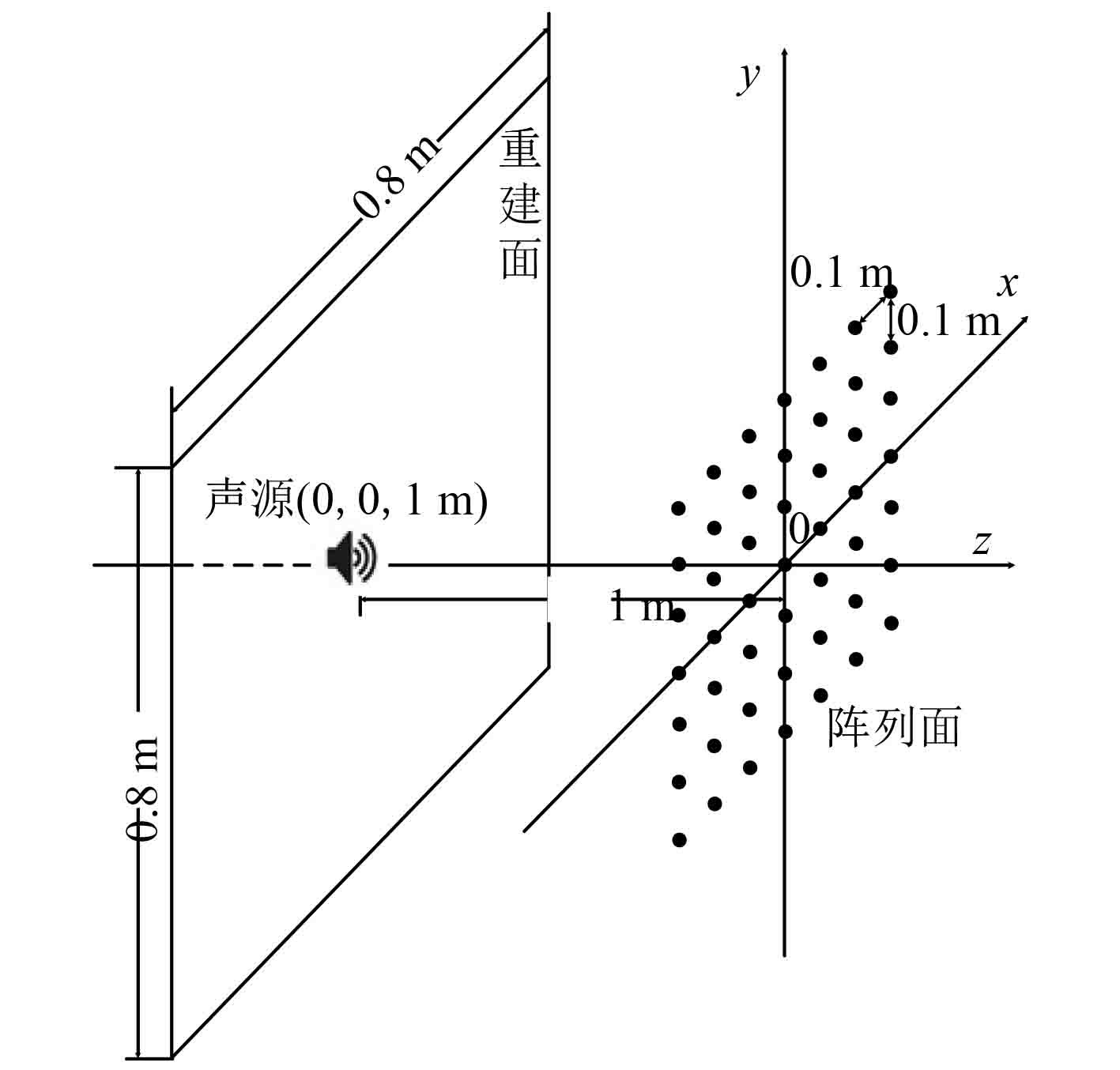
3 仿真试验验证在空间点(0,0,1 m)处布置点声源S1,源强为1 Pa,频率为6 000 Hz。设靠近声源前方的Z=0.95 m平面为波束形成重建面,将重建面离散为101×101个扫描点,扫描范围为x坐标方向–0.8~0.8 m,y坐标方向–0.8~0.8 m。阵列为7×7等间距矩形网格阵列,阵元间距0.1 m。
|
图 2 声源、阵列面和重建面几何示意图 Fig. 2 Diagram of noise source, micro-phone array and re-construction plane |
由于波束形成输出结果为声压,而改进后输出结果为等效源强度,量纲不同,因此改进前后计算出的声压或等效源强度均以相对值表示。仿真结果如表1与图3所示。
|
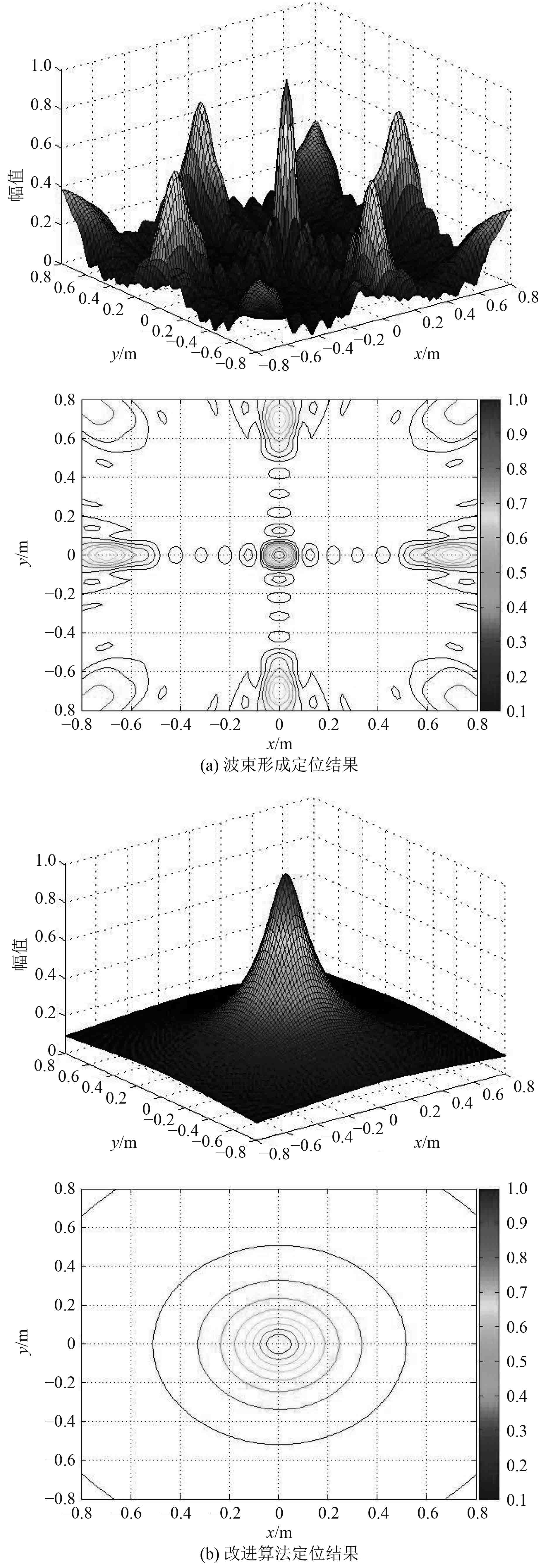
图 3 波束形成与改进算法定位结果对比 Fig. 3 Comparison of beamforming and improve algorithm |
|
|
表 1 波束形成与改进算法定位结果对比 Tab.1 Comparison of beamforming and improve algorithm |
由表1及图3(a)可知,波峰1的峰值最大,对应(0,0 m)处真实声源,这表明波束形成算法可以准确定位出真实声源,但在2~5号波峰处存在旁瓣比为68.2%的严重旁瓣效应干扰,甚至在6~9号波峰处的旁瓣比也达到24.5%,旁瓣关于实际声源位置对称出现,这是由于算法本身特点产生,并非仿真中所加噪声干扰。因此,需要对波束形成的旁瓣效应进行改进。
改进后,计算出的各个波峰处等效源强度相对值如表1中“改进算法”一列所示,真实声源对应的1号波峰处源强最大,可据此判断1号等效源表示真实声源,而2~9号虚假声源处对应的等效源强度较小,最大干扰项6号等效源的强度相对值仅为4.92%,仿真结果验证了改进算法的有效性。
基于波叠加法对波束形成进行改进后,只在(0,0 m)处存在一个明显波峰,有效地消除了波束形成算法的严重旁瓣效应,使定位图像清晰明辨。实际上,由于在旁瓣处布置有等效源,在图3(b)中这些位置处仍存在各自对应的等效源产生的声压幅值,只是由于这些等效源强度相对(0,0 m)处等效源强度较小,其产生的声压幅值被淹没,总之,基于波叠加法对波束形成改进后,其识别结果中的旁瓣效应被有效地抑制。
4 试验验证在半消音室中进行了改进算法进一步的验证试验。以扬声器作为已知单点声源,将该扬声器置于空间坐标(0,0,1 m)处,重建面为Z=0.95 m平面上的0.8 m×0.8 m区域,阵列位于Z=0 m平面,阵列中心为空间坐标系原点。扬声器发出信号频率为3 000 Hz的单频声压信号。
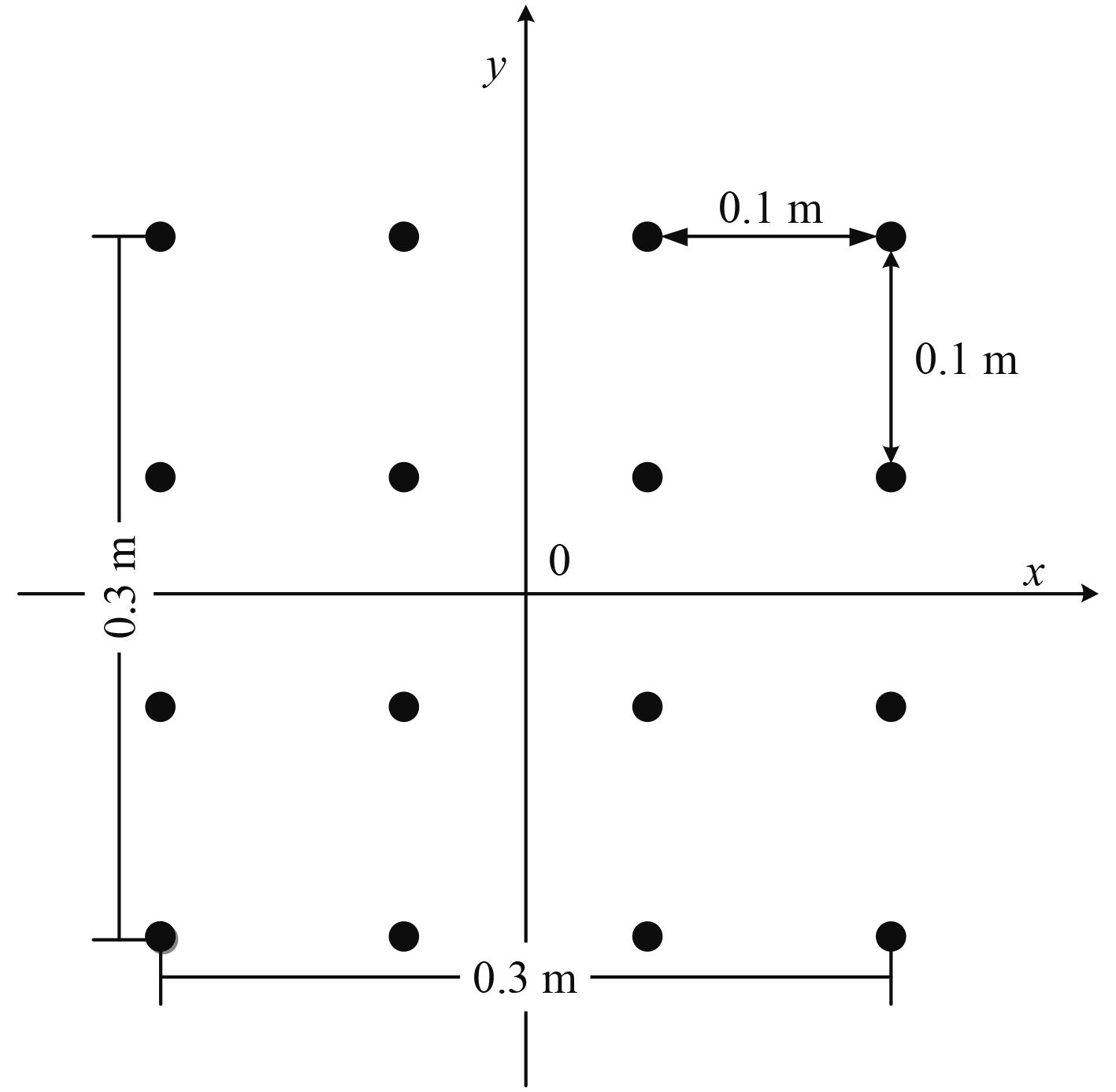
设计传声器阵列型式为4×4的16阵元等间距平面网格阵列,阵元间距0.1 m,阵列孔径0.3 m×0.3 m,如图4所示。
|
图 4 “0.3 m×0.3 m”孔径等间距网格阵列示意图 Fig. 4 Diagram of 0.3 m×0.3 m equal distance grid micro-phone array |
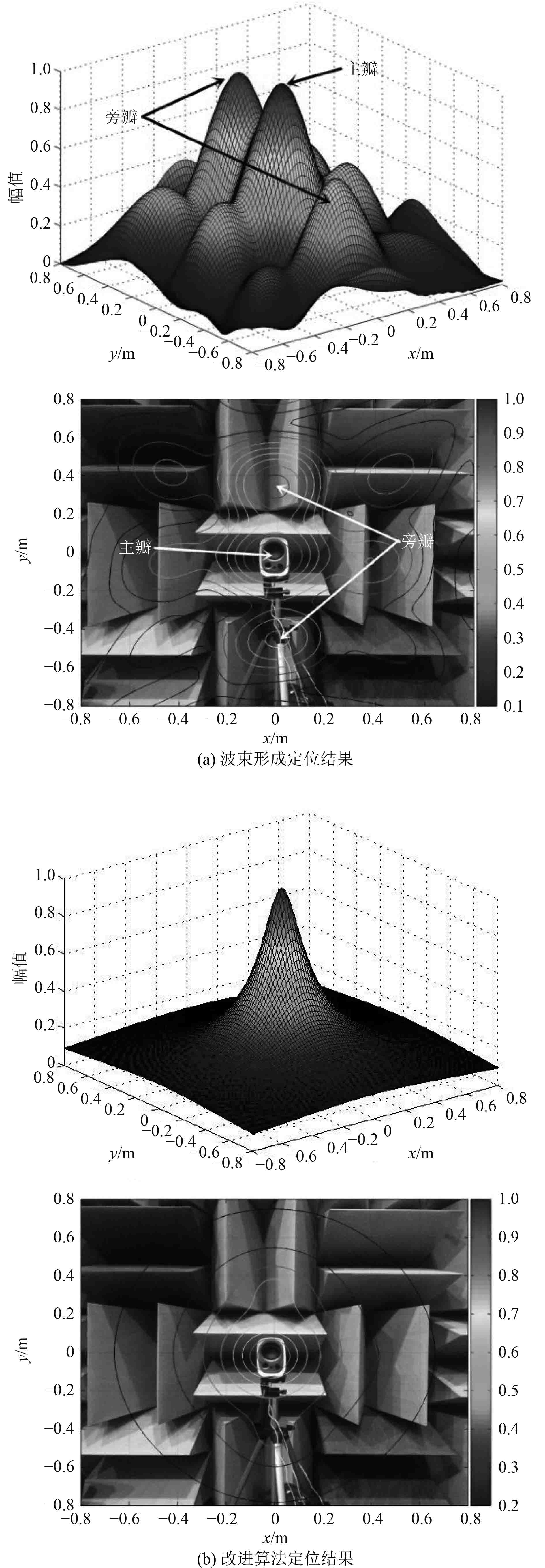
使用波束形成及改进算法对扬声器进行定位,结果如图5所示。由图5所示试验结果对比可知,波束形成技术虽然可以准确定位出目标声源,但在目标声源附近存在旁瓣效应,且旁瓣比较大,无法判断旁瓣处是否真实存在声源;而改进算法结果清晰,只在目标声源处存在幅值较大的波峰,旁瓣效应干扰被有效抑制,试验结果进一步验证了改进算法的有效性及实用性。
|
图 5 半消音室内声源定位结果对比 Fig. 5 Comparison of experiments result in semi-anechoic room |
对改进算法的有效性及实用性验证之后,设计了6L16/24型柴油机机体侧噪声源实际定位试验。设计传声器阵列为4×4的16阵元等间距网格阵列,阵列孔径为0.6 m×0.6 m,阵元间距为0.2 m,受阵列孔径及阵元间距限制,该阵列的适用频率范围约为800~1 500 Hz,阵列中心高度1.2 m,阵列所在面距离机体侧面1.7 m。

|
图 6 柴油机噪声源定位试验环境 Fig. 6 Environment of diesel engine noise source localization experiment |

|
图 7 柴油机辐射噪声频谱 Fig. 7 Frequency spectrum of radiation noise of diesel engine |
由图7知,1000 r/min、0负荷工况下,6L16/24型柴油机机体侧的辐射噪声主要集中在1 300 Hz以下频段,结合阵列适用频率范围,进行800~1 300 Hz范围内柴油机机体侧噪声源定位,800 Hz和1 300 Hz频率下噪声源定位结果如图8所示。
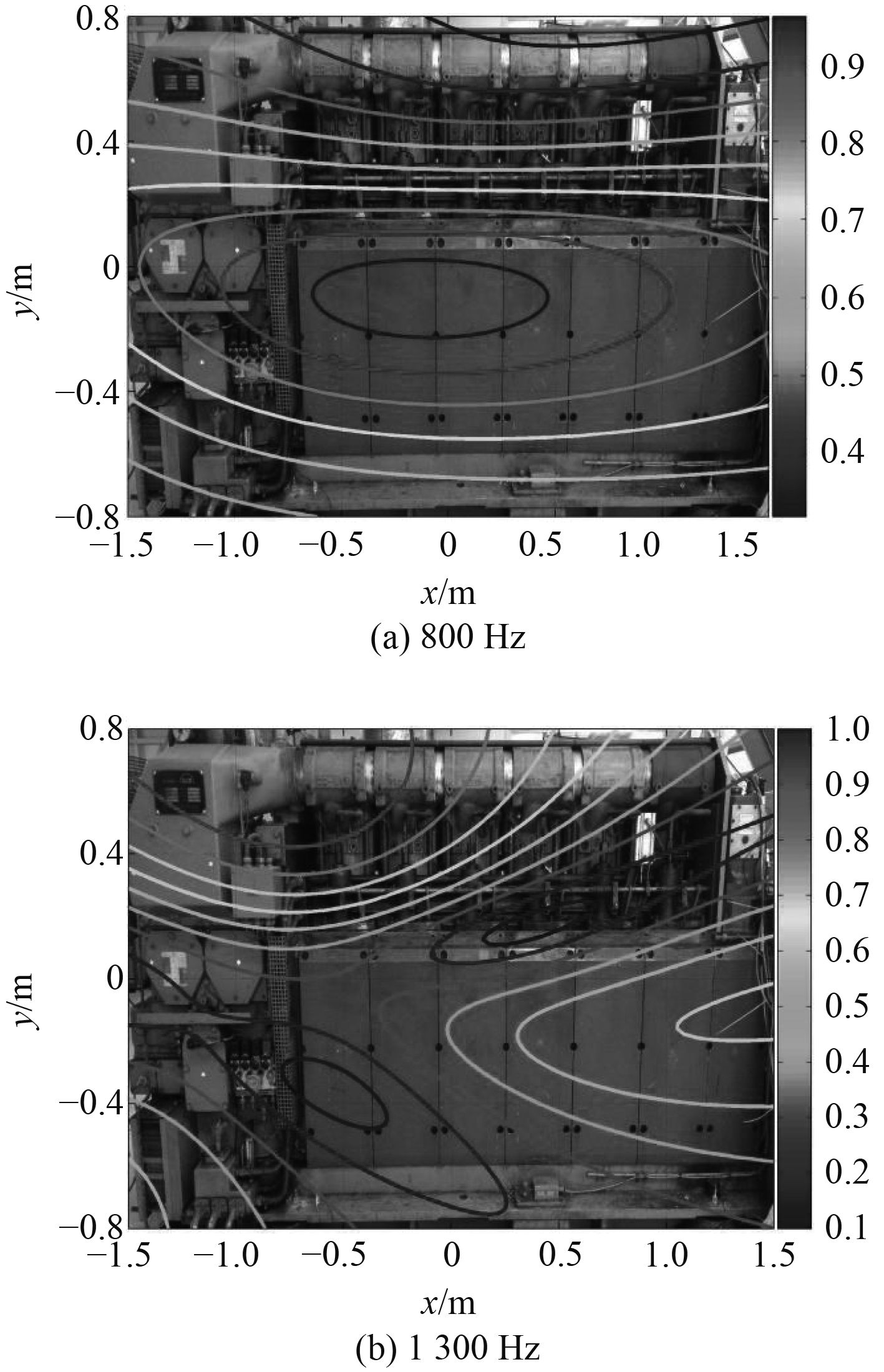
|
图 8 柴油机机体侧噪声源定位结果 Fig. 8 Results of diesel engine noise source localization experiment |
由图8所示定位结果可知,800 Hz频率下,主要噪声来源于曲轴箱附近,由曲柄连杆机构及主轴承产生,而在1 300 Hz频率下辐射噪声主要来源于涡轮增压器。在图8(b)所示1 300 Hz定位结果中,除幅值最大的主瓣之外,图像还存在少许旁瓣干扰,这是由于试验环境为轮机模拟机舱,不可避免的存在背景噪声及地面反射干扰,这些干扰源是实际存在的声源,并非波束形成算法产生的虚假旁瓣,定位结果中这些干扰声源必然存在。因此,综合判断分析认为,改进算法可以有效地消除波束形成算法本身产生的虚假旁瓣干扰。
6 结 语1)针对波束形成算法存在的旁瓣效应问题,本文根据波叠加法计算结构声辐射的基本思想,提出了基于波叠加法对波束形成旁瓣效应的改进算法;通过仿真试验、扬声器定位试验及柴油机噪声源定位试验,同时验证了改进算法可以准确定位出噪声源,且有效低消除了旁瓣效应,避免了虚假声源干扰。
2)在提出改进算法时做了一些假设,即假定各噪声源在中远距离测量时可被近似作为点声源,且采集的阵列声压信号均未滤除背景噪声干扰。尽管有上述假设的限制及噪声干扰,试验结果表明改进算法仍有较好的应用效果。
| [1] | 刘超. 基于麦克风阵列的声源定位算法研究[D]. 南京: 南京大学, 2015. |
| [2] | 王雁, 刘志红, 吴波波, 等. 识别运动声源随机阵列生成法研究[J]. 声学学报, 2015 (1): 97–103. |
| [3] | Ballesteros J A, Sarradj E, Fernández M D, et al. Noise source identification with Beamforming in the pass-by of a car[J]. Applied Acoustics, 2015, 93 : 106–119. DOI: 10.1016/j.apacoust.2015.01.019 |
| [4] | 李兵, 杨殿阁, 郑四发, 等. 基于遗传算法的动态优化波叠加噪声源识别方法[J]. 机械工程学报, 2010, 46 (12): 99–105. |
| [5] | Koopmann G H, Song L, Fahnline J B. A method for computing acoustic fields based on the principle of wave superposition[J]. Journal of the Acoustical Society of America, 1989, 86 (6): 2433–2438. DOI: 10.1121/1.398450 |
| [6] | Geng L, Zhang X Z, Bi C X. Reconstruction of transient vibration and sound radiation of an impacted plate using time domain plane wave superposition method[J]. Journal of Sound & Vibration, 2015, 344 (3): 114–125. |
| [7] | Gounot Y J R, Musafir R E. Simulation of scattered fields: Some guidelines for the equivalent source method[J]. Journal of Sound and Vibration, 2011, 330 (15): 3698–3709. DOI: 10.1016/j.jsv.2011.03.006 |
| [8] | 陈鸿洋, 商德江, 李琪, 等. 声场匹配波叠加法的水下结构声辐射预报[J]. 声学学报, 2013 (2): 137–146. |
| [9] | 吴绍维, 向阳, 李胜杨. 体积速度匹配分布源边界点法的特解源位置优化方法研究[J]. 声学学报, 2015 (3): 381–390. |
| [10] | 张永斌. 基于等效源法和质点振速测量的近场声全息技术[D]. 合肥: 合肥工业大学, 2012. |
 2018, Vol. 41
2018, Vol. 41
