近年来,我国经济的快速发展促进了船舶事业的繁荣,机舱作为船舶的动力场所,存放的各种油料和电器设施,成为火灾的高发区[1, 2]。因此,研究船舶机舱火灾对于消防训练和火灾逃生有重要意义。
测量火灾实验过程中空间内的温度分布,对研究火灾行为规律有重要意义[3, 4]。就固定空间而言,由美国NIST研究所开发的基于火灾动力学的大涡模拟软件FDS(Fire Dynamics Simulator)对火灾温度流动模拟的准确性已得到广泛认可[5]。但若改变机舱火源功率、火源面积、补风口面积、风机流速等条件,FDS就不能满足要求,所以有必要建立火灾温度预测模型。20世纪90年代Vapnik等提出的支持向量机(Support Vector Machines,SVM),是一种新的机器学习算法,并迅速在多个领域得到快速发展[6]。相比其他传统学习方法,具有良好的泛化能力,能够很好地克服维数灾难、小样本、局部极小点以及过拟合等问题[7]。因此,运用支持向量机技术求解实际工程中有关火场温度预测的问题非常适宜。
本文以船舶机舱为研究对象,采用大涡模拟方法,以火灾动力学分析软件FDS为平台,计算不同条件下的船舶机舱火场温度变化规律。以计算结果为训练样本建立船舶机舱火灾温度的支持向量机预测模型,最后将遗传算法优化支持向量机(GA-SVM)理论运用于船舶机舱火灾温度的预测。为了验证本文模型的准确性,对比了SVM模型和BP神经网络方法的船舶机舱火灾温度预测结果。预测结果表明,利用遗传算法优化支持向量机的方法的预测效果较好且准确度较高,可以作为快速预测火场温度的工程计算方法。
1 船舶机舱火灾数值模拟本文运用FDS软件对实习公司的船舶机舱实验室进行舱底油水火灾数值模拟。
1.1 船舶机舱火灾场景设计以实习公司船舶火灾实验室为模拟对象,该实验室内部尺寸15 m(长)×7 m(宽)×5 m(高),机舱内部尺寸是6 m(长)×7 m(宽)×5 m(高),舱内有2台柴油机和1台柴油发电机,以及其他一些常用机舱设备。建立的模型如图1所示。采用机械通风和自然通风,计算场景中在四面墙壁设有多个格栅作为补风口,每个格栅是0.8 m(长)×0.6 m(宽),顶部设有机械抽风口,抽风口是0.5 m(长)×0.5 m(宽)。
本文将火源置于实验舱地面左边,燃料为柴油,火源为超快速t2火,最大火源功率为1.8MW。计算场景的环境温度为20℃。墙面、地面和天花板都为304钢板表面,墙面中间填充耐热材料。通过对该场景的网格独立性分析[8],本文使用了72×36×25非均一网格系统对所有涉及样本进行计算。

|
图 1 FDS场景的几何模型 Fig. 1 The geometric model of the FDS scene |
在整个船舶机舱火灾场景中,火场温度变化的过程是一个动态过程,受多种因素的影响,本文主要考虑火源功率、补风口面积、风机流量、火灾面积这4个因素对温度场的影响,构建了表1中15组火灾场景,每组只改变一个影响因素,采用FDS分别对这15个火灾场景下的船舶机舱火灾温度变化过程进行模拟,计算其不同时刻的温度分布。在主频为2.80 GHz的Intel CPU计算速度下,表1中每组火灾场景计算到400 s需要使用CPU的时间不少于4 h。15组数据计算结果如表2所示。
|
|
表 1 FDS算例设计 Tab.1 The design of FDS scene |
表1中各符号的含义如下:Q为火灾功率,kW;T为风机启动时间,s;V为风机流速,m/s;S为补风口面积,m2。
|
|
表 2 FDS计算结果 Tab.2 The results of the FDS |
为检验算法训练的精度,需要将第1节中15组FDS计算数据划分为13个训练样本和2个测试样本,将表1中的Q,T,V,S四个主要影响因素作为支持向量机模型的输入量
| ${y'} = w \cdot \phi (x) + b\text{。}$ | (1) |
式中:w为权值向量;b为偏差。参数w和b的值由SVM采用最小化结构风险
为了使SVM有最优的性能,本文采用遗传算法对SVM模型的惩罚因子C和核参数g进行参数寻优,避免认为选择参数的盲目性。遗传算法是一种借鉴生物界自然选择和进化机制发展起来的高度并行、自适应的全局优化概率搜索算法,已被广泛应用于组合优化、机器学习、信号处理等领域[10]。
3 结果对比及分析 3.1 参数优化对比本文采用网格搜索寻优和GA参数寻优对支持向量机的惩罚系数C和核参数g进行优化分析和选择,见表3。利用网格搜索寻优法时,先粗略寻找最佳参数,再进行精细的参数选择。
|
|
表 3 网格搜索和GA优化模型参数对比 Tab.3 Comparing parameters optimized by grid-search and GA |
从表3可以看出,以上2种寻优方法对模型参数C和g寻优后,GA的适应度值0.046 691最小,模型的适应能力最好,对应的参数[C,g]=[81.192 6,0.300 69]组合最佳。由GA寻找最佳参数的适应度变化曲线图2 可知,进化代数为150次时终止进化,此时适应度值0.046 691就接近理想最优值。
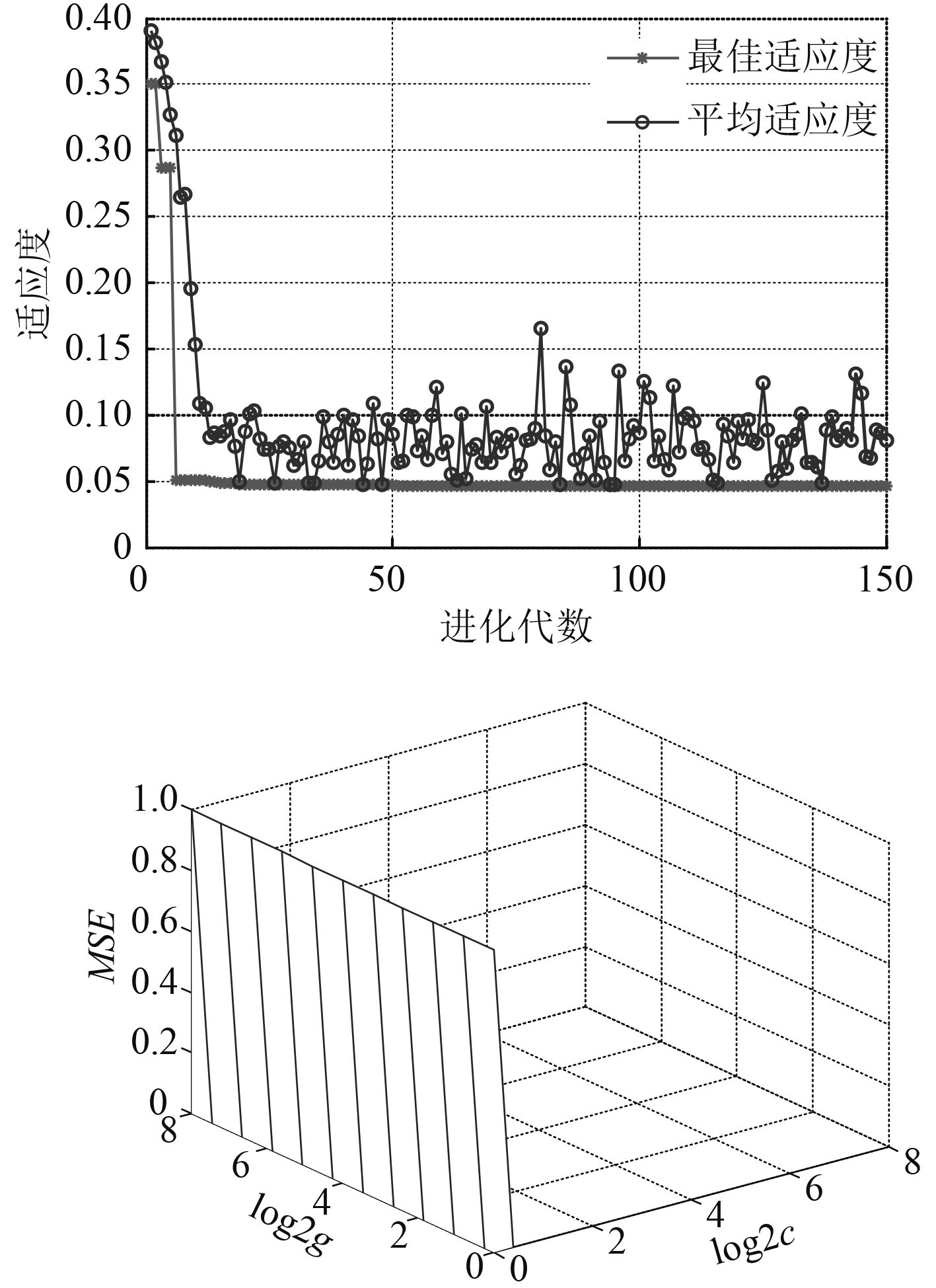
|
图 2 GA-SVM的适应度曲线和SVM的适应度曲线比较 Fig. 2 Comparing the fitness of GA-SVM and SVM |
为比较GA-SVM模型的船舶机舱火灾温度预测的性能,分别采用SVM模型和前馈型BP神经网络建模对相同的样本集进行训练和预测。GA-SVM模型选用RBF核函数,经反复参数寻优,得到满足要求的C和g分别为 81.192 6和0.300 69。利用神经网络预测时,经过反复试验,网络的输入层、隐含层、输出层的节点数分别为 4,30,21,隐含层传递函数选用tansig函数,输出层传递函数选用purelin函数,训练函数选用Levenberg-Marquardt算法,学习速率Lr=0.2,目标误差Eg=0.000 01。3种模型下船舶火灾温度预测值与FDS计算结果比较见表4,可以得出,GA-SVM模型有较强的泛化能力,对训练样本学习后,对预测输入样本进行预测,得出相应预测输出值与FDS计算结果吻合很好。
|
|
表 4 不同模型下预测值与FDS计算值比较 Tab.4 Contrast the FDS results and predict data of different models |
图3列举了采用GA-SVM模型、SVM模型和BP神经网络方法进行火灾温度预测的效果图。
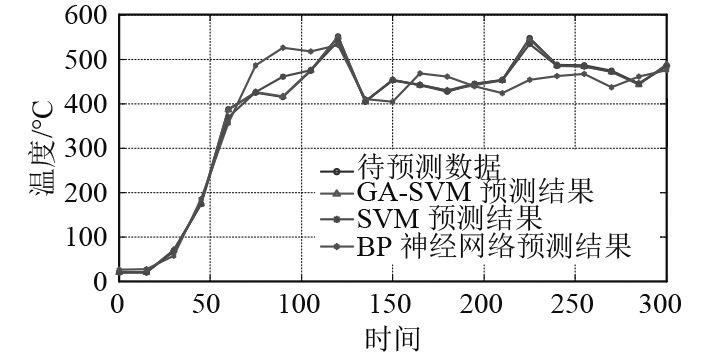
|
图 3 三种模型下的预测效果 Fig. 3 Prediction results based on different models |
图4~图6分别列举了GA-SVM模型、SVM模型和BP神经网络预测值与FDS计算结果的相对误差曲线,由图4~图6可知,3种模型的预测值与FDS计算结果的最大相对误差分别为0.005 63,0.083 81和0.200 35。最小相对误差分别为0,0和0.008 63,GA-SVM模型和SVM模型均可以达到消防工程的精度要求,且GA-SVM模型预测精度明显高于SVM模型。
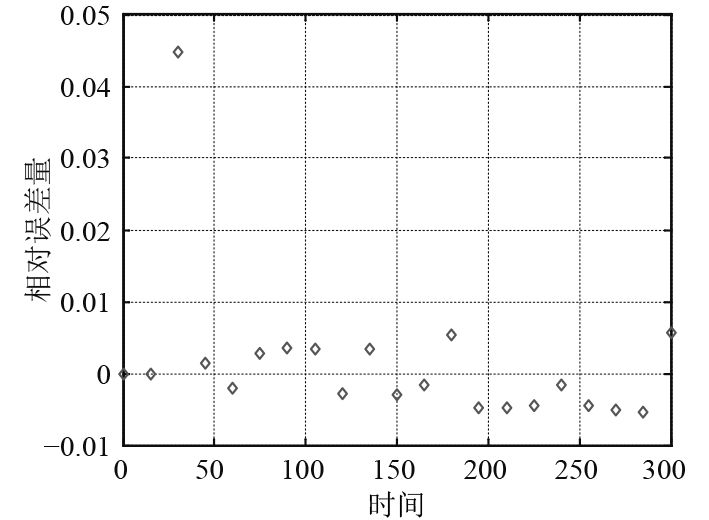
|
图 4 GA-SVM模型下相对误差 Fig. 4 Relative error based on GA-SVM |
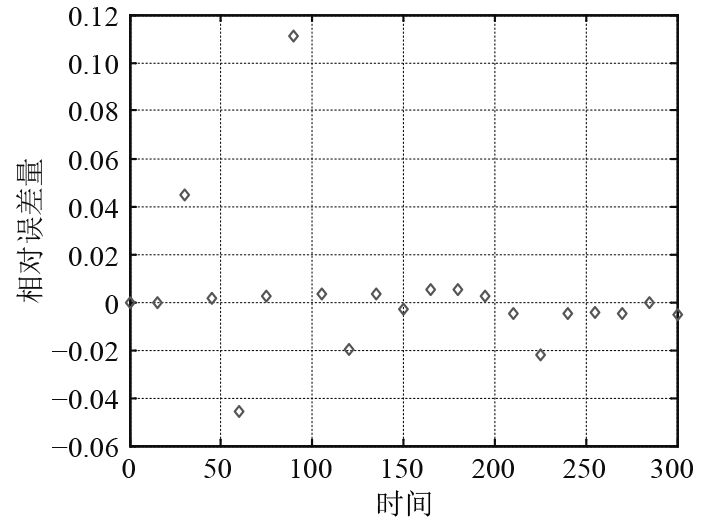
|
图 5 SVM模型下相对误差 Fig. 5 Relative error based on SVM |

|
图 6 BP神经网络下相对误差 Fig. 6 Relative error based on BP Neural Network |
3种模型预测性能结果对比见表5,用MSE,eMAPE和R三个指标进行预测性能评价。
|
|
表 5 三种模型性能比较 Tab.5 Comparison of model performance |
从表5 可看出,GA-SVM模型的均方误差MSE和平均相对误差eMAPE值分别为 0.046 691,0.001 6,远小于SVM模型和BP网络预测的相应指标值,且GA-SVM模型的相关系数R为 0.971 2,比SVM模型和BP网络模型的相关系数更接近1,其预测结果精度更高,适应性更好,表明本文模型预测性能更优。
4 结 语本文利用FDS软件对不同条件下的船舶机舱火灾场景进行模拟,以火灾功率、风机启动时间、风机流速和补风口面积这4个影响因素为输入参数,不同时刻的火灾温度为输出构造了船舶机舱火灾温度的GA-SVM预测模型。在建模过程中,采用GA对SVM回归模型的惩罚因子C和核参数g自动寻优选择,避免了人为主观经验地确定参数。通过输入火灾功率、风机启动时间、风机流速和补风口面积到GA-SVM模型中,其对火灾温度预测的效果较好。与SVM模型和BP神经网络模型的相对误差对比分析表明,GA-SVM模型具有较好的泛化能力,为船舶机舱火灾温度间接计算及预测提出了一种新方法。
本文建立的船舶机舱火灾温度的支持向量机计算模型包括4种条件参数对火灾温度的影响。在今后的工作中,可以设计更多的火灾场景,例如考虑火源位置、补风口位置、火灾空间高度、面积等因素对船舶机舱火灾温度的影响,通过FDS数值模拟构造更加全面系统的训练样本,从而完善模型功能并进一步提高预测精度。
| [1] |
贾佳, 陆守香. 船舶舱室火灾风险分析方法研究[J]. 安全与环境学报, 2014, 14(3): 132–137.
JIA Jia, LU Shou-xiang. Study of fire risk analysis method applied to ship compartment[J]. Journal of safety and environment, 2014, 14(3): 132–137. |
| [2] | 苌占星. VR技术在船舶舱室火灾处理中的应用研究[D]. 大连: 大连海事大学, 2015. |
| [3] | 周德闯. 基于虚拟现实平台的火灾场景计算和仿真研究[ D]. 合肥: 中国科学技术大学, 2010: 72–96. |
| [4] |
徐文强, 刘芳, 董龙洋, 等. 基于FDS的地下停车场火灾数值模拟分析[J]. 安全与环境工程, 2012, 19 (1): 73–76.
XU Wenqiang, LIU Fang, DONG Longyang, et al. Analysis on the fire of underground parking based on FDS numerical simulation[J]. Safety and Environmental Engineering, 2012, 19 (1): 73–76. |
| [5] | 胡靖. 船舶封闭舱室火灾温度分布特性实验研究[D]. 合肥: 中国科学技术大学, 2010: 8–10. |
| [6] |
辛喆, 王顺喜, 云峰, 等. 基于火灾模拟软件(FDS)的草原火灾蔓延规律数值分析[J]. 农业工程学报, 2013, 29 (11): 156–163.
XIN Zhe, WANG Shun-xi, YUN Feng, et al. Numerical analysis on spreading laws of grassland fire based on fire dynamics simulator (FDS)[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29 (11): 156–163. |
| [7] |
顾亚祥, 丁世飞. 支持向量机研究进展[J]. 计算机科学, 2011, 38 (2): 14–17.
GU Yafei, DING Shifei. Advances of support vector machines(SVM)[J]. Computer Science, 2011, 38 (2): 14–17. |
| [8] |
陈伟根, 滕黎, 刘军, 等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报, 2014, 29 (1): 44–51.
CHEN Wei-gen, TENG Li, LIU Jun, et al. Transformer winding hot-spot temperature prediction model of support vector machine optimized by genetic algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29 (1): 44–51. |
| [9] |
杨钟瑾. 粒子群和遗传算法优化支持向量机的破产预测[J]. 计算机工程与应用, 2013, 49 (18): 265–270.
YANG Zhong-jin. Bankruptcy prediction based on support vector machine optimized by particle swarm optimization and genetic algorithm[J]. Computer Engineering and Applications, 2013, 49 (18): 265–270. DOI: 10.3778/j.issn.1002-8331.1303-0352 |
| [10] | CHAUDHURI A, DE K. Fuzzy support vector machine for bankruptcy prediction[J]. Applied Soft Computing, 2011, 11 (2): 2472–2486. DOI: 10.1016/j.asoc.2010.10.003 |
| [11] | WANG Chunlin, ZHOU hao, LI Guoneng. Combining support vector machine and genetic algorithm to predict ash fusion temperature[J]. Proceedings of the CSEE, 2010, 27 (8): 11–15. |
 2018, Vol. 40
2018, Vol. 40
