2. 江苏恒神股份有限公司,江苏 丹阳 212300
2. Jiangsu Heng Shen Co. Ltd., Danyang 212300, China
随着世界海上贸易的迅速发展,船舶压载水带来的危害亦愈发严重。大量研究表明,任何单一的压载水处理方法都无法在满足IMO标准的前提下同等高效地处理压载水中的全部有害生物。
US技术是集高级氧化、热解等技术于一体的新型水处理技术[1]。近年来,很多实验研究表明US技术在水处理领域中具有广阔的应用前景。
赵超等[2]研究发现US能够有效地抑制水中藻类数量的增长。舒天阁等[3]利用实验研究了功率和US频率在除藻效果方面的影响,通过荧光显微镜观测验证了US具有良好的破碎效果。王小蓓[4]利用超声波-硫酸自由基法为依据,通过实验处理船舶压载水中的小球藻、扁藻等藻类,结果表明:2种技术联合处理压载水在保证3种藻的去除率达到标准的前提下,能量损耗明显降低。王晓宁等[5]研究结果表明,用超声和紫外光协同降解处理染料废水时,其降解速度大于二者单独降解速度之和,协同效应明显,脱色效率达到99.1%。以上研究证明了US技术在实际压载水处理中可行。
1 US处理器的设计 1.1 换能器的选型|
|
表 1 换能器的具体参数 Tab.1 Parameters of transducer |
本文所选用的US处理器是用来做紫外线杀菌的预处理手段,主要是利用超声波的机械剪切作用将大分子颗粒的微生物拆分并破环其细胞结构。综上分析,应选择频段为中频的超声波换能器,具体参数如表1所示。
1.2 处理器尺寸的确定US处理器的几何尺寸与声波的各种特性紧密相连,主要考虑以下2个影响因素:
1)波长因素
超声波的波长λ决定了其折射或者反射,当处理器两平行外壁间的距离为λ/4的整数倍时,超声波将会在反应器壁上发生全反射,由于超声波在液体中的衰减量很小,因此在满足这样尺寸要求的反应器中很容易发生混响,有利于超声波空化和机械剪切作用的发生[6]。波长的计算公式为:
| $c = \lambda f{\text{。}}$ | (1) |
将换能器28 kHz的频率和在海水中声波1 450 m/s传播速度代入式(1)计算得出声波的波长为51.78 mm。因此,安装换能器平行外壁间的距离应为12.95 mm的整数倍。
2)压载水管路流速因素
本文设计的US处理器的处理量为200 m3/h,根据船舶压载水的有关规定,压载或者卸载时,水在管道中的流速不能超过3 m/s[6]。在此规定下,选取处理器的入口直径为200 mm。
结合上述因素,最终将横截面为长方形的长方体定为处理器的反应腔,且长方形横截面的尺寸为259 mm×280 mm,安装换能器两壁间的距离为

|
图 1 处理器结构 Fig. 1 Processor structure |
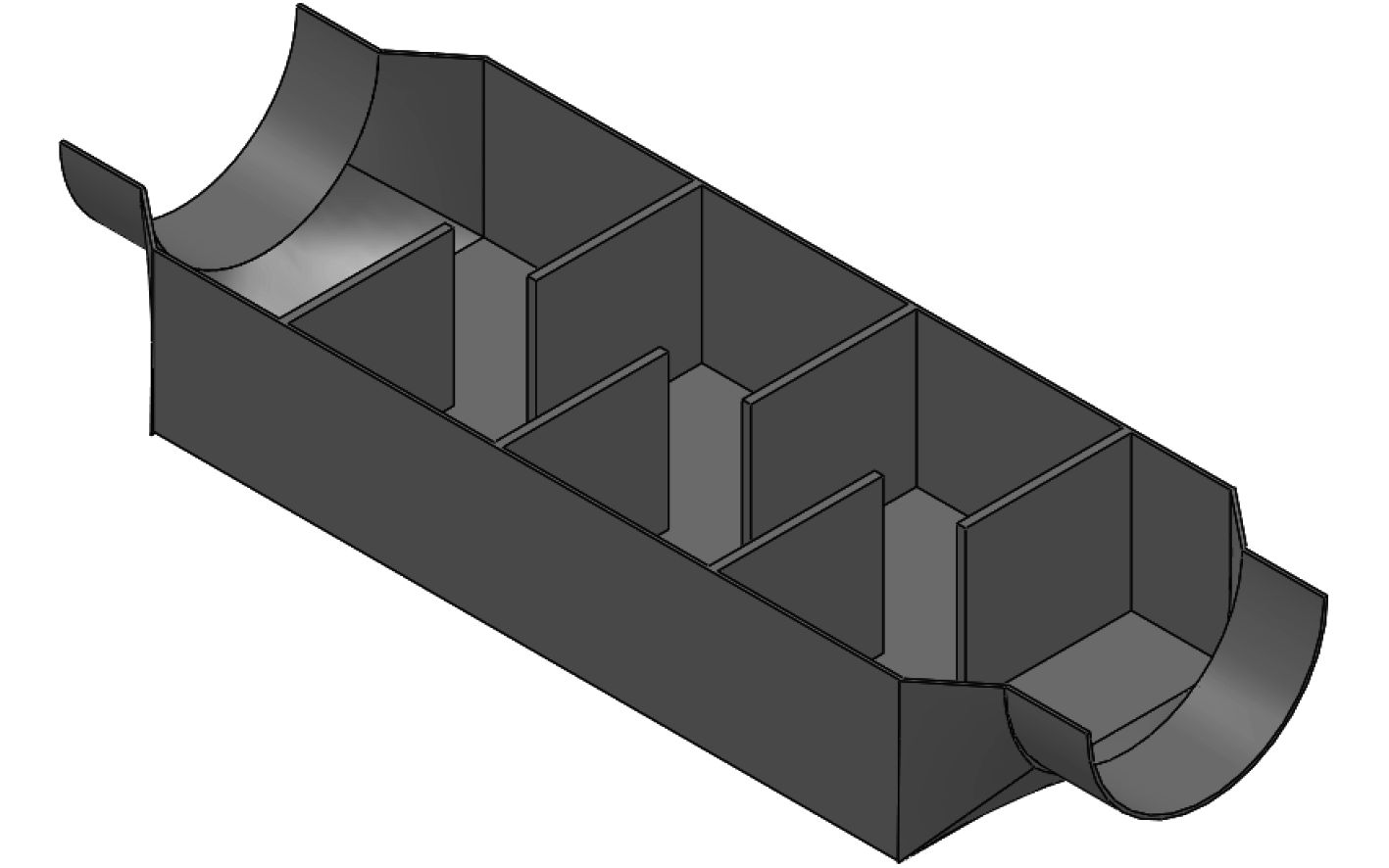
超声波的空化效应或者剪切效应只有处理内存在一定的死水区或者水流速很小(通常应小于0.2 m/s)才能发挥作用,而当压载水流经所设计的处理器时,水流速约为0.763 m/s,仍然达不到要求。因此,考虑在处理器中加装隔板,水在经过隔板时可以阻挡水流,降低大部分水流的速度。加入隔板的处理器结构如图2所示。
|
图 2 加入隔板的处理器结构 Fig. 2 Processor structure after adding the clapboards |
当处理器中液面的深度小于400 mm,并且超声波换能器安装在器壁上,超声波的功率可采用面积功率密度参数(声强I)来设计。相关研究证实,在一定的范围内提高声强I会增加超声波处理效果,但有一定的限度,一般当声强I≥3 W/cm2后,超声波处理效果将不再有明显的提高。因此,若过度增加声强会造成处理器的能耗增大;相反,若使用过小的声强则会达不到预期的处理效果。总之,从提高声处理效率和降低超声波处理器能耗的角度来看,应控制平均声强I≤3 W/cm2。根据本文所设计的超声波处理器的具体尺寸计算安装换能器两壁面的面积可得:
| $A = 2 \times W \times L = 3\;584\;{\rm{c}}{{\rm{m}}^2}\text{。}$ | (2) |
式中:W为处理器截面边长,C=280 mm;L为处理器长度,L=640 mm。s
根据一些实验经验,用来降解有机物有效声强应在2 W/cm2左右。超声波处理器作为压载水处理系统中的预处理模块,主要作用是将较大的微生物和菌胶团剪切开来,故所需的声强要小于降解有机物用的声强。在本设计中取声强I=1.8 W/cm2。因此可求得超声波换能器的总功率为:
| $P = A \times I = 3\;584 \times 1.8 = 6\;451.2\;{\rm W}{\text{。}}$ | (3) |
将总功率圆整为6 400 W,由上述所选换能器的参数可知,需要64个即可满足功率要求。
1.4 超声波发生器的选择在本设计中,由于选择的换能器都是相同频率,而且为了达到处理效果,必须要有较强的声波。经分析,单频率发振的发生器采用单一振动频率发振,且这种发振方式能够产生较强的超声波。因此,本文设计中选用单频率发振的发生器。
1.5 声场均匀化根据所设计的US处理器结构可知处理器内的声场为对射。处理器上、下2个反应壁面上的超声波相向传播,并在相对的面上形成反射,进而在处理器中形成了频率相同、传播方向相反的2列声波。选取共同的坐标原点和计时起点,则可以得到2列声波的表达式:
| ${y_1} = A\cos \omega (t - x/c), $ | (4) |
| ${y_2} = A\cos \omega (t + x/c){\text{。}}$ | (5) |
两列声波相遇时的合成波为:
| $y = {y_1} + {y_2} = 2A\cos \frac{{2\pi }}{\lambda }x \cdot \cos \omega t{\text{。}}$ | (6) |
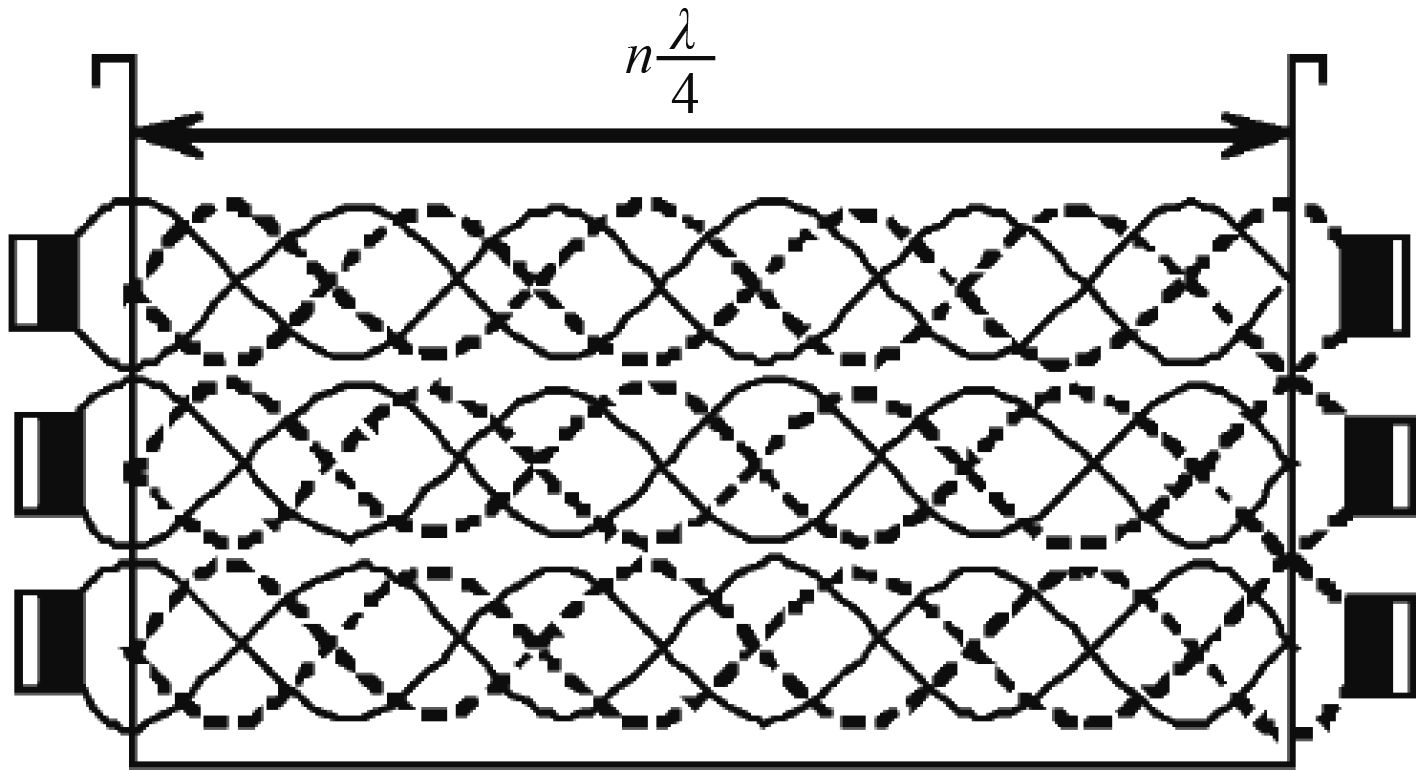
由式(6)可知,合成波上的各点都在做同一周期的简谐振动,其振动频率为
|
图 3 换能器正对分布声场的模拟 Fig. 3 Simulation of the aligned sound field |
从图3可以看出,只要换能器的对射距离为

|
图 4 反应器的内部结构 Fig. 4 The internal structure of the reactor |
通过上述设计,得到US反应器的总体结构如图5所示。

|
图 5 超声波反应器总装图 Fig. 5 US processor assembly diagram |
US处理器内的声场分布对其处理效果有显著影响,而声场的空间分布与换能器的辐射频率及处理器的结构尺寸等有关。根据平面阵列超声波换能器的指向性分布的计算方法,计算超声换能器阵列在三维空间中的辐射声场分布。
2.1 基于Matlab的超声波声场模拟US处理器内的声场分布对US处理效果有显著的影响。采用Matlab软件对所设计的US处理器内的声场进行仿真计算,仿真时,可将处理器简化为一个有上、下2个相同换能器阵列的矩形处理器。首先只考虑下面的阵列,利用上述公式可求得处理器内任意一点
由于液体中的空化效应只取决于声压幅值和声能密度的均匀性[8]。利用声压幅值的平均值
| ${P_{am}} = \frac{1}{{{V_0}}}\iiint_{{V_0}} {\left| {{P_A}} \right|}, $ | (7) |
| $N{U_I} = \frac{1}{{{P_{am}}}}\sqrt {\frac{{\iiint_{{V_0}} {{{\left( {\left| {{P_A}} \right| - \left| {{P_{am}}} \right|} \right)}^2}{\rm d}V} }}{{{V_0}}}}{\text{。}} $ | (8) |
式中V0为声场体积。那么声压幅值的平均值越大,声场非均匀性指数越小,超声波处理器在声处理均匀性和声能利用率方面的性能就越好。
|
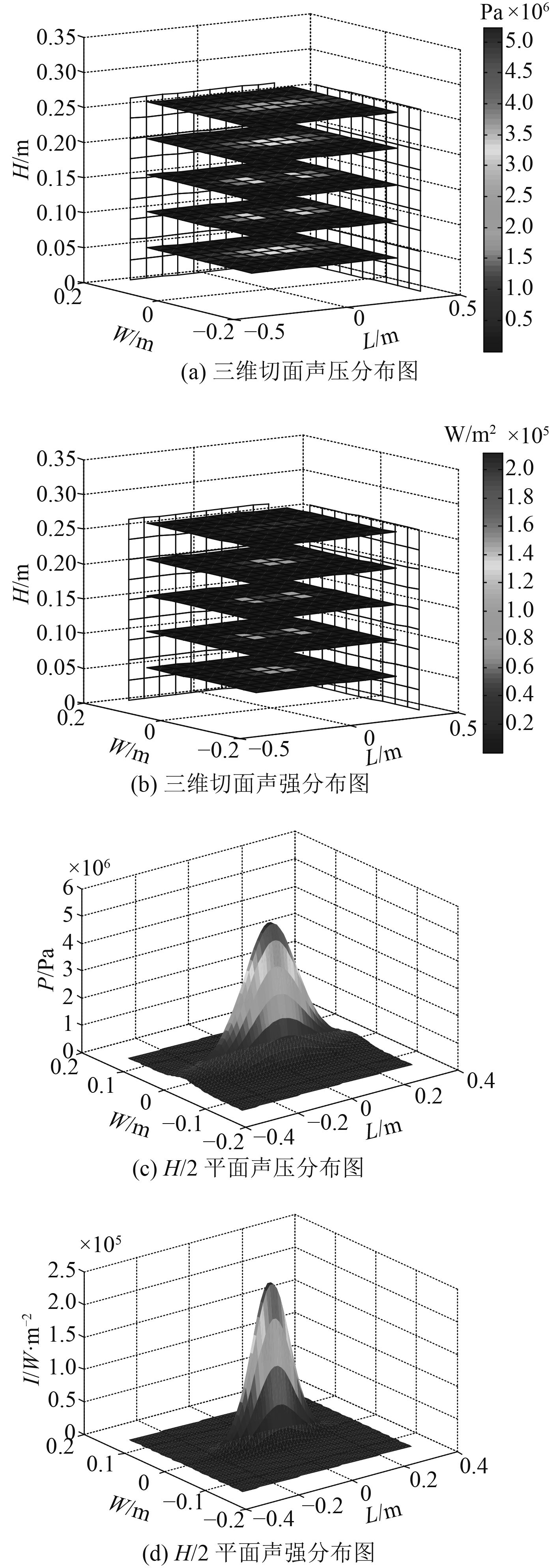
图 6 处理器内声场分布图 Fig. 6 The sound field distribution inside the processor |
根据上述理论,采用Matlab软件进行程序编写。研究处理器中液体的声压分布、声强分布、声压幅值平均值以及非均匀性指数,并比较不同结构参数下的能量利用率,对其进行结构优化,从而确定超声波处理器的最终结构。
如图6所示即为超声波处理器的声场仿真结果,其中图6(a)和图6(b)分别为处理器内声压、声强的三维切面分布图,图6(c)和图6(d)分别为高度为H/2平面上的声压、声强分布图。
根据模拟结果可以得出超声处理器所产生的声场中声压幅值的最大值为5.23×106 Pa,把上述值代入式(7)和式(8)可得声场幅值的平均值Pam为5.05×105 Pa,非均匀性指数NUI为1.216 5。
2.2 腔体高度H对声场分布的影响US处理器结构尺寸的大小对其声场分布有很大的影响,因此本节将计算不同结构尺寸的处理器液体内的声场分布。仿真时,以处理器腔体的高H(即换能器的对射距离)为研究对象,通过微调H来研究处理器内声场分布的变化规律,并得出声压幅值的平均值Pam和非均匀性指数NUI随H的变化规律。仿真时,超声频率取为28 kHz,保持腔体的长640 mm和宽280 mm不变,腔体高度在
|
|
表 2 不同腔体高度下的Pam和NUI Tab.2 Values of Pam and NUI under different heights |
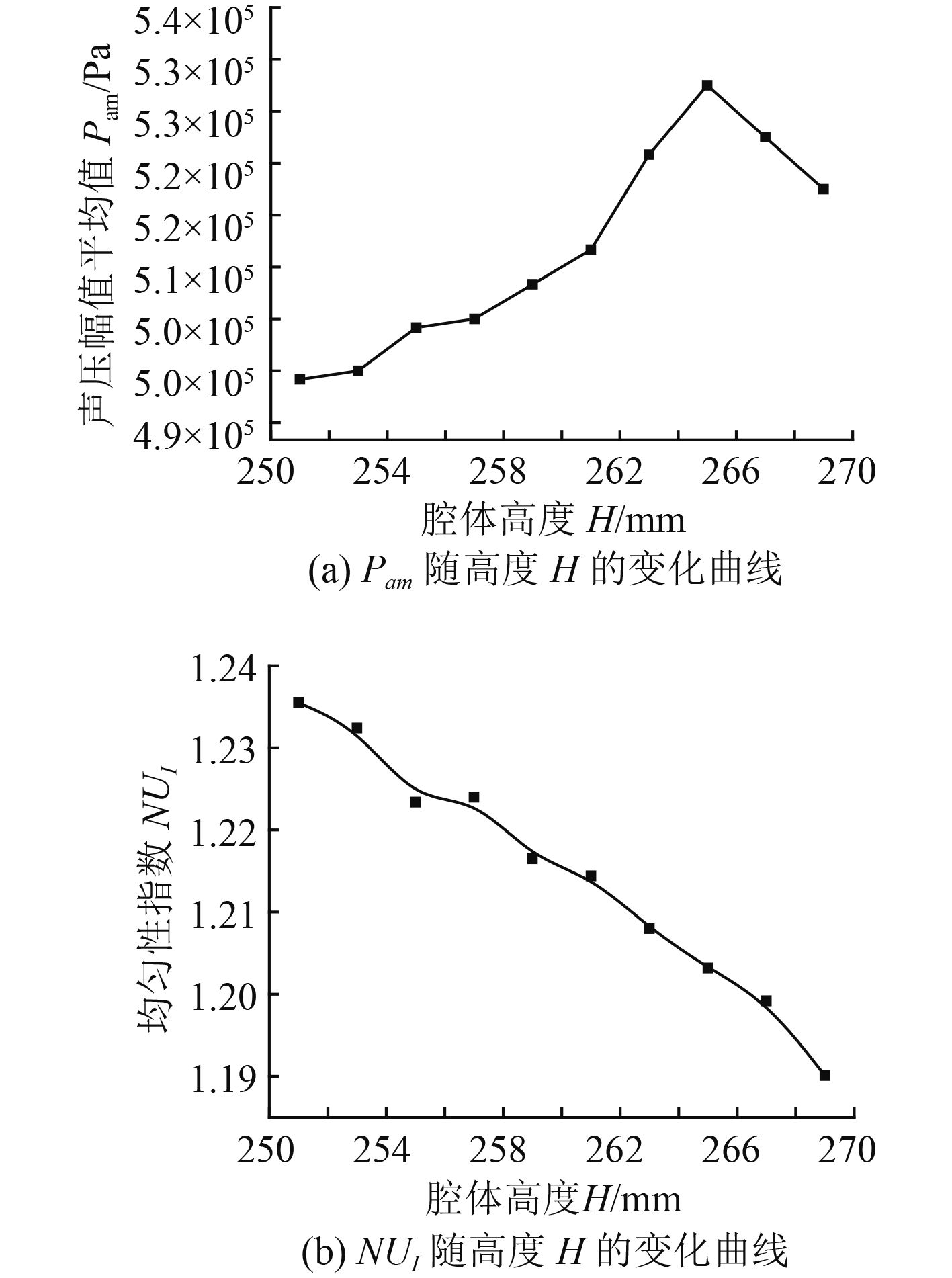
声压幅值的平均值Pam和非均匀性指数NUI值随H的变化曲线如图7所示。从图7(a)可以看出,随H的增大,压幅值的平均值Pam呈先增大后减小的变化趋势。在H由251 mm到269 mm的变化过程中,在
|
图 7 Pam和NUI随高度的变化曲线 Fig. 7 The change curves of Pam and NUI accompanied with heights |
US处理器的工作频率也会对其声场分布产生很大影响。因此,本节将主要研究在不同超声频率下,US处理器内的声场分布情况以及声压幅值的平均值Pam和非均匀性指数NUI。仿真时,保持处理器结构尺寸不变,超声频率f分别取为20 kHz,28 kHz,30 kHz,40 kHz,50 kHz,60 kHz和70 kHz,仿真结果如表3所示。
|
|
表 3 不同超声频率下的Pam和NUI Tab.3 Values of Pam and NUI under different ultrasonic frequencies |
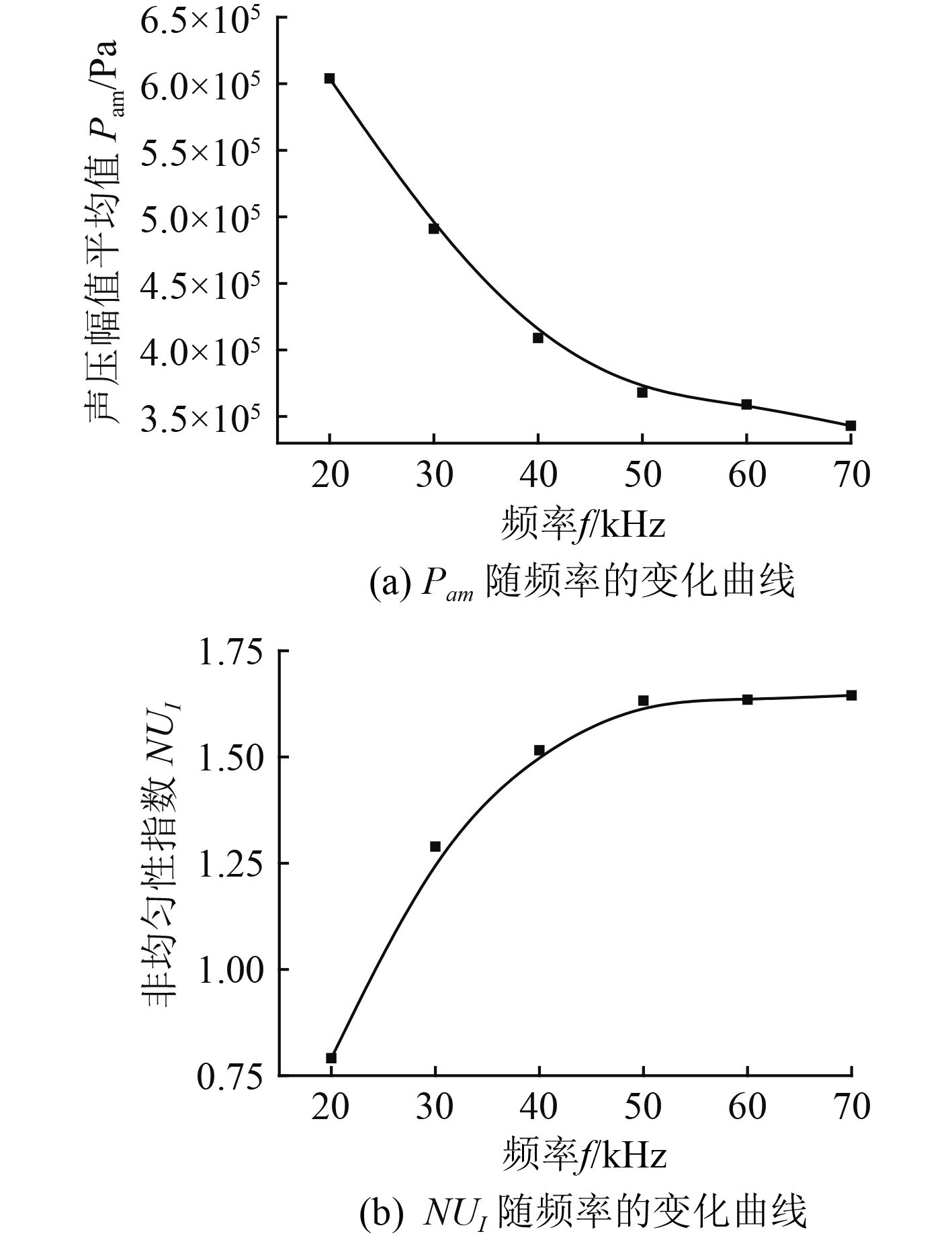
声压幅值平均值Pam和NUI随超声频率的变化曲线如图8所示。由图8(a)可以看出,声压幅值平均值Pam随频率的增高而减小,说明随着频率的增高,处理器内液体的空化效应减弱。这是因为超声频率的增高会导致声波径向周期变短,空化气核还未成长到产生空化效应的条件,即使形成空化气泡,但由于声波的轴向周期也变短,空化气泡很可能来不及破裂。此外,高频超声波在液体中的能量消耗也较快,为获得相同的处理效果,会有大量的能量消耗,可能造成得不偿失的结果。由图8(b)可以看出,非均匀性指数NUI随超声频率的增加而增大,这说明随着频率的增加,处理器的声处理均匀性和声能利用率逐渐降低。因此,对于文中的矩形US处理器来说,为了提高超声作用效果,应采用频率较低的超声波。
|
图 8 Pam和NUI随频率的变化曲线 Fig. 8 The change curves of Pam and NUI accompanied with ultrasonic frequencies |
本文首先对US处理器进行设计,完成了US处理器的建模,最后根据平面阵列换能器的指向性分布的计算方法,推导出平面阵列换能器在三维空间中声场的计算方法,利用Matlab软件编程仿真了US处理器内的声场分布,得出了腔体高度H、频率f对平均声压幅值Pam、非均匀性指数NUI以及US处理器性能的影响规律。仿真结果表明:由于声波在介质中传播时存在损耗,在理论值
| [1] | 袁易全. 近代超声原理及应用[M]. 南京: 南京大学出版社, 1996: 170–171. |
| [2] | 赵超, 于宁楼, 马万里, 等. 超声波抑藻技术效果研究[J]. 中国农学通报, 2010, 26 (22): 413–417. |
| [3] | 舒天阁, 苑宝玲, 王少蓉. 低功率超声波去除铜绿微囊藻技术[J]. 华侨大学学报: 自然科版, 2008, 29 (1): 72–75. |
| [4] | 王小蓓. 超声波一硫酸自由基技术处理船舶压载水的研究[D]. 大连: 大连海事大学. 2009. |
| [5] | 王晓宁, 卞华松, 张国莹. 超声与紫外光协同氧化法处理染料废水的工艺研究[J]. 上海环境科学, 2002, 21 (6): 331–337. |
| [6] | 孟宪振. 船舶压载水防海生物技术研究[D]. 镇江: 江苏科技大学. 2013: 19–22. |
| [7] | 周金娟. 高输出性能超声换能器结构设计及仿真实验研究[D]. 南京: 南京航空航天大学, 2012, 14–15. |
 2018, Vol. 40
2018, Vol. 40
