矢量水声传感技术是检测水中声能流方向与强度的一种新技术,其信号处理技术是水声工程领域令人瞩目的研究方向之一,利用矢量传感器能获取水下声矢量信号[1],为信号检测提供丰富的声场信息[2]。随着矢量传感器[3]制作工艺不断进步及其优越性的体现,基于矢量传感器和矢量阵列的信号处理技术也得到越来越多的研究和应用。目前在这方面占据领先地位的是俄罗斯、美国和中国。
但是由于外场试验环境的复杂性,很难对目标做出一个准确的估计,同时采集到的声源信息含有大量噪声,所以对信号进行有效降噪估计,进而结合相应的方位估计算法估计方位角就非常重要,之前对信号的处理都是直接进行傅里叶变换,简单时频分析,在强噪背景下信号的特征就不明显,计算的方位角也不太准确,所以本文提出用小波变换进行信号的降噪处理,尽可能的保留信号更多的有用信息,降低噪声的干扰。水声信号处理的目的是为了对接收到的目标信号做出估计,更好的得到目标方位信息。目前研究小波降噪[4]方面的文章比较多,但通过对比傅里叶变换降噪和小波降噪,并通过有力的数据来证明小波降噪优越性方面的文献目前还比较少。
本文以MEMS矢量水听器为硬件依托,研究单矢量水听器信号处理的基本问题,结合小波降噪通过理论分析、计算机仿真和湖试实验验证MEMS水量水听器的定向性能,为后续的工程化应用及发展奠定基础。
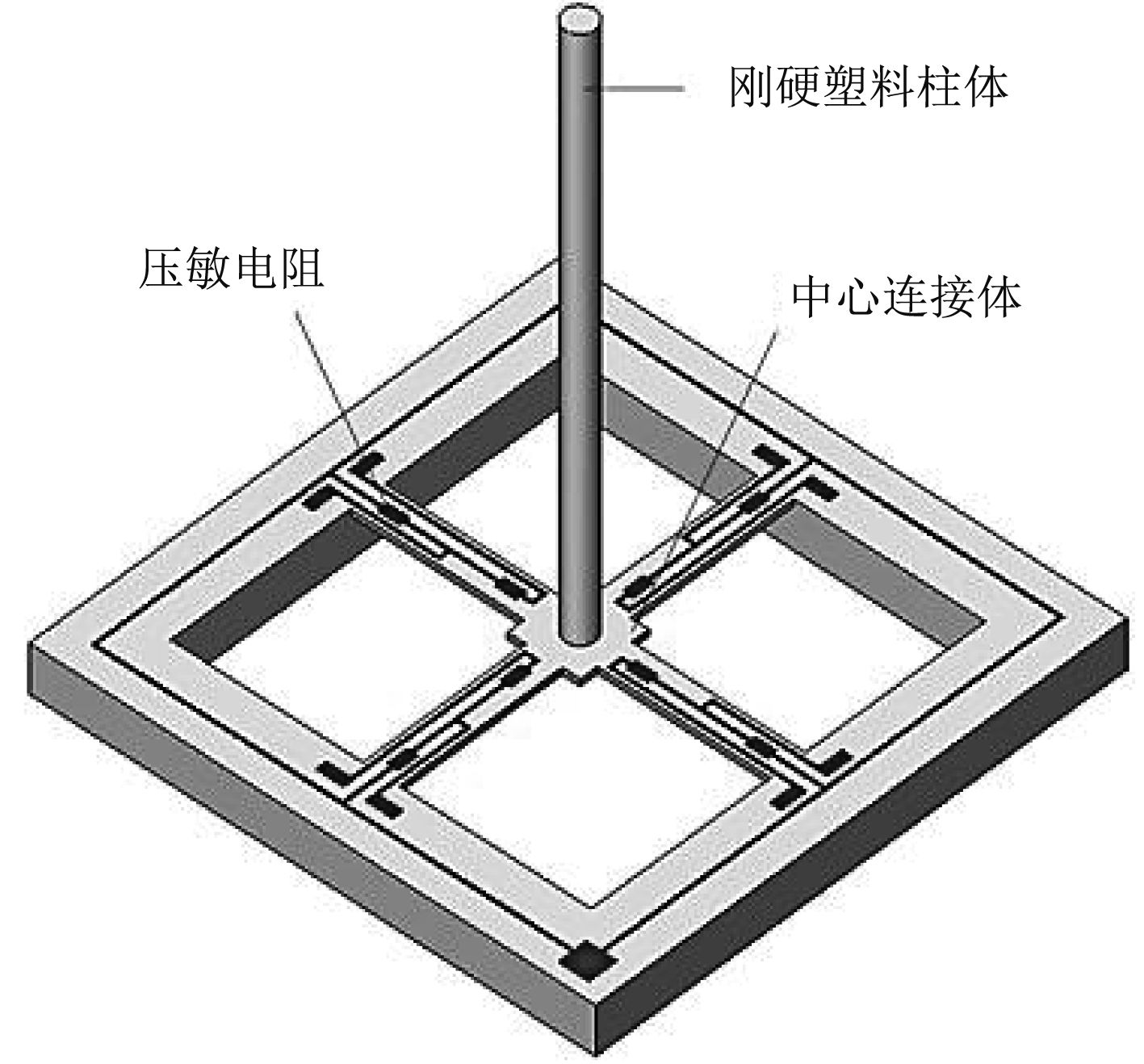
1 水声信号获取及定位原理 1.1 信号的获取纳机电矢量水听器是中北大学自行研制的新概念的矢量水听器,融合MEMS技术、仿生原理和水声原理[5]。其微结构三维示意图如图1所示。
|
图 1 微结构示意图 Fig. 1 Microstructure diagram |
在测量范围内,矢量水听器可以接收任何类型的声音信号,包括噪声和目标信号,而对于信号处理仅对目标信号感兴趣,这就需要从噪声中分离出所需信号,降噪技术显得很重要。
1.2 水声定位原理由声学理论可知平面波声压可表示为:
| $\begin{split}p(r,t) = &{p_0}{e^{j(\mathord{\buildrel{\hbox{$\scriptscriptstyle\rightharpoonup$}} \over k} \mathord{\buildrel{\hbox{$\scriptscriptstyle\rightharpoonup$}} \over r} -wt)}} = {p_0}\exp [j(kx\cos \alpha \cos \theta + \\& ky\cos \alpha \sin \theta + kz\sin \alpha -wt)]\text{。}\end{split}$ | (1) |
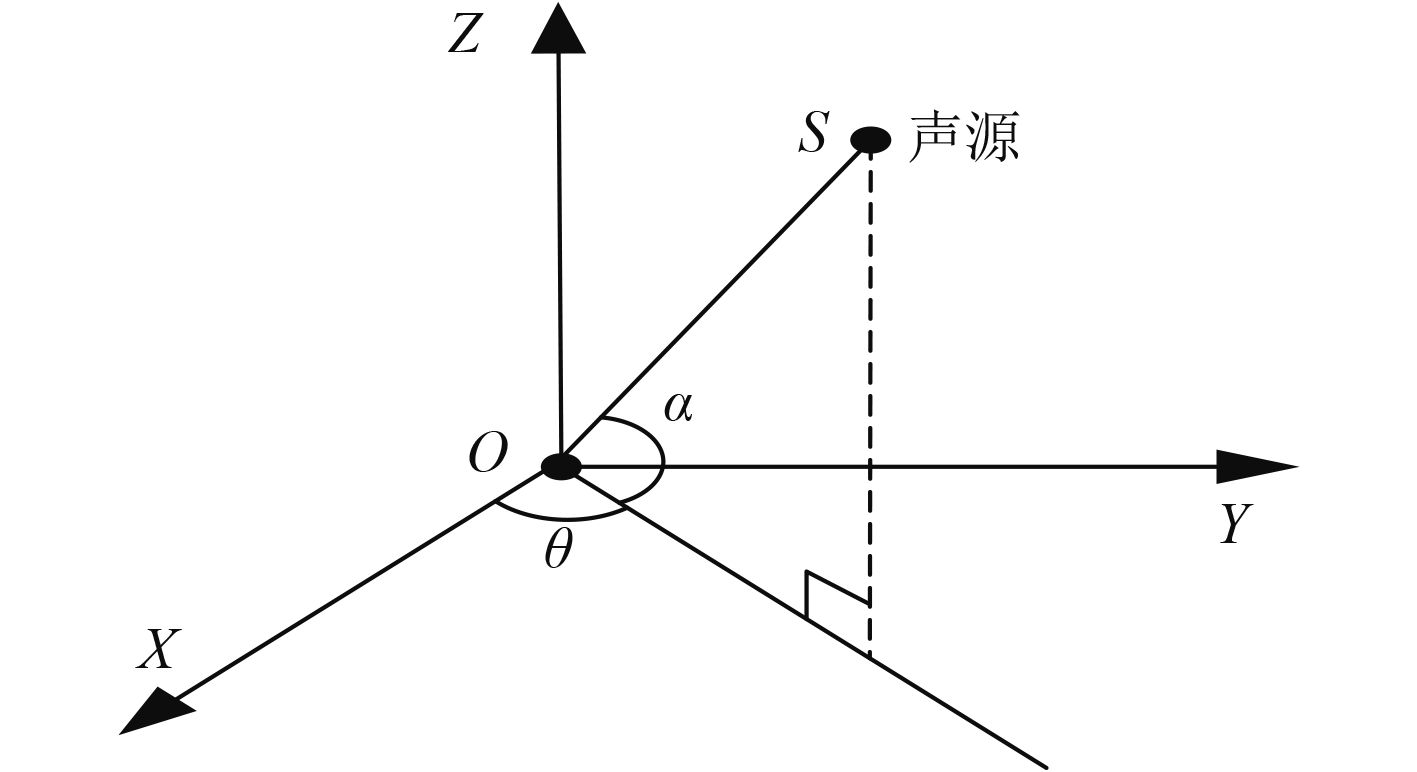
式中:k为波矢量,表示声波传播的方向,它与水平面的夹角为
|
图 2 波矢量在直角坐标系中的投影 Fig. 2 Projection of wave vector in cartesian coordinate system |
在均匀介质中,声场的运动方程为:
| $\frac{{\partial \overrightarrow v }}{{\partial t}} + \frac{1}{{{\rho _0}}}\nabla p = 0\text{。}$ | (2) |
平面波的声压与质点振速[6]三分量之间仅差一个常数,两者的波形一样,因而对平面波来说,声压与振速完全相关。可得质点振速的3个分量:
| $\begin{array}{l}{v_x} = \displaystyle\frac{p}{{{\rho _0}c}}\cos \theta \cos \alpha\text{,} \\[8pt]{v_y} = \displaystyle\frac{p}{{{\rho _0}c}}\sin \theta \cos \alpha \text{,}\\[8pt]{v_z} = \displaystyle\frac{p}{{{\rho _0}c}}\sin \alpha \text{。}\end{array}$ | (3) |
且方位角
由此可见,只要测得质点振速在水平面内的2个分量vx、vy(水听器测试的信号为电压信号,正比于振速分量),就可以由上式得到声源在水平面内的方位角θ,这就是矢量水声传感器确定声源方位的基本原理。
但实际接收到的信号中包含很多噪声,所以本文提出用傅里叶变换及小波变换对信号进行处理,为后续定位定向做好准备。
2 不同降噪方法水声信号一般是按1/3倍频程发射的连续单频正弦波,由于MEMS矢量水听器的共振峰在1 kHz左右,所以主要研究500~800 Hz范围内的信号。用信噪比来衡量一种方法的降噪性能。信噪比公式如下:
| ${\rm{SNR}} = 10\cdot\lg \frac{S}{N}\text{,}$ | (4) |
其中:S为信号功率;N为噪声能量功率。
2.1 傅里叶变换结合Matlab软件[7]用傅里叶变换对信号进行简单处理,通过直接法和Pwelch法求信号的功率谱密度。
直接法又称周期图法,它是把随机序列x(n)的N个观测数据视为一能量有限的序列,直接计算x(n)的离散傅里叶变换,得X(k),然后再取其幅值的平方并除以N,作为序列x(n)真实功率谱的估计。
对于直接法的功率谱估计,当数据长度N太大时,谱曲线起伏加剧,若N太小,谱的分辨率又不好,因此需要改进。Pwelch法将N点的有限长序列x(n)分段求周期图再平均。一是选择适当的窗函数w(n),并在周期图计算前直接加进去,加窗的优点是无论什么样的窗函数均可使谱估计非负。二是在分段时,可使各段之间有重叠,这样会使方差减小。在Matlab上可用这2种方法进行功率谱的计算。
2.2 小波阈值降噪小波分析是在傅里叶分析的基础上发展起来的,但小波分析有着极大的不同,小波变换是空(时)间和频率的局部变换,能有效从信号中提取信息。通过伸缩和平移等运算功能可对信号进行多尺度的细化分析[8],解决了Fourier变换不能解决的许多问题。
设Ψ是定义在(-∞,∞)上能量有限的函数,Ψ构成平方可积信号空间,记为Ψ∈L2(R),则生成函数族{Ψab}:
| ${\varPsi _{{\rm{ab}}}}\left( t \right) = {\left| a \right|^{-\frac{1}{2}}}\varPsi \left[ {\frac{{t-b}}{a}} \right]\text{。}$ | (5) |
Ψ(t)称为小波函数,Ψab(t)由Ψ(t)伸缩和平移生成,是小波基函数。a为伸缩因子,b为平移因子。对任一信号f(t)∈L2(R)的连续小波变换可定义为信号与小波基函数的内积。从信号学的角度看,小波去噪是一个信号滤波的问题。尽管在很大程度上小波去噪可以看成是低通滤波。但由于在去噪后,还能成功地保留信号特征,所以在这一点上又优于传统的低通滤波器。
小波去噪主要过程:
1)对接收到信号进行小波分解变化;
2)对小波系数作阈值门限处理(软硬阈值);
3)处理过的小波系数作逆变换重构信号,可得到去噪后的信号。
不同小波基以及阈值,对信号产生不同的处理效果。经过试验,选择“db4”,“sym8”这2种小波进行处理,使用4种阈值选取规则进行处理。
3 仿真研究Matlab中的小波工具箱提供了小波变换的一些基本功能,仿真实验及外场测试结果实现都在Matlab中进行,首先仿真正弦信号加入不同信噪比的高斯噪声,通过相应算法处理,得出信噪比及误差的具体对比。之后将仿真使用的信号处理方法用来处理外场信号。
3.1 FFT与小波降噪对比含高斯噪声的正弦信号,输入信噪比分别为0、10,在Matlab中进行仿真并用FFT滤波及小波降噪[9]处理,选择不同小波阈值。对比信号图如图3所示。

|
图 3 Fft及4种小波阈值降噪方法 Fig. 3 Fft and four kinds of wavelet threshold denoising methods |
从信号图看出小波降噪效果明显优于Filter滤波,输出信噪比及均方差具体比较见表1。
|
|
表 1 输出信噪比及均方差 Tab.1 Output signal to noise ratio and mean square error |
小波法对信噪比有很大的提高,当信噪比为10时,经小波不同阈值滤波提高了24 dB左右,而Filter滤波将信噪比提高到21 dB,小波法效果好;同时小波去噪后方差低于Filter滤波,所以小波对信号处理有很好的作用,不同阈值规则下效果区别不太大。
3.2 不同小波降噪对比在Matlab中,设置入射信号为500 Hz正弦信号,添加随机高斯噪声,对比信号特征,目标信号为500 Hz线谱,噪声分布在整个频率范围。可以通过小波变换把随机噪声滤掉,保留单频信息。经过多次实验发现db4和sym8小波对此目标信号滤波作用较好,同时使用heursure启发式阈值规则,对信号进行处理,2种方法的输出信噪比如表2所示。
|
|
表 2 db4和sym8小波输出信噪比及均方差 Tab.2 The signal-to-noise ratio and mean square error of db4 and sym8 wavelet output |
对比图表发现,使用同一种阈值规则,不同小波基处理的结果略有不同,sym8小波在相同输入信噪比条件下,输出信噪比高于db4小波,同时均方差也小,降噪效果更好。不论输入信噪比如何,2种方法的输出信噪比都有很大提升,信噪比为负时,均方差相对大些。所以对小波的研究很有待深入。
4 外场试验处理在太原某水库进行湖试试验,实验方案如图4所示,鱼唇换能器作为声源,发射连续正弦信号,调整声源与水听器的间距约为15 m,换能器与水听器放置在水面同一高度。实验过程中,利用NI采集卡采集数据,采样率设为4 kHz。调整水听器的位置,使得声波入射角为45°,验证单矢量水听器的目标定向能力[10]。

|
图 4 湖试现场 Fig. 4 Lake test site |
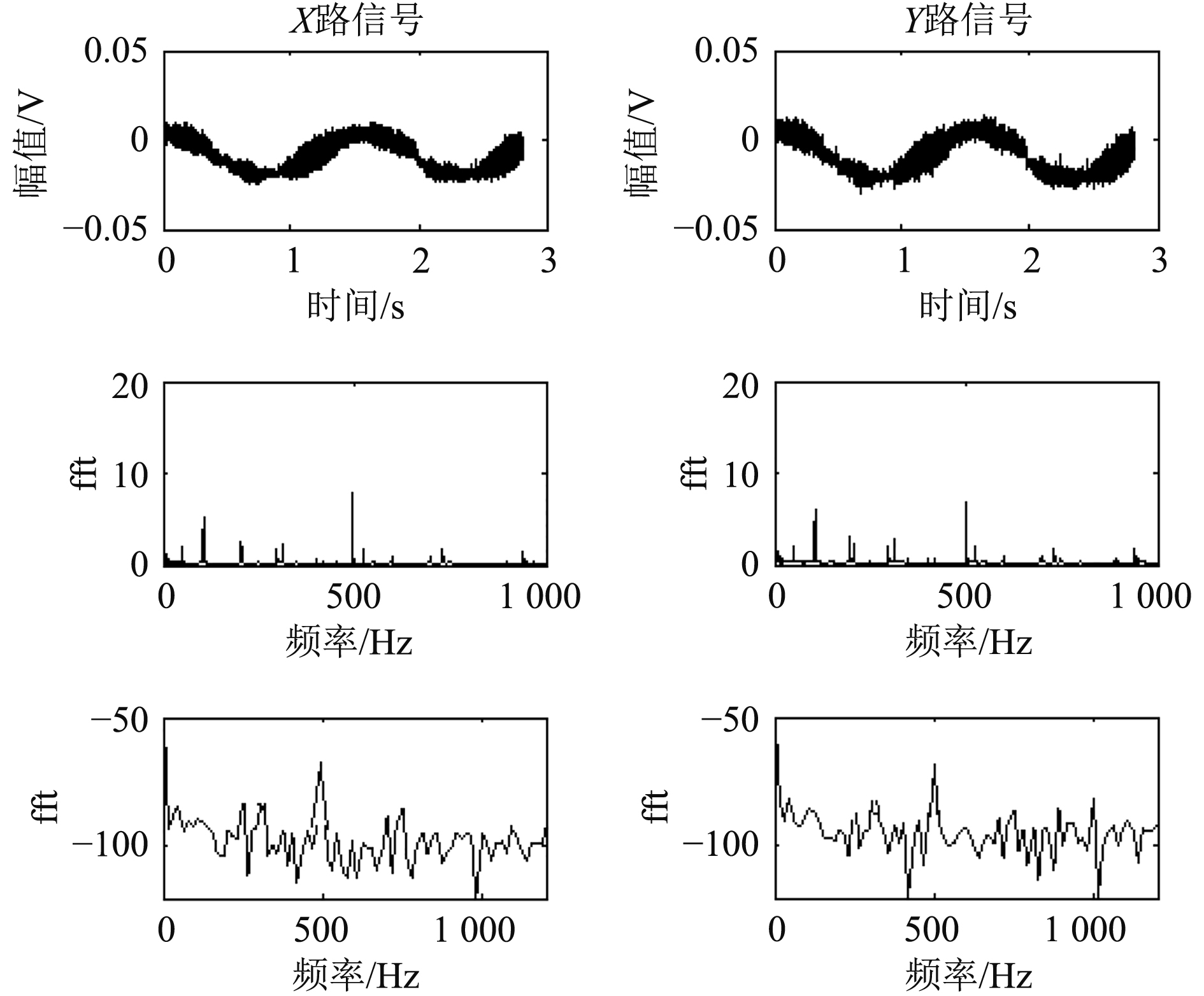
二维矢量水听器可以接收到X,Y两路声压信号,设定采样率为4 kHz,实时地进行信号采集,将采集到的数据用Matlab进行处理,画出时频信号,从图5可以看出发射的是500 Hz的信号,第1行为两路时域信号,第2行为直接傅里叶变换后频域信息,第3行为功率谱密度。由于矢量水听器的“8”字余弦指向性,从时域波形看出,由于外场环境的复杂性及不稳定性,信号含有很多的噪声成分,所以首先对信号进行简单滤波。
|
图 5 湖试信号 Fig. 5 Lake test signal |
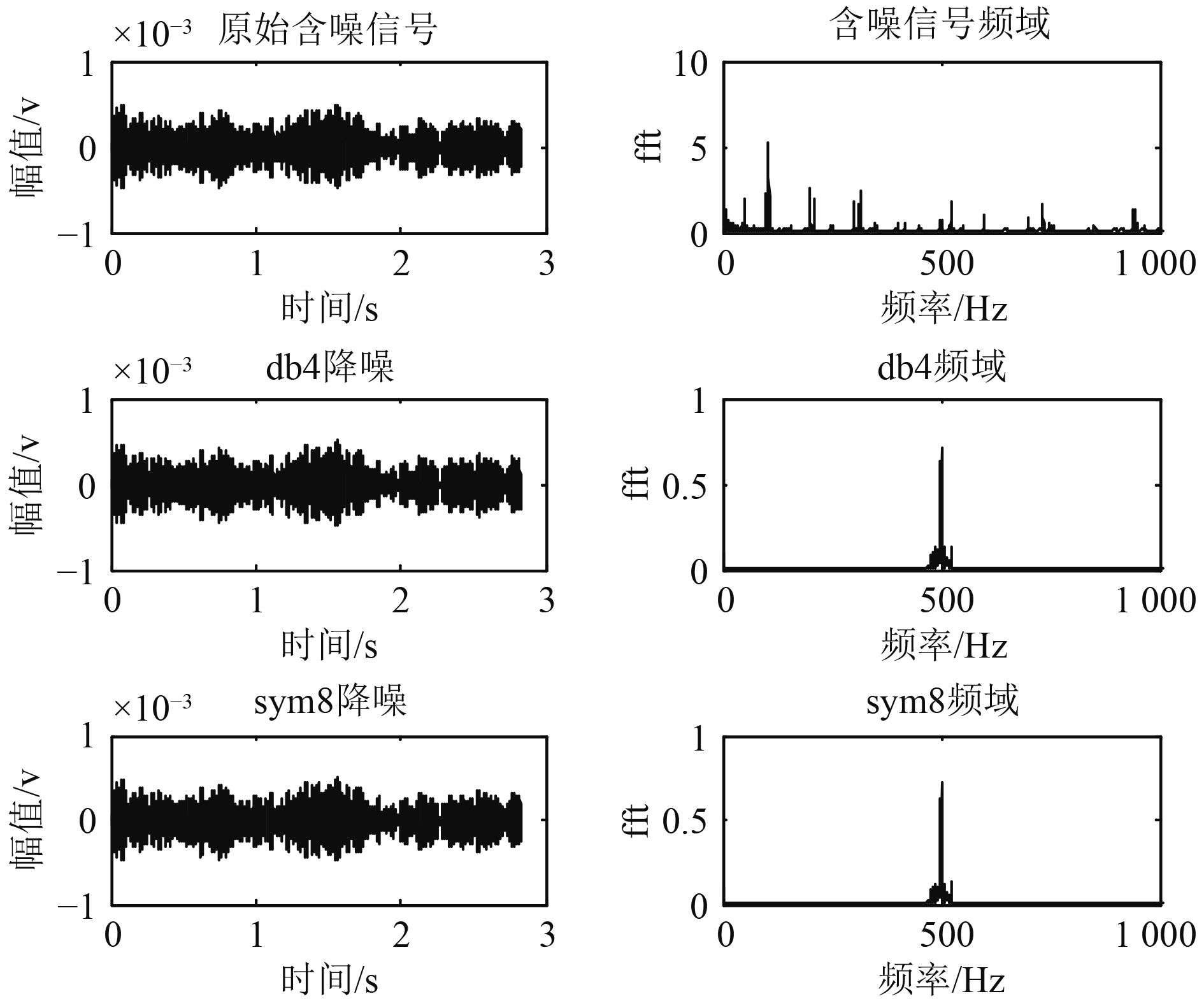
先窄带滤波,再进行小波变换;降噪信号及功率谱密度如图6和图7所示。
|
图 6 湖试信号降噪时频信息 Fig. 6 Lake test signal noise reduction time-frequency information |

|
图 7 降噪后X路信号功率谱密度 Fig. 7 Noise density of X-channel signal after noise reduction |
分析降噪后时频信号,高频部分的噪声被滤掉一部分,低频(100 Hz左右)附近的线谱是发射换能器自身的电噪声及共频干扰,原则上可以直接加窗滤掉这部分信号。经过小波变换及窄带滤波处理,信噪比得到提升。因为多次室内及外场试验使用的都是单矢量水听器,而且使用一个鱼唇换能器,所以目标声源个数为1,当有多个声源时可以用盖氏圆盘法确定信号源数,这里就不详细论述声源数目的计算算法。
最后使用降噪后信号进行方位估计,结合直方图法估计出方位角,具体原理如图8所示。

|
图 8 直方图方位估计原理图 Fig. 8 Histogram azimuth estimation |
结合MUSIC算法用直方图法计算出方位角为46°(入射角45°),定向精度在5°以内,说明小波降噪对保留信号的有用信息可取。
5 结 语本文对多个频率的信号进行多次仿真处理,研究显示:小波降噪比傅里叶变换的处理效果更好,能得到更高的信噪比,更好保留信号的有用部分,并通过外场试验数据进行验证,得到很好的降噪结果,对方位的估计更准确。整体研究的复杂之处在于阈值的选取,降噪阈值过大或过小都会影响最终的降噪效果,阈值过大会造成细节部分丢失,过小则得不到最好的降噪效果。在此基础上,还需要进一步研究,对现有方法进行改进或找出其他适合水声信号的降噪方法,达到最完美的降噪效果。由于水声环境的复杂性和可变性,对水声信号的处理与学习还需要更加充分的学习,同时矢量阵在复杂海况下的各项性能还有待进一步提高完善,仍有很多工作需要完成,本文的研究工作可能有助于该技术的深入研究和发展,推动更广泛的工程化应用。
| [1] | R. J. 尤立克. 水声原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 1990: 67–75. |
| [2] | 李启虎. 进入21世纪的声纳技术[J]. 应用声学, 2002, 21 (1): 13–18. DOI: 10.11684/j.issn.1000-310X.2002.01.005 |
| [3] | 杨德森, 洪连进. 矢量水听器原理及应用引论[M]. 北京: 科学出版社, 2009. |
| [4] | 彭玉华. 小波变换与工程应用[M]. 北京: 科学出版社, 1999. |
| [5] | 陈尚. 硅微仿生矢量水声传感器研究[D]. 太原: 中北大学, 2007. |
| [6] | 姚直象, 惠俊英, 蔡平, 等. 单矢量水听器方位估计的柱状图方法[J]. 应用声学, 2006, 25 (3): 161–167. DOI: 10.11684/j.issn.1000-310X.2006.03.009 |
| [7] | 徐明远, 刘增力. MATLAB仿真在信号处理中的应用[M]. 西安: 电子科技大学出版社, 2007: 313–316. |
| [8] | 王拴中, 朱玉田. 改进小波阈值去噪法的对比性仿真实验与分析[J]. 噪声与振动控制, 2012, 32 (1): 128–132. |
| [9] | 孙延奎. 小波分析及其应用[M]. 北京: 机械工业出版社, 2005: 224–236. |
| [10] | 李芬. 矢量水听器确定声源目标方位估计研究[D]. 哈尔滨: 哈尔滨工程大学, 2004. |
 2018, Vol. 40
2018, Vol. 40
