2. 武汉大学 地球空间信息技术协同创新中心,湖北 武汉 430072
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430072, China
海洋回波多普勒谱反映了海面的动态信息,其中多普勒频移与海面散射元的雷达径向速度相关,而谱宽则反映了该径向速度的分布特征,这使得微波海面多普勒谱特征对微波雷达海浪反演等领域具有重要的意义[1–2]。近年来,诸多学者针对海面微波散射场多普勒谱特征进行研究和实验。Plant和Keller[3]于1991年根据布拉格散射理论,由海浪谱模型推导出速度谱从而仿真获得回波的多普勒谱;姜文正等[4]2011年提出了微波散射场多普勒谱频移和谱宽的理论公式。然而这些研究都是基于岸基微波雷达,但对船载微波雷达回波多普勒谱特征研究较少。
船载雷达[5]在观测过程受海浪和海风的影响,不可避免产生六自由度运动,导致雷达回波多普勒谱的中心频率和谱宽发生变化。本文基于武汉大学自主研制的船载S波段微波多普勒雷达,结合海表面的散射模型,建立船舶运动模型,提出船载雷达回波多普勒谱的中心频率和谱宽的理论模型,并使用仿真多普勒谱的方法分析船载雷达多普勒谱,讨论了船舶不同运动状态下多普勒谱中心频率和谱宽的变化情况和规律。
1 海表面散射机理雷达回波多普勒谱与海表面的散射模型密切相关。海表面是由波峰、波谷、风浪、涌浪、碎浪、白浪以及泡沫等波浪成分组成,海面的空气扰动使得这些成分之间相互作用,从而导致海表面具有粗糙特性。当入射电磁波照射到海表面时,就形成了海杂波。
为了研究问题的方便,一般可以将海表面建模成复合散射模型[6]。海浪分为3种规模的波:第一类为毛细波,其波长与雷达发射波波长相当,与无线电波在海面产生布拉格散射;第二类为中规模波,其波长介于毛细波与雷达距离分辨率之间,主要对多普勒谱宽度有所贡献;第三类为空间可分辨的大规模波(即重力波),重力波调制了其他两类波,这种调制性的平流输送将产生多普勒速度的时间和空间序列。微波多普勒雷达利用多普勒效应测量海面较小照度区的水质点速度,利用海面轨道速度与海浪浪高之间的直接关系获取海浪谱及其他海浪参数。
2 船载S波段雷达多普勒谱 2.1 船载雷达运动模型图1是船载雷达的照射模型图,假设雷达安装在船舶的侧面,图中的6个序号分别代表6根天线。图中建立了船载坐标系O-XYZ,船的六自由度运动在X,Y,Z轴分别为:横滚和垂荡、纵摇和横荡、首摇和浮沉。

|
图 1 船载S波段雷达照射模型 Fig. 1 Irradiation model of ship-borne S-band radar |
基于武汉大学自主研发的船载S波段多普勒雷达的参数如下:工作频率为2.85 GHz,系统采用6个标准喇叭天线组成的天线结构,每根天线3 dB带宽为30°,均为垂直极化,6根天线呈半圆形排列,依次工作,扫描180°方位的海面信息。
船舶在海上运动时,不可避免地要受到海浪、海风和海流等海洋环境的影响,所以除舰船的前向运动之外,必然会存在着包括横摇、纵摇等6个自由度上的运动[7]。由于时刻作用于船体的波浪同时呈现出周期性和随机性两方面的特点,船舶在波浪中的运动规律也是周期性和随机性的结合。由于本文研究的重点在于船舶在波浪中存在运动时对架设于船上的微波雷达回波的影响,故船舶运动的模型可以在不失真实性的情况下做适当简化,提出了以周期运动为主的3次谐波统计模型来描述船舶运动的模型[8],3次谐波统计模型将船舶摇摆角看作3个谐波分量叠加而成。
根据中大型舰船的典型摇摆角时间历程,纵横摇自由度采用3次谐波叠加的方法,首摇自由度采用正弦波,可模拟海上摇摆的主要特性。为了模拟不同海况的摇摆状态,将摇摆谱分成高、中、低3档,高档对应6级海况,中档对应4~5级海况,低档对应2~3级海况,各次谐波的幅值、角频率见表1所示。
|
|
表 1 摇摆幅值、角频率 Tab.1 Swing amplitudes and angular frequency |
海面回波多普勒谱可以看成若干个独立的分量叠加而成。根据复合散射理论,海面由毛细波(布拉格相速度)、大尺度波(潮流和风漂流)和中尺度波(水质点轨道速度)组成。根据中心极限定理,多普勒谱服从高斯分布。假设微波雷达海洋回波信号的功率谱形式为:
| $S(f) = \frac{{{\sigma _{vv}}(\theta )}}{{\sqrt {2\pi \delta _f^2} }}\exp \left( { - \frac{{{{(f \pm {f_d})}^2}}}{{2\delta _f^2}}} \right),$ | (1) |
式中:
在岸基微波雷达中,多普勒频率
| ${f_d} = {f_c} + {f_o}_r + = \frac{{2{\upsilon _c}}}{{{\lambda _0}}} + \frac{{2{\upsilon _{or}}}}{{{\lambda _0}}},$ | (2) |
式中:
由于轨道速度呈现周期性运动的特点,微波多普勒谱频率不再是2个单一的频率尖峰,轨道速度的存在引入了多个频率分量,导致了微波雷达多普勒谱的展宽,谱宽的大小为:
| $\Delta {f_d} = \frac{{2\Delta {\upsilon _{or}}}}{{{\lambda _0}}} + 2{f_b}\text{。}$ | (3) |
其中:
当雷达处在船载平台之上,雷达会存在前向速度和摇晃速度,将在天线照射范围内不同方向的散射单元上产生径向速度分量,雷达接收的回波中附加了一个随方位角变化的多普勒频率,不仅会造成多普勒中心频率的偏移,而且会造成多普勒谱不同方向的展宽,船载上的微波雷达多普勒频率为:
| $\begin{split}&{f_d} = {f_c} + {f_o}_r + {f_{ship\_c}}(\theta ) + {f_{ship\_y}}(\theta ) = \frac{{2{\upsilon _c}}}{{{\lambda _0}}} + \frac{{2{\upsilon _{or}}}}{{{\lambda _0}}} +\\&\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2{\upsilon _{ship\_c}}(\theta )}}{{{\lambda _0}}} + \frac{{2{\upsilon _{ship\_y}}(\theta )}}{{{\lambda _0}}}{\text{。}}\end{split}$ | (4) |
新增加的
|
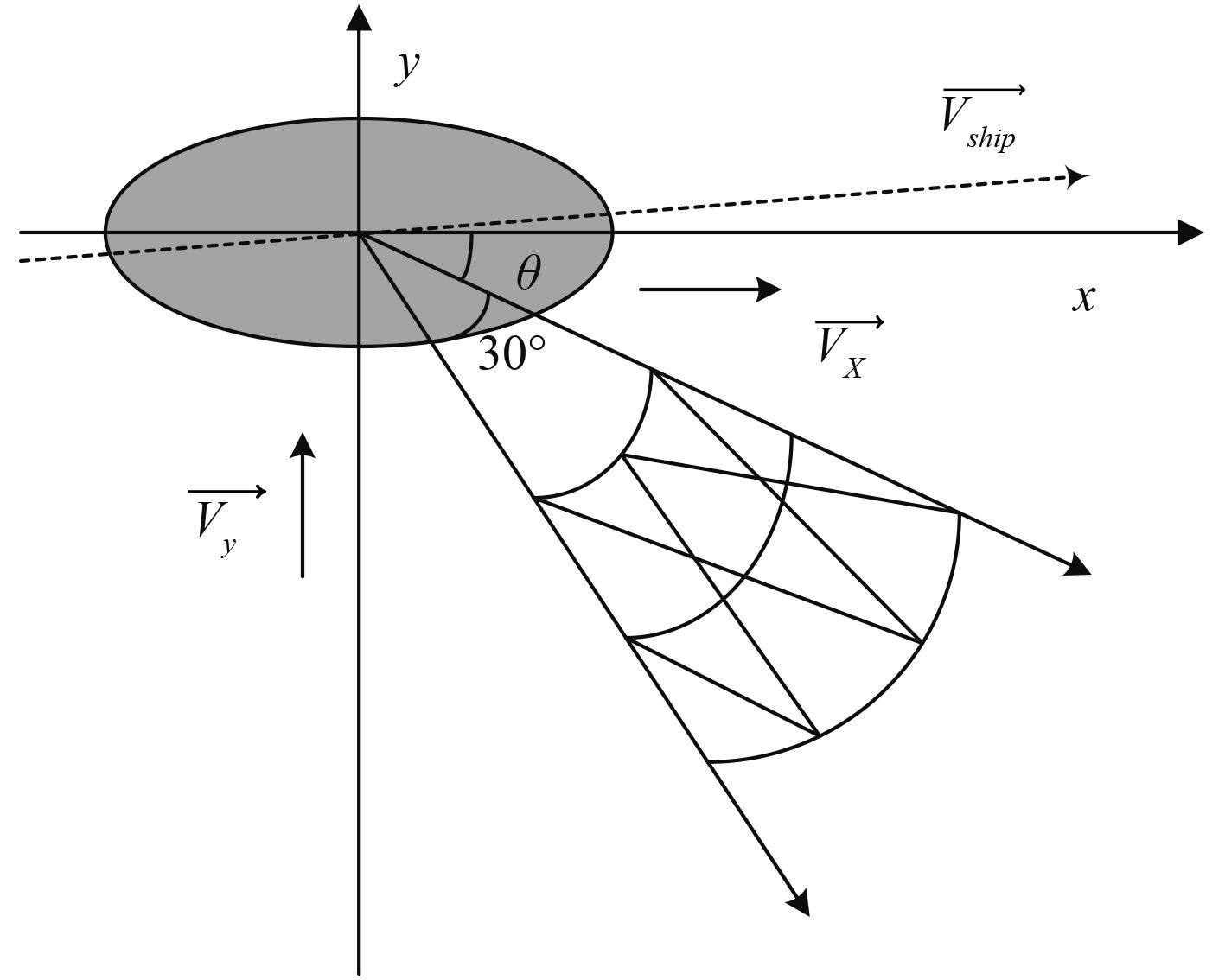
图 2 单天线照射海面俯视图 Fig. 2 The overlook view of the sea surface by a single antenna |
图2表示船载雷达单个天线照射海面的俯视图,船沿X方向行驶,天线照射范围为30°的海域,天线中心掠射角为3°,天线照射方位角为
| $\Delta {f_d} = \frac{{2\Delta \nu }}{{{\lambda _0}}} + 2{f_b} = \frac{{2({\nu _{\max }} - {\nu _{\min }})}}{{{\lambda _0}}} + 2{f_b}\text{。}$ | (5) |
其中:
由以上公式,结合Plant的方法[3],可以仿真出船载情况下的微波多普勒谱[9],并与岸基多普勒谱仿真进行对比分析。由于只考虑船前向运动、横滚和纵摇情况下的多普勒谱变化,而首摇、横荡、垂荡和浮沉影响较小,无需考虑它们对仿真带来的影响。
3 仿真结果分析多普勒谱仿真参数如下:船载雷达工作频率为2.85 GHz,采用垂直极化方式,掠射角3°,船的航向为正北方向,6根天线方位角范围分别为(0,30),(30,60),(60,90),(90,120),(120,150)和(150,180)。
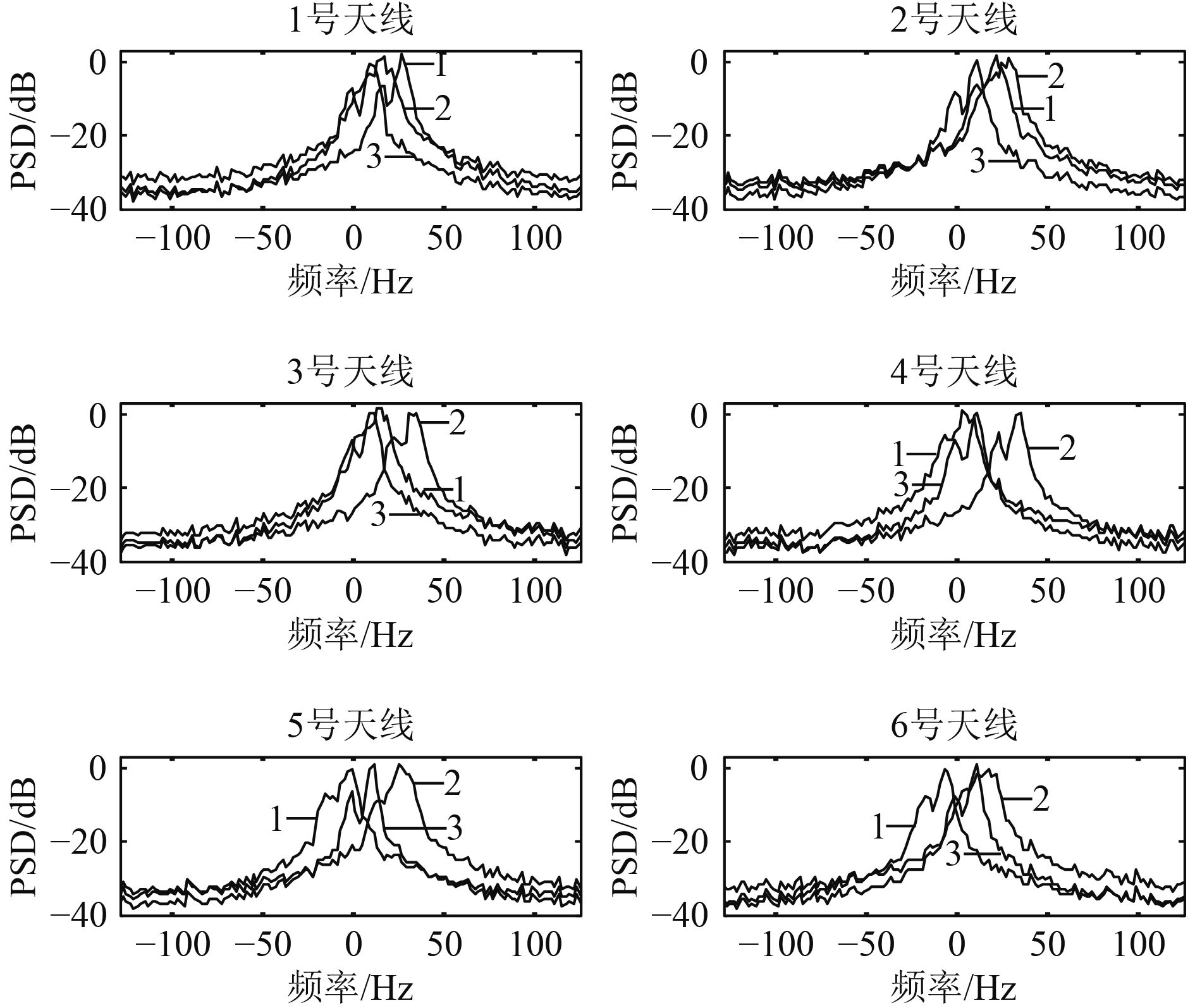
3.1 前向速度导致的多普勒谱如图所示,仿真得到的6根天线的多普勒谱中,线1代表船速为3 m/s,线2代表船速为5 m/s时、线3代表岸基无船速时。由图可见:

|
图 3 六根天线的多普勒谱 Fig. 3 Doppler spectrums of six antennas |
1)每根天线的多普勒谱特征不一样,随着船速的增大,多普勒谱中心频率偏移增大。
2)微波岸基雷达双峰比较明显,但在船载情况下展宽变得不可分辨,由于船速的存在,多普勒谱呈现出向一侧展宽的特点,使得求中心频率产生误差,船速越大,展宽宽度越大。
3)6根天线呈现相互对应的关系,1号和6号天线对应,2号和5号对应,3号和4号对应,中心频率向不同方向变化。
4)1号、6号天线与船速方向相近,得到的速度分量较大,导致中心频率的变化明显,但谱展宽宽度较小,3号和4号天线与船速方向几乎垂直,得到的速度分量较小,导致中心频率的变化较小,但谱展宽宽度较大。
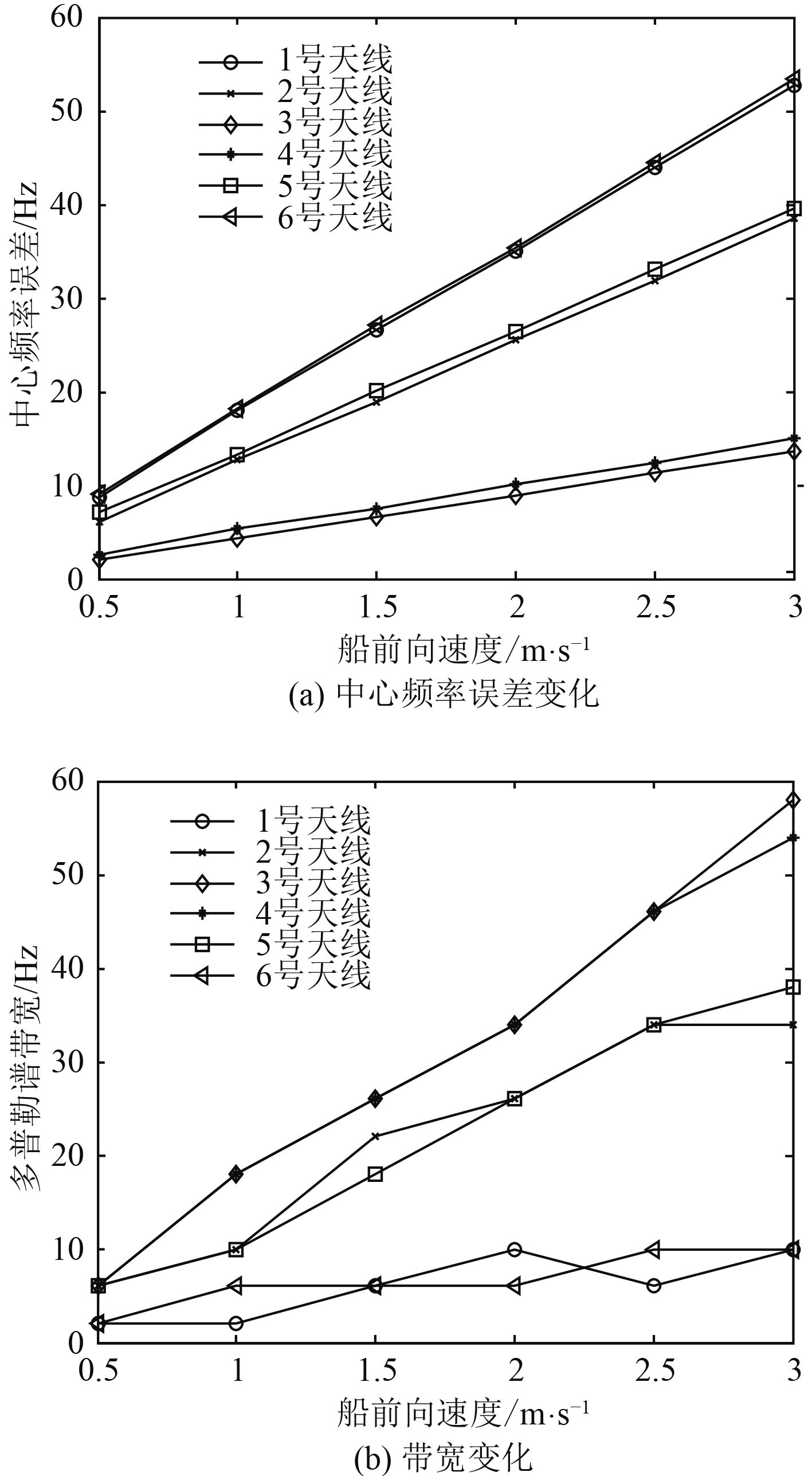
综上分析,由于船前向速度的存在,使得多普勒谱频率偏移和多普勒谱向一侧展宽,导致估计多普勒谱中心频率存在不小的误差。图5是中心频率误差和带宽变化随船速变化的关系。
|
图 4 多普勒谱中心频率和带宽变化图 Fig. 4 Changes in the center frequency and bandwidth of the Doppler spectrum |
图4表明:中心频率的误差和谱宽的变化与之前的分析一致,6根天线中心频率的误差和谱宽大小随着船速的增长而呈线性增长趋势,并且1号和6号天线中心频率误差较大,2号和5号居中,3号和4号误差较小,而谱宽大小变化与之相反。
3.2 横滚和纵摇速度导致的多普勒谱当船在海中不断发生横滚和纵摇运动时,会在X轴和Y轴产生速度变量,该速度变量值近似周期变化,根据之前建立的3次谐波运动模型,对摆动角度求导,便可得到船舶摇晃姿态的瞬时角频率,假设船舶转动圆心为重心,则可得甲板上距重心距离一定点的线速度。接下来仿真出纵摇和横滚运动导致的多普勒谱。
|
图 5 六根天线的多普勒谱 Fig. 5 Doppler spectrums of six antennas |
如图5所示,线1代表纵摇运动,线2代表横滚运动,线3代表岸基无船速时。可以发现纵摇运动在X轴产生速度分量时,6根天线多普勒谱的变化形式和趋势与前向速度引起的相一致;横滚运动在Y轴产生速度分量时,6根天线多普勒谱的变化形式和趋势与前向速度引起的正好相反,1号和6号天线主要是谱展宽明显,中心频率变化小,3号和4号天线中心频率变化明显,谱展宽较小,而且6根天线得到的速度分量都为正,中心频率和谱展宽都向正方向。
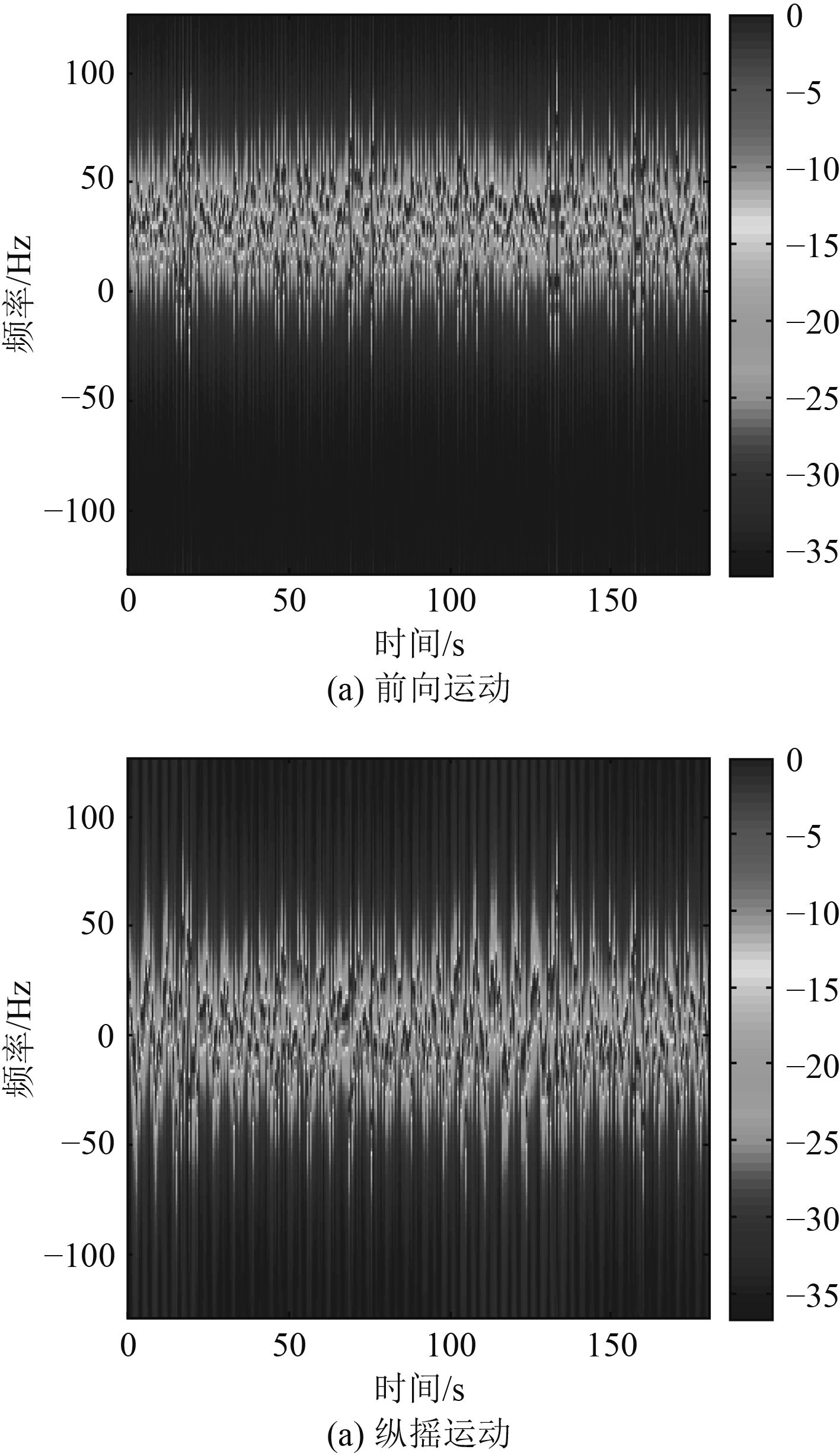
横滚和纵摇运动产生的速度变量与前向运动最主要的区别在于速度分量周期变化,其多普勒谱变化的不同主要是在时间域上,下面仿真出2号天线前向运动和纵摇运动的时间多普勒谱,规定前向运动的速度等于纵摇运动速度的最大值。
|
图 6 时间多普勒谱仿真结果 Fig. 6 Simulation results of time Doppler spectrums |
图6表明前向运动在整个时间域内引起的多普勒频移比纵摇运动大,但纵摇运动产生的谱宽比前向运动大得多,符合纵摇运动产生的速度分量是周期变化的这一规律。
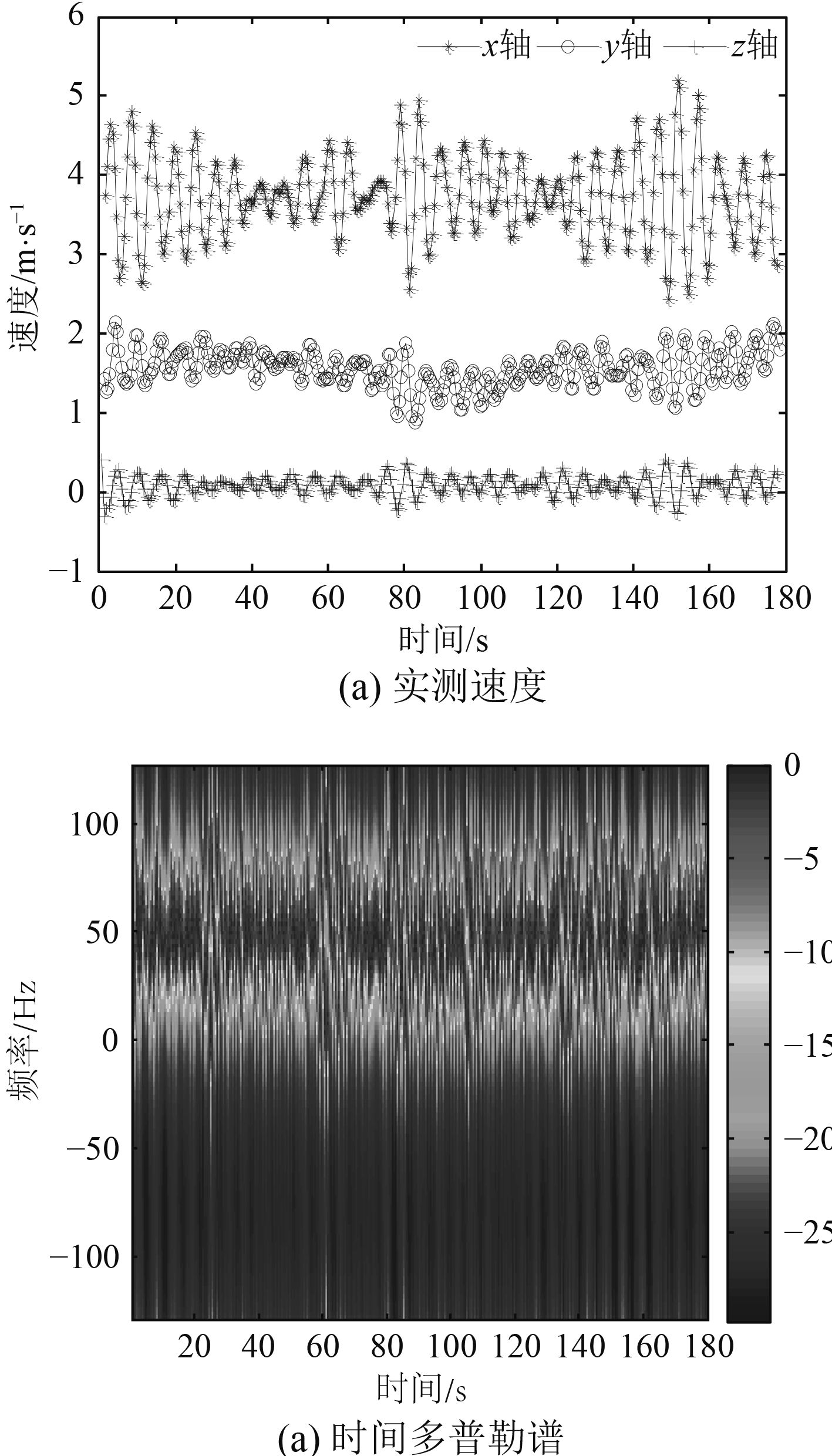
3.3 实际海况中的多普勒谱当船舶在实际海况中时,船的运动是前向运动和六自由度运动的叠加,使得多普勒谱既有前向运动谱的特征,又有横滚和纵摇运动谱的特征,导致多普勒中心频率变化更加明显,谱展宽的宽度也更宽。根据2016年6月南海实验的一段3 min实测船速,由MTI_G传感器测得,仿真得到3号天线雷达时间多普勒谱。
|
图 7 实测速度和时间多普勒谱仿真结果 Fig. 7 The measured velocity and the simulation result of the time Doppler spectrum |
可见,船的X轴和Y轴速度基本符合简谐运动的特征,由于偏航运动,X轴和Y轴都叠加了船前向速度分量,Z轴的速度基本为0。从时间多普勒谱中可以看出,中心频率的变化更加明显,且谱宽较前面单独运动时宽度也更宽。
|
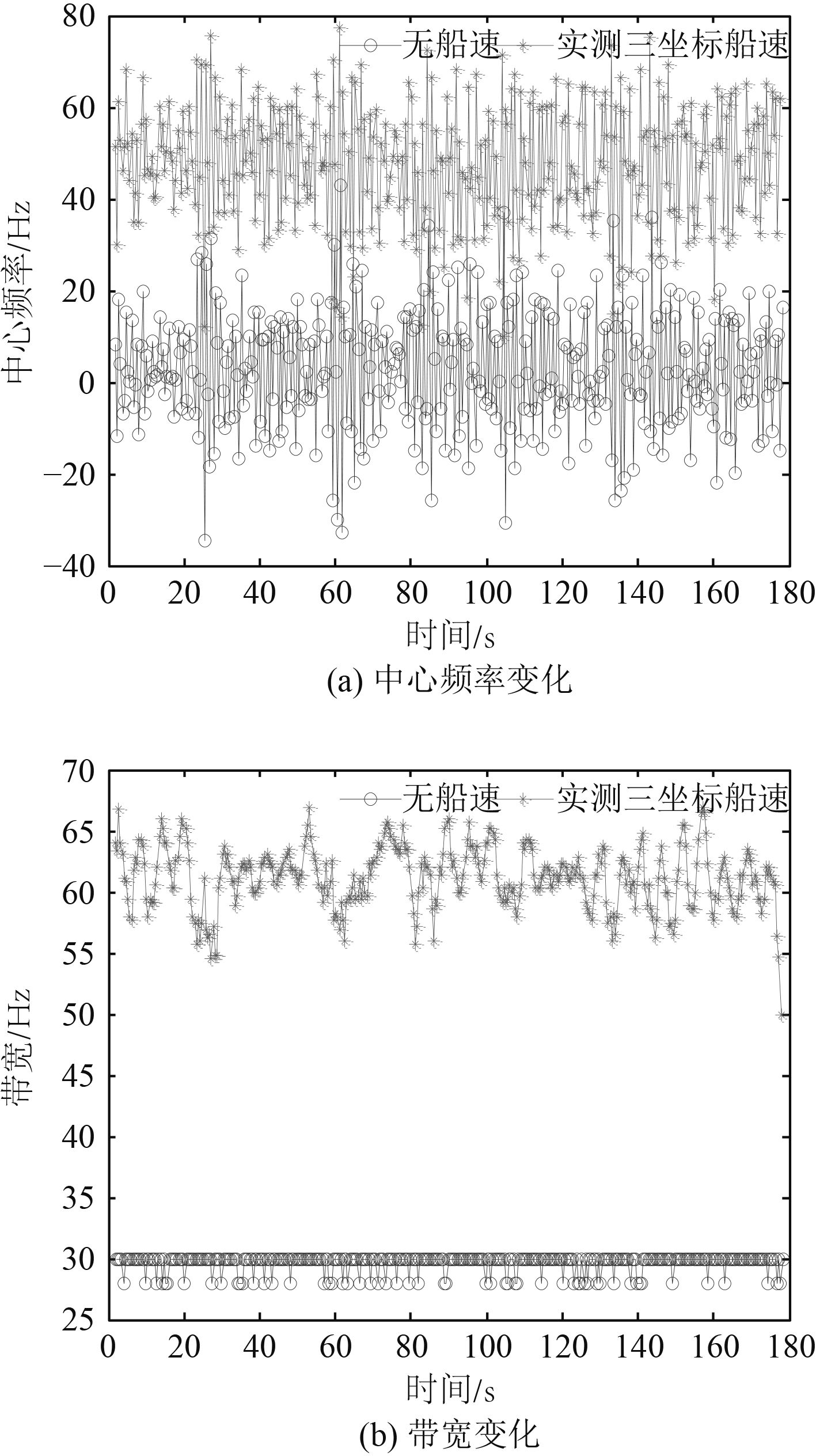
图 8 多普勒谱中心频率和带宽变化图 Fig. 8 Changes in the center frequency and bandwidth of the Doppler spectrum |
图8表明:3号天线中心频率的变化非常明显,同样谱宽也要大得多,最大接近70 Hz,与上面的分析一致。
4 结 语本文推导得到了船载S波段微波多普勒雷达回波的多普勒谱中心频率和谱宽的理论模型,并使用仿真多普勒谱的方法分析了船载雷达多普勒谱,发现船前向运动和横纵摇运动6根天线多普勒谱变化的不同点和规律,并指出了6根天线多普勒谱中心频率误差和谱宽变化与船速的关系,船速愈大,中心频率误差愈大,谱宽愈大;最后给出一段实测船速,并仿真出雷达时间多普勒谱,发现中心频率的变化明显,且谱展宽程度较大。
| [1] | MONAKOV A A, BLAGOVESHCHENSKY D V. A method of spectral moment estimation[J]. Geoscience and Remote Sensing, IEEE Transactions on, 1999, 37 (2): 805–810. DOI: 10.1109/36.752196 |
| [2] | 陈泽宗, 钟建波, 张龙刚, 等. 基于频移迭代的微波多普勒谱中心频率估算算法[J]. 华中科技大学学报(自然科学版), 2016, 44 (2): 70–74. |
| [3] | W J. Evidence of bragg scattering in microwave doppler spectra of sea return[J]. Journal of Geophysical Research, 1990, 95 (C9): 299–310. |
| [4] | 姜文正, 袁业立, 王运华, 等. 海面微波散射场多普勒谱特性研究[J]. 物理学报, 2012, 61 (12): 124213–124213. DOI: 10.7498/aps.61.124213 |
| [5] | 柳世华, 张莲芳, 沈桂明. 舰载雷达信号处理机舰速补偿的实验研究[J]. 舰船科学技术, 1993, 6 : 33–39. |
| [6] | ROMEISER R, SCHMIDT A, ALPERS W. A three-scale composite surface model for the ocean wave-radar modulation transfer function[J]. Journal of Geophysical Research Atmospheres, 1994, 99 (C5): 9785–9801. DOI: 10.1029/93JC03372 |
| [7] | 廖铭声. 船舶横摇计算公式及其应用[J]. 舰船科学技术, 1992, 2 : 39–46. |
| [8] | 李学忠, 黄守训, 林其生, 等. 船用摇摆试验台建模和控制系统设计[J]. 电气传动, 2006, 36 (11): 11–15. DOI: 10.3969/j.issn.1001-2095.2006.11.003 |
| [9] | 陈泽宗, 金燕, 等. 微波雷达海洋回波多普勒频谱的数值仿真[J]. 武汉大学学报(信息科学版), 2013, 9 (38): 1048–1051. |
 2018, Vol. 40
2018, Vol. 40
