伴随着能源危机以及环境安全问题的产生,新能源在节能减排和经济环保上的优势愈加体现。各国加强环保措施,并制定配套政策以促进新能源在船舶上的研究应用。其中以风能、核能、潮汐能、太阳能、燃料电池等为主的新能源分布式发电系统作为辅助动力也越来越多应用于船舶[1 – 2]。并网逆变器是新能源电能并入船舶电网的关键接口,其能将新能源产生的直流电能逆变为交流电能并入船舶电网[3]。相对于无穷容量的陆上电网来说,船舶电网容量有限。这种电网线路短、负荷密度大,受冲击性、波动性负载影响较大,大量使用各种电子控制设备,会产生大量的谐波。新能源并网逆变器通常采用的PWM(脉冲宽度调制)技术会产生高频谐波电流注入船舶电网,造成对船舶电网的谐波污染,对船舶电网的稳定运行不利,因此要在并网逆变器与船舶电网之间加滤波设备来抑制这些谐波[4 – 5]。
通常滤波器有L、LC、LCL型滤波器,LCL型滤波器相对于L型滤波器,更能滤除高频次谐波,而LC型滤波器,在并网状态下,由于船舶电网电压钳制作用,只有电感L起到滤波作用,电容C对于逆变器来说只是个负载,所以在船舶新能源并网逆变器系统中采用LCL滤波器。但是LCL滤波器是一个包含L1、C,L2的3阶系统,会在谐振频率处产生一个谐振尖峰,引起系统震荡,造成系统不稳定,并且传统的并网逆变器LCL滤波器参数的设计很难满足船舶新能源逆变并网要求[6 – 7],因此提出了采用遗传算法来对船舶电网网侧LCL滤波器参数进行优化设计的方法。并通过搭建仿真模型验证其优越的滤波性能。
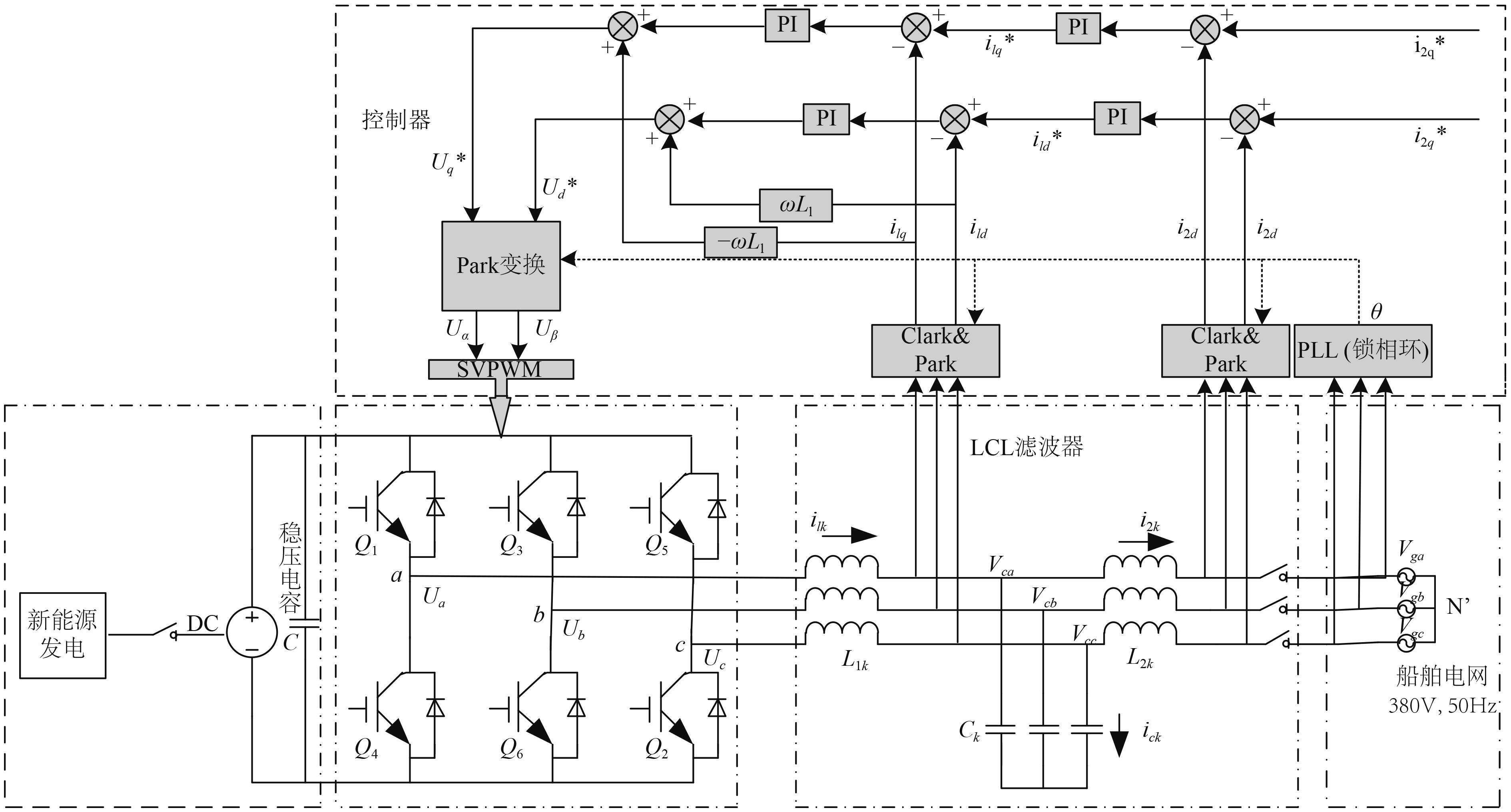
1 船舶新能源并网控制结构船舶新能源逆变并网的拓扑结构如图1所示。船舶新能源发出直流电,经过稳压电容并上逆变器,并网逆变器采用三相三桥臂两电平逆变器,将LCL滤波器采用星型连接方式并入船舶电网。其中,LCL滤波器中L1K为滤除逆变器侧谐波电感,CK为滤波电容,L2K为船舶电网测电感(k=a,b,c)。控制部分首先通过电网电压锁相环获得与d轴同相位的电网电压矢量的相角θ,再采用船舶电网侧电流外环、逆变器侧电流内环双闭环控制回路来完成。
|
图 1 船舶新能源并网控制结构 Fig. 1 New energy grid-connected control structure for ships |
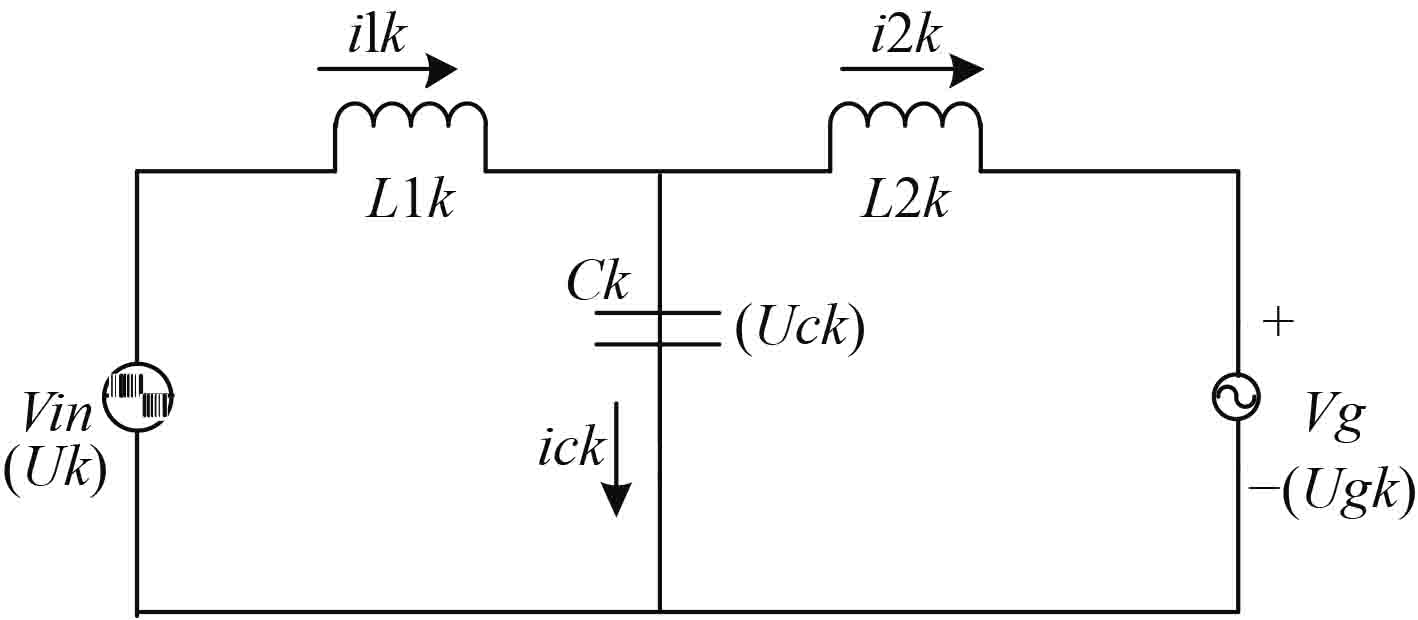
将图1三相并网LCL滤波器结构简化为如图2所示的单相逆变并网LCL滤波电路,其中vin为新能源发电通过逆变器输出电压,vg为船舶电网电压。
|
图 2 LCL滤波器单相等效电路 Fig. 2 LCL filter single-phase equivalent circuit |
在三相abc坐标系下由基尔霍夫电压定律和基尔霍夫电流定律可得到新能源逆变并网LCL滤波器的数学模型:
| $\left\{\!\!\! {\begin{array}{*{20}{c}}{{{{L}}_{1{{k}}}}\frac{{{\rm{d}}{{{i}}_{1{{k}}}}}}{{{\rm{d}}t}} = {{{u}}_{{k}}} - {{{u}}_{{{ck}}}}}, \\[8pt]{{{{L}}_{2{{k}}}}\frac{{{\rm{d}}{{{i}}_{2{{k}}}}}}{{{\rm{d}}t}} = {{{u}}_{{{ck}}}} - {{{u}}_{{{gk}}}}}, \\[8pt]{{{{C}}_{{k}}}\frac{{{\rm{d}}{{{u}}_{{{ck}}}}}}{{{\rm{d}}t}} = {{{i}}_{1{{k}}}} - {{{i}}_{2{{k}}}}}{\text{。}}\end{array}} \right.$ | (1) |
虽然abc坐标模型物理意义简单明了,但是在实际控制时由于变量为时变交流量,难以进行系统控制器的设计,因此可以将abc坐标系PARK变换到以电网电压向量角速度同步旋转的dq坐标系中进行控制。在同步旋转坐标系下并网逆变器的数学模型为:
| $\left\{ {\begin{array}{*{20}{l}}{\frac{{{\rm{d}}{i_{1{\rm{d}}}}}}{{{\rm{d}}t}} = \omega {i_{1q}} - \frac{1}{{L1}}{u_{c{\rm{d}}}} + \frac{1}{{L1}}{u_{\rm{d}}}},\\[5pt]{\frac{{{\rm{d}}{i_{1q}}}}{{{\rm{d}}t}} = - \omega {i_{1{\rm{d}}}} - \frac{1}{{L1}}{u_{c{\rm{q}}}} + \frac{1}{{L1}}{u_q}},\\[5pt]{\frac{{{\rm{d}}{i_{2{\rm{d}}}}}}{{{\rm{d}}t}} = \omega {{\rm{i}}_{2{\rm{q}}}} + \frac{1}{{{\rm{L}}2}}{{\rm{u}}_{{\rm{cd}}}} - \frac{1}{{L2}}{u_{\rm{d}}}},\\[5pt]{\frac{{{\rm{d}}{i_{2q}}}}{{{\rm{d}}t}} = - \omega {i_{2{\rm{d}}}} + \frac{1}{{L2}}{u_{cq}} - \frac{1}{{L2}}{u_q}},\\[5pt]{\frac{{{\rm{d}}{u_{c{\rm{d}}}}}}{{{\rm{d}}t}} = \frac{1}{C}{i_{1{\rm{d}}}} - \frac{1}{C}{i_{2{\rm{d}}}} + \omega {u_{c{\rm{q}}}}},\\[5pt]{\frac{{{\rm{d}}{i_{c{\rm{q}}}}}}{{{\rm{d}}t}} = \frac{1}{C}{i_{1q}} - \frac{1}{C}{i_{2q}} - \omega {u_{c{\rm{d}}}}}{\text{。}}\end{array}} \right.$ | (2) |
其中k=a,b,c表示a,b,c三相,Park变换过后,三相交流量变为两相坐标下的直流变量,进而简化了控制器的设计。可推导出vin到并网电流i2的传递函数为
| $\begin{split}{{{G}}_{{{LCL}}}}\left( {{s}} \right) \!= \frac{{{{{i}}_2}\left( {\rm{s}} \right)}}{{{{{v}}_{{{in}}}}\left( {{s}} \right)}} \!&=\! \frac{1}{{{{{s}}^3}{{{L}}_1}{{{L}}_2}{{C}} + {{s}}\left( {{{{L}}_1} + {{{L}}_2}} \right)}} \!=\\&\! \frac{1}{{{{s}}{{{L}}_1}{{{L}}_2}{{C}}{{{s}}^2}}}\frac{1}{{{{{s}}^{2 + }}{{\omega }}_{{r}}^2}},\end{split}$ | (3) |
式中:ωr为LCL滤波器的产生谐振时的角频率。
| ${\omega _r} = \sqrt {\frac{{{L_1} + {L_2}}}{{{L_1}{L_2}C}}} {\text{。}}$ | (4) |
谐振频率为
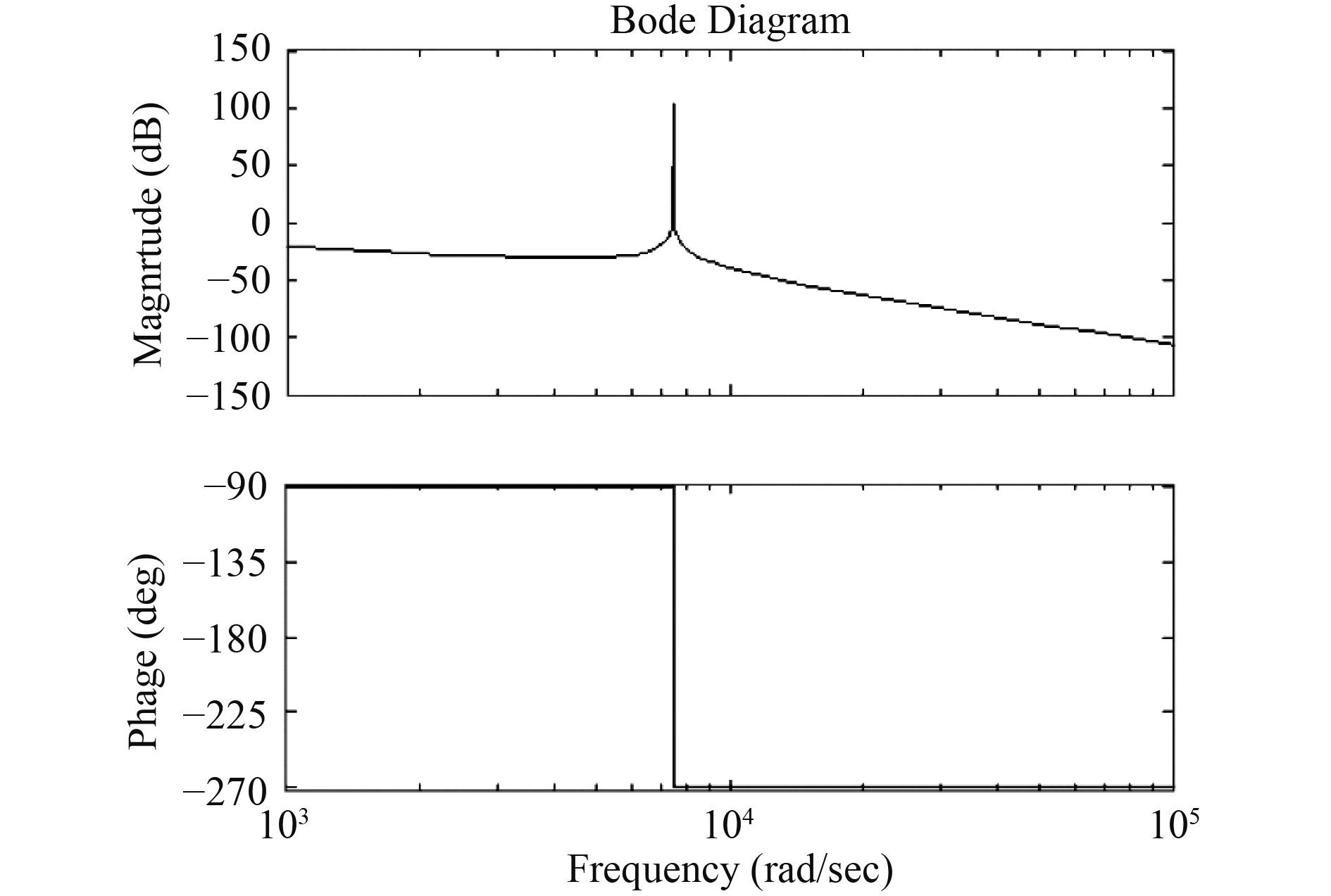
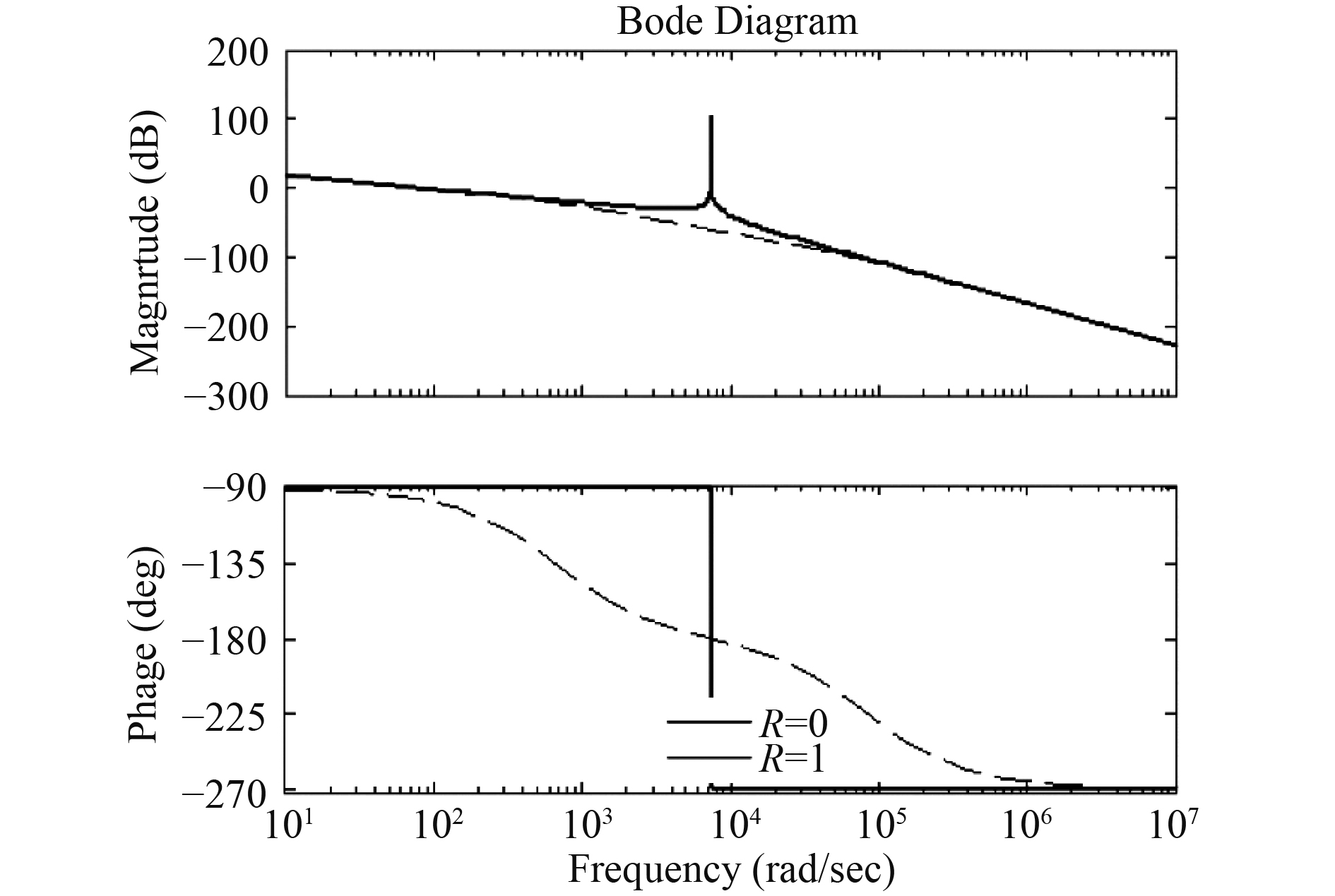
根据vin到并网电流i2的传递函数,画出如图3所示波特图,图中显示,LCL滤波器的频率响应在谐振频率fr处产生谐振尖峰,与此同时相位存在–180°跳变。因而致使在其谐振角频率ωr处的幅值增大,进而导致并入船舶电网的高次谐波含量增加。为了抑制LCL滤波器谐振尖峰,采用在滤波电容或者电感上串并联电阻的无源阻尼方法,从图4的幅频特性曲线虚线上可以看出,电阻R与电容并联时谐振尖峰得到很好抑制,而且还保留了LCL滤波器在低频段和高频段的幅频特性,从而保证了系统的高频谐波衰减能力和低频增益[8 – 12]。因此在LCL滤波器设计中与电容C并联一个电阻Rc来抑制谐振尖峰,本文取Rc=1 Ω。
|
图 3 LCL滤波器的幅频特性 Fig. 3 Amplitude-frequency characteristics of LCL filter |
|
图 4 谐振抑制幅频特性曲线 Fig. 4 Resonance suppression amplitude-frequency characteristic curve |
船舶新能源并网系统中,LCL型滤波器的电感L1是将并网逆变器的输出电压转化为并网电流i1。如果L1取值小,那么纹波电流增大。但是当L1取值偏大时,直流电压利用效率会降低,其主要是通过对并网电流变化率的抑制来影响系统的动态性能;滤波电容C和船舶电网侧L2主要是对并入船舶电网的高次谐波分量进行滤除。
滤波器设计时需要对总电感LT(LT=L1+L2)进行约束,总电感值越大滤波效果越小,但同时系统的跟踪性能会较小,所以在总电感LT设计时需要综合考虑系统的动态性和滤波效果,LT满足下式:
| ${L_T} = \frac{{{E_m} \sin\varphi + U_m^2 + \sqrt {E_m^2{\sin^2}\varphi + U_m^2 - E_m^2} }}{{\omega {I_{mp}}}},$ | (5) |
式中:Im为相电流峰值;Em为并网相电压的峰值;ω为基波角频率;φ为功率因数角;在SVPWM调制模式下,Um为逆变器输出相电压的峰值,可达到
| ${{{L}}_{{T}}} \leqslant \frac{{\sqrt {\frac{{U_{dc}^2}}{3} - E_m^2} }}{{\omega {I_m}}}{\text{。}}$ | (6) |
图(1)中当A相上面的开关管,B相,C相下面的开关管(即Q1、Q6、Q2)导通时,此时并网逆变器A相的纹波电流最大。
| $\Delta {I_{\rm ripple - max}} = \frac{{{U_{dc}}}}{{4\sqrt {3{L_T}{f_{sw}}} }},$ | (7) |
式中:fsw为逆变器开关频率;
| ${L_T} = \frac{{{U_{dc}}}}{{4\sqrt 3 \Delta {I_{\rm ripple - {\rm max}}}{f_{sw}}}}{\text{,}}$ | (8) |
根据式(6)和式(8)得[11]:
| $\frac{{{{{U}}_{{{dc}}}}}}{{4\sqrt 3 \Delta {{{I}}_{{\rm{ripple}} - {\rm{max}}}}{{{f}}_{{{sw}}}}}} \leqslant {{{L}}_{{T}}} \leqslant \frac{{\sqrt {\frac{{{{U}}_{{{dc}}}^2}}{3} - {{E}}_{{m}}^2} }}{{{\rm{\omega }}{{{I}}_{{m}}}}}{\text{,}}$ | (9) |
一般取
滤波电容C选取时,需要考虑滤波电容C在并网时产生的无功功率。引入的滤波电容C过大时,电容产生的无功功率大,逆变器的功率变换能力降低。一般滤波电容产生的基波无功功率不超过逆变并网系统额定功率的5%[13] ,则有:
| ${\rm{C}} \leqslant 5\% \times \frac{P}{{3 \times 2 \times \pi \times {f_n}E_m^2}}{\text{,}}$ | (10) |
LCL型滤波器具有低通滤波器的特性,为了更好发挥LCL滤波器的优势,高效抑制高频谐波,且对开关频率控制并网逆变器不产生影响。则谐振频率fres取值设定式(11)约束范围。
| $10{f_b} \leqslant{f_{res}} \leqslant \frac{{{f_s}}}{2}\text{。}$ | (11) |
式中:fres为谐振频率;fb为基波频率;fs为控制逆变器开关频率。
3 基于遗传算法LCL滤波器参数优化遗传算法是一种寻优算法,它借鉴了生物的物竞天择和自然遗传变异机制,将变量编译为染色体,利用编码技术,建立最优解目标函数,然后模拟遗传过程中发生的染色体复制、交叉、和变异等现象,不断迭代,产生最适宜的种群、求出最优解。
3.1 染色体编码LCL滤波器参数包括L1、L2、C和RC,其中RC用于谐振抑制取RC=1 Ω,对另外3个参数采用遗传算法寻求3个参数最优解时,可将染色体表示为向量X=[L1 L2 C]。根据式子(9),式(10),式(11)确定的LCL滤波器参数的约束条件,对变量采用二进制编码的方式,将代表的个体表示为{0,1}二进制字符。
3.2 适应度函数建立适应度函数为遗传算法在寻优过程中仅依靠的依据,直接影响遗传算法的收敛速度和最优解的寻求。由于在开关频率及其整数倍处电流谐波较大,因此,适应度函数选择开关频率次的谐波衰减度。建立的适应度函数为:
| ${{{f}}_{{{fitness}}}} = {{d}} = \frac{{{{{i}}_{\rm{g}}}\left( {{{{h}}_{{{sw}}}}} \right)}}{{{{i}}\left( {{{{h}}_{{{sw}}}}} \right)}} \approx \left| {\frac{{{{Z}}_{{{LC}}}^2}}{{{\rm{\omega }}_{{{res}}}^2 - {\rm{\omega }}_{{{sw}}}^2}}} \right|,$ | (12) |
其中d为谐波衰减率;
| $Z_{LC}^2 = {({L_2}C)^{ - 1}},\;{\omega _{res}} = 2\pi {f_{res}},\;{\omega _{sw}} = 2\pi {f_{sw}}{\text{。}}$ |
遗传算法是基于无约束的优化算法,而优化有约束的问题时,要将优化模型转化为无约束的问题通常采用罚函数方法。该方法的基本思路是:计算其适应度时,对于染色体不满足约束条件的,加入一个罚函数,使该染色体适应度降低,降低该个体被遗传到下一代群体中的机会[14]。基于此本文采用罚函数方法,建立了新的适应度函数:
| ${{{F}}_{{{fit}}}} = \left\{\!\!\!\! \begin{array}{l}{{\rm{f}}_{{\rm{fitness}}}}\;\;\;\;\;\;,\;\; x{\text{满足约束条件}}\\{{\rm{f}}_{{\rm{fitness}}}} - \infty \;\;\;,\;\; x{\text{不满足约束条件}}{\text{。}}\end{array} \right.$ | (13) |
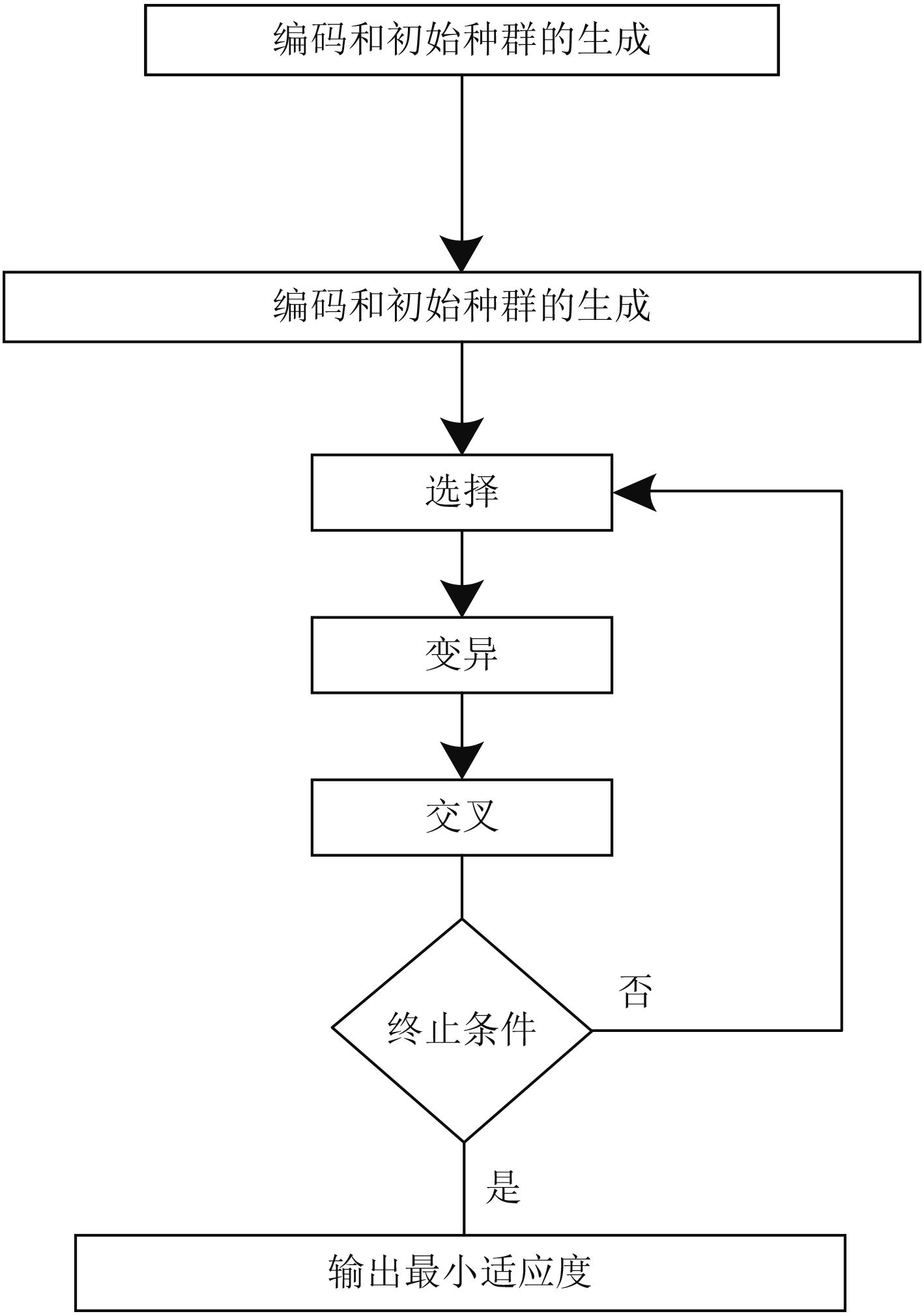
运用遗传算法在求解船舶并网逆变器LCL滤波器优化问题时,其基本求解流程如图5所示。
1)产生规模为NIND=70的初始种群;
2)经过研究比较,设定最大遗传代数MAXGEN=2 000,变异GGAP=0.1,交叉概率PM=0.8;
3)对种群中各个个体的适应度进行计算;
4)对群体进行选择运算;
5)对群体进行交叉运算;
6)变异运算,求得下一代种群;
7)终止条件判断。
|
图 5 遗传算法流程图 Fig. 5 Genetic algorithm flow chart |
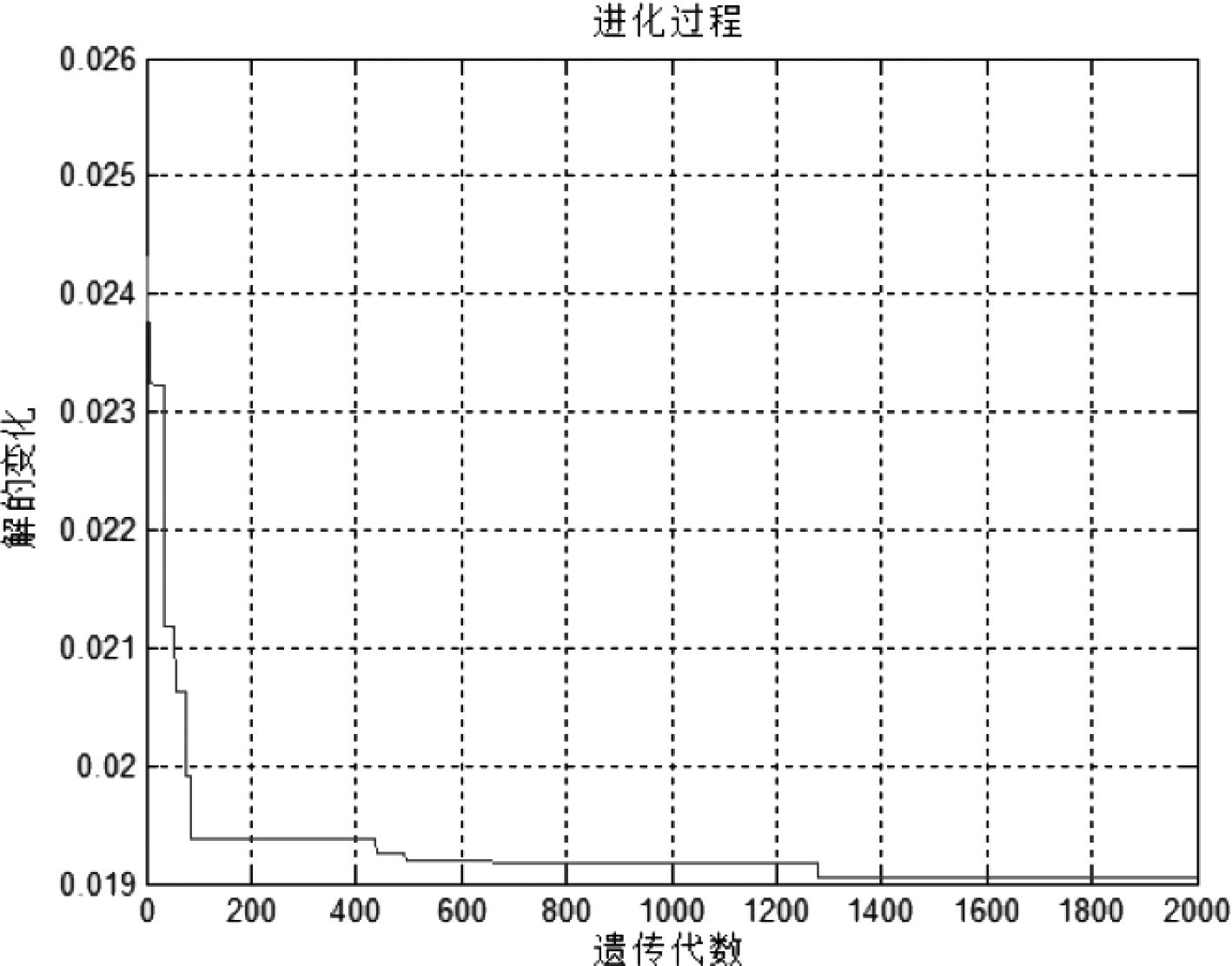
如果选择的所有个体都已经满足条件,并且连续三代计算出的适应度都小于某个设定阈值,那么就可以认为此刻算法已经收敛,然后选择最优个体作为输出,遗传算法寻找最优解结束。最终遗传算法得到最优解的过程如图6所示,输出适应度值稳定在0.019左右。
|
图 6 遗传算法寻求最优解变化图 Fig. 6 Genetic algorithm to seek the optimal solution change graph |
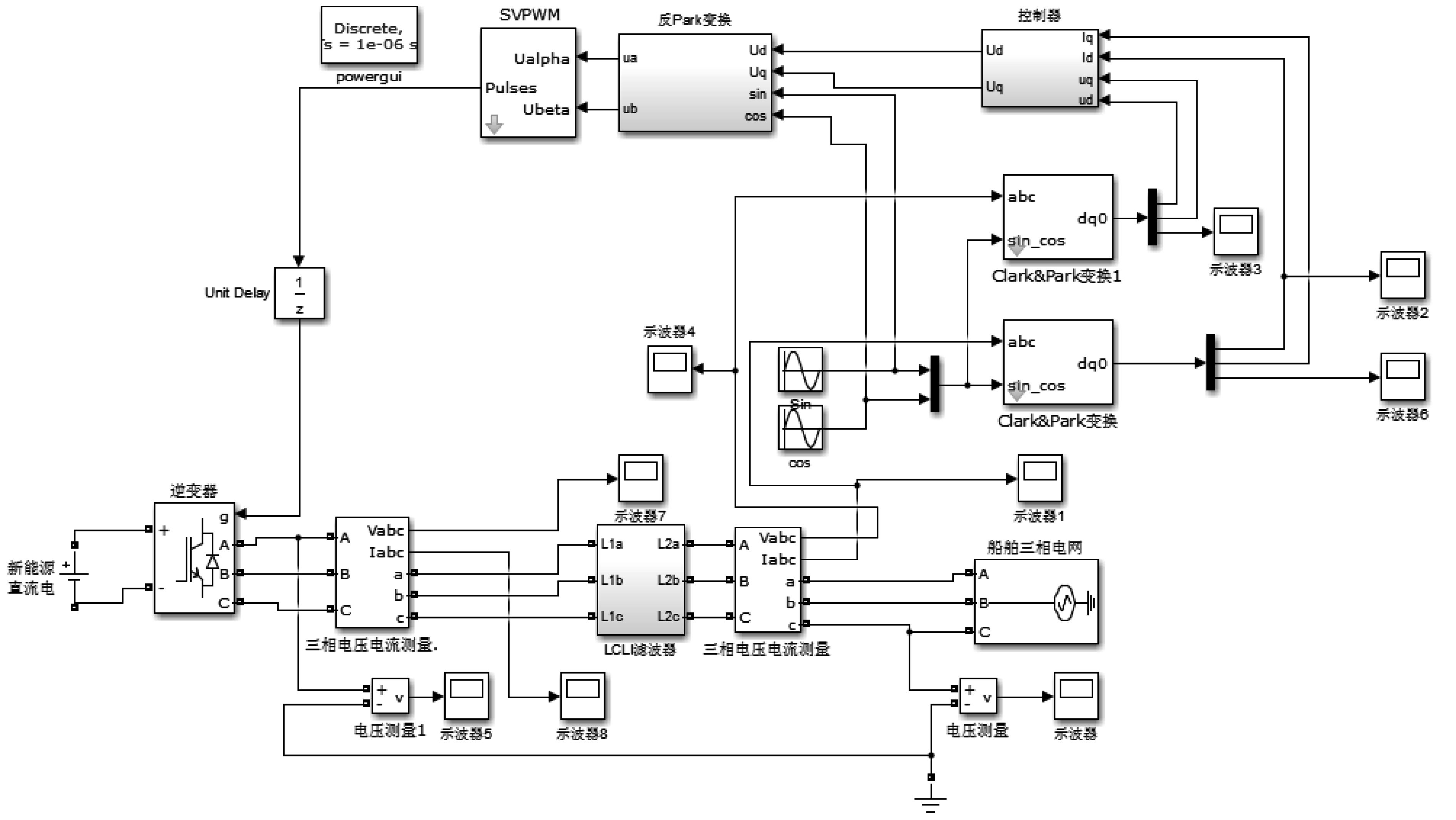
本文采用遗传算法对船舶新能源逆变并网逆变器LCL型滤波器参数优化设计,为了验证该算法寻求的最优解有效抑制谐波含量并符合并网要求,搭建了基于Matlab/Simulink新能源逆变并网系统仿真模型,如图(7)所示仿真参数为:额定功率23 kW,交流电压380 V,50 Hz,直流电压800 V,逆变器开关频率10 000 Hz。
|
图 7 基于LCL滤波器船舶新能源逆变并网仿真系统 Fig. 7 Grid connected simulation system of new energy inverter based on LCL filter |
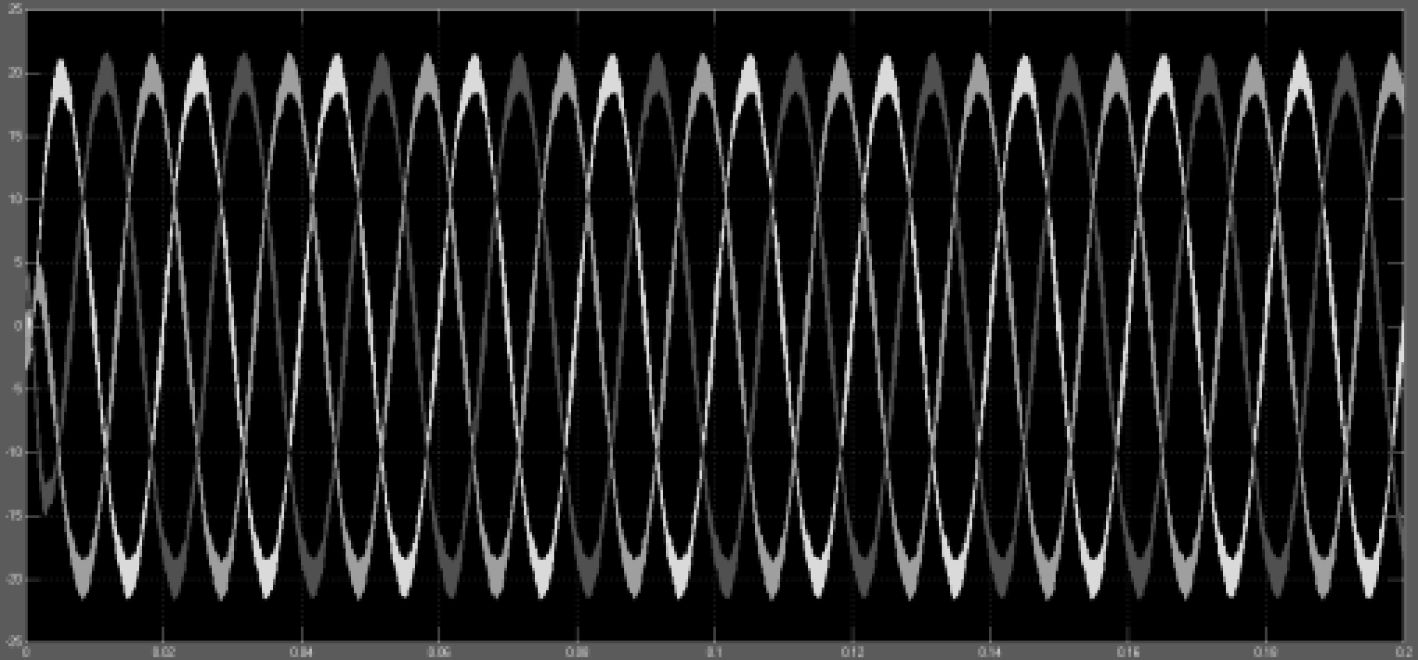
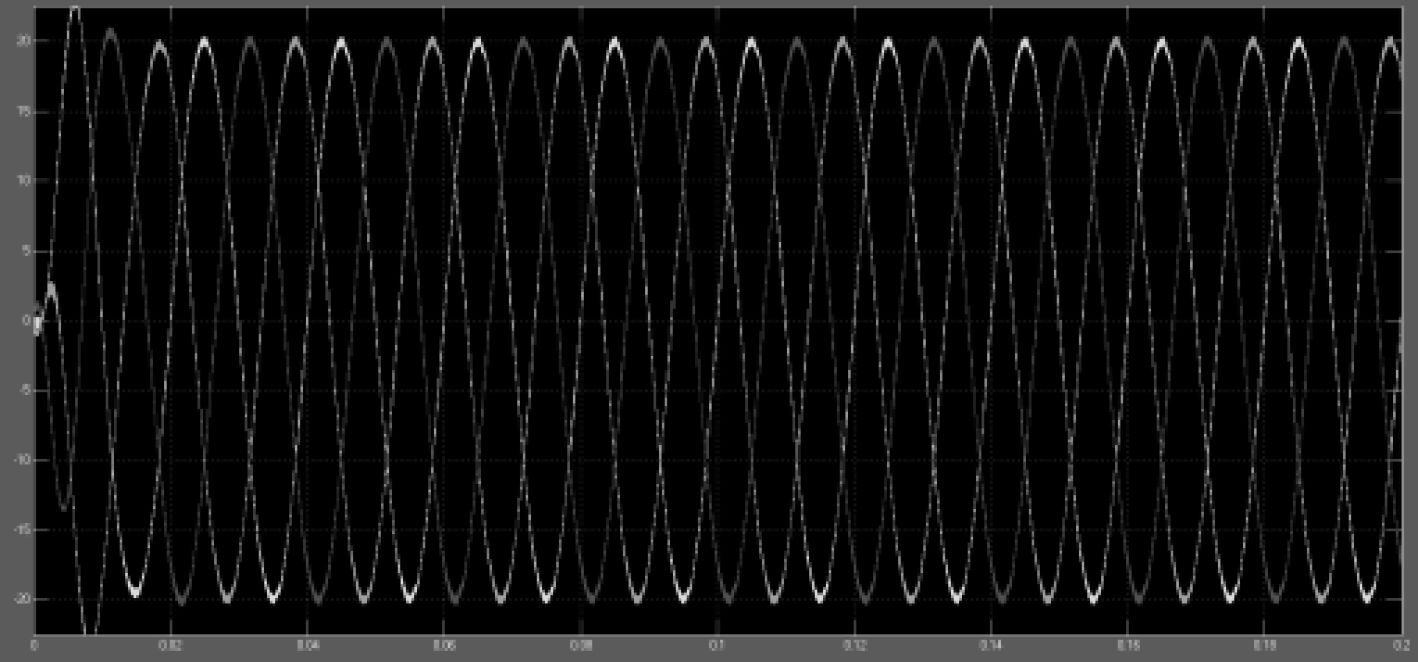
传统试凑法对LCL滤波器参数设计得到L1=0.56 mH,L2=1.53 mH,C=52 μF,仿真并网电流波形如图8所示。采用遗传算法得到L1=1.711 mH,L2=7.642 mH,C=63.677 μF,仿真并网电流波形如图9所示。
|
图 8 传统算法并网电流波形 Fig. 8 Traditional algorithm grid - connected current waveform |
|
图 9 遗传算法并网电流波形 Fig. 9 Genetic algorithm and grid - connected current waveform |
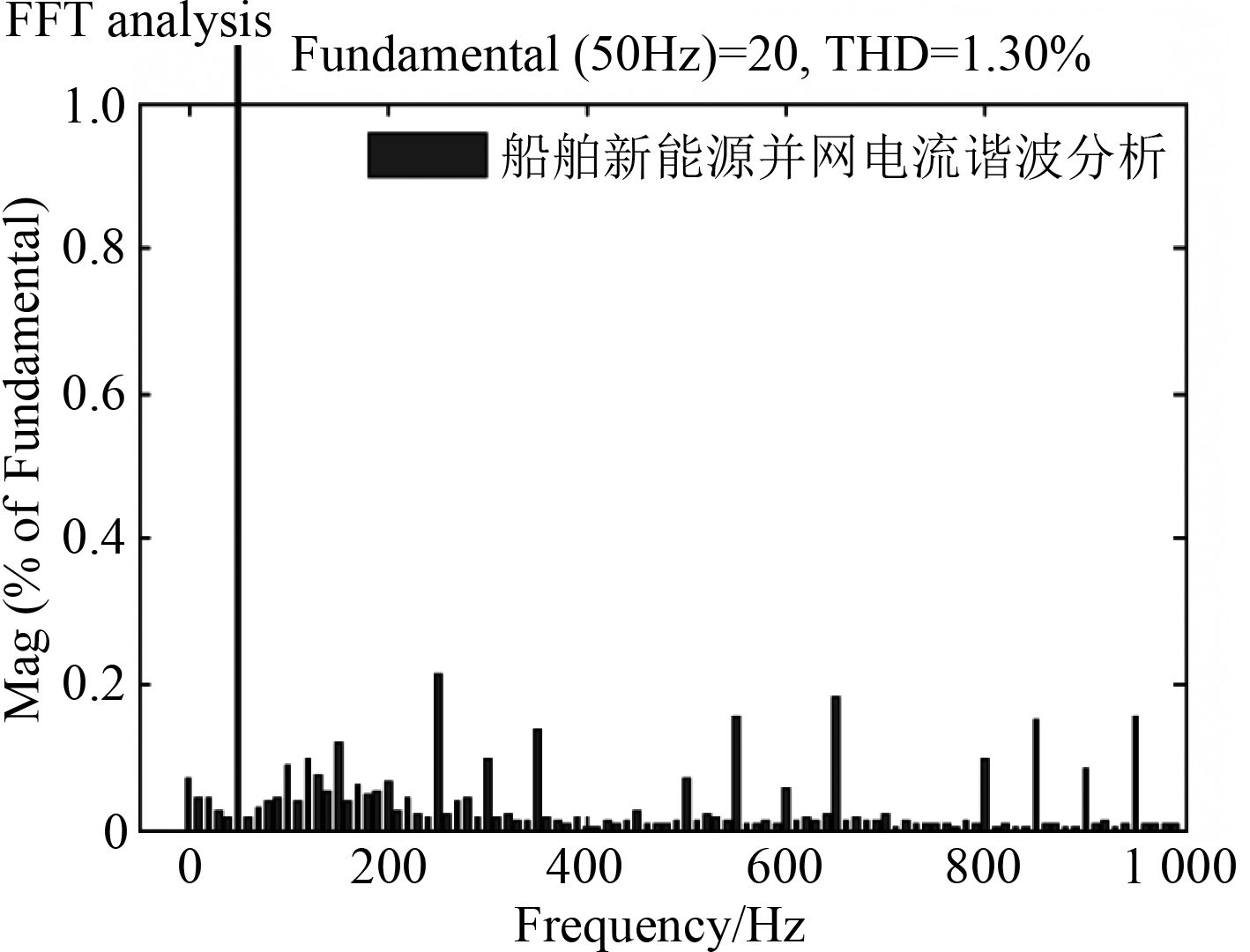
从图8和图9两种算法电流波形可以看出,传统算法电流带有明显毛刺,遗传算法仿真得到电流波形较为光滑,分别对其电流做FFT谐波分析,图10和图11为分析结果。图10显示传统算法电流谐波含量5.66%不符合并网要求,图11遗传算法分析结果谐波含量1.30%,满足船舶新能源逆变并网谐波含量低于5%的要求。

|
图 10 传统算法谐波分析 Fig. 10 Traditional algorithm harmonic analysis |
|
图 11 遗传算法谐波分析 Fig. 11 Genetic algorithm harmonic analysis |
1)本文针对船舶新能源并网系统会产生大量谐波,对本身就不稳定的船舶电网造成谐波污染的问题,采用遗传算法对其LCL滤波器参数通过编码、交叉、变异,择优进行参数最优化,最后搭建了仿真模型,比较传统算法和遗传算法优化参数得到的谐波含量,遗传算法优化的滤波器得到的并网电流谐波含量低且符合船舶新能源并网要求。
2)先前有过采用自适应遗传算法对陆地风力发电逆变并网LCL滤波器参数进行优化设计,本文采用遗传算法是对船舶新能源逆变并网LCL滤波器参数进行优化,并提出一种电容并联电阻的无缘阻尼谐振抑制的方法。
3)本文采用遗传算法对船舶新能源逆变并网LCL滤波器参数优化,最后逆变器输出电流经滤波后谐波含量降低且符合并网要求,为船舶新能源并网提供理论支持。本文只是一个仿真实验,还需要进一步通过对实船新能源逆变系统设计来验证。
| [1] |
严新平. 新能源在船舶上的应用进展及展望[J]. 船海工程, 2010, 39 (6): 111–115.
YAN Xin-ping. Progress review of new energy application in ship[J]. Ship & Ocean Engineering, 2010, 39 (6): 111–115. |
| [2] |
孙义存. 船舶新能源动力系统现状与发展趋势[J]. 中国水运, 2012, 12 (7): 87–88.
SUN Yi-cun. Present situation and development trend of marine new energy power system[J]. China Water Transport, 2012, 12 (7): 87–88. |
| [3] |
陈姝慧, 王红梅. 基于电网电压前馈的三相LCL并网逆变器电流控制方法研究[J]. 电气工程学报, 2016, 11 (1): 24–31.
CHEN Shu-hui, WANG Hong-mei. Research on current control scheme based on grid voltage feed forward for three-phase LCL-type grid-connected inverters[J]. Journal of Electrical Engineering, 2016, 11 (1): 24–31. |
| [4] | 张勇. 分布式发电系统中的LCL滤波器性能分析和设计[J]. 电力电容与无功补偿, 2013, 34 (6): 29–32. |
| [5] | 韩琳, 陈柏超, 陈晓国. 三相整流电路谐波注入滤波器方法[J]. 高电压技术, 2003, 3 (33): 42–46. |
| [6] | 李永辉. 船舶并网逆变器控制策略的研究[D]. 大连: 大连海事大学, 2014. |
| [7] | 陈东, 张军明, 钱照明. 带LCL滤波器的并网逆变器单电流反馈控制策略[J]. 中国电机工程学报, 2013, 33 (9): 10–16. |
| [8] | 张宪平, 李亚西, 等. 三相电压型整流器的LCL滤波器分析与设计[J]. 电气应用, 2007, 26 (5): 51–53. |
| [9] | 陈伟, 韦徵. 三相并网逆变器LCL滤波器的研究及新型有源阻尼控制[J]. 电工技术学报, 2014, 29 (6): 71–79. |
| [10] | J DANNEHL, FW FUCHS, S HANSEN, et al. Investigation of active damping approaches for PI-based current control of grid-connected pulse width modulation converters with LCL filters[J]. Energy Conversion Congress and Exposition, 2009, 46 (4): 1509–1517. |
| [11] | 阮新波, 王学华, 潘东华, 等. LCL型并网逆变器的控制技术[M]. 北京: 科学出版社, 2015: 60–71. |
| [12] | PEÑA-ALZOLA, et al. Analysis of the PassiAnalysis of the passive damping losses in LCL-filter-based grid convertersve Damping Losses in LCL-Filter-Based Grid Converters[J]. IEEE Transactions on Power Electronics, 2013, 28 (6): 2642–2646. DOI: 10.1109/TPEL.2012.2222931 |
| [13] | . 三相并网逆变器LCL滤波器的简明设计[J]. 通讯电源技术, 2012, 29 (2): 47–49. |
| [14] |
雷英杰, 张善文. MATLAB遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2014: 55–59.
LEI Ying-jie, ZHANG Shan-wen. MATLAB genetic algorithm toolbox and its application[M]. Xi’an: Xi'an University of Electronic Science and Technology Press, 2014: 55–59. |
 2018, Vol. 40
2018, Vol. 40
