永磁同步电机因为其结构简单、使用方便、可靠性高等优点,广泛应用于船舶电力推进[1]、工业控制应用中。随着交流调速技术取得突破进展,交流电力推进的应用情况发生了根本变化,各种新型控制算法的采用,使得船舶电力推进交流调速得以快速发展[2 – 5]。滑模变结构控制由于不受系统参数扰动和外部因素干扰,表现出极强的鲁棒性,得到越来越多学者关注并在电机伺服控制系统中得到应用。
本文采用id=0控制,并采用改进型滑模控制,设计了船舶电力推进永磁同步电机交流调速系统仿真模型,验证了系统设计的有效性。
1 永磁同步电机数学模型为了更好地分析永磁同步电机调速系统,方便建立永磁同步电机的数学模型,作如下假设:
1)假设转子的永磁场在空间上的分布为正弦波;
2)忽略定子铁心的饱和,将磁路作线性处理,电感参数保持不变;
3)不计铁心涡流和磁滞损耗;
4)转子上没有阻尼绕组。
在以上假设下,建立在dq坐标系下的永磁同步电机数学模型,其电压方程为
| $\left[ \begin{array}{l}{u_d}\\{u_q}\end{array} \right] = \left[ {\begin{array}{*{20}{c}}{{R_s} + {L_d}p} & { - {\omega _e}{L_q}}\\{{\omega _e}{L_d}} & {{R_s} + {L_q}p}\end{array}} \right]\left[ \begin{array}{l}{i_d}\\{i_q}\end{array} \right] + {\omega _e}\left[ \begin{array}{l}0\\{\psi _r}\end{array} \right],$ | (1) |
式中:ud,uq分别为d轴和q轴上的电压;id,iq分别为d轴和q轴上的电流;Ld,Lq分别为直、交轴电感;Rs为电机的定子绕组的电阻;ωe为电机的电角速度;ψr为永磁体与定子交链磁链;p为微分符号。
永磁同步电机的转矩方程为
| ${T_e} = \frac{3}{2}{n_p}[{\psi _r}{i_q} + ({L_d} - {L_q}){i_d}{i_q}],$ | (2) |
式中:Te为永磁同步电机的转矩;np为电机的极对数。对于面贴式永磁同步电机(SVPWM),有Ld=Lq=L,采用id=0矢量控制,转矩方程可以简化为
| ${T_e} = \frac{3}{2}{n_p}{\psi _r}{i_q}{\text{。}}$ | (3) |
永磁同步电机运动方程为
| ${T_e} - {T_L} - B\omega = J\frac{{{\rm d}{\omega _m}}}{{{\rm d}t}}\text{。}$ | (4) |
式中:TL为负载转矩;ωm为电机的机械角速度;B为电机的摩擦系数;J为电机转动惯量。
2 控制器的设计 2.1 滑模面的设计滑模变结构控制是一类特殊的非线性控制方法,它根据系统当时的状态、偏差及其导数值,在不同的控制区域,以理想开关方式切换控制量的大小和符号,使系统在切换线邻近区域来回运动,使系统在滑移曲线很小的领域内沿滑移换节曲线滑动。但是由于开关的空间滞后,离散系统本身以及系统惯性的存在,会不可避免存在抖振现象。由于滑膜抖振主要原因是因为控制系统开关切换不连续造成,因此减少切换项的增益,便可以有效削弱滑膜抖振现象[6 – 7]。
取永磁同步电机系统的状态变量为
| $\left\{ \begin{array}{l}{\omega _1} = {\omega ^*} - \omega, \\{\omega _2} = \int_0^t {\omega _1}{\rm d}t =\int_0^t ({\omega ^*} - \omega ){\rm d}t{\text{。}}\end{array} \right.$ | (5) |
式中:ω*和ω分别为给定的电机期望转速和实际转速。
构造积分型滑模面
为了保证系统的全局鲁棒性,在初始时刻系统轨迹需要处在滑模面,即
| $L = \int_{- \infty}^0 {\omega _2}{\rm d}t = - {\omega _2}(0),$ | (6) |
所以滑模切换面为
| $s(t) = {\omega _1} + c\int_0^t {\omega _1}{\rm d}t + L{\text{。}}$ | (7) |
当t=0时,s=0,即系统开始在滑模面运动。
2.2 控制率的求取对滑模面s求导,可得
| ${s'} = {\omega _1}' + c{\omega _1} = - \frac{{3{n_p}{\psi _r}}}{{2J}}{i_q} + \frac{B}{J}\omega + \frac{1}{J}{T_L} + c{\omega _1}{\text{。}}$ | (8) |
为提高系统的动态品质,采用指数趋近律来设计控制器,但是基于指数趋近律的滑模控制器,缺点在于其控制器输出为高频带状,使系统出现较大幅度的高频抖振,大大降低了系统的稳定性。为了弥补其自身的缺陷,在此对其进行改进,即变指数趋近律,形式如下
| ${s'} = - \varepsilon \left| {{\omega _1}} \right|{\mathop{\rm sgn}} (s) - ks\text{。}$ | (9) |
式中:ε,k均为正的常数。
结合式(8)和式(9)可得:
| $\frac{{3{n_p}{\psi _r}}}{{2J}}{i_q} - {\rm{c}}{\omega _{\rm{1}}} = \varepsilon \left| {{\omega _1}} \right|{\mathop{\rm sgn}} (s) + ks + \frac{B}{J}\omega + \frac{1}{J}{T_L},$ | (10) |
由此可得
| ${i_q} = \frac{{2J}}{{3{n_p}{\psi _r}}}\left[ {\varepsilon \left| {{\omega _1}} \right|{\mathop{\rm sgn}} (s) + ks + \frac{B}{J}\omega + \frac{1}{J}{T_L} + c{\omega _1}} \right],$ | (11) |
即相应的控制律函数Usmc为:
| ${U_{smc}} = {i_q} = \frac{{2J}}{{3{n_p}{\psi _r}}}\left[ \begin{array}{l}\varepsilon \left| {{\omega _1}} \right|{\mathop{\rm sgn}} (s) + ks + \displaystyle\frac{B}{J}\omega \\ + \displaystyle\frac{1}{J}{T_L} + c{\omega _1}\end{array} \right]\text{。}$ | (12) |
实际调速系统控制中,高频抖振是影响滑模控制最主要的问题。采用合适的方法抑制抖振,减弱抖振对系统的影响,是滑模控制的关键。积分型变指数趋近律的采用,可以很好地抑制滑模抖振,提高系统的控制性能。在远离切换面时,在常规趋近律的基础上,加入速度误差的绝对值,可以使运动点以较快的速度趋近滑模面,加快系统的动态响应;而当运动点接近切换面时,速度误差的绝对值趋近于0,速度逐渐减低,更加平滑地到达滑模面,以达到减振目的。
2.3 稳定性分析当得到滑模面(切换面)和滑动模态的控制律后,滑膜变结构控制系统就建立起来了。在选定切换和得到滑模控制率后,针对上述滑模控制器选用李雅普诺夫Lyapunov函数来证明其滑模平面稳定且存在滑动模态。稳定性条件为
| $\mathop {\lim }\limits_{s \to 0} s{s'} < 0{\text{。}}$ | (13) |
选定李雅普诺夫函数为
| $\begin{split}{V'} = &s{s'}=\\ &s[ - \varepsilon \left| {{\omega _1}} \right|{\mathop{\rm sgn}} (s) - ks]=\\ & - \varepsilon \left| {{\omega _1}} \right|s \cdot {\mathop{\rm sgn}} (s) - k{s^2}=\\ & - \varepsilon \left| {{\omega _1}} \right| \cdot \left| s \right| - k{s^2} < 0{\text{。}}\end{split}$ | (14) |
得到
为验证设计的滑模控制器的控制性能,本文利用Matlab/Simulink对控制系统实现了数字仿真。调速系统采用id=0的矢量控制方案。永磁同步电机的具体参数为电机定子相绕组电阻Rs=2.875 Ω,电枢电感Ld=Lq=15 mH,转动惯量J=0.029 kg·m2,极对数np=4,摩擦系数B=0.004 9 N·m·s,磁链ψr=0.175 Wb。图1所示为永磁同步电机矢量控制系统框图。
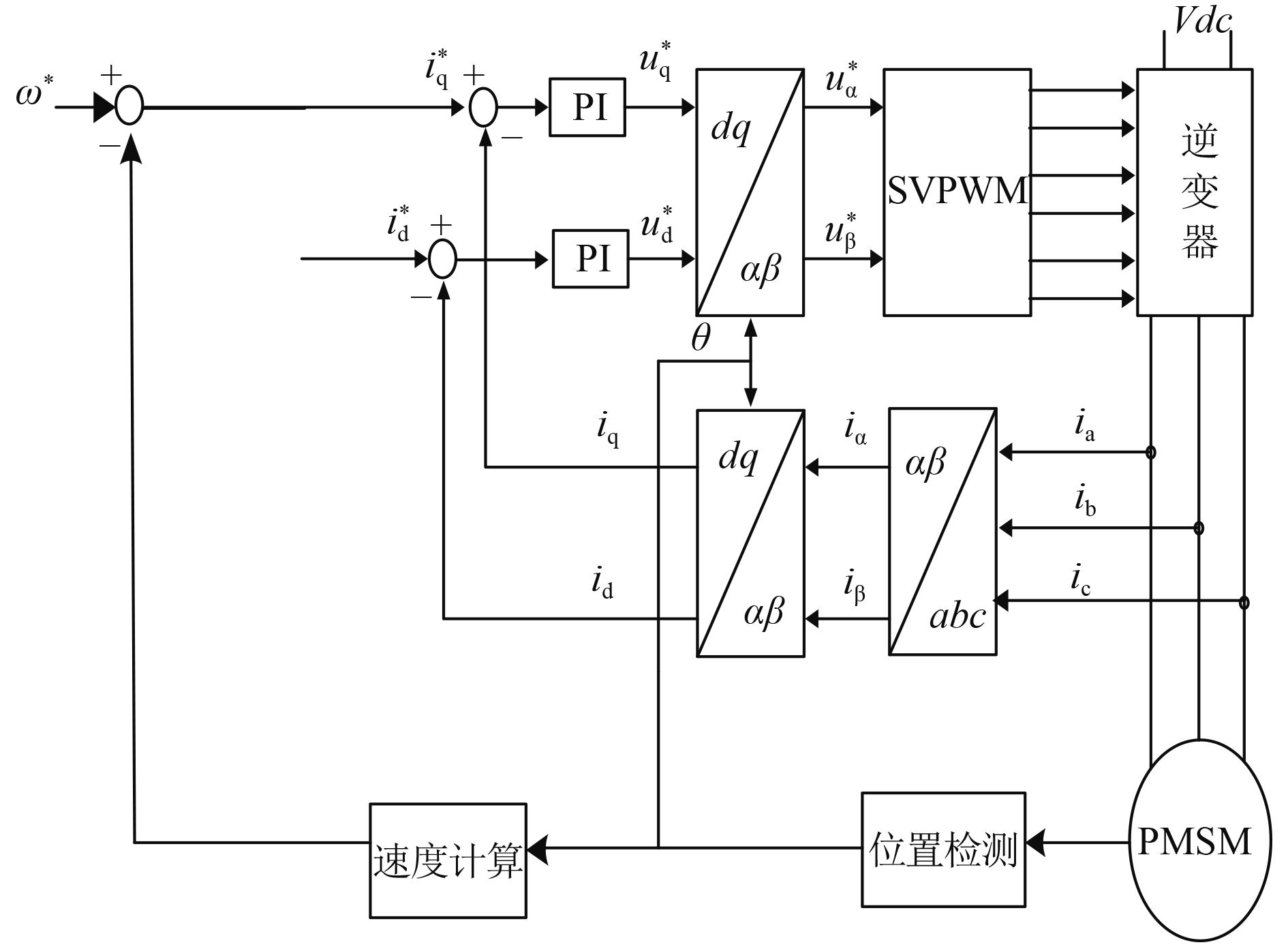
|
图 1 PMSM矢量控制系统 Fig. 1 PMSM servo control systerm |
系统给定参考转速为600 r/min。下面分3种情况进行仿真。
1)忽略负载转矩。如图2所示,常规滑模控制响应迅速,但有大约11.5 r/min的超调。图3中,本文设计的的积分变指数滑模控制响应最快,且无超调。
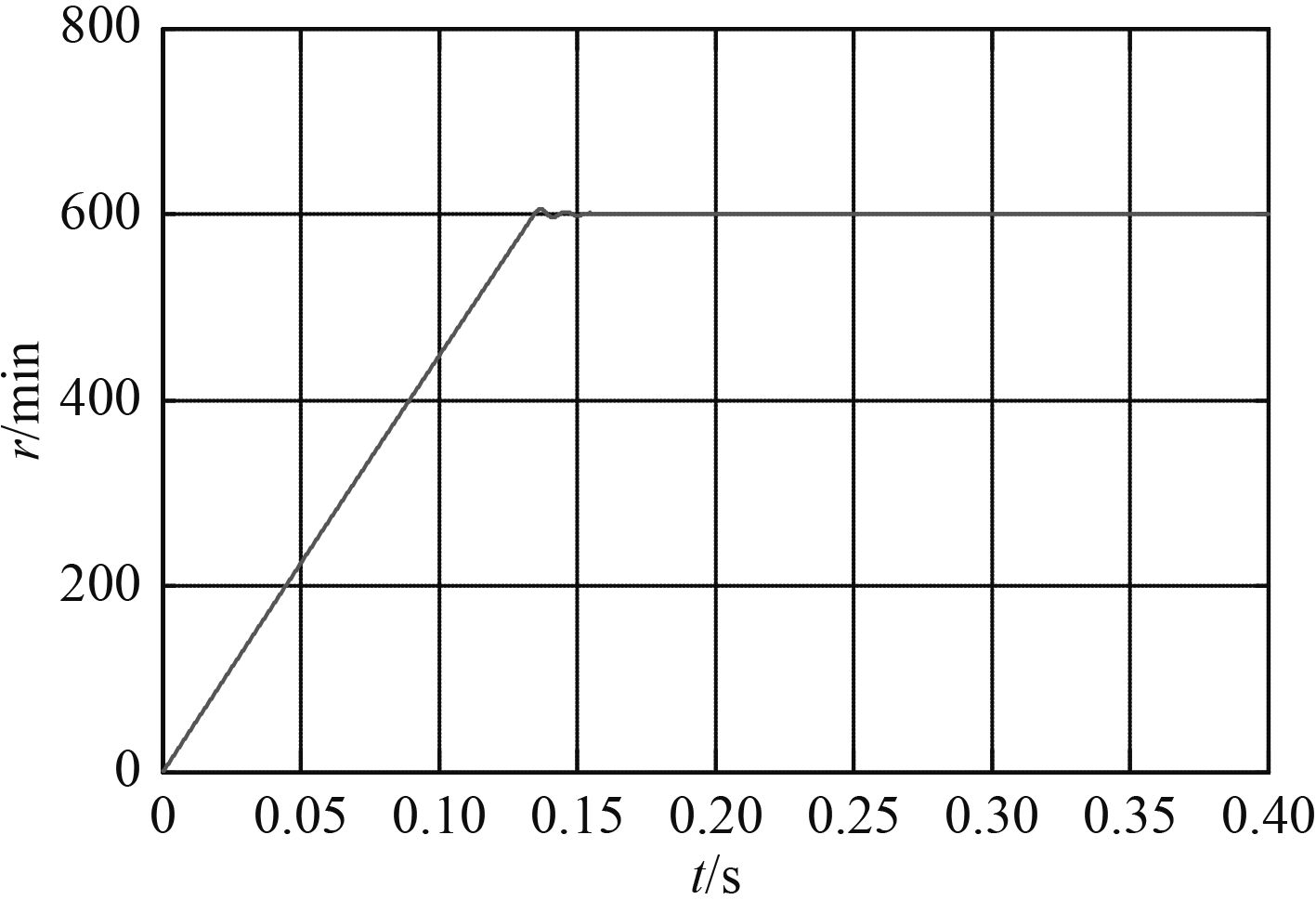
|
图 2 常规滑模控制 Fig. 2 Conventional sliding mode control |
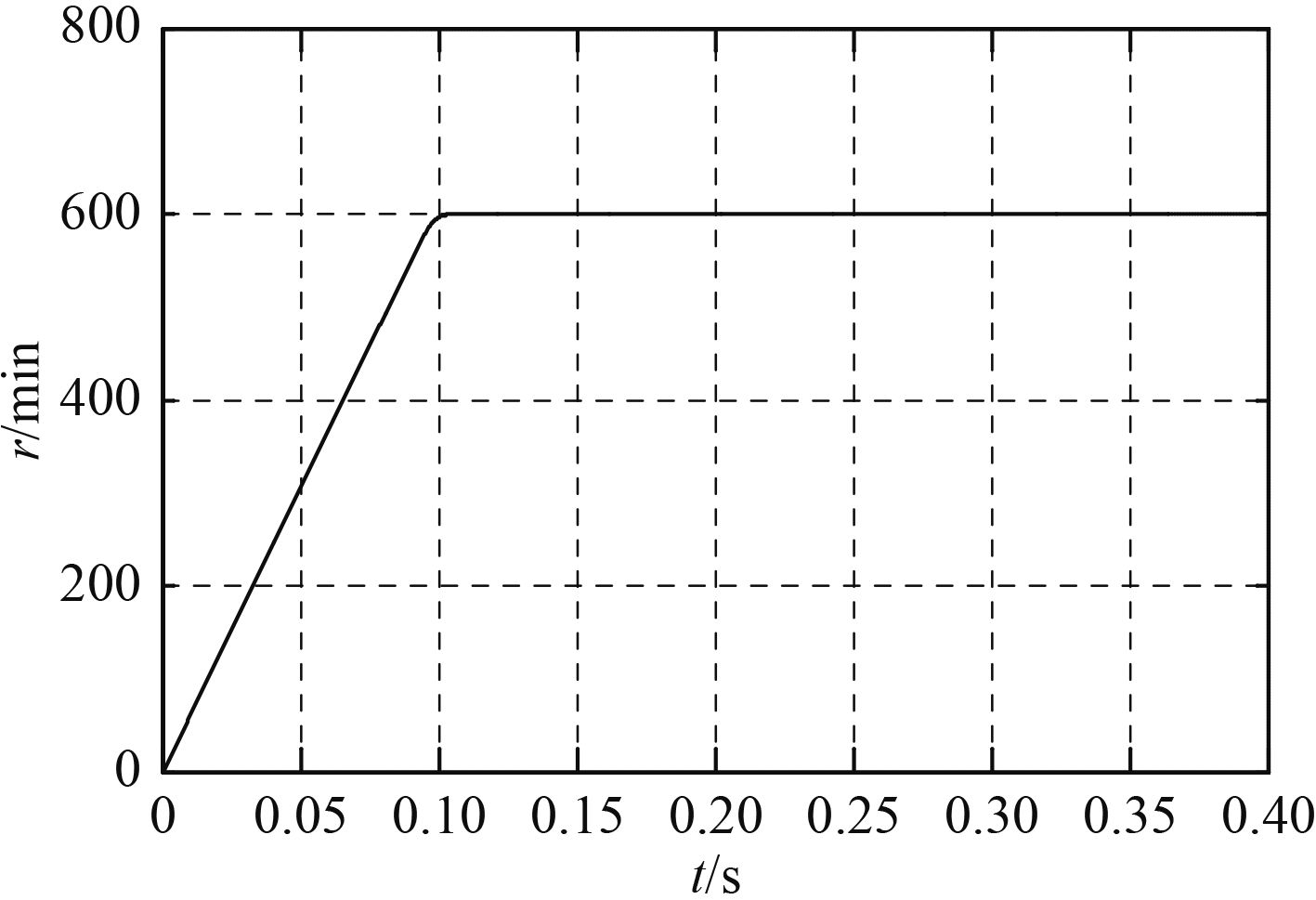
|
图 3 积分变指数滑模控制 Fig. 3 Integral variable index sliding mode control |
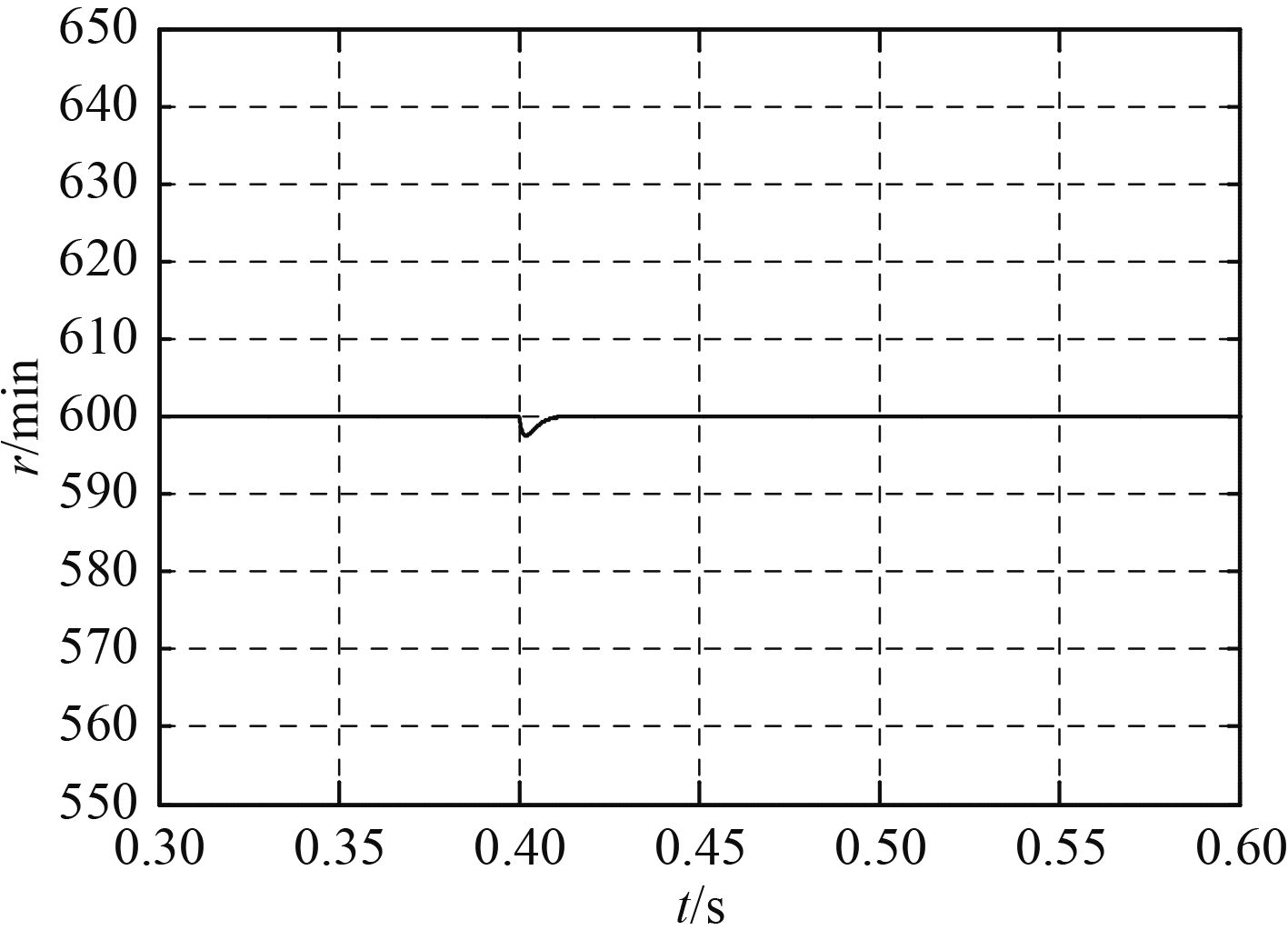
2)突增10 N·m负载。如图4所示,常规滑模控制存在10 r/min左右的扰动,并经过大约0.03 s恢复到稳态值,且超调一直存在,滑模抖振较大。图5中,本文设计的积分变指数滑模控制,扰动只有3 r/min,在0.01 s内快速恢复到稳定状态。
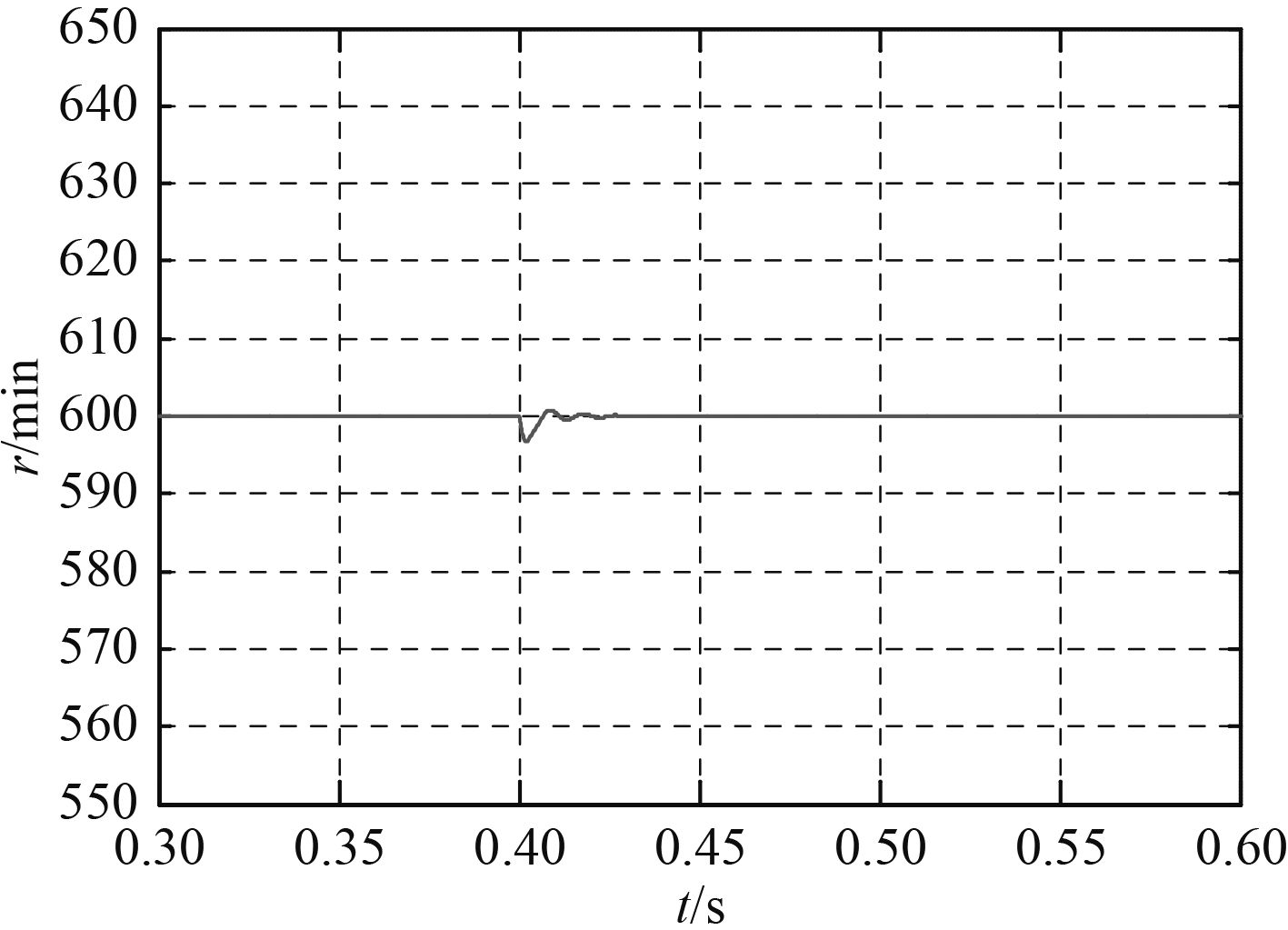
|
图 4 常规滑模控制 Fig. 4 Conventionalsliding mode control |
|
图 5 积分变指数滑模控制 Fig. 5 Integral variable index sliding mode control |
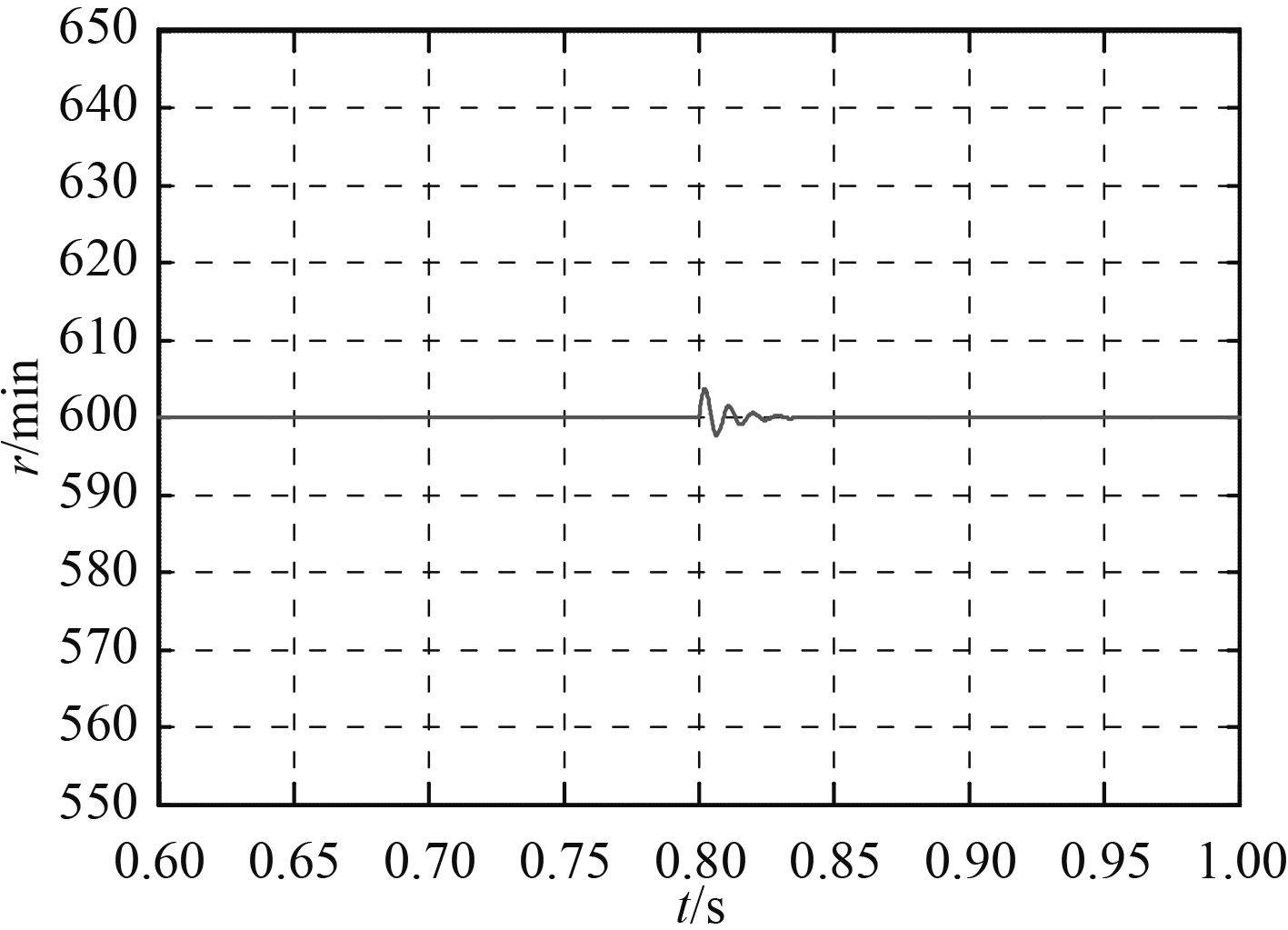
3)突卸10 N·m负载。如图6所示,常规滑模控制存在5 r/min左右的扰动,在大约0.03 s恢复稳定。图7中,本文设计的积分变指数滑模控制,扰动有5 r/min,在0.01 s内快速恢复到稳定状态。
|
图 6 常规滑模控制 Fig. 6 Conventional sliding mode control |

|
图 7 积分变指数滑模控制 Fig. 7 Integral variable index sliding mode control |
由以上仿真结果可以看出,本文所设计的积分型变指数滑模变结构控制器能够快速无超调地响应给定转速。在外部扰动时,能快速恢复到给定值,波动较小,不会出现稳态误差,鲁棒性好,较传统滑模控制,有了极大改善。完全符合船舶电力推进稳定、准确、快速响应的要求。
4 结 语在滑膜变结构控制的基础上,为了减弱滑模抖振,实现永磁同步电机调速系统的高精度控制,本文将积分型滑模面和变指数趋近律结合在一起,设计了积分型变指数滑模控制器,通过Matlab/Simulink仿真,大大降低了滑模抖振,验证了方法的可行性,取得了良好的控制效果,为船舶电气推进交流调速系统实际应用建立理论基础。
| [1] |
李新兵, 张继勇. 高性能永磁同步电机交流伺服系统的研究[J]. 机电工程, 2005, 22 (4): 30–31.
LI Xin-bing, ZHANG Ji-yong. Study on AC servo system of high performance permanent magnet synchronous motor[J]. Mechatronics Engineering, 2005, 22 (4): 30–31. |
| [2] |
朱磊, 温旭辉, 赵峰, 等. 永磁同步电机弱磁失控机制及其应对策略研究[J]. 中国电机工程学报, 2011, 31 (18): 68–71.
ZHU Lei, WEN Xuhui, ZHAO Feng, et al. Research on permanent magnet synchronous motor's weakening control mechanism and its countermeasure[J]. Chinese Journal of Engineering, 2011, 31 (18): 68–71. |
| [3] |
罗慧, 尹泉, 孙明明. 交流伺服系统参数辨识方法综述[J]. 伺服控制, 2012 (1): 27–29.
LUO Hui, YIN Quan, SUN Ming-ming. Review of AC servo system parameter identification method[J]. Servo Control, 2012 (1): 27–29. |
| [4] |
罗慧, 王军林, 尹泉. PMSM自适应观测器算法低速稳定性研究[J]. 电气传动, 2013, 43 (8): 3–7.
LUO Hui, WANG Jun-lin, YIN Quan. Low speed stability research of adaptive observer for PMSM[J]. Electric Drive, 2013, 43 (8): 3–7. |
| [5] |
李芳, 王旒顺, 张家瑞. 基于模糊PI控制的永磁同步电机的建模与仿真[J]. 工业控制计算机, 2013, 26 (8): 73–74.
LI Fang, WANG Yu-shun, ZHANG Jia-rui. Modeling and simulation based on fuzzy PI control of permanent magnet synchronous motor[J]. Industrial Control Computer, 2013, 26 (8): 73–74. |
| [6] | L M GRZESIAK, T TARCZEWSKI. PMSM servo drive control systerm with a state feedback and a load torque feed forward compensation[J]. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2012, 32 (1): 365–380. |
| [7] |
汪海波, 周波, 方斯琛. 永磁同步电机调速系统的滑模控制[J]. 电工技术学报, 2009, 27 (9): 72–76.
WANG Hai-bo, ZHOU Bo, FANG Si-chen. A PMSM sliding mode control system based on exponential reaching law[J]. Proceeding of the CSEE, 2009, 27 (9): 72–76. |
 2018, Vol. 40
2018, Vol. 40
