船舶动力装置模拟器是基于实船动力装置系统,人工建立与之相似的系统,训练人员可以操作、控制、管理模拟器系统,达到代替实船设备进行训练的目的。对于船舶而言,其动力装置系统较结构较复杂,实船训练受投入的人力、物力成本高,影响设备的寿命等因素的限制,而成本低、训练周期短的动力装置模拟器在对相关人员的培训、教学等方面优势明显。船舶模拟器起源于20世纪60年代,并随着与之依赖的虚拟现实技术的发展不断成熟,其实际应用经历单机仿真、分布式仿真、全系统大任务仿真几个发展历程后已经趋于成熟。虚拟现实因其独特的交互性、沉浸性和想象性[1],以视景仿真为主被越来越多应用到模拟器中。在船舶模拟器方面,波兰Unitest公司、挪威Kongsberg和英国Transas公司都曾先后开发过基于视景的仿真软件。在国内,虚拟现实技术引入到船舶模拟器中可以追溯到20世纪90年代。随着模拟器以及虚拟现实技术应用程度的不断提高,船舶模拟训练过程对训练过程真实感及沉浸感要求越来越高[2]。以数学模型为主要建模对象的模拟器系统,难以准确地描述模型运算过程,在实际训练过程中得到的仿真结果及船舶运动的变化也难以直观、准确地体现,影响操作人员及时对下一步操作及时进行判断和决策。建立视景仿真与数学模型的实时交互,可以将仿真中的数学参数转化为图像显示,从而使操作人员快速直观观察到参数变化引起的外部环境的变化,较快地对产生的变化进行相应的操作。实现虚拟现实与动力装置的协同仿真,需要建立虚拟视景引擎与动力装置数学模型接口之间的通道,目前主流的视景仿真引擎主要还是在C++或C#语言平台进行程序设计,使动力学数学模型的参数在视景仿真系统及编程平台的接口之间相互传递。这其中既要数学模型的计算精度、可靠性,也要考虑到参数在视景引擎接口间传递速度。从船舶领域来讲,我国对应用于模拟器的视景仿真也做过多次研究,文献[3]对救助船舶进行过基于Virtools软件的视景仿真,文献[4]基于Creator和Vega进行舰船航行的视景仿真,文献[5]基于Vega Prime对水下航行器进行视景仿真,文献[6]对超大型双桨双舵类型船舶进行船舶运动数学模型与Vega的协同仿真,类似相关文献还有很多,大多是基于运动模型、版本较早的Vega模型进行视景仿真设计,画面友好程度及模型的实用性上都有待改进。在此基础上,基于喷水推进船舶的动力装置系统,使用Vega Prime进行视景仿真。本文首先建立船舶的动力装置仿真模型实现动力装置性能仿真,基于光栅图像法及传统方法中使用的terrain vista和creator建模的方法,对以上3种地形建模方法进行改进,实现大地形快速建模。通过Vega Prime及VC++平台进行虚拟视景可视化仿真的程序开发,通过C++平台调用后台运行的Simulink模型的变化参数,将参数变化转化为Vega Prime中的物体属性变化,最终实现动力装置性能仿真与船舶航行可视化仿真的实时交互。
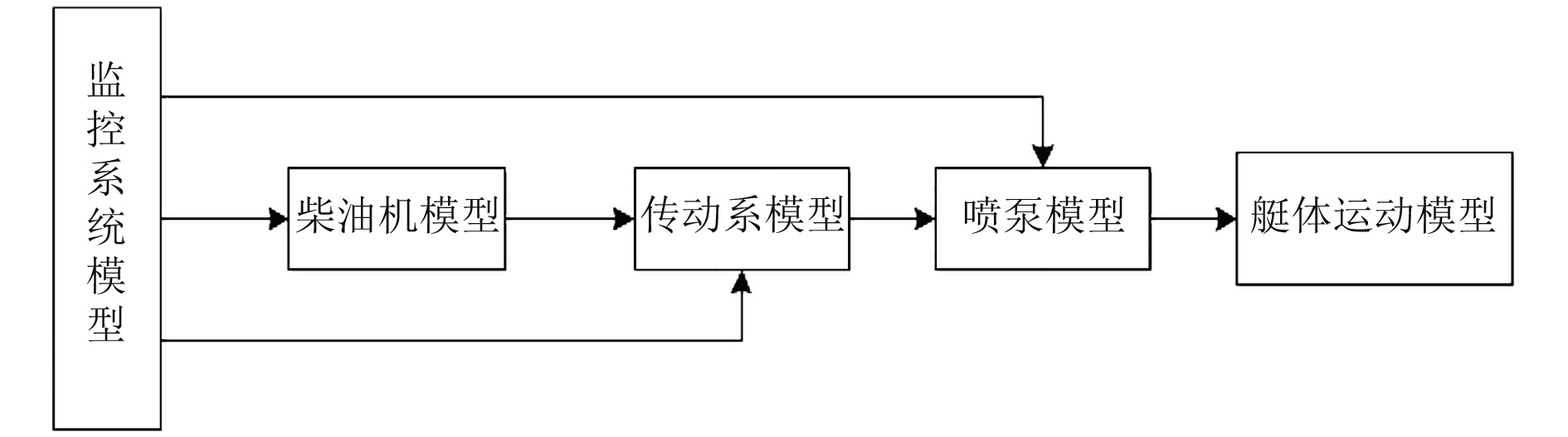
1 动力装置性能仿真建模针对船体为喷水推进船舶,其动力装置仿真系统主要包括控制系统、柴油机、传动系、喷泵以及船体运动仿真模型。图1为船舶动力装置仿真模型结构。
|
图 1 船舶动力装置系统模型简图 Fig. 1 Framework of the power plant system |
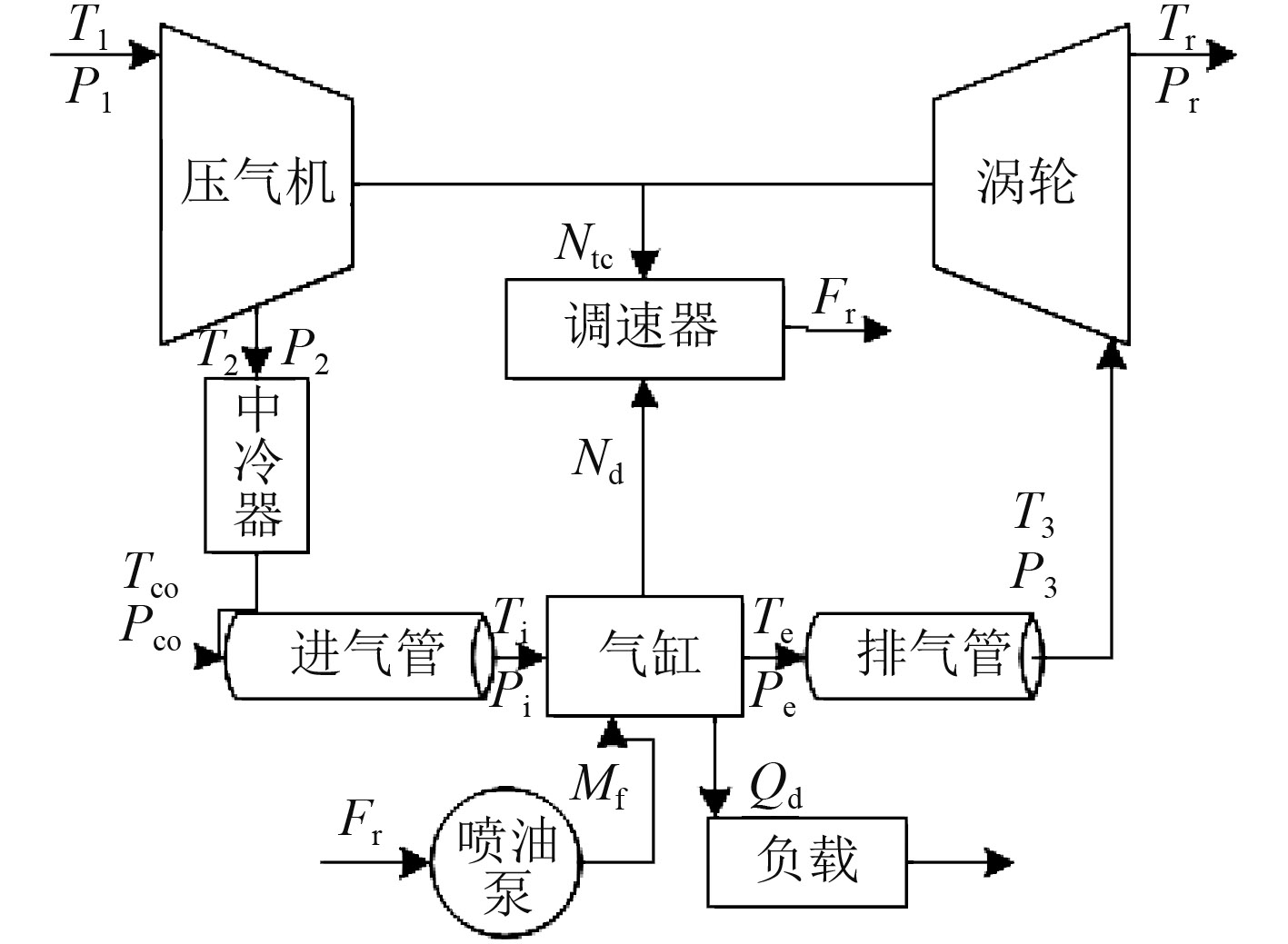
柴油机的建模技术比较成熟,传统的柴油机建模方法主要有线性化模型、准稳态非线性模型、容积法柴油机模型和压力波模型4类[7]。基于模拟器中计算精度、速度兼顾、能较准确反映内、外部性能参数变换、参数能及时传递的要求,采用准稳态法对柴油机进行建模,柴油机模型结构图如图2所示。
|
图 2 柴油机模型结构图 Fig. 2 Structure diagram of the diesel |
准稳态模型把动态过程看成一系列稳态过程组成,其基础是柴油机各部分的稳态特性、基本的动力学和热力学方程以及基于试验的经验公式。柴油机本体模型要应用牛顿第二定律,利用柴油机输出扭矩、负载扭矩和摩擦扭矩之间的平衡,得到柴油机的转速等参数。
1.2 船体运动模型根据船型和航行工况,通过求解运动微分方程,获得船舶运动参数。运动模型简图如图3所示。

|
图 3 船舶运动模型简图 Fig. 3 Framework of motion model |
对于回转运动,建立运动坐标系OXYZ,以船舶的重心为原点,OX轴取船纵向轴指向船首为正,OY轴与纵剖面垂直指向右舷为正,OZ轴垂直于水平面向下为正。运动方程为:
| $\left\{ {\begin{aligned}& {m\left( {\dot u - vr} \right) = X},\\& {m\left( {\dot v - ur} \right) = Y},\\& {{I_z}\dot r = N}\text{。}\end{aligned}} \right.$ |
| $\left\{ {\begin{aligned}& X = {X_H} + {X_R} + {X_P} = - {\lambda _{11}}\dot u + \\& \quad \quad \left( {{X_{vr}} + {\lambda _{22}}} \right)vr + {X_{vv}}{v^2} + {X_{rr}}{r^2} + {X_u}u + {X_p},\\& Y = {Y_H} + {Y_R} + {Y_P} = - {\lambda _{22}}\dot v + \\& \quad \quad {Y_v}v + \left( {{Y_r} - {\lambda _{11}}u} \right)r + \int {^{{{\left( {v + xr} \right)}^2}}} {C_D}\left( x \right){\rm d}x + {Y_p}, \\& N = {N_H} + {N_R} = - {\lambda _{66}}\dot r + \\& \quad \quad {N_v}v + {N_r}r + \int {^{{{\left( {v + xr} \right)}^2}}} {C_D}\left( x \right){\rm d}x + {N_p}{\text{。}}\end{aligned}} \right.$ |
式中:H为船体;P及R为推进和操纵系统;λ为附加质量;X为作用于船舶的水动力合力沿OX方向的分量;Y为作用于船舶的水动力合力沿OY方向的分量;N为作用于船舶的水动力合力对OZ轴的力矩。运用龙格库塔数值计算方法,可解得操纵运动参数u(t),v(t),r(t),则可求出船舶在固定坐标系中轨迹和首向角。
| $\left\{ {\begin{aligned}& {\psi \left( {\rm{t}} \right) = \int\nolimits_0^t {r{\rm d}t} },\\& {{x_0}\left( t \right) = \int\nolimits_0^t {{x_0}{\rm d}t} = \int\nolimits_0^t {\left( {u \cos\psi - v \sin\psi } \right){\rm d}t} },\\& {{y_0}\left( t \right) = \int\nolimits_0^t {{y_0}{\rm d}t} = \int\nolimits_0^t {\left( {u \sin\psi + v \cos\psi } \right){\rm d}t}\text{。} }\end{aligned}} \right.$ |
对于船体的直线运动,其数学模型可以由下面的运动学方程表示:
| $\frac{{\left( {{M_S} + {M_{SAD}}} \right)d{v_s}}}{{dt}} = {T_P} - {T_S}{\text{。}}$ |
式中:MS为船体总质量;MSAD为船体的附连水质量;TP为喷水泵提供推力;TS为船舶的阻力。船舶总的运动,由直线运动及回转运动构成。
1.3 喷水推进装置模型喷水推进系统的稳定运行依赖于3个平衡:喷泵吸收扭矩、功率与柴油机输出相平衡;喷泵扬程与系统所需扬程平衡;喷泵产生推力与船体所有阻力之和相平衡。喷泵吸收功率与柴油机输出功率平衡方程如下:
| ${N_p} = \gamma QH,$ |
式中:γ为水的重度;Q为喷泵流量;H为喷泵扬程;Nε为柴油机发出功率;Np为喷泵吸收功率。由动量定理,喷泵理想推力Tideal为水的动量增量:
| ${T_{{\rm{ideal}}}} = \rho Q\left( {{\nu _j} - {\nu _o}} \right),$ |
式中:α为边界层对进流的影响系数。喷泵产生总扬程与产生射流和克服系统管路损失所需扬程以及来流扬程的平衡方程式为:
| $H = \frac{{\left( {1 + {k_j}} \right)v_j^2}}{{2g}} + \frac{{\left( {{k_1} - \beta } \right)v_0^2}}{{2g}}\text{。}$ |
式中:kj为喷口损失系数;β为进口动能损失系数;k1为管道损失系数。根据喷泵中水流的连续性方程
| $102{N_\varepsilon }{\eta _m}{\eta _r}{\eta _p} = \frac{{\gamma Q\left( {1 + {k_j}} \right){Q^2}}}{{2g{\rm{A}}_j^2}} + \frac{{\left( {{k_1} - \beta } \right)v_0^2}}{{2g}} + \Delta h{\text{。}}$ |
其中:ηm为轴系机械传动效率;ηr为相对旋转效率;ηp为喷泵效率。
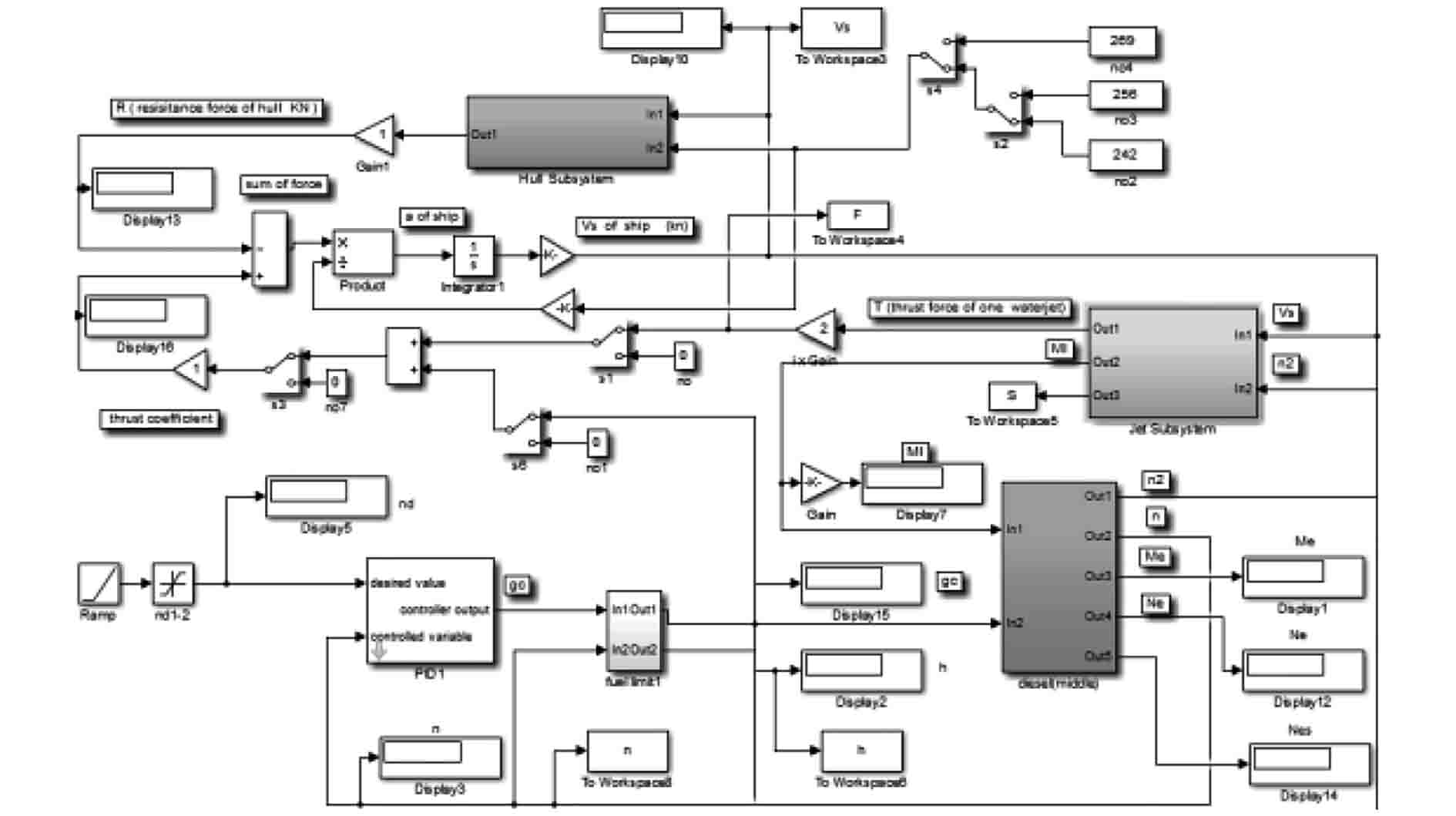
1.4 动力装置系统仿真模型对以上各子系统模型封装后,最终的动力装置仿真模型可以对单机单泵、多机多泵的直线加、减速,回转运动及换向运动等工作方式进行性能仿真。图4为整个动力装置系统的Simulink模型图。
|
图 4 动力装置仿真Simulink模型 Fig. 4 Power plant simulation model based on Simulink |
虚拟场景的建立主要是虚拟物体的实体模型,其中实体模型可分为地形模型、复杂实体模型、地物模型,根据建模的过程,实体建模包括几何建模、运动建模、物理建模、对象行为建模及模型分割。船体建模就属于复杂实体建模[10]。
船体建模可以用传统的CAD、Catia及3DMAX进行建模。Multigen-Creator建立船体模型,是基于OpenFlight数据格式实时渲染时占用内存少、具有多层次细节(LOD)及自由度控制节点方便控制等一系列优点,此种方法建立的船体模型能够较完善的将模型数据库的层次视图与建模环境集成在一起,在使用外部引用技术时,只需要将指向引用模型的指针粘贴到本场景中以节省计算机内存和空间,同时Creator本身的多种插件和模块能高效地生成实时三维数据库,能够与视景仿真软件Vega Prime紧密集合。
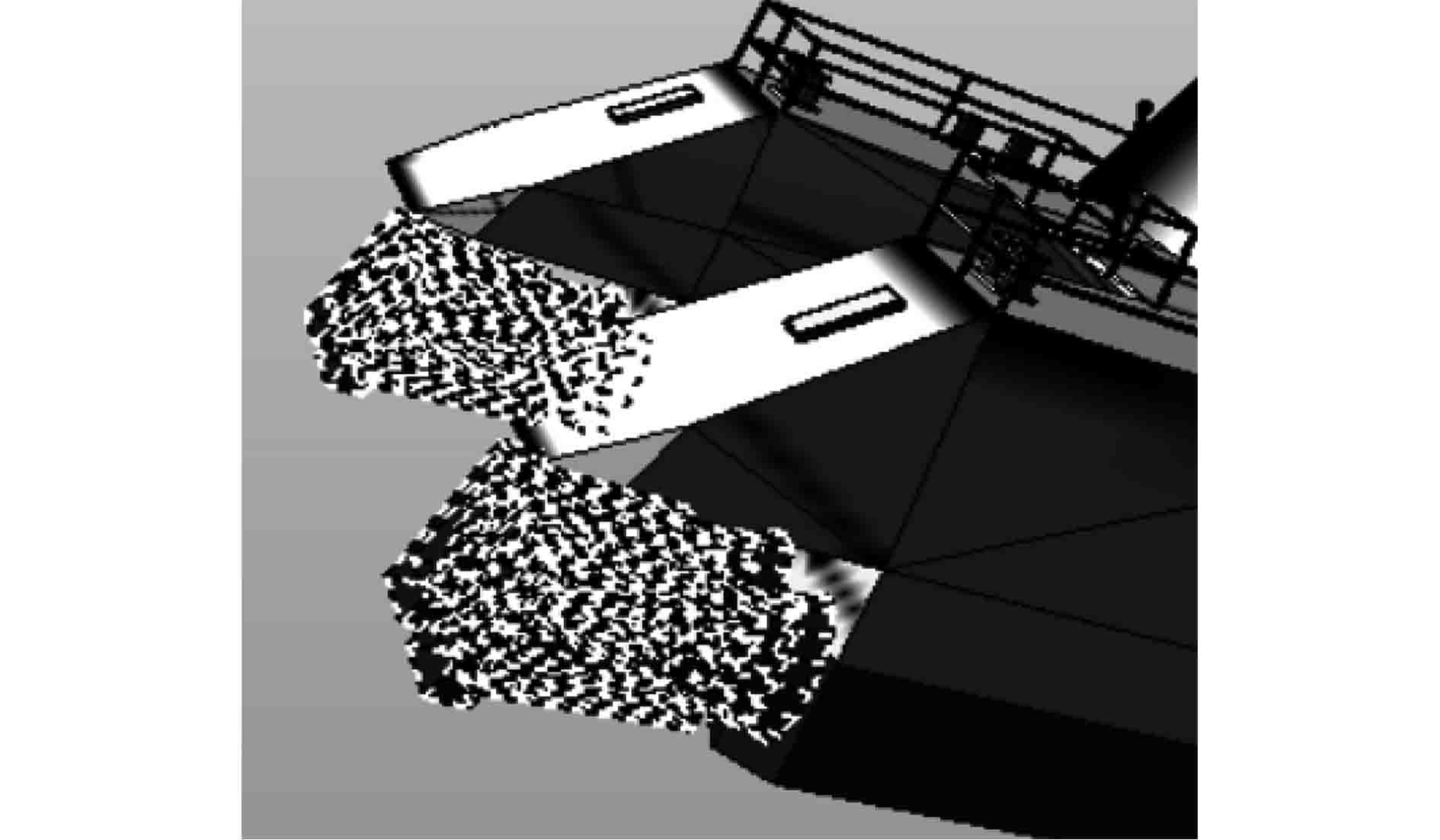
对控制船舶运动方向的倒车斗设置自由度(DOF)节点,可以实现该定义部件的铰链型关节及运动范围,实现模型的移动和旋转,设置由DOF节点的倒车斗运动装置及部分船体模型如图5所示。
|
图 5 倒车斗及船体模型 Fig. 5 Ship and reversing bucket model established on creator |
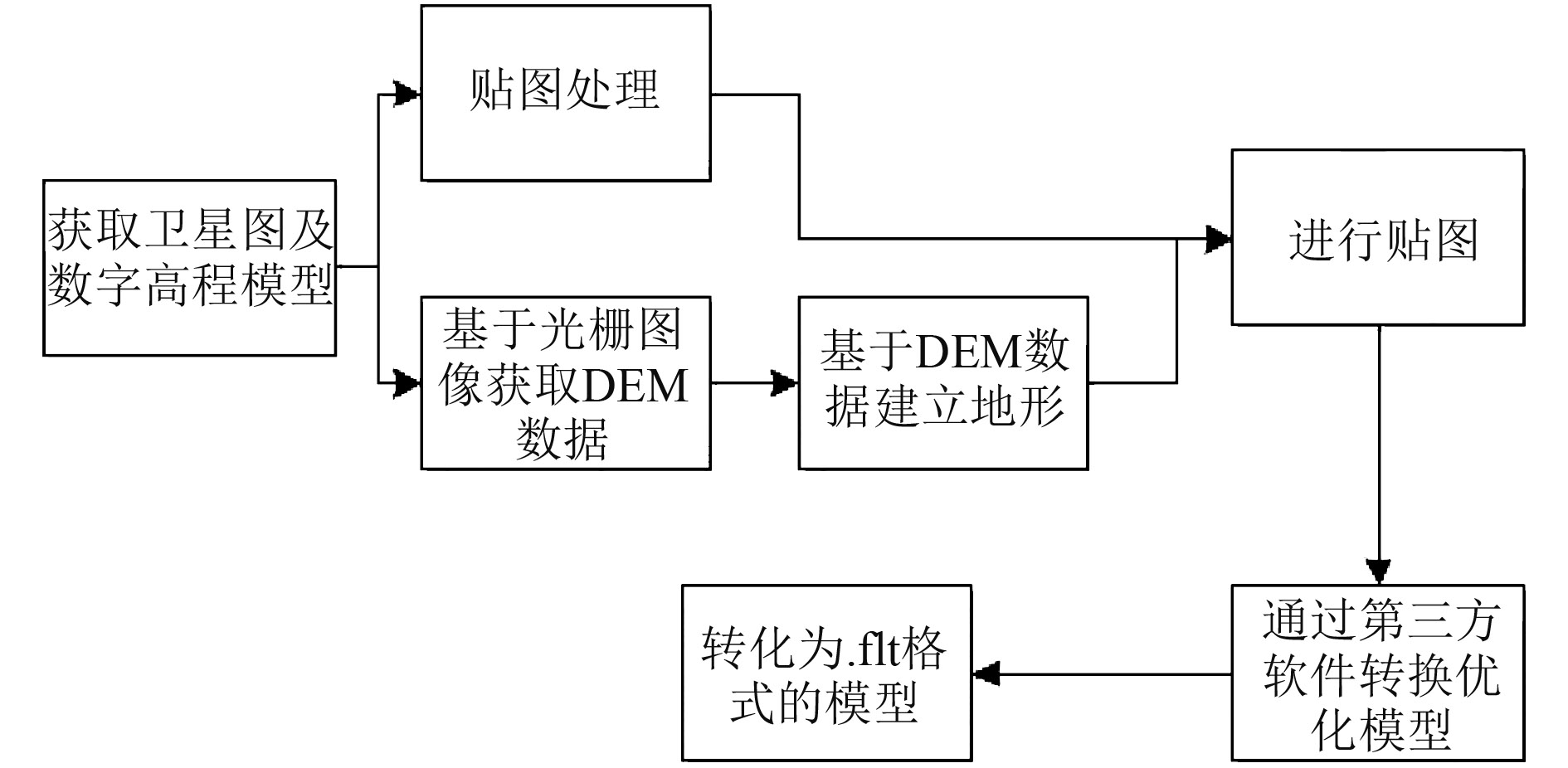
地形建模技术是实体建模的一个重要分支[10],基于Openflight格式的传统地形建模方法有光栅灰度法、Terrain及基于高程数据的Creator建模。针对大地形及群岛型的地形建模分块贴图复杂的问题,以上方法中都需要面对的问题是大地行分块及纹理贴图分块处理,采用先建模、处理纹理再将已经处理好的地形转化为OpenFlight的方法,有效减少了Creator在分块处理大地形冗余点线面过多及纹理处理的问题,大大减少了地形建模的时间。地形模型建立流程图如图6所示。
|
图 6 地形模型建立流程图 Fig. 6 Flow chart of terrain model establishment |
地形建模过程中主要需要解决的问题是预先采用非Creator建模所建立的模型在Creator中会产生许多冗余面,导致点线面错误,解决的方法是采用初始模型二次转化的方式,先将地形进行平滑处理,有效减少不规则面的个数,再转化为Openflight格式的地形。图7为处理后的地形模型。

|
图 7 地形优化模型 Fig. 7 Terrain optimization model |
使用Vega Prime中的Lynx Prime对虚拟场景进行配置,为保证视景仿真运行及参数传递的实时性,Vega Prime经常通过多线程实现虚拟可视化平台的设计。VP视景的驱动单独占用一个线程,MFC主界面使用一个或者多个线程用来开启、关闭和对VP参数进行控制。
3.2 混合编程上面已建立船舶动力装置数学模型,根据各个仿真模块进行封装。根据已经建立的Simulink模型,可以实时的获得各个时刻运动的位置、速度、舵角等数据。利用Visual C++接口功能,通过基于VC++混合编程,实现Simulink参数到Vega Prime图像渲染的实时传递。
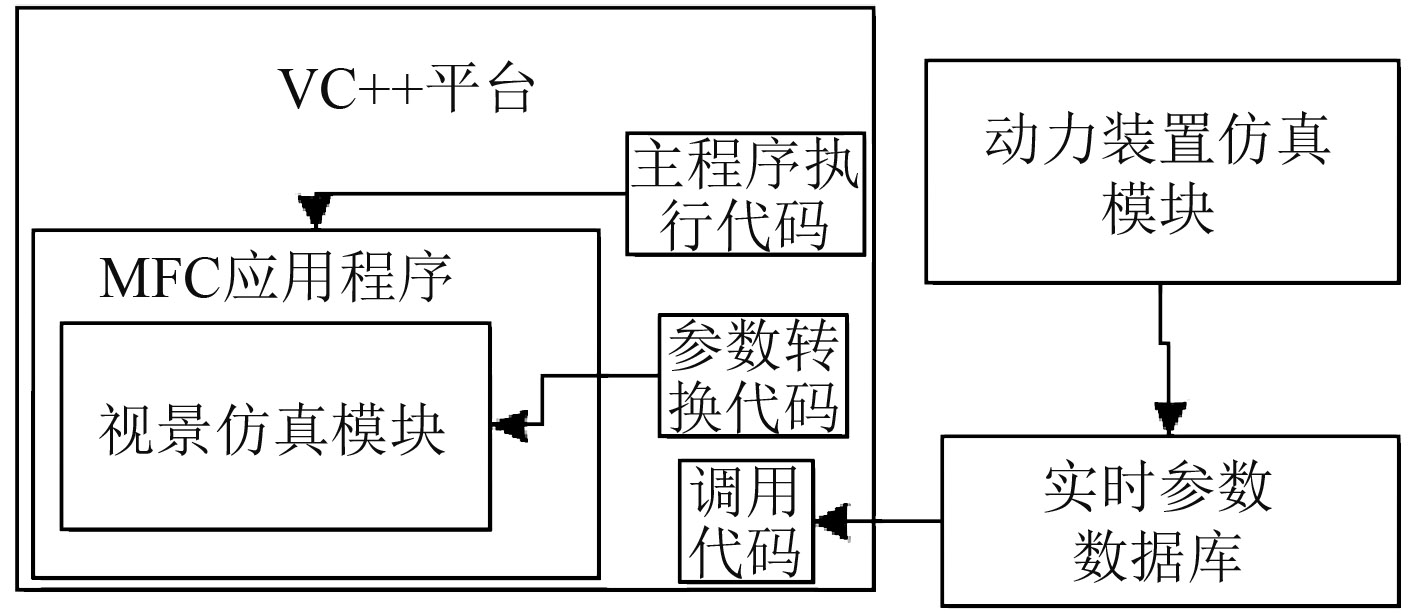
4 协同仿真运行整个协同仿真系统由动力装置仿真模、视景仿真模块组成,视景仿真模块又由Vega Prime程序模块、调用Matlab引擎程序模块以及船体运动策略模块构成,如图8所示。
|
图 8 协同仿真系统结构图 Fig. 8 Structure diagram of collaborative simulation system |
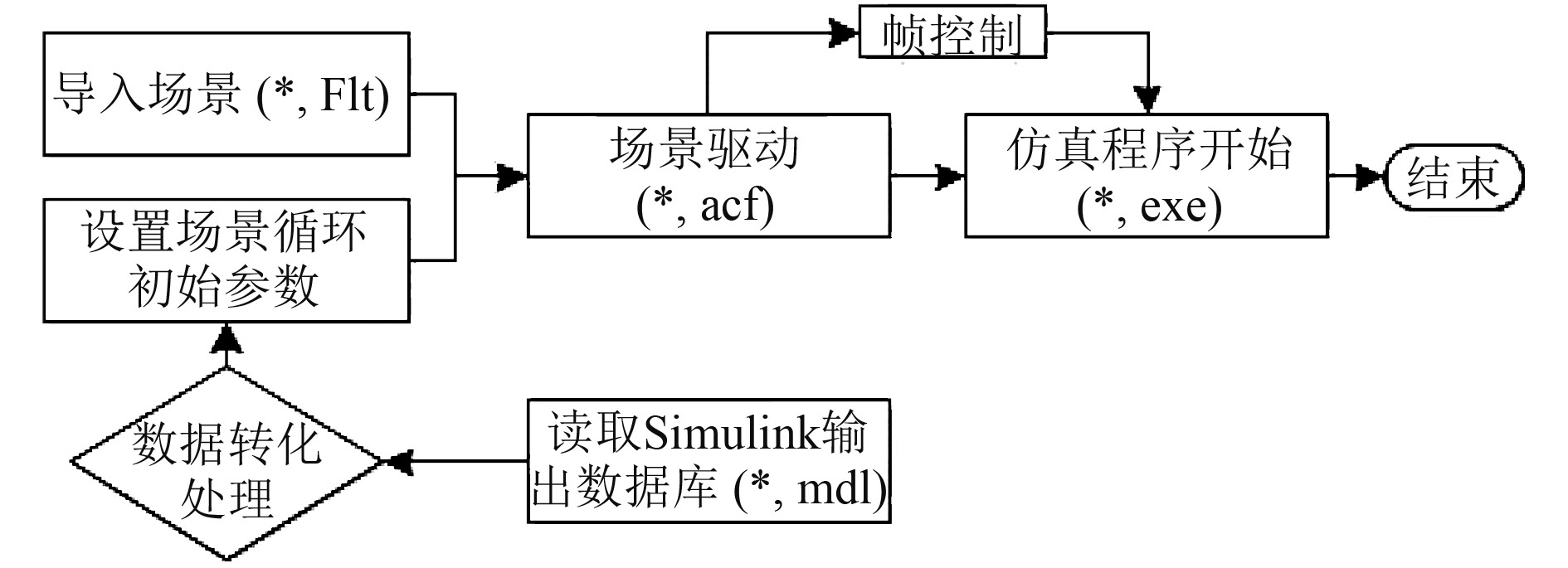
VP程序及调用Matlab模块由VS2005中的C++模块编写,完成了虚拟场景的实时配置及参数更改,Simulink输出参数的传递、获取、赋值、参数转换,船体的运动策略基于船舶运动模型进行构建,实现基于控制系统下各参数变化时船舶的协同仿真运行。整个仿真程序的流程图如图9所示。
|
图 9 程序流程图 Fig. 9 Program flow chart |
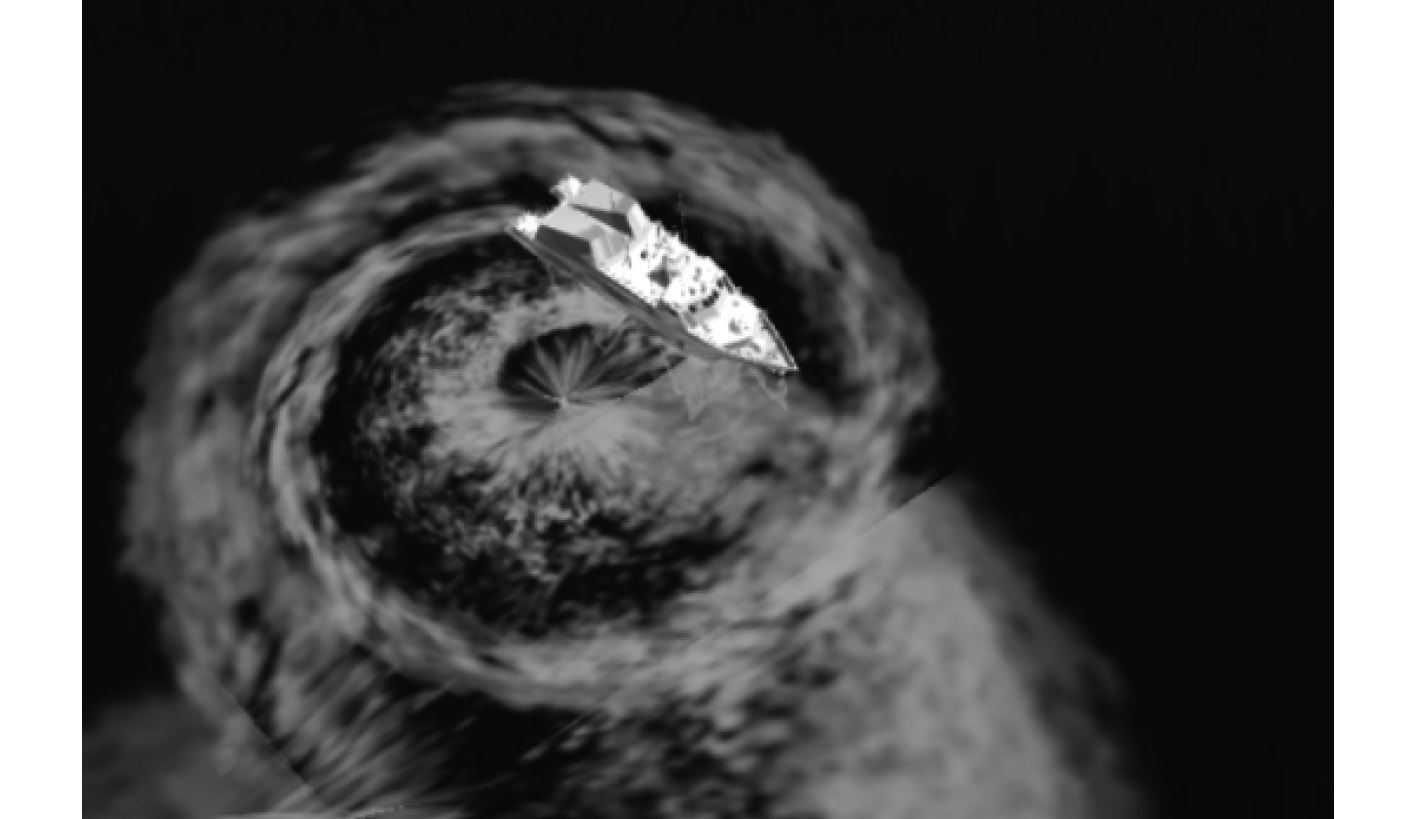
根据动力装置参数对动力装置进行操作,改变动力装置的运行参数,实现各个工况下,船舶航行姿态的展示,最终协同交互仿真如图10~图12所示。

|
图 10 船舶第一视角仿真效果图 Fig. 10 The first vision drawing |
|
图 11 船舶原地回转运动仿真效果图 Fig. 11 The inverse motion drawing of ship |

|
图 12 转向运动仿真效果图 Fig. 12 The turningmotion drawing of ship |
通过调用Matlab引擎及Simulink仿真结果的方式,实现动力装置与虚拟实景的实时交互,其结果能够很好地反映出船舶的运动状态,但基于这种方法的可视化协同仿真不能脱离数学模型的运行环境。
5 结 语本文基于喷水推进型船舶的动力装置仿真做了如下工作:
1)建立喷水推进动力装置仿真模型,模型仿真结果与试验数据准确。
2)以光栅图像法为基础,综合当前地形建模方法,改善大地形建模快速性并进行虚拟视景中地形的建模。
3)基于Vega Prime视景引擎,在C++平台进行混合编程,建立动力装置模型仿真与视景仿真的血统运行。
4)实现了视景仿真在喷水推进动力装置仿真的应用,工作原理及对进一步在喷水推进动力装置模拟器实际应用有借鉴意义。
| [1] | BURDEA G C, COIFFET D. Virtual reality technology[R]. New Jersey: Wiley – IEEE Press, 2003. |
| [2] | 吴家铸, 党岗, 刘华锋, 等. 视景仿真技术及应用[M]. 西安: 西安电子科技大学, 2001. |
| [3] | 王兴昭. 基于救助船舶模拟器的视景仿真研究[D]. 大连: 大连海事大学, 2012. |
| [4] | 吕帮俊, 邢继峰, 黄华斌, 等. 基于Mutigen和Vega的舰船航行视景仿真[J]. 仿真技术, 2006 (05): 299–301. |
| [5] | 莫剑飞. 基于Vega Prime的水下航行器视景仿真[J]. 电子设计工程, 2015, 23 (1): 13–15. |
| [6] | 郭晨, 焉丽飞, 沈海清. 超大型双桨双舵船舶运动数学模型与虚拟仿真[J]. 系统仿真学报, 2015, 27 (9): 1976–1982. |
| [7] | 孔庆福, 吴家明, 曾凡明. 船舶喷水推进系统数学建模及仿真研究[J]. 船舶工程, 2006, 28 (2): 12–16. |
| [8] | 赵希人, 陈虹丽, 艾晓庸. 船舶运动纵向受扰力和受扰力矩估算方法研究[J]. 哈尔滨工程大学学报, 2004, 25 (2): 167–170. |
| [9] | LV Shu-ping, YANG Xue-jing, ZHAO Xi-ren. The application of modeling and prediction with MRA wavelet network[J]. Journal of Marine Science and Application, 2004, 13 (1): 20–23. |
| [10] | 赵经国. 虚拟训练系统导论[M]. 长沙: 国防工业大学出版社, 2004. |
 2018, Vol. 40
2018, Vol. 40
