海面宽广,障碍物小,风力大,有利于海上风力发电。海上风机长期遭受风、波浪、流、海冰等载荷的作用,容易发生疲劳破坏。高纬度海域冬季结冰,如渤海、波罗的海等,此类区域海上风机冬季遭受海冰的作用,需考虑海冰对风机的影响。
目前关于作用在直立结构上的冰载荷计算并没有统一的规定,而且有很多冰力模型的计算结果相去甚远。Kärnä[1]根据实际测量得到的数据,提出采用保守的锯齿形冰力函数来计算海洋结构物的自激振动响应。IEC[2]采用正弦函数作为冰力函数的形式。王翎羽等[3]采用冰力振子的模型来预测冰的频率锁定挤压。岳前进[4]根据渤海海洋平台现场实测资料,发现冰激振动有准静态模型、稳态振动以及随机挤压破碎模型。
关于海上结构物的冰激疲劳研究较少,主要是运用现有冰力模型进行海洋结构物的振动与疲劳分析。Wang[5]采用Määttänen-Blenkarn模型对海上风机进行冰激振动分析。Wells[6]采用频率锁定冰力模型对带有破冰锥海上风机进行冰激振动响应分析。方华灿[7]进行冰载荷作用下具有直立桩腿的海洋平台进行疲劳寿命评估。黄焱等[8]对渤海海域三桩式风机进行了时域内的冰激振动响应分析。本文主要对海上风机在风冰2种载荷联合作用下进行动力响应分析,并在时域内提出疲劳评估方法。
1 风载荷计算风速分成:平均风速与脉动风速2部分。对于平均风速,可以采用风廓线定律确定,而脉动风速则采用功率谱模型通过数值模拟确定。
1.1 平均风速的计算计算平均风速可以采用指数定律与对数定律[9],本文采用指数定律计算平均风速,即
| $V\left( z \right) = V\left( {{z_r}} \right){\left( {z/{z_r}} \right)^\alpha }\text{,}$ | (1) |
其中:V(z)为高度z处的风速;V(zr)为相对海面高度zr处的平均风速;α为风切变指数,α=0.14。
1.2 脉动风速的模拟本文采用Kaimal谱[10]和Sandia法[11]进行脉动风速时域模拟。
1.2.1 Kaimal风速谱脉动风速场包括3个方向:纵向方向(u方向)、横向方向(v方向)以及垂向方向(w方向)[10]。3个方向的脉动风速谱为:
| ${S_K}\left( f \right) = \frac{{4\sigma _K^2{L_K}/{V_{hub}}}}{{{{\left( {1 + 6f{L_K}/{V_{hub}}} \right)}^{5/3}}}}\text{。}$ | (2) |
其中,下标K,K=u,v,w代表风场不同方向;f为频率;σK为脉动风速标准差;Vhub为轮毂处平均风速;LK为积分尺度参数,其取值如下:
| ${L_K} = \left\{ \begin{array}{l}8.10{\Lambda _U}, \;\;\;K = u\text{;}\\2.70{\Lambda _U}, \;\;\;K = v\text{;}\\0.66{\Lambda _U}, \;\;\;K = w\text{。}\end{array} \right.$ | (3) |
其中,ΛU为湍流尺度参数,取值为:
| ${\Lambda _U} = 0.7 \cdot \min (60,{Z_{hub}})\text{。}$ | (4) |
其中,Zhub为轮毂高度,m。
不同方向之间的脉动风速标准差关系为:
| ${\sigma _v} = 0.8{\sigma _u}\text{,}$ | (5) |
| ${\sigma _w} = 10.5{\sigma _u}\text{。}$ | (6) |
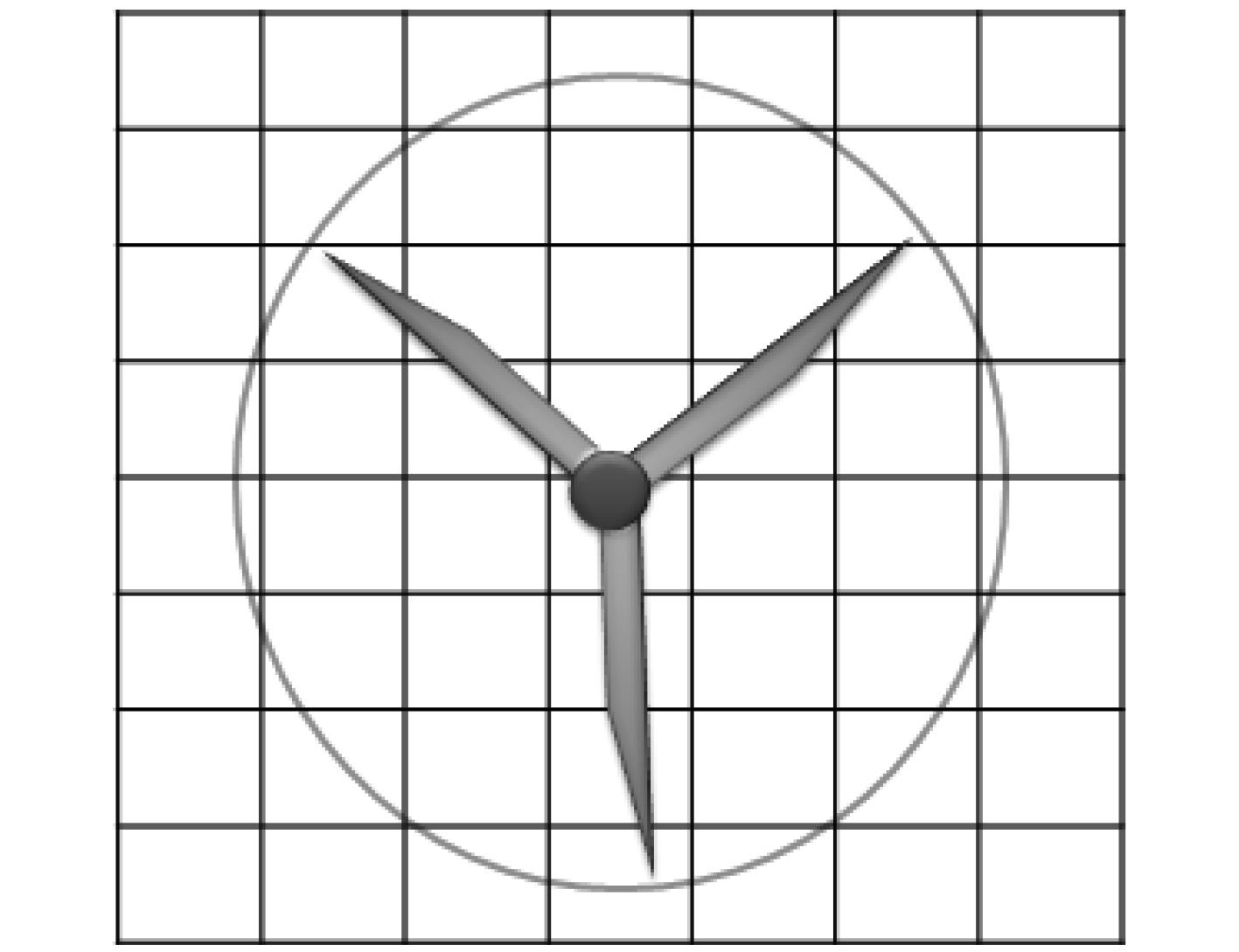
脉动风场的网格划分如图1所示。
|
图 1 脉动风速场网格划分 Fig. 1 Grids of fluctuating wind speed field |
当计算三维空间脉动风场时,必须考虑空间(见图1)各点之间的空间相干性[9]。IEC对于纵向风速场的相干性,提出了相干性系数Coh(r,f),即
| $Coh\left( {r,f} \right) = \exp \left[ { - 12\sqrt {{{\left( {\frac{{fr}}{{{V_{hub}}}}} \right)}^2} + {{\left( {0.12\frac{r}{{{L_c}}}} \right)}^2}} } \right]\text{。}$ | (7) |
其中:r为空间任意2点的距离;f为频率,Hz;Vhub为轮毂处平均风速;Lc为相干性尺度参数(Lc=8.1Λu) 。
1.2.3 Sandia法本文采用Sandia法进行脉动风速时程模拟[11],其计算步骤参考文献[11]。
1.3 气动载荷计算风机的气动载荷的计算一般采用叶素-动量理论计算[12]。该理论经常用于稳态风速下风机风载荷计算。其原理为将风机叶片沿展长方向划分成许多微段,采用动量理论计算出这些微段上力和力矩。再沿着展长方向积分就可以得到风机叶片上力与力矩。
2 冰载荷计算冰与直立桩腿之间发生相互作用,根据冰速的不同,冰的失效模式主要有间歇性挤压破碎、频率锁定挤压破碎以及连续性随机挤压破碎3种。冰绝大多数情况下以连续随机挤压破碎的形式失效[11]。对于连续性随机挤压破碎冰力函数模型主要使用Kӓrnӓ提出的冰力谱模型[13]。
Kӓrnӓ认为总的冰力Ftotal(t)应该是平均冰力分量
| ${F_{total}}(t) = \overline F + F(t)\text{,}$ | (8) |
平均冰力分量
| ${F_{\max }} = \overline F + k\sigma \text{,}$ | (9) |
| $I = \frac{\sigma }{{\overline F }}\text{。}$ | (10) |
式(9)中Fmax为冰力极值。k为一无因次量,取Fmax对应的超越概率。σ为冰力的标准差。I为强度参数,无因次量,取值范围为0.2~0.5,建议取值为0.4。由式(9)与式(10)可以求出:
| $\sigma = \frac{I}{{1 + kI}}{F_{\max }}\text{,}$ | (11) |
| $\overline F = \frac{{{F_{\max }}}}{{1 + kI}}\text{。}$ | (12) |
冰力极值Fmax的计算方法如下:
| ${F_{\max }} = {C_R}\left( {\frac{h}{{{h_1}}}} \right){\left( {\frac{w}{h}} \right)^m}hw\text{,}$ | (13) |
式中:CR为冰的压缩强度,MPa;w为桩腿在水面处的直径,m;h为冰厚,m;h1为参考冰厚,取值为1 m;m为经验常数,取值为–0.16;n为依赖于冰厚的经验常数。即
| $n = \left\{ \begin{array}{l} - 0.5 + h/5\;\text{,}\;\;h < 1.0\;m\text{,}\\{\rm{ - }}0.3\;\;\;\;\text{,}\;\;\;\;\;\;\;\;h > 1.0\;m\text{。}\end{array} \right.$ | (14) |
对于冰力的脉动分量,Kӓrnӓ基于渤海以及波罗的海的海冰连续挤压的现场试验的测量数据,建立了功率谱密度函数。
| $\tilde S\left( f \right) = \frac{{fS\left( f \right)}}{{{\sigma ^2}}}\text{,}$ | (15) |
| $\tilde S\left( f \right) = \frac{{af}}{{1 + {k_s}{a^{1.5}}{f^2}}}\text{。}$ | (16) |
式中:
由冰载荷谱进行傅里叶逆变换即可得到随时间变化的冰载荷。
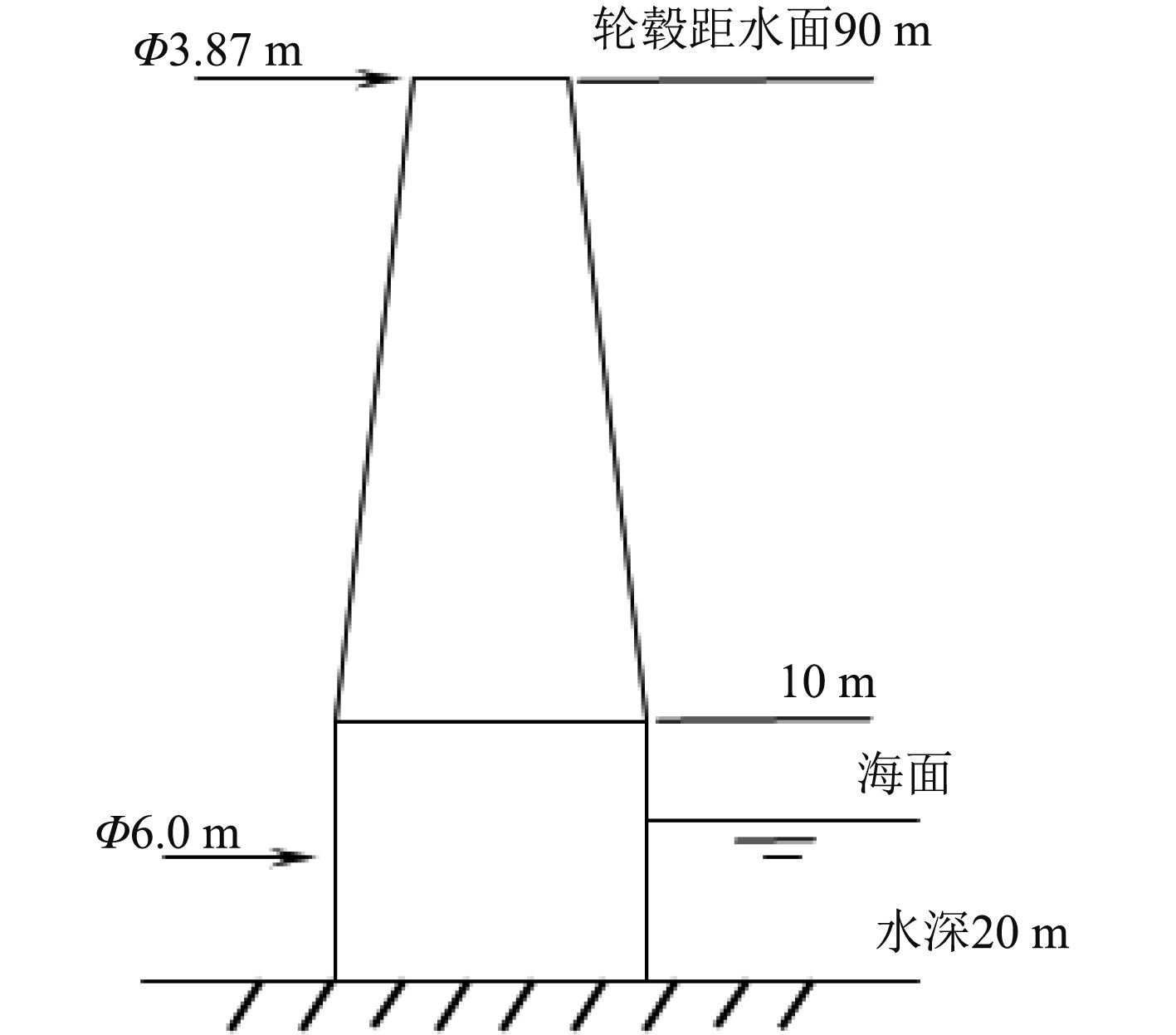
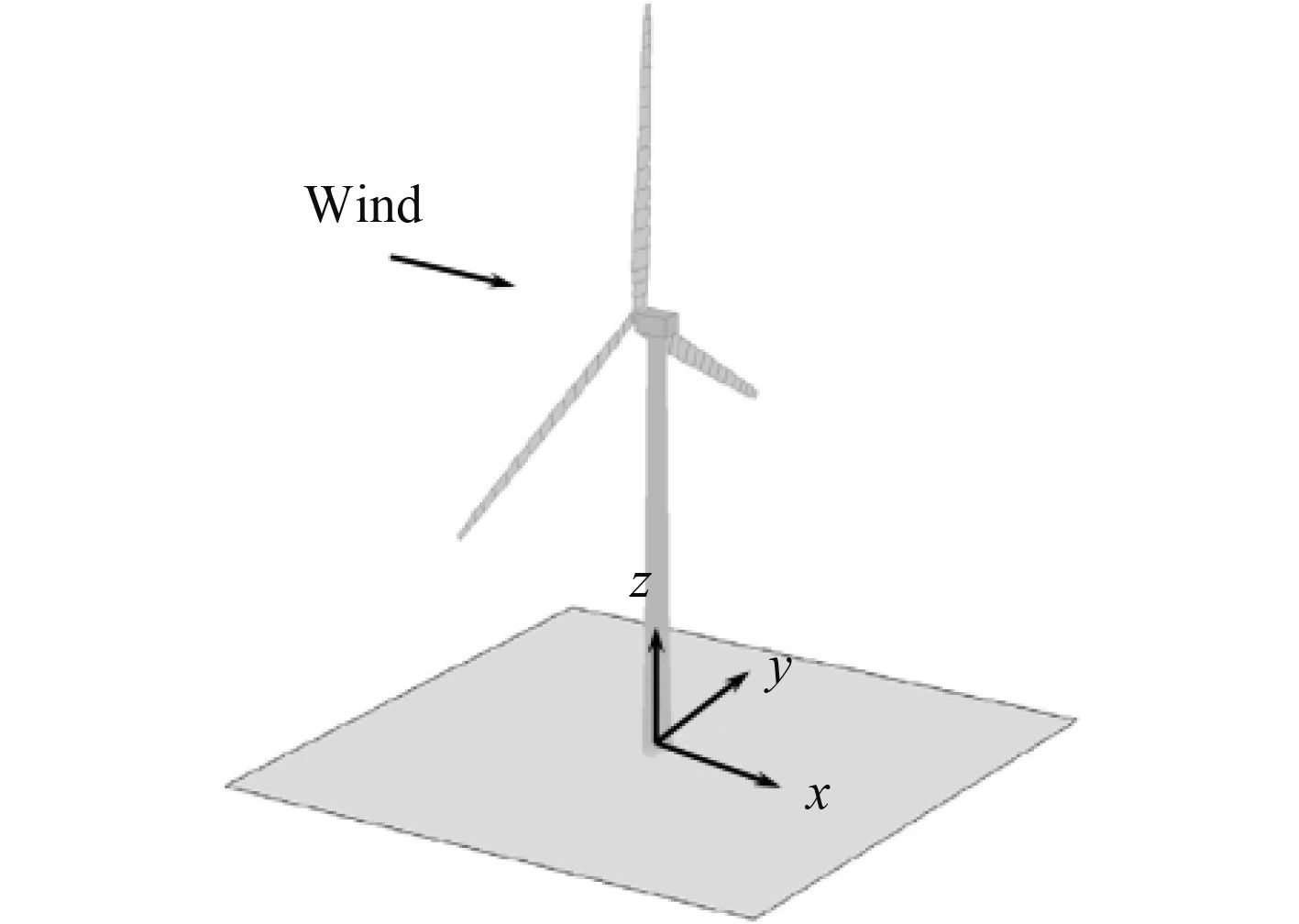
3 计算实例 3.1 风机模型本文风机建于渤海某海域,如图2所示,风机的基本参数如下:轮毂距水面高度为90 m,水深为20 m,塔架海面以下部分为薄壁圆筒结构,外径为6 m。海面10 m以上为圆锥筒形结构,顶端直径为3.87 m。
|
图 2 风机结构示意图 Fig. 2 Structural sketch of offshore wind turbine |
|
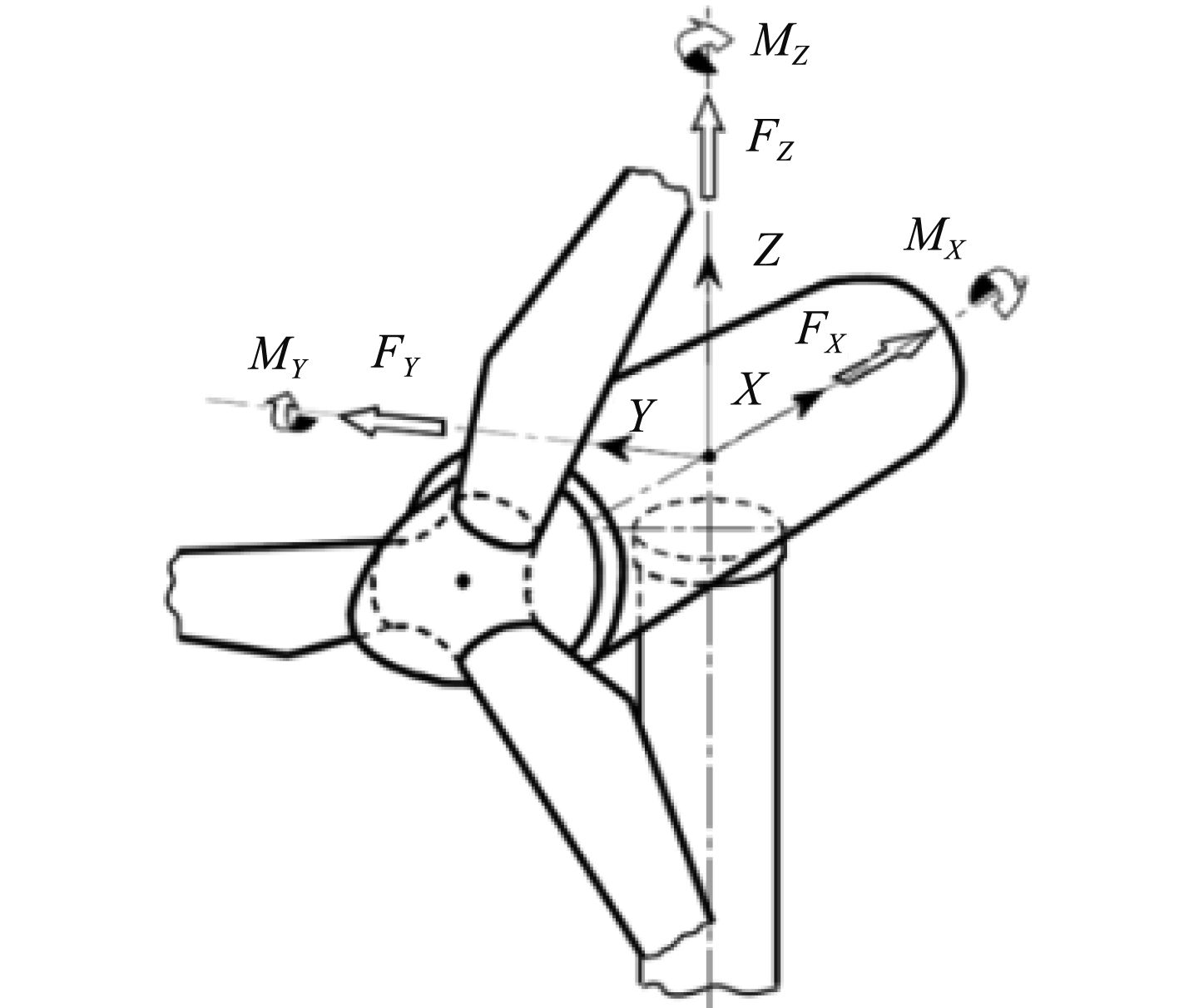
图 3 塔顶坐标系定义 Fig. 3 The definition of coordinate system at the top of tower |
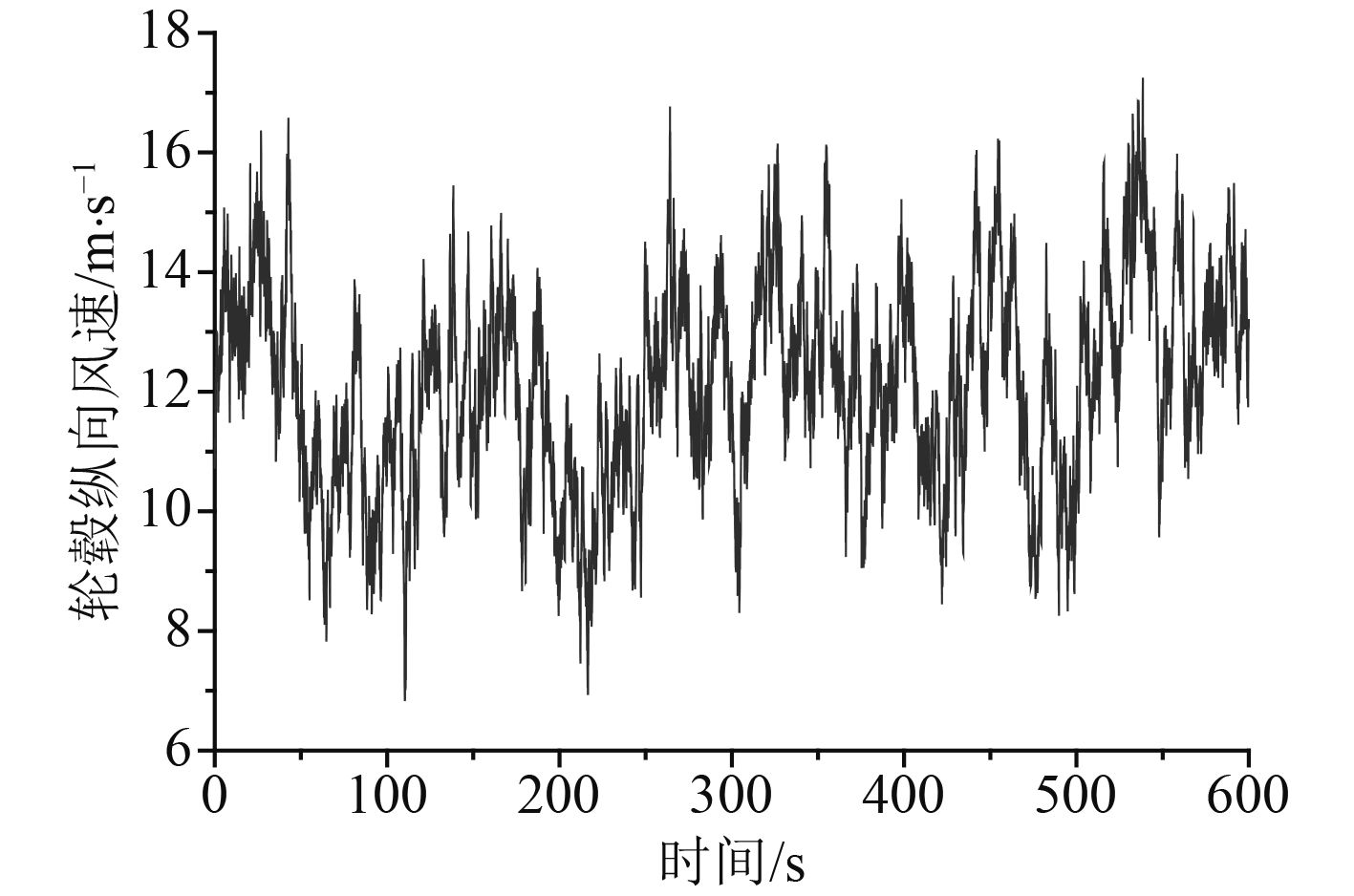
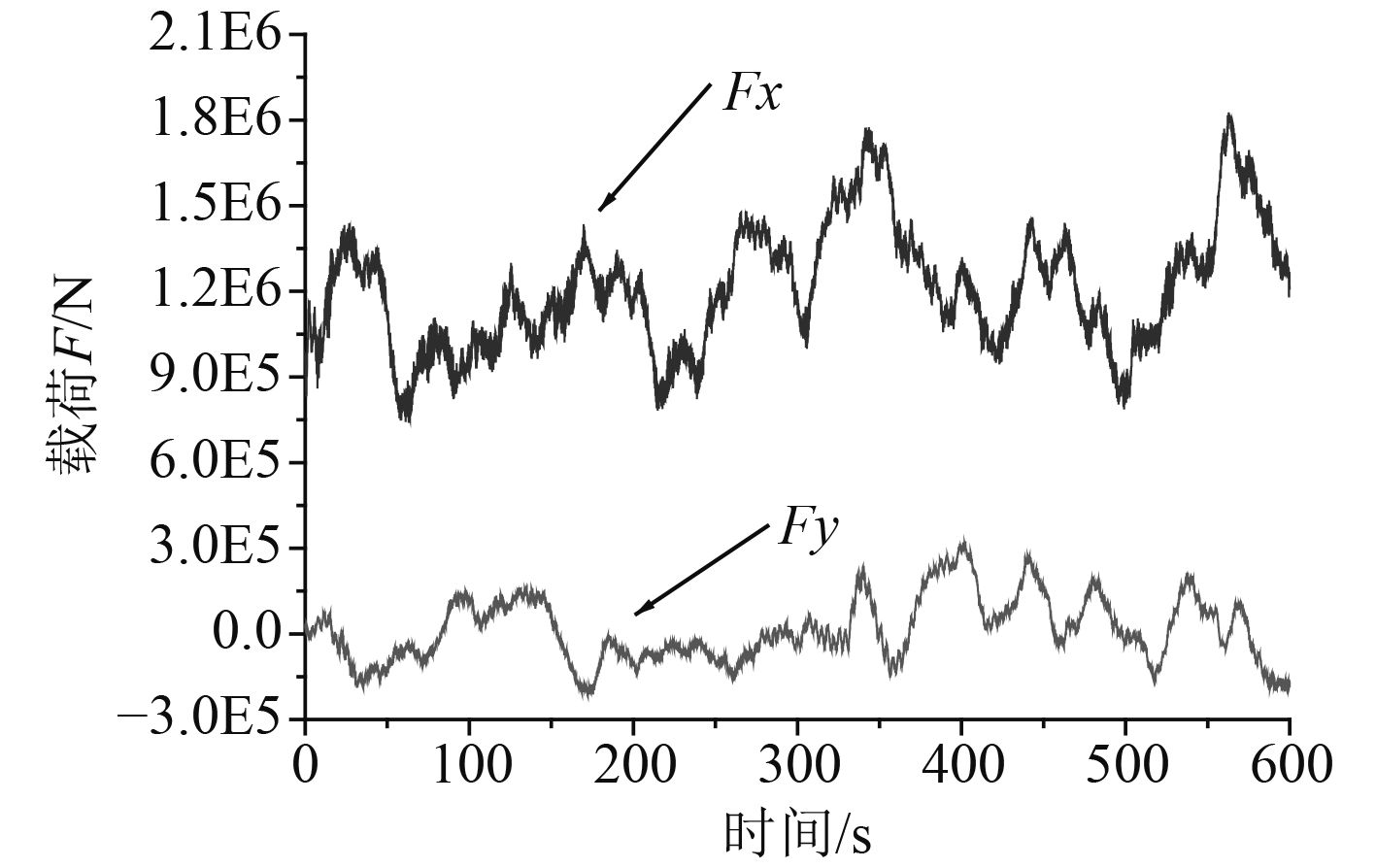
采用FAST软件计算塔顶处的风载荷,脉动风速谱采用Kaimal谱,海面10m处的平均风速为8.9 m/s[14]。轮毂处纵向湍流强度为10%。风机轮毂处坐标系定义如图3所示,x方向为纵向,y方向为横向,z方向为垂向。图4为轮毂处的纵向风速,图5为塔顶处纵向与横向载荷。
|
图 4 轮毂处纵向风速 Fig. 4 Longitudinal wind speed at hub |
|
图 5 塔筒顶端载荷 Fig. 5 Wind load at the top of tower |
|
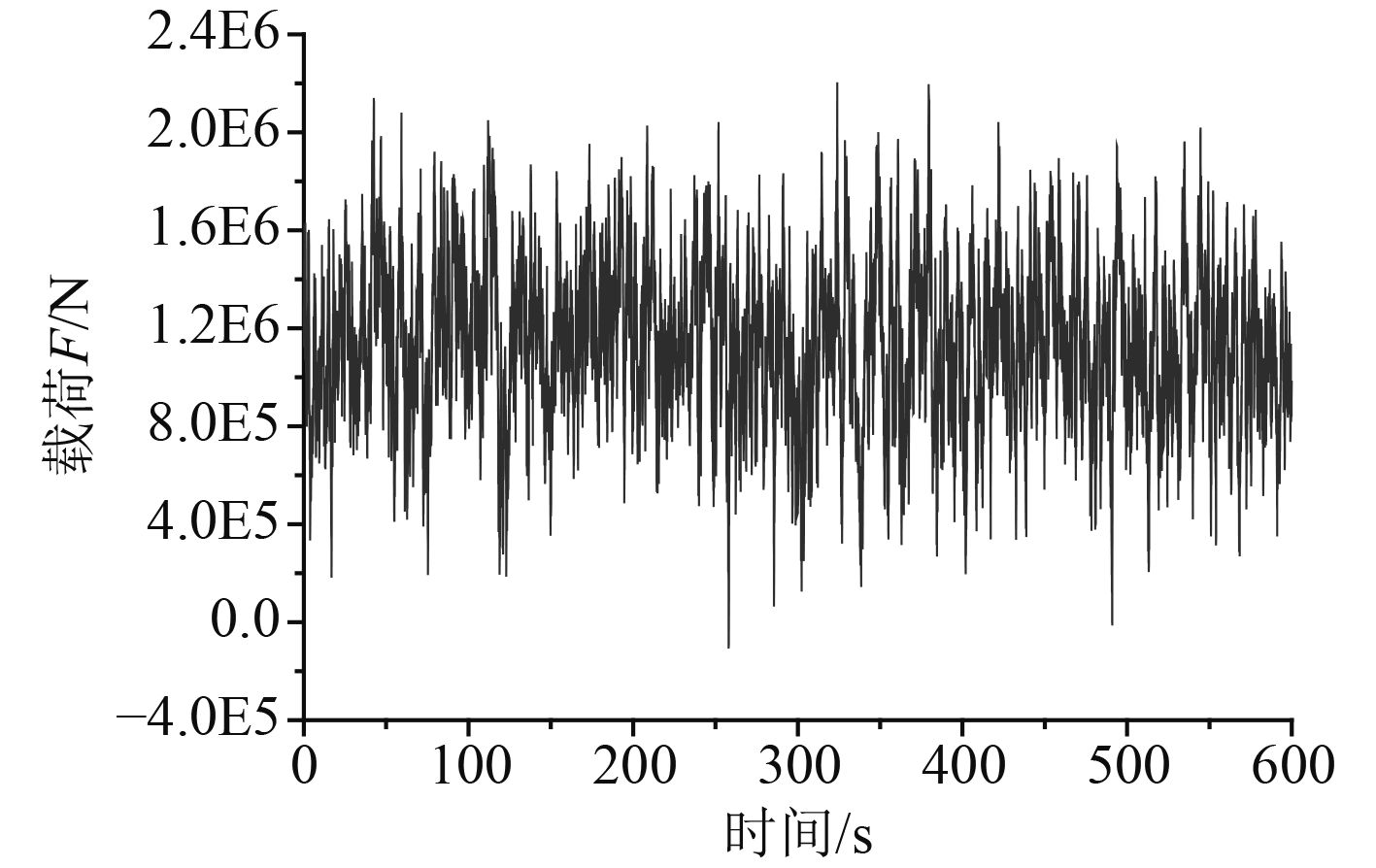
图 6 冰载荷时间历程 Fig. 6 Ice load time history |
采用IceFloe软件进行冰载荷计算。冰厚为13.1 cm,冰的压缩强度为2.02 MPa[15]。假设冰速方向与风速方向相同,忽略潮流对冰速的影响,冰漂移的风力系数为0.022[16],则平均冰速为19.6 cm/s。图6为冰载荷时间历程曲线。
3.3 风机动力响应分析风机在泥面处的坐标系定义如图7所示。
|
图 7 泥面处坐标系定义 Fig. 7 The definition of coordinate system at the mudline |
如图8所示,当风、冰载荷单独作用时,冰载荷作用下风机塔顶的纵向位移要远远小于风载荷的作用。
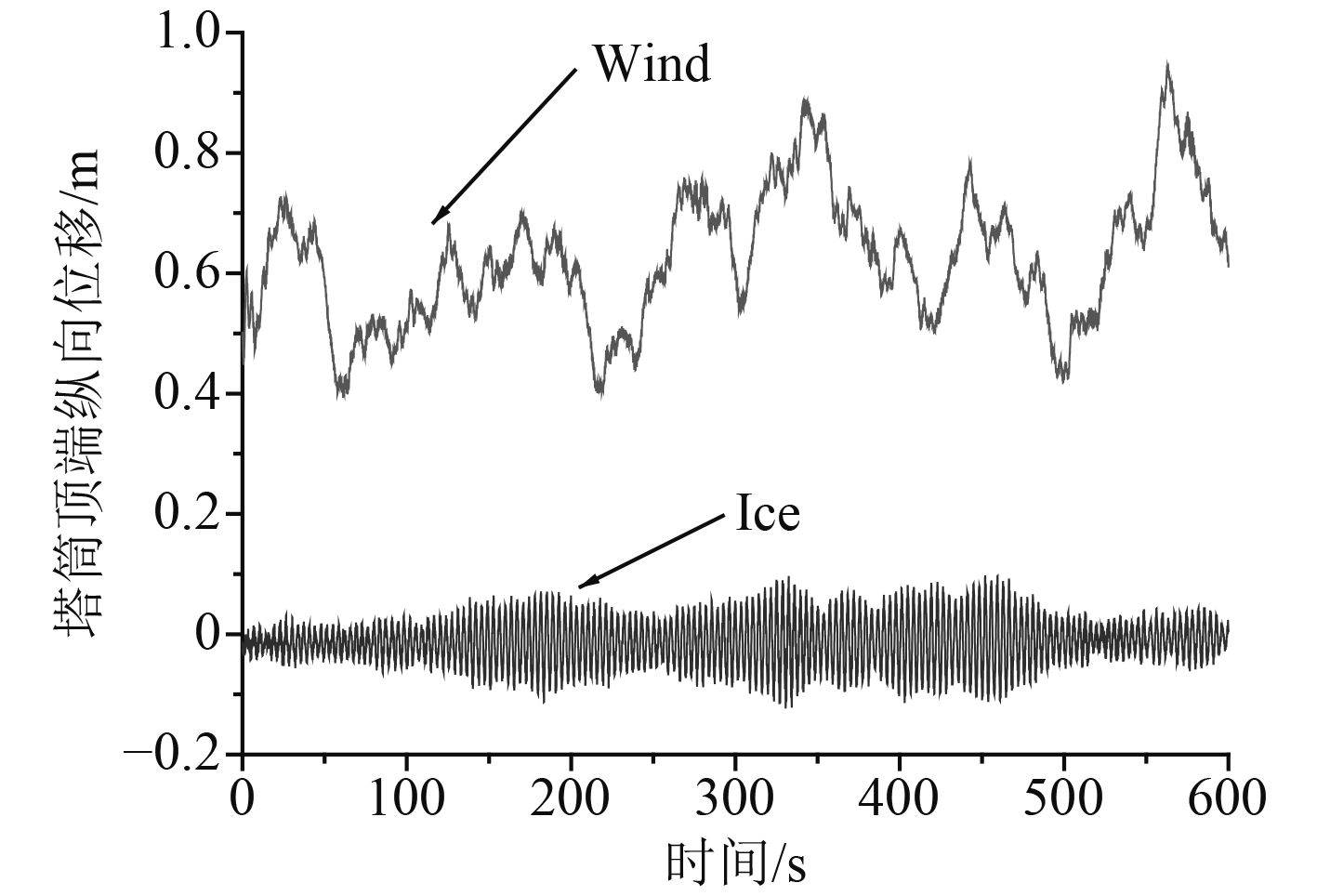
|
图 8 塔筒顶端纵向位移 Fig. 8 Longitudinal displacement at hub |
|
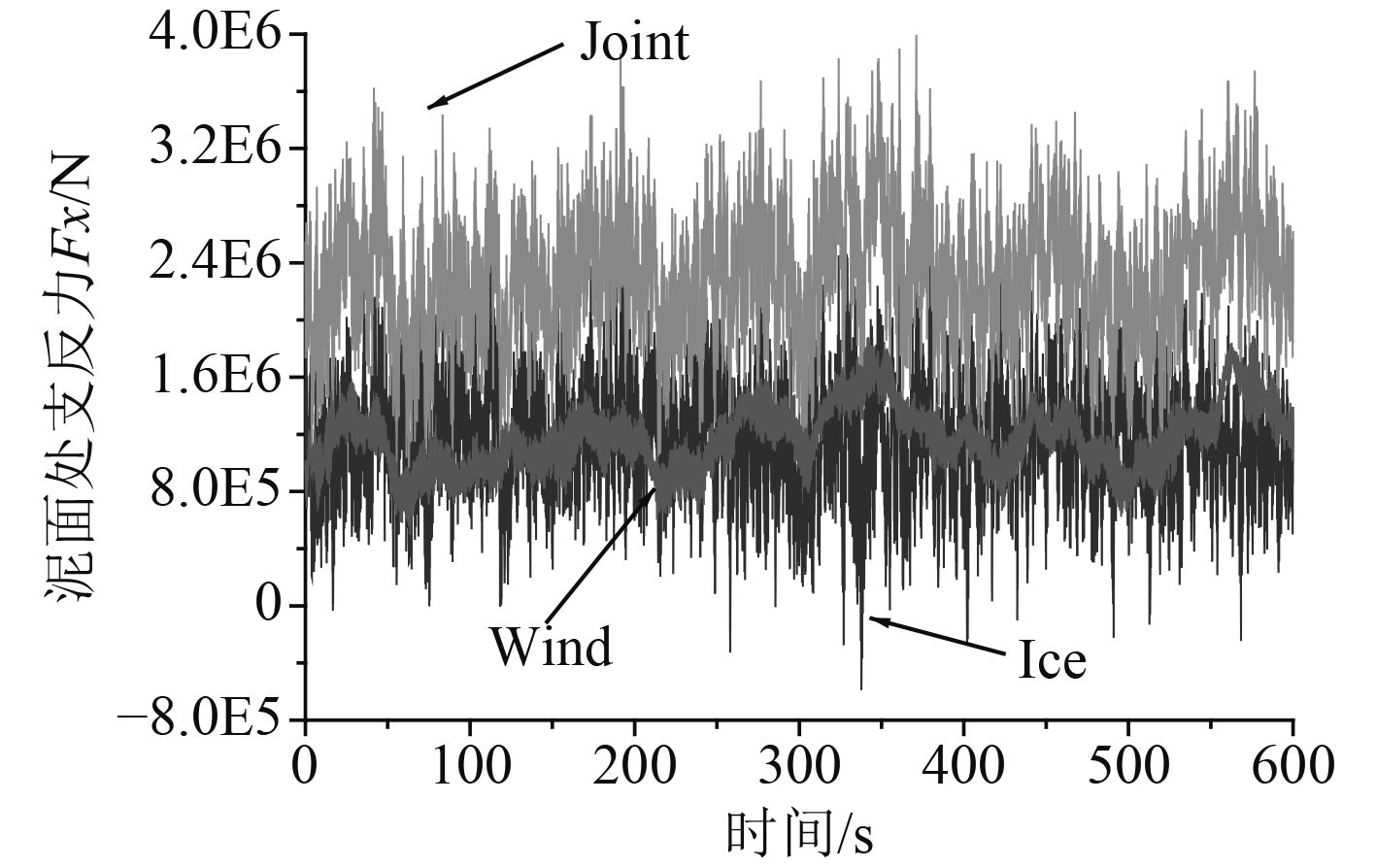
图 9 泥面处支反力Fx Fig. 9 Bearing force at the mudline |
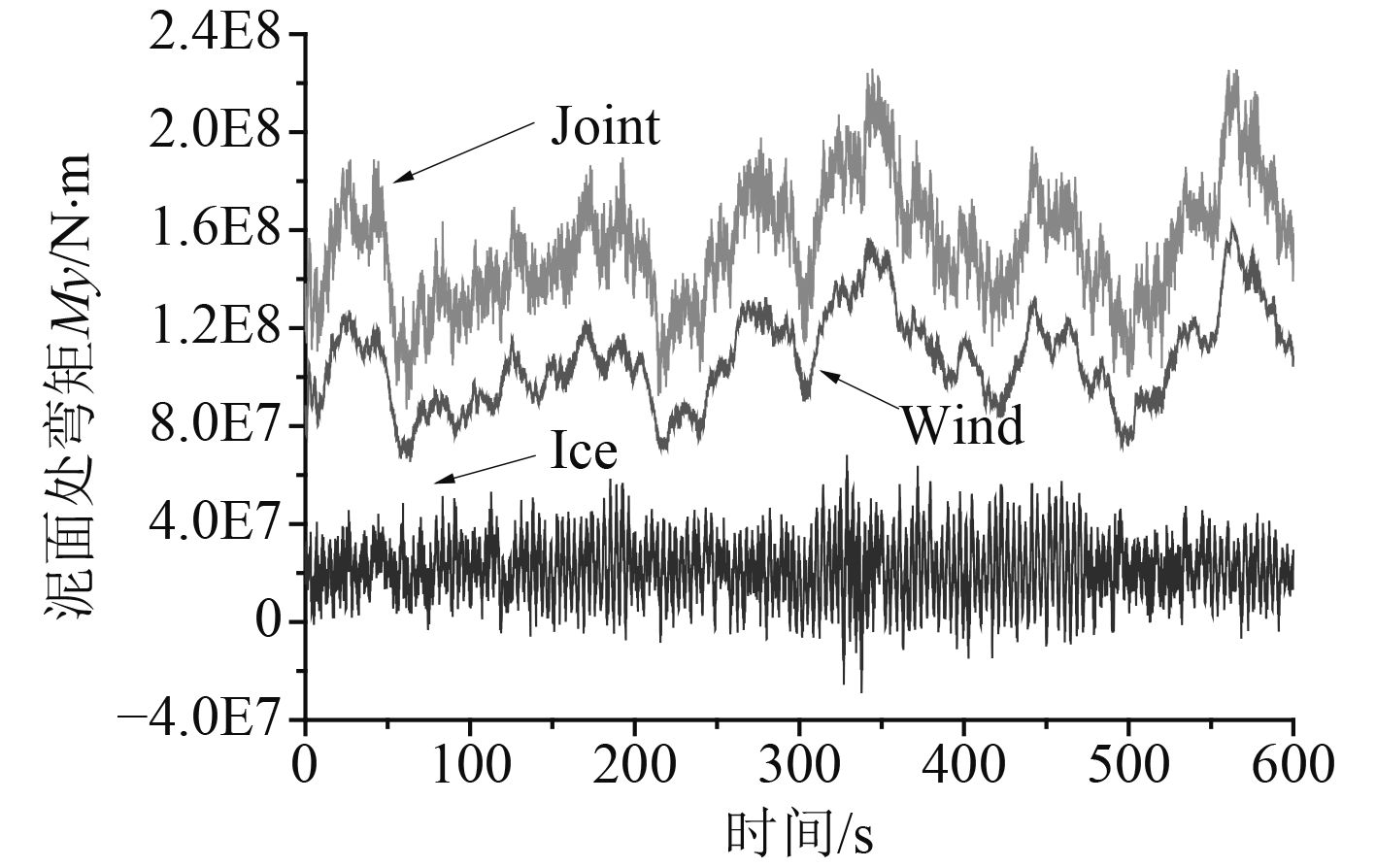
如图9所示,风冰载荷单独作用下,风机在泥面处的支反力Fx大小相当。风冰联合作用时,泥面处的支反力Fx总体上要大于2种载荷单独作用的支座反力Fx。图10中,冰载荷作用下风机在泥面处的弯矩My要低于风载荷作用时泥面处的弯矩My。当风冰联合作用时,其结果要大于2种载荷单独作用,曲线形状与风载荷单独作用基本一致,但是幅值有所不同。
|
图 10 泥面处弯矩 Fig. 10 Bending moment at the mudline |
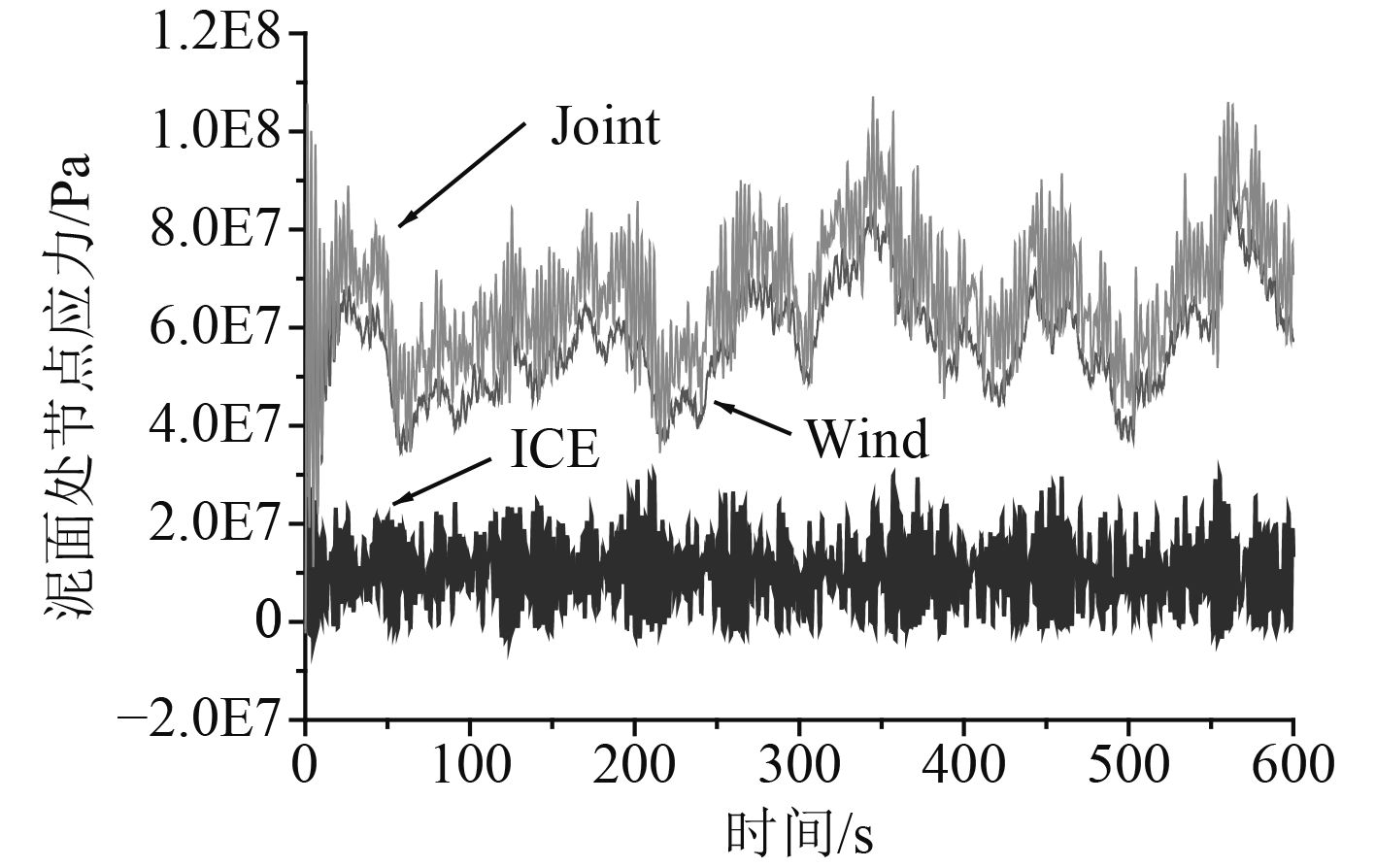
冰载荷作用下海上风机的疲劳属于2种载荷下的结构疲劳。通过有限元计算发现,风载荷与冰载荷作用下风机疲劳热点位置基本相同,均位于泥面处。图11为泥面处节点应力时程曲线。本文在时域内分别计算风载荷、冰载荷以及风冰联合作用下风机的疲劳损伤。采用Huang-Moan方法[17]、二次叠加法[18]、DNV方法[19]、Han-Ma方法[20]进行损伤组合计算,并与风冰联合作用下风机疲劳损伤比较。
|
图 11 泥面处节点应力时间历程 Fig. 11 Node stress time history at the mudline |
|
|
表 1 疲劳损伤比较 Tab.1 Comparison of fatigue damage |
由表1可知,冰载荷对风机造成的疲劳损伤要小于风载荷。以风冰联合计算损伤值为准,采用二次叠加法、Huang-Moan方法、Han-Ma方法进行损伤叠加,计算结果偏小,而DNV方法进行损伤叠加计算结果偏于保守,且误差较小。
4 结 语本文针对风冰载荷作用下的海上风机进行动力响应分析与疲劳损伤计算。研究结果表明:
1)风载荷作用下塔筒顶端的纵向位移要远远大于冰载荷作用。
2)风载荷与冰载荷单独作用下,泥面处的支反力相当。冰载荷作用下的泥面处的弯矩要要小于风载荷作用。当风冰载荷联合作用时,泥面处的支反力与弯矩均大于单一载荷的作用。
3)冰载荷对风机造成的疲劳损伤值要小于风载荷。DNV方法叠加计算得到的损伤值要大于风冰联合作用计算得到的结果,偏于保守。因此,推荐使用DNV方法。
| [1] | T. A numerical model for for dynamic ice-structure interaction[J]. Computers and Structures, 1999, 72 : 645–668. DOI: 10.1016/S0045-7949(98)00337-X |
| [2] | International Electrical Commission. IEC 61400–3, Wind turbines–Part 3: Design requirements for offshore wind turbines [S]. London, 2001. |
| [3] | 王翎羽, 徐继祖. 冰与结构动力相互作用的理论分析模型[J]. 海洋学报, 1993, 15 (3): 140–146. |
| [4] | Q. Dynamic ice forces of slender vertical structures due to ice crushing[J]. Cold Regions Science and Technology, 2009, 56 : 77–83. DOI: 10.1016/j.coldregions.2008.11.008 |
| [5] | WANG Qi. Ice-induced vibrations under continuous brittle crushing for an offshore wind turbine[D]. Delft: Technische Universiteit Delft, 2015. |
| [6] | WELLS E M. An assessment of surface ice sheet loads and their effects on an offshore wind turbine structure[D]. Toledo: The University of Toledo, 2012. |
| [7] | 方华灿, 徐发彦, 陈国明. 冰区海上平台管节点疲劳寿命计算的新方法[J]. 中国海洋平台, 1997, 12 (6): 259–263. |
| [8] | 黄焱, 马玉贤, 罗金平, 等. 渤海海域单柱三桩式海上风电结构冰激振动分析[J]. 海洋工程, 2016, 34 (5): 1–10. |
| [9] | International Electrical Commission. IEC 61400-1, Wind turbines–Part 1.: Wind turbines[S]. London, 2005. |
| [10] | VERITAS D N. DNV-RP-C205, Environmental conditions and environmental loads[S]. Oslo, 2010. |
| [11] | VEERS P S. Three-dimensional wind simulation[R]. NM: Sandia National Laboratories, 1988. |
| [12] | KUMH M. Dynamic and design optimization of offshore wind energy conversion system[D]. Delft: Technische Universiteit Delft, 2001. |
| [13] | International Organization for Standardization. ISO 19906, Petroleum and natural gas industries – Arctic offshore structures[S]. Switzerland, 2012. |
| [14] | 张增海, 曹越男, 赵伟. 渤海湾海域风况特性分析与海-陆风速对比分析[J]. 海洋预报, 2011, 28 (6): 33–39. DOI: 10.11737/j.issn.1003-0239.2011.06.006 |
| [15] | 中国海洋总公司. Q/Hsn 3000-2002, 中国海海冰条件及应用规定[S]. 北京, 2002. |
| [16] | 吴龙涛, 吴辉碇, 李万彪, 等. 渤海冰漂移对海面风场、潮流场的响应[J]. 海洋学报, 2005, 27 (5): 15–21. |
| [17] | HUANG W, MOAN T. Fatigue under combined high and low frequency loads[C]//25th International Conference on Offshore Mechanics and Arctic Engineering, Hanburg, 2006 |
| [18] | TEMPEL V D. Design of support structures for offshore wind turbines[D]. Delft: Technische Universiteit Delft, 2006. |
| [19] | Det Norske Veritas. DNV-RP-C203, fatigue design of offshore steel structure[S]. Oslo, 2011. |
| [20] | HAN C. A practical method for combination of fatigue damage subjected to low-frequency and high-frequency Gaussian random processes[J]. Applied Ocean Research, 2016, 60 : 47–60. DOI: 10.1016/j.apor.2016.08.007 |
 2018, Vol. 40
2018, Vol. 40
