2. 高新船舶与深海开发装备协同创新中心(船海协创中心),上海 200240;
3. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China;
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
近年来,由于住宅、工业以及军事用地需求增加,沿岸城市、岛屿附近土地扩张的需求日益高涨[1]。填海造地是一个可供选择的扩张陆地面积的方式,但填海造地会对洋流、海洋生态环境等造成巨大影响[2-3]。使用超大型浮体可以在扩张陆地面积的同时避免对海洋环境造成上述不良影响[4]。
超大型浮体通常由许多半潜式的单模块通过连接件首尾连接组成,其长度一般在1 000~10 000 m[5]。因此与小尺度的海洋平台相比,超大型浮体在纵向具有相当大的柔性[6],其纵向的弹性变形是目前研究的一个热点。本文研究的对象是超大型浮体的一个单模块,长度为300 m,不考虑纵向的弹性变形。
超大型浮体经常会布置在大陆海岸线周围或岛屿附近,这类海域通常具有水深极浅、海床具有一定坡度这2个特点。在这种浅水斜底的特殊海洋环境下,海洋结构物的运动响应有其特殊性,一些研究工作也印证了这一点。
Li等[7]发现,浅水情况下随着水深的减小,FPSO的波频运动会出现明显下降。Xiao等[8]也指出在浅水情况下,当水深减小时低频波浪力随之增加。除了“浅水”之外,“斜底”也对海洋结构物的运动有很大影响。Lu和Lin[9]在研究中指出,在浅水环境下,相同的波浪在海床水平与海床不水平时所产生的波浪力有极大差别。2005年Teigen[10]通过数值模拟表明,浅水中,海底地形的变化对驳船在波浪中的运动响应有深刻影响。Buchner[11]同时使用了数值模拟和模型试验的方法来研究船舶在浅水斜底环境下的运动,结果表明,当海床倾斜时,船舶运动更加剧烈并且船舶的RAO有更加明显的局部震荡。
基于海洋结构物在浅水斜底情况下动态响应的特殊性,本文分别通过OrcaFlex数值模拟和模型试验研究了超大型浮体单模块在浅水斜底情况下的动态响应,得到了单模块横荡和横摇运动的时历数据及统计结果,以及锚链张力的统计数据。本文的模型试验在上海交通大学海洋工程水池开展,单模块由一套悬链线锚链实现定位,同时考虑斜底和浅水的影响。
1 数值模拟 1.1 势流理论OrcaFlex中的数值模拟基于势流理论。在势流理论中,海水被视为没有粘性且不可压缩的流体,并且海水的流动是无旋的。因此,速度势ϕ满足以下拉普拉斯方程[12]:
| ${{\nabla ^2}\phi (x,y,z,t) = 0}\text{。}$ | (1) |
根据Haskind的理论,速度势ϕ可以被分解为3部分:入射势ϕI、辐射势ϕR以及绕射势ϕD。于是总的速度势可以通过分别求解这3部分得到:
| $\phi = {\phi _I} + {\phi _R} + {\phi _D}\text{。}$ | (2) |
其中,求解入射势、辐射势、绕射势的任何一个都需要用到边界条件,边界条件的公式如下所示:
| $\left\{ \begin{aligned}&\displaystyle\frac{{{\partial ^2}\phi }}{{\partial {t^2}}} + g\displaystyle\frac{{\partial \phi }}{{\partial z}} = 0\left| {_{z = 0},} \right.\;\;\;{\text{自由面}},\\&\displaystyle\frac{{\partial \phi }}{{\partial n}}\left| {_S = {U_n},} \right.\;\;\;\;{\text{物面}},\\&\displaystyle\frac{{\partial \phi }}{{\partial n}}\left| {_{z = - H} = 0,} \right.\;\;\;{\text{有限水深的水底}},\\&\mathop {\lim }\limits_{R \to \infty } \sqrt R (\displaystyle\frac{{\partial \phi }}{{\partial R}} + \displaystyle\frac{1}{C}\frac{{\partial \phi }}{{\partial t}}) = 0,\;\;\;{\text{无限水深}}{\text{。}}\end{aligned} \right.$ | (3) |
得到速度势后,通过拉格朗日积分可以求得整个流场的压力分布。流体施加在单模块上的作用力也可以进一步被求出[12]。
| $p(x,y,z,t) = - \rho \frac{{\partial \phi }}{{\partial t}} - \rho gz\text{。}$ | (4) |
然后,根据求得的单模块上的流体作用力,使用1阶频域运动方程可以求得单模块频域内的水动力参数。
| $({{m}_{ij}} + {\mu _{ij}}){\ddot x_j} + {\lambda _{ij}}{\dot x_j} + {{c}_{ij}}{x_j} = {f_i},{{ i、j = 1}},{\rm{2}}, \cdots {\rm{6}} {\text{。}}$ | (5) |
式中:m为质量矩阵;μ为附加质量;λ为阻尼系数矩阵;c是回复力系数矩阵;f为作用在单模块上的1阶力。
1.3 时域运动分析单模块的运动由下式决定[12]:
| $\begin{split}({M} + {a})\ddot x + {C}\dot x + {{D}_1}\dot x + {{D}_2}f(\dot x) + {K}(x)x = \\ {F_{\rm wave}} + {F_{\rm wind}} + {F_{\rm current}} + {F_{\rm moor}}{\text{。}}\end{split}$ | (6) |
式中:M和a分别为单模块的质量矩阵和附加质量矩阵;C为阻尼矩阵;D1和D2为线性和二阶的阻尼矩阵;K(x)为静回复力刚度矩阵;x(t)是单模块的六自由度运动方程;Fwind,Fwave和Fcurrent分别是风浪流施加的力;Fmoor是锚链力。
1.4 系泊力计算OrcaFlex中使用有限元方法计算锚链的系泊力。锚链被分解成若干个直的无质量分段,分段两端各有1个节点。每个分段中只建立锚链轴向和扭转特性的关系,其他的锚链参数如重力、浮力等都集中在节点位置。在线性刚度的情况下,分段的轴向有效张力可由下式计算[13]:
| ${T_{\rm{e}}} = {T_w} + ({P_e}{A_e} - {P_i}{A_i})\text{。}$ | (7) |
式中:Te为有效张力;Tw为管壁张力;Pe为外壁圧力;Pi为内壁压力;Ae为外圆横截面积;Ai为内圆横截面积。对于锚链而言,内圆横截面积Ai和内壁压力Pi都为0。管壁张力Tw可以通过下式获得:
| ${T_w} = EA \cdot \varepsilon - 2v \cdot \left( {{P_e}{A_e} - {P_i}{A_i}} \right) + EA \cdot e\left( {dL/dt} \right)/{L_0}{\text{。}}$ | (8) |
式中:EA为锚链的轴向刚度;ε为总的轴向应变;L为分段的瞬时长度;L0为分段原长;v为泊松比;e为锚链的阻尼系数;dL/dt为分段长度的增长速度。
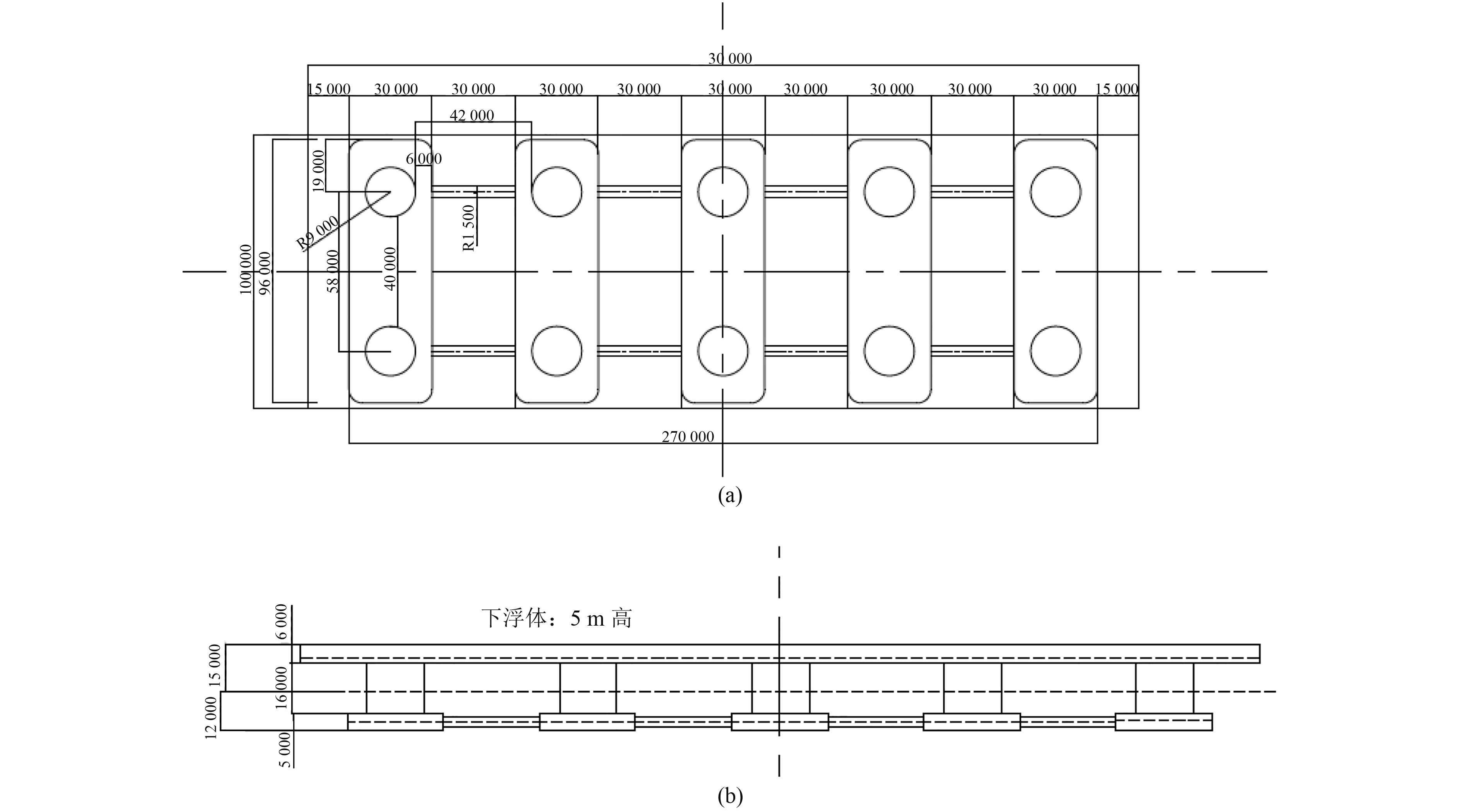
2 模型试验 2.1 单模块基本特征本文所研究的超大型浮体单模块由上部甲板、立柱、下部浮箱3部分组成,共有5个浮箱、10根立柱。单模块总长300 m,宽100 m,设计图及实物如图1所示。本文模型试验按照1:100的缩尺比进行,后文如无特别说明,所有数值均代表实型值。
|
图 1 超大型浮体单模块设计图 Fig. 1 Design plan of the single module of a very large floating structure |

|
图 2 单模块在浅水斜底中的系泊试验 Fig. 2 Single module's mooring model test in shallow water and sloped seabed |
表1给出了单模块的具体参数。
|
|
表 1 单模块的主要参数 Tab.1 Main parameters of the single module |
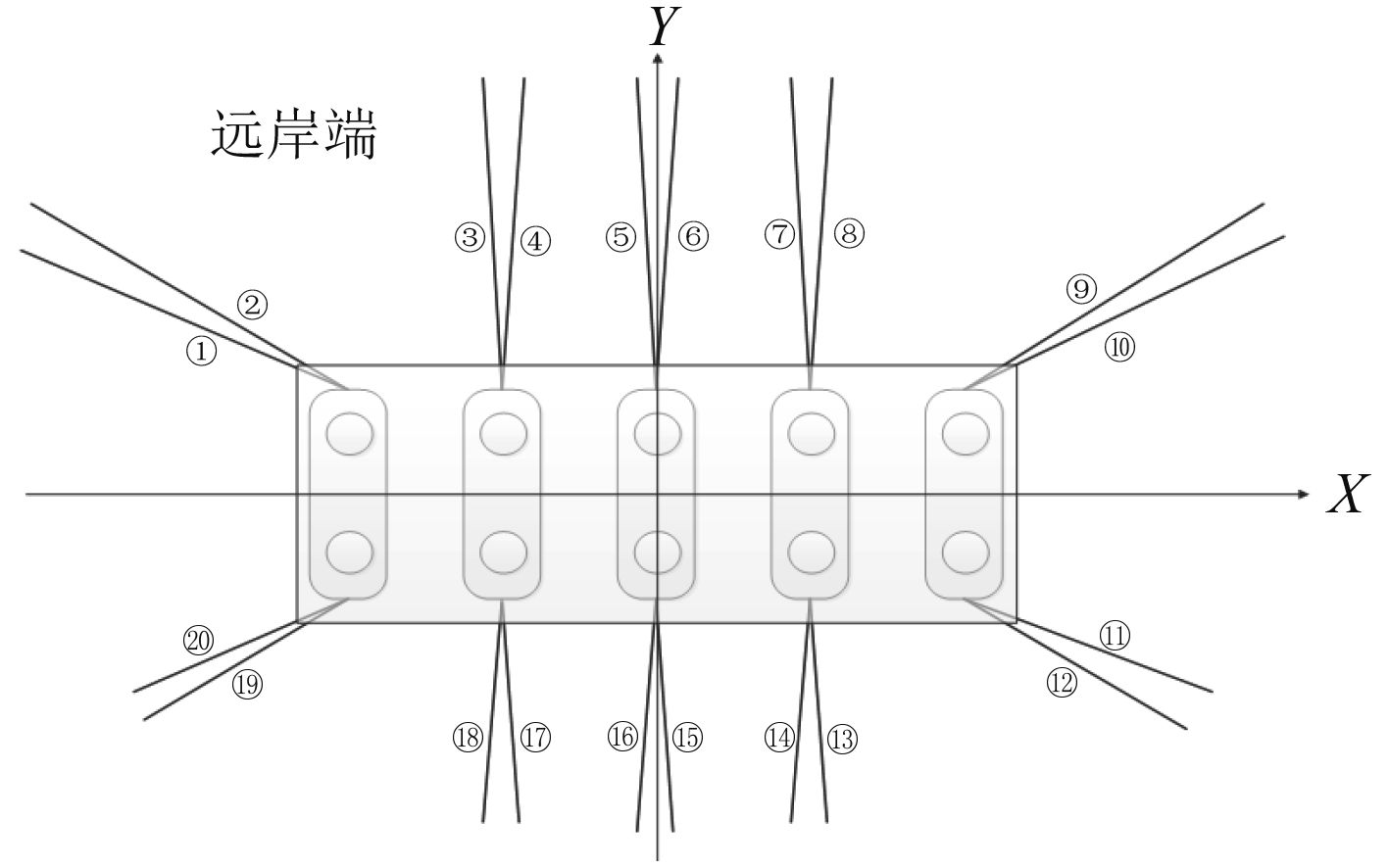
单模块由20根悬链线实现系泊,锚链的布置如图3所示,表2给出了锚链的具体参数。由于斜底的影响,系泊系统中各锚链的长度有所不同。
|
图 3 锚链布置形式 Fig. 3 Mooring line configuration |
|
|
表 2 锚链的基本参数 Tab.2 Primary parameters of the mooring lines |
模型试验中,使用1套非接触式光学运动跟踪系统来采集单模块重心处的六自由度运动;使用20个张力传感器测量锚链在导缆孔处的张力;使用6个电阻式浪高仪测量水池中的波浪时历情况。
2.4 工况设置本文研究的目标海域为岛礁附近,岛礁附近的风浪载荷主要从海洋向岛礁方向传播,因此本文中风浪载荷的方向均由远岸端传向岛礁,即图3中X轴的270°方向。
本文讨论了4种不同海况,其中不规则波由JONSWAP谱给出,风载荷为定常风,计算对应的实际海况时间为3 h。表3给出了海况信息。
|
|
表 3 模型试验工况 Tab.3 Sea states of the model test |
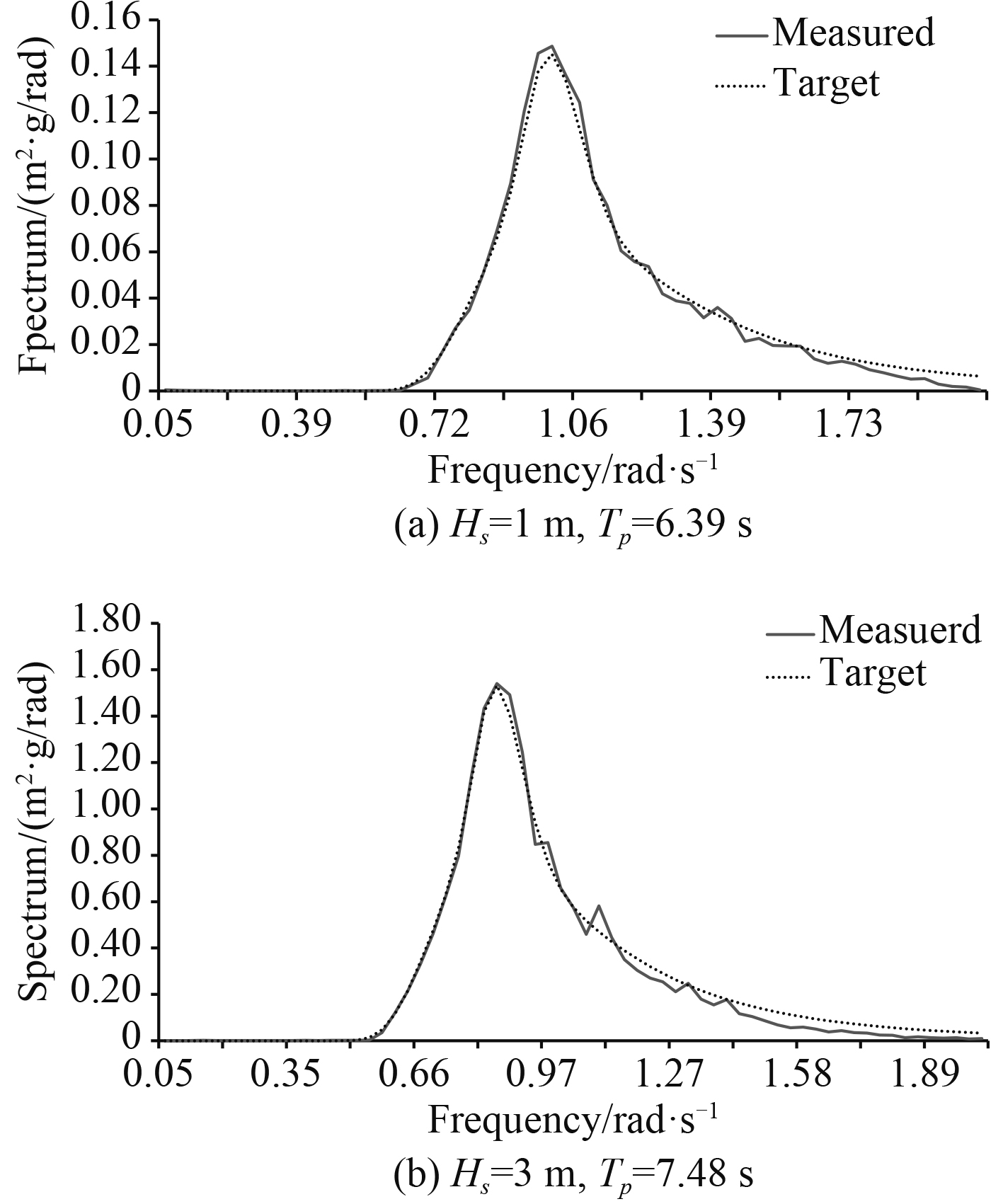
在单模块下水之前,使用浪高仪测量造波机产生的波浪以实现校波,校波结果如图4所示,可以发现造波机产生的波浪与目标值非常契合。
|
图 4 校波结果 Fig. 4 Results of wave calibration |
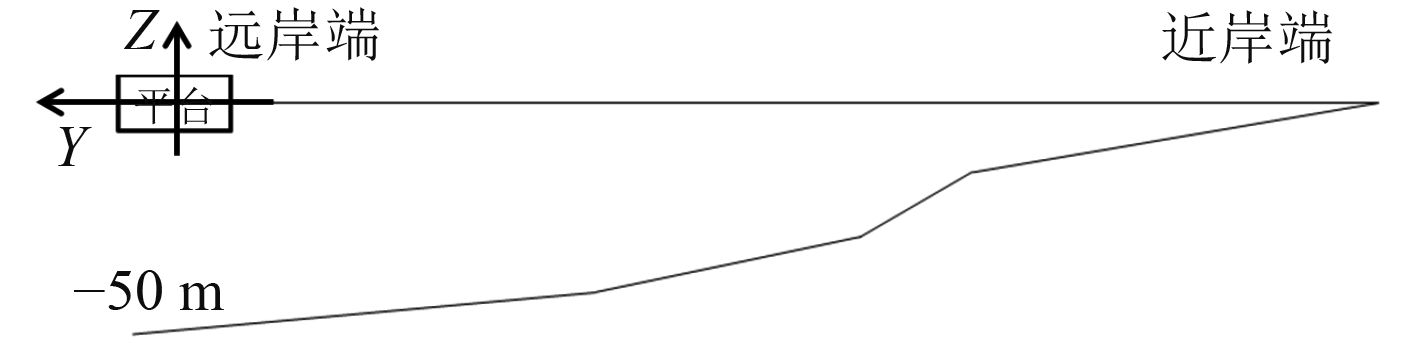
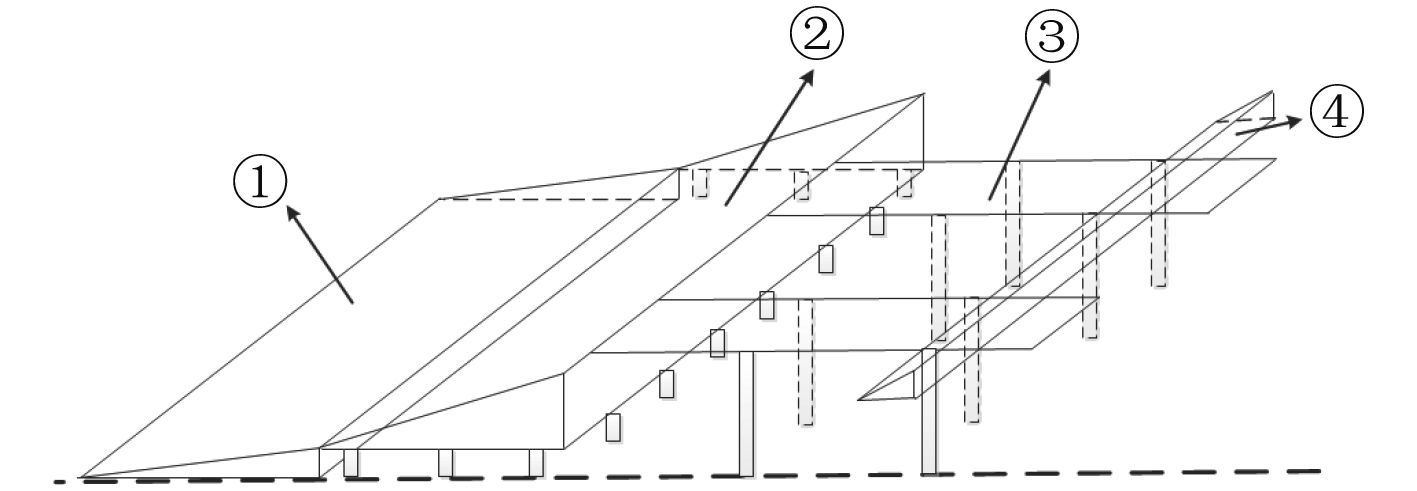
本文研究的浅水斜底地形如图5所示,在数值模拟和模型试验中,用图6所示的假底来模拟真实的海底地形。假底由2部分组成:一个2°的斜底(①),以及一个7°的斜底(②)。
|
图 5 海底地形简图 Fig. 5 The submarine topography |
|
图 6 试验中使用的假底 Fig. 6 The artificial seabed used in model test |
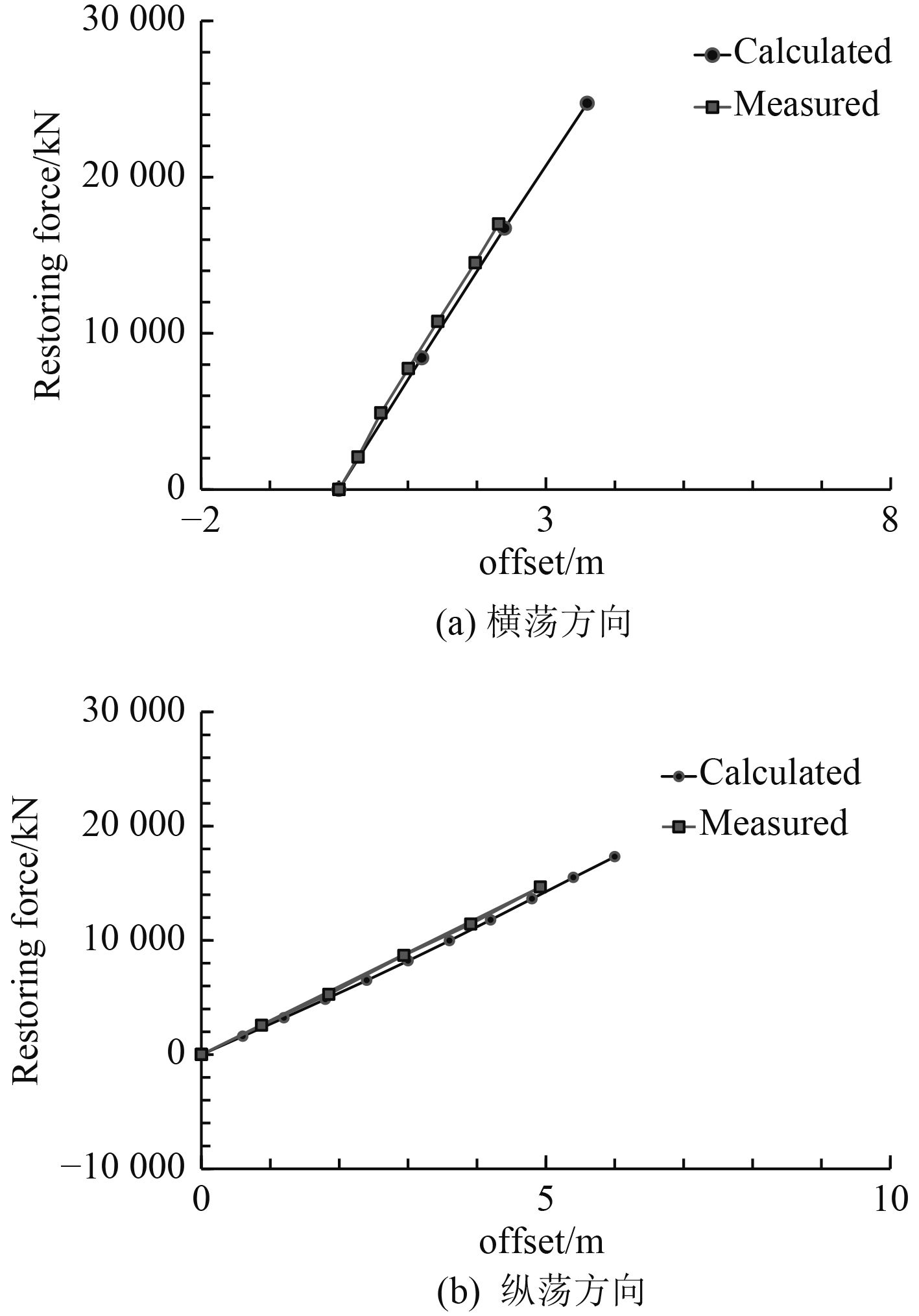
为验证用于模型试验的系统是否与设计一致,试验中首先对模型进行静态刚度试验。图7展示了试验获得的静态刚度曲线和目标静态刚度曲线之间的对比,可以发现,试验值和设计值吻合良好。
|
图 7 静态刚度试验结果 Fig. 7 Results of static stiffness test |
为了获得平台的瞬时响应,进行时域分析非常必要[14],平台的时域运动响应是评估整个系泊系统可靠性的重要依据。由于本文研究的单模块所遭遇的风浪载荷为X轴的270°方向,因此主要对单模块在风浪载荷下的横荡和横摇运动进行探究。
图8给出了数值模拟和模型试验得到的单模块时历运动结果,为使对比更加明显,图中仅给出了1 800 s的时历数据。由图8可得,数值模拟与模型试验结果吻合良好;同时,可以发现在此系泊系统下单模块的横荡和横摇运动都较为稳定,而同一海况下横荡运动的稳定性优于横摇运动。

|
图 8 数值模拟和模型试验所得横荡及横摇时历对比 Fig. 8 Comparison of sway and roll time series results between numerical simulation and model test |
表4和表5给出了单模块数值模拟和模型试验得到的横荡及横摇运动统计数据,平均值及标准差分别表征了单模块运动的位置偏差以及运动的稳定性,对考察单模块的动态响应具有重要意义。
1)风载荷对运动的影响
工况1和工况2波浪载荷相同,而工况2相较工况1而言多了10 m/s的定常风,因此2种海况下统计结果的比较可以分析风载荷对单模块运动的影响。
以表4数据为例,工况2和工况1相比,数值模拟和模型试验所得的运动平均值分别增加67.6%和80.0%,运动的标准差分别增加24.6%和4.1%。这表明风载荷的存在会使横荡运动幅值大幅增加,而横荡运动的稳定性所受影响则十分微弱。工况3和工况4的对比,以及表5所示的横摇运动也能得出相同结论。
2)波浪载荷对运动的影响
工况1和工况3两种海况的区别在于波浪载荷不同,将两者进行比较可以得出波浪载荷对单模块运动的影响。
表4数据显示,工况3和工况1相比,数值模拟和模型试验所得的横荡运动平均值分别增加96.9%和117.1%,运动的标准差分别增加307.9%和280.8%。平均值和标准差都显著增大说明波浪载荷的增大会使运动幅值大幅增加、运动稳定性大幅下降;同时,标准差增幅远大于平均值增幅,说明运动的稳定性对波浪载荷更为敏感。表5所示的横摇运动也呈现相同特征。
|
|
表 4 单模块数值模拟与模型试验统计结果比较(横荡) Tab.4 Comparison of the statistical results between numerical simulation and model test results (sway) |
|
|
表 5 单模块数值模拟与模型试验统计结果对比(横摇) Tab.5 Comparison of the statistical results between numerical simulation and model test results (roll) |
锚链张力与整个单模块系统的安全性密切相关,因此必须分析锚链张力对风浪载荷的响应。表6为数值模拟和模型试验中,各海况下锚泊系统出现的最大锚链张力。表中|A|max为最大锚链张力,λ为最大张力与锚链破断强度的比值。
从模型试验结果来看,工况2相比工况1最大张力增加7.9%,工况4相比工况3增加2.5%,这表征了相同波浪载荷下风载荷对锚链最大张力的影响;而工况3相比工况1最大张力增加21.5%表征了波浪载荷对锚链张力的影响。以上数据显示,相比于风载荷,锚链张力受波浪载荷影响更为明显,数值模拟的结果也证实了这样的结论。此外,从最大张力与锚链破断强度的比值来看,所用锚链在本文提出的4种海况中都十分安全。
|
|
表 6 数值模拟与模型试验所得最大锚链张力 Tab.6 Statistical results of maximum mooring force in numerical simulation and model test |
由于在浅水斜底情况下,浮式结构物对环境载荷的动态响应与其在深水中的表现会有较大差别,本文分别通过数值模拟和模型试验探究了超大型浮体单模块在浅水斜底海域中对风浪载荷的动态响应,通过结果的对比分析,得到以下结论:
在相同波浪载荷作用下,当所受风载荷增加时,单模块横荡和横摇运动的平均值都大幅增加,而标准差则几乎不受影响,说明定常风对单模块运动的稳定性影响较小。
当单模块所受波浪载荷增大时,横荡和横摇运动的平均值都大幅增加、标准差也大幅增加且更为显著;说明波浪载荷对单模块运动的幅值和稳定性都有很大影响,而相比运动幅值,其对运动稳定性的影响更为明显。
风载荷和波浪载荷的增大都将导致锚链张力增大,但相比于风载荷,波浪载荷对锚链张力的影响更为明显。
| [1] | MIGUEL L P, GREGORIO I, LUIS C. A review of very large floating structures (VLFS) forcoastal and offshore uses[J]. Ocean Engineering, 2015, 109 : 677–690. DOI: 10.1016/j.oceaneng.2015.09.012 |
| [2] | WATANABE E, UTSUNOMIYA T, WANG C M.. Hydroelastic analysis of pontoon-type VLFS: a literature survey[J]. Engineering Structures, 2004, 26 : 245–256. DOI: 10.1016/j.engstruct.2003.10.001 |
| [3] | ZHANG Ming-hui, CHEN Chang-ping, SUO An-ning, et al. International advance of sea areas reclamation impact on marine environment[J]. Ecology and Environmental Sciences, 2012, 21 (8): 1509–1513. |
| [4] | GAO R P, TAY Z Y, WANG C M, et al. Hydroelastic response of very large floating structure with a flexible line connection[J]. Ocean Engineering, 2011, 38 : 1957–1966. DOI: 10.1016/j.oceaneng.2011.09.021 |
| [5] | SUZUKI H, BHATTACHARYA B, FUJIKUBO M. Very large floating structures[C]// Proceedings of the 16th International Ship and Offshore Structures Congress. Southampton, 2006, UK2. |
| [6] | KIM J G, CHO S P, KIM K T, et al. Hydroelastic design contour for the preliminary design of very large floating structures[J]. Ocean Eng, 2014, 78 : 112–123. DOI: 10.1016/j.oceaneng.2013.11.006 |
| [7] | LI Xin, LI Jian-min, XIAO Long-fei. Motion analysis on a large FPSO in shallow water[C]// Proceedings of The Thirteenth (2003) International Offshore and Polar Engineering Conference. Honolulu, 2003: 235–239. |
| [8] | XIAO Long-fei, YANG Jian-min, HU Zhi-qiang. Low frequency wave forces and wave induced motions of a FPSO in shallow water[C]// Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering. San Diego, 2007: 1–7. |
| [9] | LU Y, LIN J. Nonlinear wave diffraction in shallow water over an uneven bottom[C]// ISOPE 1992, 2nd Intl Offshore & Polar Engng Conf. San Francisco, 1992: 53. |
| [10] | TEIGEN P. Motion response of a spread moored barge over a sloping bottom[C]// Proceedings of the Fifteenth (2005) International Offshore and Polar Engineering Conference. Seoul, 2005: 19–24. |
| [11] | BAS B. The motions of a ship on a sloped seabed[C]// Proceedings of OMAE 2006: 25th International Conference on Offshore Mechanics and Arctic Engineering. Hamburg, 2006: 1–9. |
| [12] | LIU Ying-zhong, LIAO Guo-ping. Theory of ship motions in waves[M]. Shanghai: Profile of Shanghai Jiao Tong University Press, 1987. |
| [13] | Orcina Ltd. OrcaFlex Manual[M]. 2012. |
| [14] | C. Very large floating structures: applications, research and development[J]. Procedia Engineering, 2011, 14 : 62–72. DOI: 10.1016/j.proeng.2011.07.007 |
 2018, Vol. 40
2018, Vol. 40
