2. 浙江水利水电学院 机械与汽车工程学院,浙江 杭州 310018
2. Mechanical and Automotive Engineering College, Zhejiang University of Water Resources and Electric Power, Hangzhou 310018
随着油气开采逐步向海洋,特别是深海推进,以深海平台及其配套设备(如系泊缆、立管等)为代表的海洋结构物的设计与优化成为海洋工程领域研究热点之一。海洋立管是海面与海底井口间的主要连接构件,是现代海洋工程结构系统的重要组成部分之一。张力腿平台(TLP)是一类较为常用的深海油气钻采平台,通常情况下TLP平台与TTR立管的连接通过张紧器实现,立管的底部则通过万向节固定于油井的井口。当立管本身的固有频率与由立管的顶张力、自重以及波浪共同作用下产生的振动频率相近时,立管会发生耦合共振,使其振动幅值急剧加大。长此以往,立管会发生疲劳损伤乃至失效,从而造成巨大的经济损失以及严重的海洋环境污染。因此,对深海立管的固有频率及其影响因素进行研究,能够有效避免因立管耦合共振而造成的立管损伤甚至失效,具有明确的理论和工程实用意义。
对水下立管力学性能的研究已有50多年的历史,最早可追溯至1950年Molole计划中对海洋立管的静力特性与动力特性的研究。自深海立管被大量投入使用以来,为确保深海油气钻采作业的安全,对立管涡激振动的研究热度从未降低。这其中,对立管固有频率和立管振动频率的研究作为立管涡激振动研究的关键部分,更是被关注。
对立管固有频率的研究主要有模型试验法和数值模拟法2种。相较于模型试验法,采用数值模拟的方法具有成本低、方便易实现等优点,因此目前该方法被广泛应用于深海立管固有频率的研究中。张杰[1]针对不同的立管分析模型,提出不同的固有振动特性简化计算公式,并在此基础上,进一步研究了平台运动对立管模态的影响[2]。雷松等[3]运用微分变换法推导了立管在悬挂状态下的固有频率和振型的数值计算方法。郭磊[4]建立了考虑内部流体作用的数值计算模型,发现立管各阶固有频率均随立管内部流体密度的变化而有规律地变化。D.J. Montoya[5]研究了立管内多相流对立管固有频率的影响。王在刚[6]编写了考虑耦合振动的立管频率Matlab计算程序,并通过与Ansys的模拟结果对比验证了该模型的正确性。王东[7]利用Ansys有限元模型分析了立管高度、风速、管径和管道两端约束方式对浅海天然气立管固有频率的影响。姜峰等[8]应用Ansys比较了立管在干、湿模态下的固有频率及振型,提出了立管结构的若干优化方法。王红霞等[9]研究了立管变张力和弯曲刚度对SCR立管固有频率的影响,结果表明弯曲刚度对前10阶频率影响不大。潘佳[10]通过Shear7对是否考虑弯曲刚度的2种模型进行了固有频率和模态分析。孙传栋等[11]则通过Abaqus模拟了不同顶张力下立管的模态,并分析了顶张力对固有频率的影响。
本文采用数值模拟的方法研究了立管的边界条件、本身物理参数和顶端张力等因素对其固有频率的影响。首先建立了简化的立管模型,并对3种不同边界条件下立管的振动特性进行分析。然后,在第3类边界条件的基础上,分析了立管的自重、长度、外径、壁厚等自身物理参数以及顶张力等因素对立管固有频率的影响。通过上述研究工作,最终得出了一些有意义的结论。
1 立管运动方程及边界条件的处理深海顶张力立管(即TTR)在顶张力的作用下,其横向运动方程可表示为:
| $EI\frac{{{\partial ^4}y}}{{\partial {z^4}}} - \left( {{T_0} + T\cos \omega t} \right)\frac{{{\partial ^2}y}}{{\partial {z^2}}} + {\rm{c}}\frac{{\partial {\rm{y}}}}{{\partial t}} + m\frac{{{\partial ^2}{\rm{y}}}}{{\partial {t^2}}} = {F_{\rm{y}}}\left( {z,t} \right),$ | (1) |
式中:E为弹性模量;I为截面惯性矩;T0为预张力;T为动张力;ω为中心激振圆频率;c为结构粘性阻尼系数;m为结构的单位长度质量。
Fy(z,t) 为沿着y方向上每单位长度的流体总作用力,可视作漩涡串作用产生的升力FL(z,t) 和张力腿由于横向运动而产生的流体阻尼力Fr(z,t) 两部分组成,即
| ${F_y}\left( {z,t} \right) = {F_L}\left( {z,t} \right) - {F_r}\left( {z,t} \right){\text{。}}$ | (2) |
其中:
| ${F_L}\left( {z,t} \right) = \frac{1}{2}\rho D{\left( {{V_c} + u} \right)^2}{C_L}\cos {\omega _s}t{\text{。}}$ | (3) |
式中:ρ为海水密度;D为张力腿直径;CL为升力系数;ωs为涡激圆频率。
而对于流体阻尼力Fr(z,t) 项,则可通过Morison方程[13]进行求解。
在实际工作状态下,TLP平台由于波流的作用会发生纵荡、纵摇等运动。这些运动会带动通过张紧器连接的立管一起运动,使立管的顶端存在一个随时间变化的位移边界条件。因此,在对立管进行有限元分析时,除了要建立立管的简化模型外,还需要确定计算的边界条件。不同的边界条件会得到不同的立管频率计算结果。本文对顶张式立管边界条件共分为3类:第1类边界条件为两端简支;第2类边界条件为下端简支,上端的边界条件为一固定位移,记为d;第3类边界条件为下端简支,上端在第2类边界条件的基础上,将其变为一个位移随时间变化的位移边界条件。3类边界条件下的立管模型如图1所示。

|
图 1 不同边界条件示意图 Fig. 1 The schematic of different boundary conditions |
对于上述3类不同边界条件下的立管模型,其边界条件可分别表示为:
| $\begin{aligned}& \!\!\!\left\{ {\begin{array}{*{20}{c}}\!\!\!{y(0,t) = y(l,t) = 0,\;\;\;\;\;}\\\!\!\!\!{\displaystyle\frac{{\partial {y^2}(0,t)}}{{\partial {z^2}}} \!\!=\!\! \displaystyle\frac{{\partial {y^2}(l,t)}}{{\partial {z^2}}} \!\!=\!\! 0}{\text{。}}\end{array}} \right.\!\!\!\!\!\;\;\left\{ {\begin{array}{*{20}{c}}\!\!\!\!{y(0,t) = 0\;\;y(l,t) = d},\\\!\!\!\!{\displaystyle\frac{{\partial {y^2}(0,t)}}{{\partial {z^2}}} \!\!=\!\! 0\;\;\displaystyle\frac{{\partial {y^3}(l,t)}}{{\partial {z^3}}}\!\! =\!\! 0}{\text{。}}\end{array}} \right.\!\!\!\;\; \\ & \left\{ {\begin{array}{*{20}{c}}{y(0,t) = 0\;\;\;\;\;\;\;\frac{{\partial y(l,t)}}{{\partial z}} = 0},\\{\displaystyle\frac{{\partial {y^2}(0,t)}}{{\partial {z^2}}} = 0\;\;\;\;\displaystyle\frac{{\partial {y^3}(l,t)}}{{\partial {z^3}}} = 0}{\text{。}}\end{array}} \right.\end{aligned}\!\!\!\!\!\!\!\!\!$ | (4) |
又由于横向位移y(z,t)可表示为:
| $y(z,t) = \sum\limits_{n = 1}^\infty {{y_n}\left( t \right)} \sin {\lambda _n}z{\text{。}}$ | (5) |
最后,计算式(5)中3种边界条件下所对应的λn,然后将式(5)代入式(1)中,即可通过伽辽金法[13]对立管的运动方程进行求解。
1.1 算例验证在Abaqus软件中建立简化的立管模型,采用Abaqus梁单元B21进行振动特性分析,单元数目为2 000个。其中,立管模型的具体参数如表1所示。
|
|
表 1 立管模型参数 Tab.1 Parameters of riser model |
等截面简支梁自由振动的频率公式:
| ${f_n} = \frac{1}{{2\pi }}{\left( {\frac{{n\pi }}{L}} \right)^2}\sqrt {\frac{{EI}}{{\rho A}}} {\text{。}}$ | (6) |
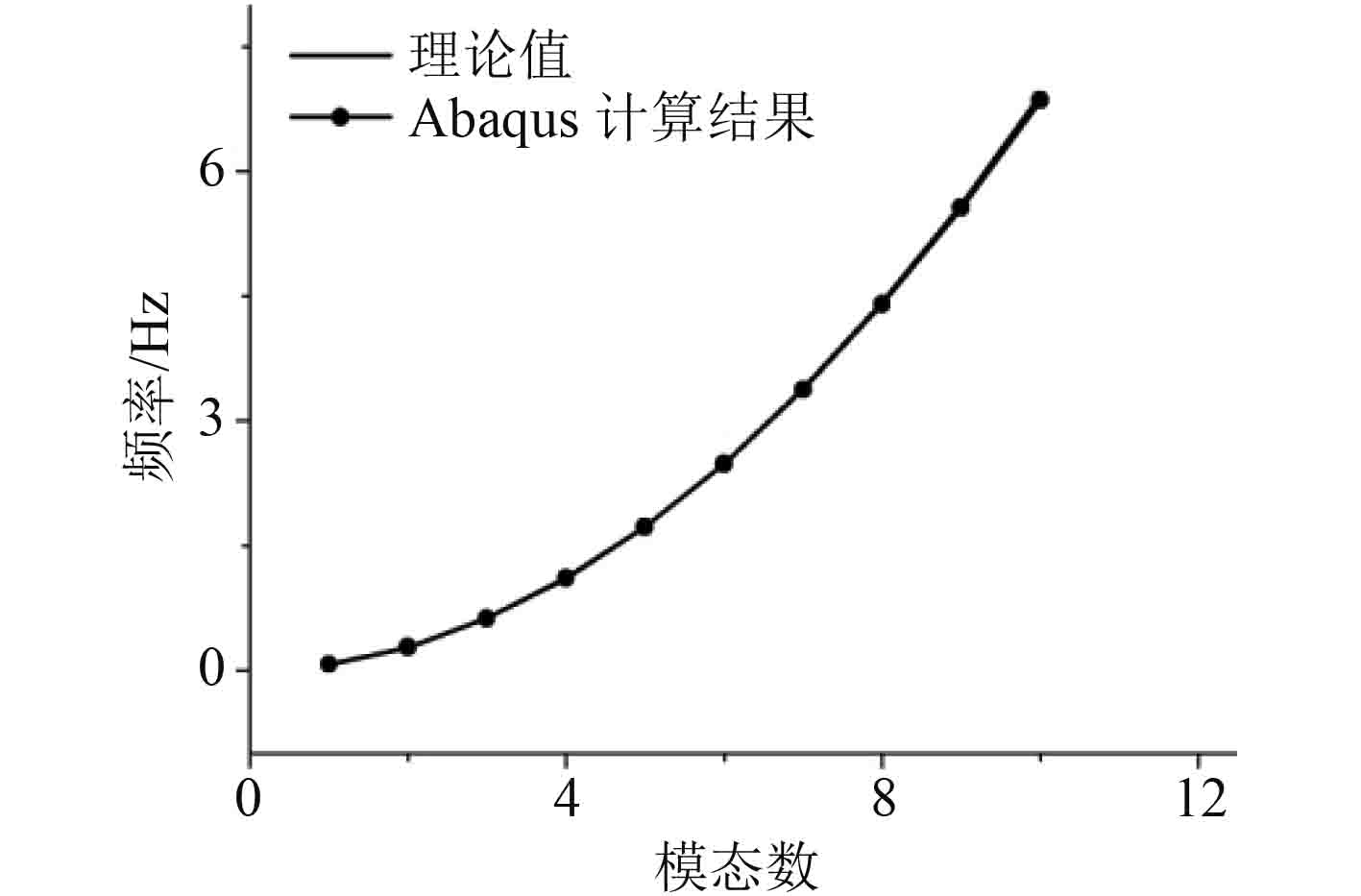
式中:n为模态数;A为立管横截面积。由式(6)可以得到前10阶频率,其与Abaqus梁单元的频率计算结果比较如图2所示,由此验证了通过Abaqus软件所得计算结果的正确性。
|
图 2 简支梁前10阶频率计算结果比较 Fig. 2 The comparison of simple-supported beam′s frequencies |
本文的研究对象为1 200 m长的深海顶张力立管。在图1所示的3种边界条件下,对其振动特性进行分析。立管自身参数以及海洋波浪环境相关参数的设定如表2所示。
|
|
表 2 立管物理参数及海洋波流环境参数 Tab.2 Riser's physical parameters and ocean wave and current environmental parameters |
|
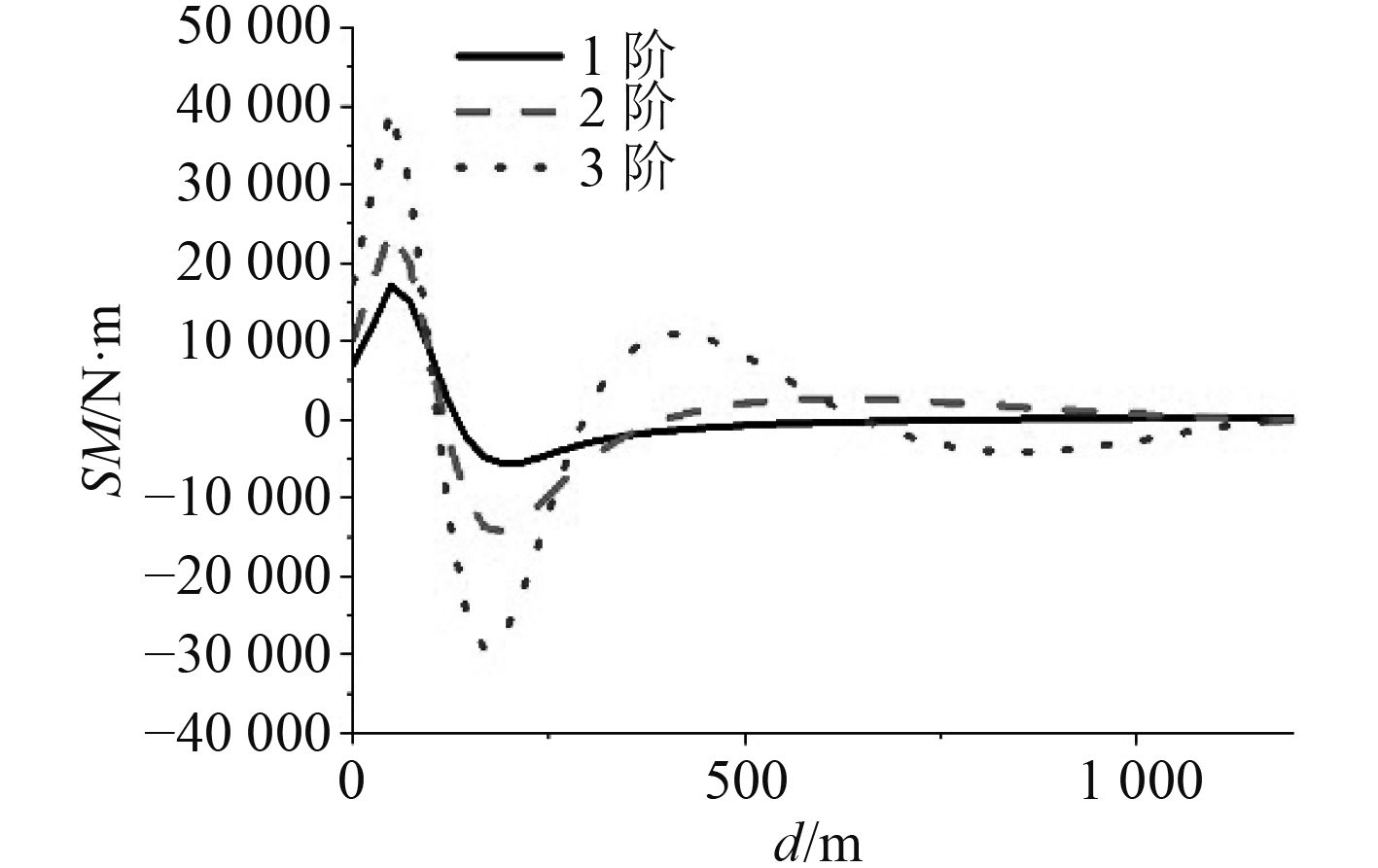
图 3 第1类边界条件 Fig. 3 The first boundary condition |
|
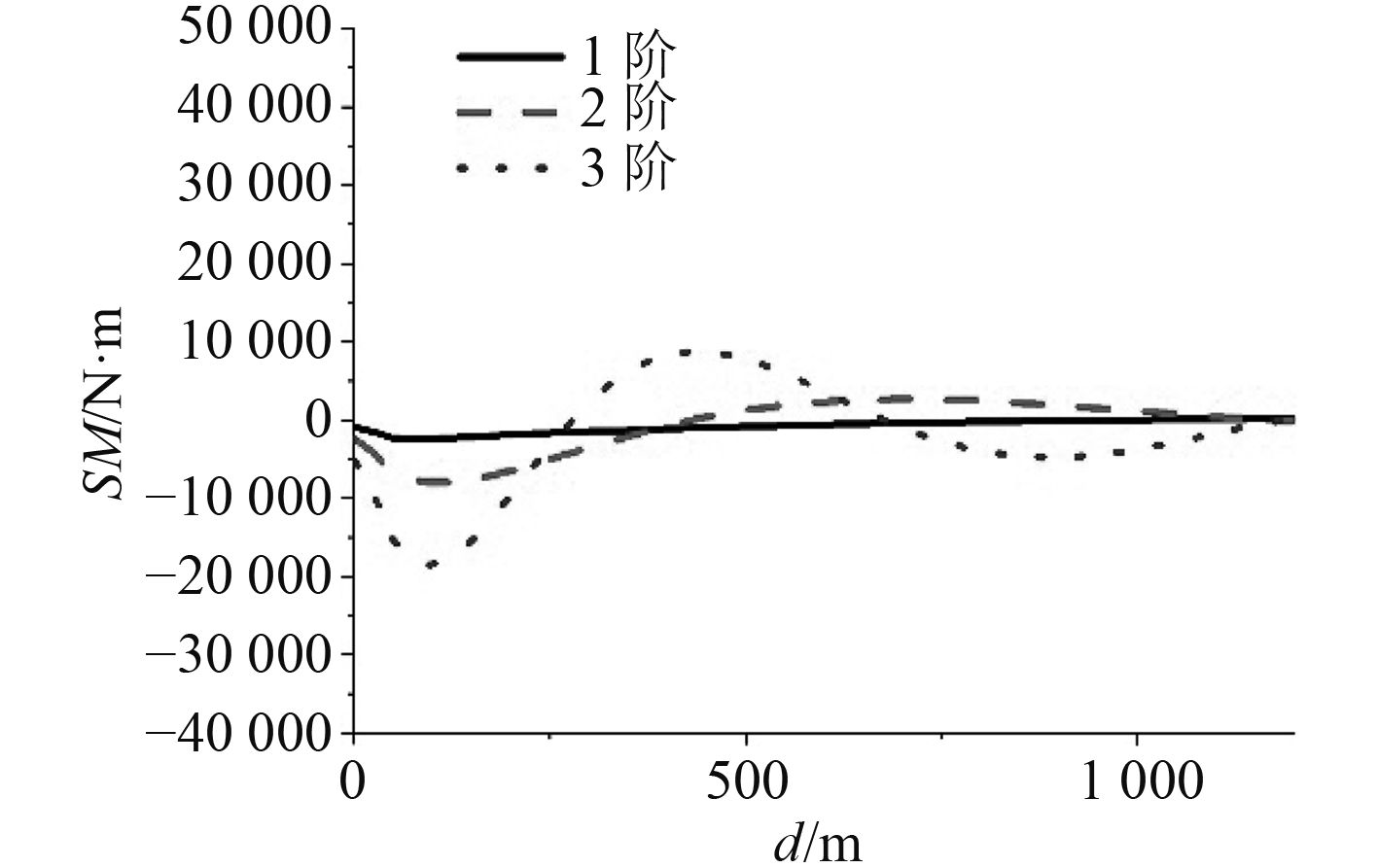
图 4 第2类边界条件 Fig. 4 The second boundary condition |
|
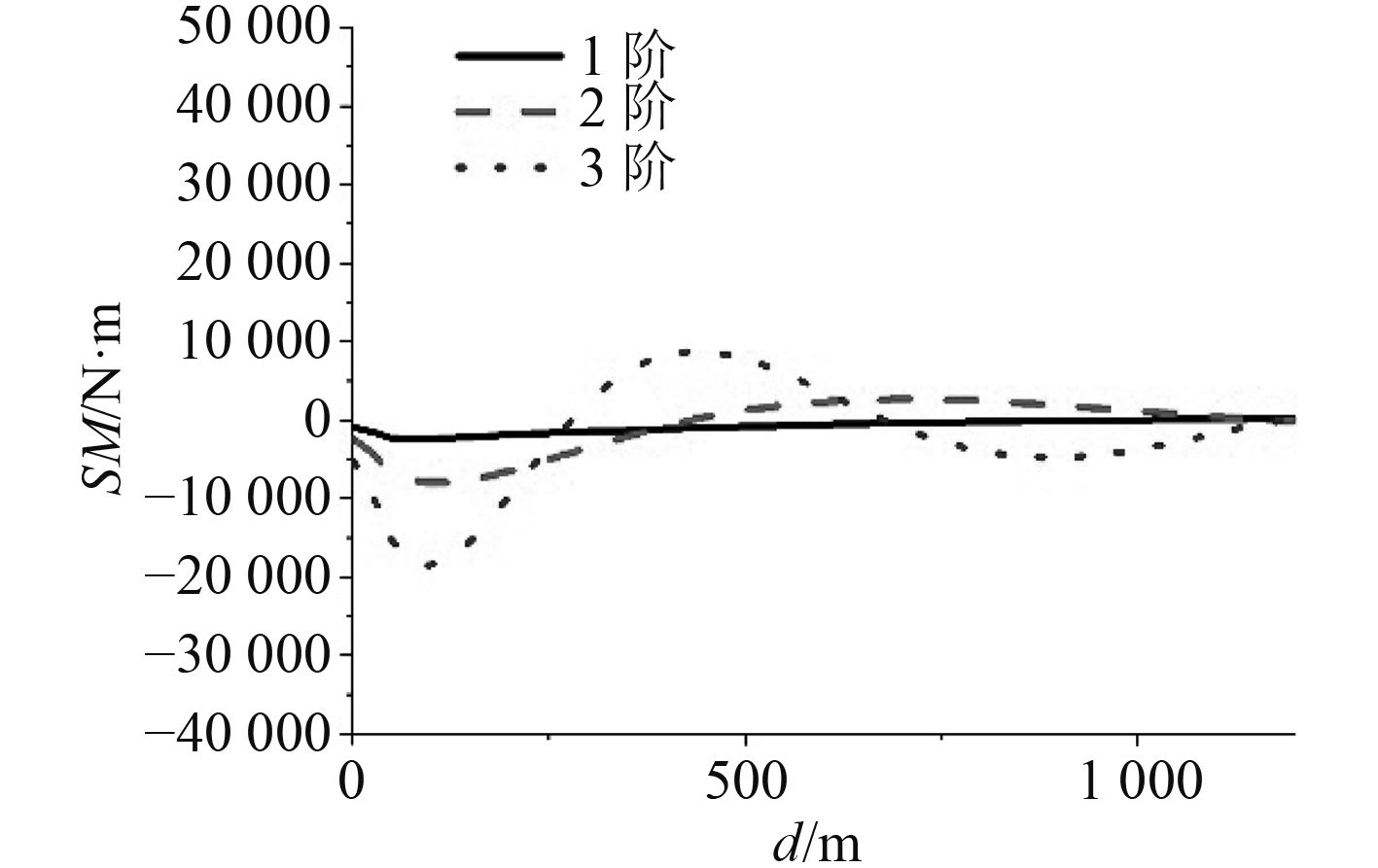
图 5 第3类边界条件 Fig. 5 The third boundary condition |
|
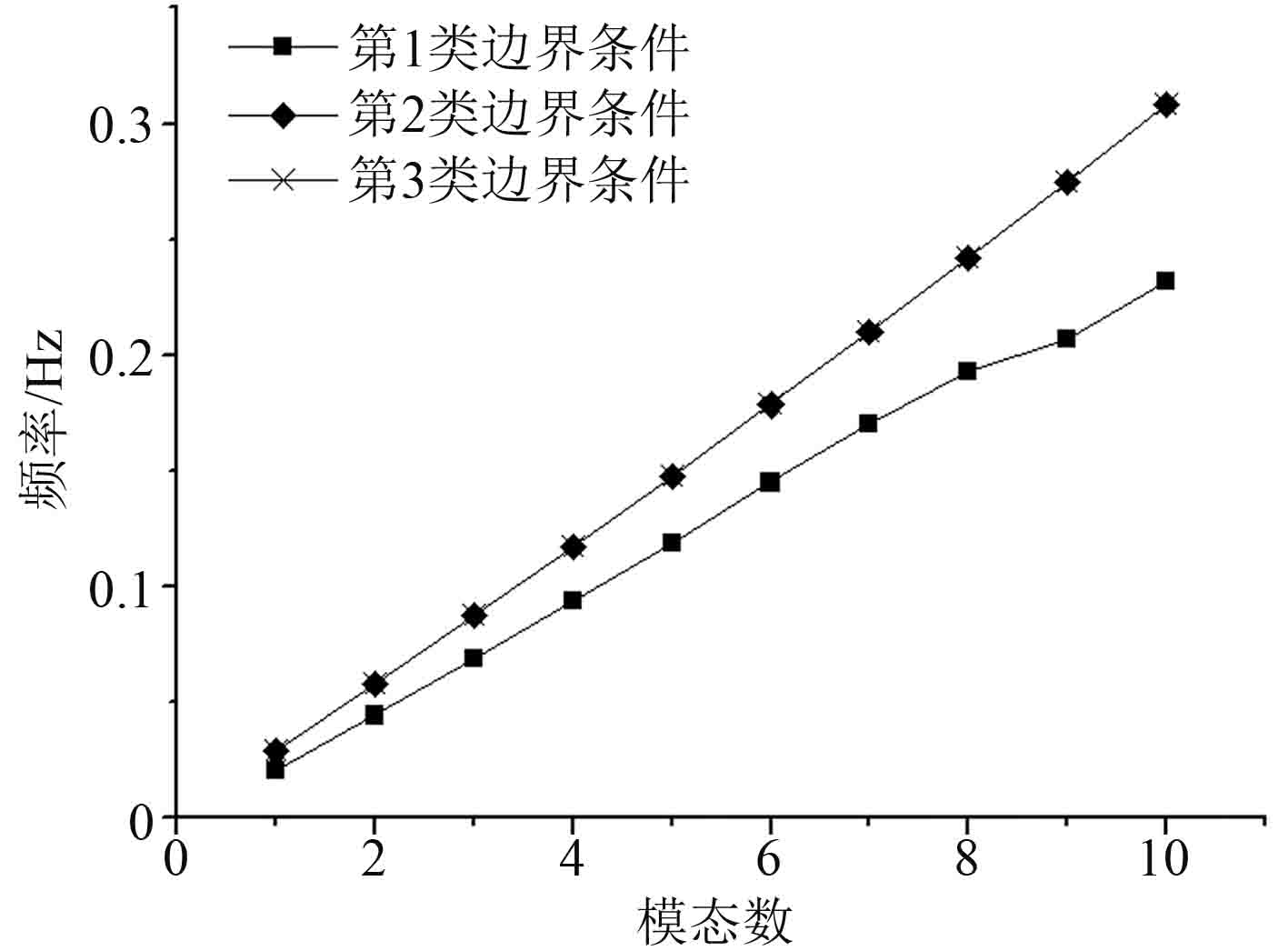
图 6 不同边界条件下的立管固有频率 Fig. 6 Riser′s natural frequencies under different boundary conditions |
在Abaqus的View模块中,可以根据需要选择相应的输出变量。图3~图5为不同边界条件下立管的前3阶模态弯矩。由图可以看出:在相同的波流环境下,同一立管在第1边界条件下的1阶模态弯矩最大值为17 025.6 N·m,而第2、3类边界条件下立管的1阶模态弯矩最大值均为2 465.75 N·m。从立管的弯矩分布图看,3种边界条件的弯矩最大值都出现在立管接近底端处。但第1类边界条件下的立管弯矩分布变化率比第2类和第3类大得多,其值也大得多。
图6为不同边界条件下立管固有频率的比较。根据计算结果,可知第2、3类边界条件下立管的固有频率在数值上基本相同,并随着模态数的增加而呈现接近线性增加的趋势。此外,第1类边界条件下立管的固有频率较第2类和第3类的小,当模态阶数较小时,两者的差值较小;不过随着模态数的增加,两者的差值越来越大。再结合图4和图5,能够断定动位移对立管固有频率的影响可以忽略不计。
2 立管固有频率的影响因素分析深海立管因所处的环境较为复杂,需综合考虑立管的各个受力对立管固有频率的影响。本文采用分块Lanczos方法,不考虑流体相对于立管的运动,将立管及其内部流体视为一个整体:在水面上的立管重量是立管材料与管内液体的重量之和;而对于水面以下的立管部分,则需考虑的是外部流体的附加质量。因此立管所处的环境管内液体密度的不同会对立管的静力特性产生较大的影响。在Abaqus中采用BEAM21梁单元计算立管的固有频率。立管的物理特性参数同样按表2进行设定。此外,与第1、2类边界条件相比,第3类边界条件下立管的响应结果更能反映实际情况。因此,本文在分析不同外部环境、立管本身物理参数以及顶端张力等因素对立管固有频率的影响时,选择第3类边界条件。
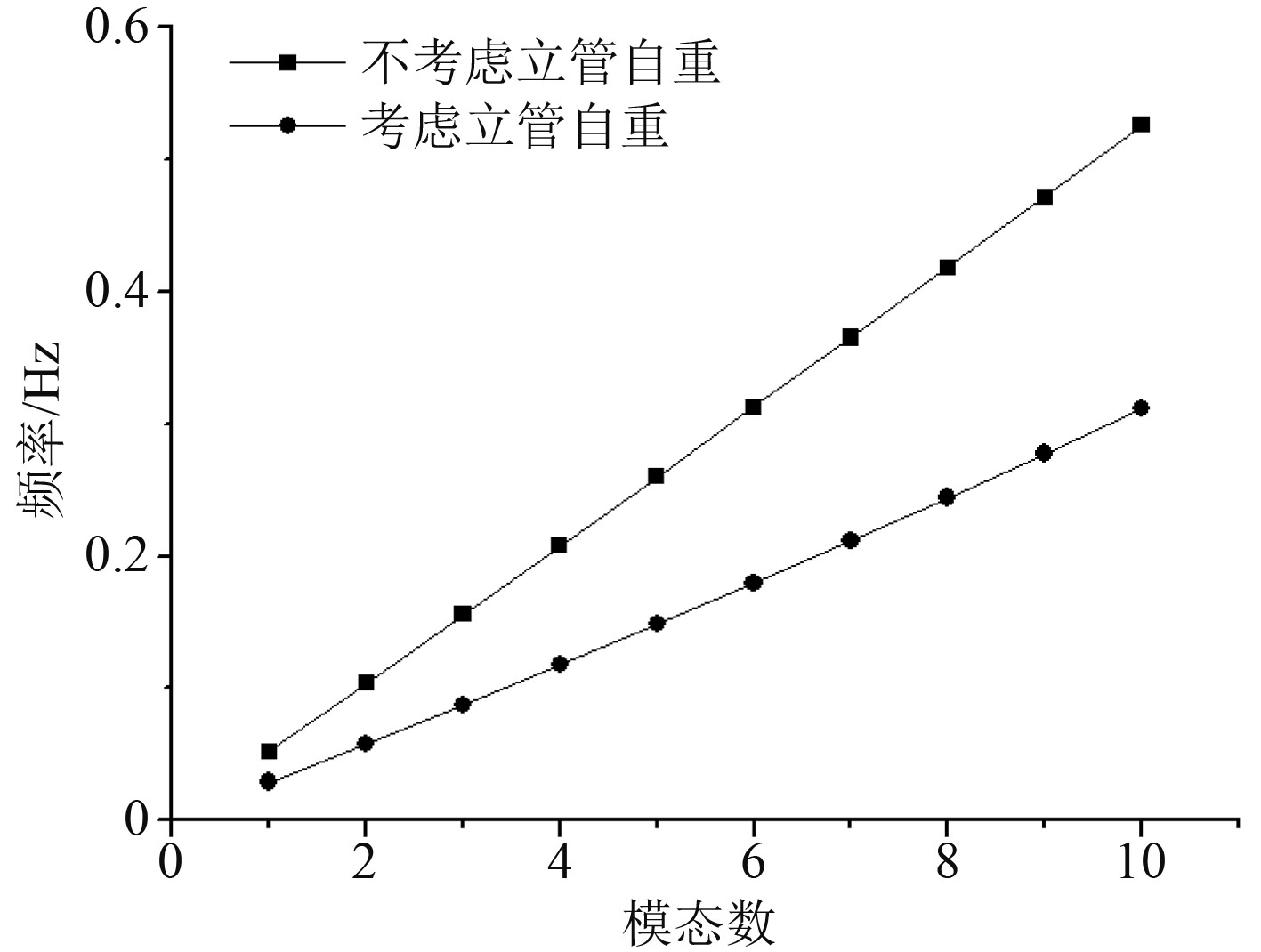
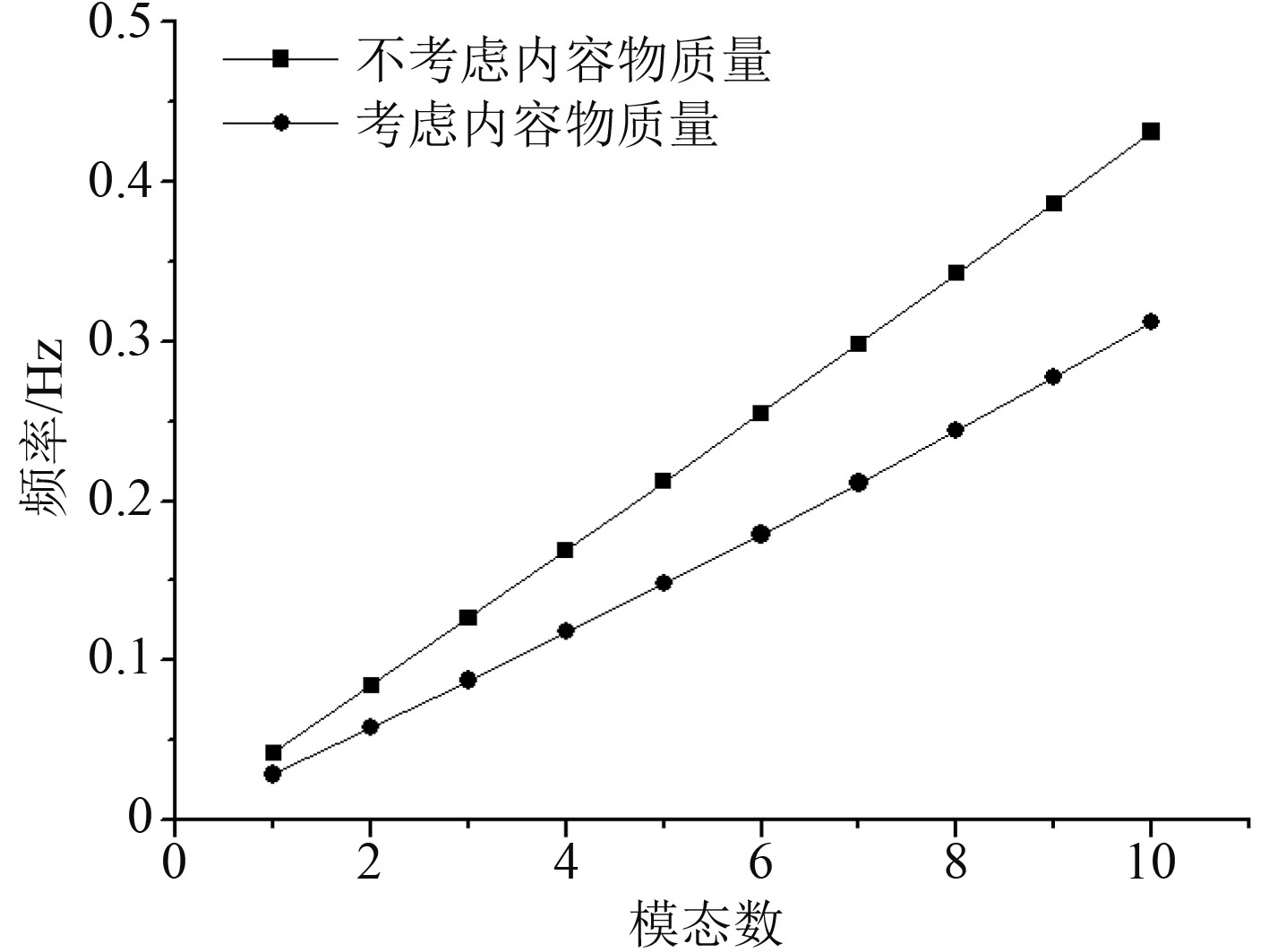
接下来,考虑到深海立管处于深海环境中,其立管固有频率受到顶张力和立管自重的影响,所以分析海洋立管在不考虑本身自重和管内流体(忽略流体运动,流体密度取1 635 kg/m3)下的立管固有频率,如图7和图8所示。由此可以看出:不考虑立管的自重和管内流体(即管内内容物质量)时,立管的前10阶频率偏大,此时立管容易发生“共振”,可能会加剧立管的疲劳乃至失效。此外,是否考虑立管自重与是否考虑管内流体的2种情况下,第1种情况对立管1阶固有频率的计算结果的影响更大。所以,只有同时考虑立管自重和管内流体对立管振动特性的影响,才能更好地保障作业安全,同时也更符合实际工况。
|
图 7 自重对立管固有频率的影响 Fig. 7 The effect of self-weight on riser′s natural frequency |
|
图 8 内容物对立管固有频率的影响 Fig. 8 The effect of contents on riser′s natural frequency |
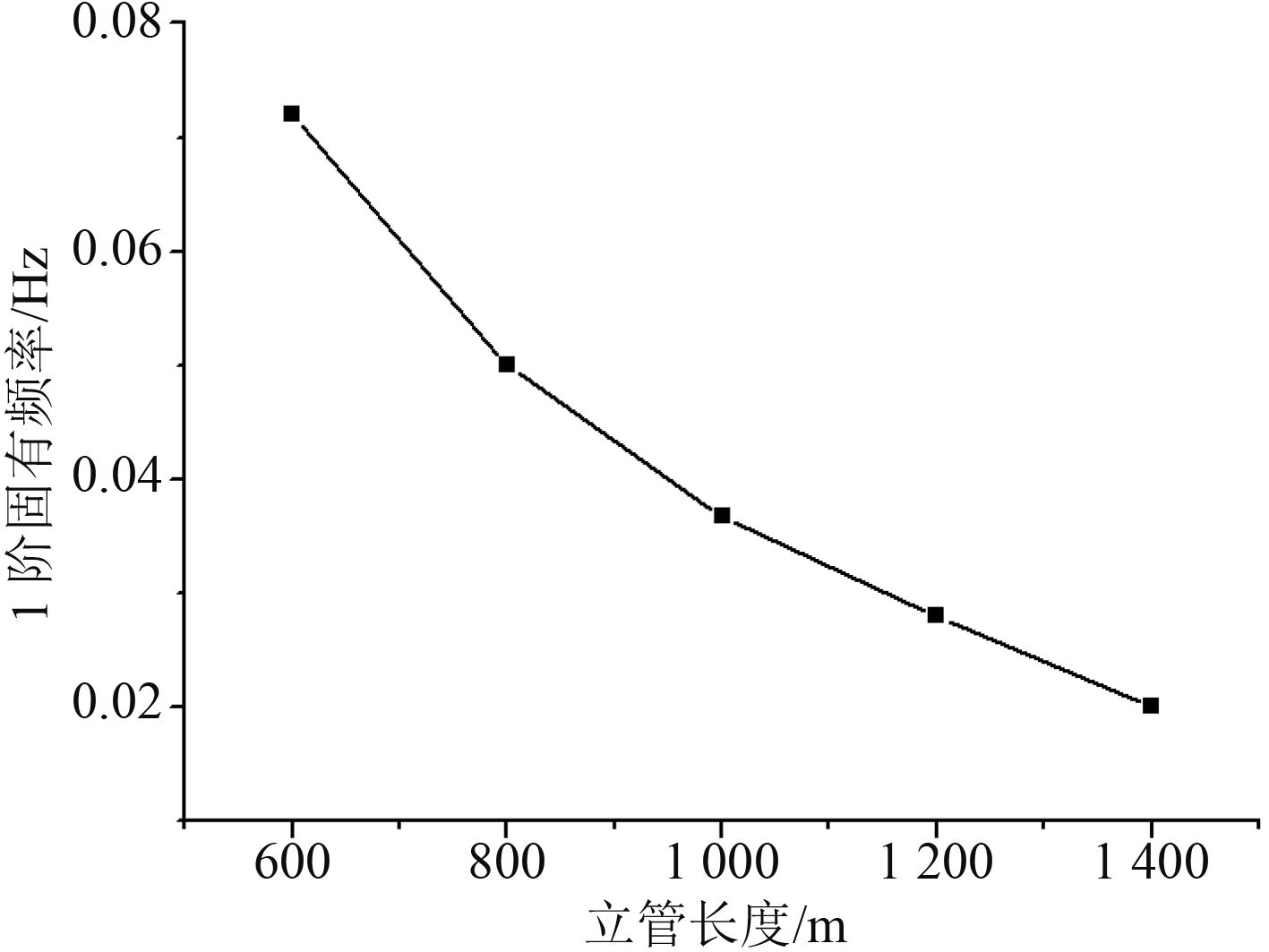
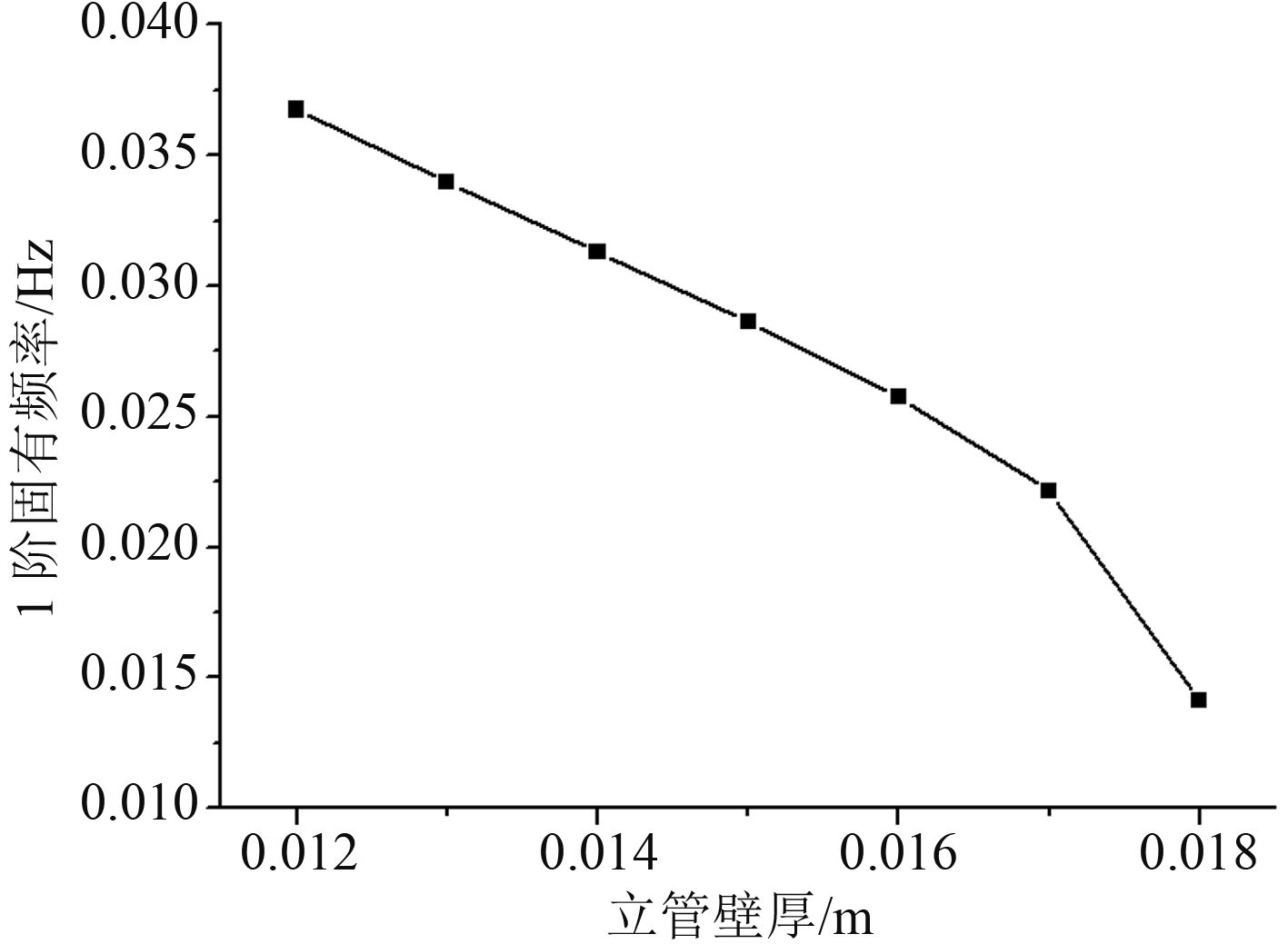
最后,分析立管自身物理参数(即立管的长度、直径和壁厚)以及顶端张力的不同对立管1阶固有频率的影响,数值模拟的结果如图9~图12所示。
|
图 9 不同长度立管1阶固有频率 Fig. 9 The first natural frequencies of different lengths |

|
图 10 不同外径立管1阶固有频率 Fig. 10 The first natural frequencies different diameter |
|
图 11 不同壁厚立管1阶固有频率 Fig. 11 The first natural frequencies of different thickness |

|
图 12 不同顶张力立管1阶固有频率 Fig. 12 The first natural frequencies of different top tensions |
1)立管的1阶固有频率随着立管长度、外径和管壁厚度的增加而减小。其中,立管长度对固有频率的影响最为显著,在设计深海石油开发平台时需进行考虑。
2)当立管的顶张力较小时,立管的1阶固有频率随着顶张力的增加而快速增加;而随着顶张力的继续增加,幅度越来越小。考虑到立管强度校核的要求,可以适当地加大立管顶张力,以预防立管发生共振。
3 总结与展望本文采用数值模拟的方法研究了立管的边界条件、本身物理参数和顶端张力等因素对立管固有频率的影响。在Abaqus软件中建立了简化的立管模型,比较了立管在3类不同边界条件下的振动特性。然后,在第3类边界条件的基础上,分析了上述因素对立管固有频率(主要是1阶频率)的影响。基于上述研究工作,得到如下结论:
1)立管的固有频率与其边界条件中的初始位移密切相关,但与该位移的运动无关;
2)立管自重和管内流体密度对立管的1阶固有频率有影响。其中,立管自重对对立管1阶固有频率的影响更大。当不考虑立管的自重和管内流体的密度时,立管的前10阶频率均会偏大;
3)随着立管长度、外径和壁厚的增加,立管的固有频率会降低。其中,立管的长度对于固有频率的影响最为显著,随着立管长度的增加,立管的固有频率急剧降低;
4)立管的顶部张力对立管的固有频率有影响。当立管的顶张力较小时,立管的1阶固有频率随着顶张力的增加而快速增加;而随着顶张力的继续增加,其增幅会越来越小。
与此同时,本文还存在一定的局限:在分析管内流体对立管振动的影响时,仅分析了管内流体质量的影响,而没有考虑管内流体与管道的相对运动对立管振动的影响。事实上,管内流体与管道的相对运动对立管振动的影响不可忽略。在今后的研究中,还应对此继续进行分析并完善。
| [1] |
张杰, 唐友刚. 深海立管固有振动特性的进一步分析[J]. 船舶力学, 2014, 18 (1-2): 165–171.
ZHANG Jie, TANG You-gang. Further analysis on natural vibration of deep-water risers[J]. Journal of Ship Mechanics, 2014, 18 (1-2): 165–171. |
| [2] |
张杰, 唐友刚, 黄磊, 等. 参数激励下深海立管多模态耦合振动特性分析[J]. 振动与冲击, 2013, 32 (19): 51–56.
ZHANG Jie, TANG You-gang, HUANG Lei, et al. Multi-mode coupled vibration behavior of a deep-water riser under parametric excitations[J]. Journal of Vibration and Shock, 2013, 32 (19): 51–56. DOI: 10.3969/j.issn.1000-3835.2013.19.010 |
| [3] |
雷松, 郑向远, 张文首, 等. 海洋立管悬挂状态的固有频率和振型[J]. 船舶力学, 2015, 19 (10): 1267–1274.
LEI Song, ZHENG Xiang-yuan, ZHANG Wen-shou, et al. Natural frequencies and mode shapes of free-hanging risers[J]. Journal of Ship Mechanics, 2015, 19 (10): 1267–1274. DOI: 10.3969/j.issn.1007-7294.2015.10.012 |
| [4] |
郭磊, 段梦兰, 张新虎, 等. 浮式平台对深水立管振动的影响及共振研究[J]. 石油机械, 2014, 42 (9): 59–64.
GUO Lei, DUAN Meng-lan, ZHANG Xin-hu, et al. The influence of floating platform on deep-water riser vibration and resonance[J]. ChinaPetroleum Machinery, 2014, 42 (9): 59–64. |
| [5] | MONTOYA-HERNÁNDEZ D J,VÁZQUEZ-HERNÁNDEZ A O, CUAMATZI R, et al. Natural frequency analysis of a marine riser considering multiphase internal flow behavior[J]. Ocean Engineering, 2014(92): 103–113. |
| [6] |
王在刚. 海洋立管流固耦合动力特性分析[D]. 兰州: 兰州理工大学, 2013.
WANG Zai-gang. Analysis on dynamic characteristics of fluid-structure interactionfor marine risers[D]. Lanzhou: Lanzhou University of Technology, 2013. |
| [7] |
王东, 任帅, 陈磊, 等. 基于ANSYS的浅海天然气立管模态分析[J]. 管道技术与设备, 2014 (3): 9–11.
WANG Dong, REN Shuai, CHEN Lei, et al. Shallow gas riser modal analysis based on Ansys[J]. Pipeline Technique and Equipment, 2014 (3): 9–11. |
| [8] |
姜峰, 郑运虎, 梁瑞, 等. 海洋立管湿模态振动分析[J]. 西南石油大学学报(自然科学版), 2015, 37 (5): 159–166.
JIANG Feng, ZHENG Yun-hu, LIANG Rui, et al. An analysis of the wet modal vibration of marine riser[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37 (5): 159–166. DOI: 10.11885/j.issn.1674-5086.2013.11.11.03 |
| [9] |
王红霞, 李喆. 钢悬链线立管振动响应影响因素分析[J]. 噪声与振动控制, 2011, 31 (4): 26–28.
WANG Hong-xia, LI Zhe. Factors analysis of influencing of steel catenary riser[J]. Noise and Vibration Control, 2011, 31 (4): 26–28. |
| [10] |
潘佳. 深水立管涡激振动响应和疲劳损伤分析[D]. 大连: 大连理工大学, 2015.
PAN Jia. Vortex-induced vibration response and damage analysis of riser in deep water[D]. Dalian: Dalian University of Technology, 2015. |
| [11] |
孙传栋, 黄维平, 曹静. Abaqus在深水顶张力生产立管模态分析中的应用[J]. 中国水运月刊, 2009, 9 (2): 181–182.
SUN Chuan-dong, HUANG Wei-ping, CAO Jing. Application of Abaqus in modal analysis of standpipe in deep water tension production[J]. China Water Transport, 2009, 9 (2): 181–182. |
| [12] | 黄祥鹿. 海洋工程流体力学及结构动力响应[M]. 上海: 上海交通大学出版社, 1992. |
| [13] |
马驰, 董艳秋. 海洋平台张力腿在两种边界条件下的涡激非线性振动的比较研究[J]. 船舶力学, 2000, 4 (1): 56–65.
MA Chi, DONG yan-qiu. Comparative study of vortex-induced nonlinear oscillation of TLP tethers under two different boundary conditions[J]. Journal of Ship Mechanics, 2000, 4 (1): 56–65. |
 2018, Vol. 40
2018, Vol. 40
