钻井船是海洋石油资源开发中非常重要的生产与生活设施,为了确保钻井船上的钻井设施能够处在一个稳定的环境下正常工作,同时为了确保开采过程安全顺利地进行,许多钻井船都带有月池。月池是从钻井船的夹板贯穿到船底结构的垂直开放水密区域,内部有自由液面,月池给船和海洋平台水下实验提供支持和保障[1]。然而,在某些共振环境下,月池内可能会发生剧烈的运动,导致潜在的安全隐患甚至实验的中止。所以,如何能够规避共振环境下月池结构潜在的安全隐患,最大限度发挥月池的优势是研究人员们一直以来的工作重点。
钻井船月池内共振情况下水的运动模式主要取决于月池形状、结构、主尺度还有入射波性质,主要运动形式分为活塞运动和晃荡运动2种[2],这2种运动形式相辅相成。活塞运动类似于垂荡运动,即在垂直平面内做上下的往复运动;而晃荡运动是在水平平面内做前后的往复运动,月池内的晃荡运动出现在月池前后边界墙之间。然而与运动相关的水动力特征很难通过非线性的自然条件来预测,而且由波浪引起的船体运动,船体向前的速度和海洋环境都可以对月池内水的状况造成影响。为了预测和量化共振环境下月池内水运动,研究人员做了大量努力,主要有理论分析、数值计算和模型试验3种方式。Molin主要通过理论分析[3 – 5],得到一系列月池内流体做活塞运动和晃荡运动时的固有频率。Faltinsen通过理论分析[6],推导月池振荡的固有周期的公式,将月池内的流体简化为一个质量——弹簧系统,得到月池内流体活塞运动的固有周期
传统数值计算的方法一般是根据Naiver-Stokes方程计算,并和实验结果作对比。本文采用势流理论和CFD数值模拟相结合的方法,对钻井船的水动力性能及其月池内的流体运动进行研究,即在势流软件中计算出钻井船在波浪中的运动,将此运动作为边界条件,在CFD软件中进行计算。
1 数学模型 1.1 运动方程由于本文采用势流理论和CFD数值模拟相结合的方法,对钻井船的水动力性能及其月池内的流体运动进行研究,所以主要数值计算理论包括三维势流理论和CFD理论。
1.1.1 三维势流理论三维势流理论假设流体是理想流体,满足无粘性、均匀、不可压缩的特点,而且流动是无旋流体,忽略表面张力的影响,则存在速度势函数,流场的基本控制方程由连续性方程和NS方程简化为拉普拉斯方程和拉格朗日积分[12]。此外,对于实际流场,还必须满足自由表面条件、物面条件、底部条件、辐射条件等边界条件,以及适当的初始条件。
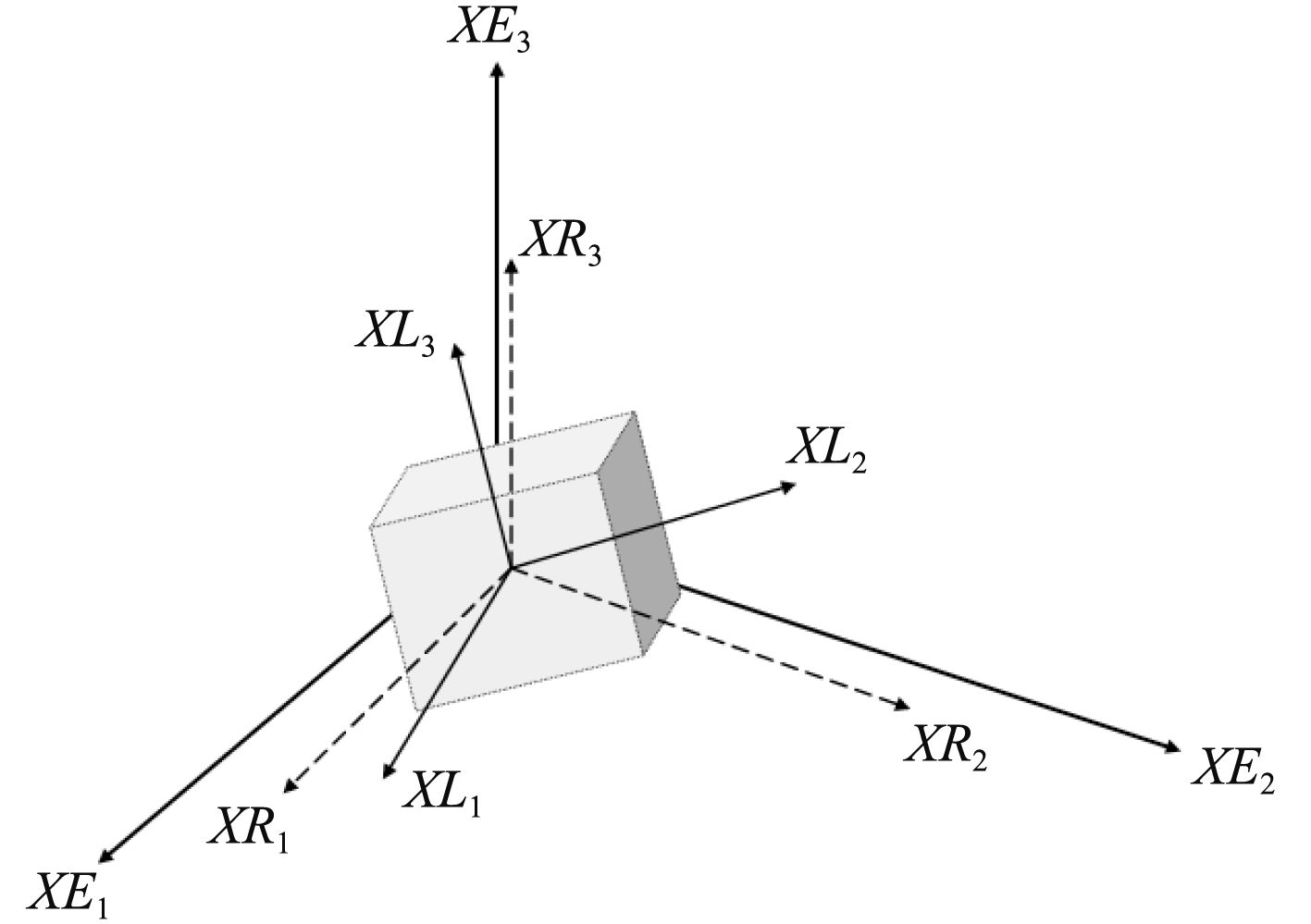
假设船体为刚体,则这艘船的运动可以分解为重心的线运动与船体绕重心的角运动的叠加,共6个自由度,其定义需要引入3个右手笛卡尔坐标系统:即大地坐标系XE、随体坐标系XL和相关坐标系XR,如图1所示。
|
图 1 描述船体运动的坐标系 Fig. 1 Coordinates system of ship motion |
基于势流理论基本假设,可用非定常速度势表示流场中流体的运动[13]。一阶速度势
拉普拉斯方程流场内
| ${\nabla ^2}\Phi (x,y,z,t) = 0,$ | (1) |
自由面条件
| $\frac{{{\partial ^2}\Phi }}{{\partial {t^2}}} + g\frac{{\partial \Phi }}{{\partial z}} = 0,\left( {z = 0} \right),$ | (2) |
物面条件
| ${\left. {\frac{{\partial \varPhi }}{{\partial n}}} \right|_s} = {U_n},$ | (3) |
底部条件
| ${\left. \frac{{\partial \varPhi }}{{\partial n}} \right|_{z = - H}}= 0\text{。}$ | (4) |
sommerfeld辐射条件。
式中:t为时间;g为重力加速度;n为船体平均湿表面上指向内部的单位法向量;Un为船体法向速度。
应用叠加原理,将总的速度势分解为入射势、绕射势和辐射势:
| $\varPhi (x,y,z,t) = {\varPhi ^I}(x,y,z,t) + {\varPhi ^D}(x,y,z,t) + {\varPhi ^R}(x,y,z,t){\text{。}}$ | (5) |
式中:
对于非理想流体,流场的控制方程包括连续性方程和动量方程,即
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho \vec u) = 0,$ | (6) |
| $\frac{{\partial \vec u}}{{\partial t}} + \vec u \cdot \nabla \vec u = - \frac{1}{\rho }\left[ {\nabla P + \nabla \cdot [\tau ]} \right] + \vec G{\text{。}}$ | (7) |
式中:t为时间;
模拟自由液面,本文采用VOF法,即通过定义一个流体体积函数F来追踪自由液面的变化[15]。这个流体体积函数F描述网格单元内流体体积占该单元总体积的比。
| $F = \left\{ {\begin{array}{*{20}{c}}0&\text{内部无流体},\\{0 < F < 1}&\text{部分被流体充满},\\1&\text{被流体充满}\text{。}\end{array}} \right.$ | (8) |
当F介于0~1之间,表明这种单元或者含有自由边界,或者存在小于该单元体积的空隙或气泡。对于自由液面单元,除了F值介于0~1之间,还需要相邻单元中至少有一个是F=0的空单元。F的控制微分方程为:
| $\frac{{DF}}{{Dt}} = 0{\text{,即}}\frac{{\partial F}}{{\partial t}} + (\vec u \cdot \nabla )F = 0{\text{。}}$ | (9) |
自由液面的法线方向可由F的梯度来决定,得出各单元的F值及其梯度之后,就可确定自由液面的位置和形状。
3)物体表面的捕捉同模拟自由液面类似,模拟物体表面,本文采用FAVOR法来对物体表面进行模拟[16]。它的基本原理是通过定义网格单元内可以让流体流动的体积分数,即开放体积分数Vf和面积分数
FAVOR方法把划分网格和定义几何体这2项分开来,大大简便了网格划分工作,从而节省了时间。
1.1.3 月池共振周期的计算Molin通过推导月池内流体做活塞运动和晃荡运动时的速度势得到其固有频率为:
| ${\omega _{piston}} = \sqrt {\frac{g}{{d + b{f_0}(b/l)}}} ,$ | (10) |
式中:d为月池吃水;l为月池长度;b为月池宽度;g为重力加速度。
| $\begin{split}&{f_0} = \frac{1}{\pi }\Biggr\{ {{{\sinh }^{ - 1}}\left( {\frac{l}{b}} \right) + \frac{l}{b}{{\sinh }^{ - 1}}\left( {\frac{b}{l}} \right) + \frac{1}{3}\left( {\frac{b}{l} + \frac{{{l^2}}}{{{b^2}}}} \right)} -\\& \left. { \frac{1}{3}\left( {1 + \frac{{{l^2}}}{{{b^2}}}} \right)\sqrt {\frac{{{b^2}}}{{{l^2}}} + 1} } \right\}\text{。}\end{split}$ | (11) |
为了在FLOW-3D软件中进行CFD计算,首先建立一个三维波浪数值水池。在建立水池时,要保证入射波经历一段时间才传播到船首,船尾距离消波滩有一定的距离,来保证消波效果,船侧距离水池边缘同样有一定距离。综合钻井船主尺度和上述要求,确定水池长25.5 m,水池深1.5 m,坐标原点位于距造波端10.5 m,初始静水面以上高0.5 m。
在数值水池的造波端造波,在没有模型船的情况下,对所造的波进行检测。根据式(10)来计算月池内流体活塞运动的固有周期为1.1 s。为了更好地观察月池内流体水动力性能,设1.1 s为输入波浪周期,在数值水池造波端进行波浪检测,并与标准的正弦曲线进行对比。
对于数值波浪水池,比较关心自由面附近的变化和形状,所以在自由面附近的区域应该进行网格垂向加密,来保证FLOW-3D软件良好地模拟出自由面升高变化和自由面形状。而对于自由液面以上较高处以及对于数值水池较深处,所关心的物理量变化梯度比较小,不是很密的网格就能完成计算。为了减少计算时间,降低计算耗费内存,距离自由液面较远处网格划分可逐步变疏,但是,由于本文采用有限差分法,如果在任一方向放大系数过大或网格细长比过大,都不能精确描述所需计算的物理量,甚至会影响计算的稳定性,所以在划分网格的过程中,放大系数不超过2,对于细长比和网格疏密度的选择,要通过网格测试来选择最佳的细长比和网格密度,来保证既能正确描述所需计算的物理量,又能计算资源消耗。
本文用来测试的规则波的波高和模型试验中的相同,为0.02 m,周期取月池共振周期1.1 s,模拟时间为30 s。在波高范围内,分别划分6个、10个和20个网格进行比较,细长比也取3,4,5三种进行比较。
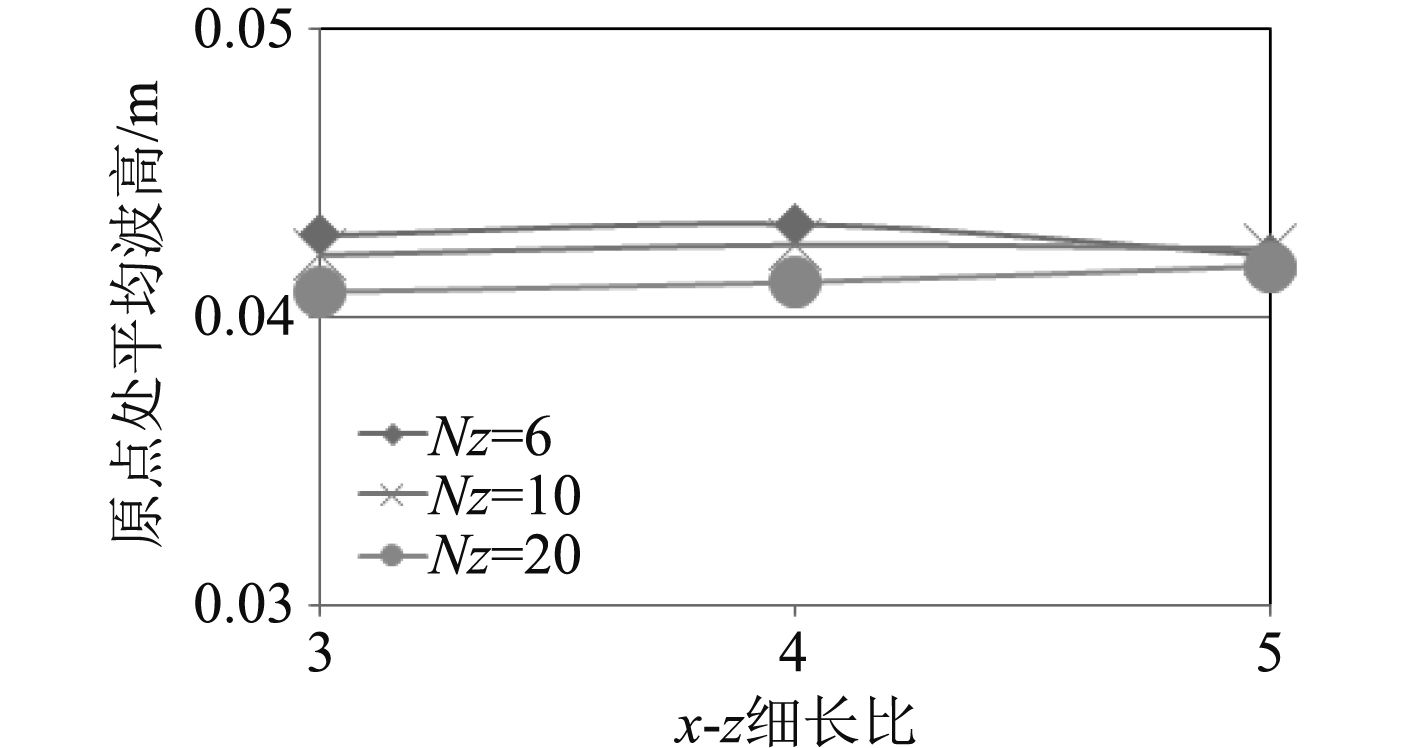
图2为原点处的平均波高随细长比和波高范围内垂向网格划分数量变化的曲线,从中可以发现,在波高范围内网格划分数量(Nz)一定的情况下,随着X-Z细长比的增加,即随着网格纵向逐渐稀疏,平均波高有所降低,逐渐接近目标波平均高度0.04 m,但程度不大;在X-Z细长比一定的情况下,增加波高范围内的网格划分数量(Nz),可以使观测点处的波高更接近于目标波高。综上,本文认为在波高范围内垂向划分20个网格,X-Z细长比选择最大值5,可以达到既保证准确描述波面,又最大程度降低总网格数的目的。
|
图 2 原点处平均波高随X-Z细长比和波高范围网格垂向划分数量(Nz)的变化 Fig. 2 Average wave height in the origin varying with aspect ratio and Nz number |
根据目标钻井船主要尺度、环境条件以及海洋深水试验池的实际设施条件,确定模型试验的缩尺比为λ=1∶50,模型制作以及海洋环境条件模拟等都需按照此缩尺比进行。试验中,需要制作的模型主要包括1艘钻井船模型和1个水平系泊系统模型。
钻井船模型以设计方案所确定的型线图和总布置图为依据,实船与模型船的主尺度,月池的尺寸以及其他参数见表1,规则波实验主要实验工况见表2,钻井船与月池模型图见图3,实船和模型船上的3个测试点坐标见表3,3个测试点方位见图4所示。
|
|
表 1 实船与模型船的主尺度与月池的尺寸 Tab.1 Principal particulars of the drillship and the moonpool |
|
|
表 2 首迎浪工况表(规则波) Tab.2 Wave angles of 180 deg test cases (regular wave) |

|
图 3 钻井船与月池模型图 Fig. 3 The vessel model graph and the moonpool graph |
|
|
表 3 实船和模型船上的3个测试点坐标 Tab.3 Position of the probes in the moonpool on the model ship and the real ship |

|
图 4 三个测试点示意图 Fig. 4 Sketch of three test probes |
将实验参数代入式(11)可得ω=1.1 s。
基于三维势流理论,应用DNV船级社所开发的Sesam软件中的HydroD,对钻井船进行建模以及频域的计算。图6为Sesam软件中对钻井船进行建模,并划分网格后的模型图。

|
图 5 在Sesam软件中对钻井船进行建模并划分网格 Fig. 5 Making model in Sesam and mesh it |
|
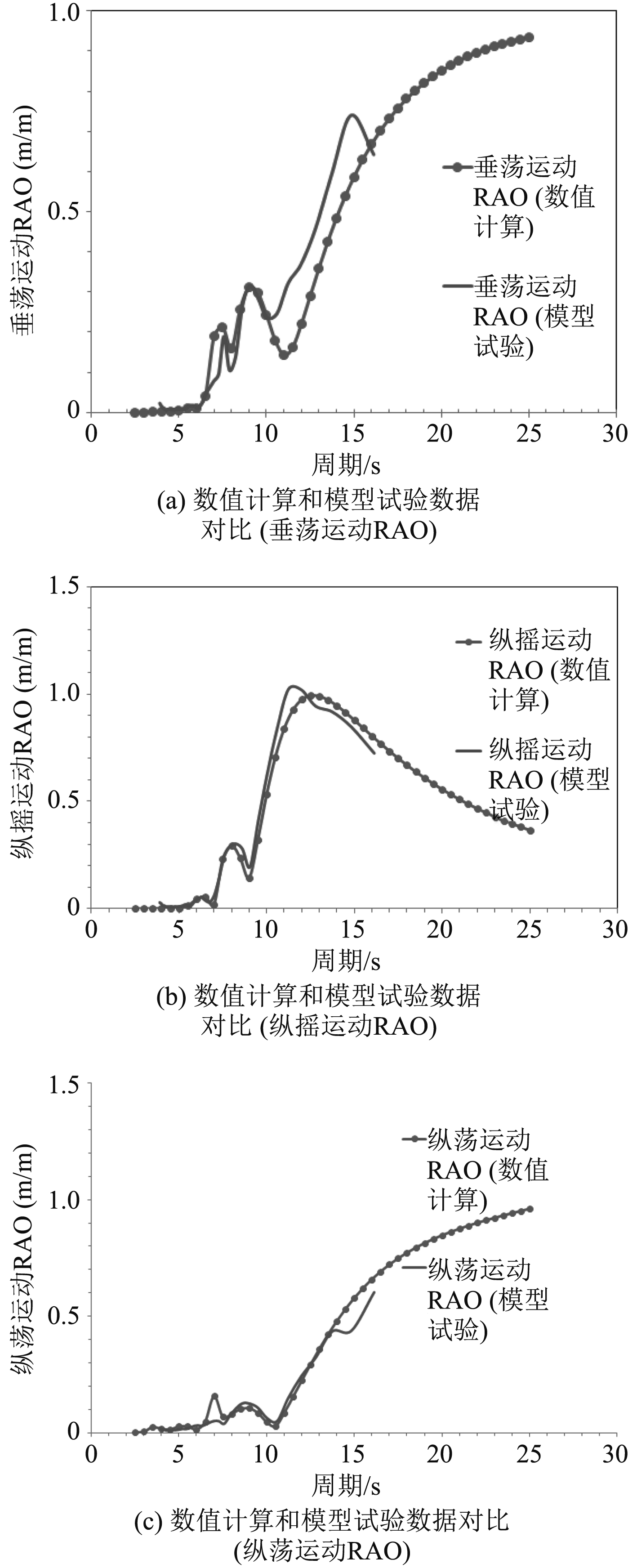
图 6 三个方向RAO数值计算结果和模型试验结果比较 Fig. 6 Comparisons between numerical and experimental results of RAO |
将钻井船在垂荡、纵荡和纵摇3个方向RAO的数值计算结果和模型实验结果相比较,可以看到:
1)钻井船纵荡运动的响应幅值随着周期的增大而增大,即具有显著的低频特性。
2)垂荡运动RAO在7.6 s左右出现峰值,总体上,垂荡运动在迎浪时响应幅值随着周期的增大而增大;
3)纵摇运动具有明显的波频特性,峰值周期大约为9.5 s。
4)通过将数值计算结果和模型试验比较,可以看出当入射波的频率和月池共振频率相差不多的时候,钻井船3个方向的RAO数值计算结果和模型试验的RAO相吻合,初步验证了数值计算的结果可信。
3.2 钻井船时域水动力性能分析将HydroD中频域计算结果导入Sesam中的Sima软件中计算时域结果,再把结果和模型试验数据对比,进一步验证数值计算结果的可信度。
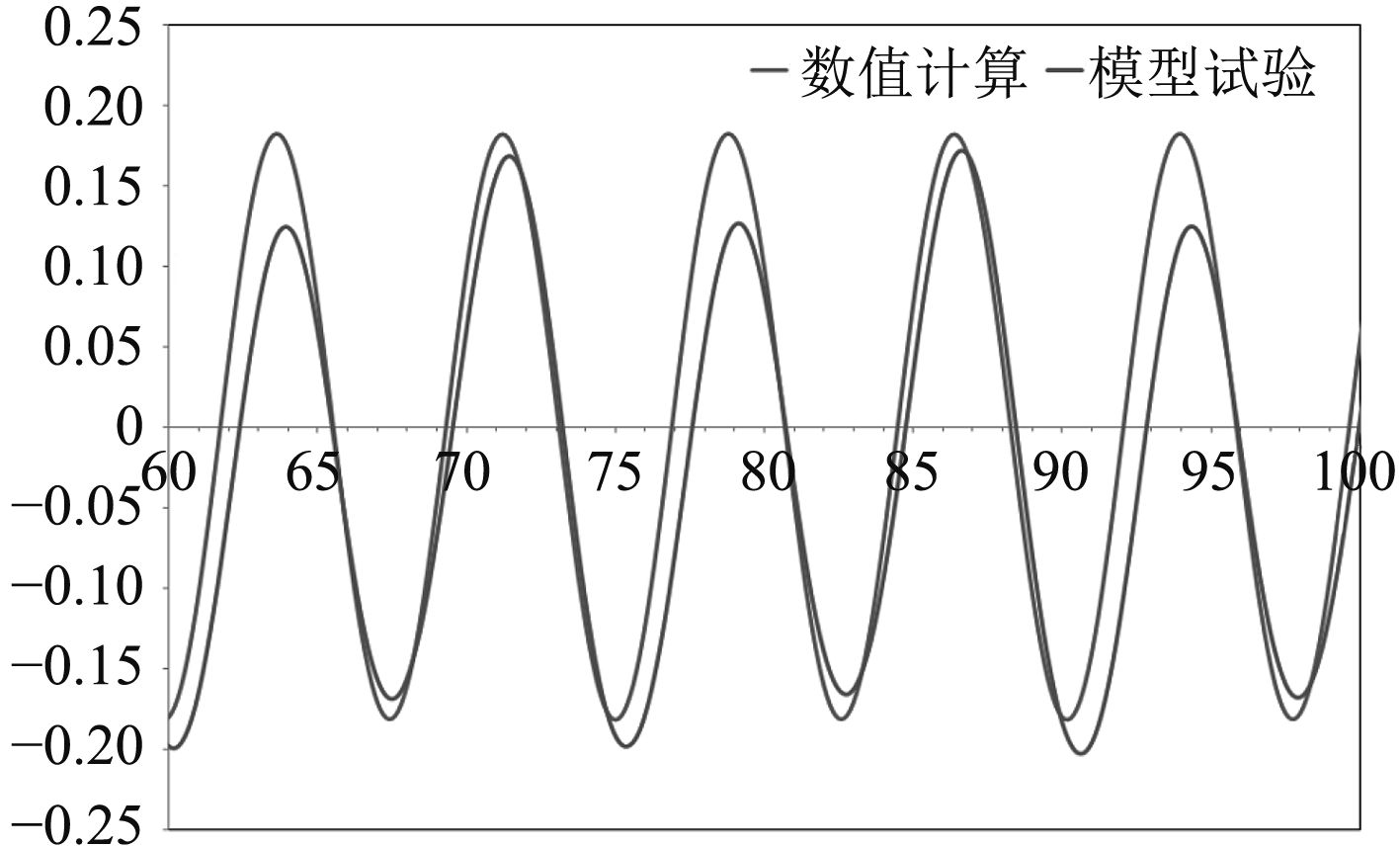
将钻井船在垂荡方向运动的数值计算结果和模拟实验结果相比较(见图7),可以看到,当入射波的频率和月池共振频率相差不多的时候,钻井船在月池共振周期附近运动数值计算结果和模型试验基本相吻合,进一步确定了数值计算结果的可信度。
|
图 7 钻井船在垂荡方向上数值计算结果和模型试验对比 Fig. 7 Comparision between numerical and experimental results of the vessel heave motion |
将月池共振周期附近的波浪下月池前中后3个位置的数值计算结果与模型试验相比较(见图8)。当入射波的频率和月池共振频率相差不多的时候,可以看到在月池共振周期附近的波浪下月池前中后3个位置的数值计算结果和模型试验结果基本符合,更进一步确定了数值计算结果的可信度。

|
图 8 月池内波浪升高数值计算结果与实验结果比较 Fig. 8 Comparision between numerical and experimental results of free surface elevation in moonpool |
图6~图8分别从RAO、运动幅值和月池内波浪升高3个方面比较了数值计算结果和实验数据,发现这3个方面的数值计算结果和实验数据基本吻合,证明数值计算方法基本可信。
3.3 共振周期下月池内波面升高的研究本文通过将势流理论软件和CFD软件相结合的方法研究讨论钻井船、波浪和月池内流体三者之间的关系。通过三维势流软件计算出钻井船在波浪中的运动,将这个运动导入到CFD软件中作为边界条件,讨论钻井船月池内流体的水动力性能。
本文将通过以下2个步骤进行讨论:首先将船体固定,计算在船体静止这个假设条件下,月池内各处流体的水动力性能;然后考虑船体在周期为月池共振周期的入射波下运动时,月池内流体的水动力性能。
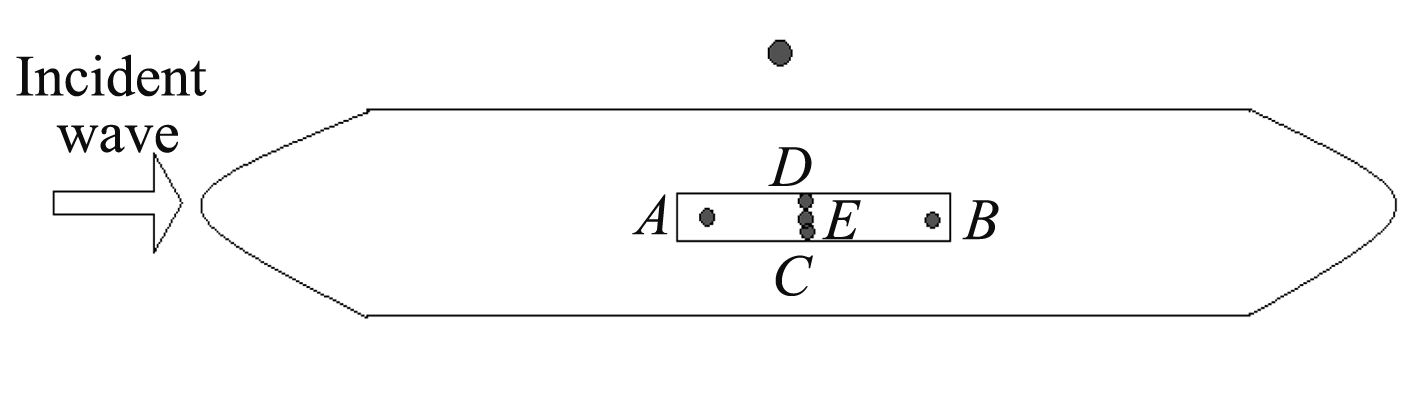
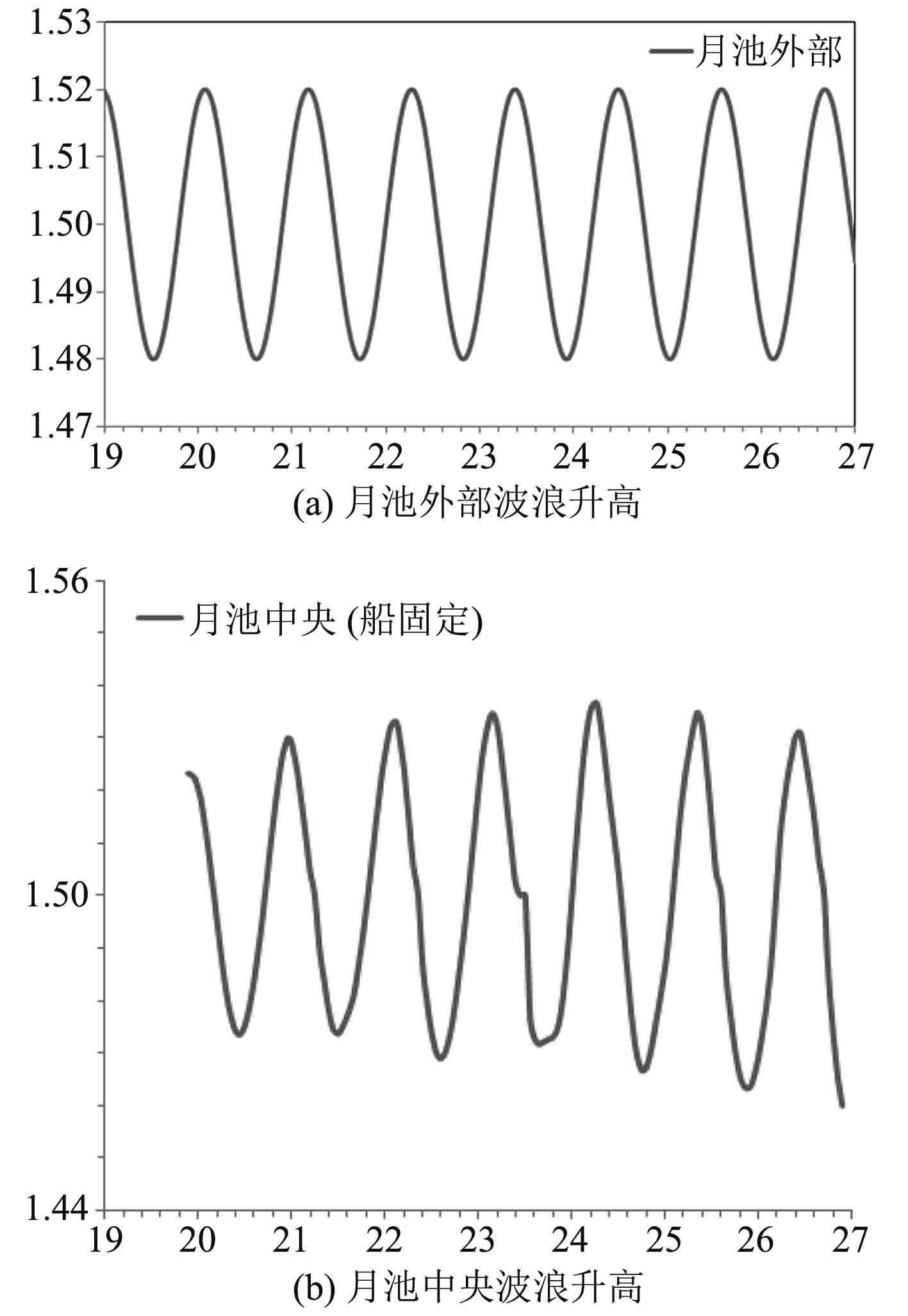
3.3.1 月池共振周期下月池内不同位置的自由液面升高比较分别对月池前端(A点)、后端(B点)、左端(C点)、右端(D点)、中央(E点)5点以及船体外与月池平行处进行浪高监测,入射波周期选择1.1 s,即月池的共振周期,以使波浪升高最大,便于观察。如图9所示,其中,月池中央E点处波面升高代表了月池内流体的活塞运动,A点与B点波面升高之差可以认为是月池纵向,即X方向的晃荡运动,C点与D点波面升高之差则认为是月池横向,即Y方向的晃荡运动。但是由于本文限制了y方向的运动,只考虑x方向和z方向运动,所以y方向的晃荡运动暂时不做研究。在180°迎浪条件下,对船体固定状态进行了数值模拟,得到波浪时历曲线(见图10)。
|
图 9 月池内浪高仪布置图 Fig. 9 Position of the wave elevation probesin the moonpool |
|
通过图10可知,共振周期下月池前端,中央和后端的波面升高均基本相同,说明:
1)月池内流体在各周期和幅值的入射波下水平运动均不激烈;
2)月池内流体波面升高均滞后于外部流场,说明月池对于外部波浪具有屏蔽作用。
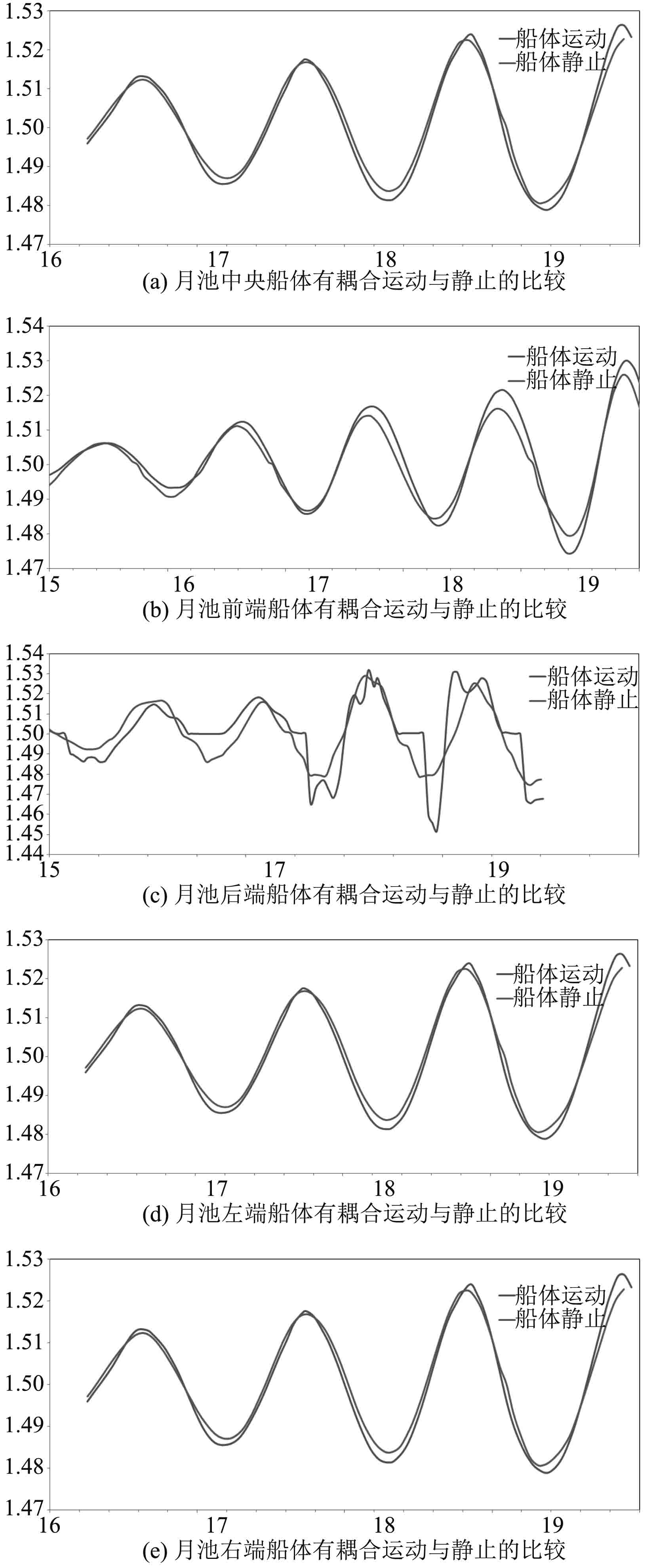
3.3.2 月池内流体在船体有运动时不同位置的自由液面升高比较上述算例无论入射波周期为共振周期还是其他周期,均做出船静止的假设,但是船体和波浪有耦合作用。船体在波浪中的运动可能会对月池内波浪运动有影响,所以考虑在利用Sima软件计算出船体运动实例后,导入FLOW3d中作为边界条件,这样就可以计算在月池共振周期下,船体随着波浪运动时,月池内流体波面的变化。于是在入射波周期为月池共振周期的情况下对对船体和波浪耦合运动状态进行模拟,得到波浪时历曲线(见图11)。
|
图 11 船体有无耦合运动时,月池内各点运动比较 Fig. 11 Comparions of wave elevation of different positions whether the vessel is fixed of not |
分析如下:
1)通过比较可以发现,与船体静止情况基本相同,月池内A,B,C,D,E五处的波面升高同样基本相同,说明船体在垂荡、纵荡和纵摇运动下,月池内流体运动不激烈,还是主要以活塞运动为主,水平晃荡运动不明显。
2)通过比较相同周期相同振幅的入射波有无船体运动2种情况可以发现,考虑船体运动,月池内各点处流体振幅比不考虑船体运动要剧烈,说明船体运动对月池内流体有加剧作用,而且说明如果要更好地模拟月池内流体运动,假设船体是静止的是不能满足的,要把船体运动也考虑进去。
4 结 语为了探索带有长矩形月池钻井船在不同周期下波浪中的运动情况,本文主要采用数值计算和模型试验2种方式进行研究。其中数值计算采用在FLOW-3D软件中建立三维数值水池的方式进行模拟,并设置多种周期和幅值的入射波,计算观察月池内不同位置流体的运动,并进行比较。而模型试验在深水池中进行,验证数值计算结果的正确性。
通过以上结果分析,可以清楚地发现:
1)在特定的振幅和周期的入射波作用下,钻井船月池后端流体的振幅显著比月池中央增大,振荡最大处流体的自由液面升高已经达到了入射波振幅的2倍左右,可能是受入射波浪向角的影响,也有可能是受月池后端台阶的影响。
2)通过比较可以发现,随着入射波的周期增大,月池内流体的运动周期也增大,响应幅值也随着增大,到月池共振周期左右达到幅值。随着入射波的幅值增大,月池内流体的运动幅值也随之增大。
3)通过比较相同周期相同振幅的入射波有无船体运动2种情况可以发现,考虑船体运动,月池内各点处流体振幅比不考虑船体运动要剧烈,说明船体运动对月池内流体有加剧作用,而且说明如果要更好地模拟月池内流体运动,假设船体是静止的是不能满足的,要把船体运动也考虑进去。
| [1] | 曲媛. 深海钻井船的总体方案分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. |
| [2] | 康庄. 月池流噪声及水动力特性的实验研究[D]. 哈尔滨: 哈尔滨工程大学. 2006. |
| [3] | MOLIN B. On the piston mode in moonpools [C]//Proc. 14th Int. Workshop on water waves & Floating Bodies, Port Huron, R. F. Beck & W. W. Schultz editors, 1999. |
| [4] | MOLIN B. On the sloshing modes in moonpools, or the dispersion equation for progressive waves in a channel through the ice sheet[C]//Proc. 15th Int. Workshop on water waves & Floating Bodies, Caesarea, Israel, 122–125, 2000. |
| [5] | MOLIN B. On the piston and sloshing modes in moonpools[J]. Journal of Fluid Mechanics, 2001, 430 : 27–50. DOI: 10.1017/S0022112000002871 |
| [6] | FALTINSEN O.M. Sea loads on ships and offshore structures [M]. Cambridge University Press, Cambridge, United Kingdom, 1990. |
| [7] | SALMAN SADIQ, KANG ZHUANG, YAO Xiong-liang. Oscillations in moonpool at static platform in waves[C]//26th Int. Conf. OMAE-29368, San Diego, California, USA, 2007. |
| [8] | KANG Zhuang, SALMAN SADIQ, YAO Xiong-liang. Acoustics and hydrodynamics of circle and square moonpool-an experimental research[C]// 26th Int. Conf. OMAE-29369, San Diego, California, USA, 2007. |
| [9] | KANG Zhuang, YAO Xiong-liang, SALMAN SADIQ. Experimental research on flow induced oscillations in moonpool encountered through waves[C]//26th Int. Conf. OMAE-29370, San Diego, California, USA, 2007. |
| [10] | SALMAN SADIQ, YAO Xiong-liang. Combined acoustic and hydrodynamic experimental data acquisition in towing tank-moonpool experiments[C]//27th Int. Conf. OMAE-57419, Estoril, Portugal, 2008. |
| [11] | AALBERS A. The water motions in a moonpool[J]. Ocean Engineering, 1984, 11 (06): 557–579. DOI: 10.1016/0029-8018(84)90001-5 |
| [12] | 刘应中, 缪国平. 船舶在波浪中的运动理论[M]. 上海: 上海交通大学出版社, 1987. |
| [13] | 戴遗山, 段文洋. 船舶在波浪中运动的势流理论[M]. 北京: 国防工业出版社, 2008. |
| [14] | 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007. |
| [15] | HIRT. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries[J]. Journal of Computational Physics, 1981, 39 : 201–225. DOI: 10.1016/0021-9991(81)90145-5 |
| [16] | 孙采微, 杨建民, 吕海宁. 波浪作用下带月池结构船体运动数值预报[D]. 上海: 上海交通大学. 2013. |
 2018, Vol. 40
2018, Vol. 40
