随着极地更多油气储量研究结果的公布[1],“北极资源战”的争夺愈演愈烈,尤其是近年来,气候升温,北极结冰面积逐年减少,表面海冰不断漂移,裂解和融化,资源开采指日可待。2015年1月19日,中集来福士为挪威建造的半潜式钻井平台“维京”号上下船体成功合拢,“维京”号是我国建造的第1座可在北极海域作业的半潜式钻井平台,也是我国首次进行深水平台冰区结构设计。但是,由于特殊的自然环境,冰载荷成为极地工作的海洋平台主要的影响因素。
浮冰与结构物的作用力即冰力主要有挤压冰力和撞击冰力2种。史庆增等[2]只考虑了浮冰的初始动能,给出了墩桩柱上作用浮冰的计算公式,并且得知冰与结构接触面宽度增加,会引起局部挤压系数的变化,浮冰撞击力的上限值就是同样厚度冰排的挤压力。通过现场结构实验,岳前进等[3]在研究冰与直立结构产生挤压破坏过程中,得出冰力形式与冰速相关,伴随着冰速的增大,相应引起结构准静态振动,稳态振动和随机振动响应。现在大多数平台碰撞特性研究中都只是针对船舶与平台的作用,冰对平台结构损伤研究甚少,金书成等[4]分析了阻塞冰载荷下的平台极限承载力,获得了不同冰厚对应的抗冰能力曲线。狄少丞等[5]采用了粘接-破碎效应离散元模型,大规模计算海洋平台结构与海冰的作用,得到了平台不同桩腿上的冰力时程曲线。欧进萍等[6]在对海洋平台结构冰力作用研究中提出统一静冰力模型,分析了冰激振动产生的条件并计算了单自由度结构的响应。
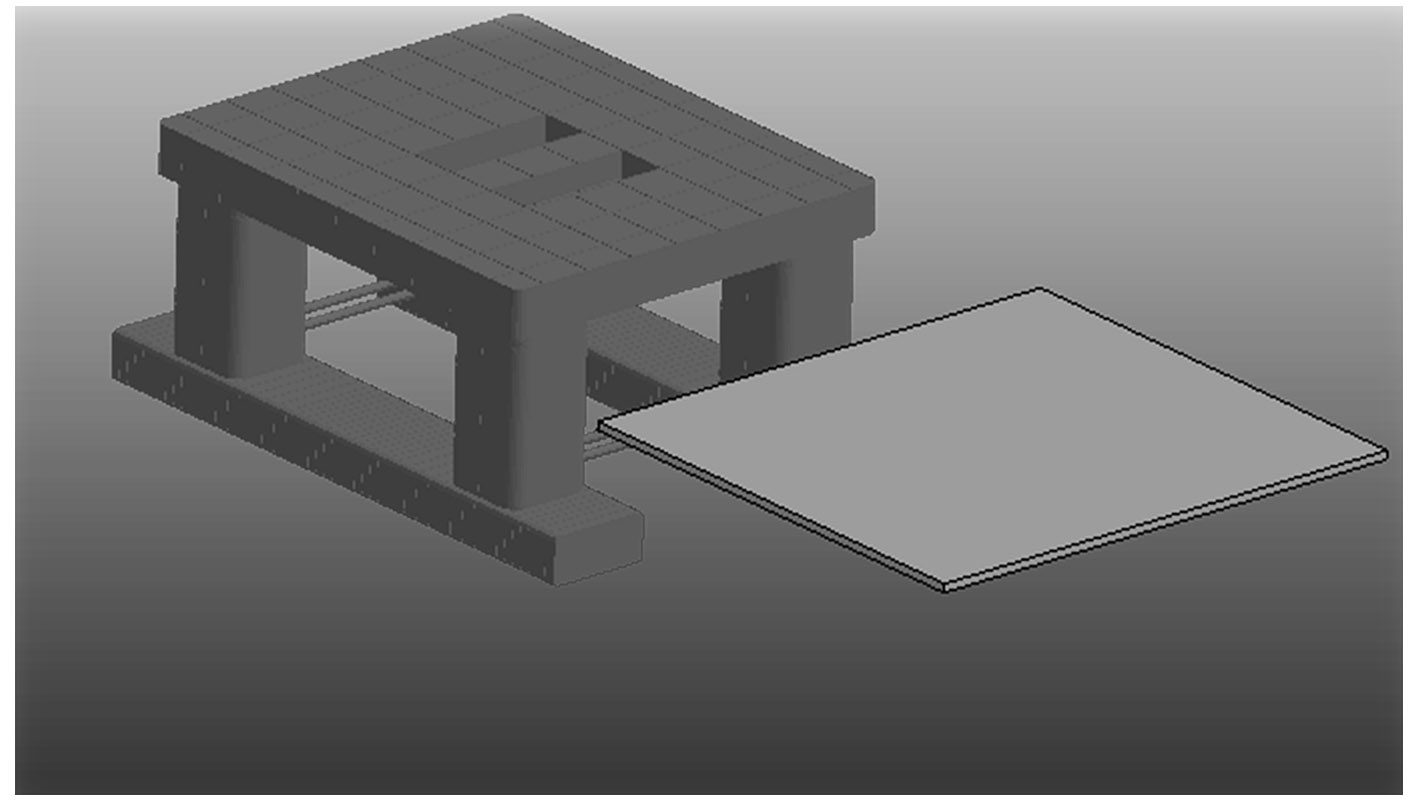
本文运用显式非线性有限元软件Ansys/LS-DYNA,建立了某半潜式海洋平台立柱和浮冰相互作用的模型,如图1所示。由于平台大多数都处于作业和生存阶段,根据吃水情况,故选择立柱为发生碰撞区域。极地浮冰面积都偏大,且大多为多年冰,厚度可达3 m,因此浮冰尺寸定为80 m×100 m×1.5 m。根据某平台图纸通过型值点和型线由外而内光顺得到外壳,甲板等,其尺寸如表1所示。给定浮冰一定的初始动能,从浮冰和平台的耗散能以及平台立柱不同区域的应力应变分析了平台的损伤情况,讨论了碰撞过程中平台的振动响应,并获得了平台碰撞力和初始动能的关系曲线。
|
图 1 有限元模型 Fig. 1 The finite element model |
|
|
表 1 平台尺寸 Tab.1 The dimension of platform |
在有限元方法中常采用显示中心差分的方式来求解短时间高度非线性问题,平台-冰碰撞方程可以表达为:
| $ {M} \alpha + {C} v + {K } d = F^{\rm{ex}}{\text{。}}$ | (1) |
式中:M为系统质量矩阵;C为系统的阻尼矩阵;K为系统的刚度阵;α为加速度向量;v为速度向量;d为位移向量;Fex为外力向量。
而为了计算简便,碰撞方程常常简化为如下形式:
| $ {M} \alpha =F^{{re}} {\text{。}}$ | (2) |
式中:
冰的材料非常复杂,与时间、含盐度、孔数和周遭水域等有关,本构模型是数值模拟中的关键点也是难点。翟帅帅等[7]采用Derradji-Aouat多重失效面准则来模拟海冰在碰撞中的力学行为,重点研究了应变率、拉压强度以及横观各向异性等影响因素,张充霖[8]在研究船首在冰载荷作用下损伤中则是基于Tsai-Wu屈服准则采用Elas-Plas基本材料。目前,研究的材料模型大致可以归为4类,即黏塑性模型、弹塑性模型、黏-弹-塑性模型和各向异性断裂损伤模型。本文采用DYNA中13号材料各向同性弹塑性断裂模型(*MAT-ISOTROPIC-ELASTIC-FAILURE),各材料参数如表2所示。其压强-面积曲线与ISO-ALIE推荐曲线基本上一致[9],采用的屈服准则von Mises,主应力表达式为:
|
|
表 2 冰材料模型参数 Tab.2 Material properties of ice model |
| ${\left( {{\sigma _1} - {\sigma _2}} \right)^2} + {\left( {{\sigma _2} - {\sigma _3}} \right)^2} + {\left( {{\sigma _3} - {\sigma _1}} \right)^2}{\rm{ = 2}}\sigma _{\rm{s}}^2 = 6{K^2}{\text{。}}$ | (3) |
式中:σs为材料屈服点;K为材料剪切屈服强度。
1.2.2 平台材料模型大多数的金属材料中应变率对屈服极限有很明显的影响,平台-冰的碰撞属于动力响应的过程,需要考虑平台出现大的变形和损伤。本文采用Ansys/LS-DYNA提供的塑性动态模型(Plastic Kinematic Model),材料参数如表3所示。运用Cowper-Symonds本构方程反应屈服应力和应变率的关系,其表达式为:
| ${\sigma _{\rm{y}}} = \left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{C}} \right)}^{\frac{1}{P}}}} \right]\left( {{\sigma _0} + \beta {E_P}\varepsilon _P^{eff}} \right){\text{。}}$ | (4) |
式中:σ0为初始屈服应力;
|
|
表 3 平台材料参数 Tab.3 Material properties of platform |
平台与浮冰的接触-碰撞属于状态非线性范畴,通常很难知道接触的区域,对接触和分开时间难以精确估计,接触面的设置会影响分析结果,本文采用面-面侵蚀接触(*CONTACT_ERODING_SURFACE_TO_SURFACE),并且将动静摩擦系数都设置为0.15。为了减少计算时间且保证计算结果的准确性,在网格划分时只将平台立柱的碰撞区域进行细化。
2 碰撞分析本文中碰撞的作用水线面与半潜式海洋平台作用吃水线保持一致。海冰漂移速度主要由风和流以及海冰内力决定[10],风速、流速、海冰密集度越大,冰速越大;根据北极海冰情况[11],以及平台相对运动,取了偏危险的速度,定为1.5 m/s,因此浮冰的初始动能是13.68 MJ,并且将半潜式海洋平台浮体设置为刚性固定。
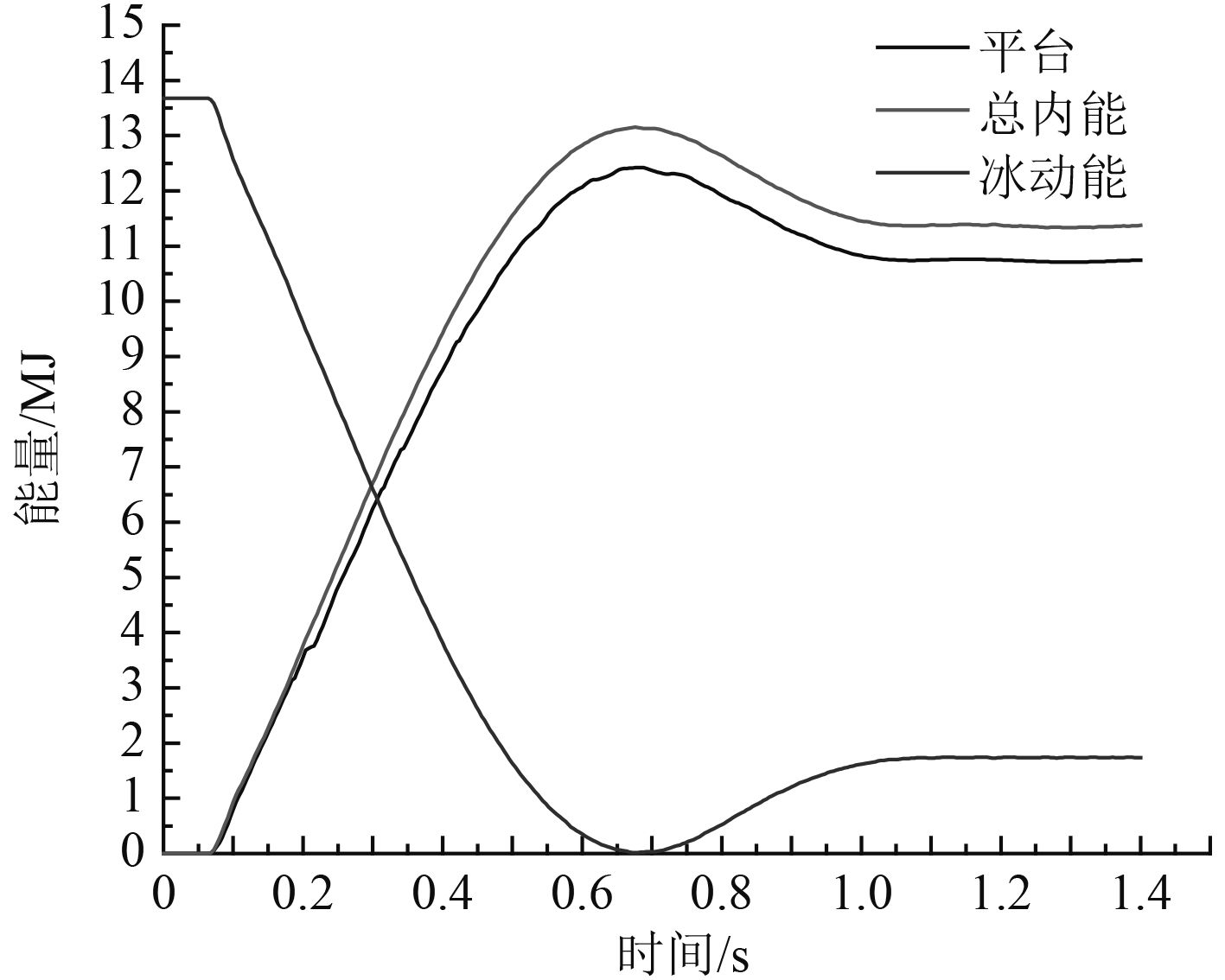
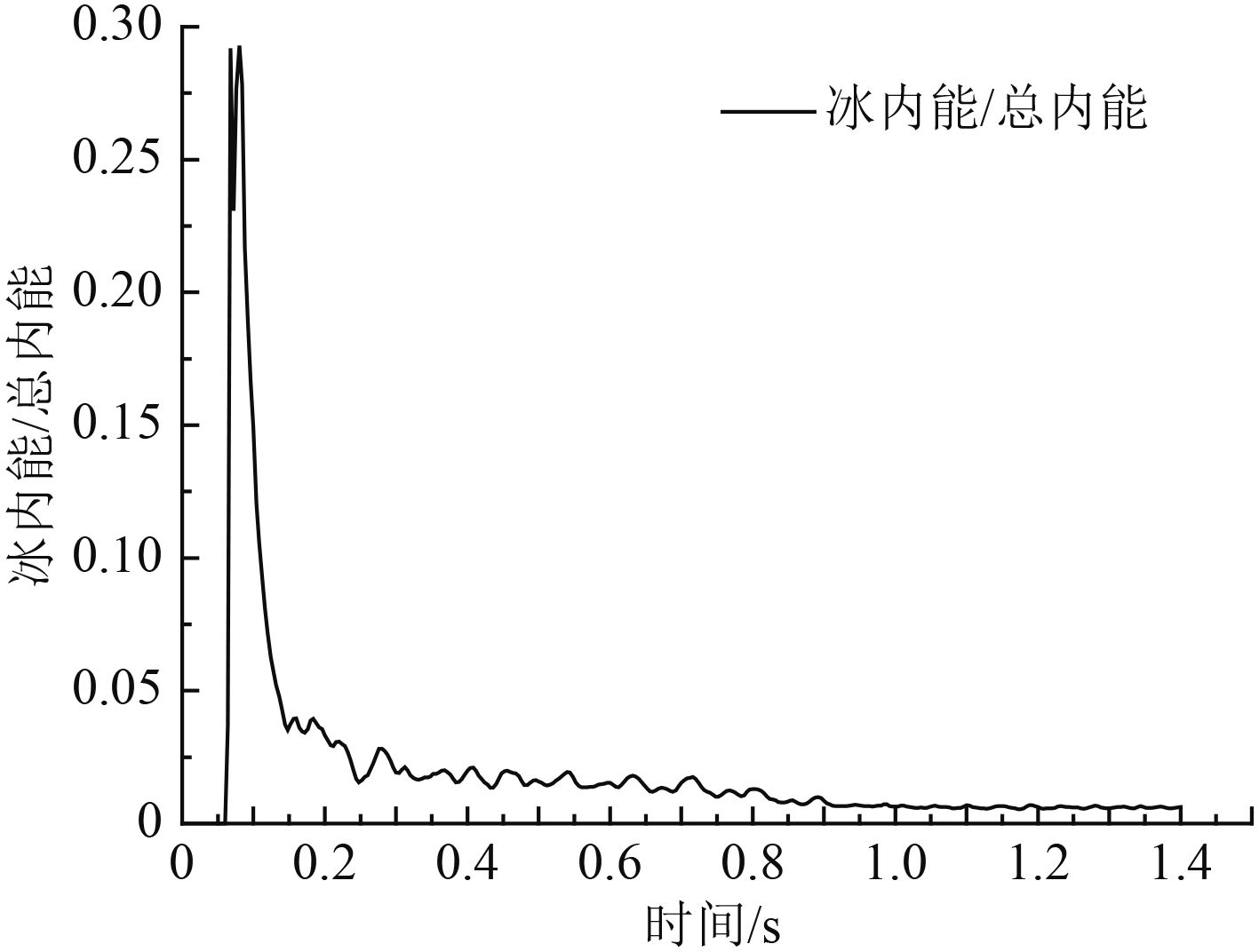
2.1 能量分析图2是海洋平台受浮冰撞击后变形能的时程曲线。大约在0.07 s,浮冰与平台发生碰撞,浮冰的动能迅速减少,平台的变形极速增加,但是大约在0.68 s之后,平台的变形能量逐渐减少,并最终达到了稳定值,约为1.075E7J,这是由于浮冰在0.68 s后速度为0并开始往回运动,随着外力的减小平台弹性形变开始恢复。从整个碰撞过程来看,浮冰的动能几乎全都转化为了平台的势能,能量转化率达到78.58%。而冰在整个碰撞过程也消耗了能量,图3中初始阶段,冰耗散能与总耗散能的比值接近0.3,这表明了碰撞初始平台变形与冰变形同时开始,随后冰单元表现较为坚硬,比值迅速降低,最终稳定值约为1%。此变化说明了在碰撞过程中平台的变形占主要的,并且在碰撞模拟过程中可以明显看出冰单元失效较少,从2图中看出平台的变形是主要吸收耗散能的部分。
|
图 2 能量转化时程曲线 Fig. 2 The energy transformation curve |
|
图 3 耗散能的比值时程曲线 Fig. 3 The energy dissipation ratio curve |
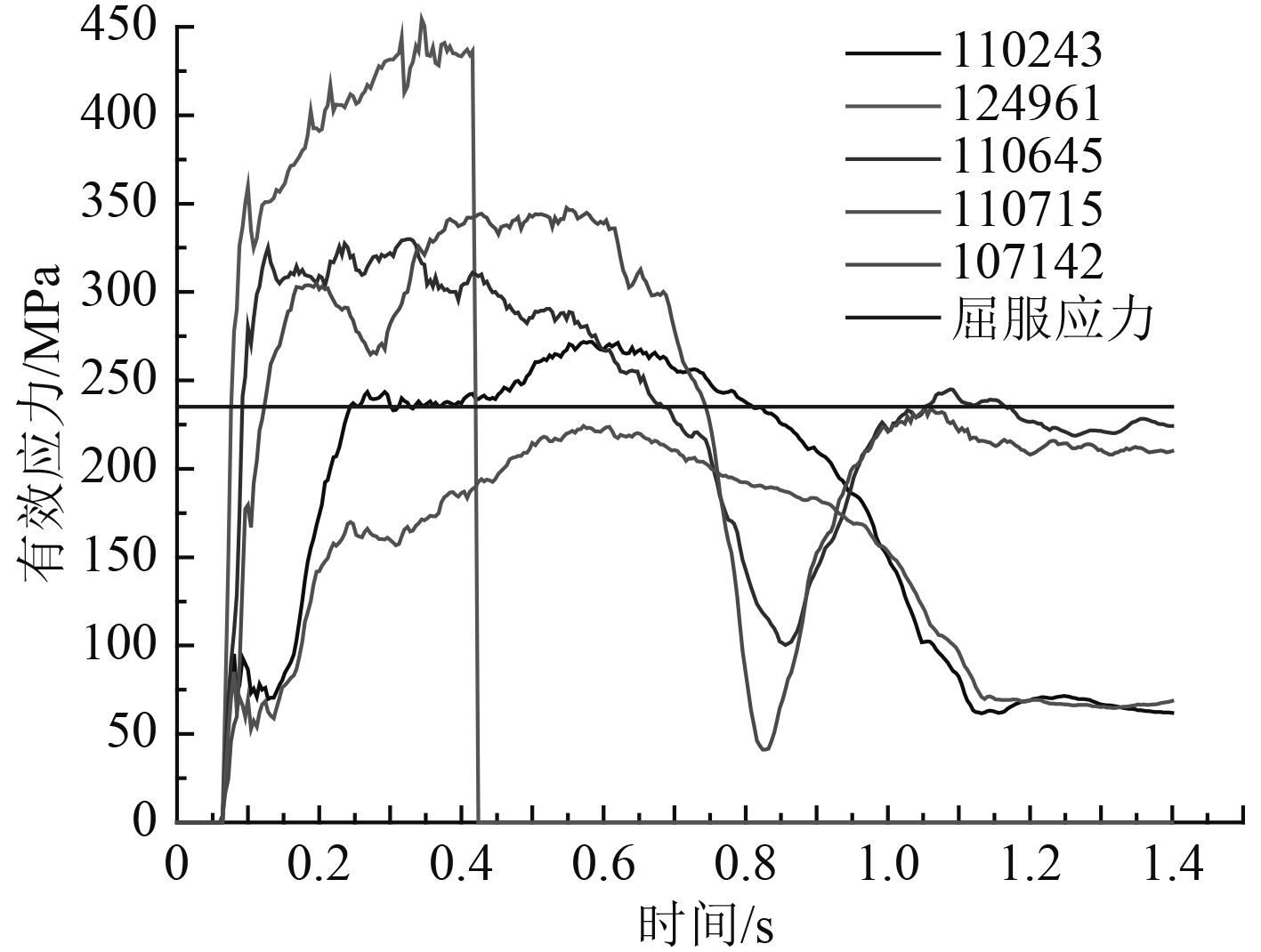
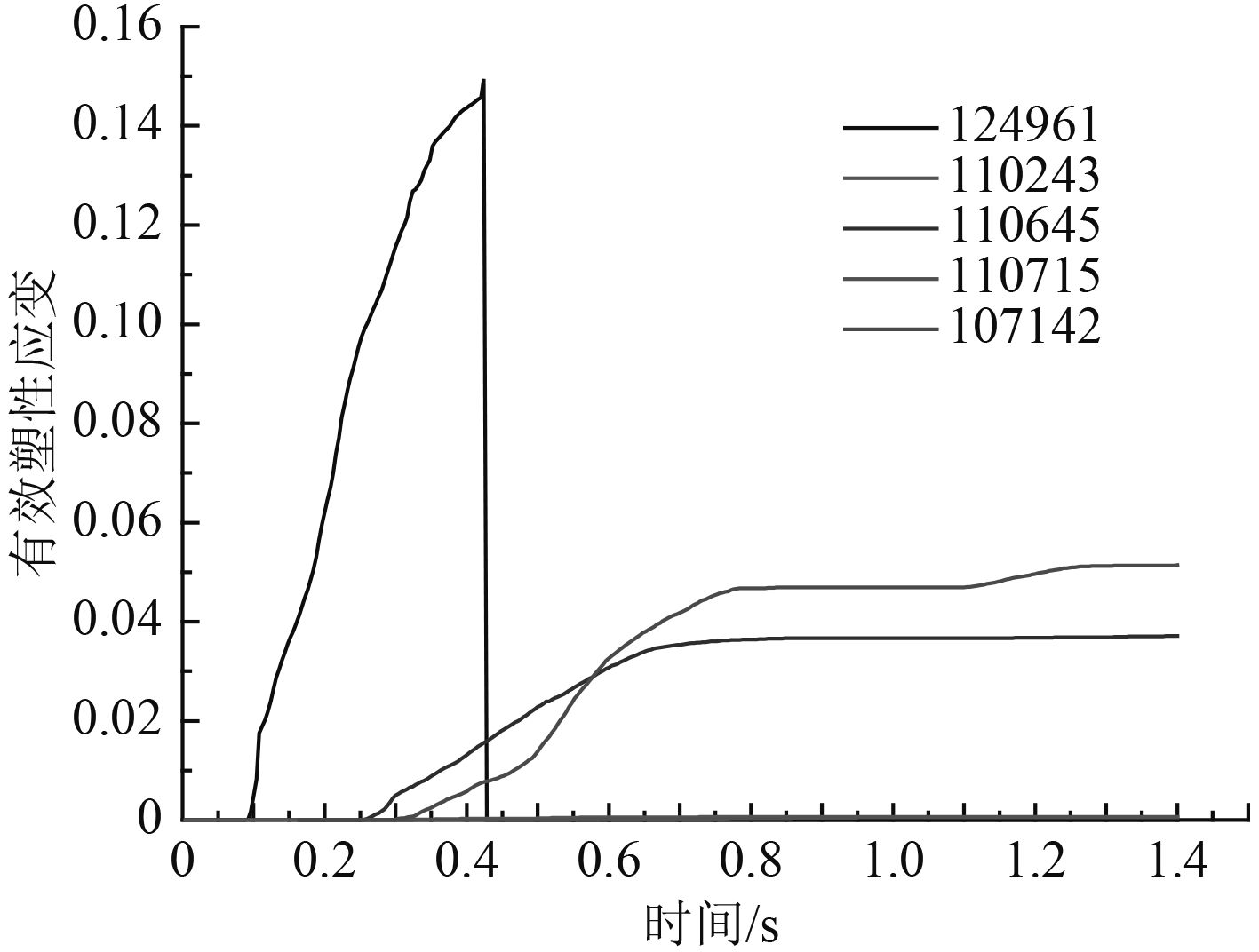
图5和图6为选取碰撞区域立柱外板几个单元的有效应力和有效塑性应变时程图(单元124961,110243,110645,110715,107142的位置见图4)。应力时程曲线图中,单元124961、单元107142和单元110645在碰撞的初始时刻应力迅速达到屈服极限,进入塑性阶段,而且一直持续到外力作用消失,弹性阶段的时间极短。而单元110243在接触之后一段时间才达到屈服极限并且只是持续一段时间,在外力未消失时就进入弹性阶段,在塑性变形图中可以看出几乎没有产生塑性变形,单元110715应力从未达到屈服极限,一直处于弹性阶段,表明中间区段单元主要处于弹性变形阶段。在图5中,单元124961进入到塑性阶段之后,约0.43 s时由于塑性变形积累到失效应变0.15,从而单元产生失效行为,不再承受应力,即有效应力剧变为0。而单元107142和单元110645一直处于塑性变形积累阶段,且在外力消失时由于塑性变形不可恢复而达到稳定,但是由于弹性变形减小,在碰撞结束时应力出现了减小。由此表明立柱中心和两外侧是主要受力区域,最易发生损伤破坏,需要重点加强保护位置。

|
图 4 单元位置分布 Fig. 4 The locations of elements |
|
图 5 单元有效应力时程曲线 Fig. 5 The elements of effective stress curve |
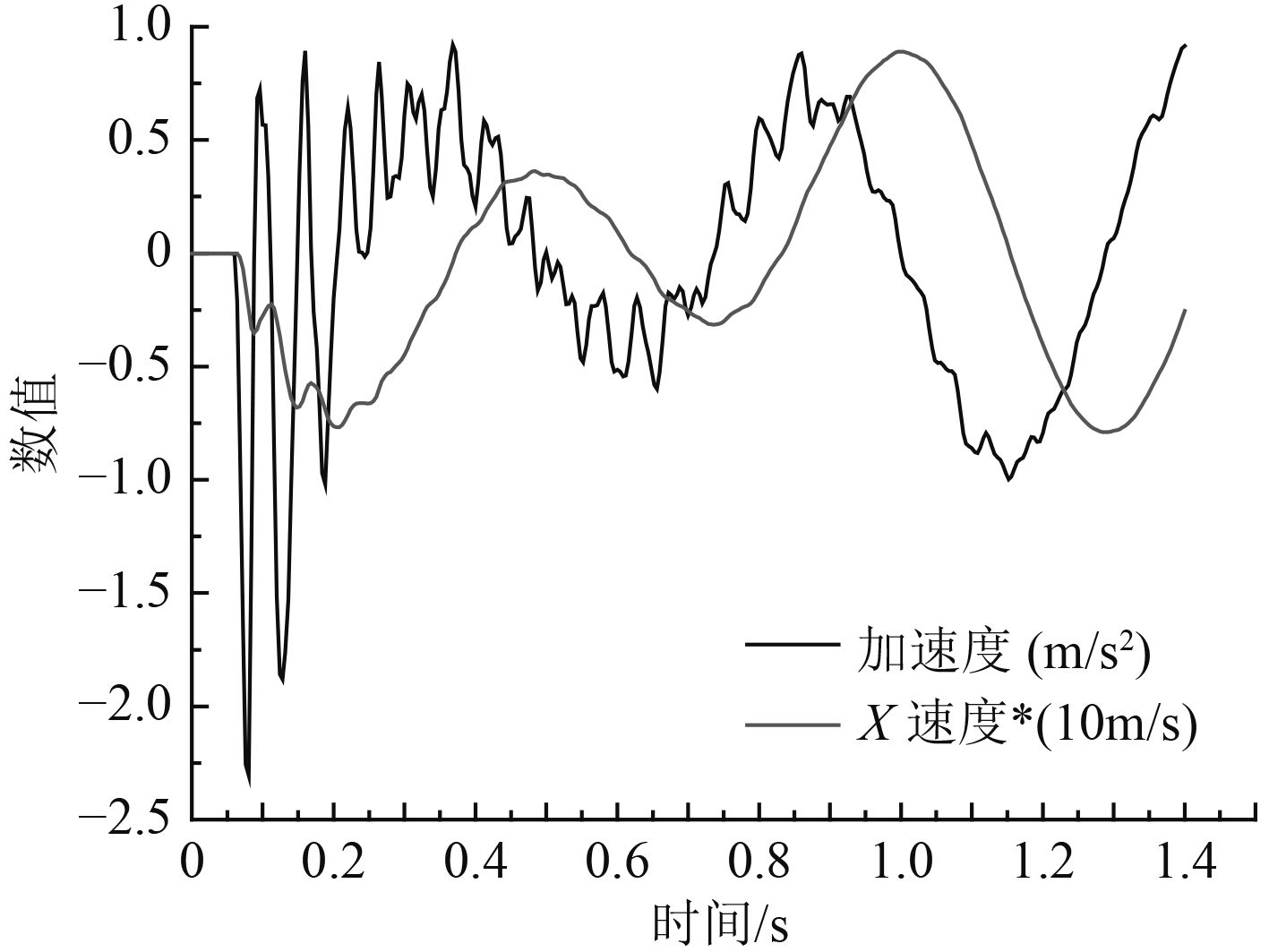
图7是半潜式海洋平台在X方向的速度加速度-时间曲线。刚开始接触阶段,平台在X方向的加速度呈现剧烈波动,最大值接近2.4,变化时间非常短,平台受到强大的外力产生强迫振动,但是随着结构的变形增加,吸收了部分能量后速度和加速度的改变明显减缓,尤其是当浮冰开始往回运动之后,呈现相对平稳的状态。这种海洋平台强烈冰激振动严重影响工作人员的舒适和上层建筑设施,尤其精密仪器的损害,对于长期处于冰载荷环境工作状态下的平台来说,由于振动时间较长,也会引起部分结构的疲劳。
|
图 6 单元有效塑性应变时程曲线 Fig. 6 The effective plastic strain curve |
|
图 7 平台X方向速度加速度-时间曲线 Fig. 7 The velocity and acceleration curve |
在与浮冰的碰撞过程中,浮冰的尺寸、速度、强度等都会影响冰力值的大小,本文主要考虑浮冰厚度,考查碰撞力与浮冰初始动能的关系。
从表4可以知道失效时间[10]并不随着初始动能的增加而变长,在任何时刻下都可能会出现最大碰撞力,单元失效是一个随机的过程。当初始动能增大,平均碰撞力和最大碰撞力也会随着增加,但是最大碰撞力的增加趋势却是逐步减缓。
|
|
表 4 不同初始动能下的碰撞力 Tab.4 The impact forces under different initial kinetic energy |
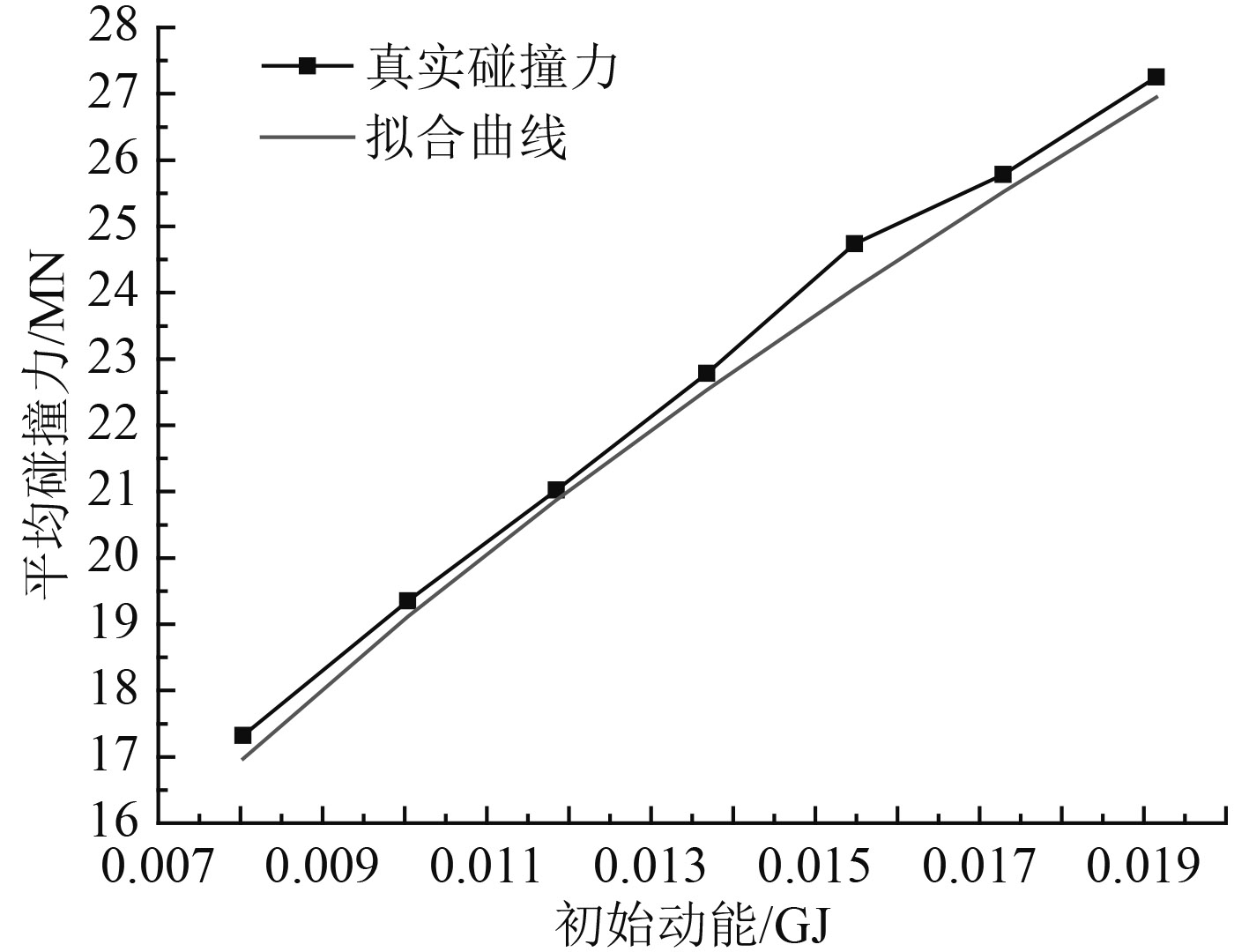
G.W.Timco[12]通过不同区域的海冰与海洋结构物撞击实验,给出了平均碰撞力和动能的关系:
|
图 8 平均碰撞力-初始动能曲线 Fig. 8 The averageimpact force- initial kinetic energy curve |
本文分析了半潜式海洋平台受到一初始动能的浮冰撞击过程中的力学性能,得出了海洋平台变形能和应力应变时程结果和平台冰激振动。同时,也分析了不同初始动能下的最大碰撞力、平均碰撞力和失效时间的关系。得出以下结论:
1)海洋平台受到浮冰撞击之后,浮冰的动能几乎转化为平台的势能,但是在碰撞初期,浮冰和平台同时产生变形,由于冰表现强硬,随后平台的变形远远超过冰变形,冰消耗的能量逐渐降低。尽管在碰撞过程中,浮冰和平台都消耗了能量,但是平台的变形还是主要耗能部分。
2)平台受到浮冰撞击,立柱的损伤程度不同。在撞击中心和最外侧位置,弹性形变时间很短,可以认为几乎没有,主要是处于塑性变形阶段,所以其损伤程度最严重,尤其是中心区域,而中心偏两侧部位大多数时间都处于弹性形变范围,没有进入到塑性变形阶段。立柱损伤程度由中心区域最严重,最外侧次之,中心偏内侧最轻。这说明极地工作的平台对立柱的中心和外侧区域应重点加强防护。
3)海洋平台与冰碰撞中会产生冰激振动效应。碰撞初期,平台受到强大的外力产生强迫振动,加速度变化剧烈,但是随着变形增加,消耗了大部分能量后趋势趋于平缓,当外力消失后,平台整体振动处于相对平稳的状态。
4)碰撞力和浮冰的初始动能是处于同增同减的关系,但是碰撞力增加量却随着动能的增加逐步减缓。从平均碰撞力来看,数值分析得出的结果和实验结果基本一致。尽管碰撞力随着动能增加而增大,但是失效时间是随机,任何时候都可能发生。
| [1] | Arctic ocean oil and natural gas potential[R]. Energy Information Administration, 2009, 10. |
| [2] | 史庆增. 墩(桩)柱上流冰撞击力的研究与试验[J]. 海洋工程, 1994 (4): 8–13. |
| [3] | 岳前进, 杜小振, 毕祥军, 等. 冰与柔性结构作用挤压破坏形成的动荷载[J]. 工程力学, 2004 (1): 202–208. |
| [4] | 金书成, 杨炎华. 冰荷载对导管架海洋平台的作用研究[J]. 中国海洋平台, 2010 (5): 15–19. |
| [5] | 狄少丞, 季顺迎. 海冰与自升式海洋平台相互作用GPU离散元模拟[J]. 力学学报, 2014 (4): 561–571. DOI: 10.6052/0459-1879-13-400 |
| [6] | 欧进萍, 王刚, 段忠东. 海洋平台结构的冰力作用模型[J]. 海洋工程, 2002 (1): 7–14. |
| [7] | 张充霖. 冰载荷作用下船首结构碰撞数值仿真计算与分析[J]. 中国海上油气, 2014 (S1): 6–10. |
| [8] | 翟帅帅, 高俊. 基于Derradji-Aouat海冰本构模型的船冰碰撞数值模拟[J]. 船舶设计通讯, 2016 (S1): 51–59. |
| [9] | 史江海, 桂洪斌, 李丹. 船首形状对船-冰碰撞性能的影响研究[J]. 舰船科学技术, 2016 (1): 8–13. |
| [10] | 岳前进, 张希, 季顺迎. 辽东湾海冰漂移的动力要素分析[J]. 海洋环境科学, 2001 (4): 34–39. |
| [11] | 苏洁, 徐栋, 赵进平, 等. 北极加速变暖条件下西北航道的海冰分布变化特征[J]. 极地研究, 2010 (2): 104–124. |
| [12] | TIMCO G W. Isolated ice floe impacts[J]. Cold Regions Science and Technology, 2011, 68(1–2): 35–48. |
 2018, Vol. 40
2018, Vol. 40
