国际海事组织一直致力于解决船舶碰撞和安全问题。尽管这样,仍有大量数据表明,国际上每年失事船舶中有超过40%是因为碰撞导致的,且其中近80%的事故是人为原因造成的[1 – 3]。日益拥挤的海上交通环境、快速发展的航海技术以及与人为失误有关的海难事故,促使船舶避碰的研究进一步深入,而自动避碰决策是其中的核心和难点问题,一个较成熟的自动避碰决策系统要求在满足避碰规则(对于港口水域既包括“国际海上避碰规则”也包括“地方规则”)的前提下,适时自动避让来船(可能是多艘船舶)以及其他障碍物,保证驶过让清后选择安全经济的航线复航。
海上环境复杂多变,因此决策的实时性要求较高,此外还需要考虑对避碰规则的严格遵守、能见度、水域受限情况以及船舶类型、操纵性能等,满足以上条件的自动避碰决策系统将非常复杂,且在未完全感知的环境中进行多船避让,且规则未对避碰行为进行要求,本身就属于NP困难问题,最优解难以保证,因此航海界一直致力于寻找更智能、优化的算法来解决船舶避碰决策问题。针对这个问题,学术界在避碰决策模型方面开展了广泛的研究,一些启发式进化算法,如遗传算法、蚁群算法、粒子群算法、模拟退火算法(SA)等[4 – 7],以及一些确定性避碰决策方法相继取得一定的成果。但对于多种算法的混合策略研究不够,不能全面提高算法的速度和计算结果的精度,存在局部和全局收敛不足的问题,算法的实时性也有待提升。
现代避碰决策技术已经向智能化方向发展。应用较多的避碰决策方法是专家系统(ES),如英国利物浦大学、东京商船大学、广州舰艇学院等研究单位均研究了用于船舶避碰的专家系统[8 – 10],这些避碰专家系统采用咨询式辅助避碰手段,针对不同的会遇局面给出避碰决策结果。李丽娜[11]提出拟人化智能避碰决策方法,模仿经验丰富的避碰决策,这种方法较专家系统更为快速,能在短时间内进行局面判断,精确计算及预测避碰效果,提供决策支持,既可用于单船避碰,又可用于多船避碰。郑中义和孙立成等[12 – 14]分别从信息熵理论和神经网络理论出发研究了船舶避碰决策方法。刘以安等[15]采用模拟退火算法计算多船会遇局面下本船的转向幅度,并进行3种会遇态势下的避碰仿真验证。
在多船会遇态势下,船舶转向避碰是采用频率最高的一种避碰方法。本文从多目标函数全局优化问题出发,基于船舶碰撞危险度和航程损失的多目标函数优化,通过分级变异动态克隆选择优化算法,在《国际海上避碰规则》约束的可行域空间内,从而在可行空间中找出满足多目标函数和约束条件的全局范围内的最优转向幅度。
1 船舶碰撞危险度计算模型本文的研究是基于开阔水域下多船会遇态势下的转向避碰幅度最优解计算,通过碰撞几何原理分析可知,影响船舶碰撞危险度大小的因素很多,且互相制约,判断船舶是否存在碰撞危险度的主要依据是基于船舶领域和动界的概念,对DCPA和TCPA进行综合考虑。确定了最近会遇距离(DCPA)、最近会遇时间(TCPA)、两船距离、相对方位、船速比5个主要影响因素的隶属度函数,并考虑航行区域状况、能见度情况和船舶的操纵性能等对船舶碰撞危险度的隶属度函数修正,利用模糊规则和模糊综合评价方法进行船舶复合碰撞危险度的计算,考虑了船舶微观和主观碰撞危险度因素。
基于模糊综合评价的碰撞危险度计算结果可以作为主观和客观评价,通过减小其影响因素来得到最佳的计算结果。所以,本文不采用DCPA和TCPA加权的方法计算碰撞危险度,而是采用模糊综合评价的方法计算碰撞危险度。文献[16]中把DCPA、TCPA、两船距离、相对方位、船速比5个因素作为基本评判参数,并考虑航行区域状况、能见度情况和船舶的操纵性能等对船舶危险度的隶属度函数修正。为了更加符合海上避碰行动实际,主要考虑以下5个影响因素:任意时刻目标船和本船的距离、目标船的方位、船速比、DCPA和TCPA。所以,目标影响因素的论域为:
| $u = \{ d,\theta ,K,{t_{{\rm{CPA}}}},{d_{{\rm{CPA}}}}\}{\text{。}}$ | (1) |
目标影响因素的模糊权重分配如下,权重值根据文献[16],取为:wd=0.14,wθ=0.10,wk=0.08,
| $\left\{ \begin{aligned}& A = {w_d},{w_\theta },{w_k},{w_{{d_{{\rm{CPA}}}}}},{w_{{t_{{\rm{CPA}}}}}},\\& {w_d} > 0,{w_\theta } > 0,{w_k} > 0,{w_{{d_{{\rm{CPA}}}}}} > 0,{w_{{t_{{\rm{CPA}}}}}} > 0,\\& {w_d} + {w_\theta } + {w_k} + {w_{{d_{{\rm{CPA}}}}}} + {w_{{t_{{\rm{CPA}}}}}} = 1{\text{。}}\end{aligned} \right.$ | (2) |
目标评价矩阵如下,其中rd,rθ,
| ${B} = \left[ {\begin{array}{*{20}{c}}{{r_d}}\\{{r_\theta }}\\{{r_{{d_{{\rm{CPA}}}}}}}\\{{r_{{t_{{\rm{CPA}}}}}}}\end{array}} \right]{\text{。}}$ | (3) |
由文献[17]可知,船舶间距离越小,船舶间碰撞危险度越大。任意时刻船舶间距离的隶属度函数如下:
| $u(d) = \left\{ \begin{array}{l}\begin{array}{*{20}{c}}1, & {} & {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{} & {} & {} & {}\end{array}} & {} & {d \leqslant {d_1}},\end{array}}\end{array}\\{[({d_2} - d)/({d_2} - {d_1})]^2}, \;\;\;\;{d_1} < d \leqslant {d_{\rm{2}}}, \\\begin{array}{*{20}{c}}0, & {} & {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{} & {} & {} & {}\end{array}} & {} & {d > {d_2}}{\text{。}}\end{array}}\end{array}\end{array} \right.$ | (4) |
d1和d2的大小取决于航行区域的状况、能见度以及人为因素的影响。动界是以驾驶员开始采取行动以避免紧迫局面时与他船的距离为基础的超级领域。英国学者Davis等通过大量的调查统计得到了动界模型的具体数据,在进行平滑其边界后,得到了一个半径为2.7 n mile的圆的数学模型。令其区域半径为R,可以得到其表达式:
| ${d_1} = {K_1} \cdot {K_2} \cdot {K_3} \cdot {D_{{L}}},$ | (5) |
| ${d_2} = {K_1} \cdot {K_2} \cdot {K_3} \cdot R, $ | (6) |
| $R = 1.7\cos (\theta - {19^\circ }) + \sqrt {4.4 + 2.89{{\cos }^2}(\theta - {{19}^\circ })}{\text{。}} $ | (7) |
式中:d1为船舶最晚避让距离;d2为船舶协调避让的距离;K1取决于能见度;K2取决于水域情况;K3取决于人为因素;DL为最晚施舵距离,一般取12倍船长[18];R为任意时刻船舶动界的半径。
不同方位的目标船对本船所构成的危险程度不同,一般来说右舷大于左舷,正横前大于正横后。
任意时刻目标船相对方位角的隶属度函数,式中θ与本船与目标船的船速比
| $u(\theta ) = \left\{ \begin{aligned}& \frac{1}{{1 + {{(\theta /{\theta _0})}^2}}},\;\;\;\;\;\;\;\;0 \leqslant \theta < {180^\circ }, \\& \frac{1}{{{{(\frac{{{{360}^\circ } - \theta }}{{{\theta _0}}})}^2}}},\;\;\;\;\;\;\;\;{180^\circ } \leqslant \theta < {360^\circ }{\text{。}}\end{aligned} \right.$ | (8) |
| ${\theta _0} = \left\{ \begin{array}{l}\begin{array}{*{20}{c}}{{{40}^\circ }}, & {K < 1},\end{array}\\\begin{array}{*{20}{c}}{{{90}^\circ }}, & {K = 1},\end{array}\\\begin{array}{*{20}{c}}{{{180}^\circ }}, & {K > 1}{\text{。}}\end{array}\end{array} \right.$ | (9) |
如果其他参数相同,船速比不同时,其碰撞危险度也不相同。船速比越大,船舶碰撞危险度越大,令W≥0,W=2,0°≤C<180°,船速比的隶属度函数:
| $u(K) = \frac{1}{{1 + \frac{W}{{K\sqrt {{K^2} + 1 + 2K\sin C} }}}}{\text{。}}$ | (10) |
DCPA小于船舶安全会遇距离时,船舶存在碰撞危险,该值越小,碰撞危险程度越大。任意时刻DCPA的隶属度函数[21]:
| $ u({d_{{\rm{CPA}}}}) \!=\!\! \left\{\!\!\!\!\!\! {\begin{array}{*{20}{c}}1\\{\displaystyle\frac{1}{2} \!-\! \displaystyle\frac{1}{2}\sin \left[ {\displaystyle\frac{{\rm{\pi }}}{{{d_{{\rm{CP}}{{\rm{A}}_0}}} \!-\! \lambda }}\left( {{d_{{\rm{CPA}}}} \!-\! \displaystyle\frac{{{d_{{\rm{CP}}{{\rm{A}}_0}}} \!+\! \lambda }}{2}} \right)} \right]}{\text{。}}\\ 0 \end{array}} \right.\!\!\!\!$ | (11) |
适用于开阔水域的基于船舶领域的船舶安全会遇距离计算时,需要考虑船舶领域存在的模糊边界FBD[19],船舶领域进行平滑连续后大小和模糊边界值的计算如下[20]:
| $domain{\rm{ = }}\left\{ {\begin{aligned}& {0.85 - \frac{{{\theta _t}}}{{{{180}^\circ }}} \times 0.2},\\& {1.8 - \frac{{{\theta _t}}}{{{{180}^\circ }}} \times 0.73},\\& {1.02 - \frac{{{{360}^\circ } - {\theta _t}}}{{{{180}^\circ }}} \times 0.57},\\& {{\rm{0}}{\rm{.85}} - \frac{{{{360}^\circ } - {\theta _t}}}{{{{180}^\circ }}} \times 0.3},\end{aligned}} \right.$ | (12) |
| $FBD = 0.267{D_S}{\text{。}}$ | (13) |
1)当能见度不良时,
| ${d_{{\rm{CP}}{{\rm{A}}_0}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}}{{K_1} \cdot {K_2} \cdot {K_3} \cdot \left( {{D_S}{\rm{ - }}FBD} \right)},\\{{K_1} \cdot {K_2} \cdot {K_3} \cdot \left( {1{\rm{ - }}0.276} \right){D_S}}{\text{。}}\end{array}} \right.$ | (14) |
2)
TCPA值大小与碰撞危险度的关系与DCPA类似,任意时刻TCPA的隶属度函数:
| $u({t_{{\rm{CPA}}}}) = \left\{ {\begin{aligned}& 1, & {} & {{t_{{\rm{CPA}}}} < {t_1}},\\& {\frac{{{t_2} - {t_{{\rm{CPA}}}}}}{{{t_2} - {t_1}}}}, & {} & {{t_1} < {t_{{\rm{CPA}}}} \leqslant {t_2}}, \\& 0, & {} & {{t_{{\rm{CPA}}}} > {t_2}}{\text{。}}\end{aligned}} \right.$ | (15) |
| ${t_1} = \frac{{\sqrt {\left( {d_1^2 - {\lambda ^2}} \right)} }}{{{v_s}}},\;{t_2} = \frac{{\sqrt {\left( {d_{\rm{m}}^2 - d_{{\rm{CP}}{{\rm{A}}_0}}^2} \right)} }}{{{v_s}}}{\text{。}}$ | (16) |
根据模糊综合评价方法得到目标危险度所有因素的综合评判结果:
| $\begin{aligned}& CRI = {A} \cdot {B} = \\& \left[ {\begin{array}{*{20}{c}}{{w_d}}\!\!\!\!\! & \!\!\!\!\!\!\!{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{w_\theta }} \! & \! {{w_k}}\end{array}} \!\!\! & \!\!\! {{w_{{d_{{\rm{CPA}}}}}}}\end{array}} \!\!\! & \!\!\! {{w_{{t_{{\rm{CPA}}}}}}}\end{array}}\end{array}} \right] \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{r_d}}\\{{r_\theta }}\end{array}}\\{{r_k}}\end{array}}\\{{r_{{d_{{\rm{CPA}}}}}}}\end{array}}\\{{r_{{t_{{\rm{CPA}}}}}}}\end{array}} \right]{\text{。}} \end{aligned}$ | (17) |
任意时刻的碰撞危险度C2为:
| $CRI \!=\! {w_d}{u_d} \!+\! {w_\theta }{u_\theta } \!+\! {w_k}{u_k} \!+\! {w_{{d_{{\rm{CPA}}}}}}{u_{{d_{{\rm{CPA}}}}}} \!+\! {w_{{t_{{\rm{CPA}}}}}}{u_{{t_{{\rm{CPA}}}}}}{\text{。}}$ | (18) |
经过计算可以得到目标船的碰撞危险度大小。如果CRI=0,船舶间不存在碰撞危险;如果CRI=1,船舶间一定存在最大碰撞危险;如果CRI∈[0,1],CRI越大,船舶碰撞危险性越大。
2 转向避碰多目标函数模型本文将多船会遇态势下的转向避碰作为一类多目标函数优化问题,应用分级变异动态克隆选择优化算法,从《国际海上避碰规则》约束的可行域空间中找出满足目标函数和约束条件的最优转向避碰幅度,使得让路船采取转向避碰决策时满足:1)与各目标船间的碰撞危险度尽量减小;2)转向避碰幅度尽量小;3)尽量减小转向到复航过程中的航程损失[21]。
2.1 碰撞危险度目标函数确定了最近会遇距离(DCPA)、最近会遇时间(TCPA)、两船距离、相对方位、船速比5个主要因素的隶属度函数,并考虑航行区域状况、能见度情况和船舶的操纵性能等对船舶碰撞危险度的隶属度函数修正。因此,设碰撞危险度目标函数为
| ${f_1}({x_i}) = \mathop {\max }\limits_{i = 1}^N {f_i}({u_{{d_i}}},{u_{{\theta _i}}},{u_{{K_i}}},{u_{{d_{CP{A_i}}}}},{u_{{t_{CP{A_i}}}}}){\text{。}}$ | (19) |
式中:
航海避碰实践中,考虑到《国际海上避碰规则》对避碰行动“大幅度”的要求,航向变化至少为30°;考虑到要减小航程损失,要求转向幅度尽可能小。因此,航程损失目标函数为
| ${f_2}({x_i}) = \frac{1}{{60}} \times ({x_i} - 30)(90 - {x_i}){\text{。}}$ | (20) |
式中:xi为转向幅度,向右为“+”,向左为“–”;
假设上述多目标函数函数权重分配为8:2,则转向避碰目标函数为
| $f = \sum\limits_{i = 1}^N {\left\{ {1{\rm{ - }}\left[ {0.8{f_1}({x_i}){\rm{ + 0}}{\rm{.2}}{f_2}({x_i})} \right]} \right\}}{\text{。}} $ | (21) |
克隆选择算法(Clonal Selection Algorithm)是模拟免疫系统防御外来侵袭的一种学习进化过程。免疫克隆选择算法是通过无性繁殖(克隆、变异)连续传代形成群体,通过抗体克隆群的变异来提高免疫力(亲和度)从而实现种群的进化。克隆选择算法虽然克服了遗传算法局部搜索能力差且常出现进化缓慢现象的问题,但是用较小的变异概率来提高局部搜索能力,降低了全局搜索能力;而较大的变异概率虽然全局寻优速度提高,但收敛的精度下降。因此,其全局搜索能力和局部搜索能力矛盾。
3.2 分级变异动态克隆选择算法采用[0,1]区间内的浮点数编码,以搜索全局最优解为目标,依据抗体与抗原的亲和度将种群分化为功能不同的子种群,高亲和度抗体在较小领域内精细搜索局部最优解,中亲和度抗体在较大邻域进行全局粗搜索,低亲和度抗体则死亡并随机再生以保持种群多样性,且在进化中动态调整参数[22]。
设第g代抗体群
设
已知本船为“育鲲”轮在开阔水域,以航向000°,航速15 kn航行,本船船长为116 m,满载排水量为5 778.8 t,此时海上能见度良好,船舶操纵者驾驶状况良好(取K1=1,K2=1,K3=1)。他船船长152 m,满载排水量为9 879.6 t。与3艘目标船(TS1,TS2,TS3)形成多船会遇态势,存在碰撞危险且本船为让路船,采取转向避碰决策。本船与目标船的会遇态势如表1所示。
|
|
表 1 本船与多目标船会遇态势 Tab.1 Multi-ship encounter situation |
初始种群规模设为N0=100,初始克隆数目nc0=10,对于多目标函数,初始变异尺度变换因子n10=0.05,n20=1.5,分级变异概率为
该算法随机独立运算100次,算法性能评价准则采用计算量和阻滞次数表示。目标函数变量范围在[30,90],目标函数评估次数为12 596±2 153,阻滞次数为0次。
|
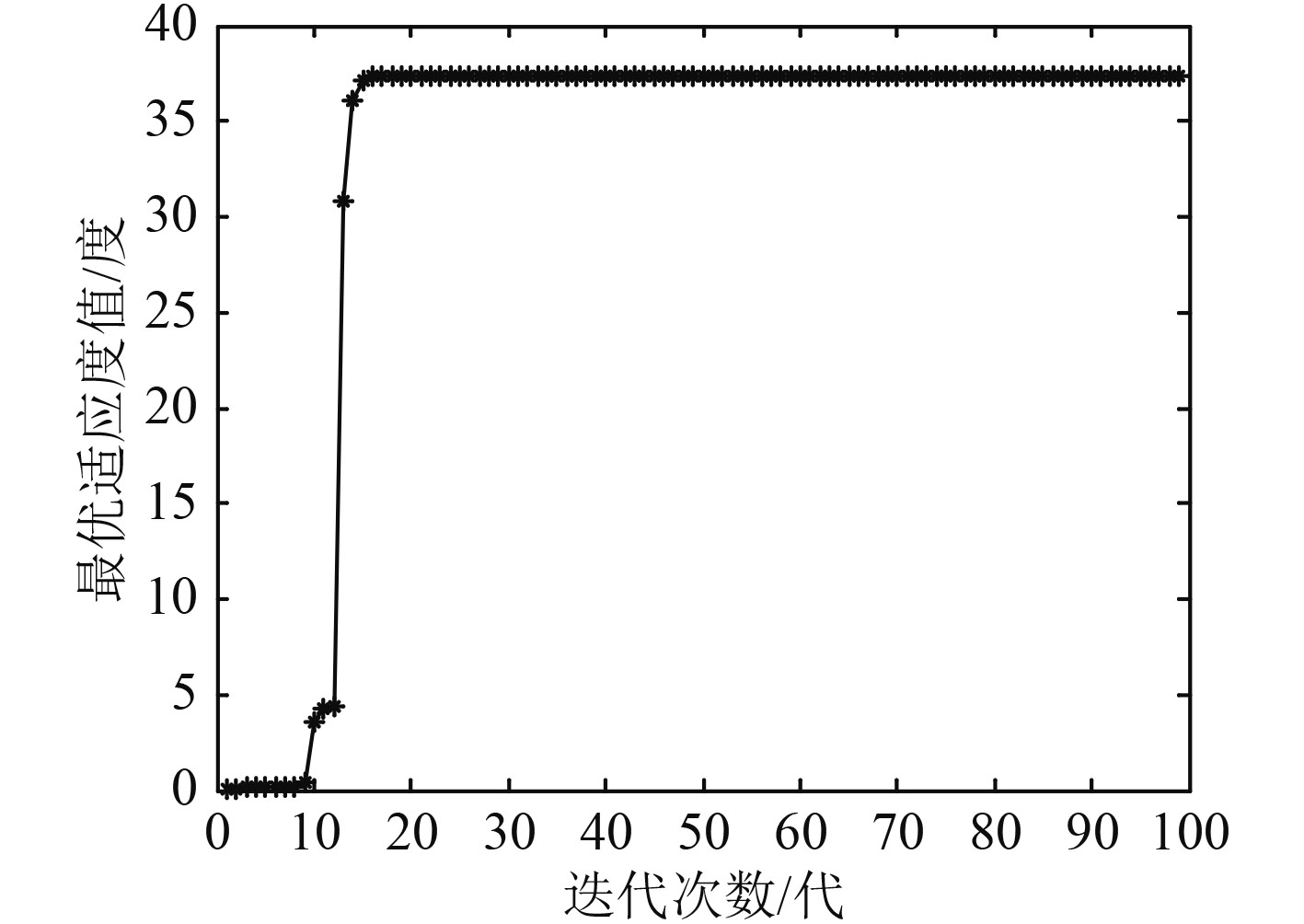
图 1 最优解迭代变化 Fig. 1 Optimal evolution for iteration |
可知分级变异克隆选择优化算法计算量小,算法稳定。图1为各代最优解,即本船最优转向避碰幅度。最终结果收敛于某个固定值,100代内能够快速趋于稳定,收敛速度快,算法执行耗时4~10 s,能够保证多船避碰决策的实时性。结果表明,本船作为让路船在该会遇态势下应向右转向约38.5°。转向后,本船对各目标船(按TS1,TS2,TS3顺序)的碰撞危险度分别为(0.233 8,0.334 6,0.273 7),船舶间碰撞危险度均明显减小,能够有效避免碰撞。
5 结 语将分级变异动态克隆选择优化算法应用到多船转向避碰决策研究中,综合考虑影响船舶转向避碰幅度的多种因素,在《国际海上避碰规则》作为可行域约束的限制条件下,建立了相应合理的多目标函数,并考虑到各种因素之间的差异,对目标函数进行权重分配,使模型更加符合航海实际。结果表明:该算法可行、有效、能满足实时决策等要求,为船舶驾驶员提供转向避碰决策支持。
| [1] | AHNA J H, RHEE K P, YOU Y J. A study on the collision avoidance of a ship using neural networks and fuzzy logic[J]. Applied Ocean Research, 2012 (37): 162–173. |
| [2] | 孙立成, 王逢辰, 夏国忠, 等. 驾驶员避碰行为的统计研究[J]. 大连海事大学学报, 1996, 22 (1): 1–6. |
| [3] | 江立军, 郑凯, 王国峰, 等. 现代船舶避碰系统研究进展[J]. 上海船舶运输科学研究报, 2015 . |
| [4] | 邹晓华, 倪天权. 遗传算法在船舶转向避碰幅度决策中的应用研究[J]. 舰船电子对抗, 2006 . |
| [5] | 何祖军, 齐亮. 基于蚁群算法的AUV动目标避碰规划的方法研究[J]. 舰船科学技术, 2007, 06 : 86–89. |
| [6] | 王得燕, 刘以安. 粒子群算法在多船避碰决策中的应用[J]. 计算机工程与设计, 2009, 14 : 3380–3382. |
| [7] | 刘以安, 刘静, 吴洁, 等. 模拟退火算法在船舶转向避碰幅度决策中的应用[J]. 中国造船, 2007 . |
| [8] | HASEGAWA K, FUKUTO J. An intelligent ship handling simulator with automatic collision avoidance function of target ships [C]// INSLC 17-International Navigation Simulator Lecturers’ Conference. Rostock, Germany, 2012: F23-1–10. |
| [9] | 鹤田三郎. 船舶航行专家系统的基础研究[J]. 国外航海科技, 1988 (5): 55–58. |
| [10] | 王敬全. 船舶避碰专家系统[M]. 广州: 海军广州舰艇学院出版社, 1994. |
| [11] | 李丽娜, 杨神化, 曹宝根, 等. 船舶避碰智能决策自动化研究[J]. 集美大学学报(自然科学版), 2006 (2): 188–192. |
| [12] | 吕红光, 尹勇, 尹建川. 混合智能系统在船舶自动避碰决策中的应用[J]. 大连海事大学学报, 2015 (4): 29–36. |
| [13] | 史国友, 贾传荧. 航海模拟器中DCPA TCPA的算法[J]. 大连海事大学学报, 1999 (3): 17–20. |
| [14] | BUKHARI A C, TUSSEYEVA I, LEE Byung-gli, et al. An intelligent real-time multi-vessel collision risk assessment system from VTS view point based on fuzzy inference system[J]. Expert Systems with Applications, 2013 : 1220–1230. |
| [15] | FENG Ming-kui, LI Yong-jin. Ship intelligent collision avoidance based on maritime police warships simulation system [C]// IEEE Symposium on Electrical & Electronics Engineering (EEESYM). Kuala Lumpur, Malaysia, 2012: 293–296. |
| [16] | KOIKE T, OKAZAKI T. Development of ship simulator system for designing auto-pilot [C]// World Automation Congress (WAC). Kobe, Japan, 2010: 1–5. |
| [17] | SUI Jiang-hua. An AND-OR fuzzy neural network, ant colony optimization-methods and applications [C]// IEEE International Conference on Robotics and Biomimetic. Sanya, China, 2007: 1194–1199. |
| [18] | 薛彦卓, 魏伊, 孙淼. 基于避碰重点船算法的多船避碰模拟[J]. 大连海事大学报, 2014 (1): 13–16. |
| [19] | HASEGAWA K. Automatic collision avoidance system for ship using fuzzy control [C]// Proc Eighth Ship Control Systems Symposium (SCSS). The Hague, Netherlands, 1987: 34–58. |
| [20] | 于家根, 刘正江, 卜仁祥, 等. 基于拟态物理学优化算法的船舶转向避碰决策[J]. 中国航海, 2016 (1): 36–38, 109. |
| [21] | 胡江强, 郭晨, 尹建川, 等. 分级变异的动态克隆选择算法[J]. 控制与决策, 2007 (6): 608–612. |
 2018, Vol. 40
2018, Vol. 40
