2. 海军九〇二厂,上海 200083
2. Navy 902 Factory, Shanghai 200083, China
船舶运动模型的建立是船舶控制的基础工作,对于控制方法的研究以及自动舵的研制和陆基条件下的检测具有重要意义。中低速船运动过程中横摇角较小,对首摇运动的耦合作用可忽略不计,进行仿真试验时可只考虑包括横荡、纵荡、首摇的平面运动三自由度模型。然而高速舰船的操纵性和普通中低速船较为不同,回转运动中横摇角的幅值较大,对首摇运动的回转力矩产生一定的影响,使用三自由度模型进行仿真会产生较大的误差。为了全面精确地进行船舶操纵运动仿真,必须建立四自由度运动模型。目前,考虑横摇耦合的四自由度运动还没有一个统一的数学模型,常见的有孙景浩提出的和平野提出的两类模型[1]。本文使用平野给出的四自由度模型对DTMB5415船进行操纵运动仿真试验,将2次仿真结果与水池试验数据进行对比及误差分析, 验证了该数学模型的适用性。
另一方面,现实中船舶航行时会受到风浪流等环境干扰的影响,其中波浪干扰最为复杂,干扰作用也最为明显。波浪干扰不仅会使船舶的航迹产生漂移,还会引起摇荡运动,其中对横摇的影响尤为明显[4]。对于波浪中的船舶操纵性能,Kijima[2]建立了1阶及2阶波浪力影响下的四自由度船舶运动模型,Yasukawa[3]对S175船进行了波浪中的自航模试验及基于MMG的仿真回转试验。本文在上述研究的基础上建立了海浪干扰力模型,对DTMB5415船在随机波浪干扰下的运动进行仿真,分析了波浪对高速舰船操纵运动的影响。
1 静水中的船舶运动模型三自由度的MMG模型如下所示:
| $\left\{ {\begin{array}{*{20}{l}}{(m + {m_x})\dot u - (m + {m_y})vr = {X_H} + {X_P} + {X_R} + {X_W}}\text{,}\\{(m + {m_y})\dot v + (m + {m_x})ur = {Y_H} + {Y_R} + {Y_W}}\text{,}\\{({I_{ZZ}} + {J_{ZZ}})\dot r = {N_H} + {N_R} + {N_W}}\text{。}\end{array}} \right.$ | (1) |
式中:下标H,P,R,W分别为船体水动力,桨的推进力,舵力及波浪干扰力。
平野模型在三自由度MMG模型的基础上给出了横摇模型,并且考虑了横摇耦合对横向流体动力YH及NH的影响,将这2项分解为受到横摇耦合影响和不受横摇影响的2项,即
| $\left\{ {\begin{array}{*{20}{l}}{{Y_H} = {Y_0}(v,r) + {Y_1}(v,r,\phi )}\text{,}\\{{N_H} = {N_0}(v,r) + {N_1}(v,r,\phi ) - {Y_H} \cdot {x_C}}\text{。}\end{array}} \right.$ | (2) |
式中:Y0,N0为横摇角为0时的流体动力及力矩,依照三自由度模型的估算方法进行计算;Y1,N1即为横摇耦合造成的附加力和力矩,由平野的研究有:
| $\left\{ {\begin{array}{*{20}{l}}{{Y_1}(v,r,\phi ) = 0}\text{,}\\{{N_1}(v,r,\phi ) = {N_\phi }\phi + {N_{v\phi }}v\left| \phi \right| + {N_{r\phi }}r\left| \phi \right|}\text{。}\end{array}} \right.$ | (3) |
其中,水动力系数
平野给出横摇自由度的动力学方程如下式:
| $({I_{xx}} + {J_{xx}})\ddot \phi = {L_H} + {L_R} + {L_W}\text{。}$ | (4) |
式中:LH由横摇阻尼力矩、恢复力矩及横向流体动力YH对x轴的力矩这3项组成,如下式所示:
| ${L_H} = - N(\dot \phi ) - W \cdot GZ(\phi ) - {Y_H} \cdot {z_H}\text{。}$ | (5) |
横摇阻尼力矩当横摇角在10°以内时,可采用线性横摇阻尼力矩的形式进行计算,即
理想流体中,船舶在波浪中的运动可以看作是高频运动和低频运动的叠加[5]。1阶波浪力即高频波浪干扰力,主要引发船舶的摇荡运动,而对于纵荡、横荡和首摇运动的影响较小。2阶波浪力即波浪漂移力,与波高的平方成正比。波浪漂移力是非线性的,具有慢时变特性,对于船舶航向航迹变化的影响较大。综上,本文对于平面运动的3个自由度方程只考虑2阶波浪漂移力的影响而对于横摇方程仅考虑1阶波浪干扰力的影响[6]。
2.1 不规则波的数学描述不规则波主要是采用线性叠加原理来进行描述,即可以将不规则波的波面看作由一系列不同频率、波数、波幅以及初相位角和传播方向的规则波叠加而成。通过余弦序列权重系数法可以由波谱密度得到波面历时值:
| $\zeta (t) = \sum\limits_{i = 1}^m {\sqrt {2{S_\zeta }({\omega _i})\Delta \omega } } \cos (\frac{{{\omega _i}^2}}{g}\xi - {\omega _i}t + {\varepsilon _i})\text{。}$ | (6) |
式中:波谱密度
| ${S_\xi }(\omega ) = \frac{A}{{{\omega ^5}}}\exp ( - \frac{B}{{{\omega ^4}}})\text{。}$ | (7) |
式中:参数
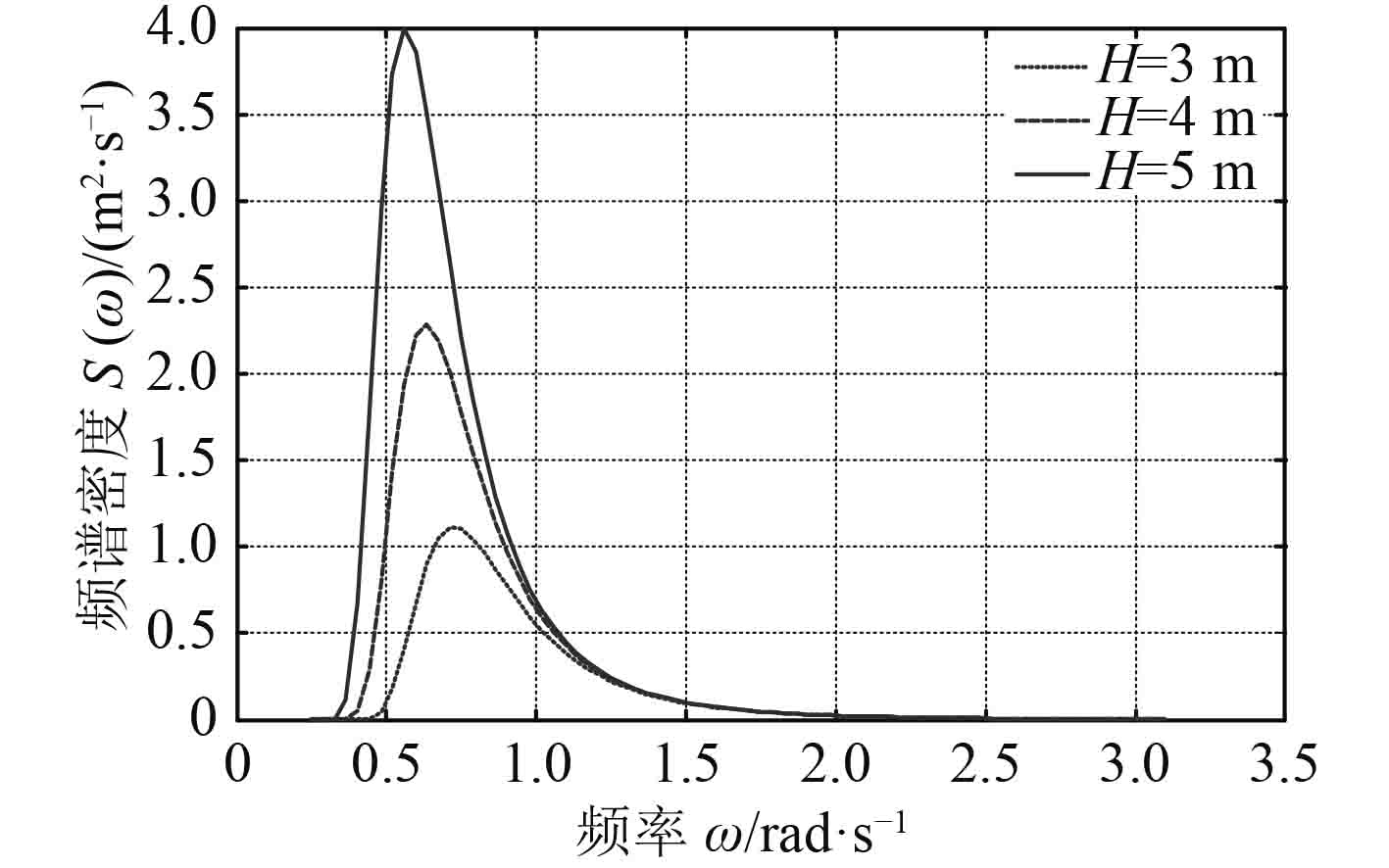
|
图 1 海浪波谱密度曲线 Fig. 1 The spectrum curve of wave |
对于1阶波浪干扰力,目前有2种较为常用的方法,一种是应用长峰波随机海浪叠加原理求解,另一种是通过脉冲响应求解。本文使用第1种方法。由于1阶波浪力对船舶平面运动的影响很小,故只对横摇这一个运动模态下的干扰力进行计算:
| ${L_{wave}}(t) = \sum\limits_{i = 1}^n {{L_{wave}}({\omega _i}) \cdot \zeta (t)}\text{。} $ | (8) |
式中,
由于不规则波可以看作是各种频率的规则波的叠加,可以通过叠加的方法计算不规则波的波浪漂移力。
| $\left\{ {\begin{array}{*{20}{c}}{X_{wave}^D = \frac{1}{2}\rho L\cos \chi \sum\limits_{i = 1}^m {C_{Xw}^D({\lambda _i}){a_i}^2} }\text{,}\\{Y_{wave}^D = \frac{1}{2}\rho L\sin \chi \sum\limits_{i = 1}^m {C_{Yw}^D({\lambda _i}){a_i}^2} }\text{,}\\{N_{wave}^D = \frac{1}{2}\rho {L^2}\sin \chi \sum\limits_{i = 1}^m {C_{Nw}^D({\lambda _i}){a_i}^2} }\text{。}\end{array}} \right.$ | (9) |
式中:ai为波幅,可由波谱密度函数得到;χ为波浪遭遇角,考虑深水波时,
本文以DTMB5415驱逐舰作为研究对象进行仿真试验。该船主要参数如表1所示[7]。
|
|
表 1 DTMB5415船主要参数 Tab.1 The major parameters of ship DTMB5415 |
使用Simulink作为仿真平台,将船舶运动模型分为推进系统模型、舵系统模型、船体水动力模型及波浪干扰力模型、波浪漂移力模型等几个模块,仿真原理框图如图2所示。
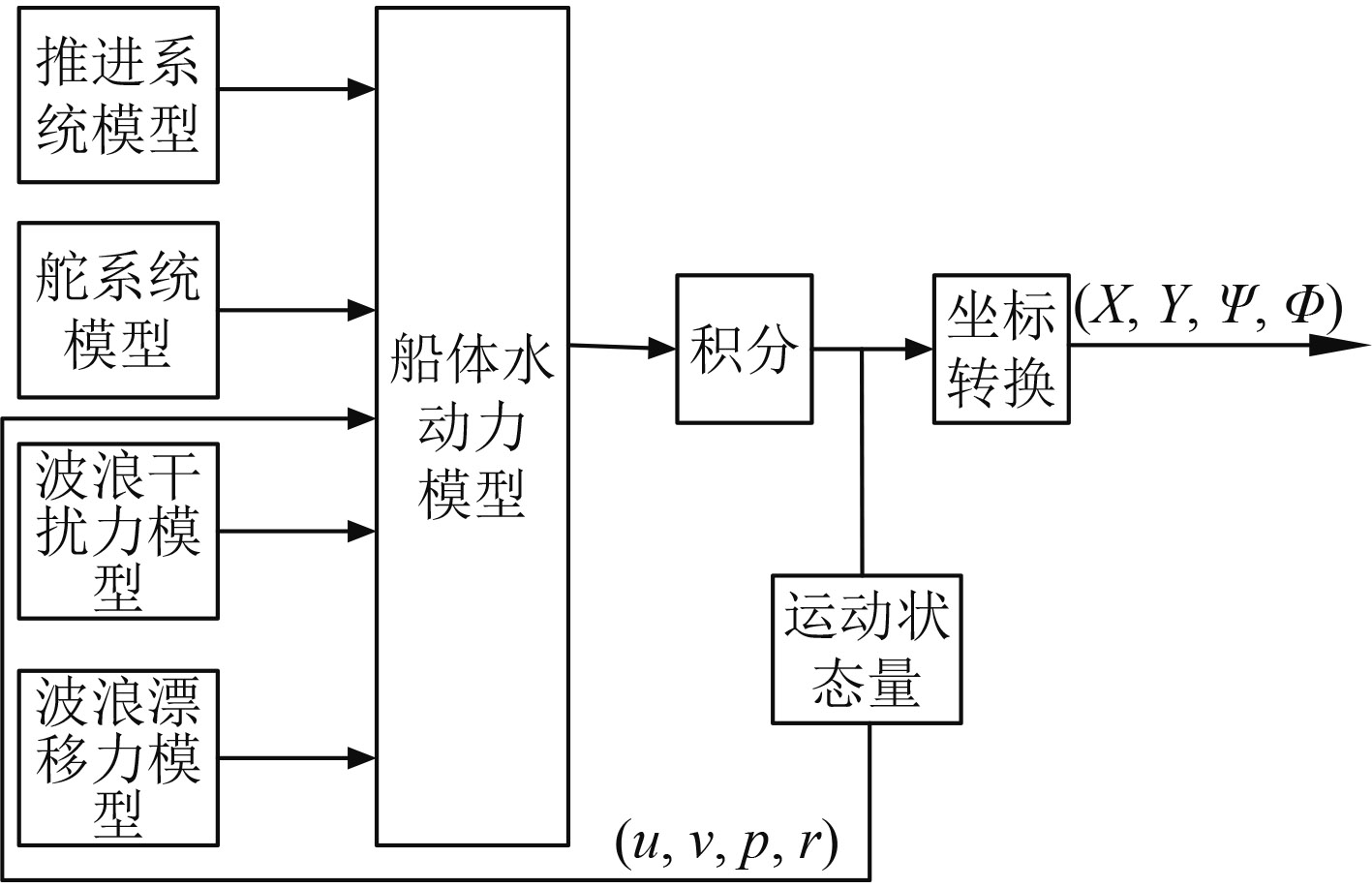
|
图 2 仿真原理框图 Fig. 2 The block diagram of simulation |
静水中对DTMB5415船分别在不考虑横摇运动及考虑横摇运动耦合2种情况下进行回转操纵仿真试验并且将2次仿真实验结果与水池试验数据进行对比。航速设定为最大航速30 kn,转舵速率为9(°)/s,指令舵角分别设定为35°和25°。仿真实验结果如下:

|
图 3 35°舵角下DTMB5415船的回转运动仿真图 Fig. 3 The simulation diagram of DTMB5415 under the rudder angle of 35° |
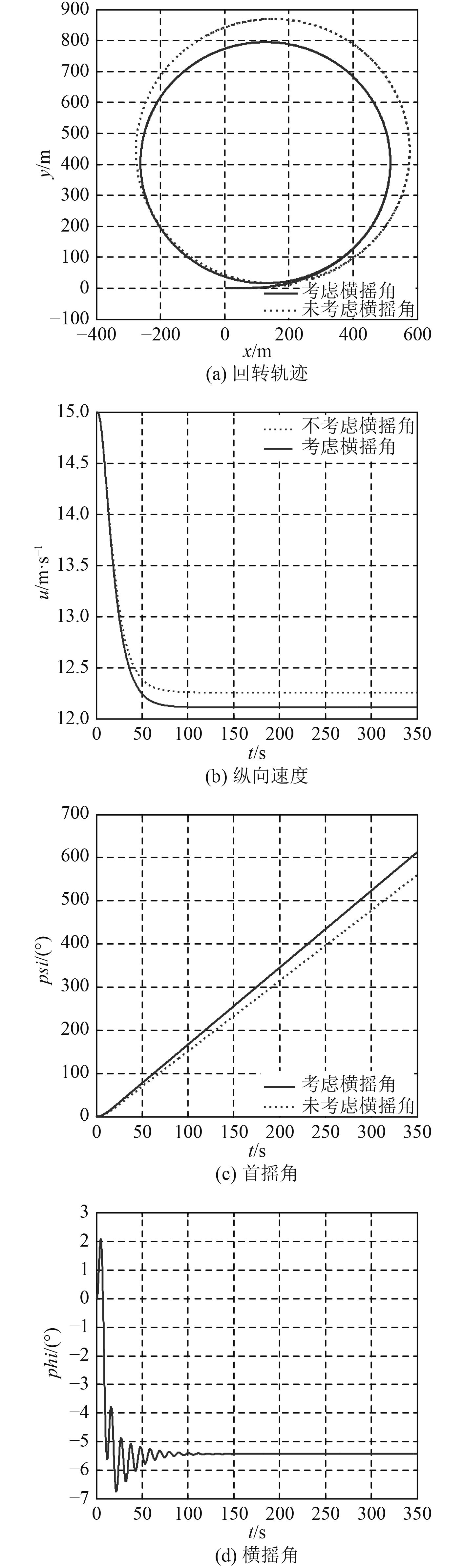
|
图 4 25°舵角下DTMB5415船的回转运动仿真图 Fig. 4 The simulation diagram of DTMB5415 under the rudder angle of 25° |
回转过程中横摇角的变化如图3(d)及图4(d)所示,船舶回转过程中的横摇角呈周期性变化规律。转舵阶段由于作用于船舶重心的横向惯性力指向内侧,作用于舵面积中心的横向舵力指向外侧,故产生短时间的船舶内倾。过渡阶段,伴随角速度及漂角的增大,船体惯性力变化为指向外侧,与横向舵力方向相同,但由于其数值相比舵力要大得多,船舶会产生外倾。定常回转阶段横摇角趋于稳定。当船舶进入定常回转阶段,横摇角的变化率,横向加速度以及首摇角加速度均为0。忽略舵力的影响,可近似认为作用于船体的惯性力引起了船舶的横倾外力矩。
由图3和图4可以看出,横摇耦合对DTMB5415船的回转运动仿真结果有较为明显的影响。为验证仿真实验的可行性,以进距(AD)和战术直径(TD)作为回转运动主要特征参数,将水池试验[7]得到的数据均值与2次仿真实验的结果进行比较并进行误差分析。比较结果如表2所示。
|
|
表 2 水池试验与两次仿真实验结果 Tab.2 Results of pool test and two simulation experiments |
由表2可以看出,横摇运动对于首摇运动的影响主要是增大了船体水动力对于Z轴的回转力矩,从而增大了回转角速度,减小了回转半径。不考虑横摇耦合的情况下仿真实验相对水池试验的误差超过了10%。考虑横摇运动耦合的影响,仿真实验相对水池试验的误差下降到5%以内,上述对比结果反映了横摇耦合对高速舰船回转性的影响,同时验证了仿真实验方法的可行性。
3.2 波浪干扰下的船舶回转运动仿真在上述仿真实验的基础上加上波浪干扰作用,对DTMB5415船进行波浪中的直航运动仿真。设定航速30 kn,初始遭遇角χ为90°,有义波高分别为4 m和5 m,船舶直航时横摇角的变化曲线如图5所示。
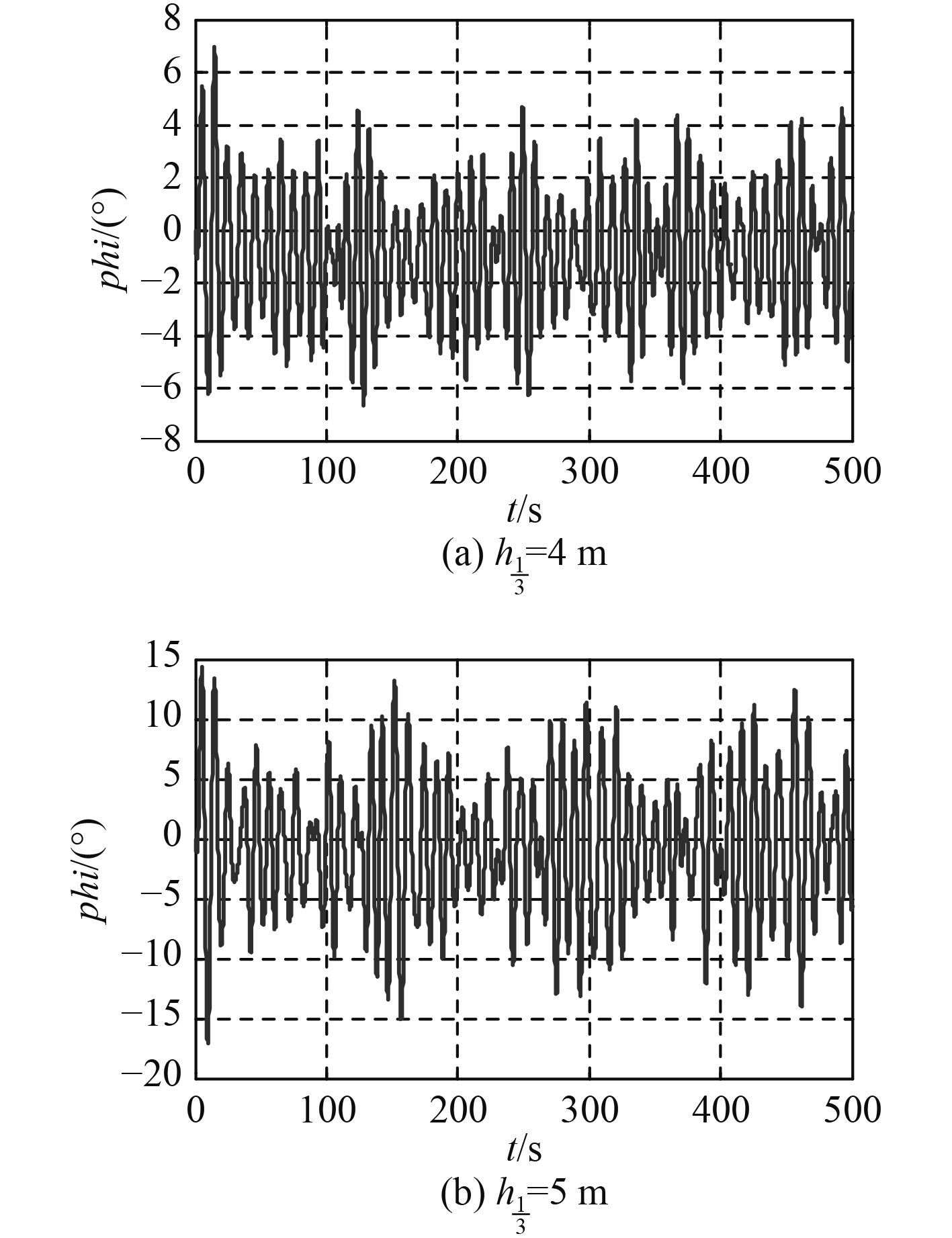
|
图 5 波浪干扰下DTMB5415船的横摇角变化曲线 Fig. 5 The curve of rolling angle of ship DTMB5415 under the wave interference |
如图5所示,直航时横摇角的变化幅度随时间变化,这是由于波浪漂移力的作用使首摇角发生偏移,导致波浪遭遇角的变化,使得波浪对船体干扰的幅度大小产生变化。另外,由于初始阶段船舶的非线性阻力较小,可以看出横摇幅值较大。比较图5(a)和图5(b)可以看出有义波高为较大时,横摇角幅度明显增大。
对DTMB5415船进行波浪中的回转运动仿真。设定有义波高4 m,初始航速30 kn,舵角35°,舵速为9(°)/s,初始遭遇角χ分别为45°和90°。船舶回转运动轨迹及横摇角变化曲线如图6所示。
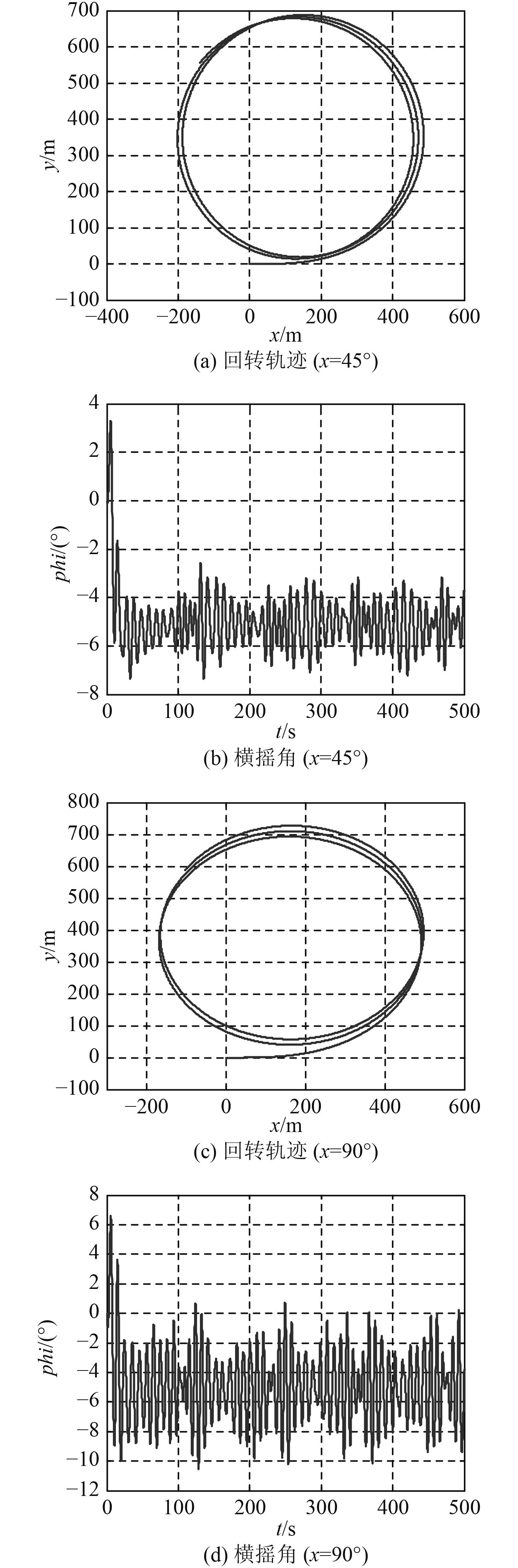
|
图 6 波浪干扰下DTMB5415船回转运动仿真图 Fig. 6 The simulation diagram of ship DTMB5415 under the wave interference |
由图6可见,在波高4 m,不同初始遭遇角的不规则波浪中,由于船体水动力、舵力以及1阶波浪干扰力的作用,船舶在稳定横摇角周围进行幅值不定的摆动。其横摇幅值随遭遇角的变化而改变,可以看出,横浪中的横摇幅值较首尾斜浪中的横摇幅值要大。另一方面,可以看出船舶由于波浪漂移力的作用,回转轨迹都产生了明显的偏移, 偏移方向由初始遭遇角决定。
4 结 语本文通过Matlab对DTMB5415船分别进行了三自由度运动建模以及加入横摇的四自由度运动建模,通过仿真操纵实验得到了回转运动过程中的纵向速度、首摇角、横摇角等运动状态量,分析了回转运动中横摇角的变化规律,可以看出对于高速舰船,大舵角回转时的稳定横摇角可以达到5°以上。另一方面,横摇运动耦合作用增大了绕Z轴的回转力矩。通过将不同舵角下加横摇、不加横摇2次仿真的回转圈的特征参数与水池试验结果进行对比及误差分析,可以看出:由于回转过程中较大的横摇角,三自由度运动方程已不能够满足实用的要求,加横摇运动模型相对于水池试验结果的误差比不加横摇的三自由度运动模型大大降低。
在上述模型的基础上叠加波浪力和力矩,模拟不同初始遭遇角的波浪干扰下的船舶直航运动和回转操纵运动,对比分析了不同运动状态下船舶横摇角和回转圈的变化规律,为进一步研究高速舰船的操纵性及运动控制打下了基础。
| [1] | 贾欣乐, 杨盐生.舰船运动数学模型 [M].大连: 大连海事大学出版社, 1999. |
| [2] | KIJIMA K, FURUKAWA Y. Ship maneuvering performance in waves[C]//3rd International Stability Workshop, 1997. |
| [3] | YASUKAWA H, et al. Simulations of ship maneuvering in waves(1st report: turning motion)[J]. Journal of the Ship and Ocean Engineering Society of Japan, 2006 (4): 163–170. |
| [4] |
尹茜, 陈红卫. 随机海浪下船舶摇荡的计算机仿真[J]. 微电子学与计算机, 2007, 24 (6): 191–193.
Yin Qian, Chen Hong-Wei. The simulation of ship’s motion on random wave[J]. Microelectronics & Computer, 2007, 24 (6): 191–193. |
| [5] | NONAKAK. On the maneuvering motion of a ship in waves[J]. Transaction of the West–Japan Society of Naval Architects, 1991 (80): 73–86. |
| [6] | 陶尧森. 船舶的耐波性[M]. 上海: 上海交通大学出版社, 1985. |
| [7] | SERGE T, FRANS V W, RINK H. Manoeuvring and seakeeping tests for 5415M [R]. Maritime Research Institute (MARIN), Wageningen/Delft University of Technology, The Netherlands Maritime Research Institute (MARIN), Wageningen. |
| [8] |
陈宁, 龚苏斌. 船舶回转运动仿真[J]. 舰船科学技术, 2013, 35 (3): 9–14.
CHEN Ning, GONG Su-bin. The research on the ship turning movement based on Simulink[J]. Ship Science and Technology, 2013, 35 (3): 9–14. |
 2018, Vol. 40
2018, Vol. 40
