近年来,高速船在商业和军事领域得到广泛应用,备受关注[1]。由于高速船船体刚度比其他常规舰船船体刚度小,高频率的激振引起的船体振动幅值也比其他常规舰船振动幅值大很多,从而影响高速船舶的结构强度与疲劳强度,因此高速船的振动问题比其他常规舰船的振动问题更为复杂与敏感[2]。在以往的船舶振动研究中,大多数是针对常规舰船振动问题的计算或研究,而对于高速船舶的振动问题研究较少。本文着眼于高速船舶领域,针对某一船型,结合其船体结构特点及振源类型,采用有限元模态计算分析对振动问题比较敏感的位置进行振动强度评估,对高速船型船体振动的评估校核及高速船舶的设计具有借鉴意义。
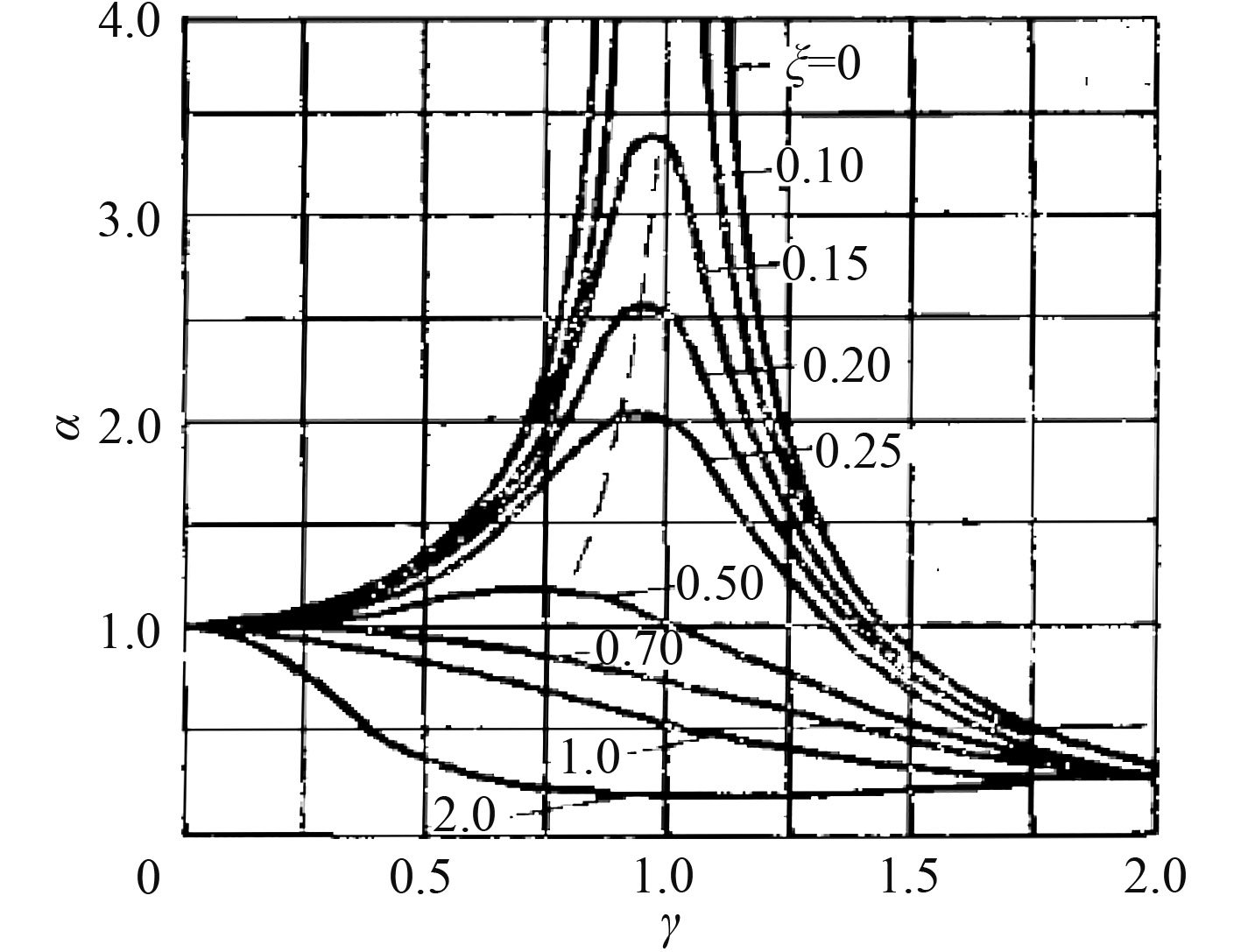
1 高速船振动衡量准则 1.1 固有频率储备衡量准则在高速船振动问题的研究过程中,根据船舶类型明确其主要激振源,从而确定激振源的额定频率。激振源频率与船体结构固有频率的比值γ对动力放大系数α的影响如图1所示,此曲线为振动位移幅值的频率响应曲线,也称为共振曲线[3]。
|
图 1 幅频响应曲线 Fig. 1 Amplitude-frequency response curve |
从图1中可以看出,当γ接近1时,即激振力频率接近结构固有频率时,动力放大系数α将急剧增加,并且达到最大值,即出现共振现象;若γ很小或γ很大时,则动力放大系数α比较小,此时激振力的作用可视为静力作用,故在CCS《船上振动控制指南》等相关的文献中,选取的共振的区域为γ接近于1的范围[4]。又由于在共振区域中,振幅的大小与阻尼有关,因此对于不同的船体结构,根据阻尼的不同,选取的γ范围也有所不同。
一般把
其中,fi为船体结构的固有频率,Hz;fe为激振力额定频率,Hz。
按照《舰船通用规范》中对不同船体结构频率储备的要求,高速船的固有频率值应满足下式要求:
| $\frac{1}{\gamma } \leqslant 0.6\text{或}\frac{1}{\gamma } \geqslant 1.3{\text{。}}$ |
目前,在国内的船体规范中尚未提供明确的高速船振动响应衡量准则,所以在对高速船的振动响应进行校核时,本文借鉴DNV《Rules for Classification of High Speed, Light Craft and Naval Surface Craft》对于高速船振动响应进行衡准[5]。
|
|
表 1 对船舶不同区域适居性评价准则 Tab.1 The habitability evaluation criteria of the different regions for ship |
本文以国内某气垫船为例,根据其振源类型,针对其尾部的桨塔与发动机短舱振动敏感位置进行振动问题研究。根据CCS《船上振动控制指南》的相关规定,在计算船舶局部结构的固有频率时,如梁、板、板架等不是孤立结构,而是与其他结构相连接,它们的边界条件严格地讲是弹性固定边界条件。为了计及相邻构件的影响,在有限元计算中将其相邻构件也计入有限元模型之内进行计算,然后再分离出指定结构得到其固有振动频率[6]。根据上述建模原则,计算模型选取该气垫船的整个型深及型宽,型长跨过振源范围[7]。
在短舱结构内,按照推进主机基座的结构图纸对主机基座进行有限元建模,在推进主机重心位置建立MPC点与推进主机基座相连,将推进主机重量施加到MPC点上。对于其他设备,如带导流罩的空气螺旋桨、空气螺旋桨的传动装置、导管、舵等均在其重心位置建立MPC进行配重,从而实现与实船重量分布相同。
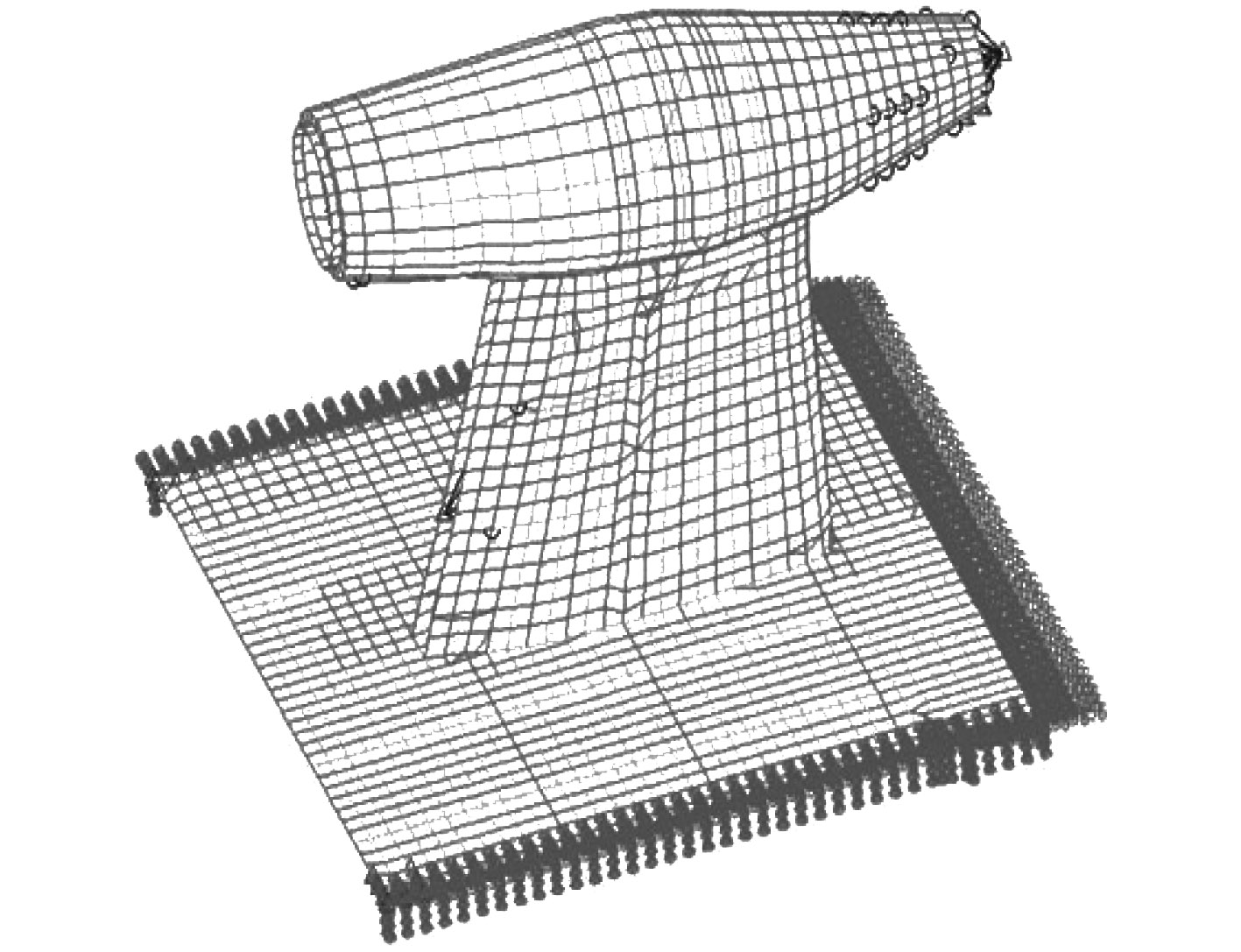
在计算桨塔与发动机短舱舱段固有频率时,对其下方边界进行刚性固定[8],如图2所示。
|
图 2 边界条件示意图 Fig. 2 Schematic diagram of boundary condition |
桨塔与短舱结构的固有频率计算结果见表2,有限元模型及振型如图3~图6所示。表中各符号的含义如下:
fi为结构固有频率;fet为推进主机额定频率;fez为螺旋桨轴频率;fey为螺旋桨叶频率;YES为满足频率储备的要求;NO为不满足频率储备的要求。
|
|
表 2 固有频率计算结果 Tab.2 The result of inherent frequency |

|
图 3 f=2.748 Hz(横向振型) Fig. 3 f=2.748 Hz (transverse vibration mode) |
|
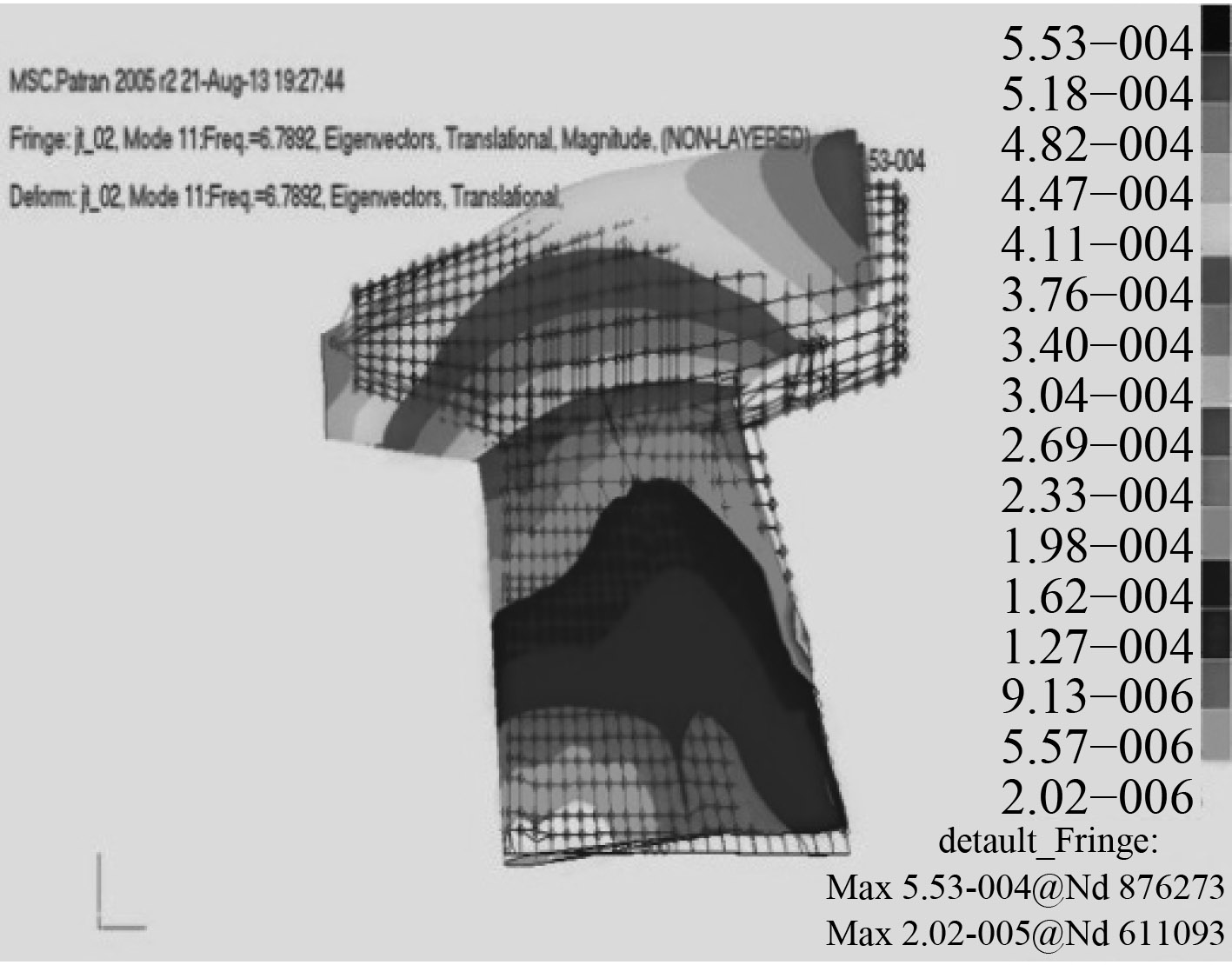
图 4 f=6.789 Hz(纵向振型) Fig. 4 f=6.789 Hz (longitudinal vibration mode) |
|
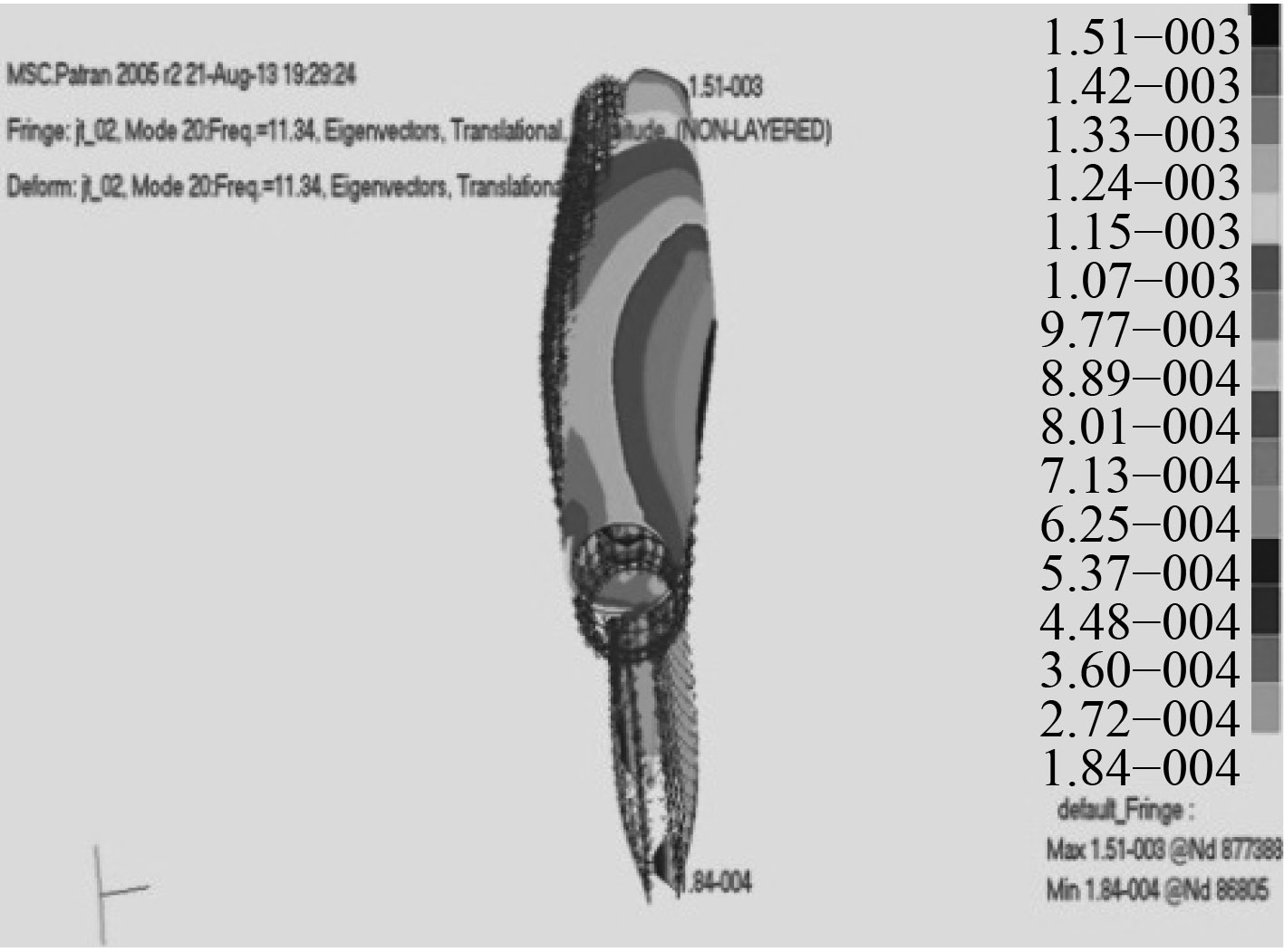
图 5 f=11.34 Hz(扭转振型) Fig. 5 f=11.34 Hz (retortion vibration mode) |
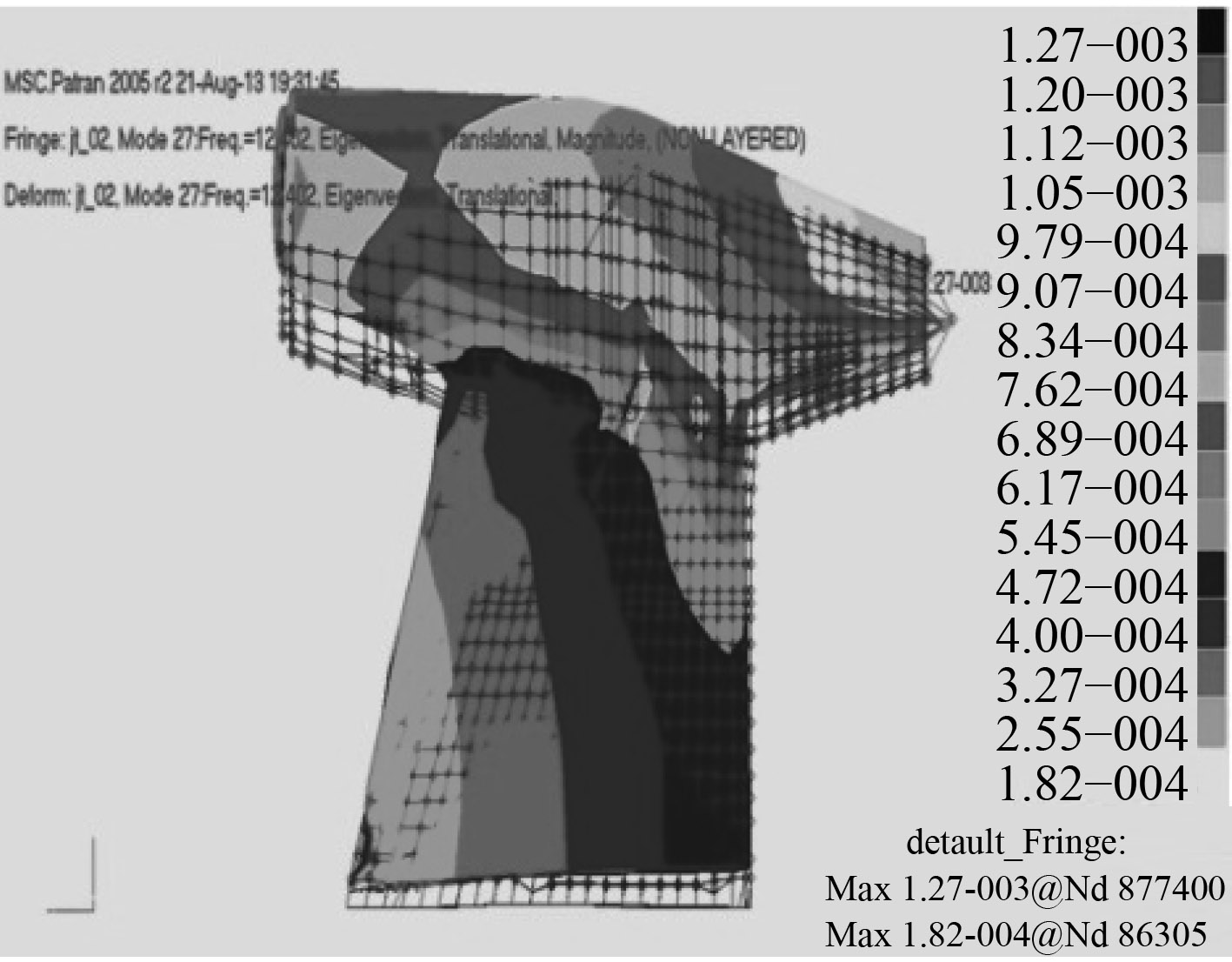
|
图 6 f=12.402 Hz(垂向振型) Fig. 6 f=12.402 Hz (vertical vibration mode) |
由上节固有频率计算结果可知,在空气螺旋桨的额定激振下,桨塔与发动机短舱结构不满足频率储备的要求,因此需要计算该局部结构在空气螺旋桨激振作用下的振动响应。振动响应是以桨塔与发动机短舱的有限元模型为计算模型,对其进行频域瞬态响应分析。在计算该结构在空气螺旋桨激振作用下的响应时,选取的计算频率为0~14 Hz(轴频)、0~54 Hz(叶频),计算频率的个数分别为35个、120个。最终提取桨塔与发动机短舱结构中频率储备较小区域单元的速度值与加速度值。
4.1 激振力的计算空气螺旋桨单个桨叶质量为
空气螺旋桨转子动量:
| $\vec P = mv\cos wt\vec i - mv\sin wt\vec j, $ |
| $\frac{{{\rm d}\vec P}}{{{\rm d}t}} = {F_X}\vec i + \left( {{F_y} - mg} \right)\vec j{\text{。}}$ |
所以转子动态激振力幅值
|
|
表 3 空气螺旋桨激振力数据 Tab.3 The excited force date of propeller |
在空气螺旋桨重心位置建立MPC点与短舱外壁相连,将空气螺旋桨不平衡力施加在空气螺旋桨重心处,通过MPC点传递给船体。具体作用形式如图7所示。
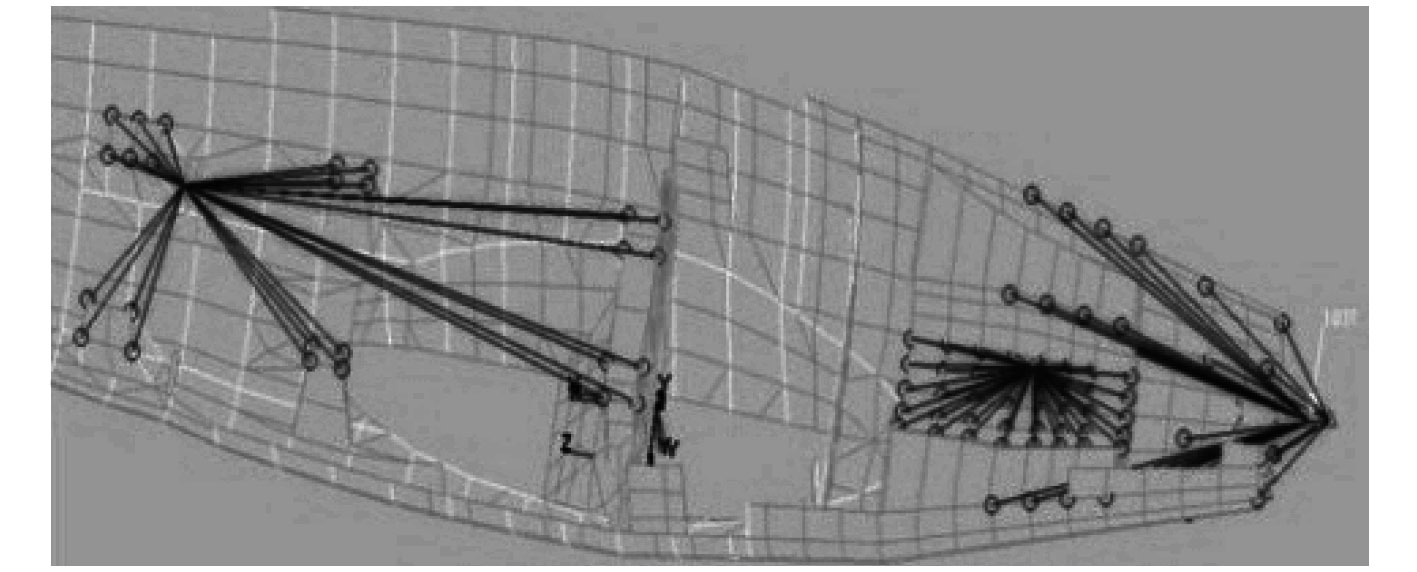
|
图 7 激振力施加示意图 Fig. 7 Schematic diagram of applying excited force |
根据上述振动响应计算模型的选取及激振力的详细确定,对桨塔与发动机短舱结构计算其在空气螺旋桨的振动响应分析。最终提取桨塔与发动机短舱结构中频率储备较小区域单元的速度值或加速度值。
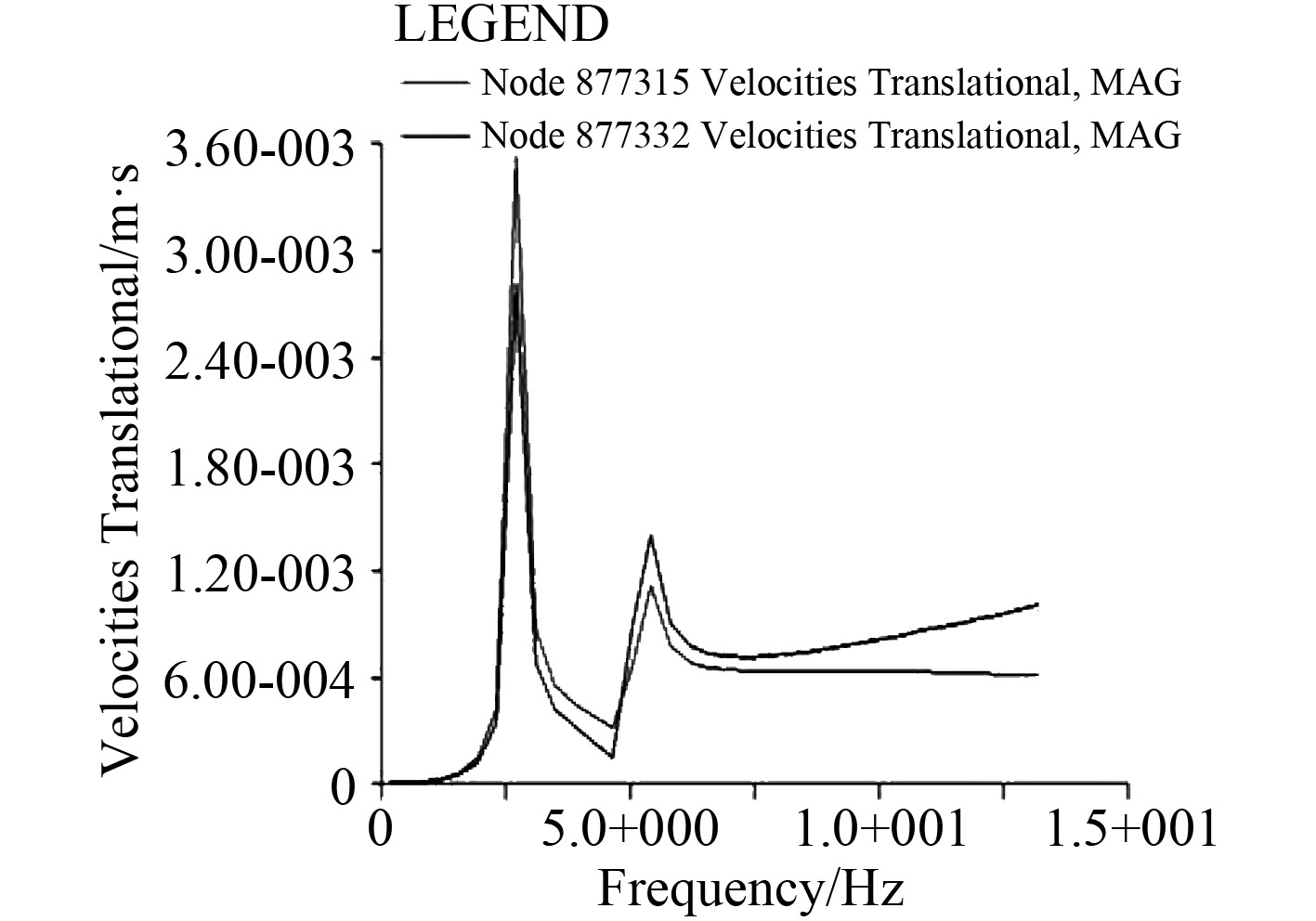
|
图 8 激振力下的速度响应曲线 Fig. 8 Velocity response curve |
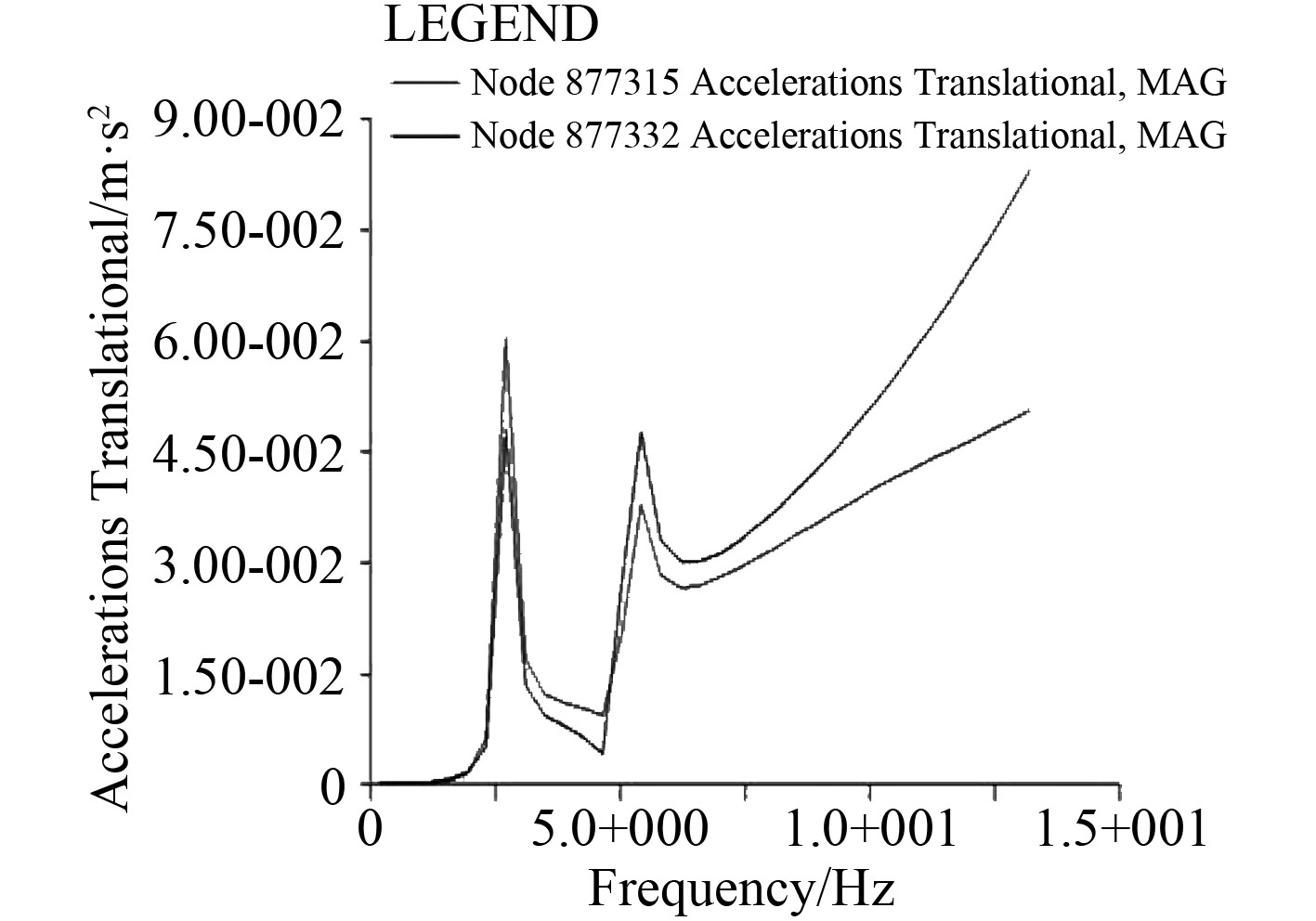
|
图 9 激振力下的加速度响应曲线 Fig. 9 Acceleration response curve |
|
|
表 4 振动响应计算结果 Tab.4 The calculation of vibration response |
由上述数据可知,气垫船桨塔与发动机短舱在空气螺旋桨的激振力作用下的加速度响应均小于
高速船的振动是一个十分复杂的问题,对其进行准确的预报是船舶设计成败的关键。本文采用有限元法进行模态分析对高速船局部结构进行了振动强度评估,按照《舰船通用规范》对于振动敏感位置进行按照固有频率的计算,对于不满足频率储备的局部结构进行振动响应分析,按照DNV《Rules for Classification of High Speed, Light Craft and Naval Surface Craft》进行衡准。本文为船舶设计人员在船舶设计建造中预报船舶振动强度提供了一条新的途径。
| [1] | 吴卫国. 高速船的振动特点及预报[J]. 江苏造船, 2008, 17 (4): 45–47. |
| [2] | 吴家鸣. 高性能船舶的类型及特点[J]. 广东造船, 2012, 4 : 2–5. |
| [3] | GJB4000-2000舰船通用规范[S]. 2000. |
| [4] | 中国船级社. 船上振动控制指南[S]. 北京:人民交通出版社, 2012. |
| [5] | DNV. Rules for Classification of High Speed, Light Craft and Naval Surface Craft [S]. July 2006. |
| [6] | 翁长俭. 我国船舶振动冲击与噪声研究进展[J]. 中国造船, 2009, 42 (3): 12–14. |
| [7] | 王昕. 高速船轻型结构声辐射的振动模态分析[D]. 武汉: 武汉理工大学, 2013. |
| [8] | 李宁. 具有弹性基础的气垫船细长轴系横向振动特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2007. |
 2018, Vol. 40
2018, Vol. 40
