2. 武汉理工大学 交通学院船舶、海洋与结构工程系,湖北 武汉 430063
2. Departments of Naval Architecture, Ocean and Structural Engineering, School of Transportation, Wuhan University of Technology, Wuhan 430063, China
当爆炸发生在舰船舱室内部时,由于冲击波传播过程中受到舱室壁面限制,将产生冲击的多次反射和汇聚,以及持续时间较长的准静态压力,对内部结构和人员产生更加严重的毁伤效应。近年来,国内外学者针对内爆炸特性和计算方法方面做了大量的研究工作。
WU等[1]开展了封闭舱室内爆炸实验,研究了炸药形状和起爆位置对爆炸冲击波载荷的影响规律。侯海量等[2] 实验研究了舱室内爆炸冲击波载荷特性。孔祥韶等[3]实验研究了药量、角隅结构形式对舱内爆炸载荷影响规律。侯海量等[4]采用MSC.DYTRAN软件数值研究了舱室内爆炸冲击波载荷特性。孔祥韶等[5]采用MSC.DYTRAN软件数值模拟了舰船舱室内部战斗部爆炸及爆炸毁伤效应。樊壮卿等[6]基于LS-DYNA软件,数值模拟了大体积复杂舱室内爆炸载荷传播特性。陈攀等[7]采用AUTODYN软件数值研究了舱室内爆工况下不同区域爆炸冲击波载荷特性及爆点位置对舱室内爆炸冲击波特性的影响规律。
炸药爆炸属于高压比、高密度比问题,其对激波捕捉格式提出较为严格的要求。传统的商用软件(MSC.DYTRAN,LS-DYNA,AUTODYN)主要采用低阶精度的黎曼求解器和FCT欧拉算法,针对爆炸载荷的计算比较粗糙,且当前发展比较成熟的激波捕捉算法还没有嵌入到商用程序中,因此自主开发高精度爆炸载荷数值计算程序显得更有意义。
目前,激波捕捉格式众多,如TVD格式[8]、ENO格式[9]、NND格式[10]等,本文主要关注被广泛采用的WENO格式(weighted essentially non-oscillation scheme),LIU等[11]于1994年提出了该格式,SHU等[12–14]发展了该格式。WENO在格式的有效性、通量的光滑性和收敛解的稳定性方面均优于ENO格式。
本文基于FORTRAN平台,采用3阶、5阶、7阶WENO有限差分格式,开发了舱室内爆炸载荷高精度三维数值计算程序。采用所开发的程序开展了封闭舱室、泄压舱室内爆炸载荷数值计算,研究了WENO格式精度对舱室内爆炸载荷影响规律,为结构抗爆设计提供一定的参考和指导。
1 控制方程假定炸药瞬时爆轰,将凝聚相炸药等效为高压、高密度气体,流场的控制方程采用三维可压缩欧拉方程进行描述,
| ${\overrightarrow U _t} + {\overrightarrow E _x} + {\overrightarrow F _y} + {\overrightarrow G _z} =0\text{,}$ | (1) |
其中:
| $\begin{array}{l}\overrightarrow U = \left( \begin{array}{l}\rho \\\rho u\\\rho v\\\rho w\\E\end{array} \right){\rm{ }}\overrightarrow E = \left( \begin{array}{l}\rho u\\\rho {u^2} + p\\\rho uv\\\rho uw\\u\left( {E + p} \right)\end{array} \right){\rm{ }}\text{,}\\[8pt]\overrightarrow F = \left( \begin{array}{l}\rho v\\\rho vu\\\rho {v^2} + p\\\rho vw\\v\left( {E + p} \right)\end{array} \right){\rm{ }}\overrightarrow G = \left( \begin{array}{l}\rho w\\\rho wu\\\rho wv\\\rho {w^2} + p\\w\left( {E + p} \right)\end{array} \right)\text{,}\end{array}$ | (2) |
| $E = \rho e + \frac{1}{2}\rho {u^2} + \frac{1}{2}\rho {v^2} + \frac{1}{2}\rho {w^2}\text{,}$ | (3) |
| $p = \left( {\gamma - 1} \right)\rho e\text{。}$ | (4) |
式中:
程序中采用3阶、5阶、7阶WENO有限差分格式对欧拉方程进行数值离散和求解,下面给出不同精度WENO格式的离散过程。
2.1 三阶WENO格式3阶WENO格式(WENO-JS3)的数值离散和推导过程如下:
单元面中心
| $f_{i + 1/2}^0 = - \frac{1}{2}{f_{i - 1}} + \frac{3}{2}{f_i}\text{,}$ | (5) |
| $f_{i + 1/2}^1 = \frac{1}{2}{f_i} + \frac{1}{2}{f_{i + 1}}\text{。}$ | (6) |
利用上述2种模板的凸组合计算数值通量
| ${f_{i + 1/2}} = {\omega _0}f_{i + 1/2}^0 + {\omega _1}f_{i + 1/2}^1\text{。}$ | (7) |
对于光滑情形,有
| ${f_{i + 1/2}} = \frac{1}{2}\left( {{f_i} + {f_{i + 1}}} \right) - \frac{1}{2}{\omega _0}\left( {{D_0} - {D_1}} \right)\text{,}$ | (8) |
式中:
| ${D_0} = {f_{i - 1}} - {f_i},{D_1} = {f_i} - {f_{i + 1}}\text{。}\qquad \qquad \qquad \qquad \, $ | (9) |
上式即为本文程序中采用的3阶WENO格式的最终形式,对于含激波间断流场,式中的
| ${\omega _k} = \frac{{{\alpha _k}}}{{\sum\limits_{s = 0}^1 {{\alpha _s}} }},{\alpha _k} = \frac{{{d_k}}}{{{{\left( {\varepsilon + {\beta _k}} \right)}^2}}},k = 0,1\text{。}$ | (10) |
式中:ε为避免分母为0,取
| ${\beta _0} = D_0^2,{\beta _1} = D_1^2\text{。}$ | (11) |
五阶WENO格式(WENO-JS5)的数值离散和推导过程如下:
单元面中心
| $f_{i + 1/2}^0 = \frac{1}{3}{f_{i - 2}} - \frac{7}{6}{f_{i - 1}} + \frac{{11}}{6}{f_i}\text{,}$ | (12) |
| $f_{i + 1/2}^1 = - \frac{1}{6}{f_{i - 1}} + \frac{5}{6}{f_i} + \frac{1}{3}{f_{i + 1}}\text{,}$ | (13) |
| $f_{i + 1/2}^2 = \frac{1}{3}{f_i} + \frac{5}{6}{f_{i + 1}} - \frac{1}{6}{f_{i + 2}}\text{。}$ | (14) |
利用上述3种模板的凸组合计算数值通量
| ${f_{i + 1/2}} = {\omega _0}f_{i + 1/2}^0 + {\omega _1}f_{i + 1/2}^1 + {\omega _2}f_{i + 1/2}^1\text{。}$ | (15) |
对于光滑情形,有
| $\begin{split}& {f_{i + 1/2}} = \displaystyle\frac{1}{{12}}\left( { - {f_{i - 1}} + 7{f_i} + 7{f_{i + 1}} - {f_{i + 2}}} \right) +\\& \displaystyle\frac{1}{3}{\omega _0}\left( {{D_0} - 2{D_1} + {D_2}} \right)+\\ & \displaystyle\frac{1}{6}\left( {{\omega _2} - \frac{1}{2}} \right)\left( {{D_1} - 2{D_2} + {D_3}} \right)\text{。}\end{split}$ | (16) |
式中:
| $\left\{ {\begin{array}{*{20}{l}}{{D_0} = {f_{i - 2}} - {f_{i - 1}},{D_1} = {f_{i - 1}} - {f_i}}\text{,}\\{{D_2} = {f_i} - {f_{i + 1}},{D_3} = {f_{i + 1}} - {f_{i + 2}}}\text{。}\end{array}} \right. $ | (17) |
式(16)即为本文程序中采用的5阶WENO格式的最终形式,对于含激波间断流场,式中的
| ${\omega _k} = \frac{{{\alpha _k}}}{{\sum\limits_{s = 0}^2 {{\alpha _s}} }},{\alpha _k} = \frac{{{d_k}}}{{{{\left( {\varepsilon + {\beta _k}} \right)}^2}}},k = 0,1,2\text{。}$ | (18) |
其中,光滑因子
| $\left\{ \begin{array}{l}{\beta _0} = {D_0}\left( {4{D_0} - 11{D_1}} \right) + 10D_1^2\text{,}\\{\beta _1} = {D_1}\left( {4{D_1} - 5{D_2}} \right) + 4D_2^2\text{,}\\{\beta _2} = {D_2}\left( {10{D_2} - 11{D_3}} \right) + 4D_3^2\text{。}\end{array} \right. $ | (19) |
7阶WENO格式(WENO-JS7)的数值离散和推导过程如下,单元面中心
| $f_{i + 1/2}^0 = - \frac{1}{4}{f_{i - 3}} + \frac{{13}}{{12}}{f_{i - 2}} - \frac{{23}}{{12}}{f_{i - 1}} + \frac{{25}}{{12}}{f_i}\text{,}$ | (20) |
| $f_{i + 1/2}^1 = \frac{1}{{12}}{f_{i - 2}} - \frac{5}{{12}}{f_{i - 1}} + \frac{{13}}{{12}}{f_i} + \frac{1}{4}{f_{i + 1}}\text{,}$ | (21) |
| $f_{i + 1/2}^2 = - \frac{1}{{12}}{f_{i - 1}} + \frac{7}{{12}}{f_i} + \frac{7}{{12}}{f_{i + 1}} - \frac{1}{{12}}{f_{i + 2}}\text{,}$ | (22) |
| $f_{i + 1/2}^3 = \frac{1}{4}{f_i} + \frac{{13}}{{12}}{f_{i + 1}} - \frac{5}{{12}}{f_{i + 2}} + \frac{1}{{12}}{f_{i + 3}}\text{。}$ | (23) |
利用上述4种模板的凸组合计算数值通量
| ${f_{i + 1/2}} = {\omega _0}f_{i + 1/2}^0 + {\omega _1}f_{i + 1/2}^1 + {\omega _2}f_{i + 1/2}^2 + {\omega _3}f_{i + 1/2}^3\text{。}$ | (24) |
对于光滑情形,有
| $\begin{split}{f_{i + 1/2}} \!=\! \displaystyle\frac{1}{{60}}\left( {{f_{i - 2}} \!-\! 8{f_{i - 1}} \!+\! 37{f_i} \!+\! 37{f_{i + 1}} \!-\! 8{f_{i \!+\! 2}} \!+\! {f_{i + 3}}} \right) \!-\! \!\!\!\!\\\displaystyle\frac{1}{{12}}\left[ \begin{array}{l}{\omega _0}\left( {3{D_0} - 10{D_1} + 12{D_2} - 6{D_3} + {D_4}} \right)\\ + \left( {{\omega _1} - \displaystyle\frac{1}{5}} \right)\left( { - {D_1} + 3{D_2} - 3{D_3} + {D_4}} \right)\\ + \left( {{\omega _3} - \displaystyle\frac{1}{5}} \right)\left( { - {D_2} + 3{D_3} - 3{D_4} + {D_5}} \right)\end{array} \right] \text{,}\end{split}$ | (25) |
式中:
| $\left\{ {\begin{array}{*{20}{l}}{{D_0} = {f_{i - 3}} - {f_{i - 2}},{D_1} = {f_{i - 2}} - {f_{i - 1}}}\text{,}\\{{D_2} = {f_{i - 1}} - {f_i},{D_3} = {f_i} - {f_{i + 1}}}\text{,}\\{{D_4} = {f_{i + 1}} - {f_{i + 2}},{D_5} = {f_{i + 2}} - {f_{i + 3}}}\text{。}\end{array}} \right. $ | (26) |
式(25)即为本文程序中采用的7阶WENO格式的最终形式,对于含激波间断流场,式中的
| ${\omega _k} = \frac{{{\alpha _k}}}{{\sum\limits_{s = 0}^3 {{\alpha _s}} }},{\alpha _k} = \frac{{{d_k}}}{{{{\left( {\varepsilon + {\beta _k}} \right)}^2}}},k = 0,1,2,3\text{。}$ | (27) |
其中,光滑因子
| $\left\{ {\begin{array}{*{20}{l}}{{\beta _0} = {D_0}\left( {547{D_0} - 2788{D_1} + 1854{D_2}} \right) + }\\{{D_1}\left( {3708{D_1} - 5188{D_2}} \right) + 2107D_2^2\text{,}}\\[12pt]{{\beta _1} = {D_1}\left( {267{D_1} - 1108{D_2} + 494{D_3}} \right)+} \\{{D_2}\left( {1468{D_2} - 1428{D_3}} \right) + 547D_3^2\text{,} }\\[12pt]{{\beta _2} = {D_2}\left( {547{D_2} - 1428{D_3} + 494{D_4}} \right) + }\\{{D_3}\left( {1468{D_3} - 1108{D_4}} \right) + 267D_4^2\text{,}}\\[12pt]{{\beta _3} = {D_3}\left( {2107{D_3} - 5188{D_4} + 1854{D_5}} \right) + }\\{{D_4}\left( {3708{D_4} - 2788{D_5}} \right) + 547D_5^2\text{。}}\end{array}} \right.$ | (28) |
时间项采用3阶TVD-RK法求解,格式如下[17]:
| $\left\{ \begin{aligned}& {u^{\left( 1 \right)}} = {u^n} + \Delta tL\left( {{u^n}} \right)\text{,}\\& {u^{\left( 2 \right)}} = \displaystyle\frac{3}{4}{u^n} + \displaystyle\frac{1}{4}{u^{\left( 1 \right)}} + \displaystyle\frac{1}{4}\Delta tL\left( {{u^{\left( 1 \right)}}} \right)\text{,}\\& {u^{n + 1}} = \displaystyle\frac{1}{3}{u^n} + \displaystyle\frac{1}{3}{u^{\left( 2 \right)}} + \displaystyle\frac{2}{3}\Delta tL\left( {{u^{\left( 2 \right)}}} \right)\text{。}\end{aligned} \right.$ | (29) |
为了初步考察上述格式(WENO-JS3,WENO-JS5,WENO-JS7)的计算性能,选取3个经典一维黎曼算例进行计算。
3.1 Sod激波管该算例初始条件如式(30)所示[18],网格数为400,计算结束时间为0.18。图1给出计算结束时刻密度曲线图及局部放大图。
| ${\left( {\rho ,u,p} \right)^{\rm T}} = \left\{ \begin{array}{l}{(1,0,1)^{\rm T}},0 \text{≤} x < 0.5; \\{(0.125,0,0.1)^{\rm T}},0.5 \text{≤} x \text{≤} 1{\text{。}}\end{array} \right.$ | (30) |
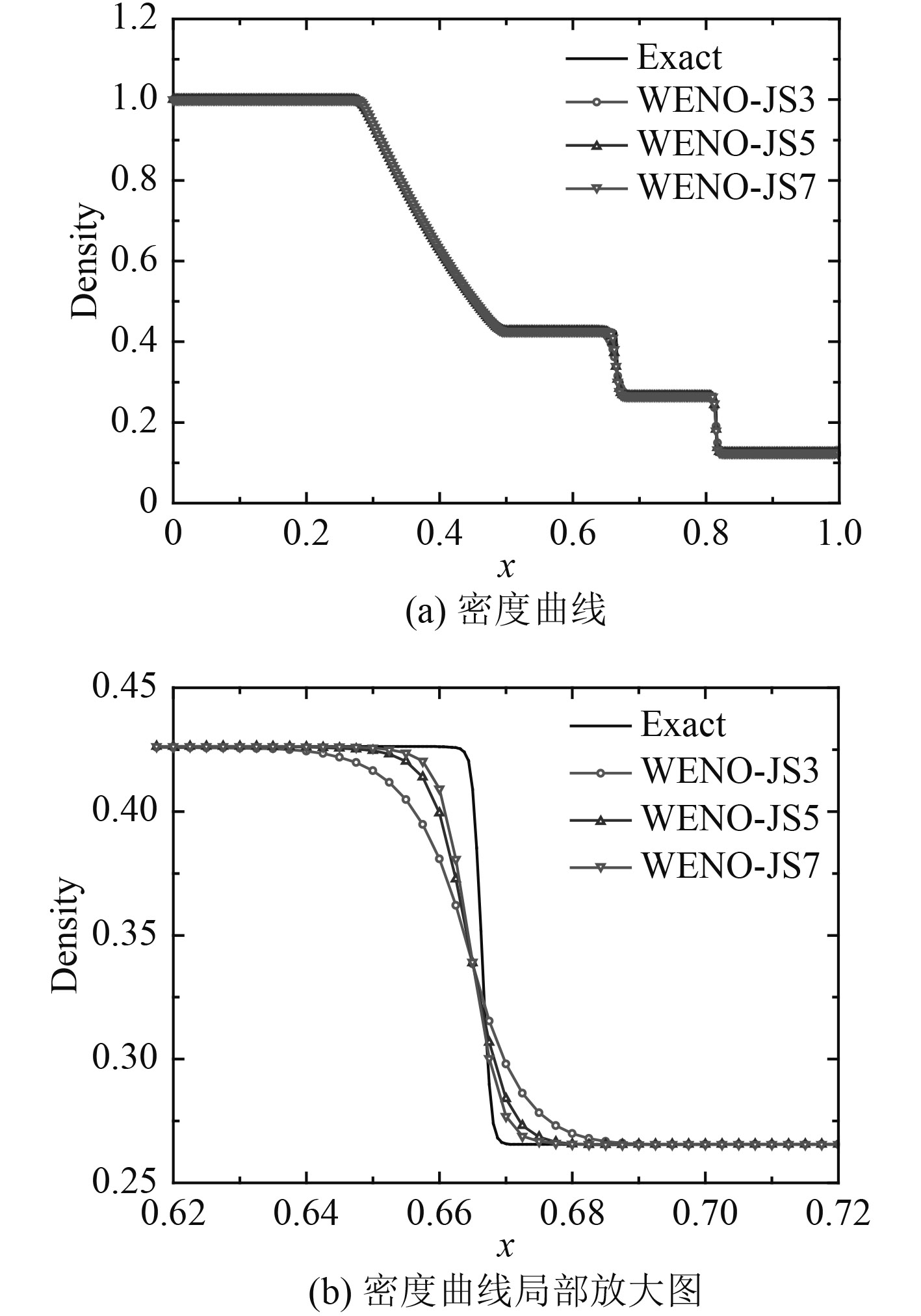
|
图 1 计算结束后密度曲线及局部放大图 Fig. 1 Density curve and partial enlarged details |
该算例初始条件如式(31)所示[19],网格数为400,计算结束时间为0.038。图2给出计算结束时刻密度曲线图及局部放大图。
| ${\left( {\rho ,u,p} \right)^{\rm T}} = \left\{ \begin{array}{l}{\left( {1,0,1000} \right)^{\rm T}},0 \text{≤} x < 0.1;\\{\left( {1,0,0.01} \right)^{\rm T}},0.1 \text{≤} x \text{≤} 0.9;\\{\left( {1,0,100} \right)^{\rm T}},0.9 \text{≤} x \text{≤} 1{\text{。}}\end{array} \right.$ | (31) |
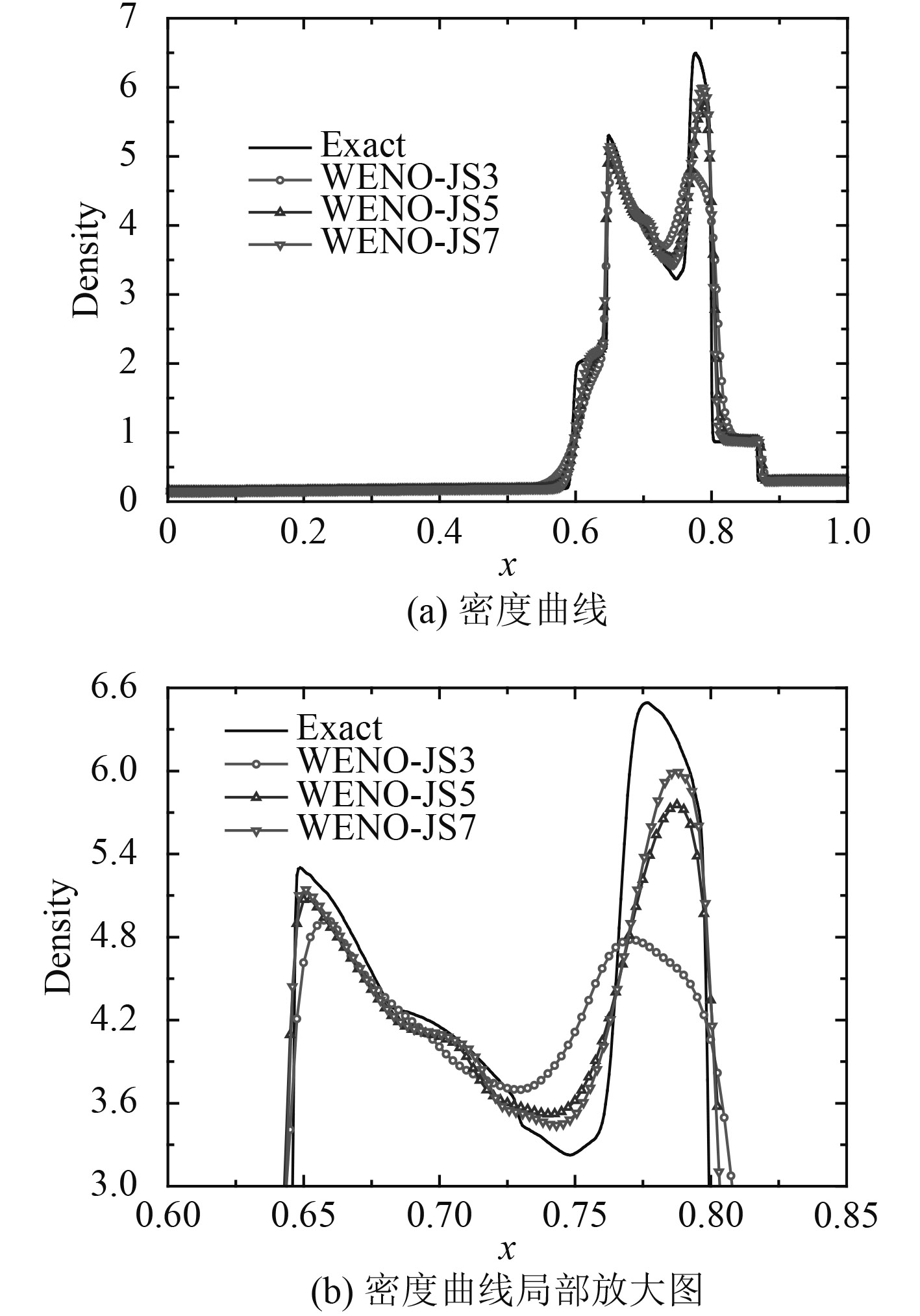
|
图 2 计算结束后密度曲线及局部放大图 Fig. 2 Density curve and partial enlarged details |
该算例初始条件如式(32)所示,网格数为400,计算结束时间为1.8。图3给出计算结束时刻密度曲线图及局部放大图。
| ${\left( {\rho ,u,p} \right)^{\rm T}} = \left\{ \begin{array}{l}{\left( {3.857143,2.629369,10.33333} \right)^{\rm T}},\\ - 5 \text{≤} x < - 4;\\{\left( {1 + 0.2\sin 5x,0,1} \right)^{\rm T}},\\ - 4 \text{≤} x \text{≤} 5{\text{。}}\end{array} \right.$ | (32) |
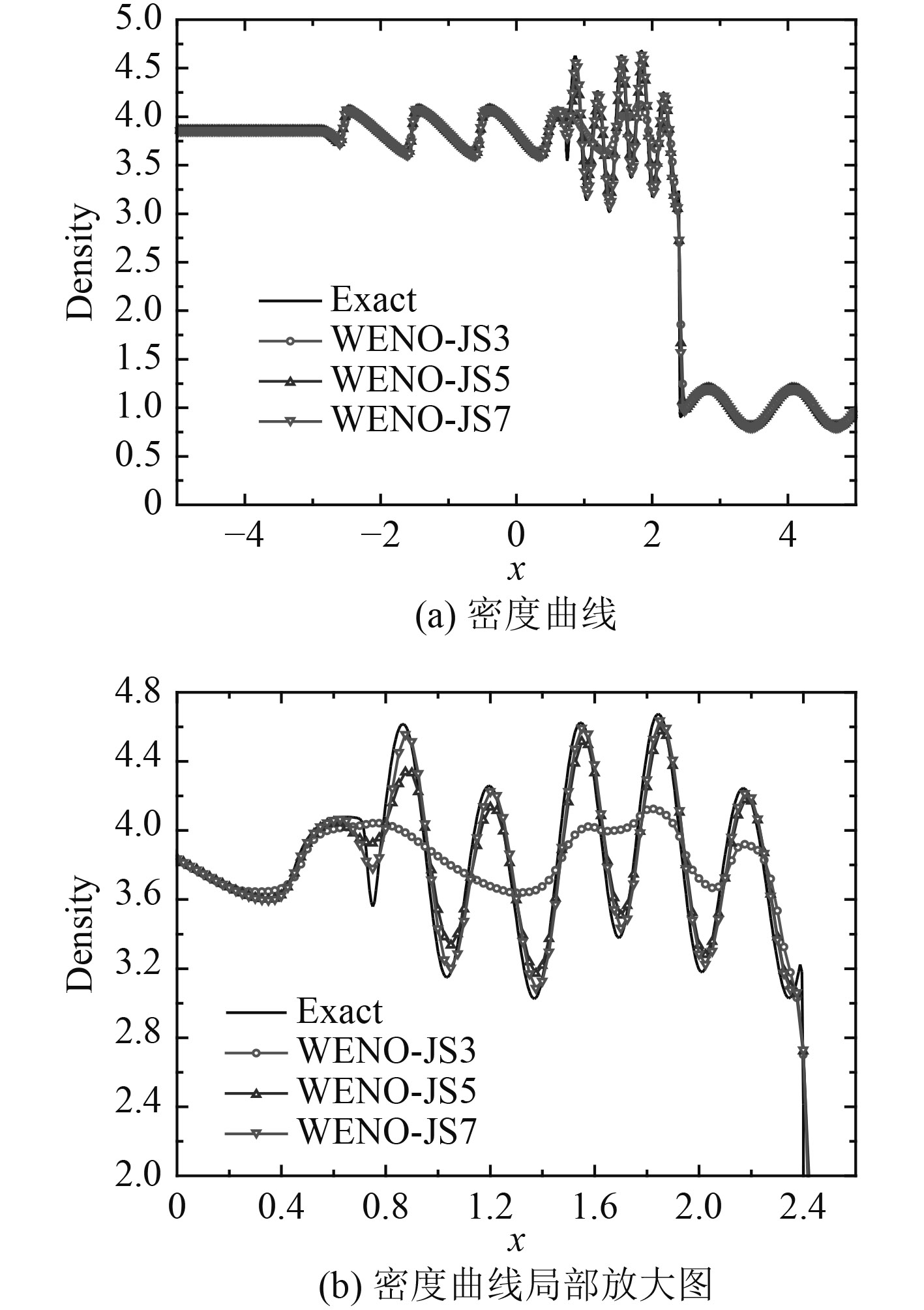
|
图 3 计算结束后密度曲线及局部放大图 Fig. 3 Density curve and partial enlarged details |
根据上述计算结果,评估各格式的计算性能发现:WENO-JS7格式计算性能最优,WENO-JS5格式次之,WENO-JS3格式计算性能最低。即高精度WENO格式对含激波间断流场具有更低的耗散特性和更高的分辨率。
4 舱室内爆炸载荷计算为了考察不同精度WENO格式对舱室内爆载荷的影响规律,采用所开发的三维程序开展封闭舱室和泄压舱室内爆炸载荷数值计算。
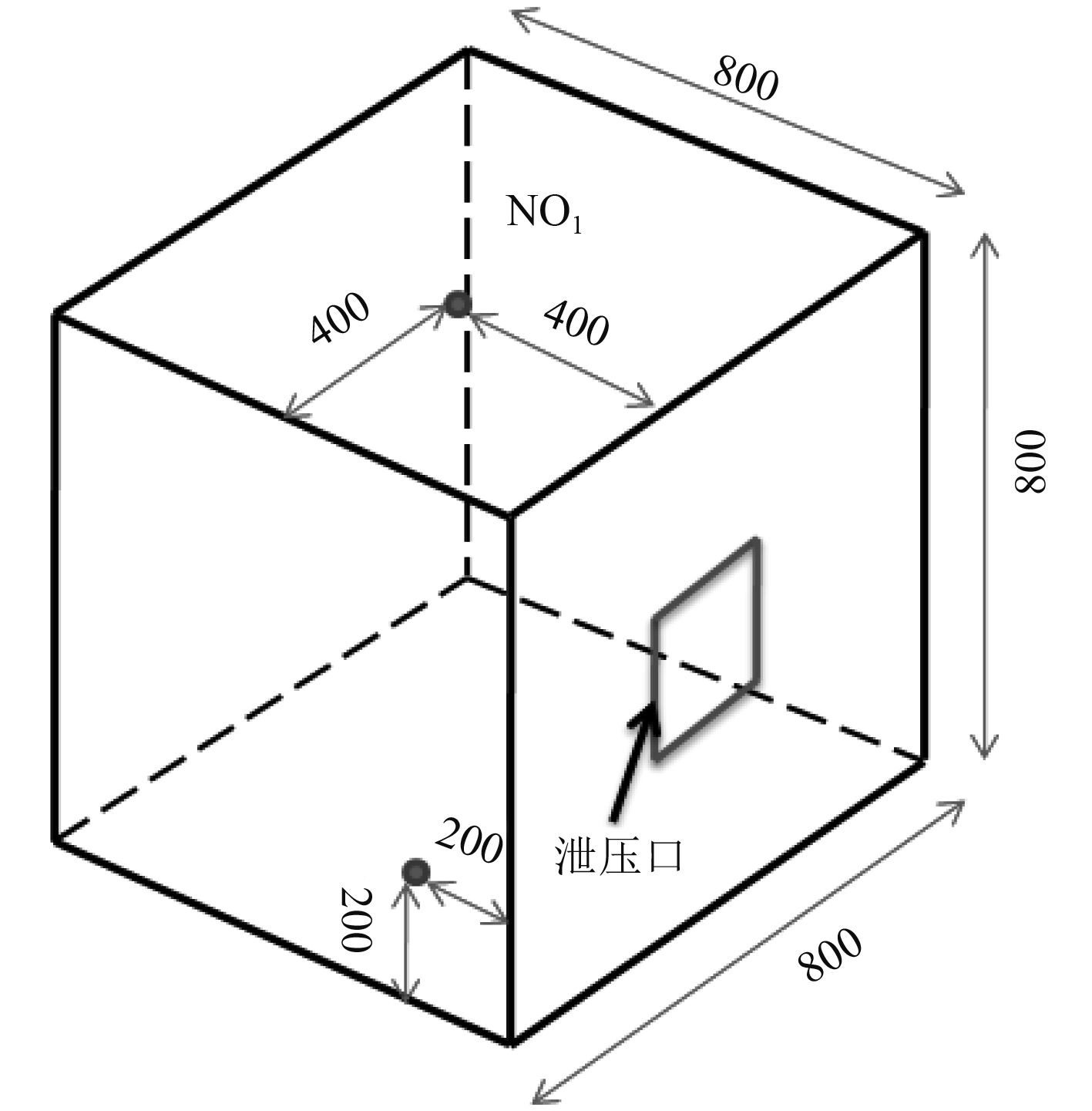
4.1 密闭舱室内爆炸 4.1.1 初始条件设置密闭舱室尺寸为800×800×800 mm,壁面上设置2个测点,分别编号为NO1,NO2对爆炸超压时间历程进行输出(见图4)。
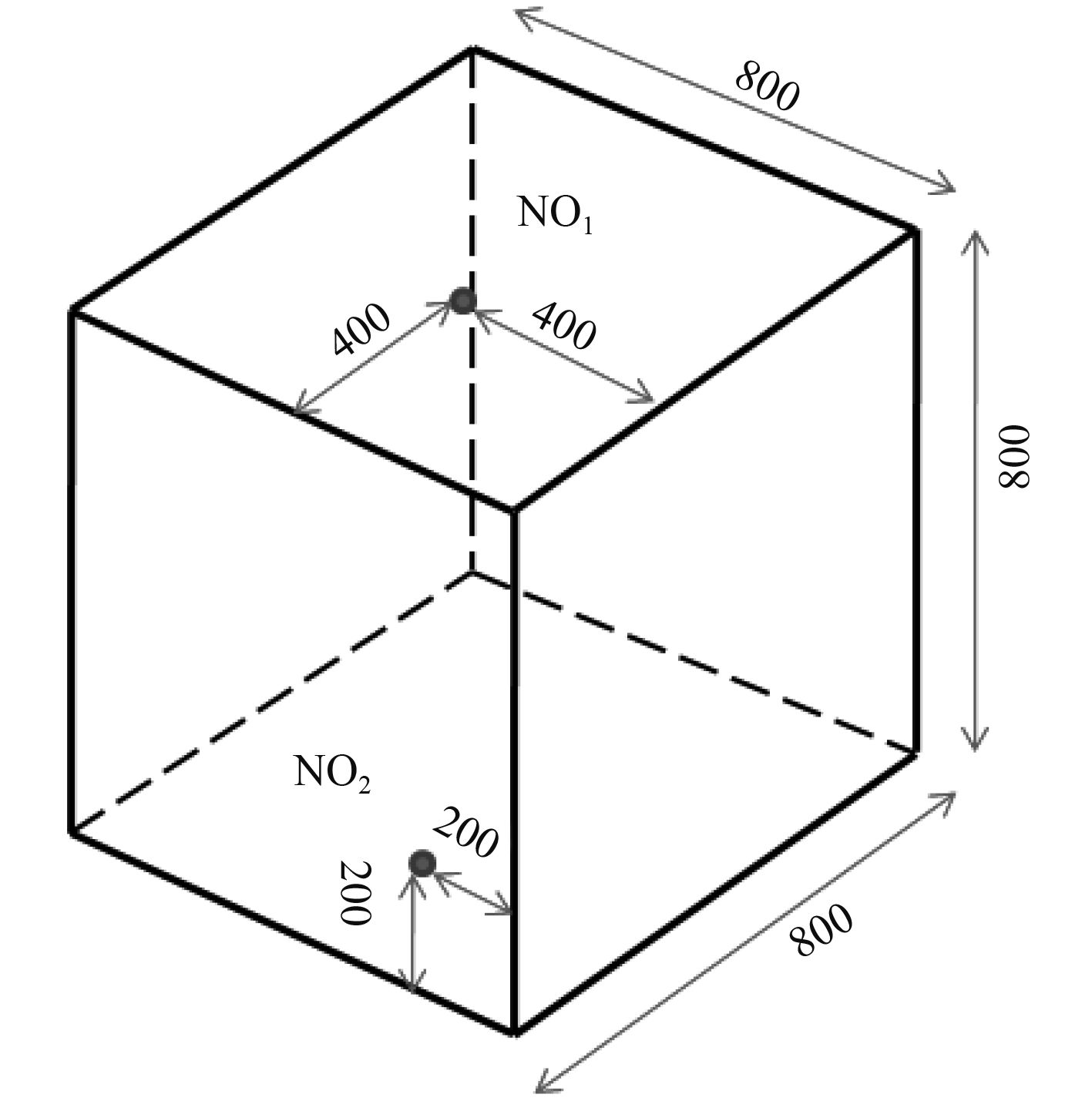
|
图 4 舱室及测点分布 Fig. 4 Cabin and gauging points |
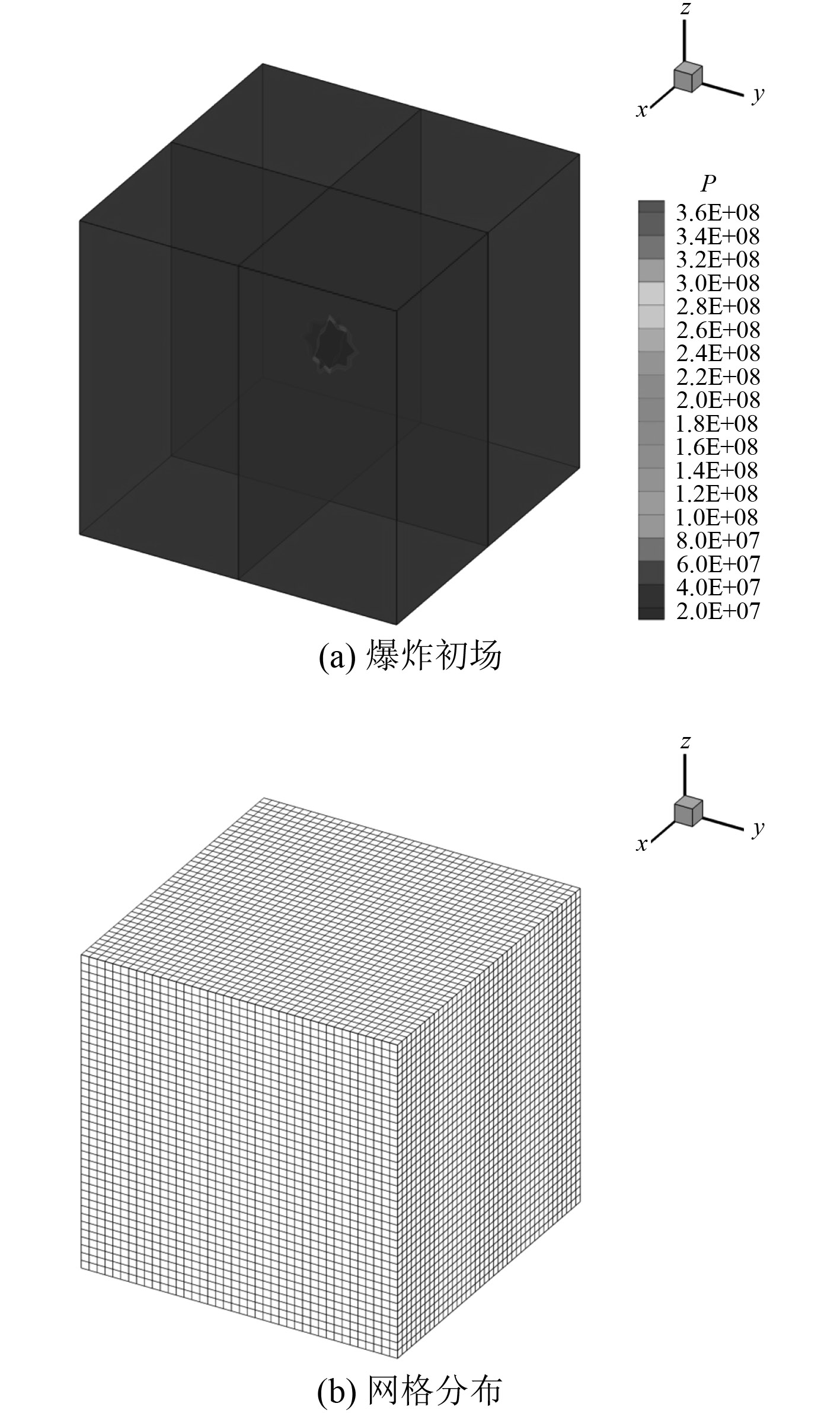
球形炸药(200 g)位于舱室中间,等效后的高压、高密度气体参数:半径为61.65 mm,密度为203.75 kg/m3,压力为3.791×108 Pa。计算初始条件见图5(a)。考虑计算时间及精度的要求,经多次数值试验,网格数为40×40×40,见图5(b)。壁面边界条件设置为反射边界。
|
图 5 爆炸初场及网格分布 Fig. 5 Initial condition and mesh distribution |
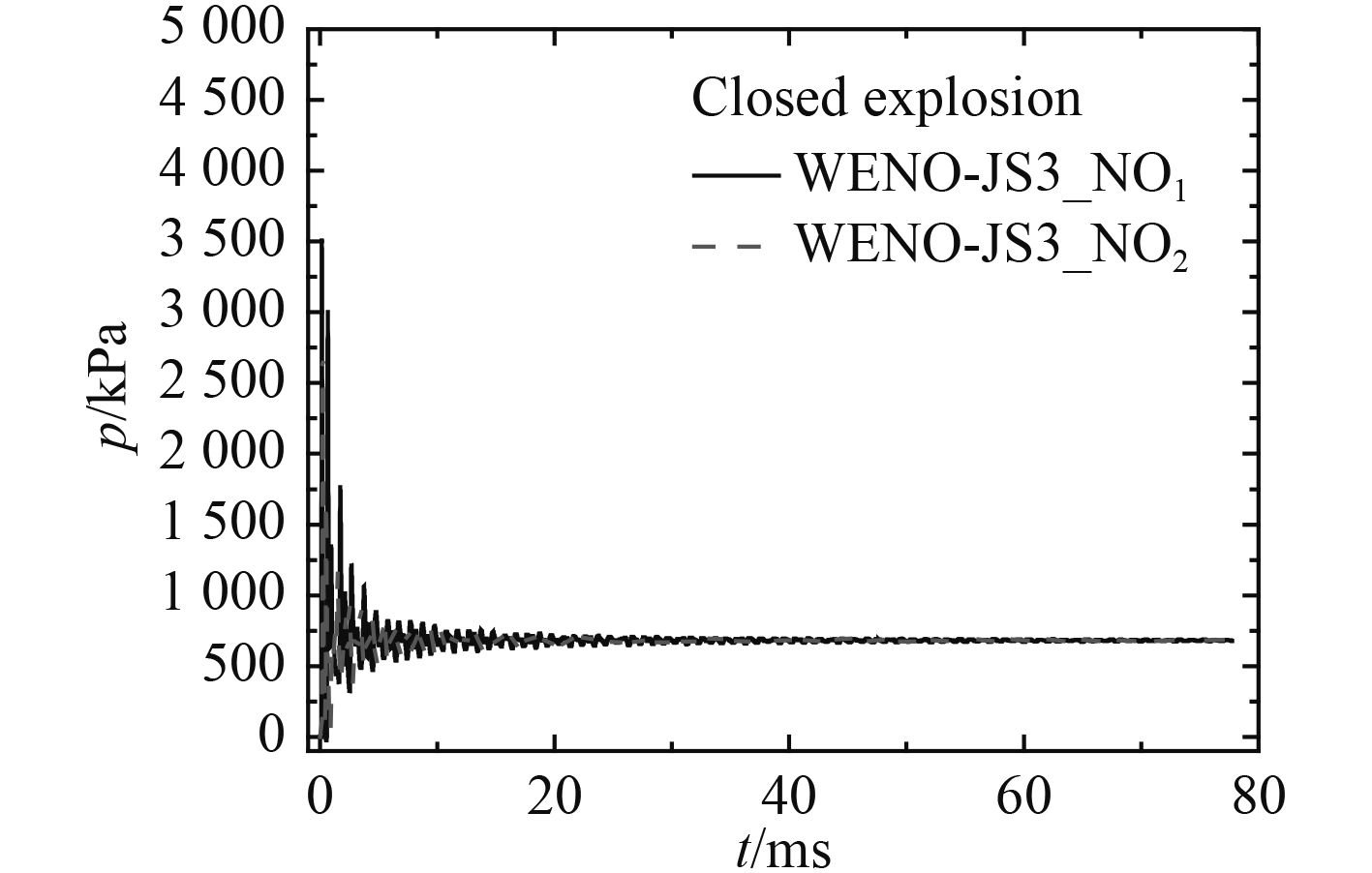
图6给出封闭舱室内爆炸壁面测点NO1和NO2超压时间历程曲线。从图6可知,封闭舱室内爆炸载荷主要包含多峰值、强度逐渐衰弱的冲击波和持续时间较长、保持稳定的准静态超压。根据测点NO1和NO2的对比可知,测点的位置对爆炸前期爆炸波超压峰值有较大的影响,而对最终形成的准静态超压峰值几乎没有影响,说明封闭舱室内部爆炸形成的准静态超压峰值在空间上近似均匀。
|
图 6 封闭舱室内爆炸超压时间历程曲线 Fig. 6 Overpressure time histories of all the gauging points in closed cabin |
为了探讨不同精度WENO格式对封闭舱室内爆炸载荷影响规律,选取壁面典型测点NO1对爆炸载荷进行输出。
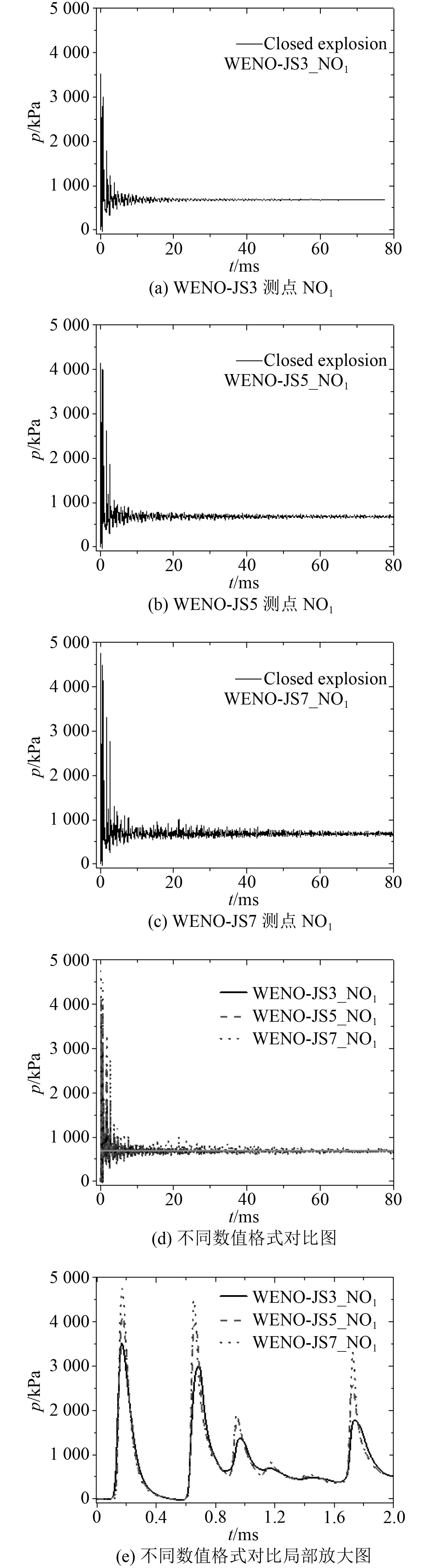
图7(a)~图7(c)给出不同精度WENO格式,测点NO1爆炸超压时间历程曲线,通过对比发现,高精度WENO格式能分辨出更精细的爆炸载荷特征,即高精度WENO格式具有更低的耗散特性和更高的分辨率。
图7(d)和图7(e)分别给出3种精度WENO格式爆炸载荷对比图及局部放大图。从图7(d)和图7(e)可知,随着WENO格式精度的提高,爆炸冲击波载荷峰值得到较大的提高,即高精度WENO格式对于激波间断具有更低的耗散特性。然而,不同精度WENO格式对最终形成的准静态超压峰值影响较小,见图7(d)中的粗实线。
|
图 7 封闭舱室内爆炸不同精度WENO格式测点NO1爆炸超压时间历程曲线 Fig. 7 Overpressure time histories of gauging point NO1 for different schemes in closed cabin |
计算初始条件同4.1.1小节,唯一的不同是,泄压舱室壁面上设置一个边长为160 mm的方形泄压口(见图8)。壁面边界条件设置为反射边界,泄压口处边界条件设置为透射边界。
|
图 8 舱室及测点分布 Fig. 8 Cabin and gauging points |
图9给出泄压舱室内爆炸壁面上测点NO1和NO2超压时间历程曲线。从图9可知,泄压舱室内爆炸载荷主要包含多峰值、强度逐渐衰弱的冲击波和持续时间较长、呈现指数衰减规律[20]的准静态超压。根据测点NO1和NO2的对比可知,测点的位置对爆炸前期爆炸波超压峰值有一定的影响,而对准静态超压时间历程几乎没有影响,说明泄压舱室内爆炸形成的准静态超压时间历程在空间上近似均匀。
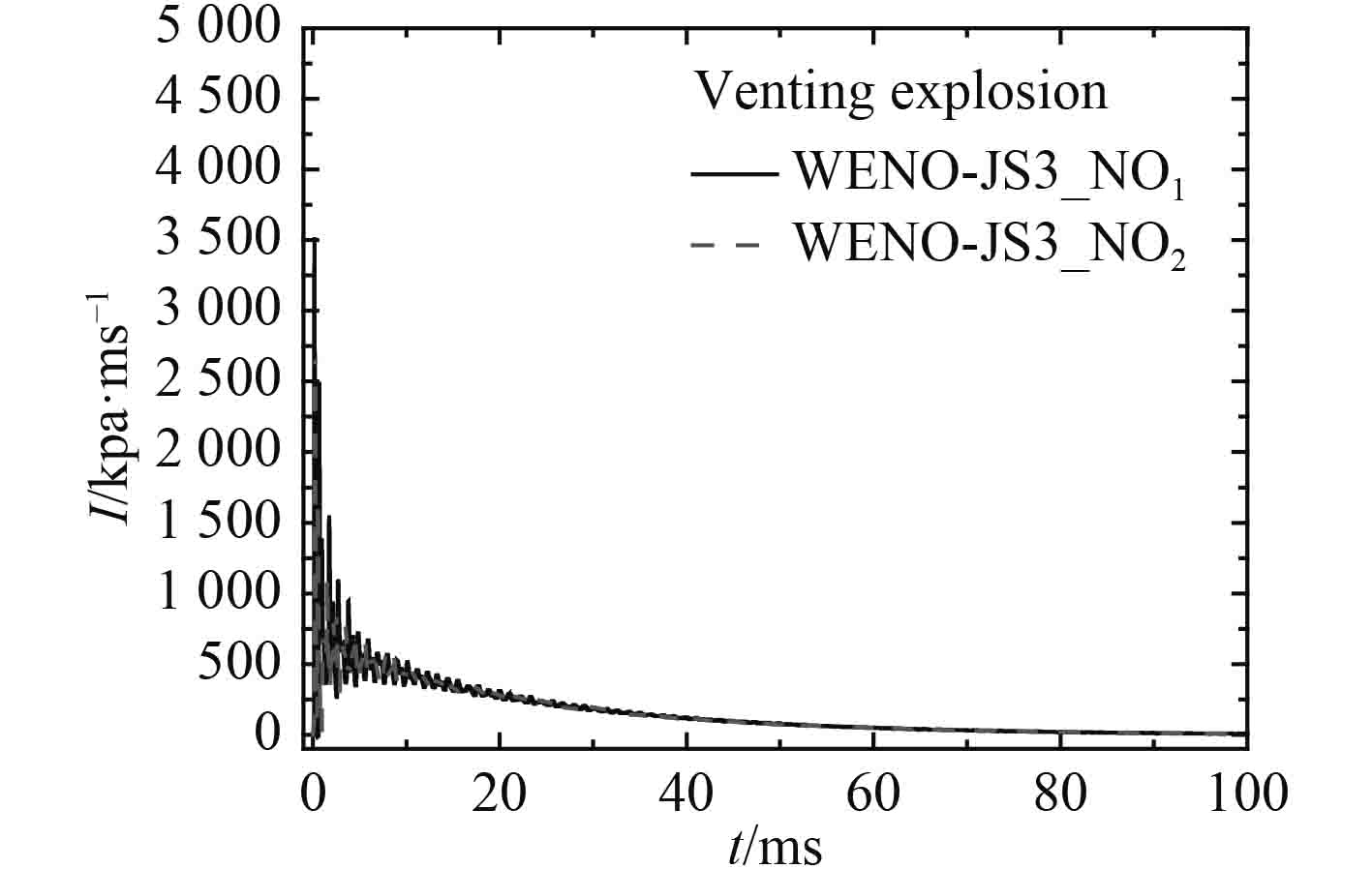
|
图 9 泄压舱室内爆炸超压时间历程曲线 Fig. 9 Overpressure time histories of all the gauging points in venting cabin |
为了探讨不同精度WENO格式对泄压舱室内爆炸载荷影响规律,选取壁面典型测点NO1对爆炸载荷进行输出。
图10(a)~图10(c)给出不同精度WENO格式,测点NO1爆炸超压时间历程曲线,通过对比发现,高精度WENO格式能分辨出更精细的爆炸载荷特征,即高精度WENO格式具有更低的耗散特性和更高的分辨率。
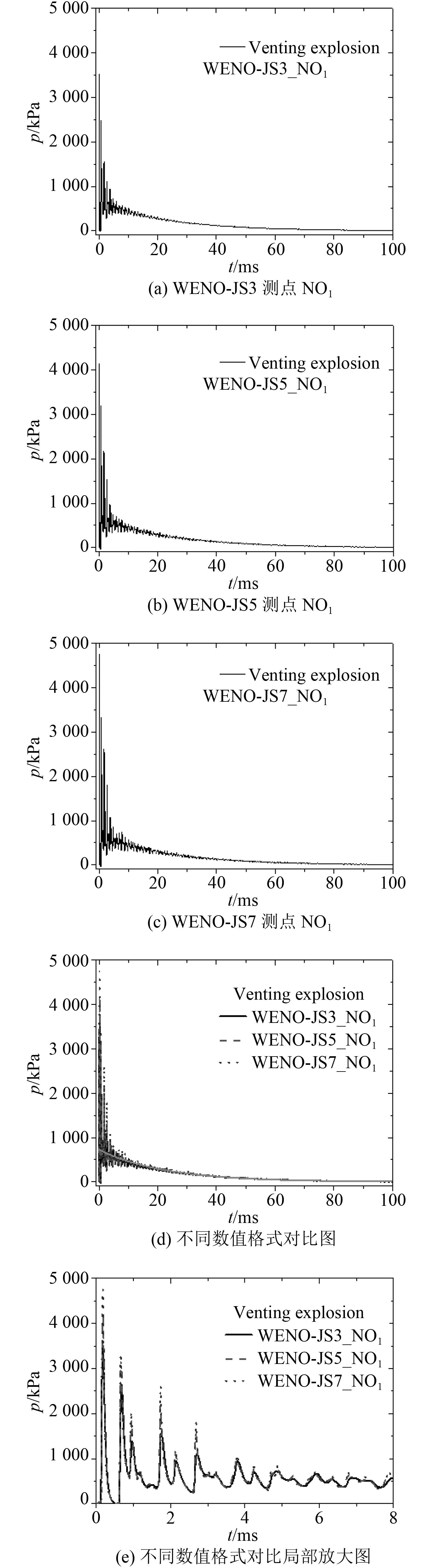
|
图 10 泄压舱室内爆炸不同精度WENO格式测点NO1爆炸超压时间历程曲线 Fig. 10 Overpressure time histories of gauging point NO1 for different schemes in venting cabin |
图10(d)和图10(e)分别给出3种精度WENO格式爆炸载荷对比图及局部放大图。从图10(d)和图10(e)可知,随着WENO格式精度的提高,爆炸冲击波载荷峰值得到较大的提高,即高精度WENO格式对于激波间断具有更低的耗散特性。然而,不同精度WENO格式对逐渐形成的、呈现指数衰减规律的准静态超压影响较小,见图10(d)中的粗实线。
5 结 语基于自主开发的高精度舱室内爆炸三维数值计算程序研究了WENO格式精度对舱室内爆炸载荷影响规律,通过本文的研究主要得到以下4点结论:
1)高精度WENO格式对含激波间断流场具有更低的耗散特性和更高的分辨率。
2)WENO格式精度对舱室内爆炸冲击波载荷影响较大,高精度WENO格式给出更陡峭的激波峰值。
3)WENO格式精度对舱室内爆炸准静态超压(封闭舱室内爆炸形成的保持不变的准静态超压、泄压舱室内爆炸形成的呈指数衰减的准静态超压)载荷影响较小。
4)本文所开发的三维程序可用于舰船舱室内爆炸载荷数值计算,为结构抗爆设计提供载荷依据。
| [1] | WU C, LUKASZEWICZ M, SCHEBELLA K, et al. Experimental and numerical investigation of confined explosion in a blast chamber[J]. Journal of Loss Prevention in the Process Industries, 2013, 26 (4): 737–750. DOI: 10.1016/j.jlp.2013.02.001 |
| [2] |
侯海量, 朱锡, 李伟, 等. 舱内爆炸冲击载荷特性实验研究[J]. 船舶力学, 2010, 14 (8): 901–907.
HOU Hai-liang, ZHU Xi, LI Wei, et al. Experimental studies on characteristics of blast loading when exploded inside ship cabin[J]. Journal of Ship Mechanics, 2010, 14 (8): 901–907. |
| [3] |
孔祥韶, 吴卫国, 李俊, 等. 角隅结构对舱内爆炸载荷影响的实验研究[J]. 中国造船, 2012 (3): 40–50.
KONG Xiang-shao, WU Wei-guo, LI Jun, et al. Experimental research of influence of corner structure on blast loading under inner explosion[J]. Chinese Journal of Ship Research, 2012 (3): 40–50. |
| [4] |
侯海量, 朱锡, 梅志远. 舱内爆炸载荷及舱室板架结构的失效模式分析[J]. 爆炸与冲击, 2007, 27 (2): 151–158.
HOU Hai-liang, ZHU Xi, MEI Zhi-yuan. Study on the blast load and failure mode of ship structure subject to internal explosion[J]. Explosion and Shock Waves, 2007, 27 (2): 151–158. DOI: 10.11883/1001-1455(2007)02-0151-08 |
| [5] |
孔祥韶, 吴卫国, 李晓彬, 等. 舰船舱室内部爆炸的数值模拟研究[J]. 中国舰船研究, 2009, 4 (4): 7–11.
KONG Xiang-shao, WU Wei-guo, LI Xiao-bin, et al. Numerical simualtion of cabin structure under inner explosion[J]. Chinese Journal of Ship Research, 2009, 4 (4): 7–11. |
| [6] |
樊壮卿, 王伟力, 黄雪峰, 等. 典型舱室内爆炸仿真分析[J]. 工程爆破, 2015, 21 (3): 13–17.
FAN Zhuang-qing, WANG Wei-li, HUANG Xue-feng, et al. Simulation analysis on typical cabin internal explosion[J]. Engineering Blasting, 2015, 21 (3): 13–17. |
| [7] |
陈攀, 刘志忠. 舱室内爆冲击波载荷特性及影响因素分析[J]. 舰船科学技术, 2016, 38 (3): 43–48.
CHEN Pan, LIU Zhi-zhong. Research on loading of explosive and influencing factors inside closed cabin[J]. Ship Science and Technology, 2016, 38 (3): 43–48. |
| [8] | HARTEN A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 135(3): 357–393. |
| [9] | HARTEN A, ENGQUIST B, OSHER S, et al. Uniformly high order accurate essentially non-oscillatory schemes, III[J]. Journal of Computational Physics, 1987, 71 (2): 231–303. DOI: 10.1016/0021-9991(87)90031-3 |
| [10] | ZHANG H, ZHUANG F. NND schemes and their applications to numerical simulation of two-and three-dimensional flows*[M]//JOHN W H, THEODORE Y W. Advances in Applied Mechanics. Elsevier. 1991: 193–256. |
| [11] | LIU X D, OSHER S, CHAN T. Weighted Essentially Non-oscillatory Schemes[J]. Journal of Computational Physics, 1994, 115 (1): 200–212. DOI: 10.1006/jcph.1994.1187 |
| [12] | JIANG G S, SHU C W. Efficient Implementation of Weighted ENO Schemes[J]. Journal of Computational Physics, 1996, 126 (1): 202–202. DOI: 10.1006/jcph.1996.0130 |
| [13] | SHU C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws [M]. Springer Berlin Heidelberg. 1998: 325–432. |
| [14] | SHU C W. High Order Weighted Essentially Nonoscillatory Schemes for Convection Dominated Problems[J]. Siam Review, 2009, 51 (1): 82–126. DOI: 10.1137/070679065 |
| [15] |
谢昌坦. 气—水可压缩流物质界面的R-M不稳定性研究 [D]. 哈尔滨: 哈尔滨工程大学, 2011.
XIE Chang-tan. The study on R-M instability of the material interface in gas-water compressible flow[D]. Harbin: Harbin Engineering University Master of Engineering, 2011. |
| [16] | BALSARA D S, SHU C W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy[J]. Journal of Computational Physics, 2000, 160 (2): 405–452. DOI: 10.1006/jcph.2000.6443 |
| [17] | SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1988, 77 (2): 439–471. DOI: 10.1016/0021-9991(88)90177-5 |
| [18] | SOD G A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J]. Journal of Computational Physics, 1978, 27 (1): 1–31. DOI: 10.1016/0021-9991(78)90023-2 |
| [19] | WOODWARD P, COLELLA P. Colella, P. The numerical simulation of two-dimensional fluid flow with strong shocks[J]. Journal of Computational Physics, 1984, 54(1): 115–173. |
| [20] | ANDERSON C E, BAKER W E, WAUTERS D K, et al. Quasi-static pressure, duration, and impulse for explosions (e. g. HE) in structures[J]. International Journal of Mechanical Sciences, 1983, 25 (6): 455–464. DOI: 10.1016/0020-7403(83)90059-0 |
 2018, Vol. 40
2018, Vol. 40
