随着船用发电机技术的进步,其向着单机大容量和小型化的趋势发展,发电机在工作时产生的能量损耗增加,使得发电机内各部件的温度升高,直接影响发电机的安全性和可靠性。转子作为船用发电机的高速旋转的运动部件,目前还没有直接有效的方法来测量其内部的温度分布情况,而采用数值模拟技术是对转子内部的温度场进行数值分析的常用手段[1, 2]。因此发电机的温度场的数值模拟对该型船用发电机的设计、优化与安全运行有至关重要的指导意义。
随着计算技术的发展,目前主要的数值模拟方法为有限元法和有限体积法,刘清等[3]采用有限体积法计算了电机内部的流场分布。邰永等[4]建立了感应电机的3D有限元模型,考虑热源损耗对转子、定子阻值和温度分布的影响,模拟了电机在额定负载下的瞬态温度场变化。丁树业等[5]根据共轭传热原理,建立了包含散热翅片与接线盒等结构部件的流动与传热的三维模型,在变频供电的情况下,对永磁同步驱动电机内各部件的温升及流动进行数值模拟。佟文明等[6]采用有限体积法对高速永磁电机的流场与温度场进行耦合计算,得到了电机内空气的流动特性和各部件的温度分布。李东和等[7]基于CFD建立了电机热仿真模型,通过有限元软件仿真得到了额定工况下的电机内部温度分布规律。冯桂宏等[8]通过有限元方法进行了电机的三维稳态温升计算,获得了电机整机及关键部件的温度场分布。王晓远等[9]建立了轮毂电机温度场的分析模型,得到轮毂电机各部件的温升曲线和温度场分布。王越等[10]利用Ansys仿真计算了不同绕线方式的电机温度场。赖林松等[11]基于Ansys建立了永磁直流电机的传热模型,计算得到电机的温度场分布。
综上所述,电机内温度场的数值模拟逐渐成熟,但是电机内热过程非常复杂,涉及电磁理论、结构学、流体力学、传热学等学科,包含了流场、温度场、电磁场等多物理场,而各物理场相互影响、相互制约,具有一定耦合关系。然而目前针对电机温度场与流场的研究主要集中在单一场的计算分析上,耦合场的研究还很少,而且边界条件多采用经验公式,对计算结果造成一定的误差。另外由于发电机的转子在工作时高速旋转,使得转子内部流动的气体与固体壁面间的耦合传热进行分析求解变得更加复杂,这也是本文的困难之处。本文在前人工作的基础上,采用有限体积的方法对船用电机的转子和内部冷却空气的耦合温度场进行数值模拟。
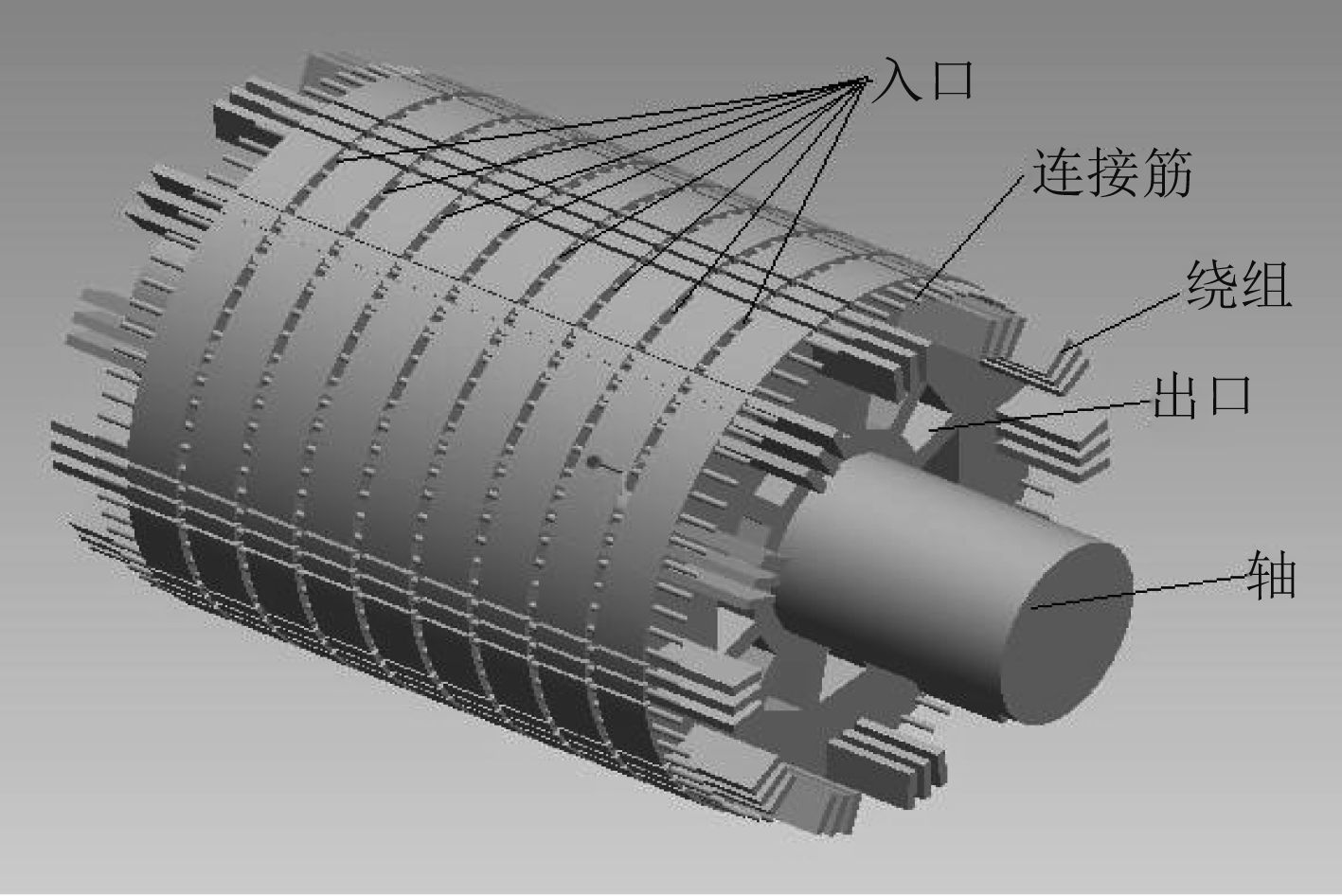
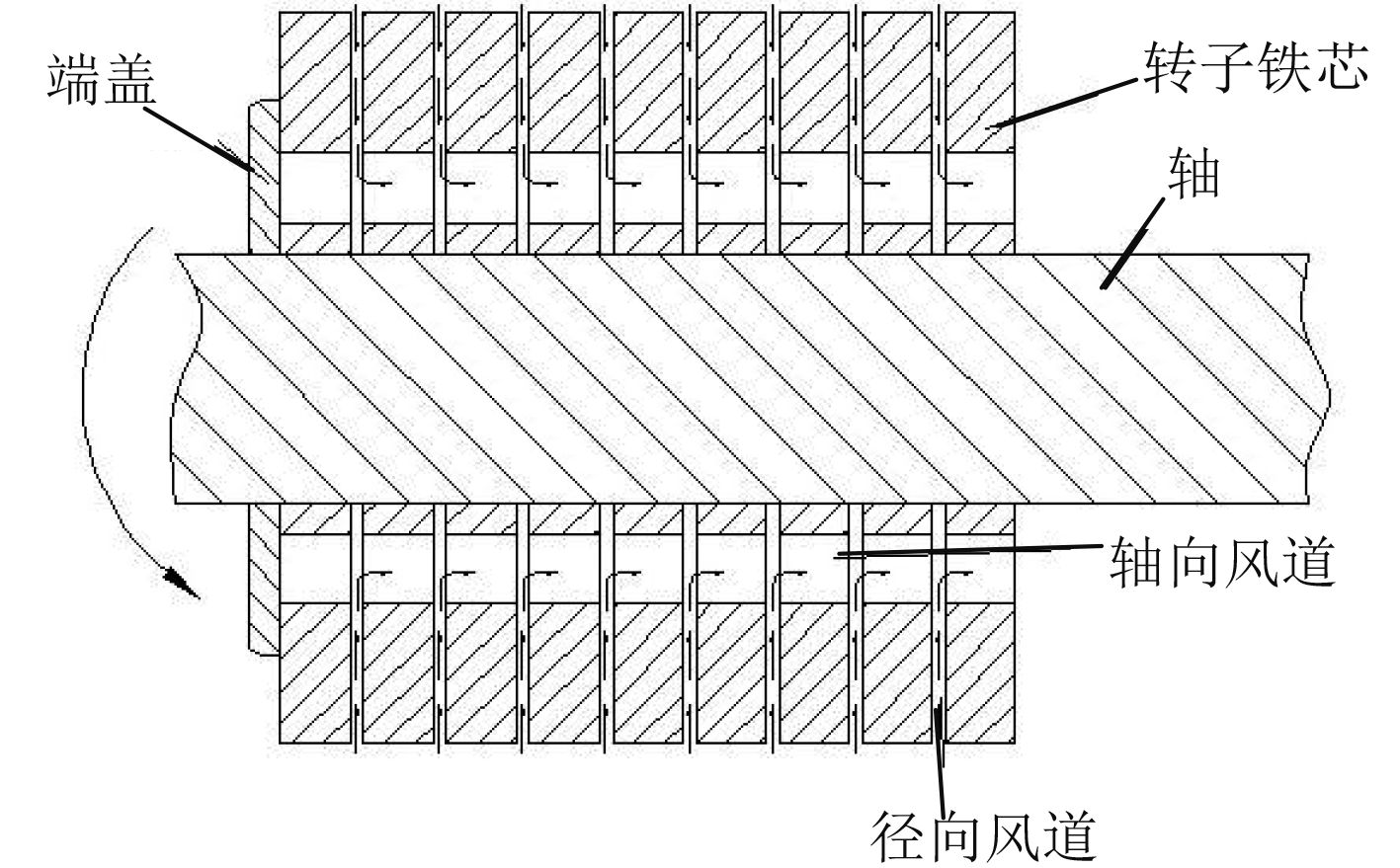
1 物理模型本文以某型船用发电机的转子作为研究对象,转子整体的3D模型图如图1所示,图2所示为转子的结构简图,从图中可以看出,该转子的通风道是径-轴向混合式冷却风道,冷却空气从定子与转子之间的气隙层,垂直于转子柱表面的入口沿径向流入径向风道,与转子表面发生强制对流换热,最后冷却空气汇集在轴向风道,沿着其排出,带走热量,起到冷却作用。冷却空气的流向如图2中箭头所示。
|
图 1 转子几何模型图 Fig. 1 The figure of geometric model |
|
图 2 转子结构简图 Fig. 2 The structure diagram of the rotor |
由于该型发电机的转子在结构上具有高度的对称性和周期性,在不影响计算结果准确性的前提下,为了计算方面快捷,选取转子整体的1/12作为计算区域。另外,有几何模型到物理模型,需要进行合理的简化,本文主要从以下几个方面进行简化:
1)把由叠压的硅钢片组成的转子铁芯段作为整体来考虑。转子铁芯是在强大的冲击力的作用下由一片片的硅钢片叠压而成,使得硅钢片之间紧固的接触,将形成的铁芯段作为一个整体考虑。
2)将转子线圈槽内的多匝线圈也作为整体考虑并忽略转子的端部效应。转子绕组的两端结构尺寸小而复杂,而且不与冷却空气发生对流换热,所以在建模时将其忽略不考虑,对结果的影响不大。
3)忽略转子铁芯与转轴之间键槽结构的影响。键槽结构实现了转轴和转子之间的动力传递,而其与转子铁芯和转轴采用同种灰铸铁材料,而且尺寸比较小,所以忽略键槽结构对温度场的计算结果影响甚微。
4)假设转子绕组与转子铁芯之间紧密接触,忽略其中的细小缝隙。
经过上述的简化后,模拟船用发电机转子温度场的3D物理模型如图3所示,该计算物理模型主要包括冷却风道中的流体部分和转子铁芯、连接筋、转子绕组3个固体部分。

|
图 3 计算区域三维物理模型 Fig. 3 The 3D physical model of the solution domain |
在柱坐标系中建立数学模型相对容易,根据冷却风道中冷却空气的稳态流动特性,分别建立流动与传热的稳态控制方程,主要包括连续方程、N-S方程以及能量守恒方程[12],并依据上述的简化步骤对数学模型进行简化。本文采用Fluent工具进行模拟,考虑到冷却流体的湍流特性以及转子的结构特点,本文采用湍流的
网格划分的质量直接影响结果的准确性,由于该计算区域有固体和流体部分,存在流体和固体接触、固体和固体接触的情形,所以本文采用分区划分网格的方法,这样不仅能保证整个计算区域采用的是COOPER网格类型,而且也能极大地降低网格数量,还可以减小计算误差,确保正确性。
3.2 边界条件的确定和载荷的施加1)入口边界:本文入口为速度入口,发电机冷却风扇的基本结构参数和转速如表1所示,按照参考文献[13]中的经验计算公式,得到转子出口处风扇带走冷却空气的体积流量Q=1.714 m3/s,已知入口尺寸得到入口面积为0.132 4 m2,推算出在径向上垂直于入口的平均速度为13 m/s,同时转子旋转会对入口速度产生影响,由转子的转速得到冷却气流在周向上的速度为21 m/s。
|
|
表 1 风扇结构参数表 Tab.1 The table of fan's structural parameters |
2)出口边界:给定出口边界为压力出口,出口的相对压力设置为900 Pa。
3)固壁边界:固壁与气流之间采用无滑移边界条件,空气的周向流速等于固壁的转速(750 r/min)。
4)周期性边界:由于计算模型是整体转子的1/12,所以计算区域两径向切面边界设置为周期性边界条件。
5)将流体和固体接触面、固体和固体导热的接触面均定义为耦合边界,在耦合面上能够实现各个物理量的耦合传递。
6)高温的转子的柱表面与四周环境对流换热,根据文献[13]中的理论公式计算得到,转子柱表面向环境的散热系数为212.24
7)将发电机转子的绕组损耗(主要是基本损耗和附加损耗)当作体积热源处理,假设热源项分布均匀,由文献[13]得到热源密度为7 047 450 W/m3。
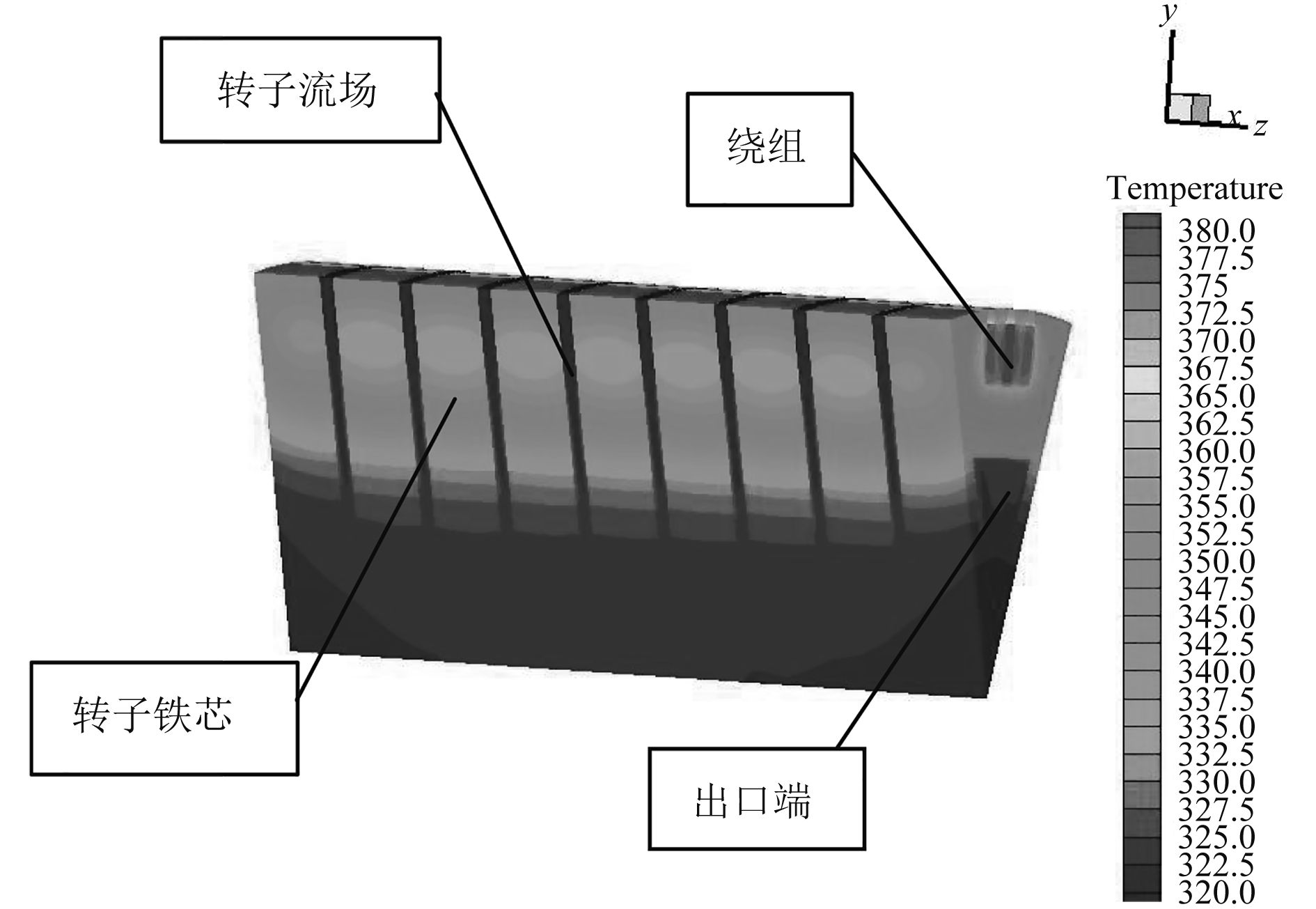
4 计算结果及分析本文采用FVM对耳钉工况下船用发电机转子的求解域进行三维耦合温度场的求解,本文的结果为采用SIMPLE算法获得,计算得到了转子内部的温度场分布云图,如图4所示。
|
图 4 转子计算区域整体温度分布图 Fig. 4 The temperature distribution of the rotor's whole solution domain |
在图4中,左端面为封闭端,右端面则为冷却气流的出口端,从温度分布云图可以看出转子的整体温度介于320 K~377.7 K之间,而且沿轴向上,转子的温度变化不是非常明显,但出口端附近区域的温度略低于封闭端区域的温度,其主要原因是由于出口端的冷却气流的流速相对较快,导致对流换热作用较强,热量更多地传递给冷却空气,所以在出口端附近区域的温度略低。
图5所示为与转子铁芯接触位置处(z=0)连接筋截面上的温度分布云图,图6所示为与冷却空气接触位置(z=0.03)处连接筋在截面上的温度分布云图,将连接筋从左至右依次编号为1~6号。从连接筋的温度分布图中看出,连接筋整体温度介于342.7 K~368.4 K之间。另外,3号、4号连接筋的温度明显高于1号、6号连接筋,造成这种现象的的原因主要是中间的连接筋距离转子绕组近,绕组位于其正下方,起到热源加热作用,所以绕组对该处的连接筋加热作用明显。通过比较图5和图6发现转子铁芯固体域中的连接筋温度高于冷却风道中与流体接触的连接筋部分。相比图6,图5中连接筋的温度在径向上出现了温度分布不均的情况,主要原因是该处连接筋处在冷却风道中,冷却空气绕流连接筋,迎风面的对流换热强度要高于背风面,所以出现迎风面的温度要低于背风面。

|
图 5 连接筋截面温度图(z=0) Fig. 5 The temperature distribution of the connecting bars (z=0) |

|
图 6 连接筋截面温度图(z=0.03) Fig. 6 The temperature distribution of the connecting bars (z=0.03) |
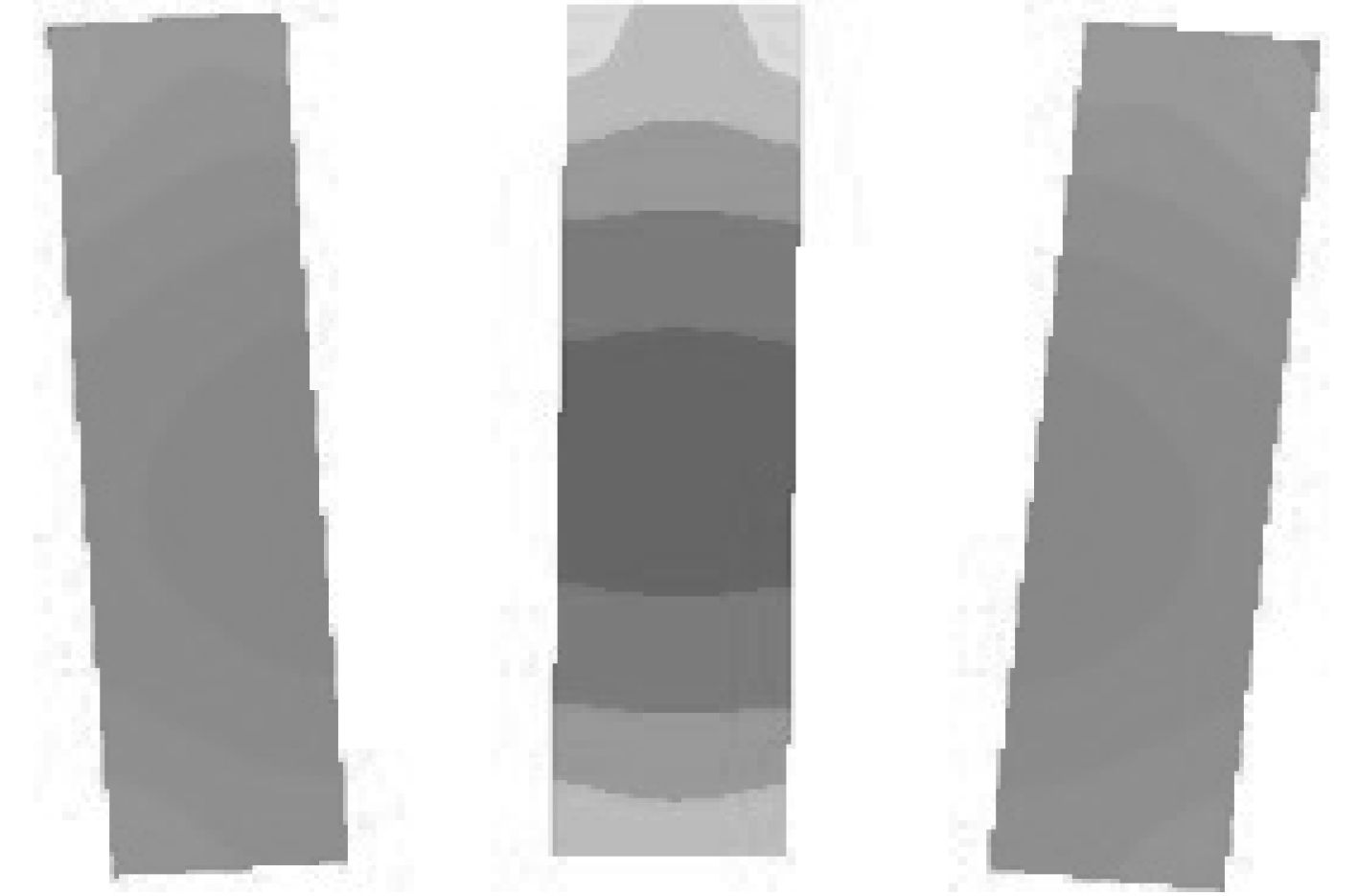
图7为与转子铁芯接触处(z=0)绕组的截面温度场分布,图8为冷却风道中与冷却空气接触的绕组部分(z=0.03)的截面温度场分布。本文将绕组的损耗作为转子的热源项进行处理,起到加热转子的作用,所以其温度比较高,温度范围为371.7 K~377.7 K。转子绕组的温度分布情况与连接筋的类似,绕组中上下两侧的温度明显低于中间区域的温度,这是由于两侧的绕组与转子铁芯发生导热现象或者与冷却空气发生对流换热,将热量传递给铁芯或者空气,所以两侧的温度要相比中间的低。通过图7和图8的比较分析发现,固体域中的中间绕组和流体域中的中间绕组温度分布范围和大小基本相同,但是由于z=0.03处的绕组和冷却空气发生对流作用,导致绕组的热量传递给空气,而且由于迎风面的风速大于背风面,所以迎风面的温度要略低于背风面。
|
图 7 绕组截面温度图(z=0) Fig. 7 The temperature distribution of windings (z=0) |
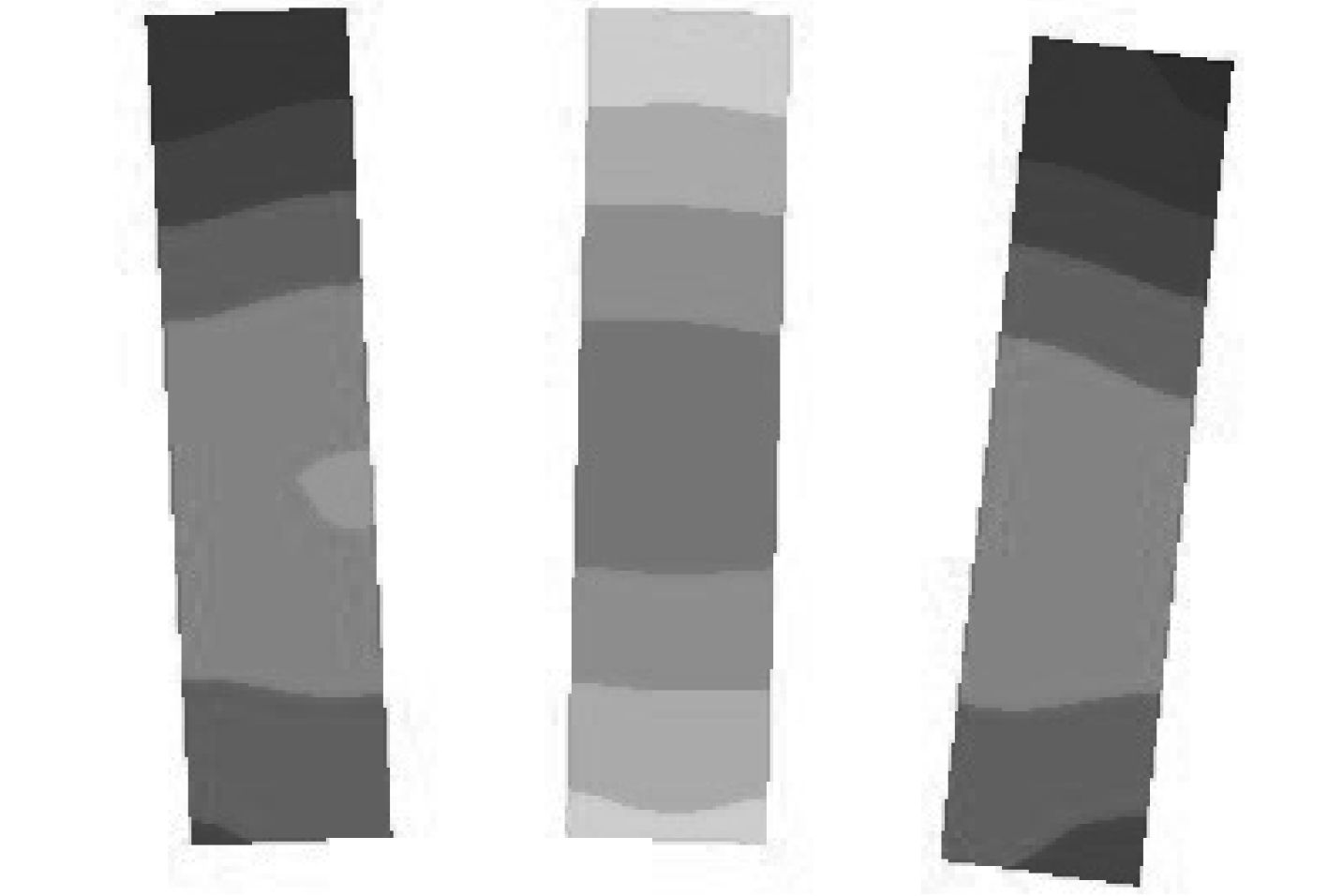
|
图 8 绕组截面温度图(z=0.03) Fig. 8 The temperature distribution of windings (z=0.03) |
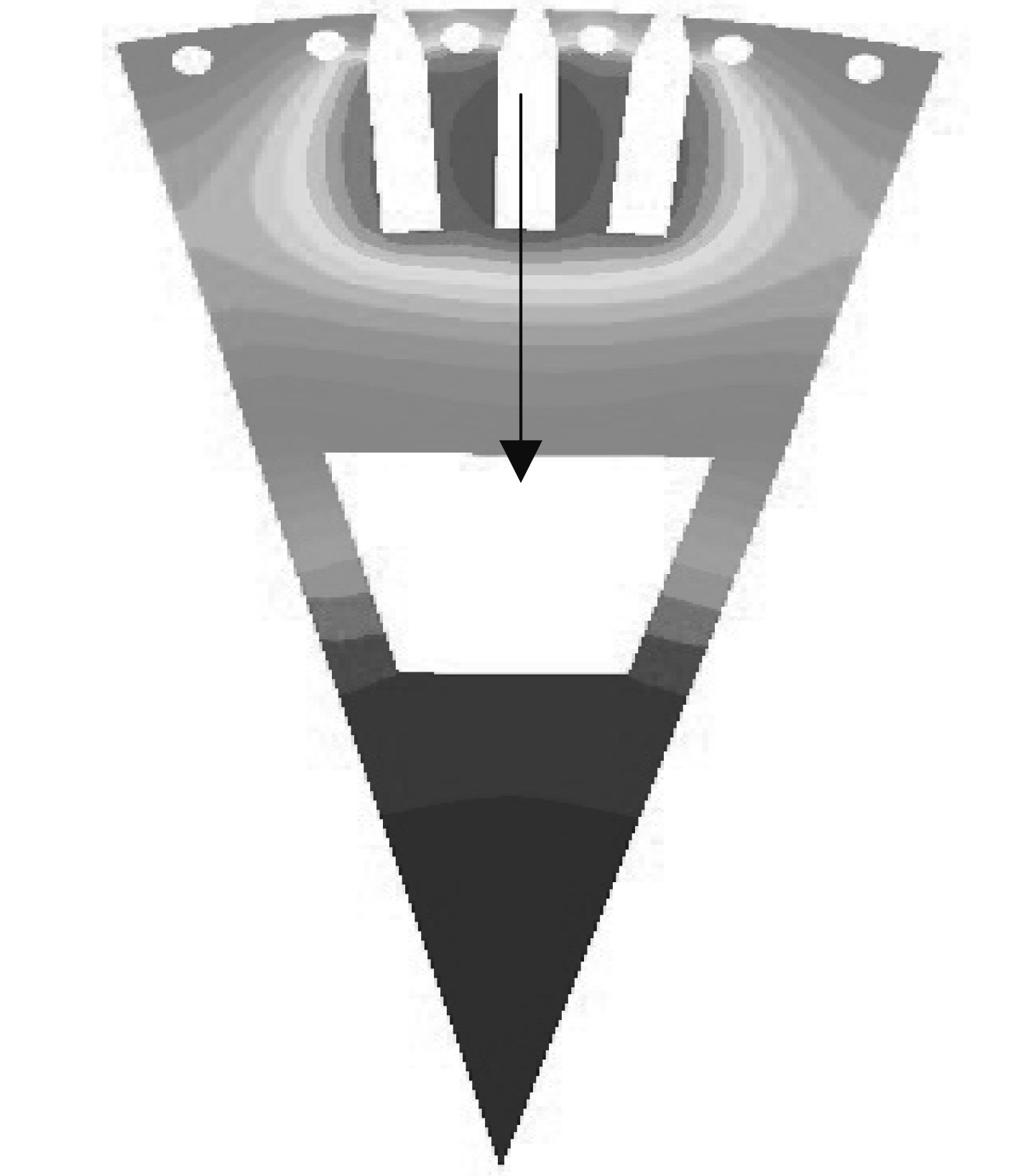
转子铁芯截面(z=0)的温度分布图如图9所示,从图中可知铁芯的温度范围为321.3 K~377.4 K,而且铁芯中的高温区域主要集中在与转子绕组接触的部分,主要由于绕组的加热作用造成。另外,温度沿图中箭头方向逐渐降低,原因是与绕组的距离变远,轴向风道与铁芯的对流换热作用在逐渐增强,所以温度降低;而在轴向风道下方,铁芯的温度变化很小,这是由于流场中的气流带走了大部分热量的缘故。
|
图 9 转子铁芯截面温度图(z=0) Fig. 9 The temperature distribution of rotor core (z=0) |
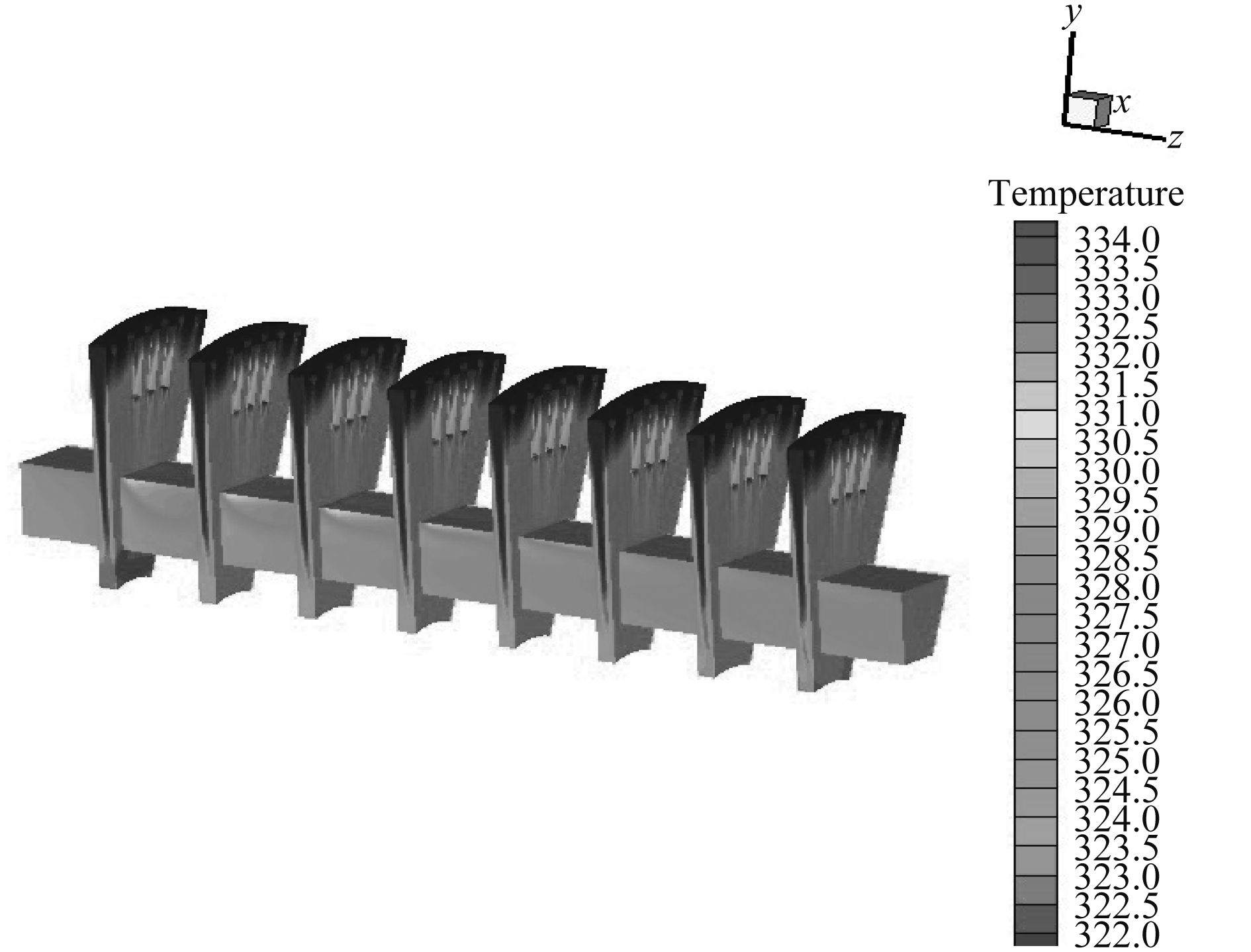
转子内部冷却空气的温度分布如图10所示,其温度范围是320 K~334.4 K。图11和图12则分别是靠近轴向风道区域和绕组区域的温度分布的局部放大图。综合图10~图12可知,在径向风道中,绕组背风面的冷却空气的温度都比较高,主要由以下2个原因造成:1)该区域靠近绕组,而且与铁芯接触,绕组和铁芯对冷却空气的综合加热作用比较强;2)该区域位于绕组的背风面,相比于迎风面,对流换热作用不强,所以温度相对迎风面较高。在轴向通风道中,上壁面的温度高于其他区域,其主要原因是冷却气流由径向风道流入轴向风道时,冷却空气的运动状态发生改变,在此处形成涡流,下壁面处的冷却空气的流速相对上壁面大,所以换热效果好,下壁面温度较上壁面低。
|
图 10 流场区域温度分布图 Fig. 10 The temperature distribution of the fluid region |

|
图 11 流场区域局部放大温度分布图 Fig. 11 The local amplificatory temperature distribution of fluid region |

|
图 12 流场区域局部放大温度分布图 Fig. 12 The local amplificatory temperature distribution of fluid region |
本文以某型船用发电机的转子为研究对象,采用有限体积法对发电机转子与冷却空气的耦合温度场进行模拟,模拟结果为优化该型船用电机温度提供理论依据,并得到如下结论:
1)发电机稳态工作时转子的最高温度为377.7 K,最低温度为320 K,转子的温度在轴向上变化不大,而在径向上温度变化较大。
2)发电机连接筋的温度介于342.7 K~368.4 K之间,绕组的温度范围为371.7 K~377.7 K。这2个部分的温度呈现中间高,两边低。由于绕组的加热作用,所以绕组温度高于其他部分,但是由于两边的绕组对流换热比中间强,所以温度较低。而中间部分的连接筋温度高,主要是由于中间部分的连接筋靠近热源。两者的温度呈现迎风侧的温度低于背风侧,由于迎风侧的对流换热强度大。
3)铁芯的温度范围为321.3 K~377.4 K,而且铁芯中的高温区域主要集中在与转子绕组接触的部分,主要是由于绕组的加热作用造成的。
4)冷却流体的温度范围是320 K~334.4 K,在径向风道中,绕组背风面的冷却空气的温度都比较高,在轴向风道中,靠近风道上壁面的温度高于其他区域。
| [1] |
路义萍, 李伟力. 大型空冷汽轮发电机转子温度场数值模拟[J]. 中国电机工程学报, 2007, 27 (12): 7–13.
LU Yi-ping, LI Wei-li. Numerical simulation of temperature field in rotor of large turbo generator with air-coolant[J]. Proceedings of the CSEE, 2007, 27 (12): 7–13. DOI: 10.3321/j.issn:0258-8013.2007.12.002 |
| [2] |
殷忠敏, 赵海志, 袁媛. 船舶发电机智能诊断系统设计与研究[J]. 舰船科学技术, 2016, 38 (6A): 85–87.
YIN Zhong-min, ZHAO Hai-zhi, YUAN Yuan. Design and research of marine generator intelligent diagnosis system[J]. Ship Science and Technology, 2016, 38 (6A): 85–87. |
| [3] | 刘清, 王滔. 用数值模拟仿真法计算电机内部流场分布[J]. 电机技术, 2015 (06): 10–12. DOI: 10.3969/j.issn.1000-3983.2015.06.003 |
| [4] |
邰永, 刘赵淼. 感应电机全域三维瞬态温度场分析[J]. 中国电机工程学报, 2010, 30 (30): 114–120.
TAI Yong, LIU Zhao-miao. Analysis on three-dimensional transient temperature field of induction motor[J]. Proceedings of the CSEE, 2010, 30 (30): 114–120. |
| [5] | 丁树业, 郭保成, 冯海军, 等. 变频控制下永磁同步电机温度场分析[J]. 中国电机工程学报, 2014, 34 (9): 1368–1375. |
| [6] | 佟文明, 程雪斌, 舒圣浪. 高速永磁电机流体场与温度场的计算分析[J]. 电工电能新技术, 2016, 35 (5): 23–28. |
| [7] | 李东和. 车用油冷电机温度场分析[J]. 微特电机, 2016 (07): 37–40. DOI: 10.3969/j.issn.1004-7018.2016.07.010 |
| [8] |
冯桂宏, 张书伟, 张炳义, 等. 挤塑机直驱永磁电机温度场的计算[J]. 机电工程, 2016, 33 (01): 96–100.
FENG Gui-hong, ZHANG Shu-wei, ZHANG Bin-gyi, et al. Temperature field calculation of the extrusion molding machine direct-drive permanent magnet motor[J]. Journal of Mechanical & Electrical Engineering, 2016, 33 (01): 96–100. DOI: 10.3969/j.issn.1009-9492.2016.01.025 |
| [9] | 王晓远, 高鹏. 电动汽车用油内冷永磁轮毂电机三维温度场分析[J]. 电机与控制学报, 2016, 20 (03): 36–42. |
| [10] |
王越, 张学义, 史立伟, 等. 绕线方式对永磁同步电动机温度场的影响分析[J]. 微电机, 2016, 49 (03): 18–21.
WANG Yue, ZHANG Xue-yi, SHI Li-wei, et al. Analysis of temperature field for permanent magnet synchronous motor with winding mode[J]. Micromotors, 2016, 49 (03): 18–21. DOI: 10.3969/j.issn.1001-6848.2016.03.005 |
| [11] | 赖松林, 曹卉, 刘崇军, 等. 大推力永磁直线同步电机温度场计算与分析[J]. 微电机, 2016, 49 (04): 35–37. |
| [12] |
温志伟, 顾国彪. 实心同极电动机转子温度场计算[J]. 大电机技术, 2005 (02): 1–5.
WEN Zhi-wei, GU Guo-biao. Calculation of rator temperature field for solid pole synchronous motor[J]. Large Electric Machine and Hydraulic Turbine, 2005 (02): 1–5. DOI: 10.3969/j.issn.1000-3983.2005.02.001 |
| [13] | 魏永田, 孟大伟, 温嘉斌. 电机内热交换[M]. 北京: 机械工业出版社, 1998. |
 2017, Vol. 39
2017, Vol. 39
