2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
无人水面艇(Unmanned Surface Vehicle,USV)作为海洋机器人的一种,是构建未来海洋机器人集群和网络的重要组成部分[1]。通过搭载不同类型的传感器和任务载荷,USV能够完成的任务呈现多样性,包括海洋环境监测、水文调查、中继通信、情报收集等[2, 3]。然而为使各类高精尖传感器工作稳定、可靠,USV的艇型设计作为影响其稳定性和耐波性的重要因素已经逐渐成为研究热点。
小水线面双体船(Small Waterplane Area Twin-Hull,SWATH)已经广泛服务于交通运输、海洋监测等重要领域。由于其具有较小的水线面,该船型具有常规船型不具备的水动力特征,包括优良的耐波性和适航性,良好的操纵性等,目前该船型已成为发展迅速的新型高性能船型[4 - 5]。与此同时,研究USV的人们也开始关注这一船型,并将其应用于USV的研制,开展水域监视、海底测绘、路由跟踪,或是作为空中与水下的通信中继等[6 – 8]。小水线面双体无人艇宽阔的甲板方便布置各类任务载荷,吃水较深的潜体适合水声设备的正常工作,优良的稳定性和耐波性为各类声、光、电载荷提供了优良的工作环境。
潜体和支柱的外形是影响小水线面无人艇水动力特性的主要因素,在水动力外形优化设计过程中,对其进行参数化建模有着直接需求。小水线面船的传统建模方法是将控制船舶尺寸和外形的参数划分为主要尺寸参数(主尺度)和型线控制参数,对于生成潜体或支柱部分的型线一般采用圆、椭圆、抛物线或任意曲线经拼接、拟合得到[9 – 11]。另有研究人员基于切比雪夫多项式结合小水线面船型的特征来生成潜体和支柱的相关曲线[12]。这类型线生成方法在曲线局部位置的光顺性方面存在一定不足。为了满足参数化建模的需求并提高型线的光顺性,由一系列特征多边形顶点控制生成的B样条曲线已被应用到小水线面无人艇的建模,保证了建模过程中的光顺性要求[13]。然而,相对于大型船舶,USV的尺度要小得多,其内部布置紧凑的各类部件对局部外形尺度调节能力要求较高。为获得优良的水动力特性,USV对局部外形的曲率调节能力也有一定要求。而目前已有的参数化建模方法在局部外形尺度和曲面曲率调节方面无法满足USV外形优化及总布置设计的要求。
本文针对小水线面双体无人艇潜体和支柱建模过程中局部外形尺度和端部曲率需任意控制的要求,提出了一种由型值点和特征多边形顶点同时控制的均匀有理B样条曲线控制方法,作为潜体和支柱参数化建模过程中的型线,实现小水线面双体无人艇潜体和支柱的参数化建模过程。
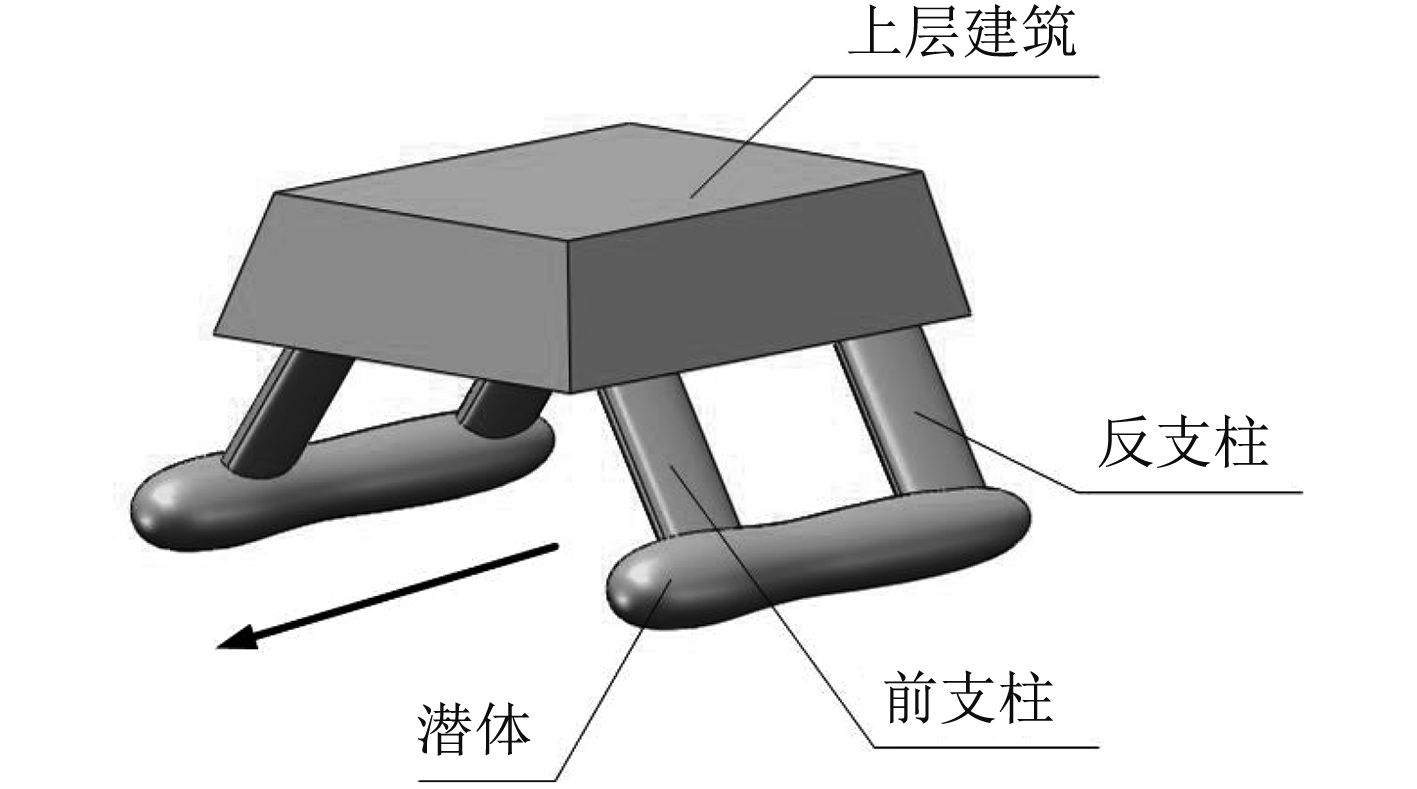
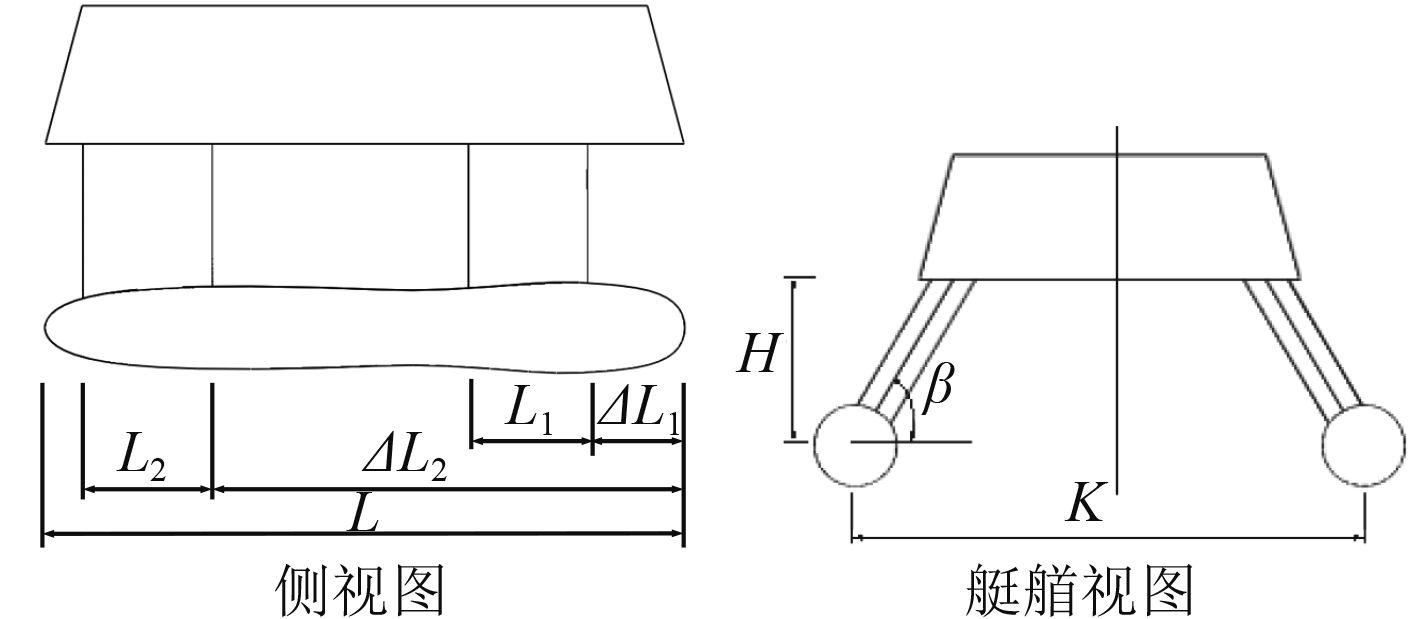
1 研究对象及艇型参数本文的研究对象是一种双体四支柱式小水线面双体无人艇,其结构如图1所示,本文主要研究与水动力性能直接密切相关的潜体和支柱的参数化建模方法。开展参数化建模研究应先确定艇型的主要尺寸参数和潜体、支柱的型线控制参数。主要尺寸参数描述了无人艇的主体尺度和各部件间的相对位置。小水面无人艇在航行过程中不仅要求艇体各部位外形具有很好的流线形特征,各部件相对位置(主要是前后支柱的相对位置和角度)对小水线面无人艇的水动力特性也有一定影响。为使其在航行过程中各部件产生有利干扰,降低航行阻力,提高推进效率,合理的设置主要尺寸参数很必要。主体尺寸参数越多,表达的含义越丰富,为后续优化过程提供更广阔的寻优空间。双体四支柱式小水线面无人艇的主要尺寸参数如图2和表1所示。
|
图 1 小水线面双体无人艇 Fig. 1 USV with SWATH |
|
图 2 小水线面双体无人艇主要尺寸 Fig. 2 Main sizes of USV with SWATH |
|
|
表 1 小水线面双体无人艇的主要尺寸参数 Tab.1 Main sizes parameters of USV with SWATH |
主要尺寸参数定义了小水线面双体无人艇的主要特征尺度,对于潜体和支柱的外形则由型线控制参数和造型方法确定。
2 均匀有理B样条型线参数化表达方法 2.1 小水线面双体无人艇的型线生成方法潜体和支柱型线控制参数主要用于三维模型的生成,并且这些控制参数是与水动力性能密切相关的参数。主要尺寸参数中如潜体长径比、方形系数等要依赖于潜体的型线控制参数的变化而改变。型线控制参数由生成型线的曲线类型确定,不同类型的曲线具有不同数量的控制参数。现阶段用于参数化模型生成的曲线主要有贝赛尔曲线、样条曲线(如均匀有理B样条、非均匀有理B样条)等。不同类型的曲线表达能力不同,表达能力越强的曲线其控制参数越多,曲线控制越灵活,模型曲面的建立越复杂,后续的优化设计工作越困难。本文中针对小水线面双体无人艇潜体和支柱的参数化建模以B样条曲线理论为基础,根据已知的型值点反求出特征多边形顶点,结合附加特征多边形顶点生成样条曲线作为潜体和支柱型线,控制潜体和支柱的外形变化。
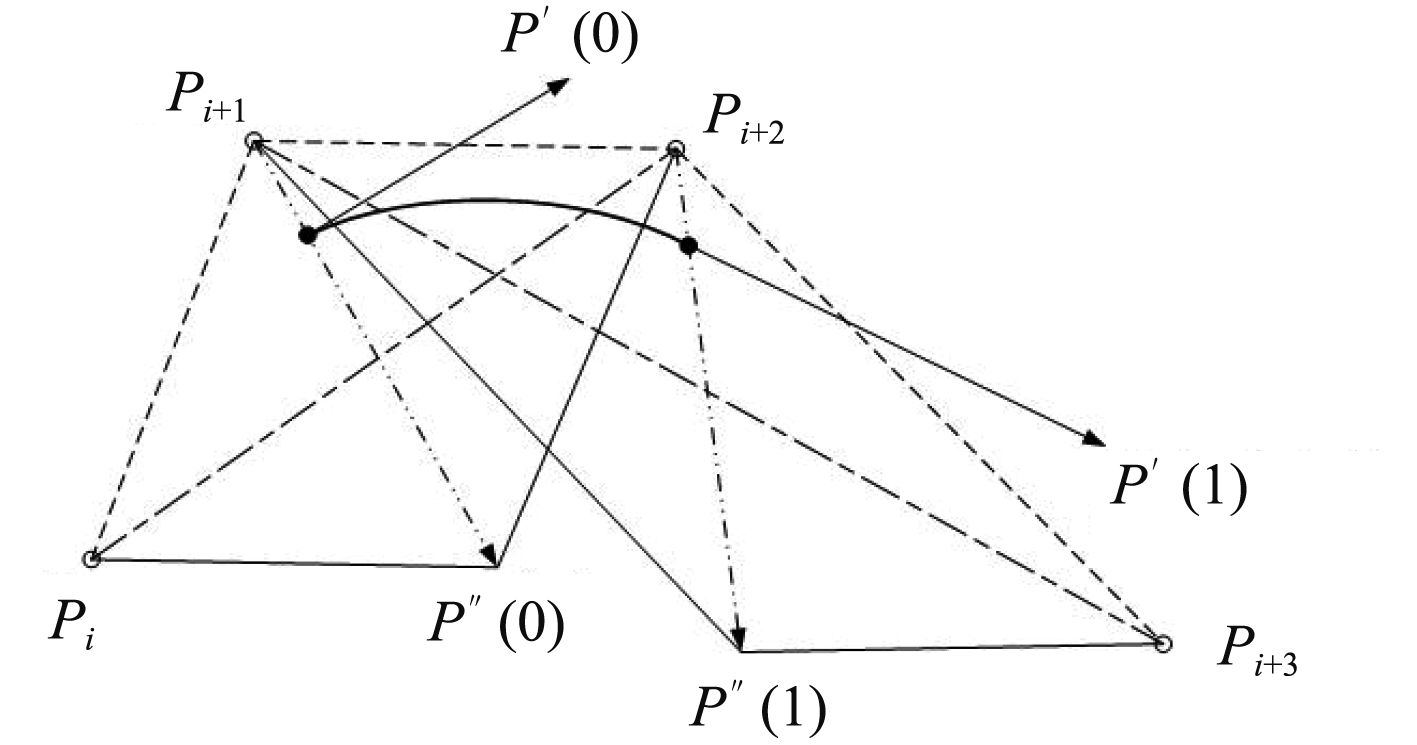
2.2 B样条基本理论均匀三次B样条曲线各个曲线段的首末点具有二阶连续性,满足模型的光顺性要求。空间n+1个控制顶点Pi(i=0,1,2,…,n)可构造n-2段三次(k=3,四阶)均匀B样条曲线段,每相邻4个点可定义一曲线段Pi(u),(i=1,……,n-2)。如任意4个顶点Pi,Pi+1,Pi+2,Pi+3作为特征多边形构造的均匀三次B样条曲线段的方程Pi(u)可表达为:
| $\begin{split}\!\!& {P_i}\left( u \right) = \sum\limits_{j = 0}^3 {{N_{j,3}}\left( u \right){P_{i + j}}}= \\ & \left[ {\begin{array}{*{20}{c}}{{u^3}}&{{u^2}}&u&1\end{array}} \right]\frac{1}{6}\left[ {\begin{array}{*{20}{c}}{ - 1}&3&{ - 3}&1\\3&{ - 6}&3&0\\{ - 3}&0&3&0\\1&4&1&0\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{P_i}}\\{{P_{i + 1}}}\\{{P_{i + 2}}}\\{{P_{i + 3}}}\end{array}} \right]=\!\!\!\!\\ & {N_{0,3}}\!\left( u \right){P_i} \!+\! {N_{1,3}}\!\left( u \right){P_{i + 1}} \!+\! {N_{2,3}}\!\left( u \right){P_{i + 2}} \!+\! {N_{3,3}}\!\left( u \right){P_{i + 3}},\end{split}$ | (1) |
式中:
曲线段2个端点的表达式及其导数如下:
| $\\[-12pt]$\left\{\begin{aligned}{p_i}\left( {\rm{0}} \right) & = \frac{{\rm{1}}}{{\rm{6}}}\left( {{p_i} + {\rm{4}}{p_{i + {\rm{1}}}} + {p_{i + {\rm{2}}}}} \right),\\{{\dot p}_i}\left( {\rm{0}} \right) & = \frac{{\rm{1}}}{{\rm{2}}}\left( {{p_{i + {\rm{2}}}} - {p_i}} \right),\\{{\ddot p}_i}\left( {\rm{0}} \right) & = {p_i} - {\rm{2}}{p_{i + {\rm{1}}}} + {p_{i + {\rm{2}}}},\\{p_i}\left( 1 \right) & = \frac{{\rm{1}}}{{\rm{6}}}\left( {{p_{i + 1}} + {\rm{4}}{p_{i + 2}} + {p_{i + 3}}} \right),\\{{\dot p}_i}\left( 1 \right) & = \frac{{\rm{1}}}{{\rm{2}}}\left( {{p_{i + 3}} - {p_{i + 1}}} \right),\\{{{\rm{\ddot p}}}_i}\left( 1 \right) & = {p_{i + 1}} - {\rm{2}}{p_{i + 2}} + {p_{i + 3}}\text{。}\end{aligned}\right.$$ | (2) |
由以上推导可知,曲线的切矢与Pi+2Pi平行,模为
|
图 3 B样条曲线段的定义 Fig. 3 Definition of B spline segment |
然而在实际设计过程中,往往知道曲线上的型值点,而不知道特征多边形顶点位置。如在潜体参数化建模过程中,为满足结构紧凑性要求,较精确的控制潜体某一位置的尺寸,对型线上某些位置的型值点坐标有较高要求,因此为了构造B样条曲线,需要根据这些型值点反求出曲线特征多边形的顶点。
已知1条三次B样条曲线通过型值点列Bi(i=1,2,…,n-1),求出这一B样条曲线的特征多边形顶点Pi(i=0,1,…,n)。由曲线端点的性质可得下列线性方程组:
| $\\[-3pt]$\begin{aligned}&{B_i}\left( {\rm{0}} \right) = \frac{{\rm{1}}}{{\rm{6}}}\left( {{P_i} + {\rm{4}}{P_{i + {\rm{1}}}} + {P_{i + {\rm{2}}}}} \right),\\&{B_i}\left( 1 \right) = \frac{{\rm{1}}}{{\rm{6}}}\left( {{P_{i + 1}} + {\rm{4}}{P_{i + 2}} + {P_{i + 3}}} \right)\text{。}\end{aligned}. | (3) |
可得:
再补充2个边界条件即可得到唯一解,例如已知2个端点的切矢
| ${P_2} - {P_0} = 2B{'_1},{P_n} - {P_{n - 2}} = 2B{'_{n - 1}}\text{。}$ | (4) |
将其写成矩阵形式为:
| $\left[ {\begin{array}{*{20}{c}}{ - 1}&0&1&{}&{}&0\\1&4&1&{}&{}&{}\\{}&1&4&1&{}&{}\\{}&{}&{...}&{...}&{...}&{}\\0&{}&{}&1&4&1\\{}&{}&{}&{ - 1}&0&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{P_0}}\\{{P_1}}\\{{P_2}}\\{...}\\{{P_{n - 1}}}\\{{P_n}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{2B{'_1}}\\{6{B_1}}\\{6{B_2}}\\{...}\\{6{B_{n - 1}}}\\{2B{'_{n - 1}}}\end{array}} \right]\text{。}$ | (5) |
由此求出B样条特征多边形的顶点Pi,即可生成相应的B样条曲线。
2.3 特征多边形顶点与型值点共同控制的均有有理B样条仅仅有型值点虽然能够构造成B样条曲线,但是曲线局部位置的曲率变化很难控制,如在潜体首部和尾部设计过程中,首尾沿纵向的曲率变化对水动力性能有较重要影响,而仅根据已知型值点反求出的曲线特征多边形顶点唯一,即曲线不能再被操作,因此无法满足造型过程中曲面曲率变化要求。为此,在根据型值点反求出特征多边形控制顶点的过程中,在首部和尾部各引入一个附加的特征多边形顶点,首尾3个特征多边形顶点决定了首尾型值点切矢的大小和方向,决定了潜体首尾的曲率变化。这样,在特征多边形顶点和曲线型值点的双重驱动下能够生成满足参数化建模要求的B样条曲线。
从B样条反求过程可以看出,已知型值点列Bi(i=1,2,…,n-1)和2个端点的切矢边界条件
| ${P_0} - 2{P_1} + {P_2} = B'{'_1},{P_{n - 2}} - 2{P_{n - 1}} + {P_n} = B'{'_{n - 1}}\text{。}$ | (6) |
为保证求解的唯一性和有效性,需在P1和Pn-1后引入2个未知的特征多边形的顶点P1+、Pn+,两端型值点B1、Bn-1的边界条件为
| ${P_{1 + }} - {P_0} = 2B{'_1},{P_{n + }} - {P_{n - 1}} = 2B{'_{n - 1}},$ | (7) |
| ${P_0} - 2{P_1} + {P_{1 + }} = B'{'_1},{P_{n - 1}} - 2{P_n} + {P_{n + }} = B'{'_{n - 1}}\text{。}$ | (8) |
将其写成矩阵形式为:
| $\left[ \!\!\!{\begin{array}{*{20}{c}}1 \!\! & \!\!{ - 2}\!\! & \!\!1\! & \!\!{}\!\! & \!\!{}\!\! & \!\!{}\! & \!\!{}v\! & \!\!0\\{ - 1}\!\! & \!\!0 \!\! & \!\!1\!\! & \!\!{}\!\! & \!\!{} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {}\\1 \!\! & \!\! 4 \!\! & \!\! 1 \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {}\\{} \!\! & \!\! {} \!\! & \!\! 1 \!\! & \!\! 4 \!\! & \!\! 1 \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {}\\{} \!\! & \!\! {} \!\! & \! \! {} \!\! & \!\! {...} \!\! & \!\! {...} \!\! & \!\! {...} \!\! & \!\! {} \!\! & \!\! {}\\{} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! 1 \!\! & \!\! 4 \!\! & \!\! 1\\{} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! { - 1} \! & \! 0 \! & \! 1\\0 \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! {} \!\! & \!\! 1 \!\! & \!\! { - 2} \!\! & \!\! 1\end{array}} \right]\left[ \!\!\!\!{\begin{array}{*{20}{c}}{{P_0}}\\{{P_1}}\\\begin{array}{l}{P_{1 + }}\\{P_2}\end{array}\\{...}\\{{P_{n - 1}}}\\\begin{array}{l}{P_n}\\{P_{n + }}\end{array}\end{array}}\!\!\!\!\!\!\! \right] \!=\! \left[ \!\!\!\!\!{\begin{array}{*{20}{c}}\begin{array}{l}B'{'_1}\\2B{'_1}\end{array}\\{6{B_1}}\\{6{B_2}}\\{...}\\{6{B_{n - 1}}}\\\begin{array}{l}2B{'_{n - 1}}\\B'{'_{n - 1}}\end{array}\end{array}}\!\!\!\!\!\!\! \right ]$ | (9) |
由此矩阵求得特征多边形顶点可以确定n段三次B样条曲线,其中B1B2之间两段,Bn-2Bn-1之间两段,其它相邻型值点之间各一段。由此矩阵计算的结果如下:
| $\left\{\begin{aligned}&{P_0} = {B_1} - B{'_1} + \frac{1}{3}B'{'_1};\\&{P_1} = {B_1} - \frac{1}{6}B'{'_1};\\&{P_{1 + }} = {B_1} + B{'_1} + \frac{1}{3}B'{'_1};\\&{P_i} = f\left( {B'{'_1},B{'_1},{B_1},...,{B_{n - 1}},B{'_{n - 1}},B'{'_{n - 1}}} \right),\\&\ \ \; i = 2,3,...,n - 2;\\&{P_{n - 1}} = {B_{n - 1}} - B{'_{n - 1}} + \frac{1}{3}B'{'_{n - 1}};\\& {P_n} = {B_{n - 1}} - \frac{1}{6}B'{'_{n - 1}};\\& {P_{n + }} = {B_{n - 1}} + B{'_{n - 1}} + \frac{1}{3}B'{'_{n - 1}}\text{。}\end{aligned}\right.$ | (10) |
根据均匀三次有理B样条曲线段特点,令首末型值点位置的导矢为0,则首末型值点的切矢始于该型值点,切矢方向与首末3个特征多边形顶点共线。即令
| $\left\{\begin{aligned}& {P_0} = {B_1} - B{'_1};\\& {P_1} = {B_1};\\& {P_{1 + }} = {B_1} + B{'_1};\\& {P_i} = f\left( {0,B{'_1},{B_1},...,{B_{n - 1}},B{'_{n - 1}},0} \right),\\& \ \ \; i = 2,3,...,n - 2;\\ &{P_{n - 1}} = {B_{n - 1}} - B{'_{n - 1}};\\& {P_n} = {B_{n - 1}};\\& {P_{n + }} = {B_{n - 1}} + B{'_{n - 1}}\text{。}\end{aligned}\right.$ | (11) |
即P1与B1重合,Pn-1与Bn-1重合,P0与P1+关于P1对称,Pn-1与Pn+关于Pn对称,首末型值点切矢的模分别为
将2个新增的特征多边形顶点P1+、Pn+作为已知量,可求得:
| $\left\{\begin{aligned}& {P_0} = 2{B_1} - {P_{1 + }};\\& {P_1} = {B_1};\\& B{'_1} = {P_{1 + }} - {B_1};\\& {P_i} = f\left( {0,{P_{1 + }} - {B_1},{B_1},...,{B_{n - 1}},{P_{n + }} - {B_{n - 1}},0} \right),\\& \ \ \; i = 2,3,...,n - 2;\\& B{'_{n - 1}} = {B_{n - 1}} - {P_{n - 1}};\\& {P_n} = {B_{n - 1}};\\& B{'_{n - 1}} = {P_{n + }} - {B_{n - 1}}\text{。}\end{aligned}\right.$ | (12) |
由上式可以得到由2个已知的特征多边形顶点和多个型值点确定的三次均匀有理B样条曲线,型值点能够精确的确定曲线某位置的坐标,2个特征多边形的顶点可以直观地反映曲线在首末端点位置的斜率大小和曲率变化影响程度。在特征多边形添加顶点的曲线表达方法理论上是在样条曲线反算过程中通过添加端点的导矢边界条件实现(曲线在B1、Bn-1点位置的曲率),然而在造型过程中不如特征多边形顶点直观。
3 小水线面双体无人艇的参数化建模本文对直接影响水动力性能的潜体和支柱的参数化建模方法开展研究。
3.1 潜体的建模潜体的建模方式通常是采用单个或多个剖面沿某一引导线经过扫描或放样完成,以单一圆形剖面潜体为例,通过在引导线的控制下沿纵向扫描,形成潜体的基本外形。引导线的型线特征和尺寸便是控制潜体外形和尺度的主要因素。
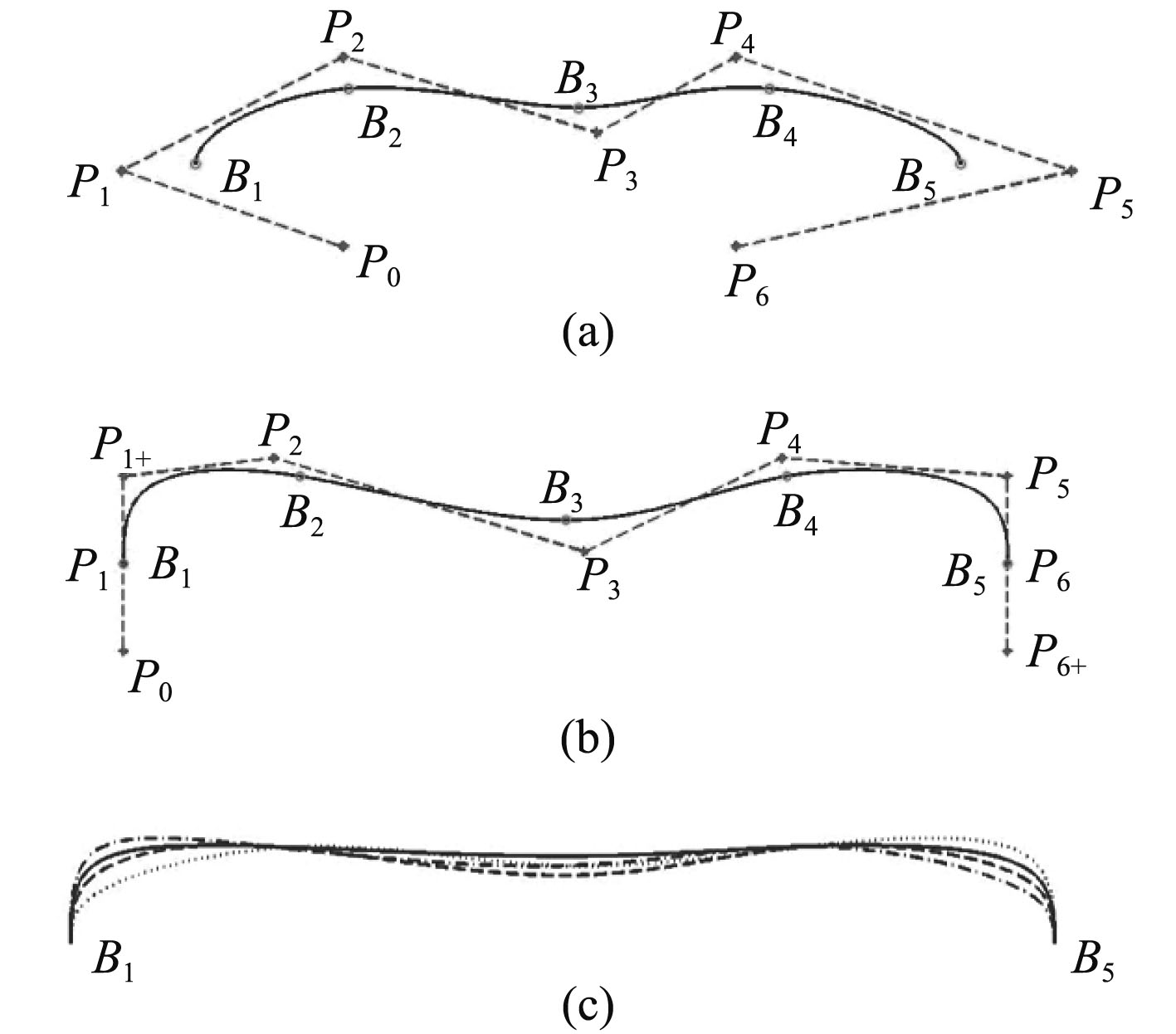
在引导线生成过程中,以5个型值点B1~B5为例作为控制潜体外形和尺度的基本参数,能够反求出均匀三次有理B样条的特征多边形顶点P0~P6。如图4(a)所示,在特征多边形中引入P1+和P6+顶点,P1+与B1连线、P6+与B5连线垂直于潜体轴向,使潜体端部不会产生尖点,生成由5个型值点和2个特征多边形顶点同时控制的引导线如图4(b)所示。各型值点和顶点位置的作用如表2所示。
|
|
表 2 潜体各型值点和顶点作用 Tab.2 Effect of molded value points and characteristics polygon vertexes on submerged bodies |
|
图 4 潜体的引导线 Fig. 4 Guided lines of submerged bodies |
B1,B5由L确定,成为主要尺寸参数,B2~B4,P1+和P6+成为外形控制参数。当主要尺寸参数中的L确定后,在不同外形参数控制下产生的引导线如图4(c)所示。以单一圆形作为潜体剖面形状,通过沿不同参数控制下的引导线造型生成的潜体如图5所示。

|
图 5 潜体的三维模型 Fig. 5 3-D models of submerged bodies |
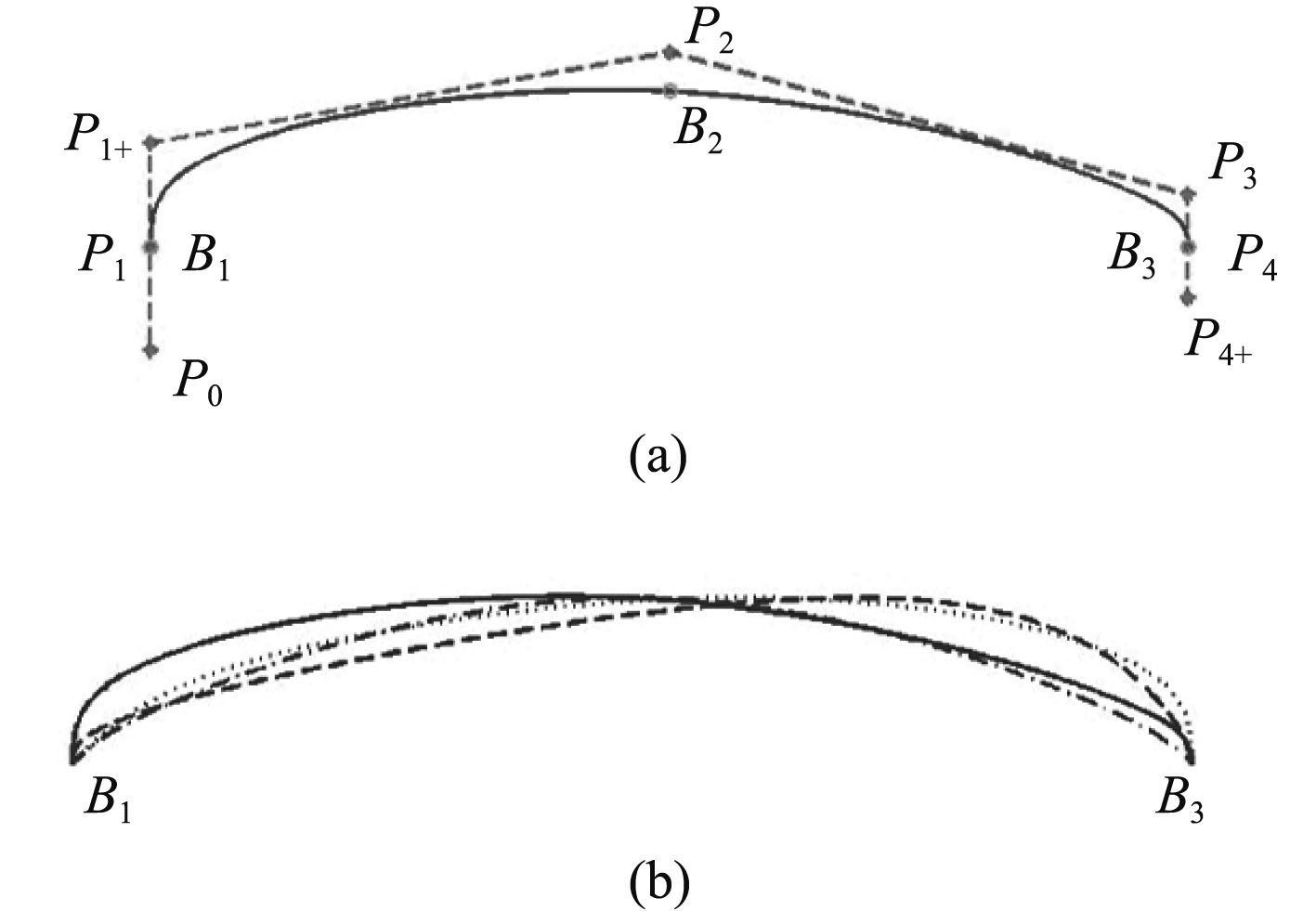
支柱的建模过程主要是支柱剖面线的生成。采用与潜体引导线相同的生成方法,对于支柱单侧剖面线,选取3个型值点B1~B3和2个特征多边形顶点P1+,P3+作为控制参数,生成的支柱单侧剖面线的外形如图6(a)所示。各型值点和顶点确定方法和作用如表3所示。
|
|
表 3 支柱各型值点和特征多边形顶点作用 Tab.3 Effect of molded value points and characteristics polygon vertexes on struts |
|
图 6 支柱半侧剖面线 Fig. 6 Half section lines of struts |
支柱另一侧剖面线可以根据对称或非对称的要求用同一方法生成。不同的型值点和特征多边形顶点控制下的单侧剖面线如图6(b)所示。
参数化建模过程中,主要尺寸参数(如L,K,H,β,ΔL1,L1,ΔL2,L2)决定了无人艇的主要尺度、潜体和支柱的尺度和前后支柱的相对位置,型线控制参数(潜体和支柱型线中的非端部型值点和附加的特征多边形顶点)决定了潜体和支柱的外形变化。采用本文提出的参数化建模和B样条生成方法,通过设定各参数建立的小水线面无人艇潜体和支柱的参数化模型示例如图7所示。

|
图 7 小水线面无人艇潜体与支柱的参数化模型 Fig. 7 Parametric model of submerged bodies and struts on USV with SWATH |
基于CFD的船舶水动力学研究已经得到越来越广泛的应用。目前大部分商业CFD求解器普遍基于求解N-S方程的方法,结合湍流模型的应用求解流域内流体的运动特征,采用VOF方法捕捉求解过程中自由液面的变化,结合动网格的应用,CFD技术可以准确获得船舶运动过程中阻力和姿态的变化。以小水线面双体无人艇模型为计算对象,经网格划分、前处理、求解和后处理等过程,得到无人艇模型在不同傅汝德数下的兴波特征和阻力特性如图8和图9所示。

|
图 8 小水线面双体无人艇兴波特征 Fig. 8 Wave performance of the SWATH USV |
|
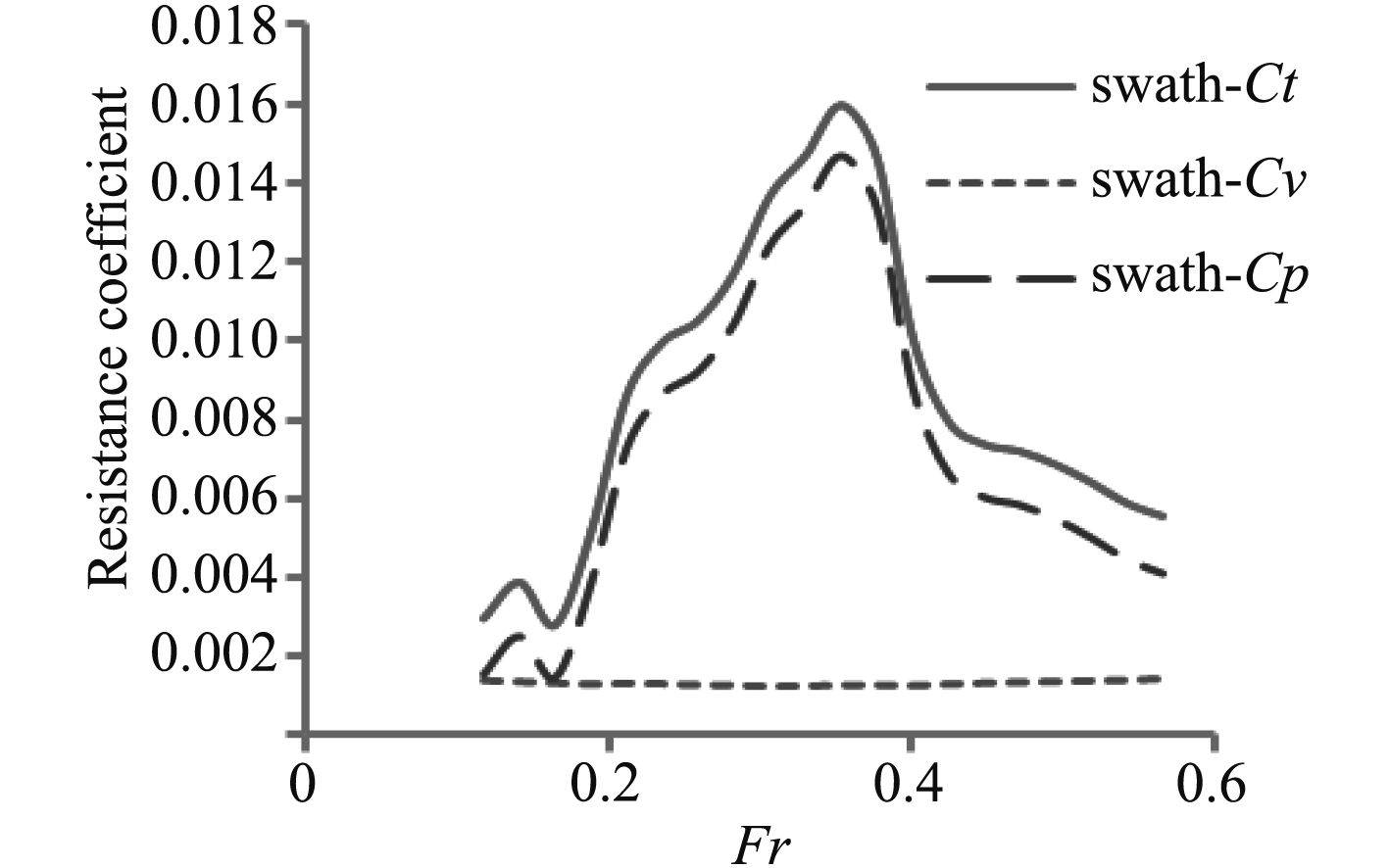
图 9 阻力系数随长度傅汝德数Fr变化 Fig. 9 Change of resistance coefficient with length Froude number Fr |
小水线面双体无人艇的兴波和阻力特征与常规的小水线面双体船相似。由于其水线面积较小,其兴波阻力相对常规排水型船舶要小得多,特别是随着速度的上升,小水线面双体无人艇的阻力系数达到极大值后会迅速下降(图9中Fr约为0.35位置)。尤其当前后支柱的兴波形成有利干扰时,小水线面双体无人艇阻力会大大降低,这对于提高无人艇的总体性能具有很大优势。
5 结 语本文提出了一种由型值点和特征多边形顶点同时控制生成的三次均匀有理B样条曲线表达方法,满足了小水线面双体无人艇参数化过程中对局部外形尺度和端部曲面曲率的自由调节需求。相对于其他型线生成方式(如简单曲线的拼接、多项式表达或传统B样条生成方法),本文提出的型线生成方法,型值点作为外形设计变量,在模型局部尺度方面具有更高的调节精度和较强的调节能力,附加的特征多边形顶点能够直观地调节模型端部曲面的斜率和曲率变化。利用本文提出的型线生成方法建立了小水线面双体无人艇的参数化模型,型值点和附加的特征多边形顶点为后续针对水动力性能的优化提供了多个可供选择的设计变量和广阔的设计空间。
本文建立的小水线面无人艇参数化模型采用了简单的回转体潜体,并对模型开展了阻力特性的数值计算。未来将基于本文提出的型线生成方法根据模型需求建立具有复杂非回转体潜体外形的无人艇参数化模型,并针对水动力特性开展参数化模型的优化设计工作。
本文提出的由型值点和特征多边形顶点同时控制的均匀有理B样条曲线生成方法不仅仅适用于小水线面双体无人艇的参数化建模过程,同样适用于其他要求具有局部尺度和曲面曲率调节能力的光顺曲面特征对象建模过程。
| [1] |
封锡盛, 李一平, 徐红丽. 下一代海洋机器人-写在人类创造下潜深度世界纪录10912米50周年之际[J]. 机器人, 2011, 33 (1): 112–118.
FENG Xi-sheng, LI Yi-ping, XU Hong-li. The Next Generation of Unmanned Marine Vehicles-Dedicated to the 50 ANNIVERSARY OF THE Human World Record Diving 10912 m[J]. Robot, 2011, 33 (1): 112–118. |
| [2] | MOHAMED Z. YAAKOB O., HANAFIAH M. S., etc, Development of unmanned surface vehicle (USV) for sea patrol and environmental monitoring[C]// International Conference on Marine Technology, Kuala Terengganu, Malaysia, 2012, 10, 20–22. |
| [3] | JAMES C. Autonomous mission planning and execution for unmanned surface vehicles in compliance with the marine rules of the road[M]. Washington, University of Washington, 2007. |
| [4] | 黄鼎良. 小水线面双体船性能原理[M]. 北京: 国防工业出版社, 1993. |
| [5] |
李水才, 许晟, 杨帅. 高速小水线面双体船船型研究[J]. 舰船科学技术, 2012, 34 (Supplement 2): 78–82.
LI Shui-cai, XU Sheng, YANG Shuai. Research on high-speed SWATH hull form[J]. SHIP SCIENCE AND TECHNOLOGY, 2012, 34 (Supplement 2): 78–82. |
| [6] | MARCO Bovio Stefano Brizzolara, ALESSANDRO F, GIULIANO V. Hydrodynamic design of a family of hybrid SWATH unmanned surface vehicles[C]// 11th International Conference on Fast Sea Transportation, Honolulu, Hawaii, USA, 2011 September. |
| [7] | Sapto Adi Nugroho Muljowidodo K. , Nico Prayogo, Munif Sudaryono. Design and Analysis of Laminar Hull SWATH Based Unmanned Surface Vehicle[J]. Indian Journal of Geo-Marine Science, 2011, April, 40 (2): 214–221. |
| [8] | Paul Mahacek Christopher Kitts, Thomas Adamek, et al. Field operation of a robotic small waterplane area twin hull boat for shallow-water bathymetric characterization[J]. Journal of Field Robotics, 2012, 29 (6): 924–938. DOI: 10.1002/rob.v29.6 |
| [9] |
程操红, 林焰, 纪卓尚, 陆丛红, 等. 小水线面双体船型线设计方法研究[J]. 中国造船, 2005, 29 (6): 924–938.
CHENG Cao-hong, LIN Yan, JI Zhuo-shang, LU Cong-hong, et al. Rerearch on Method of SWATH Ship Form Design[J]. Shipbuilding of China, 2005, 29 (6): 924–938. |
| [10] |
毛筱菲, 谭廷寿. 小水线面双体船(SWATH)优化设计及数值方法[J]. 船舶力学, 2010, 14 (7): 749–756.
MAO Xiao-fei, TAN Ting-shou. Numerical Method and Program for SWATH Ship Optimization Design[J]. Journal of Ship Mechanics, 2010, 14 (7): 749–756. |
| [11] |
郑义, 卢晓平, 董祖顺, 郦云, 等. 小水线面单体船船型与阻力研究[J]. 船舶力学, 2007, 11 (4): 553–563.
ZHENG Yi, LU Xiao-ping, DONG Zu-shun, LI Yun, et al. An Investigation of SWATH Ship Forms and Resistance[J]. Journal of Ship Mechanics, 2007, 11 (4): 553–563. |
| [12] |
金亨哲, 刘亚东, 谭家华. 一种生成小水线面双体船型线的简单方法[J]. 造船技术, 2006 (2): 10–16.
JIN Heng-zhe, LIU Ya-dong, TAN Jia-hua. A Simple Method to Generate SWATH Line[J]. Marine Technology, 2006 (2): 10–16. |
| [13] | Stefano Brizzolara, Tom Curtin, Marco Bovio, Giuliano Vernengo. Concept design and hydrodynamic optimization of an innovative SWATH USV by CFD methods[J]. Ocean Dynamics, 2011, 62 (2): 227–237. |
 2017, Vol. 39
2017, Vol. 39
