0 引　言

故障模式与影响分析（FMEA）是一种产品设计阶段用来识别、确定和排除在系统或子系统中潜在的故障模式的工程技术。它通过分析系统或子系统中所有可能对系统造成影响的故障模式及故障原因，判断这种影响的危害度有多大，从而找出系统中潜在的薄弱环节，并采取必要的预防措施，以避免造成不必要的损失和人员伤亡^[1]。

传统FMEA分析方法是通过分析系统设计或产品中潜在的故障模式来确定每种故障模式的发生频率（Occurrence Probability Ranking），严重度（Effect Severity Ranking），难检测度（Detection Difficulty Ranking），进而计算各故障模式的风险等级并进行风险排序^[2]。但传统的FMEA方法存在以下不足：①传统的FMEA方法对故障发生频率（O）、故障影响严重度（S）、检测难易程度（D）进行打分，通过三者乘积得到RPN值由此来确定各个故障模式的风险排序。但其认为三者重要性一样，没有考虑到三者的相对重要性，因此得到的结果并不准确。②在进行FMEA过程中，由于各个专家会使用不同的术语来评价，也可能使用不同标准的语言、数字和符号来描述评价结果，因此传统FMEA方法很难对专家的经验做出准确判断。

由于传统FMEA方法的缺陷，FMEA方法受到许多国内外学者的研究与改进。TAY K M等^[3]提出一种简化的FMEA模糊评价模型，但这样的结果并不准确。BOWLES 等^[4]将FMEA方法与模糊理论相结合，采用了一种基于模糊逻辑的FMEA方法，在模糊术语中采纳专家的知识和经验。李雯^[5]采用模糊理论将O，S，D三个风险因子模糊化，然后根据专家权重对模糊数去模糊化从而对各个故障模式进行风险排序。

本文首先用专家的知识和经验来建立模糊术语集和其对应的模糊数，对各个故障模式进行评价，然后对评价结果进行清晰化处理。最后，利用灰色关联度理论计算各种故障模式的灰色关联度，通过计算结果对各个故障模式进行风险顺序^{[6 – 10]}。

1 建立O，S，D的模糊术语集

传统FMEA方法将3个风险因子O，S，D看作模糊语言变量，本文将专家知识和经验应用到模糊集理论中，从而建立O，S，D的模糊术语集和相应的模糊数，为各个故障模式进行模糊评价提供依据。

1.1 建立O，S，D的模糊术语集

3个风险因子O，S，D是模糊语言变量，每个语言变量的评语集为：O/S/D={很低（R）、低（L）、中等（M），高（H），很高（VH），模糊术语的具体含义见表1。

1.2 模糊术语对应的模糊数

模糊信息可以用模糊数来定量化描述。有很多种模糊数，这里采用三角模糊数定量化处理模糊术语。三角模糊数的表达式：N=（a，b，c），其隶属函数为:

${\lambda _N}(x) = \left\{ \begin{array}{l}0\text{，}\quad \quad \quad \quad \quad \quad x \leqslant a\text{，}\\(x - a)/(b - a)\text{，}\quad \,a < x \leqslant b\text{，}\\(c - x)/(c - b)\text{，}\quad \;b < x \leqslant c\text{，}\\0\text{，} \quad \quad \quad \quad \quad \quad x > c\text{。}\end{array} \right.$

(1)

通过专家的知识和经验可以来确定三角模糊数。假设n个专家中第i个专家的权重是α_i，对故障模式其中一变量的模糊评价术语为μ_i，三角模糊数的表达形式为 ${\mu _i} = ({l_i},{m_i},{u_i})$ ，由式（2）~式（4）可得到该变量的模糊术语对应的三角模糊数：

$l = \sum\limits_{i = 1}^n {{\alpha _i}{l_i}} \text{，}$

(2)

$m = \sum\limits_{i = 1}^n {{\alpha _i}{m_i}}\text{，} $

(3)

$u = \sum\limits_{i = 1}^n {{\alpha _i}{u_i}}\text{。} $

(4)

1.3 三角模糊数去模糊化

模糊数清晰化的方法有多种，它是应用灰色关联理论的依据。这里尝试用模糊概率方法处理三角模糊数，具体公式如下：

$\begin{split}A(x) = &\displaystyle\frac{1}{{2(1 + N)}}l + \frac{{N + 2NM + M}}{{2(1 + N)(1 + M)}}m+\\ & \frac{1}{{2(1 + M)}}u\text{。}\end{split}$

(5)

式中：M，N的值由l，u与m的偏离程度来确定，分别表示确定结果是m的可能性大小是u的M倍。同样，确定结果是m的可能性大小是l的N倍。

2 基于灰色关联度的风险排序

灰色关联理论是对运行机制与物理原型不清晰或者根本缺乏物理原型的关系序列化、模式化，能为复杂系统的建模提供重要的技术分析手段^[7]。它的基本思想是将各因素的样本数据作为依据。然后计算各因素间的灰色关联度，通过计算结果描述各因素间的关系强弱。如果结果反映两因素变化趋势基本一致，则它们之间关联度较强；反之，关联度较弱。本文在已建立的模糊术语集对故障模式做出评价的基础上，利用灰色关联决策方法计算灰色关联度并用计算结果对各种故障模式进行风险排序。

2.1 建立比较判断矩阵

假设某系统故障模式集为： $X = \{ {x_1},{x_2}, \cdots {x_n}\} $ ，其中第j种故障模式为x_j。因为每种故障模式均有O，S，D三个风险因子，因此故障模式的比较判断矩阵是一个n×3矩阵。通过式（5）计算可以得到该矩阵中各个元素的具体数值，则比较判断矩阵为：

$\{ {x_j}(i)\} = \left( \begin{array}{l}{x_1}\\{x_2}\\ \vdots \\{x_n}\end{array} \right) = \left( {\begin{array}{*{20}{c}}{{x_1}(1)}&{{x_1}(2)}&{{x_1}(3)}\\{{x_2}(1)}&{{x_2}(2)}&{{x_2}(3)}\\ \vdots & \vdots & \vdots \\{{x_n}(1)}&{{x_n}(2)}&{{x_n}(3)}\end{array}} \right)\text{。}$

本文共有5中故障模式，因此取n=5，则有比较矩阵 $\{ {x_j}(t)\} $ ：

$\{ {x_j}(i)\} = \left\{ {\begin{array}{*{20}{c}}{{x_1}(1)}&{{x_1}(2)}&{{x_1}(3)}\\{{x_2}(1)}&{{x_2}(2)}&{{x_2}(3)}\\{{x_3}(1)}&{{x_3}(2)}&{{x_3}(3)}\\{{x_4}(1)}&{{x_4}(2)}&{{x_4}(3)}\\{{x_5}(1)}&{{x_5}(2)}&{{x_5}(3)}\end{array}} \right\}\text{。}$

2.2 建立参考矩阵

参考矩阵由故障模式中所有风险因子的理想水平决定，本文参考矩阵可选择最低水准，则参考矩阵表示为：

$\left\{ {\mathit{\boldsymbol{x_0}}\left( {t} \right)} \right\} = \left( {\begin{array}{*{20}{c}}{{h_{11}}}&{{h_{11}}}&{{h_{11}}}\\ \vdots & \vdots & \vdots \\{{h_{11}}}&{{h_{11}}}&{{h_{11}}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{10}&{10}&{10}\\{10}&{10}&{10}\\{10}&{10}&{10}\\{10}&{10}&{10}\\{10}&{10}&{10}\end{array}} \right)\text{。}$

2.3 计算灰色关联系数

由式（6）可计算得到所有故障模式关于每个风险因子的关联系数^[11]：

$\begin{split}{l}&\varepsilon ({x_0}(t),{x_j}(t)) = \\&\displaystyle\frac{{\mathop {\min }\limits_j \;\mathop {\min }\limits_t \;\;\left| {{x_0}(t) \!-\! {x_j}(t)} \right|\! +\! \xi \mathop {\max }\limits_j \;\mathop {\max }\limits_t \;\;\left| {{x_0}(t) - {x_j}(t)} \right|}}{{\left| {{x_0}(t) \!-\! {x_j}(t)} \right| \!+\! \xi \mathop {\max }\limits_j \;\mathop {\max }\limits_t \;\;\left| {{x_0}(t) - {x_j}(t)} \right|}}\end{split}\text{。}\!\!$

(6)

式中：j为故障模式，t为风险因子， $\xi $ 为灰色关联分辨系数。分辨系数只影响故障模式风险的相对值，不改变故障模式的风险优先顺序，通常取0.5。

2.4 计算灰色关联度

在FMEA过程中，每个风险因子的影响程度决定了它们的权重，设故障模式O，S，D三个风险因子的权重向量为： $\omega = {(0.4,0.4,0.2)^{\rm T}}$ 。则可由式（7）得到第j种故障模式与参考基准的灰色关联度：

$\Gamma ({x_0},{x_{_j}}) = \sum\limits_{t = 1}^3 {{\omega _t}\{ } \varepsilon ({x_0}(t),{x_j}(t))\}\text{。} $

(7)

式中： $\displaystyle\sum\limits_{t = 1}^3 {{\omega _t} = 1} $ 。

2.5 风险排序

灰色关联度代表故障模式风险水平与理想水平的关系，由于本文选择最低水平作为参考基准，则某一故障模式的灰色关联度越高则其风险水平越高，按照计算得到的灰色关联度对故障模式进行风险排序。

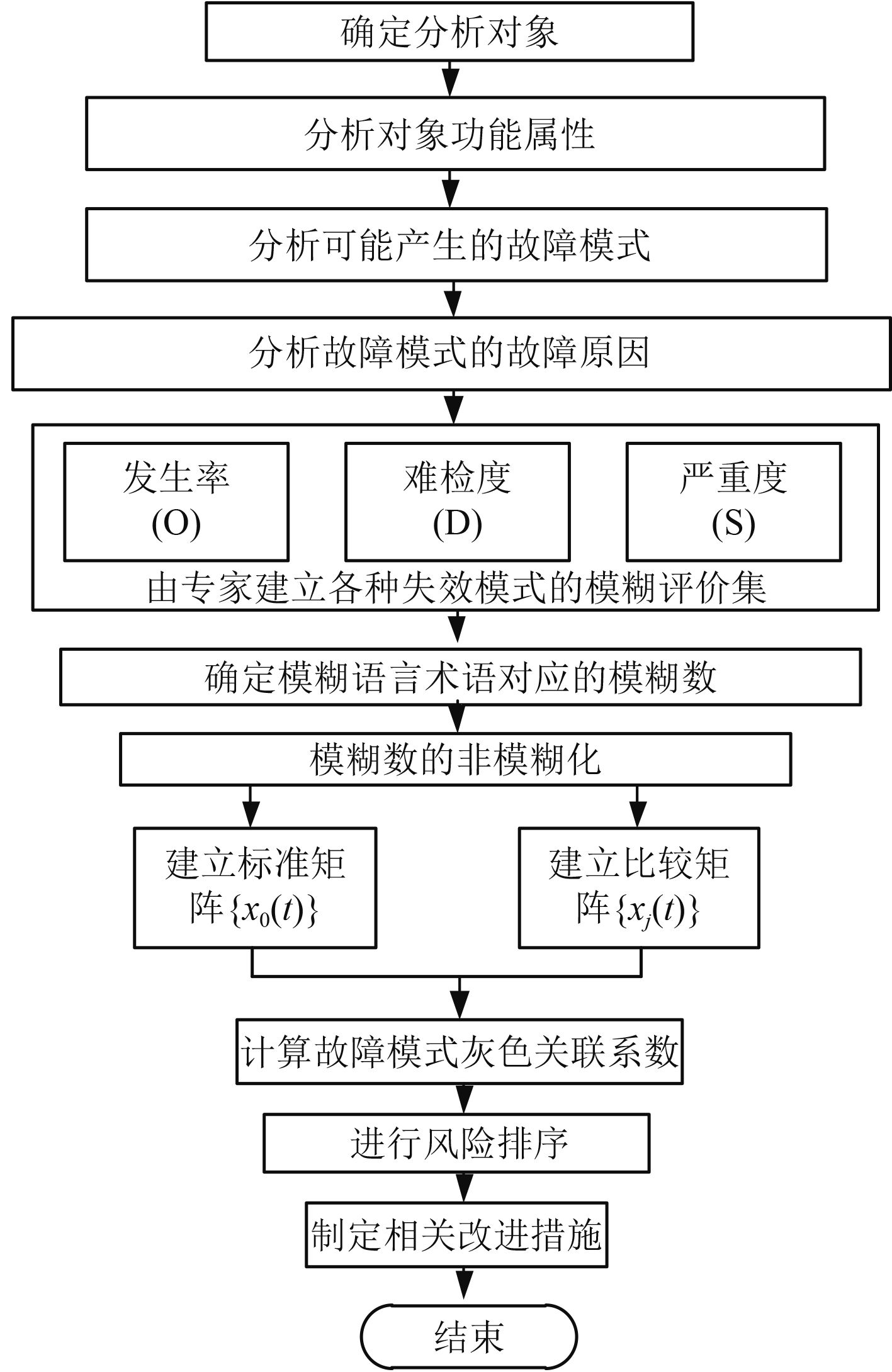
改进的FMEA流程如图1所示。

3 实例分析 3.1 确定模糊术语及模糊数

本文以YH6020多用途拖轮的动力定位系统操作面板为例，选择4位专家对故障模式的发生率（O）进行评价，评价结果见表2。根据式（2）~式（4）可以得到模糊术语对应的三角模糊数，本文3个风险因子O，S，D采用相同的模糊数。

根据式（5） 将三角模糊数进行清晰化，见表3。

3.2 评价各种故障模式

根据表2和表3对故障模式进行评价，结果见表4

3.3 应用灰色关联理论计算风险排序

1）根据表3和表4建立比较矩阵：

$\{ {x_j}(i)\} = \left\{ {\begin{array}{*{20}{c}}H&M&M\\M&L&M\\H&L&L\\L&L&M\\L&H&M\end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}}8&{5.6}&{5.6}\\{5.6}&{3.3}&{5.6}\\8&{3.3}&{3.3}\\{3.3}&{3.3}&{5.6}\\{3.3}&8&{5.6}\end{array}} \right\}\text{。}$

2）参考矩阵选择最低水平，则参考矩阵如下：

$\left\{ {{x_0}\left( {\rm{i}} \right)} \right\} = \left( {\begin{array}{*{20}{c}}{{h_{11}}}&{{h_{11}}}&{{h_{11}}}\\ \vdots & \vdots & \vdots \\{{h_{11}}}&{{h_{11}}}&{{h_{11}}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{10}&{10}&{10}\\{10}&{10}&{10}\\{10}&{10}&{10}\\{10}&{10}&{10}\\{10}&{10}&{10}\end{array}} \right)\text{。}$

3）计算灰色关联系数

由式（6）可计算得到所有故障模式关于每个风险因子的关联系数，具体计算过程如下：

令 ${X_0} = {(10,10,10,10,10)^{\rm T}}\text{，}$

第1步：求各个序列值的像：

$\begin{array}{l}{X_0} = {(10,10,10,10,10)^{\rm T}},\\{X_1} = {(8,5.6,8,3.3,3.3)^{\rm T}},\\{X_2} = {(5.6,3.3,3.3,3.3,8)^{\rm T}},\\{X_3} = {(5.6,5.6,3.3,5.6,5.6)^{\rm T}}\text{。}\end{array}$

第2步：求X₁，X₂，X₃与X₀像对应分量之差的绝对值序列

由 ${\Delta _i}\left( {\rm{t}} \right) = \left| {x_0'\left( {\rm{t}} \right) - x_i'\left( {\rm{t}} \right)} \right|$ ；i=1，2，3，得 ${X_3} = (5.6,5.6,$ 3.3,5.6,5.6)^T，

$\begin{array}{l}{\Delta _1} = \left( {0,0.3,0,0.587\;5,0.587\;5} \right)\text{，}\\{\Delta _2} = \left( {0.3,0.587\;5,0.587\;5,0.587\;5,0} \right)\text{，}\\{\Delta _3} = \left( {0,0,0.41,0,0} \right)\text{。}\end{array}$

第3步：求 ${\Delta _i}\left( {\rm{t}} \right) = \left| {x_0'\left( {\rm{t}} \right) - x_i'\left( {\rm{t}} \right)} \right|$ ；i=1，2，3；k=1，2，3，4，5的最大值与最小值。

$\begin{array}{l}M = \mathop {\max }\limits_i \mathop {\max }\limits_t {\Delta _i}\left( t \right) = 0.587\;5\text{，}\\m = \mathop {\min }\limits_i \mathop {\min }\limits_t {\Delta _i}\left( t \right) = 0\text{。}\end{array}$

第4步：求关联系数

一般取 $\zeta = 0.5$ ，有

${\varepsilon _{1i}}(t) = \frac{{m + \zeta M}}{{{\Delta _i}(t) + \zeta M}} = \frac{{0.5 \times 0.587\;5}}{{{\Delta _i}(t) + 0.5 \times 0.587\;5}}\text{。}$

代入计算得到故障模式各风险因子与参考基准间的关联系数:

$\varepsilon ({x_0}(t),{x_j}(t)) = \left( {\begin{array}{*{20}{c}}1&{0.495}&1\\{0.495}&{0.333}&1\\1&{0.333}&{0.417}\\{0.333}&{0.333}&1\\{0.333}&1&1\end{array}} \right)\text{。}$

4）计算灰色关联度

根据专家的经验、知识确定风险因子O、S、D的系数分别为： ${\lambda _1} = 0.4,{\lambda _2} = 0.4,{\lambda _3} = 0.2,$ 则权重向量为： $\omega = {(0.4,0.4,0.2)^{\rm T}}$ 。

关联度矩阵R为：

$\begin{array}{l}{R} = \varepsilon ({x_0}(t),{x_j}(t)) * \omega = \left( {\begin{array}{*{20}{c}}1&{0.495}&1\\{0.495}&{0.333}&1\\1&{0.333}&{0.417}\\{0.333}&{0.333}&1\\{0.333}&1&1\end{array}} \right)\\ * {(0.4,0.4,0.2)^{\rm T}} = \left( {\begin{array}{*{20}{c}}{0.798}\\{0.531\;2}\\{0.616\;6}\\{0.466\;4}\\{0.733\;2}\end{array}} \right)\text{。}\end{array}$

5）风险排序，见表5。

3.4 比较分析

根据传统FMEA方法分析得到的风险排序结果如表6所示。

通过表5和表6的比较可以看出，两者的排序情况相吻合，证明了该方法的有效性。但本文方法综合考虑了各风险因子的相对重要程度，确定了各风险因子的权重，较传统方法更客观细致。使FMEA方法更具有准确性和灵活性。

4 结　语

本文根据传统的FMEA方法提出了一种基于模糊评价与灰色关联理论的动力定位FMEA方法。首先建立风险因子的模糊术语集及相应的模糊数，然后进行清晰化处理。最后通过灰色关联理论计算各故障模式的灰色关联度进行风险排序。本文考虑到各风险因子的相对重要性，对3个风险因子设定了不同的权重。这使得改进后的方法更具准确性和灵活性。