2. 武汉第二船舶设计研究所,湖北 武汉 430064;
3. 中国舰船研究设计中心,湖北 武汉 430064
2. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China;
3. China Ship Development and Design Center, Wuhan 430064, China
结构冲击入水是涉及到固、液、气三者之间相互作用的典型流固耦合问题,针对该问题的研究方法主要有解析方法、试验方法和数值方法3种。最早对冲击现象进行理论研究的是Karman[1],将水上飞机降落过程简化为二维楔形体入水的数学模型,并把流体对结构的作用用附加质量来代替,提出用附加质量法计算结构入水的冲击载荷,同时基于动量守恒定律推导出入水冲击载荷的计算公式。随后,Wagner[2]对Karman的方法进行完善,考虑到水面的抬升现象提出了小斜升角模型的近似平板理论。
试验是早期研究入水问题的主要方法。Worthington[3]早在1900年就利用当时的闪光摄影技术观测小球在落入不同液体时的飞溅及空泡现象,并采用高速摄像技术捕捉到刚性球入水过程图像。率先发现平底结构冲击入水过程中空气垫存在的是Chuang[4],通过平底箱入水实验观测到在结构与水面接触瞬间在结构底部与水面之间始终存在着一层气泡,该气泡持续一段时间并最终消失,此外采用2只Mainer船型的二维分段膨体模型来研究结构的弹性对冲击力的影响。黄震球等[5]研究了在平底体两侧设置不同翼缘高度和翼缘间距对减小平底体冲击压力的影响。李国钧等[6]拟合出一组底部倾角与冲击压力峰值关系的计算公式。
21世纪以来,随着计算机技术的发展,人们开始通过数值仿真方法研究结构入水问题。卢炽华等[7]研究了二维弹性结构的入水冲击问题的数值方法,通过耦合有限元方程和边界元方程来求解流场和结构动力响应的相互作用的运动方程。夏斌等[8]对平底结构入水问题进行仿真研究,讨论了冲击速度、底部平板厚度、弹性模量与弯曲刚度对结构冲击压力峰值的影响,并通过正交实验分析了各参数对冲击压力峰值的影响程度。进一步,陈震等[9 – 12]利用MSC. Dytran模拟出空气层与水面的混合情况,并对空气垫的形成、底部压力峰值及分布作了详尽分析,还基于神经网络方法对底部冲击压力作出预报。Matej Vesenjak等[13]基于LS-DYNA评估了不同的方法对简易容器盒里流体晃荡问题的计算结果,并与试验观测结果进行对比。Oger等[14]用无网格SPH(Smoothed Particle Hydrodynamics)方法模拟了二维楔形结构冲击入水的流固耦合过程。Gong等[15]则对二维楔形结构冲击入水SPH模型的边界条件作出改进,通过在边界加上实体海绵层来模拟无反射边界条件。吴家鸣等[16]利用Fluent软件的VOF(Volume of Fluid)方法模拟大型平底结构在一定高度自由下落冲击限制水域引起的三维流体动力现象。Hu等[17]采用同样的方法在2013年海底作业工具入水过程数值仿真的研究报告中分析了二维平底模型匀速垂直进入静水的水动力问题。
本文针对二维平底结构等速冲击入水过程,采用ALE方法对不同质量、刚度、入水速度及底部斜升角情况下的入水冲击动力特性进行研究。
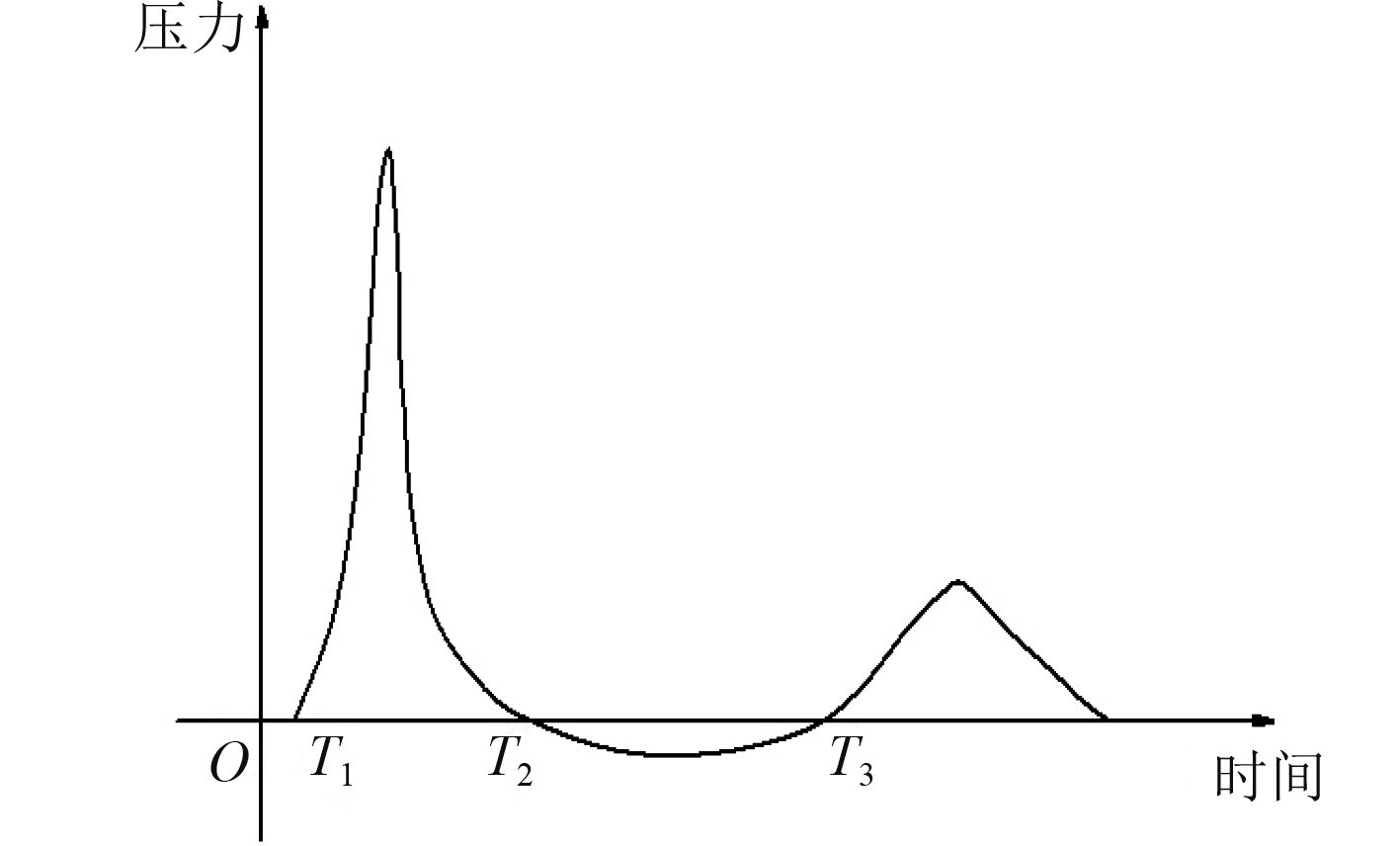
1 基本理论 1.1 弹性平底结构的入水过程一般情况下弹性平底结构入水过程可分为3个阶段[8],如图1所示。0~T1时结构以速度V从空中垂直冲向水面。由于结构距水面的距离较长,空气可向四周逃逸,此时结构底部的压力载荷几乎为0。t=T1时刻结构下降到距水面某极近处,结构底部的压力载荷迅速上升。此时自由液面充当空气的动边界,空气介质被迅速压缩,密度、内能及压力迅速升高,冲击开始。冲击压力在极短时间T1~T2内产生第1个峰值并快速衰减下去。该阶段也叫做气体压缩阶段(The Compression Phase)。T2~T3时间内,在重力、静水压力的作用下结构继续下降。结构对水平面造成扰动使静水液面升高,当V(入水速度)较大时可能产生飞溅效应。此期间冲击压力会产生第2个峰值,与第1个峰值相比,该峰值明显较小而且时间周期长。故称该阶段为液体运动阶段(The Fuild-Displacement Phase)。当结构的刚度不够时在此阶段可能产生负压的情况。通常对于结构强度设计来说,重点关注的是第1个峰值的大小。
|
图 1 弹性平底结构入水历程 Fig. 1 Water inlet course of elastic flat-bottom structure |
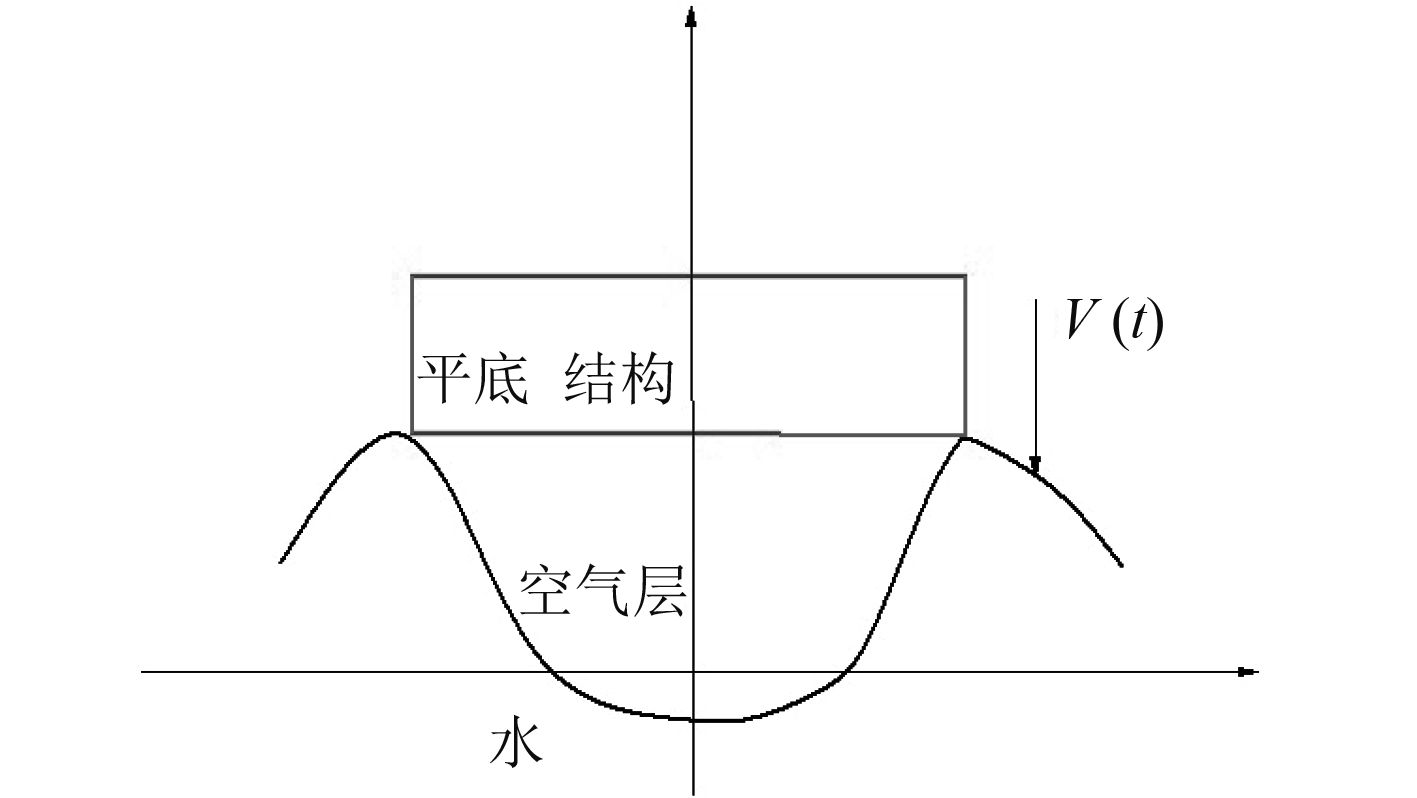
空气垫的理论模型如图2所示,假设空气为可压缩的理想气体,水为无粘不可压缩理想流体。Chuang通过分析平底箱冲击入水试验的结果总结出:在平底结构冲击入水时,一些空气也会随同压入水中,破碎成气泡并引起自由液面变形。由于平底结构与水面之间存在空气垫,作用在平底结构上的压力峰值实际上比理论值小很多,使得冲击压力持续时间延长。空气垫并非完全以一相状态存在,而是一些脱离水面的水质点与空气混合在一起形成的气水混合物。它的状态和流动形式很不稳定,气水比例也发生变动,这给理论描述带来了困难。近期试验表明,混合区域首先是出现在平底边缘,尺寸为平底结构半宽的1/3,而其他区域此时还没有接触到水面,之后底部被困的空气通过边缘的混合区域向四周逃逸。由于冲击的瞬态性以及试验条件的限制,目前尚无法达到对空气垫的各种物理属性进行精确测量,这给空气垫的定量分析带来困难。
|
图 2 平底结构的空气垫理论模型 Fig. 2 Theoretical model of air cushion with flat-bottom structure |
通常动力学计算可采用Lagrange,Euler和ALE(Arbitrary Lagrangian-Eulerian)3种算法:Lagrange算法以物质坐标为基础,应用于固体结构的应力应变分析。其结构变形与网格变形相对应,物质在网格单元之间不会有流动。该算法的主要优点是能够较精确地描述结构边界的运动,而本身算法的限制在处理大变形问题时网格会有严重的畸变现象,对计算结果有影响。Euler算法以空间坐标为基础,应用于流体分析。网格和结构相互独立,可视为2层网格叠加在一起,其中一层网格在空间中固定不动,另一层网格随材料流动。材料网格发生变形而后将材料单元的状态变量映射到空间网格中。该方法适于处理大变形问题如流体的流动,但在物质边界的捕捉上较为困难。ALE方法基于流体动力学数值模拟问题中的有限差分法。该方法兼有前2种算法的优点,即先用Lagrange方法处理结构的运动边界,跟踪物质结构边界运动,再用Euler算法划分网格,使网格独立于结构,让物质可以在网格间流动。因此ALE网格在求解过程中可根据定义的参数适当调整网格,以免网格出现严重畸变。该方法也适用于处理空间大位移、结构大变形等问题。
不可压缩流体的运动微分方程可以描述为:
| $\frac{{\partial u}}{{\partial t}} + u\nabla u - 2{u^F}\nabla \varepsilon (u) + \nabla p = b{\text{,}}$ | (1) |
| $\nabla \cdot u = 0{\text{,}}$ | (2) |
其中u为流速;p为压力;初始条件及边界条件分别为:
| $\sigma = - pl + 2{v^F}\varepsilon (u){\text{,}}$ | (3) |
| $\varepsilon (u) = \frac{1}{2}(\nabla u + {(\nabla u)^{\rm{T}}}){\text{。}}$ | (4) |
在ALE算法中引入除Lagrange和Euler坐标之外的另一个任意的参照坐标系,此参照坐标系属性可用式(5)的微分关系来表征:
| $\frac{{\partial f({X_i},t)}}{{\partial t}} = \frac{{\partial f({x_i},t)}}{{\partial t}} + {w_i}\frac{{\partial f({x_i},t)}}{{\partial {x_i}}}{\text{,}}$ | (5) |
其中,Xi为Lagrange坐标;xi为Euler坐标;wi为两者相对速度。
因此,由材料及参考几何构型的时间导数之间的逻辑关系可推得所求的ALE方程。
假设物质速度为v,网格速度为u,为简化上述方程可以引入相对速度w=v–u。ALE算法的微分方程可由下述方程给定:
1)质量守恒方程
| $\frac{{\partial \rho }}{{\partial t}} = - \rho \frac{{\partial {v_i}}}{{\partial {x_i}}} - {w_i}\frac{{\partial \rho }}{{\partial {x_i}}}{\text{。}}$ | (6) |
2)动量守恒方程
在固定控制域上,根据给定的初始边界条件,得出Navier-Stokes方程的ALE表述:
| $v\frac{{\partial {v_i}}}{{\partial t}} = {\sigma _{ij,j}} + \rho {b_i} - \rho {w_i}\frac{{\partial {v_i}}}{{\partial {x_j}}}{\text{。}}$ | (7) |
应力张量σij用式(8)表示:
| ${\sigma _{ij}} = - p{\delta _{ij}} + \mu ({v_{i,j}} + {v_{j,i}}){\text{。}}$ | (8) |
式(8)与式(9)、式(10)联立求解:
| ${v_i} = U_i^0{\text{,}} {\text{在}}\varGamma 1{\text{域上}}{\text{,}}$ | (9) |
| ${\sigma _{ij}}{n_i} = 0{\text{,}} {\text{在}}\varGamma 2{\text{域上}}{\text{。}}$ | (10) |
其中:
| ${\varGamma _1}\bigcup {{\varGamma _2} = \varGamma } \;\;\;{\text{,}}{\varGamma _1}\bigcap {{\varGamma _2} = 0} {\text{。}}$ | (11) |
式中:Г为完整的计算域边界,Г1和Г2为Г的部分域。上标参数表示初始的定值。ni为边界外法线的单位向量,δij为Kronecker δ函数。若给定了整个计算域在t=0时刻的速度场,即
| ${v_i}({x_i},0) = 0{\text{。}}$ | (12) |
3)能量守恒方程
| $\rho \frac{{\partial E}}{{\partial t}} = {\sigma _{ij}}{v_{i,j}} + \rho {b_i}{v_i} - \rho {w_j}\frac{{\partial E}}{{\partial {x_j}}}{\text{。}}$ | (13) |
流体力学中有2种方法表示欧拉观点,因此求解ALE方程也有2种方法:第1种是用计算流体力学方法求全耦合问题。但该方法只能控制单个单元的单一属性;另一种方法是算子分离计算法,此方法通过时间步来划分,每个时间步上又分成2个阶段。首先采用Lagrange方式,即网格随着物质一起运动,其中由计算速度、内外力引起的内能改变量平衡方程为:
| $\rho \frac{{\partial {v_i}}}{{\partial t}} = {\sigma _{ij,j}} + \rho {b_i}{\text{,}}$ | (14) |
| $\rho \frac{{\partial E}}{{\partial t}} = {\sigma _{ij}}{v_{i,j}} + \rho {b_i}{v_i}{\text{。}}$ | (15) |
由于单元的边界没有物质流过,因此满足质量守恒。在第2个对流阶段,对边界上的质量输运、动量以及内能进行计算,可以认为是将Lagrange过程中移位网格重新映射至初始位置或者任意位置。
对每个节点,将其速度和位移表达式重新述写:
| ${u^{n + 1/2}} = {u^{n - 1/2}} + \Delta t{{M}^{ - 1}}({F_{\rm ext}}^n + {F_{{\mathop{\rm int}} }}^n){\text{,}}$ | (16) |
| ${x^{n + 1}} = {x^{n - 1}} + \Delta t{u^{n + 1/2}}{\text{。}}$ | (17) |
式中:
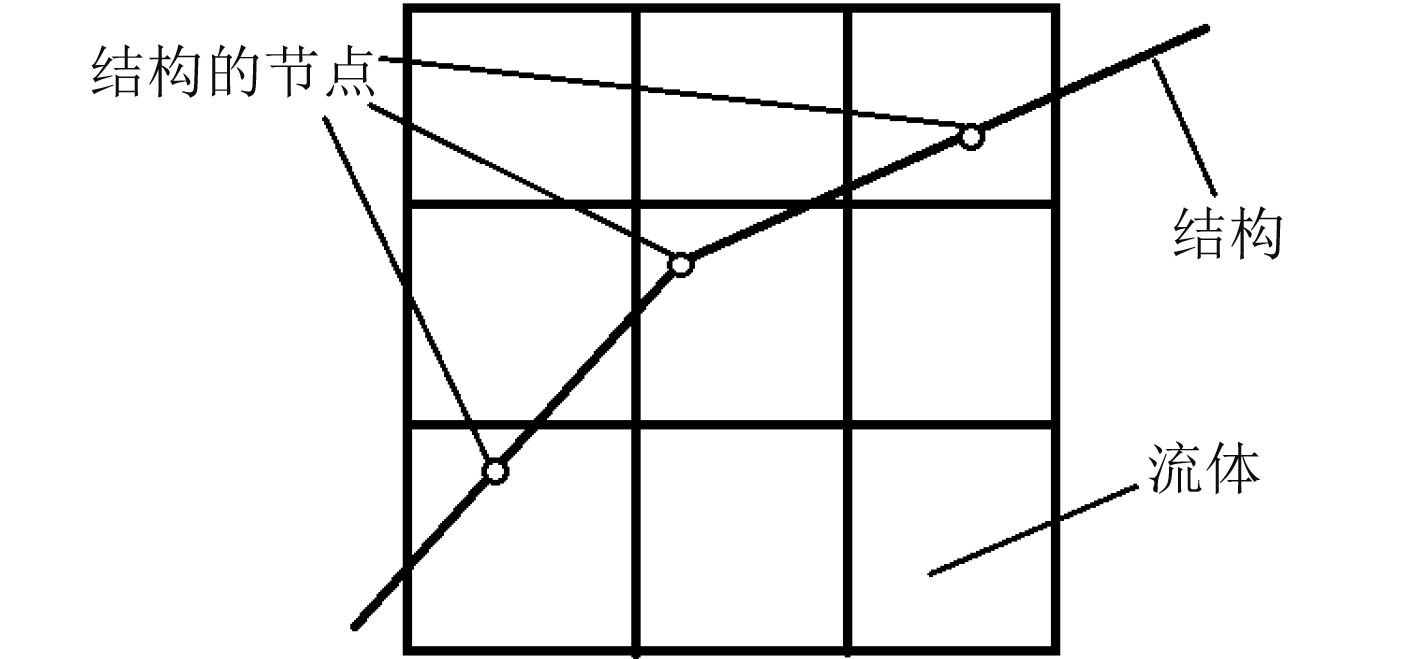
ALE算法。基本单元是定义一个流固耦合面即结构和流体的交界面,如图3所示,结构和流体分别采用Lagrange单元和Euler单元,通过约束条件将两者耦合起来,从而力学参量即可联系在一起。此算法中欧拉材料的流动产生的压载荷会自动作用到结构网格上,与此同时结构网格产生的变形又会影响欧拉材料的流动及对应的压力值。因此完全耦合的流体-结构响应可以用此方法表达。
|
图 3 ALE算法结构单元 Fig. 3 ALE algorithm structure unit |
在数值计算中,Euler算法需要稳定的时间步∆t,即需满足:
| $\Delta t < \frac{{\Delta x}}{{c + u}}{\text{,}}$ | (18) |
其中∆x为单元特征长度,c为材料声速,u为质点速度函数。
时间步∆t还应满足Courant稳定条件(Hallquist 1998):
| $\Delta t < \frac{{\Delta x}}{{Q + {{({Q^2} + {c^2})}^{1/2}}}}{\text{,}}$ | (19) |
| $\begin{array}{l}Q = {C_1}c + {C_2}\left| {div(u)} \right|;\\[7pt]div(u) < 0;\;Q = 0\;\;div(u) \geqslant 0{\text{。}}\end{array}$ | (20) |
式中:∆x为单元特征长度;Q为冲击波粘度的导出项;C1为冲击波粘度线性系数;C2为2次项系数。当材料被拉伸时,Q取0;当材料被压缩时,Q取正值。
固体物质的材料声速为:
| ${c_2} = \frac{{0.75G + k}}{{{\rho _o}}}{\text{,}}$ | (21) |
| $k = {\rho _o}\frac{{\partial P}}{{\partial \rho }} + \frac{P}{\rho }\frac{{\partial P}}{{\partial e}}{\text{。}}$ | (22) |
式中:ρ为材料密度;G为剪切模量;P(ρ,e)为状态方程压力;式(22)右边第2项可以计算当材料受压时由于内能变化导致的硬化效应数。
若为流体物质则:
| $k = {\rho _o}{c^2}{\text{,}}$ | (23) |
式中:ρ0为流体质量密度;c为声速;计算声速时忽略流体物质的粘度。
对位移x矢量以及速度u矢量进行更替:
| ${x^{n + 1}} = {x^n} + {u^{n + 1/2}}\Delta {t^n}{\text{,}}$ | (24) |
| ${u^{n + 1/2}} = {u^{n - 1/2}} + \frac{1}{2}{a^n}(\Delta {t^n} + \Delta {t^{n + 1}}){\text{。}}$ | (25) |
其中:加速度矢量an=Fn/M;Fn为节点上总的力矢量;M为质量矩阵。再将式(25)中的加速度项代入则有:
| ${u^{n + 1/2}} = {u^{n - 1/2}} + \frac{{{F_n}}}{{2{\mathit{\boldsymbol{M}}}}}(\Delta {t^n} + \Delta {t^{n + 1}}){\text{。}}$ | (26) |
节点上总的力矢量包括内力矢量
| ${F^n} = {F_{{\mathop{\rm int}} }}^n + {F_{{\rm{ext}}}}^n{\text{,}}$ | (27) |
由于节点内力可表达为应力σn的函数,该应力包括偏应力项-PnI
d及材料强度
| ${F_{{\mathop{ int}} }}^n = \int\limits_V {x{B^t}} {\sigma ^n}d{\text{,}}$ | (28) |
| ${\sigma ^n} = - {P^n}{I_d} + {\sigma _d}^n{\text{。}}$ | (29) |
式中:Bt为应变-位移矩阵;Id为应变张量的第一不变量。外力矢量
Lagrange结构(从物质)和Euler流体(主物质)间的相对位移d。检查每一个从节点相对于主物质表面的情况,如果不贯穿就无需做任何操作。如果贯穿,界面力F应分布至Euler流体物质的节点上。其中界面力F的大小与贯穿数量有如下关系:
| $F = {k_i} \cdot d{\text{。}}$ | (30) |
式中ki为基于节点质量模型特性的刚度系数。
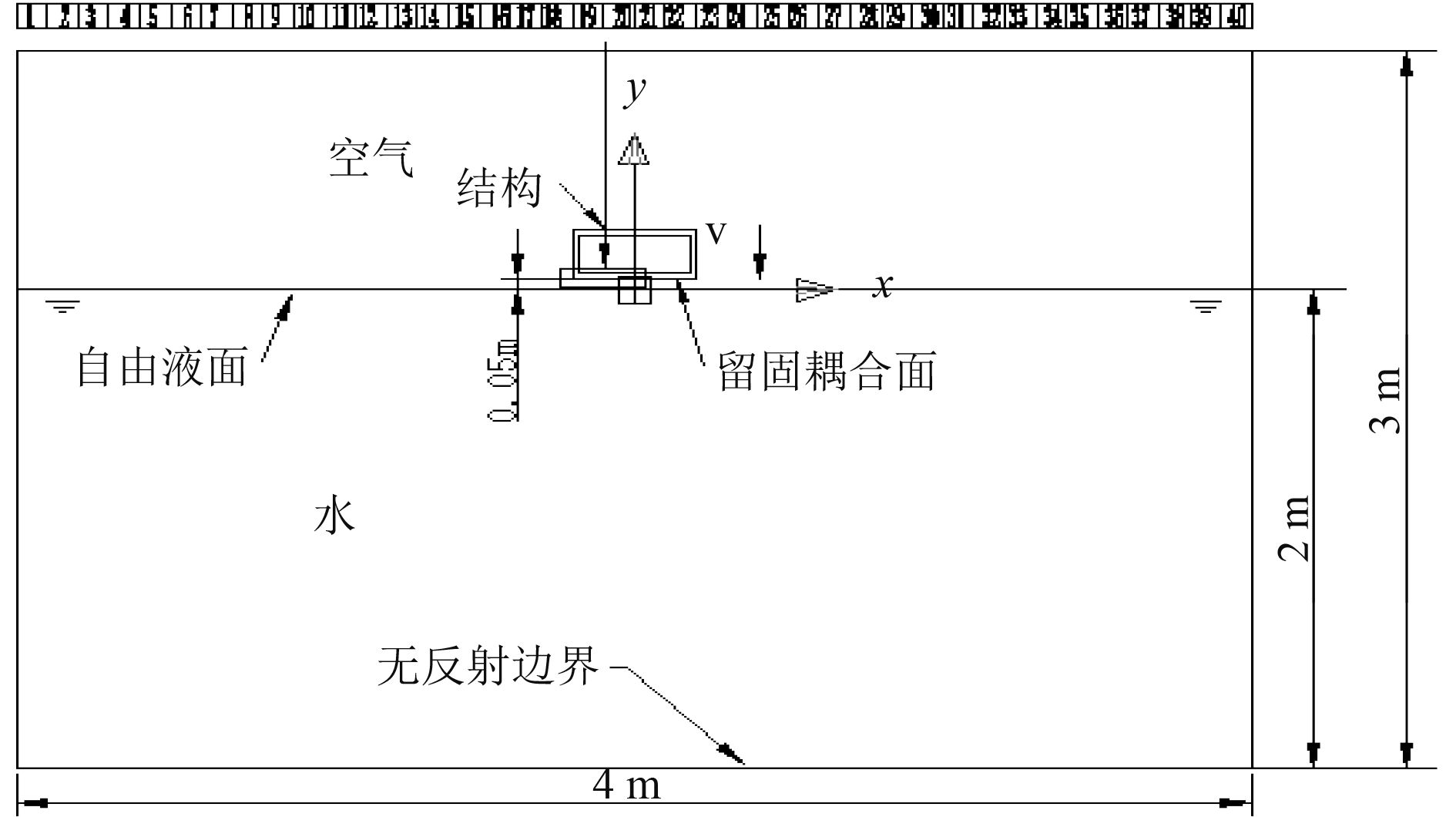
2 仿真模型 2.1 几何模型为减小数值仿真的计算量,忽略长度方向的影响,将实际三维的平底结构入水冲击模型简化为“二维”,即整个模型在厚度方向只取一个单元,并约束整个模型沿厚度方向的位移。本文所采用的二维平底结构入水冲击模型如图4所示,空气域宽4 m、高1 m,水域宽4 m、深2 m,结构宽0.4 m、高0.2 m、厚0.02 m,结构距水面的初始距离为0.05 m,整个模型厚度方向取1 mm。
为抑制冲击波在边界产生反射导致反射波与结构发生耦合作用,需模拟无限流体域,即在流体域的边界定义无反射边界条件。同时无反射边界条件的定义使得整个流体域不需要很大,这有利于降低计算成本。实际上从结构开始下落到冲击入水有很长一段距离,模拟这一段过程需消耗大量的计算成本,因此忽略结构自由下落过程,初始状态取结构在距水面一小段距离处以等速冲击入水,以提高计算效率。
|
图 4 二维平底结构入水冲击模型 Fig. 4 Water impact model of two-dimensional flat-bottom structure |
结构采用Lagrange单元,流体(空气、水)采用Euler单元,结构的外表面为流固耦合面,采用ALE算法。在结构底部取40个观测点,用来拟合整个底面上的压力情况。空气和水的网格需共节点,结构与流场不共节点。结构和流场均取Solid 164实体单元,结构划分为Lagrange单元,流场划分为Euler单元,采用ALE罚函数耦合算法计算流固耦合作用。为提高计算精度需将网格细化,考虑到计算成本,本文对流固耦合区域的网格进行局部细化,比例为10:1,如图5所示。

|
图 5 网格划分 Fig. 5 Meshing |
本文研究弹性平底结构的冲击入水过程,结构的材料模型采用密度为7 800 kg/m3、弹性模量为2.1×1011 Pa、泊松比为0.3的线弹性材料。水的密度为998 kg/m3,动力粘性系数为0.87×10–3。空气的密度为1.25 kg/m3,动力粘性系数为1.74×10–5。空气和水分别采用线性多项式状态方程和Gruneisen状态方程进行描述。
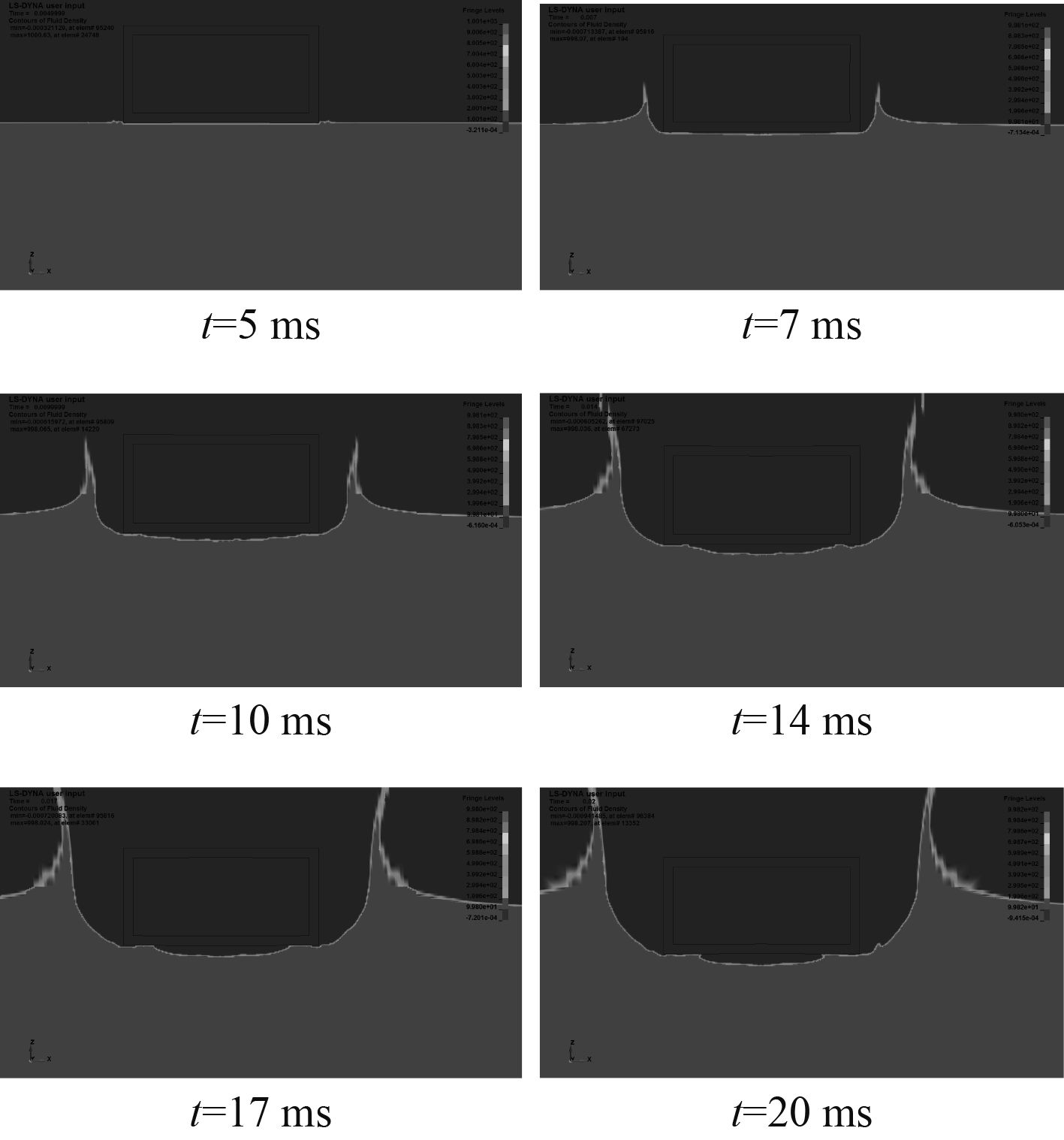
2.3 收敛性验证采用入水速度为10 m/s为典型模型来研究平底结构冲击入水全过程。取t =5 ms,7 ms,10 ms,14 ms,17 ms,20 ms六个时刻的结果图,可以观察到出入水过程中自由液面的变化情况、空气垫的形成过程及飞溅效应。
|
图 6 ALE方法入水过程云图 Fig. 6 ALE method into the water process cloud |
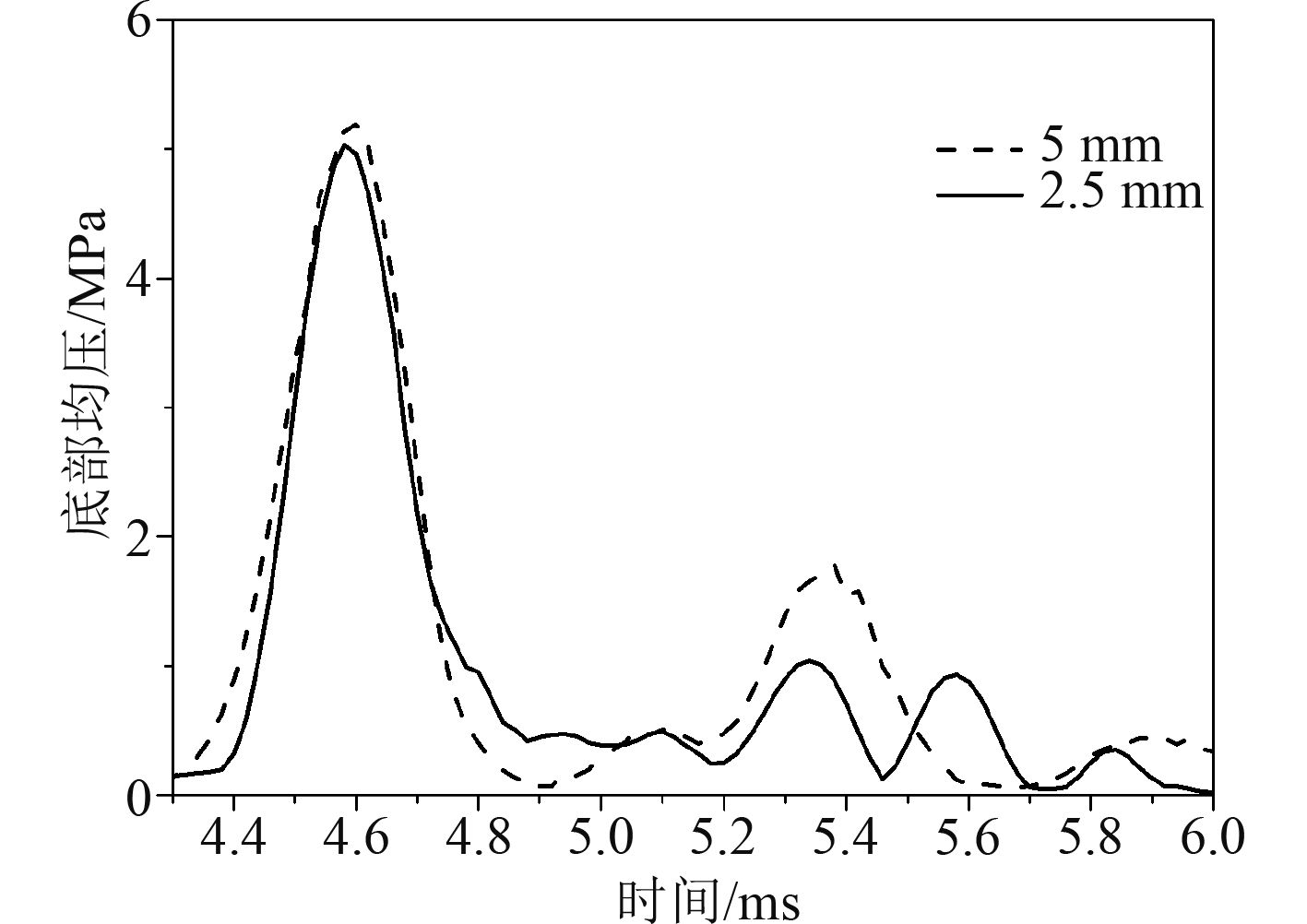
网格划分对数值结果收敛性至关重要。网格越小相应计算成本也越大,但只有在网格细化到一定程度时数值计算结果才会收敛。本文采用的结构-流体网格比例为1:1,图7对比了5 mm网格和2.5 mm网格的底部均压的计算结果,通过该图可以看出5 mm时网格已经收敛。图中5 mm网格时第1峰压为5.195 MPa,2.5 mm网格时第1峰压为5.026 MPa,相对误差仅为3.36%,小于5%,符合工程预报的要求。本文采用2.5 mm网格进行计算。
|
图 7 5 mm网格和2.5 mm网格底部均压对比 Fig. 7 Comparison of 5 mm grid and 2.5 mm grid bottom pressure |
此外,将仿真结果Chuang经验公式、李国钧试验公式对比发现,10 m/s入水速度时Chuang经验公式计算出的刚性压力理论值为5.048 MPa,李国钧试验公式计算出的理论值为4.802 MPa,均与该数值仿真结果相近,较5 mm的网格2.5 mm网格的结果精度较高,2种网格的计算误差分别为0.44%和4.66%。
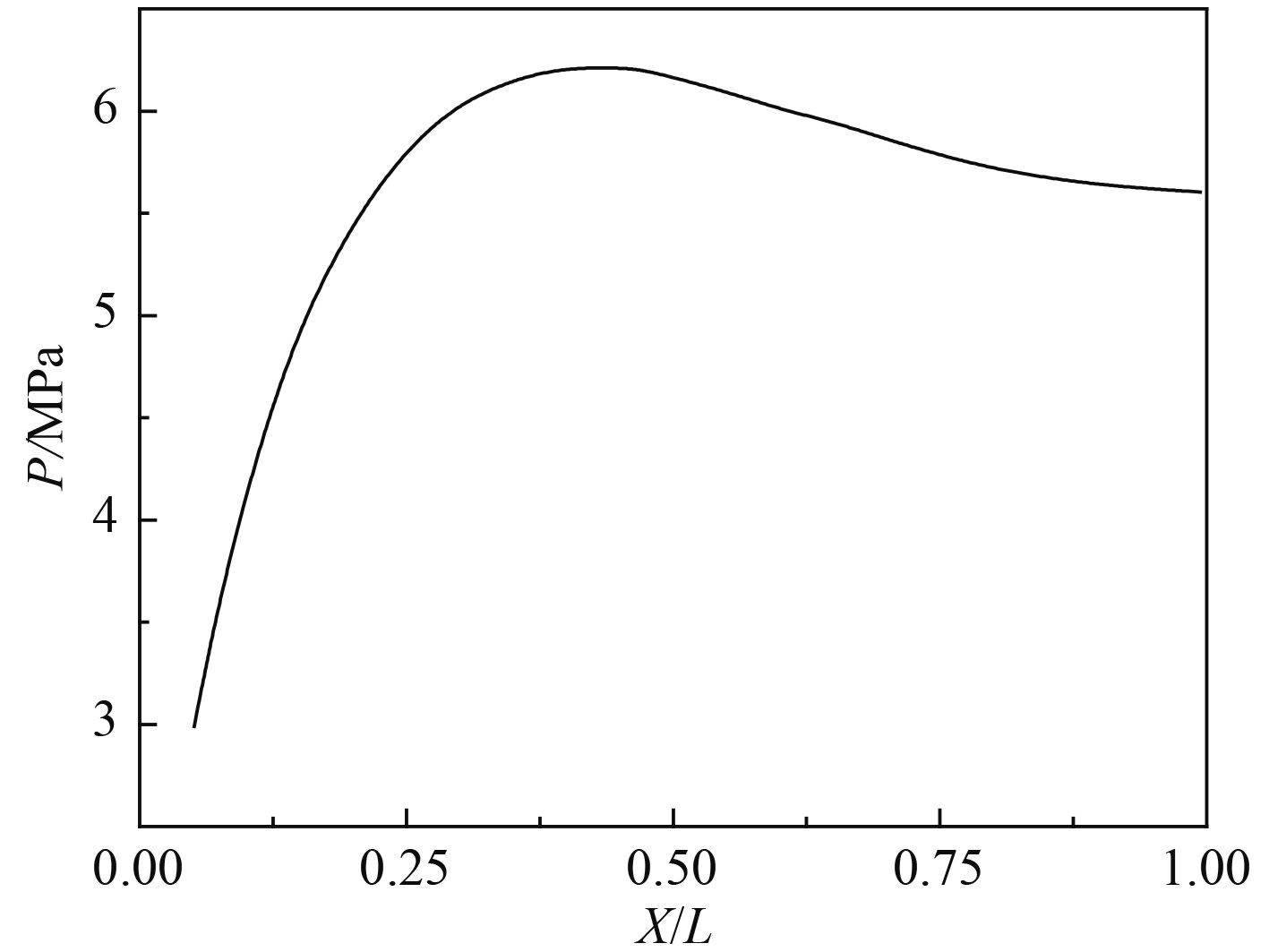
3 结果分析 3.1 底部压力将所有观测点的压力峰值沿宽度方向表示可得到结构底部压力分布情况,如图8所示。该图的横坐标与纵坐标均采用无量纲量表示,横坐标为无量纲量X/L,X为底部取值点距边缘的距离,L为结构半宽;纵坐标P为底部取值点的压力值。图中可以得出,当X/L=1时P为5.596 MPa,由于空气垫对中心区域的冲击产生缓冲作用使得结构底部压力值从中心点沿宽度方向向两侧递增,并在X/L=0.425时出现最大值,为6.219 MPa,随后急剧衰减。
|
图 8 底部压力分布 Fig. 8 Bottom pressure distribution |
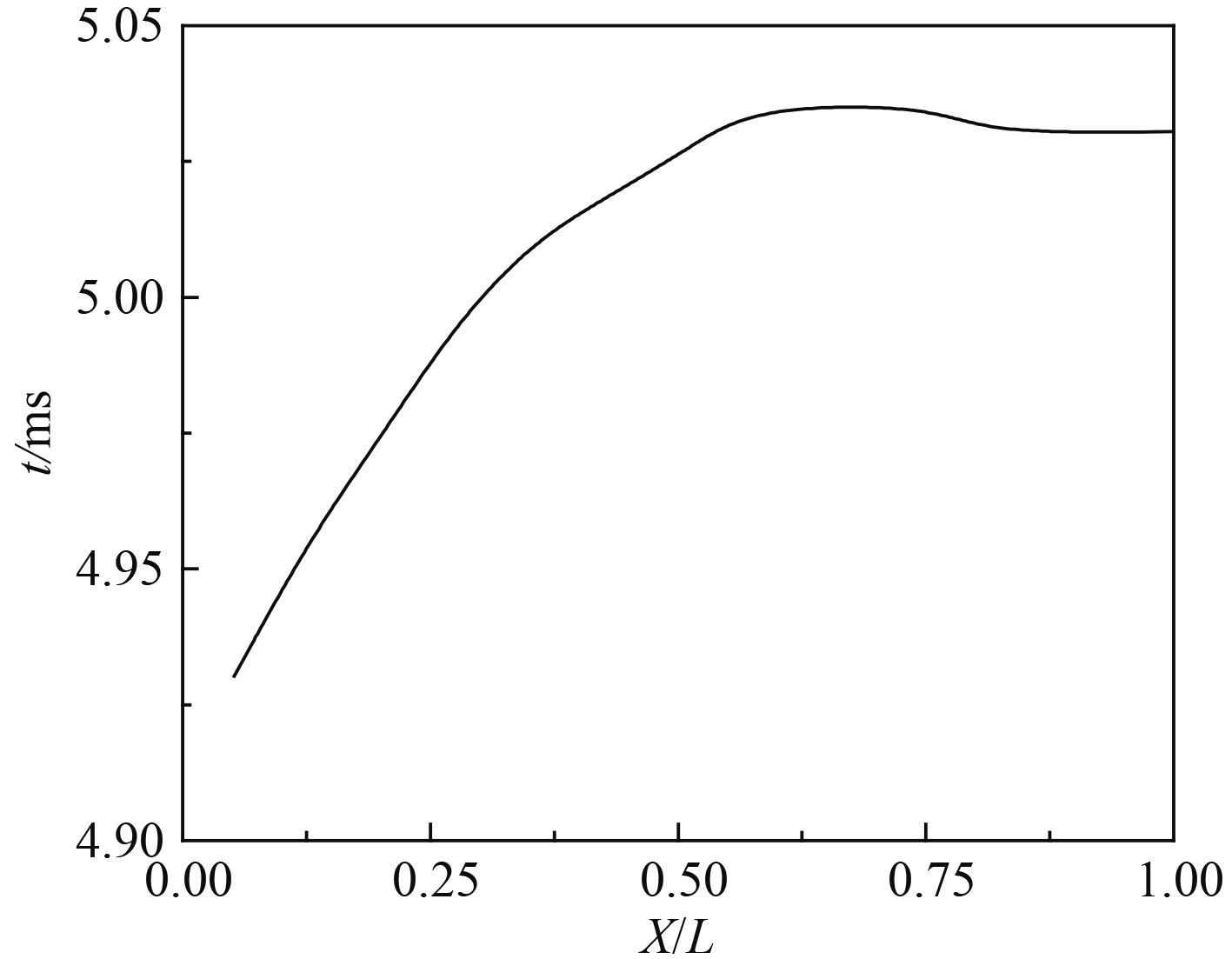
|
图 9 所有观测点出现峰值的时刻 Fig. 9 The time of peak of all observation points |
从图9可以看到底部边缘处最先达到峰值,随后沿宽度方向向中心依次出现压力峰值。空气垫的缓冲作使得中心区域几乎同时达到最大值,其中中心点附近会略先达到最大值。
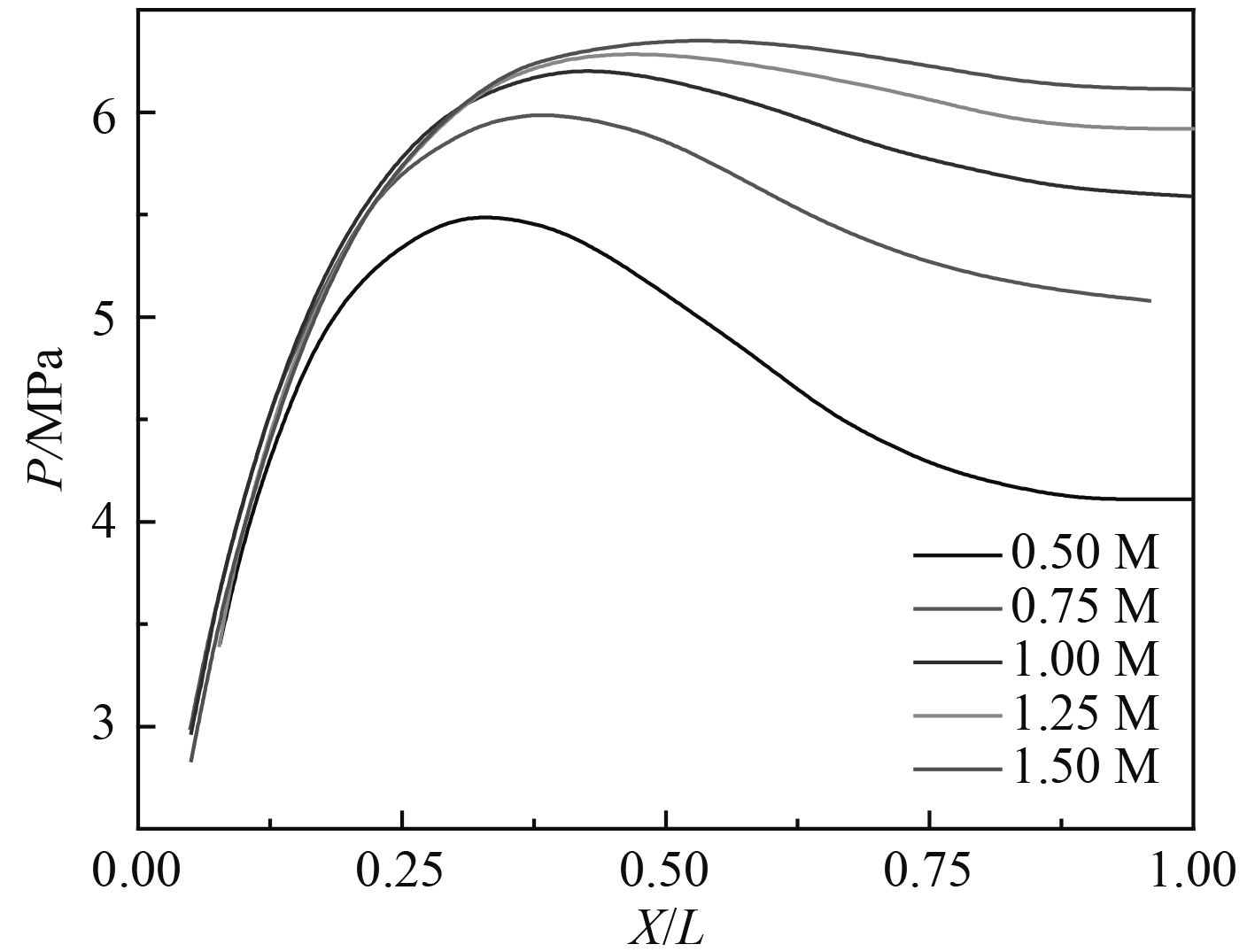
3.2 结构质量对冲击压力的影响根据Karman理论,冲击压力的大小与结构入水时的动量有关,本文采用统一的模型,通过仅改变结构的密度参数来讨论结构质量对冲击压力的影响。取3 900 kg/m3,5 850 kg/m3,7 800 kg/m3,9 750 kg/m3,11 750 kg/m3五种密度作对比,计算出结构的质量分别为:0.087 36 kg,0.131 04 kg,0.174 72 kg,0.218 40 kg,0.262 08 kg。其中0.174 74 kg为典型模型的质量,记为M,于是这5种结构的质量可转化为0.5 M,0.75 M,M,1.25 M,1.5 M,从而可得结果图10。
|
图 10 质量对冲击压力的影响 Fig. 10 Effect of mass on pressure |
从图10中取5条曲线中心点的值记为P0,最大值记为Pmax,Pmax–P0为最大值与中心点处的差值,P0/Pmax为中心点的值与最大值之比,Xmax为出现最大值的位置,列出表1。
|
|
表 1 质量对冲击压力峰值的影响 Tab.1 Effect of mass on pressure |
表中可以得出,随着质量的增大,冲击压力值增大。而Pmax–P0减小,P0/Pmax增大则表明空气垫的作用随之减弱,最大值的位置沿宽度方向向中心移动。
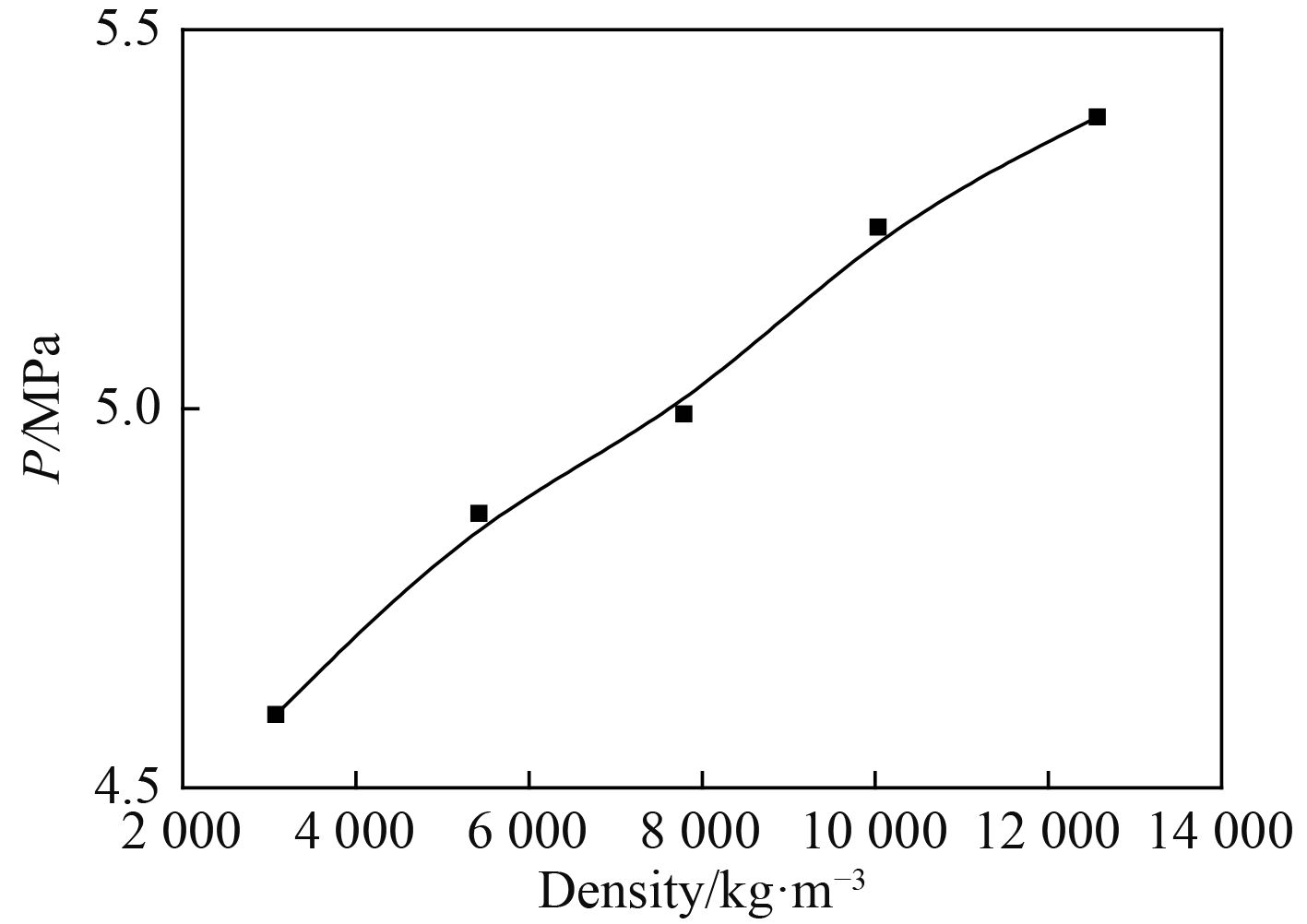
由于结构的质量由密度与体积2个参数同时决定。当结构质量为M时,取上述5种密度并将结构改为相应的板厚,讨论质量不变情况下不同密度对冲击压力的影响如图11所示。从图中可以得出,质量相同时密度越大冲击压力越大。
|
图 11 结构密度对冲击压力的影响 Fig. 11 Effect of structural density on pressure |
在结构入水冲击问题中平底结构的弹性效应一直都是人们关注的重点内容。在结构静力学中,弯曲刚度D是表征结构弹性特征的一个重要物理量。当载荷和边界条件确定时,结构的变形完全由弯曲刚度决定。本文采用统一的模型,通过改变结构的弹性模量和泊松比来讨论结构刚度对冲击压力的影响。
| $D = \frac{{{{E}}{{{t}}^{\rm{3}}}}}{{{\rm{12}}\left( {{\rm{1 - }}{\mu ^{\rm{2}}}} \right)}}{\text{。}}$ | (31) |
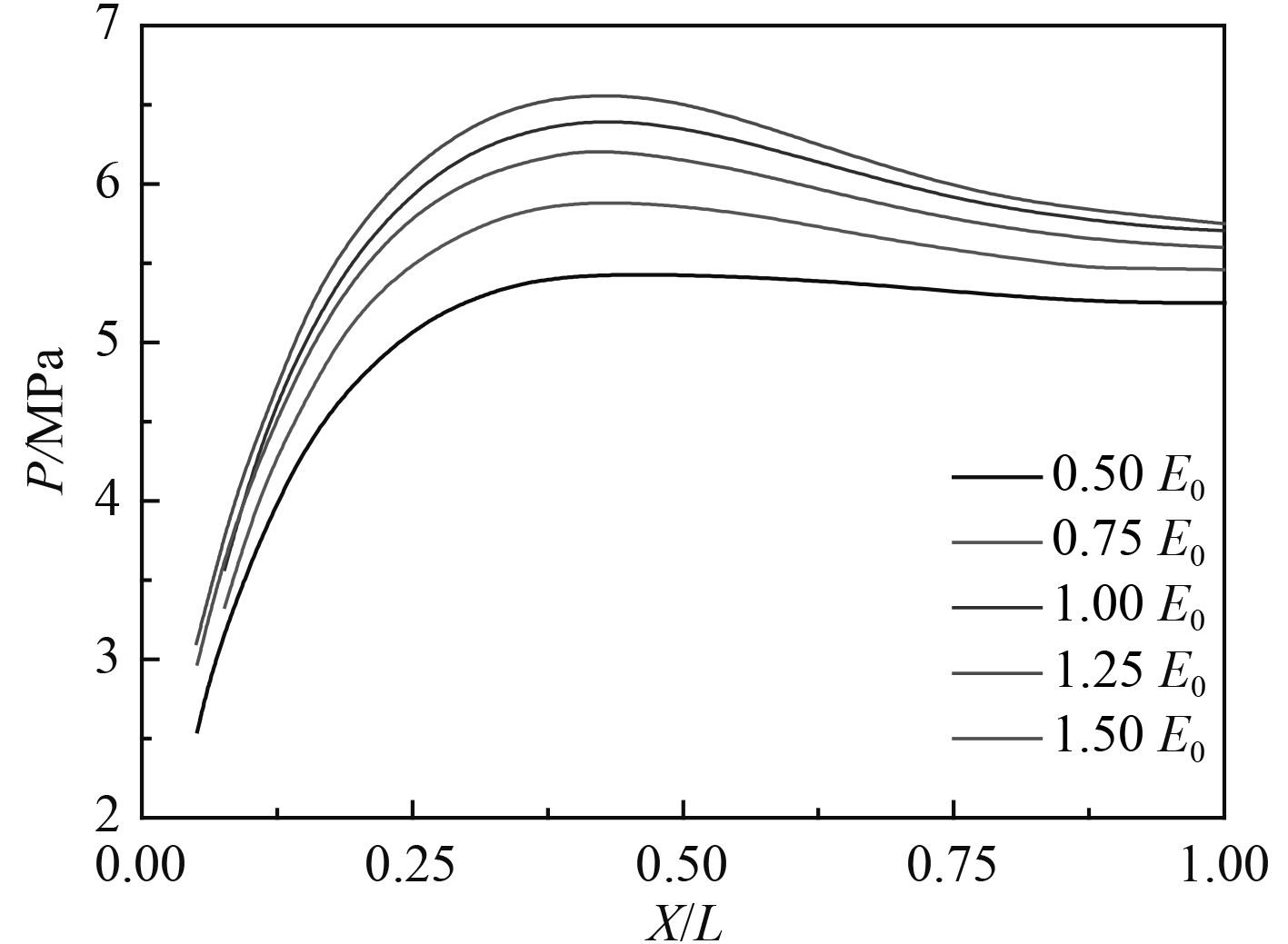
取1.05×1011 Pa,1.575×1011 Pa,2.1×1011 Pa,2.65×1011 Pa,3.15×1011 Pa五种弹性模量作对比分析,如图 12所示,其中2.1×1011 Pa为典型模型的弹性模量,记为E0,于是其他4种弹性模量可转化为0.5 E0,0.75 E0,E0,1.25 E0,1.5 E0。
|
图 12 不同弹性模量对冲击压力的影响 Fig. 12 Effect of different elastic moduli on pressure |
取不同的弹性模量作对比分析绘制表2,从表中可看出,随着弹性模量的增大,弯曲刚度增大,冲击压力值增大。而Pmax–P0增大,P0/Pmax减小则表明空气垫的作用随之增强,最大值的位置基本不变。
|
|
表 2 不同弹性模量对冲击压力的影响 Tab.2 Effect of different elastic moduls on pressure |
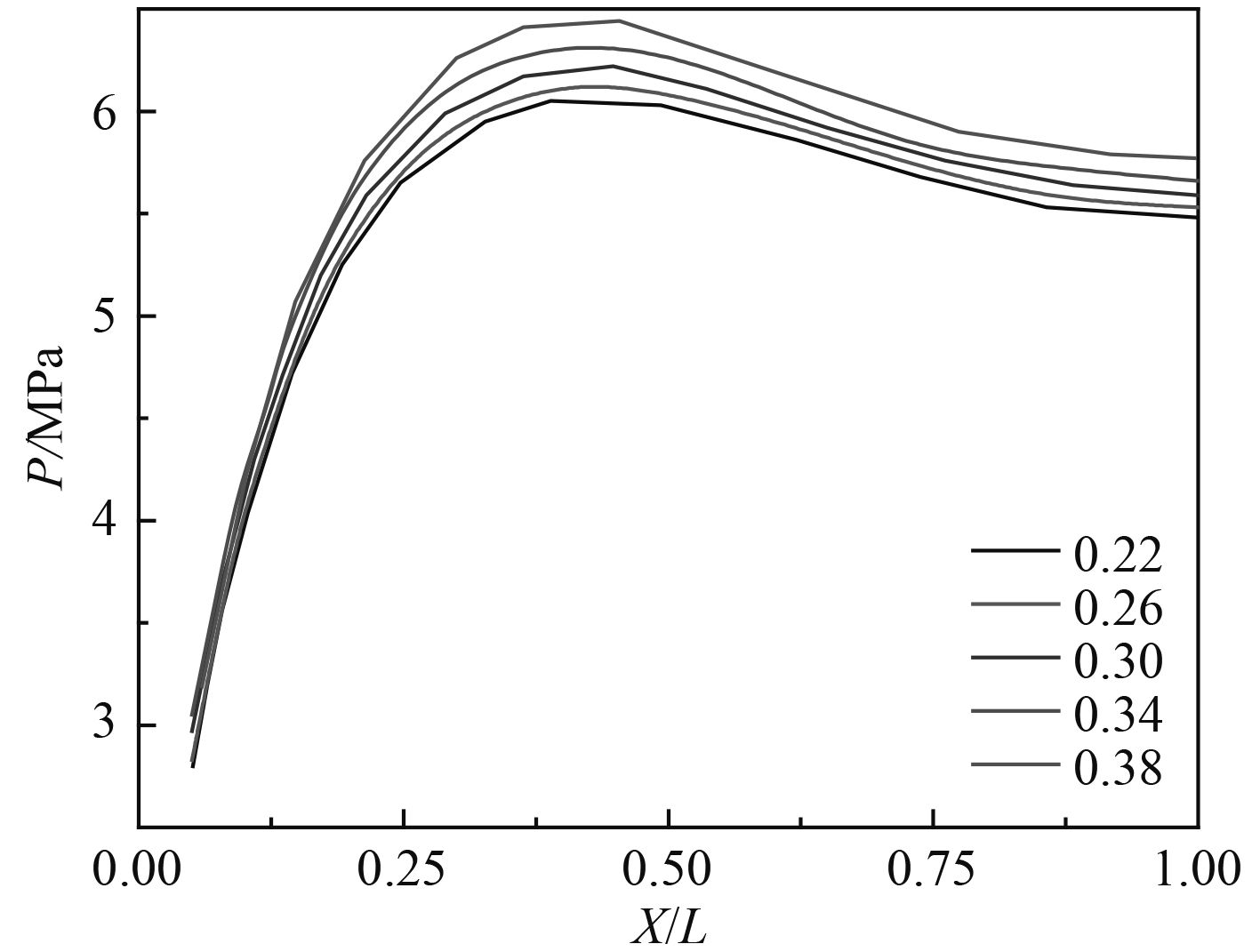
|
图 13 不同泊松比对冲击压力的影响 Fig. 13 Impact of different Poisson ratios on pressure |
取0.22,0.26,0.3,0.34,0.38五种泊松比作对比分析绘制表3。表中可以得出,随着泊松比的增大,冲击压力值增大。而Pmax–P0增大,P0/Pmax减小则表明空气垫的作用随之增强,最大值的位置基本不变。
|
|
表 3 不同泊松比对冲击压力的影响 Tab.3 Impact of different poisson ratios on pressure |
在Karman理论中,冲击压力的大小与结构入水时的动量有关,而影响动量大小的另一个重要因素就是速度。入水速度与结构下落的高度有关,因此讨论结构入水速度对冲击压力的影响从侧面反映了下落高度对入水冲击压力的影响。本节取7 m/s,12 m/s,17 m/s,22 m/s,27 m/s,32 m/s,37 m/s七种入水速度进行对比,从图中可以看出,速度对底部压力分布情况的影响不显著。

|
图 14 入水速度对冲击压力的影响 Fig. 14 Influence of water inlet velocity on pressure |
取7 m/s,12 m/s,17 m/s,22 m/s,27 m/s,32 m/s,37 m/s七种入水速度进行对比。表中可以得出,随着速度的增大,冲击压力值增大。而Pmax–P0出现波动,P0/Pmax增大,最大值的位置在小范围内波动,可见速度对空气垫作用的影响较为复杂。
|
|
表 4 入水速度对冲击压力的影响 Tab.4 The impact of water velocity on pressure |
在船舶与海洋工程领域的实际应用中,船体结构底部会有一定角度的斜升角。前人通过一系列不同斜升角的楔形体模型入水冲击实验来研究斜升角对结构底部压力的影响。其中,李国钧等[7]通过对该问题进行实验研究得出的结论为:从0°开始峰值压力P随倾角β的增大而增大,在达到临界倾角β*(β*=2°~3°)后又会随β的增大而减小。
本节取1°,2°,3°,4°,5°五种底部斜升角讨论其对冲击压力峰值的影响情况,其余参数与典型模型保持一致。如图15所示。0°~2°时冲击压力峰值随底部斜升角的增大而增大,在约2°时达到峰值后又会随底部斜升角的增大而减小,3°之后其值趋于稳定。该结果与李国钧得出的结论基本一致。
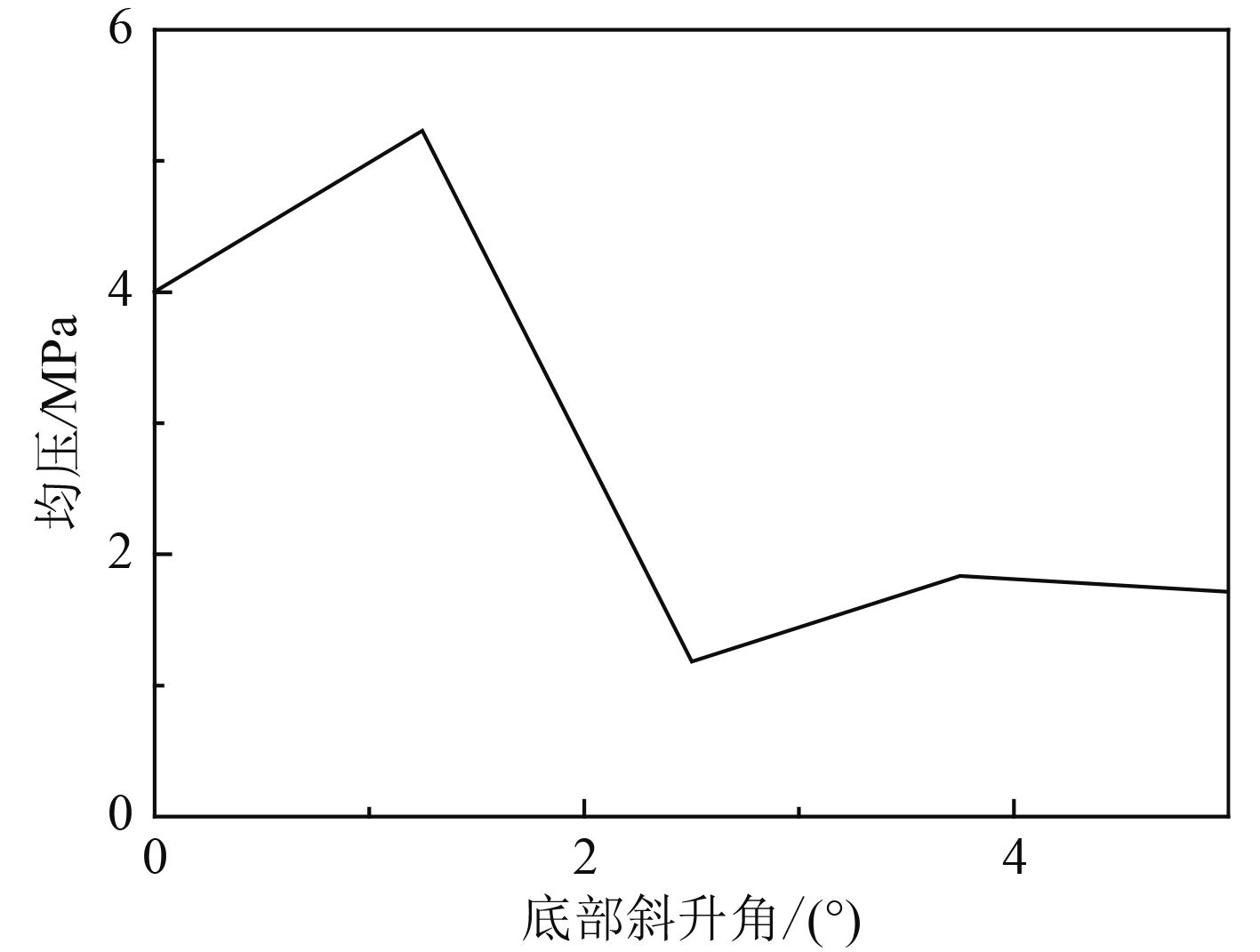
|
图 15 不同底部斜升角入水冲击的均压值 Fig. 15 Pressure value of different bottom inclined angle into water |
本文采用ALE方法对二维弹性平底结构等速冲击入水过程进行数值模拟仿真研究,得出了如下主要结论:
1)平底结构入水冲击过程中,底部边缘处最先达到峰值,随后沿宽度方向向中心依次出现压力峰值。底部中心区域(X/L=0~0.6)形成空气垫,空气垫对该区域的冲击产生缓冲作用。其缓冲作用在中心点处最明显,并沿宽度方向向两侧减弱,在X/L=0.6处为空气垫的边缘,出现压力最大值。
2)结构等速冲击入水后的运动为自由振动。冲击压力的峰值随结构质量的增大而增大。不同质量下底部均压的峰值几乎出现在同一时刻,压力分布曲线的形状基本一致,质量越小整个底部的压力值均越小。同时,质量越小空气垫的作用越明显,空气垫边缘的位置会随结构质量的增大向底部中心移动。
3)冲击压力的峰值随刚度的增大而增大。不同刚度下底部均压峰值出现的时刻随刚度的减小而顺延,冲击作用时间的长短会随弹性模量的减小而延长,压力分布曲线的形状基本保持一致。同时,刚度越大空气垫的缓冲作用越明显,且不同刚度下空气垫的边缘位置几乎不变。
4)冲击压力峰值与速度呈线性关系,随速度的增大而增大。速度对底部压力分布情况的影响并不显著。
5)底部斜升角对冲击压力峰值的影响十分显著。0°~2°时冲击压力峰值随底部斜升角的增大而增大,2°~3°时随底部斜升角的增大而减小,3°之后其值趋于稳定。
| [1] | KARMAN TV The impact of seaplane floats during landing[R]. Washington DC, USA: National Advisory Committee for Aero-nautics, NACA Technical Notes 321, 1929. |
| [2] | WAGNER V H. Phenomena associated with impacts and sliding on liquid surfaces[J]. Z Angew Math Mech, 1932, 12 (4): 193–215. DOI: 10.1002/(ISSN)1521-4001 |
| [3] | WORTHINGTON A M. Impact with a liquid surface studied with aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society of London, 1900, 194A : 175–199. |
| [4] | S. Experiments on flat-bottom slamming[J]. Journal of Ship Research, 1966, 10 (1): 10–27. |
| [5] | 黄震球, 张文海. 减小平底体砰击的试验研究[J]. 武汉造船工程学会年会论文集(下), 1985 : 245–252. |
| [6] | 李国钧, 黄震球. 平底物体对水面的斜向冲击[J]. 华中理工大学学报, 1995, 23 (1): 145–147. |
| [7] | 卢炽华, 何友声. 二维弹性结构入水冲击过程中的流固耦合效应[J]. 力学学报, 2000, 36 (2): 129–140. |
| [8] | 夏斌, 陈震, 肖熙. 弹性平底海洋结构物入水冲击的仿真分析[J]. 中国海洋平台, 2005, 20 (1): 22–28. |
| [9] | 陈震, 肖熙. 平底结构砰击压力峰值分析[J]. 上海交通大学学报, 2006, 40 (6): 983–987. |
| [10] | 陈震, 肖熙. 平底结构砰击压力的分布[J]. 中国造船, 2005, 46 (4): 97–103. |
| [11] | 陈震, 肖熙. 空气垫在平底结构入水砰击中作用的仿真分析[J]. 上海交通大学学报, 2005, 39 (5): 670–673. |
| [12] | 陈震, 肖熙. 基于神经网络的平底结构砰击压力预报[J]. 海洋工程, 2005, 23 (2): 26–31. |
| [13] | MATEJ V, STPHAN M, HEINER M, et al. Fluid models in LS-DYNA and their interaction with a structure in dynamic simulations[C]// ASME Pressure Vessels and Piping Division Conference. 2005. |
| [14] | OGER G, DORING M, ALESSANDRINI B, et al. Two-dimensional SPH simulations of wedge water entries[J]. Journal of Computational Physics, 2005, 213 : 803–822. |
| [15] | GONG Kai, LIU Hua, WANG Benlong. Water entry of a wedge based on SPH model with an improved treatment[J]. Journal of hydrodynamics, 2009, 21 (6): 750–757. DOI: 10.1016/S1001-6058(08)60209-7 |
| [16] | 吴家鸣, 龚国围, 朱良生. 平底结构砰击作用下限制水域的流体动力特性[J]. 华南理工大学学报, 2008, 36 (10): 97–107. DOI: 10.3321/j.issn:1000-565X.2008.10.020 |
| [17] | HU Xiao-zhou, RAO Qiu-hua, ZHENG Hong-qiang. Numerical simulation of flatted-bottom seafloor mining tool and water entry process[C]// Fifth Conference on Measuring Technology and Mechatronics Automation. 2013. |
 2017, Vol. 39
2017, Vol. 39
