随着水下探测技术的不断发展,水声信道受到了越来越多的关注。由于海水的复杂性,水声信号在传播过程中存在多径效应,会对水声信号造成明显的衰减和畸变,严重影响水声信号的探测。要消除多径效应的干扰,采取水声信道均衡、信道匹配[1]等方式实现水声通信与水下信号检测,需要了解水声信道特性并对其进行建模。
随着水下信道研究的发展,学者对此进行了大量研究:高分辨率谱估计技术越来越多的被用于水下信道模型仿真,同时也出现了许多其他的水声信道仿真方法[2],最新的方法包括:非线性最小二乘法[3 – 5]、最大熵法[6]、最大似然法[7, 8]、期望值最大算法[9]、反演滤波法[10]、交替投影法、自相关算法等。
本文首先简要分析了水声在浅海中的传播特性及信道模型,包括声速建模、传播衰减建模及本征声线的搜索模型;其次,基于以上理论模型,本文在Matlab平台模拟产生了信道冲激响应结果;最后为了满足实时性要求,在GPU平台上用OpenCL实现了实时信道冲激响应的模拟。
1 水声传播特性及信道模型分析水声信道的特点是环境噪声干扰严重、信号传播衰减大、随机信道等。本文对水声信道的模拟主要包括声速模拟、传播衰减模拟以及本征声线搜索模拟3个方面。
1.1 声速模型对于声速模型的模拟采用乌德公式:
| $c = 1\;450 + 4.21T - 0.037{T^2} + 1.14(S - 35) + 0.175P\text{。}$ | (1) |
由式(1)可知,声速c随温度T、盐度S、压力P的增加而增加。对P的求解可以转化为深度的求解,水深下降10 m时,增加大约一个大气压。温度T与盐度S随纬度变化规律如图1所示。
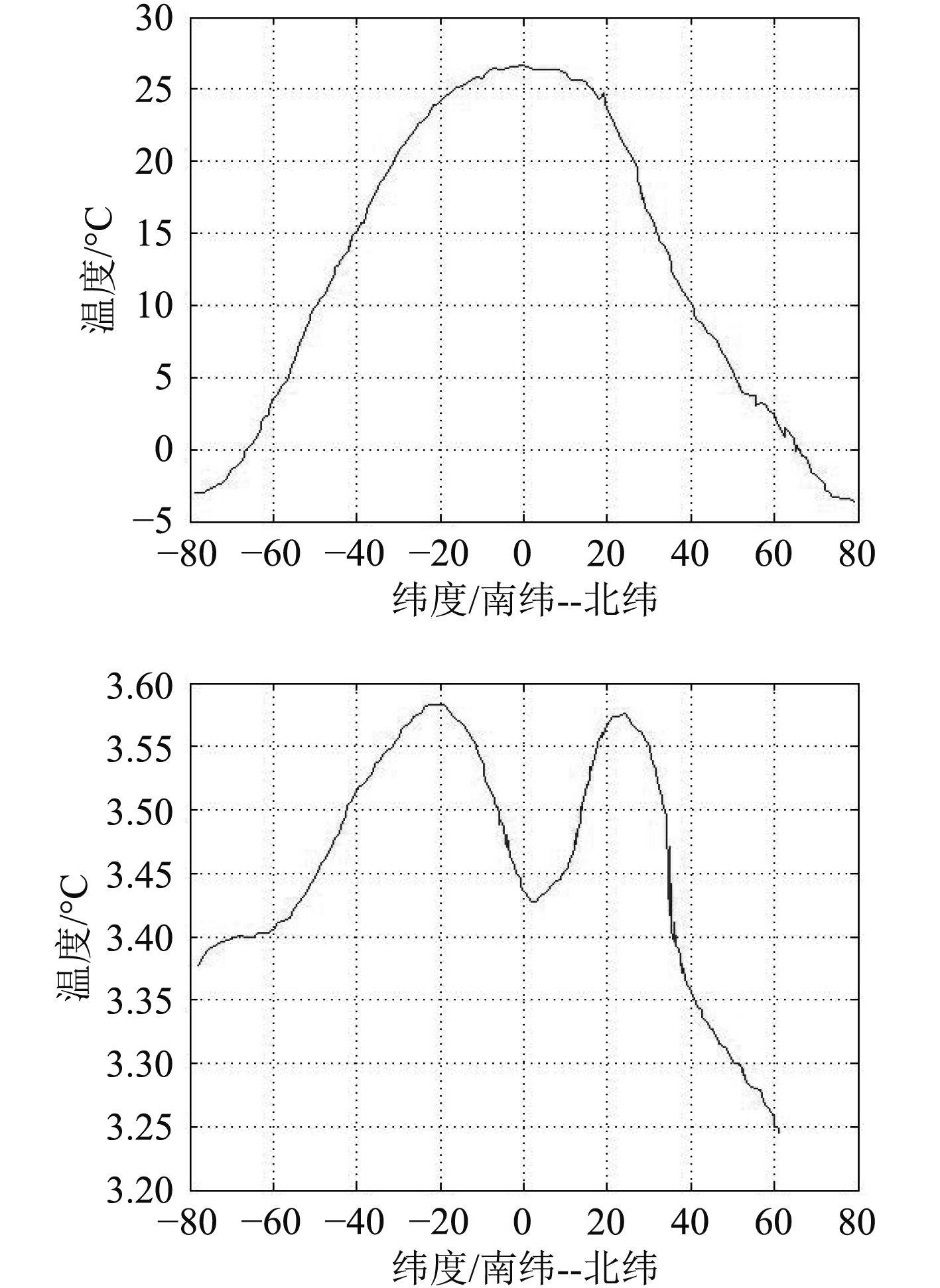
|
图 1 海洋表面温度与盐度随纬度变化规律 Fig. 1 Variation law of ocean surface temperature and salinity with latitude |
声波在海水中的传播损失主要包括传播扩展损失、介质吸收损失和海面海底散射损失。
其中,扩展损失公式为:
| $TL = n \cdot 101{\rm g}r\;\left( {\rm dB} \right)\text{。}$ | (2) |
声波的传播形式为平面波时,n近似取0;声波的传播形式为柱面波时,n近似取1;声波在浅海传播时,n近似取1.5;声波的传播形式为球面波时,n近似取2;r为声源发射点与接收点间的距离,m。
吸收损失采用Thorp公式:
| $a = \frac{{0.1{f^2}}}{{1 + {f^2}}} + \frac{{40{f^2}}}{{4\;100 + {f^2}}} + 2.75 \times {10^{ - 4}}{f^2} + 0.003\text{。}$ | (3) |
式中:a为吸收损失,dB/km;f为工作频率f,kHz。
散射损失主要为界面衰减,分为海面衰减与海底衰减,海面平均反射系数为:
| ${V_s} = 1 - 0.45 \cdot {(f \cdot H)^{3/2}} \cdot \cos {\theta _0}\text{。}$ | (4) |
式中:f为工作频率,kHz;H为海浪平均高度,m[11]。
海底反射系数与入射角及斜率之间的基本特征由三参数模型来反映:
| $ - \ln \left| {{V_{b0}}(\theta )} \right| = \left\{ {\begin{aligned}& {Q \cdot \theta\text{,} \quad\quad\quad\quad\quad\quad\quad 0 < \theta < {\theta _0}}\text{,}\\& { - \ln \left| {{V_{b0}}(\theta )} \right| = {\rm{const}}\text{,}\quad{\theta _0} < \theta < \displaystyle\frac{\pi }{2}}\text{。}\end{aligned}} \right.$ | (5) |
式中:θ0为海底反射系数临界角;Q为入射角小于临界角时,海底反射系数随入射角变化的斜率;Vb0为入射角大于临界角时海底的反射系数。
1.3 本征声线搜索模型声场是有声波存在的弹性媒质所占有的空间,通常采用射线来描述声波在声场中的传播,射线起点为声源发射点,按照声线传播的曲线到达接收点,接收点接收到的声线构成了接收点的声场。本征声线定义为所有到达接收点的声线。由于声线在海水(非真空)中传输,因此相应地有一定的时延和传播衰减。本文采用Snell折射定律来计算水平方向上非均匀海洋环境的声场。Snell折射定律为:
| $\frac{{\cos \alpha }}{c} = \frac{{\cos {\alpha _0}}}{{{c_0}}} = const \text{。}$ | (6) |
掠射角α为声线传播方向与水平面的夹角,c为声线所在深度的海洋声速。α0和c0为声线出射处的夹角和声速对应值。若声线出射角和声速随深度的分布c(z)给出,可以按照式(5)求出海洋中任意深度处声线传播方向与水平面的夹角。
根据Snell定律可导出:
| ${\rm tan}\alpha = \sqrt {({n^2}(z) - {{\cos }^2}{\alpha _1}/\cos {\alpha _1}}\text{,}$ | (7) |
其中
| $x = \cos {\alpha _1}\int_{{z_1}}^z {\frac{{{\rm d}z}}{{\sqrt {({n^2}(z) - {{\cos }^2}{\alpha _1}} }}} \text{。}$ | (8) |
声速因深度而异,声线经过微元ds距离所需要的时间
| $t = \int {\frac{{{\rm d}s}}{c}} = \int_{{z_1}}^z {\frac{{{\rm d}z}}{{c(z)\sin \alpha (z)}}}\text{,}$ | (9) |
| $S = \int {{\rm d}s} = \int_{{z_1}}^z {\frac{{{\rm d}z}}{{\sin \alpha (z)}}}\text{。}$ | (10) |
根据Snell定律,
| $t = \frac{1}{{{c_1}}}\int_{{z_1}}^z {\frac{{{n^2}(z){\rm d}z}}{{\sqrt {({n^2}(z) - {{\cos }^2}{\alpha _1}} }}}\text{。}$ | (11) |
采用声线跨度法搜索本征声线[12]:当接收点深度大于发射点深度时,海洋中本征声线传播到接收点时的路径可以分为4种基本情况[13],如图2所示。
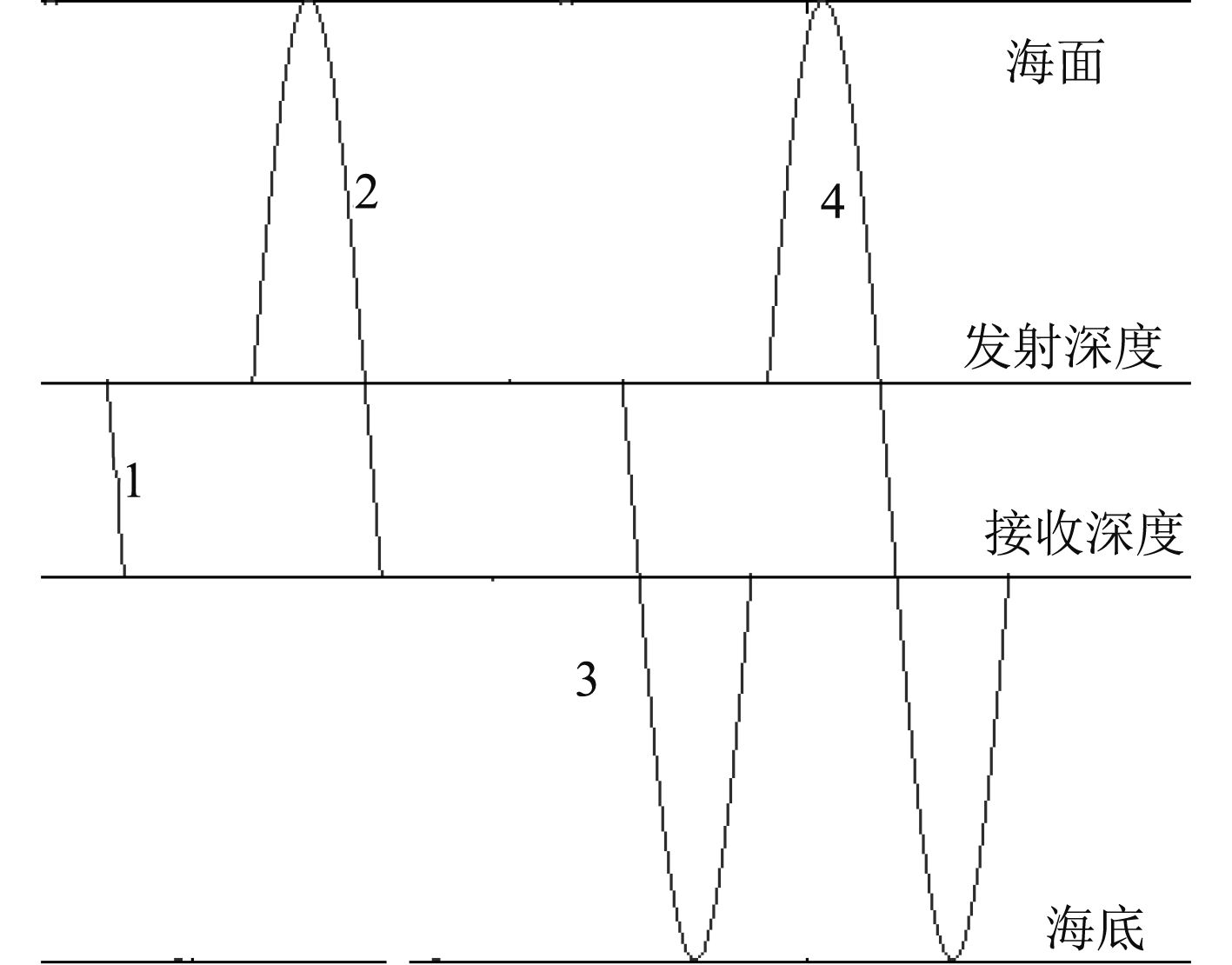
|
图 2 本征声线的几种到达形式 Fig. 2 Several forms of the sign of the eigen ray |
分析1,2,3,4的声线传播形式,不难发现4种声线传播形式的排列组合可以表示所有发射点到接收点的声线。为了使计算更简洁,定义4种声线传播形式的水平传播距离为子跨度,如图3所示。
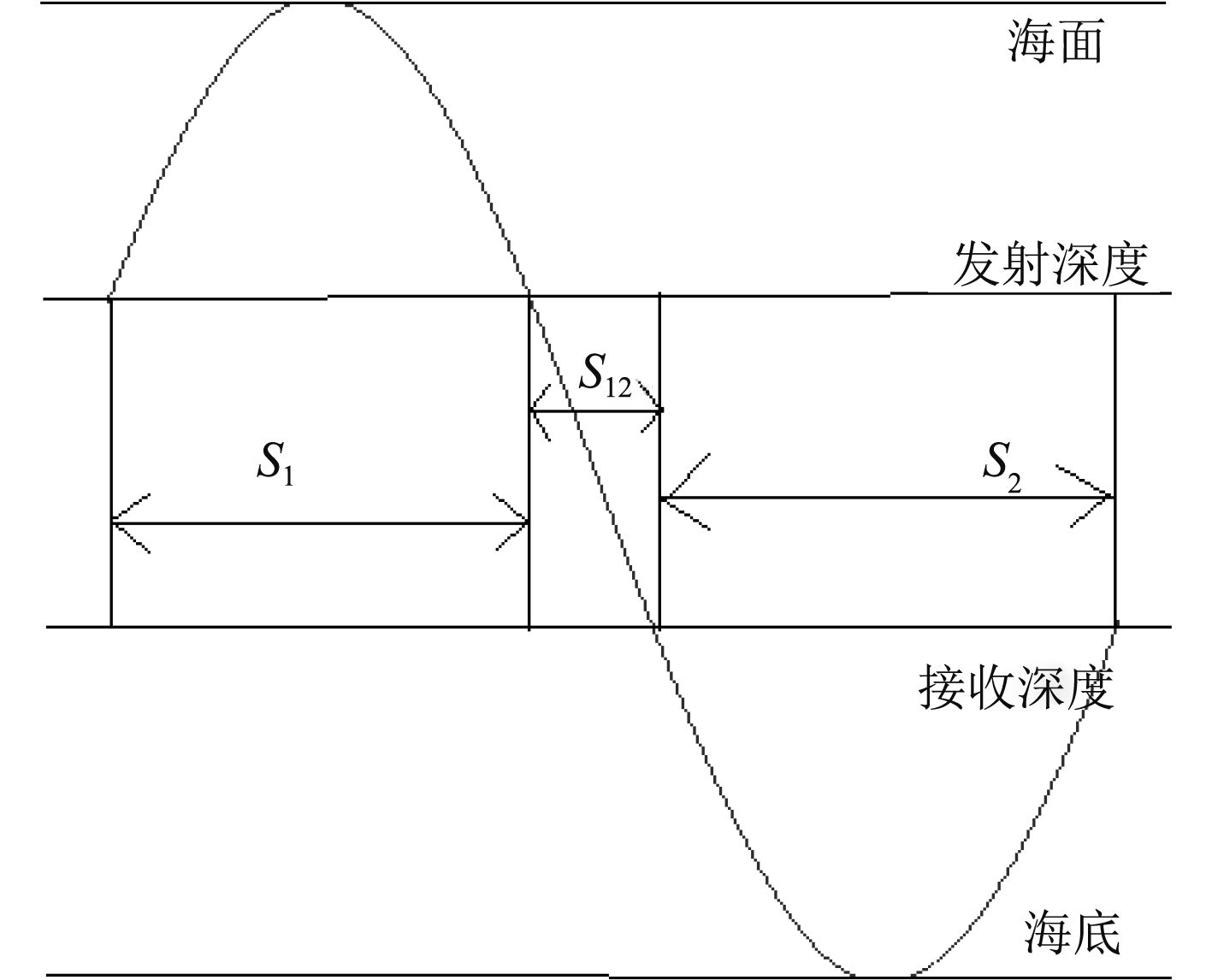
|
图 3 4种子跨度的具体形式 Fig. 3 Four specific forms of subspecies |
其中,S1表示声线发射后第1次到达声源发射点所在深度经过的水平距离,S12表示声线从声源发射点到接收点的水平距离,S2表示声线从接收点所在深度到接收点的水平距离。S1,S12与S2可由式(9)求得。当接收点深度小于发射点深度时,可看作是该子跨度形式的逆过程。
远距离传输时,以该过程为一个周期,声线会经历m个周期,m表示本征声线经过的整数跨度。
因此,本征声线远距离传输时的水平传播距离可由这4种子跨度及经历过的周期数来表示:
| $D = mS + a{S_1} + {S_{12}} + b{S_2}\text{。}$ | (12) |
其中,a和b只能取0或1。不同的m与a,b的组合形式表示了不同到达形式的本征声线。
图4画出了从发射点到接收点的一个周期下,全部4种本征声线的轨迹:
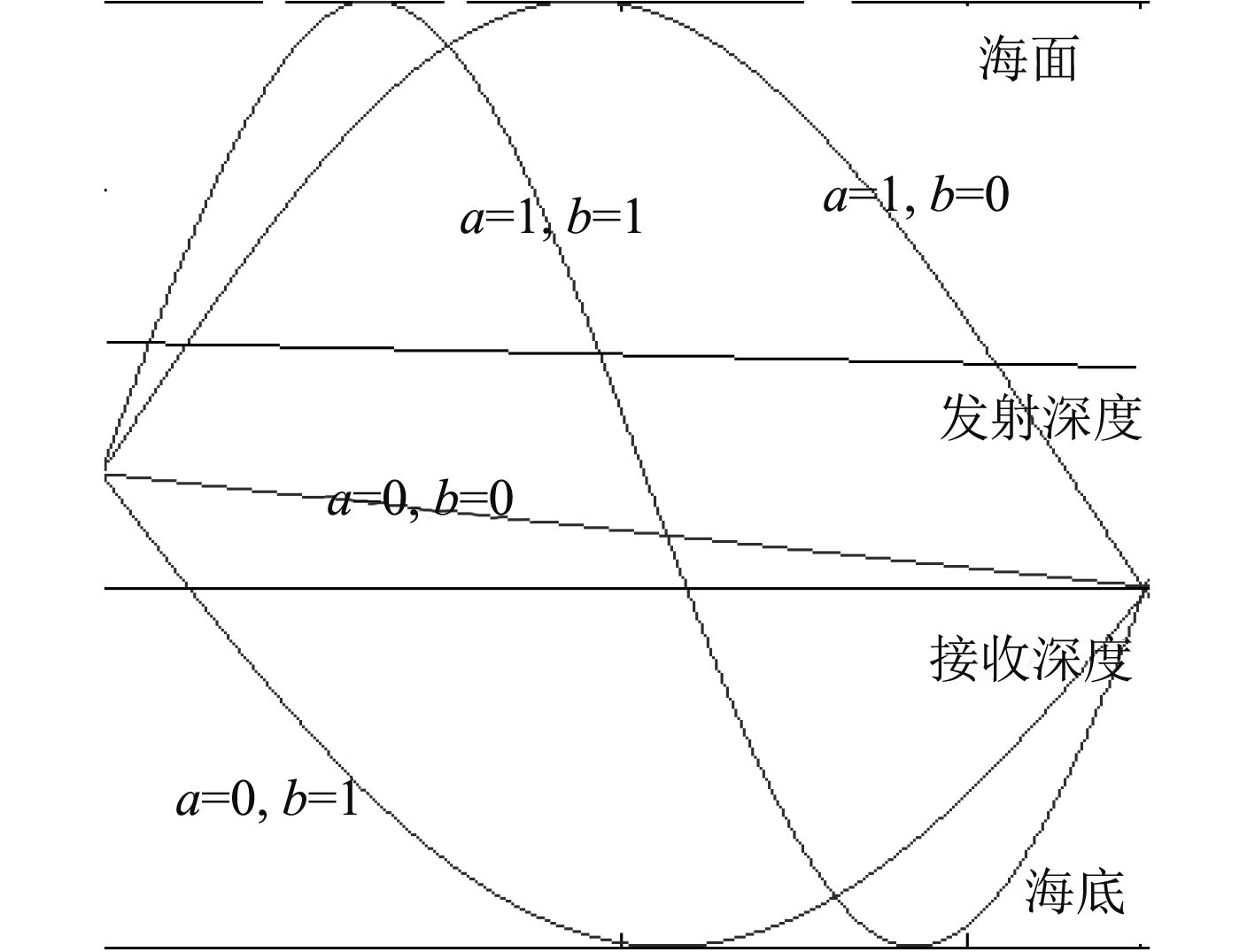
|
图 4 几种声线到达形式声线轨迹 Fig. 4 Several sound lines arrive in the form of sound line trajectory |
该解组合方程组的方法在计算上比普通打靶法更加简练。角度分辨率是求取本征声线的关键,若角度分辨率太大,在远距离传输时,本征声线的搜索会出现很大偏差;若角度分辨率太小,则搜索速度会大大降低,对水声信道估计的实时性造成很大影响。角度分辨率通常需要根据实际系统的要求,通过多次实际操作来验证[14]。
2 水声信道建模仿真实验 2.1 仿真实验条件基于以上声速梯度、传播衰减以及本征声线搜索这3种理论模型,设置仿真实验条件,假设海洋深度为300 m,纬度为北纬30°,声源发射点深度为80 m,接收点深度为200 m,两者水平距离为3 km。角度搜索范围为–50°~+50°,声线数目为200根,即角度分辨率为0.5°。
2.2 仿真实验过程首先,根据仿真实验条件得到模型背景下声速梯度如图5所示。
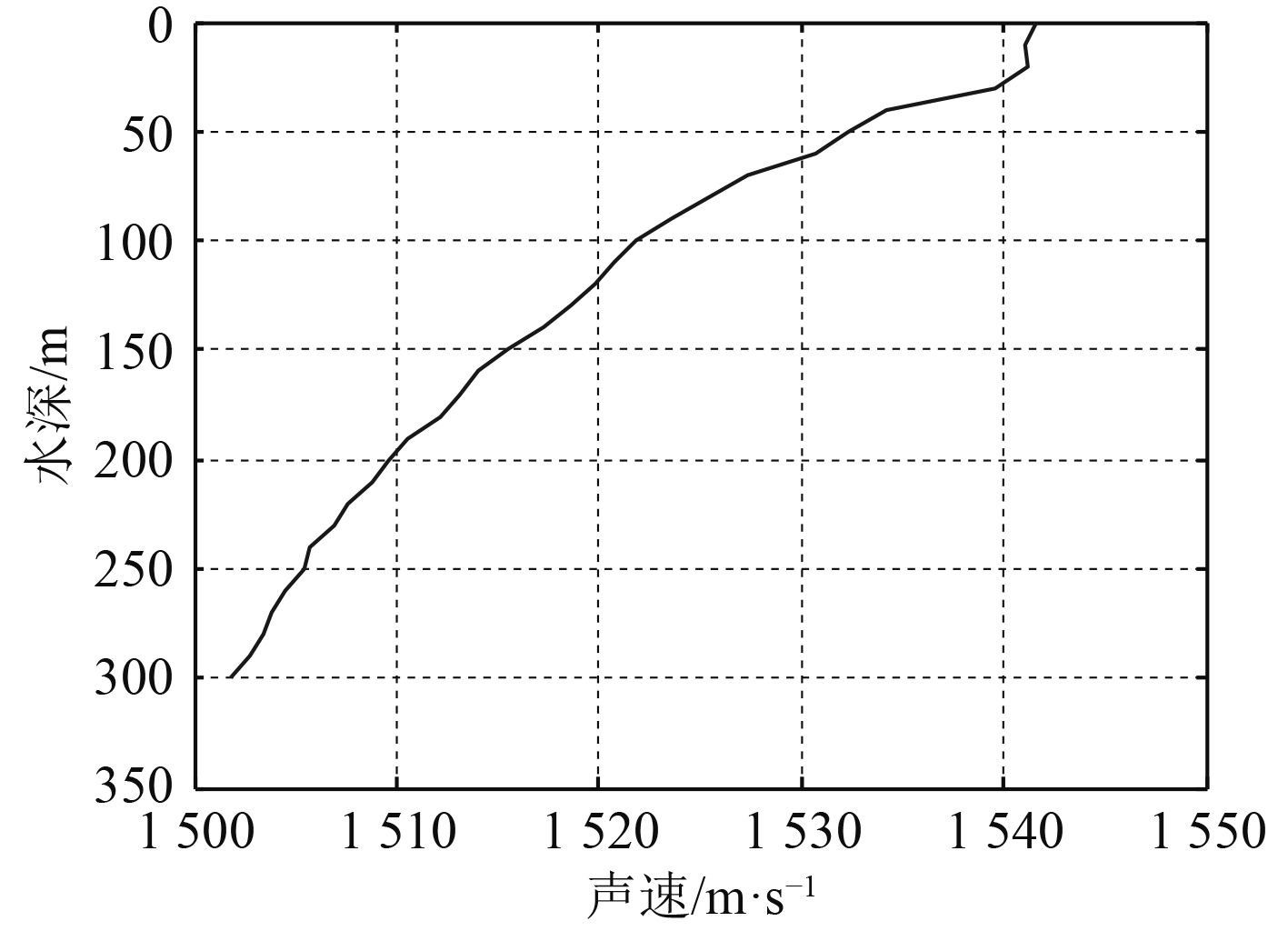
|
图 5 水下声速梯度 Fig. 5 Underwater velocity gradient |
其次,基于此声速梯度,将传播衰减与本征声线搜索模型相关公式代入,得到的本征声线结果如图6所示,其所对应的时延-衰减即信道冲激响应如图7所示。
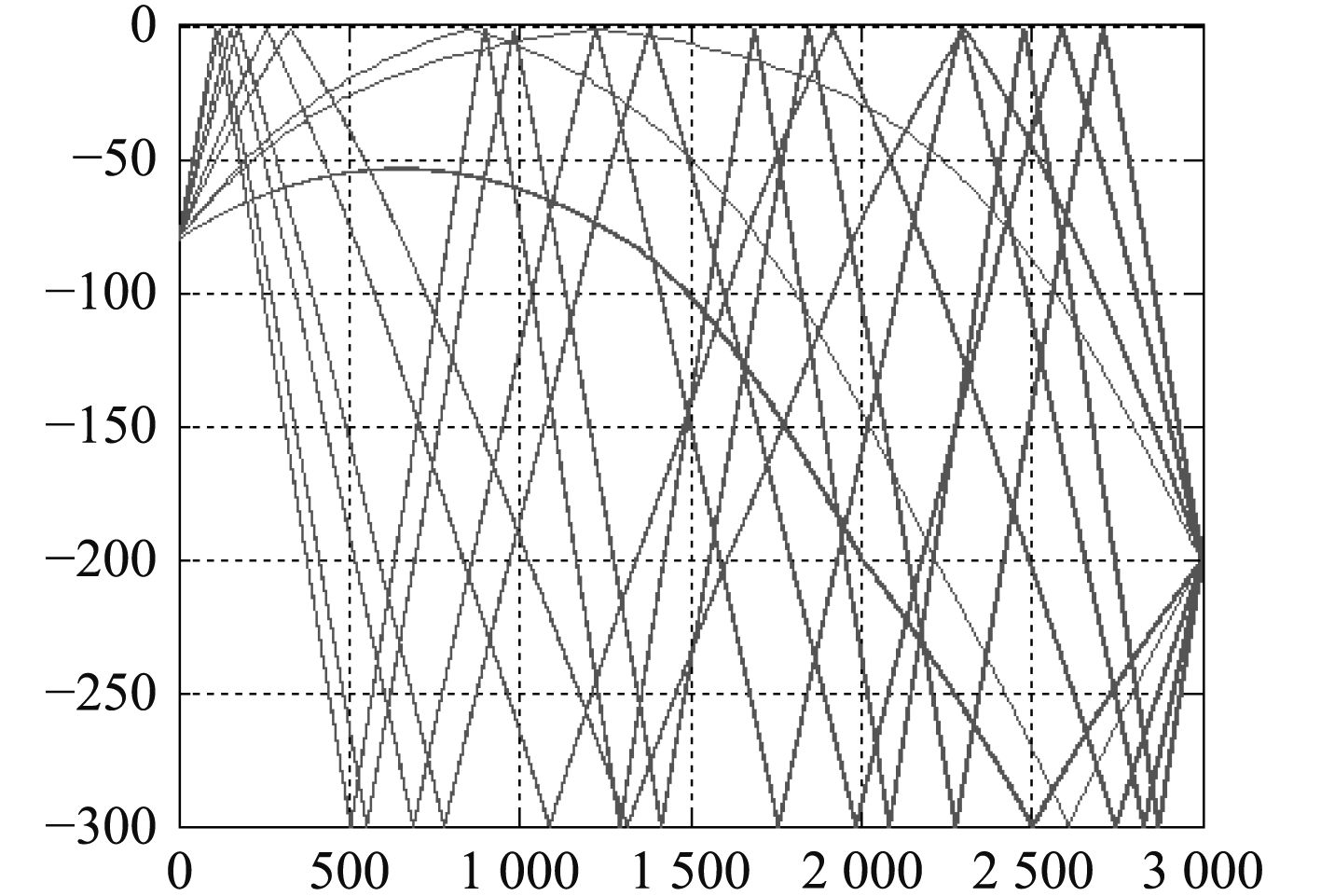
|
图 6 声源-目标传播本征声线 Fig. 6 Sound source-target propagation |
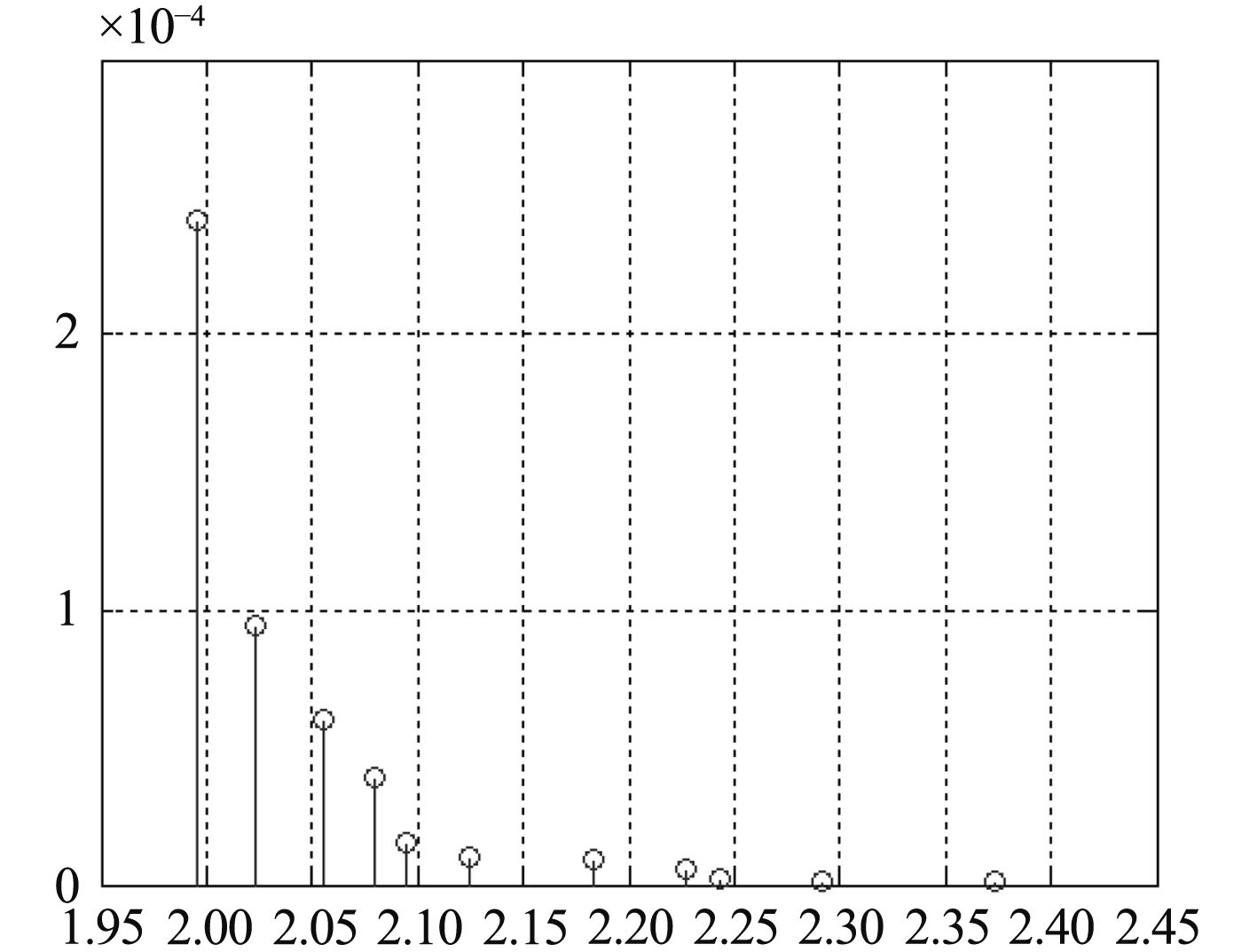
|
图 7 声源-目标信道冲激响应 Fig. 7 Sound source-target channel impulse response |
声源-目标信道时延-衰减结果如表1所示。
|
|
表 1 声源-目标信道时延-衰减结果 Tab.1 Sound source-target channel delay-attenuation result |
分析上述仿真结果,发现本文基于声速梯度以及本征声线传播搜索模型成功得到了浅海环境下声源与目标之间的传播信道以及相应的衰减与时延信息,理论上验证了算法的正确性。为了满足工程实践要求,本文将移植这种算法至GPU平台,以高运算速度满足工程实时性需求。
3 水声信道估计实时性实现 3.1 OpenCL简介随着体系结构的技术演进,计算机处理器晶体管数目不断增加,增长的晶体管数目驱动体系结构向“异构系统”演进。软件依靠硬件性能,尤其是主频提升而获得性能提升,这种“免费午餐”已经结束。在新的异构计算时代,程序员需要转变思维,拥抱新的编程模式。
异构计算系统是将一系列拥有不同指令集的机算单元整合在一起,共同工作执行一个应用程序的系统。最简单的一个异构计算系统就是CPU+GPU,GPU面向大量并行化数据的运算,计算能力可以达到CPU的几百倍。OpenCL是一个异构平台下编写程序的编程环境[15]。
本文采用的异构平台是CPU+GPU,由一个主机连接一个GPU设备构成。GPU型号为nVIDIA GeForce GTX 560,显存频率为4 008 MHz。其中,主机程序用C语言编写,负责管理内核程序在GPU设备上的运行,即GPU的资源分配。内核程序用OpenCL C语言编写,负责大量循环运算,实时计算出水声信道冲激响应。
3.2 结果分析不同平台上信道模拟用时对比(每次运行时间可能与处理器所处状态有关,应控制不同平台进行信道模拟时处理器状态相同并进行多次实验求运行时间均值):
|
|
表 2 不同平台上信道模拟用时对比 Tab.2 Time comparison of channel simulation on different platforms |
其中,实验1角度搜索范围为–50°~+50°,声线数目为200根,即角度分辨率为0.5°。实验2角度搜索范围为–50°~+50°,声线数目为1 000根,即角度分辨率为0.1°。由结果可以看出,角度分辨率为0.5°时使用GPU编程满足了实时模拟信道冲激响应的要求,可以根据信道冲激响应进行信道均衡与信道匹配,消除信道干扰,检测出声源信号。
4 结 语本文简要分析了水声在浅海中的传播特性及信道模型,包括声速建模、传播衰减建模及本征声线的搜索模型。基于以上模型,模拟了浅海条件下信道的冲激响应,通过仿真验证,证实了模型算法的正确性,其次实现了GPU平台下的算法移植,利用其高速运算特性实现了水声信道估计的实时性这一要求,满足了工程实践需求,对于信道均衡、水下目标模拟、水下目标检测、水下目标跟踪定位、水下通信等水下无人系统仿真与通信技术等研究方向均有重要作用。
| [1] |
兰英, 章新华, 熊鑫. 浅海水声多途信道建模与仿真[J]. 《舰船科学技术》, 2010, 32 (9): 120–122.
LAN Ying, ZHANG Xin-hua, XIONG Xin. Modeling and simulation on shallow water acoustic multi-path channels[J]. 《Editorial Department of Ship Science and Technology》, 2010, 32 (9): 120–122. |
| [2] |
蒋德军, 胡涛. 时延估计技术及其在多途环境中的应用[J]. 声学学报, 2001, 26 (1): 34–40.
JIANG De-jun, HU Tao. Time-delay estimation and its application in multipath environment[J]. Journal of Acoustics, 2001, 26 (1): 34–40. |
| [3] | CHEN J T, PAULRAJ A, REDDY U. Multichannel maximum-likelihood sequence estimation(MLSE) equalizer for GSM using a parametric channel model[J]. Communications, IEEE Transactions on, 1999, 47 (1): 53–63. DOI: 10.1109/26.747813 |
| [4] | CHAMPAGNE B, EIZENMAN E, PASUPATHY S. Exact maximum likelihood time delay estimation for short observation intervals[J]. Signal Processing, IEEE Transactions on, 1991, 39 (6): 1245–1257. DOI: 10.1109/78.136531 |
| [5] | MANICKAM T G, VACCARO R J, TUFTS D W. A least-squares algorithm for multipath time-delayestimation[J]. Signal Processing, IEEE Transactions on, 1994, 42 (11): 3229–3233. DOI: 10.1109/78.330381 |
| [6] | WU R, LI J. Time-delay estimation via optimizing highly oscillatory cost functions[J]. Oceanic Engineering, IEEE Journal of, 1998, 23 (3): 235–244. DOI: 10.1109/48.701196 |
| [7] | EVANS A, FISCHL R. Optimal least squares time-domain synthesis of recursive digital filters[J]. Audio and Electroacoustics, IEEE Transactions on, 1973, 21 (1): 61–65. DOI: 10.1109/TAU.1973.1162433 |
| [8] | SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. Antennas and Propagation, IEEE Transactions on, 1986, 34 (3): 276–280. DOI: 10.1109/TAP.1986.1143830 |
| [9] | FEDER M, WEINSTEIN E. Parameter estimation of superimposed signals using the EM algorithm[J]. Acoustics, Speech and Signal Processing, IEEE Transactions on, 1988, 36 (4): 477–489. DOI: 10.1109/29.1552 |
| [10] | SENMOTO S, CHILDERS D G. Signal resolution via digital inverse filtering[J]. Aerospace and Electronic Systems, IEEE Transactions on, 1972 (5): 633–640. |
| [11] | 林旺生. 水声信道仿真与声线修正技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2009. |
| [12] | 欧晓丽. 水声信道建模及其仿真平台的实现[D]. 厦门: 厦门大学, 2007. |
| [13] |
王百合, 冯西安, 黄建国, 孙静, 等. 一种分层海洋中求取本征声线的新方法[J]. 微处理机, 2006 (1): 63–65.
WANG Bai-he, FENG Xi-an, HUANG Jianguo, SUN Jing, et al. A new method for finding the intrinsic line of sound in a layered ocean[J]. Microprocessor, 2006 (1): 63–65. |
| [14] |
魏莉, 许芳, 孙海信. 水声信道的研究与仿真[J]. 声学技术, 2008 (01): 25–29.
WEI Li, XU Fang, SUN Haixin. Research and simulation of underwater acoustic channel[J]. Acoustics, 2008 (01): 25–29. |
| [15] |
陈钢, 吴百锋. 面向OpenCL模型的GPU性能优化[J]. 《计算机辅助设计与图形学学报》, 2011, 23 (4): 571–581.
CHEN Gang, WU Baifeng. GPU performance optimization for OpenCL model[J]. Journal of Computer Aided Design and Graphics, 2011, 23 (4): 571–581. |
 2017, Vol. 39
2017, Vol. 39
