在水下目标识别过程中,为了得到更好的分类识别效果,研究人员采用不同方法提取水下目标信号的多域特征。特征数目的增加导致处理这些数据所需的时间和空间急剧增加,分类器的设计更加困难,影响了自动识别系统的工作效率。且提取到的特征中多含有冗余特征、不相关特征和噪声特征,降低了分类识别正确率。因此,对数据进行特征选择以选取优化特征子集,对水下目标识别系统至关重要。
根据训练样本集中是否使用了类标,可将特征选择方法分为有监督特征选择方法[1–3]和无监督特征选择方法[4–6]。有监督特征选择方法通过类标的指导来评价特征的重要性。无监督特征选择方法由于缺少类标信息,则需要挖掘数据内在的结构信息,然后评价特征。在水下目标识别过程中,水声目标样本的获取已经比较容易,但有类标样本的获取比较困难且成本较高,所获取的样本多为无类标样本,因此无监督特征选择对水声目标的识别有重要意义。
近来提出的特征选择算法中,基于相似度保持的特征选择框架具有良好的性能。典型方法包括拉普拉斯评分法[7]、谱特征选择[8]、多簇特征选择[9]、嵌入式学习和谱回归联合学习[10]。然而,这些方法将流形学习和谱回归作为独立的步骤进行学习,预先构建的图可能无法满足后续的特征选择任务。
因此,本文中提出一种新的特征选择算法—基于图学习的无监督特征选择方法(UFSGL),该方法将图的构建整合到数据转换中,得到了图的构建和转换矩阵优化的联合框架,并采用
对于训练样本集
| ${\left\| A \right\|_{r,s}} = {\left( {\sum\limits_{i = 1}^e {{{\left( {\sum\limits_{j = 1}^f {{{\left| {{A_{ij}}} \right|}^r}} } \right)}^{s/r}}} } \right)^{1/s}}\text{。}$ | (1) |
局部保留投影(Locality Preserving Projection,LPP)[11]通过数据的近邻信息构建近邻图。利用图的拉普拉斯谱,通过最优地保持数据的局部近邻信息,计算一种映射,将数据投影到低维子空间。LPP通过优化以下目标函数得到线性映射W。
| $\arg \mathop {\min }\limits_W \sum\limits_{i,j = 1}^n {{{\left\| {{W^{\rm T}}{x_i} - {W^{\rm T}}{x_j}} \right\|}^2}{S_{ij}}}\text{。}$ | (2) |
LPP的基本思想是,寻找转换矩阵W,将高维数据X转换到低维矩阵XW,以用于最大化地保持X的局部结构的连接,最小化式(2)以确保当xi和xj相邻时,
最近的研究结果表明,保留数据的局部结构对无监督特征选择有更重要的作用,而基于图的学习方法能够有效地保留数据的流形结构。因此构建一个有效的图对后续学习算法至关重要。通常采用KNN(K Nearest Neighbors)法来构建数据的近邻图。
2.1 图的构建给定图
对于训练样本集
| ${{S}_{ij}}= {e^{ - \displaystyle\frac{{{{\left\| {{x_i} - {x_j}} \right\|}^2}}}{{2{\delta ^2}}}}}\text{。}$ | (3) |
式中:δ为参数;若xi和xj不互为k近邻,则
在得到图的相似度矩阵后,构造度量矩阵D,其对角元素
| ${L} ={D} - {S}\text{。}$ | (4) |
现实应用中,很难估计得到合适的近邻大小,且不同应用环境下的最佳近邻大小也不相同。受到LPP算法的启发,提出一种同时进行图的构建和转换矩阵优化的学习框架。此外,为了更好地进行特征选择,采用来
| $\begin{array}{l}\mathop {\min }\limits_{S,W} \sum\limits_{i,j = 1}^n {\left( {\left\| {{W^{\rm T}}{x_i} \!-\! {W^{\rm T}}{x_j}} \right\|_2^2{S_{ij}}} \right)} \!+\! \alpha \sum\limits_{i,j = 1}^n {S_{ij}^{}} \!+\! \beta {\left\| W \right\|_{2,1}}\\\begin{array}{*{20}{c}}{\rm s.t.} & {0 \leqslant {S_{ij}} \leqslant 1,{W^{\rm T}}{S_t}W = I}\text{。}\end{array}\end{array}$ | (5) |
式中:
算法目标函数的第1项与LPP函数式(2)的相似,主要用于保持数据的局部结构,并得到转换矩阵;第2项采用
注意到
| ${U_{ii}} = \frac{1}{{2{{\left\| {{w_i}} \right\|}_2}}}\text{。}$ | (6) |
可以将目标函数重写为
| $\begin{array}{l}\mathop {\min }\limits_{S,W,U} tr\left( {{{W}^{\rm T}}{X}{{L}_S}{{X}^{\rm T}}W} \right) + \beta tr\left( {{{W}^{\rm T}}{UW}} \right)\text{,}\\\begin{array}{*{20}{c}}{\rm s.t.}&{{{W}^{\rm T}}{{S}_t}{W} = I}\text{。}\end{array}\end{array}$ | (7) |
首先,固定S,更新W和U,目标函数等价于
| $\begin{array}{l}\mathop {\min }\limits_{W,U} tr\left( {{{W}^{\rm T}}\left( {{X}{{L}_S}{{X}^{\rm T}} + \beta {U}} \right){W}} \right),\\\begin{array}{*{20}{c}}{\rm s.t.}&{{{W}^{\rm T}}{{S}_t}{W} = I}{\text{。}}\end{array}\end{array}$ | (8) |
式(8)是典型的广义特征值分解问题。当U固定时,最优解是
为了更好地学习数据结构,对相似度矩阵S进行更新学习,使其在当前状态下对算法保持最优。采用拉格朗日乘数法对S进行优化。设
| ${L}({S_{ij}}) =\!\!\! \sum\limits_{i,j = 1}^n {\left( {\left\| {{{W}^{\rm T}}{x_i} \!-\! {{W}^{\rm T}}{x_j}} \right\|_2^2{{S}_{ij}}} \right)} \!\!+\!\! \alpha \sum\limits_{i,j = 1}^n {{{S}_{ij}}} + {\psi _{ij}}{{S}_{ij}}\text{。}$ | (9) |
对其求偏导可得
| $\frac{{\partial {L}({{bm S}_{ij}})}}{{\partial {S_{ij}}}} = \left\| {{{W}^{\rm T}}{x_i} - {{W}^{\rm T}}{x_j}} \right\|_2^2 + \alpha + {\varPsi _{ij}}\text{。}$ | (10) |
由KKT(Karush-Kuhn-Tucker)条件可得,
| $\left( {\left\| {{{W}^{\rm T}}{x_i} - {{W}^{\rm T}}{x_j}} \right\|_2^2 + \alpha } \right){{S}_{ij}} = 0\text{。}$ | (11) |
从而得到
| ${{\hat {S}}_{ij}} = \frac{{\alpha {{S}_{ij}}}}{{\left\| {{{W}^{\rm T}}{x_i} - {{W}^{\rm T}}{x_j}} \right\|_2^2}}\text{。}$ | (12) |
式中,
为了得到式(5)的最优解,采用循环交错优化方法。在每次循环中,转换矩阵W通过对
经过有限次的循环优化后,
|
|
表 1 UFSGL算法流程 Tab.1 The processing flow of UFSGL |
为了验证所提算法的有效性,利用UCI数据库的sonar数据集对算法进行实验验证。
4.1 数据介绍本文实验中所用的sonar数据主要用于识别声呐信号反射金属圆柱和粗糙的圆柱形岩石。数据集包含138个样本,通过在不同的角度和不同的条件下声呐信号反射金属圆柱壳获得。声呐信号是一种频率已调制过的唧唧声,其频率不断升高。该数据包含了由不同条件下生成的圆柱壳和岩石反射信号。每个样本都包含了60个从0.0到1.0的特征值。每个值代表了一个特定频带范围内的能量,并且整合了一定的时间段。高频信号在时间上出现的比较晚。因为这些频率在传输时会有延迟。如果研究的对象是岩石,那么与每一段声音录制相关联的类标都包含了字母“R”,如 果是矿山(金属圆柱壳)则是“M”。数据说明如表2所示。
|
|
表 2 数据集说明 Tab.2 Data specification |
本算法包含2个平衡参数

|
图 1
|
由图1可以看出,
在得到最优参数
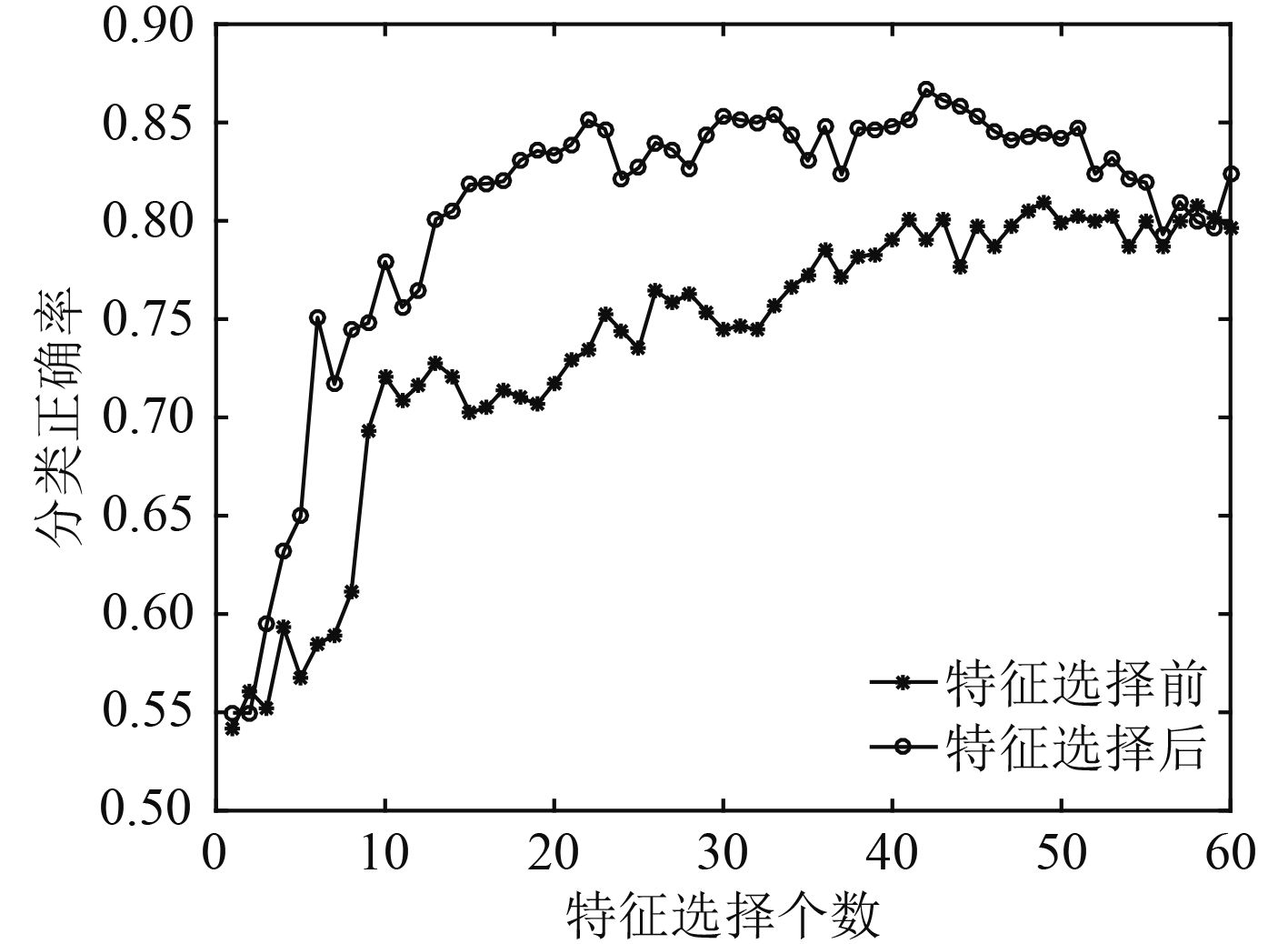
|
图 2 特征选择前后SVM分类识别正确率 Fig. 2 The SVM classification accuracy before and after the feature selection |
由图2可以看出,随着特征数目的增加,SVM分类识别正确率逐渐上升,并在特征数目达到一定个数后,趋于平稳。特征选择后的分类识别正确率相较于特征选择前有很大提升,特征选择后只需13个特征就能达到特征选择前60个特征所拥有的分类识别正确率。这说明UFSGL算法能够有效地排除冗余特征和噪声特征,选出对分类识别任务最优的特征子集,降低了运算量,提高了分类识别系统的运行效率,同时,分类识别正确率也有一定提升。
5 结 语针对水下目标识别过程中,由于数据集中存在冗余特征和噪声特征,导致识别任务效率降低、性能不佳的问题,提出了基于图学习的无监督特征选择方法。该方法利用局部保留投影得到将数据从高维转换到低维的转换矩阵,利用正则化方法优化近邻图中边的光滑度,最后采用稀疏化方法进行特征选择。并采用sonar数据对算法性能进行实验验证,实验结果表明,该方法能有效地去除冗余特征和噪声特征,选出最优特征子集,并提高分类识别正确率。
| [1] | ROBNIKŠIKONJA M, KONONENKO I. Theoretical and Empirical Analysis of ReliefF and RReliefF[J]. Machine Learning, 2003, 53 (1-2): 23–69. |
| [2] | DUDA R O, HART P E, STORK D G. Pattern classification. 2nd ed.[J]. Pattern Analysis & Applications, 2001, 1 (1): 142–143. |
| [3] | PENG H, LONG F, DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2005, 27 (8): 1226. |
| [4] | MITRA P, MURTHY C A, PAL S K. Unsupervised Feature Selection Using Feature Similarity[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2002, 24 (3): 301–312. |
| [5] | DY J G, BRODLEY C E. Feature Selection for Unsupervised Learning[J]. Journal of Machine Learning Research, 2004, 5 (4): 845–889. |
| [6] |
申昇, 杨宏晖, 袁帅. 用于水声目标识别的互信息无监督特征选择[J]. 声学技术, 2013, 32 (6): 30–33.
SHEN S, YANG HH, YUAN S. Unsupervised Feature Selection Approach Based on Mutual Information for Underwater Acoustic Target Classification[J]. Technical Acoustics, 2013, 32 (6): 30–33. |
| [7] | HE X, CAI D, NIYOGI P. Laplacian score for feature selection[C]//International Conference on Neural Information Processing Systems. MIT Press, 2005: 507–514. |
| [8] | ZHAO Z, LIU H. Spectral feature selection for supervised and unsupervised learning[C]//Machine Learning, Proceedings of the Twenty-Fourth International Conference. DBLP, 2007: 1151–1157. |
| [9] | CAI D, ZHANG C, HE X. Unsupervised feature selection for multi-cluster data[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2010: 333–342. |
| [10] | HOU C, NIE F, LI X, et al. Joint embedding learning and sparse regression: a framework for unsupervised feature selection[J]. IEEE Transactions on Cybernetics, 2014, 44 (6): 793. DOI: 10.1109/TCYB.2013.2272642 |
| [11] | X NIYOGI, " Locality preserving projections,” in Neural information processing systems. MIT, 2004. |
 2017, Vol. 39
2017, Vol. 39
