当前对水下目标固频信号的探测手段较少且比较单一,大多是建立声基阵,由于所需基线长、需要的操作平台较大、作用距离不够,并且接受的数据难以处理。赵安邦等[1]制作出1套激光声水下目标探测系统,提高我国海洋监察能力;林伟等[2]针对水下探测系统探测船舶磁场信号,结合BP神经网络对低频量进行训练学习,提取出特征信号,可以显著提高信噪比,实现对船舶信号的检测能力;孙岚等[3]提出利用重力梯度进行潜艇探测新方法,对不同位置重力分析,最终可以实现1 000 m范围的探测。
本文提出利用压电阻抗技术识别所测信号的频率,结合BP神经网络将实验系统测得数据分类存储作为训练材料,从而实现对目标固频信号定位。
1 EMI与ANN模型的建立 1.1 EMI技术EMI技术是利用压电智能材料的压电特性,通过分析PZT与结构的耦合特性得出耦合结构电阻抗与机械阻抗之间的关系,由测量电阻抗间接测得机械阻抗[4]。
1.1.1 机械阻抗
|
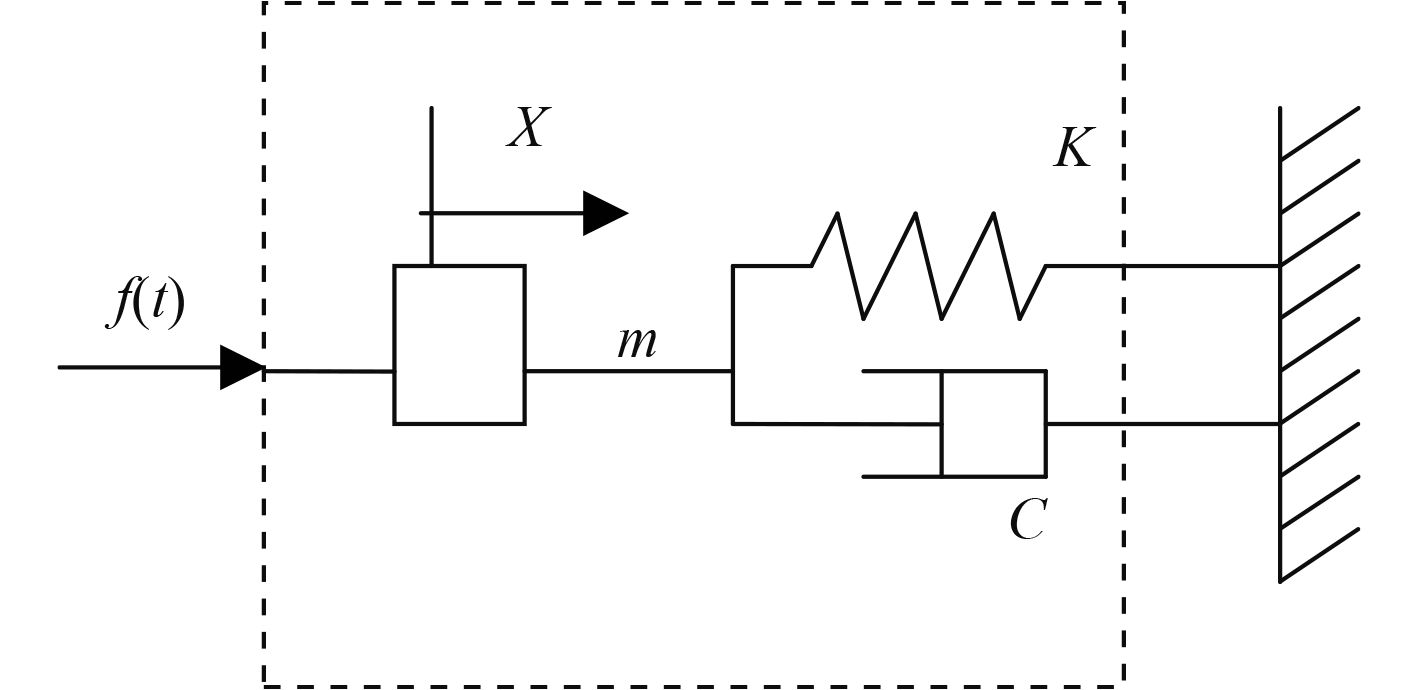
图 1 单自由度机械系统 Fig. 1 Single freedom mechanical system |
假设系统初始相位为0,则该单自由度系统的运动方程为:
| $m\ddot X + C\dot X + KX = f(t)\text{。}$ | (1) |
将激振力换成复数力
于是微分方程可化为:
| $( - {\omega ^2}m + j\omega C + K)X = F\text{,}$ | (2) |
令
| ${Z_D} = \frac{F}{X} = K - {\omega ^2}m + j\omega C\text{,}$ | (3) |
同理可得
| ${Z_v} = \frac{F}{V} = C + j\omega m + \frac{K}{{j\omega }}\text{,}$ | (4) |
| ${Z_A} = \frac{F}{A} = m - \frac{K}{{{\omega ^2}}} + \frac{C}{{j\omega }}\text{。}$ | (5) |
其中:ZD,ZV,ZA分别为位移阻抗,速度阻抗和加速度阻抗;F为产生单位的位移响应,速度响应及加速度响应所需要提供的激振力。
1.1.2 机电耦合压电阻抗技术是将机械结构和压电材料耦合在一起,利用耦合的双方相互依赖、相互影响,且压电材料在极化后具有正压电效应和逆压电效应特性,由压电材料的性质得出机械机构的性质。

|
图 2 压电陶瓷与结构的机电耦合模型 Fig. 2 Electromechanical coupling model of PZT-structure |
对PZT压电陶瓷片施加z方向的交变电压,产生x方向的变形,则PZT在无约束的自由状态下x方向的振动为:
| ${v^2}\frac{{{\partial ^2}u(x,t)}}{{\partial {x^2}}} = \frac{{{\partial ^2}u(x,t)}}{{\partial {t^2}}}\text{。}$ | (6) |
PZT与构造物的耦合的协调性、平衡性可描述为:
| ${\left. {{T_1}} \right|_{x = {l_{PZT}}}} = - j\omega \frac{{{{\left. {{Z_S}\overline u } \right|}_{x = {l_{PZT}}}}}}{{{w_{PZT}}{h_{PZT}}}}{e^{j\omega t}}\text{。}$ | (7) |
求得整个耦合系统的振动位移为:
| $x = \frac{{{d_{31}}\overline {{E_3}} }}{{k\cos (k{l_{PZT}}) + j\omega \frac{{\overline s _{11}^E}}{{{w_{PZT}}{h_{PZT}}}}\sin (k{l_{PZT}})}}\sin (kx){e^{j\omega t}}\text{。}$ | (8) |
因此,PZT振动的速度为:
| ${v_{PZT}} = {\dot x_{PZT}} = j\omega \frac{{{d_{31}}\overline {{E_3}} }}{{k\cos (k{l_{PZT}})}}\sin (k{l_{PZT}}){e^{j\omega t}}\text{。}$ | (9) |
设图2所示耦合系统所加的电场为
| ${x_f} = {l_{PZT}}{d_{31}}{E_3} = {l_{PZT}}{d_{31}}\overline {{E_3}} {e^{j\omega t}}\text{。}$ | (10) |
由压电方程组中力与位移的关系知,自由端等效激励力为:
| ${f_{PZT}} = \overline {{K_{PZT}}} {x_f} = \overline {{K_{PZT}}} {l_{PZT}}{d_{31}}\overline {{E_3}} {e^{jwt}}\text{。}$ | (11) |
其中:
根据机械阻抗的定义Z=F/V可求得PZT的机械阻抗值为:
| ${Z_{PZT}} = \frac{{{f_{PZT}}}}{{{v_{PZT}}}} = \frac{{\overline {{K_{PZT}}} {l_{PZT}}{d_{31}}\overline {{E_3}} {e^{j\omega t}}}}{{j\omega \frac{{{d_{31}}\overline {{E_3}} }}{{k\cos (k{l_{PZT}})}}\sin (k{l_{PZT}}){e^{j\omega t}}}} = \frac{{\overline {{K_{PZT}}} k{l_{PZT}}}}{{j\omega \tan (k{l_{PZT}})}}\text{。}$ | (12) |
简化后,可得整个振动系统的振动位移方程:
| ${\left. x \right|_{x = {l_{PZT}}}} = \frac{{{Z_{PZT}}\tan (k{l_{PZT}}){d_{31}}\overline {{E_3}} }}{{({Z_{PZT}} + {Z_S})k}}{e^{j\omega t}}\text{,}$ | (13) |
计算得PZT的电位移为:
| $\overline {{D_3}} = \frac{{{Z_{PZT}}d_{31}^2\overline c _{11}^E}}{{{{\rm{Z}}_{{\rm{PZT}}}} + {Z_{PZT}}}}\frac{{\cos (kx)}}{{\cos (k{l_{PZT}})}} + (\overline \varepsilon _{33}^{\rm T} - d_{31}^2\overline c _{11}^E)\overline {{E_3}} \text{。}$ | (14) |
令
| $\begin{split}&\overline I = \iint {\overline {{D_3}} dxdy = j\omega \overline {{E_3}} {w_{PZT}}{l_{PZT}}} (\frac{{d_{31}^2\overline c _{11}^E{Z_{PZT}}}}{{{Z_S} + {Z_{PZT}}}}\frac{{\tan (k{l_{PZT}})}}{{k{l_{PZT}}}} +\\ &\;\;\;\;\;\;\;\;\;\;\;\;\overline \varepsilon _{33}^T - d_{31}^2\overline c _{11}^E)\text{。}\end{split}$ | (15) |
其中,大多数智能材料在应用时的频率范围低于其一阶共振频率,可以认为
| ${Z_{PZT}} = - j\frac{{{h_{PZT}}}}{{\omega {w_{PZT}}{l_{PZT}}}}{[\overline \varepsilon _{33}^{\rm T} - \frac{{{Z_{PZT}}}}{{{{\rm{Z}}_{{\rm{PZT}}}} + {Z_{PZT}}}}d_{31}^2\overline c _{11}^E]^{ - 1}}\text{。}$ | (16) |
ANN技术即人工神经网络技术,神经网络是一种使用数目庞大的简单计算单元间的相互连接,这些简单计算单元就是“神经元”或者“处理单元”。
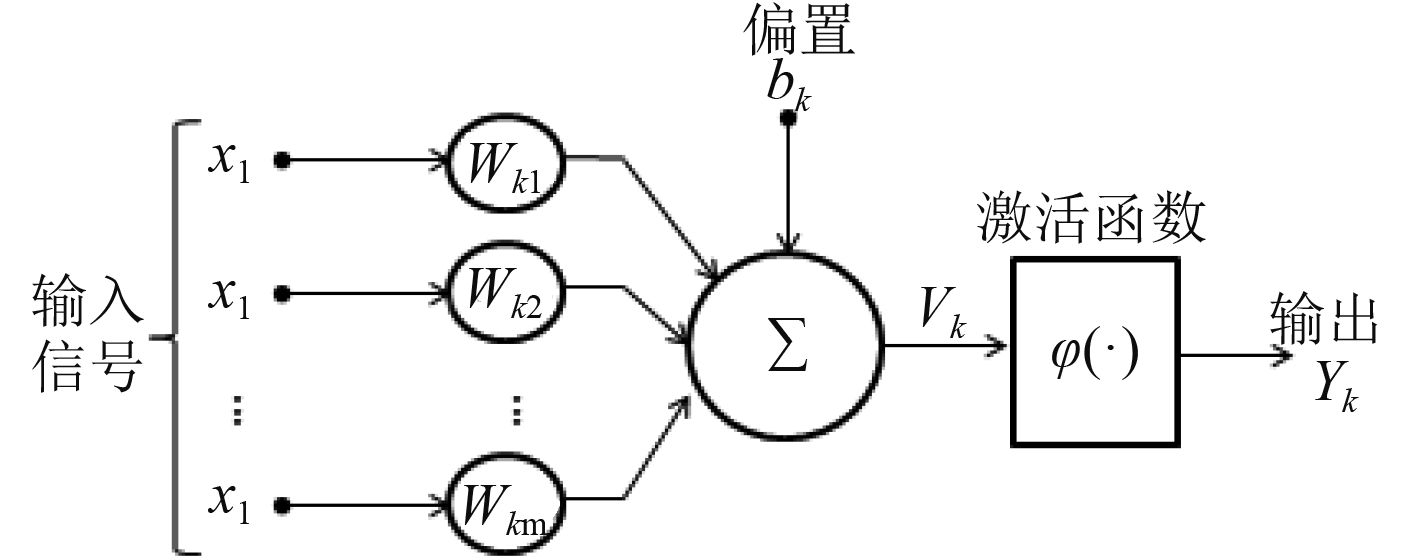
神经元的模型如图3 所示,单个神经元拥有突触、加法器、激活函数3种基本元素。每个突触都有一个有范围的权值作为基本特征。加法器用于求出经过突触加权后的输入信号之和。激活函数也称压制函数,是将输出限制在允许范围之内,一般为单位闭区间[0,1]或[–1,+1]。
|
图 3 神经元模型 Fig. 3 Neural model |
BP神经网络(Back Propagation)是一种按照逆向传播算法训练的多层前馈神经网络,具有非线性特性、大量并行分布结构以及学习和归纳能力,对于无法用明确的模型表示的数据是一种很好的处理方法,可以实现对于目标位置的识别。该神经网络结构有2个显著特点:1)信号向前传播;2)误差反向传播。
用BP网络设计并编写出针对超声信号识别的神经网络,对于水下固定频率目标的位置识别,采取的办法是利用ANN技术,将探测到的不同位置的频率信号位置参数输入BP网络,用于完成对水下目标随机位置的识别测试,完成所设计网络对水下目标位置的识别。
2 基于EMI和ANN的水下目标探测系统该水下目标探测系统主要分为2部分:一是探测主体,一种具有测量阻抗能力的水下潜航器;一是探测方法,以确保探测范围足够大,搜索方式更高效、更具有针对性。
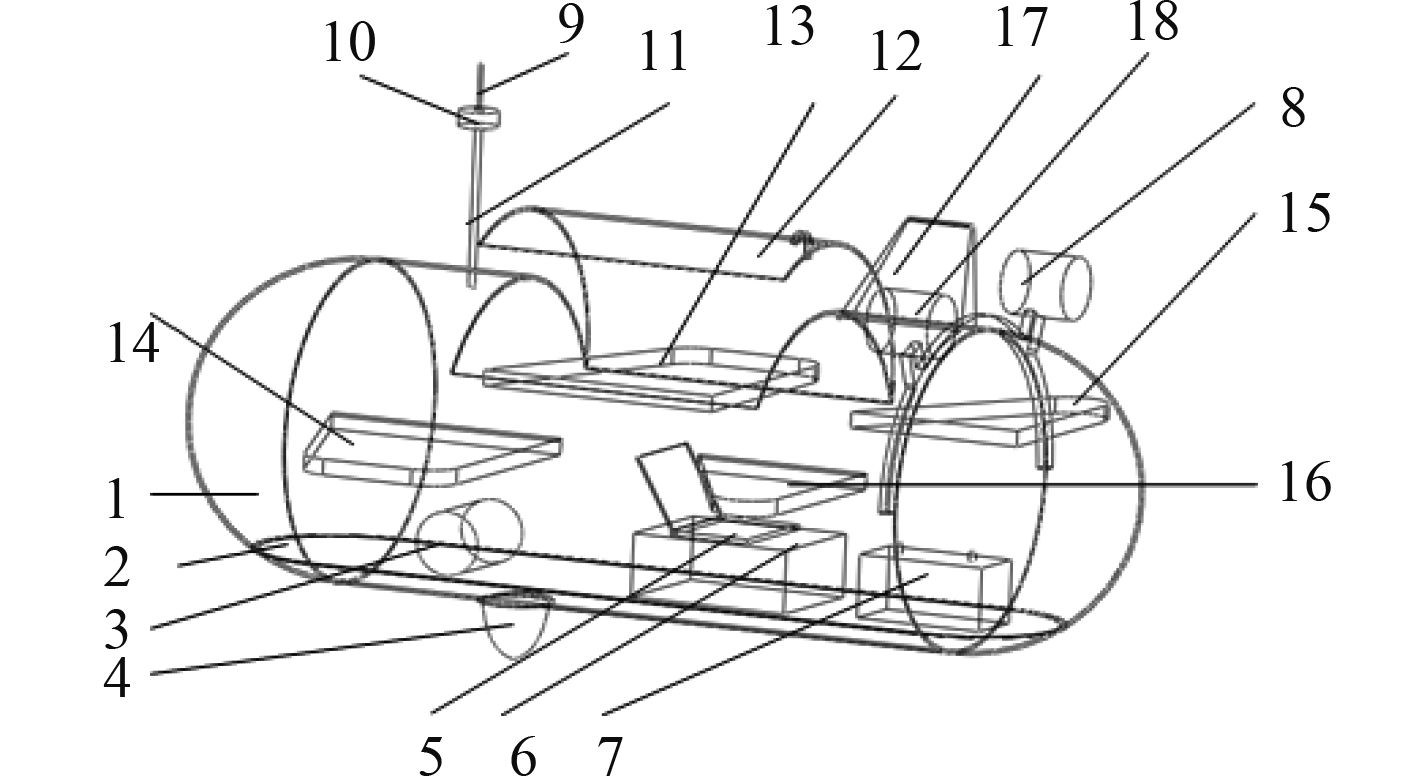
2.1 水下潜航器结构如图4所示为潜航器[5]的基本结构图,该装置主要由上浮下潜、测量、动力和无线通信4部分组成。上浮下潜主要是指由纯水液压泵和水箱共同工作来控制潜航器在水中的深度位置;测量部分由PZT压电传感器和阻抗分析仪为主要部分组成,其中PZT压电传感器基座是铸铝制成的,内部均匀地烧结一层PZT压电陶瓷;动力部分主要由推进装置和电源等部分组成;无线通讯部分主要由包裹天线的双头螺纹管和稳定天线的浮标以及天线组成。
|
图 4 潜航器结构图 Fig. 4 Autonomous underwater vehicle structure |
潜航器在水中应具有基本的上浮下潜、行走、收发数据、突发事件应急处理的能力。由于数目庞大的潜航器在水中行驶,因此使用远程控制潜航器自主作业的方式进行搜索更方便。水上测量船主要负责调动潜航器以及分析潜航器发送的数据,与潜航器之间的交流主要通过无线通信的方式[6]。
2.2 水下目标探测原理由于海底背景噪音复杂[7],而压电阻抗技术进行声探测的基本原理是对所接收的声波频率与PZT陶瓷片的扫描激励频率进行同频共振放大[8],因此应先探测出被搜索目标工作时所辐射噪声的功率谱来进行水下目标的定位。
由图5可以看出压电阻抗法可以很好的得到物体的固有特性,且准确度较高。

|
图 5 某物体声振FRF结果和压电阻抗法所得阻抗图形 Fig. 5 The FRF result of vibration noise and the resistance result of piezoelectric impedance |
在某海域有一个水下移动潜体a,则探测方法如下所述[9]:
以水下移动潜体a位置固定,且水下移动潜体a发出频率40 kHz的噪声为例来说明水下移动潜体a位置的识别方法。
1)将潜航器b、潜航器c、潜航器d上的阻抗分析仪的扫频范围设定为39.9~40.1 kHz,将40 kHz的水下移动潜体a放入目标海域,通过测量船基站向潜航器发出扫频指令,扫频后把数据传回测量船基站进行分析,当潜航器都能扫频到稳定的40 kHz的水下移动潜体a时,说明潜航器b,c,d都进入到水下移动潜体a所在附近海域;
2)基于ANN的水下目标识别数据库
将采集的数据进行归一化处理,在对水下移动潜体a探测定位中,位置编码能显示水下移动潜体a的位置,设置位置为对比信号50 m,500 m,1 000 m,2 000 m,3 000 m;则不同位置的编码用6阶单位矩阵E表示;
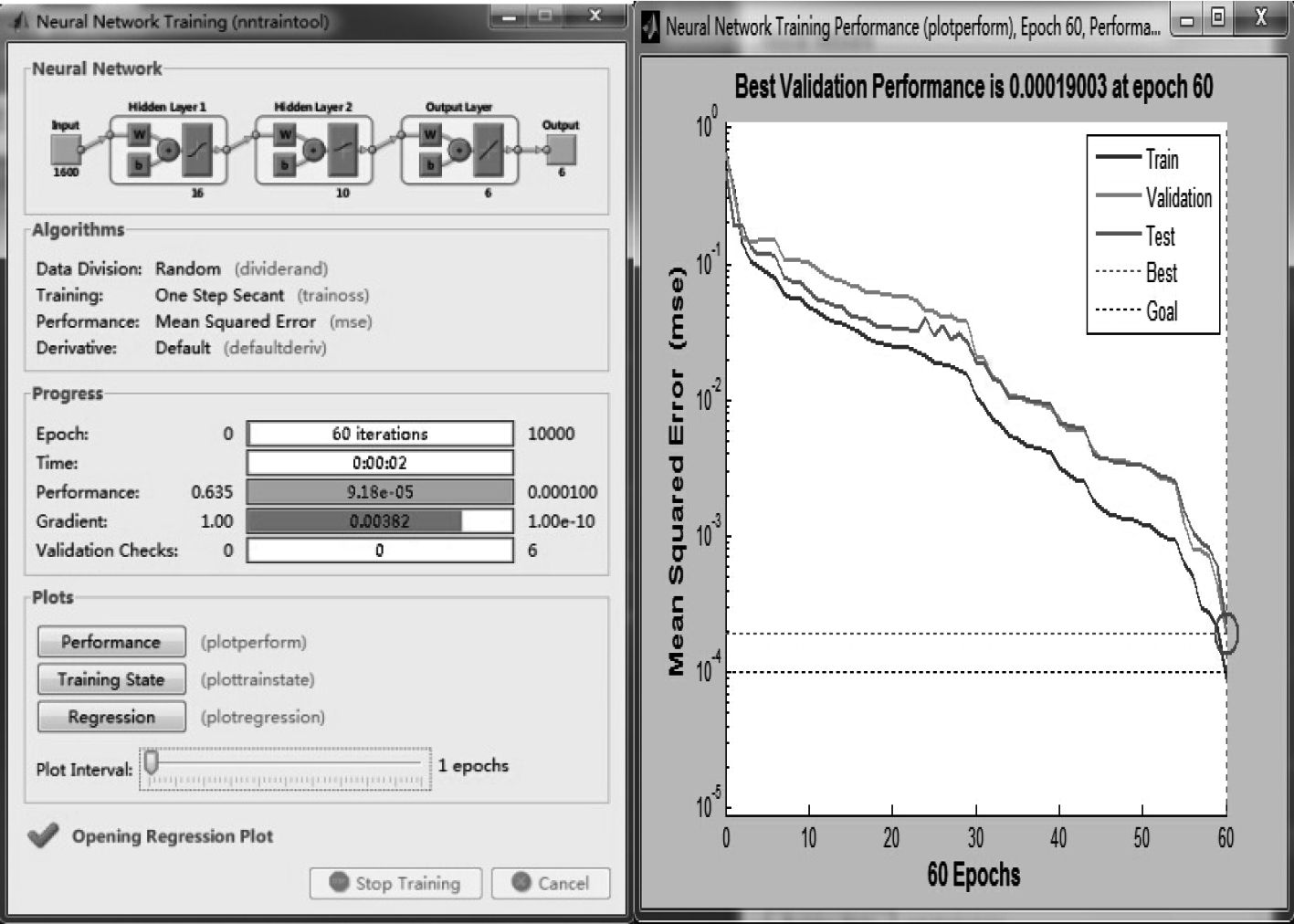
设置网络测试次数的上限定为1 000次,网络的收敛率为0.01,网络的测试误差定为0.001;网络的隐藏层节点数为16,网络的输出层节点为6;最终的目标输出向量E1与E一致时,探测定位水下移动潜体a的网络满足要求;
|
图 6 探测超声信标位置神经网络分析图 Fig. 6 The analysis chart of underwater target detection |
以距离为1 900 m的测试数据为例,输入图6神经网络进行数据检验分析,测得水下移动潜体a在距离潜航器a 2 000 m附近,该神经网络有效。
3)确定水下移动潜体a的位置
当潜航器b检测到信号时,则水下移动潜体a在该潜航器b测量范围内,此时,操控其余潜航器c和潜航器d分别往该潜航器b的四周运动,并检测信号,直到潜航器c和潜航器d能分别检测到目标信号为止;在t时刻,潜航器b、潜航器c、潜航器d的空间坐标

|
图 7 空间三球定位原理 Fig. 7 Positioning principle of the three ball |
利用图7空间三球定位原理,三潜航器坐标
| ${\left( {x - {x_1}} \right)^2} + {\left( {y - {y_1}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {L_1}^2\text{,}$ | (17) |
| ${\left( {x - {x_2}} \right)^2} + {\left( {y - {y_2}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {L_2}^2\text{,}$ | (18) |
| ${\left( {x - {x_3}} \right)^2} + {\left( {y - {y_3}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {L_3}^2\text{。}$ | (19) |
在t时刻的交点
| $x = \frac{{(L_2^2 - L_1^2)({y_1} - {y_3}) - (L_3^2 - L_1^2)({y_1} - {y_2})}}{{2\left[ {({x_1} - {x_2})({y_1} - {y_3}) - ({x_1} - {x_3})({y_1} - {y_2})} \right]}}\text{,}$ | (20) |
| $y = \frac{{(L_2^2 - L_1^2)({x_1} - {x_3}) - (L_3^2 - L_1^2)({x_1} - {x_2})}}{{2\left[ {({x_1} - {x_3})({y_1} - {y_2}) - ({x_1} - {x_2})({y_1} - {y_3})} \right]}}\text{,}$ | (21) |
| $z = - \sqrt {{\rm{L}}_1^2 - {{\left( {{\rm{x}} - {{\rm{x}}_1}} \right)}^2} - {{\left( {{\rm{y}} - {{\rm{y}}_1}} \right)}^2}} + {z_0}\text{。}$ | (22) |
当得到水下移动潜体a位置后可以根据所测得数据确定水下移动潜体a的运动轨迹,具体方式如下:
同理,在下一个t1时刻的水下移动潜体a的位置坐标
在t2时刻的水下移动潜体a的位置坐标
在t3时刻的水下移动潜体a的位置坐标
…
在tn的水下移动潜体a的位置坐标
由时间坐标t,t1,t2,…,tn与位置坐标
1)基于压电阻抗法探测声波信号时,信号源与探测器间的距离与实验所测得阻抗值直接相关,距离越小,阻抗值越大;信号源的发射频率与探测器检测到的频率一致。该实验直接表明使用压电阻抗法在水下检测发射固定频率声波信号的目标可行。
2)使用BP神经网络训练完成后的网络在验证样本测试下基本与训练样本保持一致;结合三球定位原理,使用BP神经网络建立的用于定位探测到的水下固频信号的神经网络系统,实现了对目标信号空间位置更精确的定位。
| [1] |
赵安邦, 董海防, 孙国仓. 一种应用于水下目标探测的激光声系统[J]. 声学技术, 2009, 28 (1): 14–16.
ZHAO An-bang, DONG Hai-Fang, SUN Guo-Cang. A laser-acoustic system for underwater target detection[J]. TECHNICAL ACOUSTICS, 2009, 28 (1): 14–16. |
| [2] |
林伟, 苑秉成, 张坚. 基于滤波与BP神经网络的水下探测信号检测算法[J]. 海军工程大学学报, 2012 (03): 57–60.
LIN Wei, FAN Bing-Cheng, ZHANG Jian. Signal detection algorithm of underwater detection based on band-pass filter and BP neural network[J]. Journal of Naval University of Engineering, 2012 (03): 57–60. |
| [3] |
孙岚, 李厚朴, 边少锋, 李宏武, 周超烨, 等. 基于重力梯度的潜艇探测方法研究[J]. 海洋测绘, 2010 (02): 24–27+45.
SUN Lan, LI Hou-Pu, BIAN Shao-Feng, LI Hong-Wei, Zhou Chao-Ye, et al. Study on the Submarine Detection Method Based on the Gravity Gradient[J]. HYDROGRAPHIC SURVEYING AND CHARTING, 2010 (02): 24–27+45. DOI: 10.3969/j.issn.1671-3044.2010.02.007 |
| [4] | 陶娟. 基于EMI与ANN技术的构造物健康诊断研究[D]. 淮南: 安徽理工大学, 2013. |
| [5] |
田军, 余亚军, 蔡龙. 针对持续性跟踪无人艇的探测技术[J]. 舰船科学技术, 2013, 35 (4): 98–101.
TIAN Jun, YU Ya-Long, CAI Long. Research on detection technology on ACTUV[J]. Ship Science and Technology, 2013, 35 (4): 98–101. |
| [6] |
苏镇. 一种基于超声波的潜艇数据传输系统[J]. 舰船电子工程, 2012, 32 (12): 142–143.
SU Zhen. Data Transmission System for Submarine Based on Ultrasonic Waves[J]. Ship Electronic Engineering, 2012, 32 (12): 142–143. DOI: 10.3969/j.issn.1627-9730.2012.12.049 |
| [7] |
王永浩, 陆铭华, 林晓峰, 章阳, 高劼, 等. 基于水声探测条件下潜射反舰导弹攻击中远程目标可行性研究[J]. 飞航导弹, 2013 (2): 49–51.
WANG Yong-Hao, LU Ming-Hua, LIN Xiao-Feng, ZHANG Yang, GAO Jie, et al. Feasibility study of underwater launched anti-ship missile attacking medium and long-range targets based on underwater acoustic detection condition[J]. Aerodynamic Missile Journal, 2013 (2): 49–51. |
| [8] | 郭榜增. 基于EMI与ANN技术的声波信号探测机理研究[D]. 淮南: 安徽理工大学, 2015. |
| [9] | 汪天博. 基于EMI与ANN技术水下固定频率信号探测研究[D]. 淮南: 安徽理工大学, 2015. |
 2017, Vol. 39
2017, Vol. 39
