随着海洋开发技术的发展,单自治水下机器人(Unmanned Underwater Vehicle,UUV)越来越难完成复杂的军事及民事任务,从而使得多UUV协同系统在海洋探索及开发、军事作战等方面拥有越来越重要的作用[1]。定位技术是协同作业的前提条件和关键技术。由于多UUV协同定位具有各UUV独自定位所不具有的多种优势,因此多UUV协同定位正逐步成为一个热门研究课题[2],设计能够提高多UUV定位精度的协同定位算法具有重要的理论价值和现实意义。
如果多UUV群体在定位时存在着相对观测,那么通过一定的信息交换,就可以实现UUV间定位信息的共享,达到提高多UUV系统整体定位能力的目的,这种定位方法称为“协同定位(Cooperative Localization,CL)”。多UUV协同定位具有下列优势:能够充分利用系统中某些UUV的高精度导航信息,从而使得装备低精度导航设备的UUV可以提高自身的导航精度[3];在多UUV系统中,部分UUV具有有界定位误差的导航能力,通过协同定位实现定位信息共享,可以使得系统中每个UUV都具有误差有界的定位能力;当某些UUV由于传感器或环境因素丧失独立导航能力时,协同定位可以在一定程度上恢复这些平台的定位能力。
多无人平台协同定位的研究始于20世纪90年代,研究对象包括移动机器人、水面无人艇、无人机、卫星、水下自治潜器等。目前,多UUV协同定位技术的研究总体上处于理论向工程实践转化的阶段,美国麻省理工大学的John J. Leonard教授带领的团队在2009年前后系统的提出了一系列多UUV协同定位方法,并进行了工程实践[4],但是他们的协同定位方法存在着不足,各UUV的导航传感器精度都比较高,协同仅仅作为一种保证定位精度的辅助手段引入,也就意味着协同定位精度与UUV自身导航定位精度差别不大。Leonard教授的博士Alexander Bahr在他的博士论文中[5],根据几何学原理,提出了一种基于主定位器相对观测确定的从潜航器定位区域,然后利用Kullback—Leibler原理,提出一种新的优化目标函数,在上述优化区域内按照这种优化目标函数值最小的原则对潜器进行定位,仿真结果证明了这种优化方法的可行性,这种优化方法理论比较简单,但是由于要在大量区域内寻优,每一次寻优过程都需要进行复杂的寻优计算。
欧盟资助的多水下潜航器项目MAUVs GREX的一个研究成果是只依靠航迹推算和潜航器之间的距离测量信息,在不使用水声定位的情况下,实现潜航器的相对定位[6]。Corp公司研究了地球同步卫星协同定位的分散式算法[7],同时该公司资助悉尼大学自主系统研究中心以机器人协同定位为背景,开展了相关的定位算法研究。
我国对多UUV协同定位技术的研究起步较晚。西北工业大学的徐德民院士团队提出了一种利用移动长基线技术的多AUV协同定位方法,并设计了AUV协同导航系统的运动学模型,对主AUV的精确定位信息、主从AUV之间的距离测量信息以及从AUV的自身定位信息进行了数据融合尝试[8]。国防科技大学的穆华等[9]提出了一种基于增广信息和高斯贝叶斯分布的移动机器人协同定位算法,并且对比分析了分散式信息滤波算法和分散式经典卡尔曼滤波算法的不同。
近年来,随着滚动优化理论的不断发展以及计算机计算能力的提升,基于滚动优化原理的滚动时域估计方法受到越来越多的关注并在许多领域获得成功应用。MHE的基本原理是在系统运行过程中选取一个固定时长的移动时间段作为估计窗口;然后建立性能指标函数,主要包括估计时域初始时刻状态估计误差、时域内量测噪声以及状态噪声,将系统状态硬性约束作为优化约束条件引入;最后以性能指标函数为目标函数,求解约束优化问题得到系统最优解。随着时间推移,估计窗口也相应的向前推移,为了保证估计窗口的时长不变,将旧数据移出估计窗口,加入新数据,再次执行优化算法,从而实现动态优化[10]。
1 多UUV协同定位状态空间模型 1.1 状态方程假设多UUV群体中有N个主UUV,M个从UUV,为了研究方便,先考虑2个主UUV对1个从UUV进行协同定位的情况,定义tk时刻系统状态为
| $\left\{ \begin{array}{l}{x_{ik + 1}} = {x_{ik}} + \delta t \cdot {V_{ik}}\sin {\phi _{ik}}\text{,}\\{y_{ik + 1}} = {y_{ik}} + \delta t \cdot {V_{ik}}\cos {\phi _{ik}}\text{,}\\{\phi _{ik + 1}} = {\phi _{ik}} + \delta t \cdot {\omega _{ik}}\text{。}\end{array} \right.$ | (1) |
定义
| $\left\{ \begin{array}{l}{V_{ik}} = {{\bar V}_{ik}} + {w_{ivk}}\text{,}\\{\omega _{ik}} = {{\bar \omega }_{ik}} + {w_{i\omega k}}\text{。}\end{array} \right.$ | (2) |
其中:
| ${\mathit{\boldsymbol{Q}}_{ik}} = E\left[ {{\mathit{\boldsymbol{w}}_{ik}}\mathit{\boldsymbol{w}}_{ik}^{\rm T}} \right] = \left[ {\begin{array}{*{20}{c}}{q_{i{v_k}}^2} & 0\\0 & {q_{i{\omega _k}}^2}\end{array}} \right]\text{。}$ | (3) |
则上述3个UUV协同定位系统的状态方程为:
| ${\mathit{\boldsymbol{X}}_{k + 1}} = f({\mathit{\boldsymbol{X}}_k},{\mathit{\boldsymbol{u}}_k},{\mathit{\boldsymbol{w}}_k})\text{。}$ | (4) |
若假设各UUV的运动相互之间无影响,则可以将式(4)分解为3个UUV的方程:
| ${\mathit{\boldsymbol{X}}_{k + 1}} = \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{X}}_{1k + 1}}}\\{{\mathit{\boldsymbol{X}}_{2k + 1}}}\\{{\mathit{\boldsymbol{X}}_{3k + 1}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{f_1}({\mathit{\boldsymbol{X}}_{1k}},{\mathit{\boldsymbol{u}}_{1k}},{\mathit{\boldsymbol{w}}_{1k}})}\\{{f_2}({\mathit{\boldsymbol{X}}_{2k}},{\mathit{\boldsymbol{u}}_{2k}},{\mathit{\boldsymbol{w}}_{2k}})}\\{{f_3}({\mathit{\boldsymbol{X}}_{3k}},{\mathit{\boldsymbol{u}}_{3k}},{\mathit{\boldsymbol{w}}_{3k}})}\end{array}} \right]\text{。}$ | (5) |
结合式(1)中的UUV运动学方程,利用EKF原理可将第i个UUV的状态方程线性化:
| ${\mathit{\boldsymbol{X}}_{ik + 1}} = {\mathit{\boldsymbol{F}}_{ik}}{\mathit{\boldsymbol{X}}_{ik}} + {\mathit{\boldsymbol{G}}_{ik}}{\mathit{\boldsymbol{w}}_{ik}}\text{,}$ | (6) |
其中:
| $\left\{ \begin{array}{l}{F_{ik}} = I + \delta t \cdot \frac{{\partial {f_1}}}{{\partial X{{_{ik}^{}}^T}}} = \\\;\;\;\;\;\;\;\;\;\;\;I + \delta t \cdot \left[ {\begin{array}{*{20}{c}}1&0&{\delta t \cdot {V_{ik}}\cos {\phi _{ik}}}\\0&1&{ - \delta t \cdot {V_{ik}}\sin {\phi _{ik}}}\\0&0&1\end{array}} \right]\text{,}\\{G_{ik}} = \frac{{\partial f}}{{\partial {w_{ik}}^T}} = \left[ {\begin{array}{*{20}{c}}{\delta t \cdot \sin {\phi _{ik}}}&0\\{\delta t \cdot \cos {\phi _{ik}}}&0\\0&{\delta t}\end{array}} \right]\text{。}\end{array} \right.$ | (7) |
将i=1,2,3时,3个UUV的状态方程联合起来,则两主一从协同定位系统的线性状态方程定义为:
| $\begin{split}&{\mathit{\boldsymbol{X}}_{k + 1}} = {\mathit{\boldsymbol{F}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{G}}_k}{\mathit{\boldsymbol{w}}_k}=\\& \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{F}}_{1k}}} & {\bf{0}} & {\bf{0}}\\{\bf{0}} & {{\mathit{\boldsymbol{F}}_{2k}}} & {\bf{0}}\\{\bf{0}} & {\bf{0}} & {{\mathit{\boldsymbol{F}}_{3k}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{X}}_{1k}}}\\{{\mathit{\boldsymbol{X}}_{2k}}}\\{{\mathit{\boldsymbol{X}}_{3k}}}\end{array}} \right]+\\& \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{G}}_{1k}}} & {\bf{0}} & {\bf{0}}\\{\bf{0}} & {{\mathit{\boldsymbol{G}}_{2k}}} & {\bf{0}}\\{\bf{0}} & {\bf{0}} & {{\mathit{\boldsymbol{G}}_{3k}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{w}}_{1k}}}\\{{\mathit{\boldsymbol{w}}_{2k}}}\\{{\mathit{\boldsymbol{w}}_{3k}}}\end{array}} \right]\text{。}\end{split}$ | (8) |
假设UUV1在tk时刻与从UUV进行协同定位,则UUV3在tk时刻接收到的相对观测信息包括UUV1在tk时刻的位置信息为
则根据主UUV1、从UUV3之间的几何位置关系有:
| ${r_{13k}} = \sqrt {{{({x_{1k}} - {x_{3k}})}^2} + {{({y_{1k}} - {y_{3k}})}^2}} + {v_r}\text{。}$ | (9) |
选取
| $\begin{split}&{\mathit{\boldsymbol{Z}}_{13k}} = h({\mathit{\boldsymbol{X}}_k}) + {v_{13k}} = \left[ {\begin{array}{*{20}{c}}{{x_{1k}}}\\{{y_{1k}}}\\{{r_{1k}}}\end{array}} \right] + {v_{13k}}=\\& \left[ {\begin{array}{*{20}{c}}{{x_{1k}}}\\{{y_{1k}}}\\{\sqrt {{{({x_{1k}} - {x_{3k}})}^2} + {{({y_{1k}} - {y_{3k}})}^2}} }\end{array}} \right] + {\mathit{\boldsymbol{v}}_{13k}}\text{。}\end{split}$ | (10) |
其中:
| $\begin{split}&{\mathit{\boldsymbol{Z}}_{13k}} = \left[ {\begin{array}{*{20}{c}}{{x_{1k}}}\\{{y_{1k}}}\\{\sqrt {{{({x_{1k}} - {x_{3k}})}^2} + {{({y_{1k}} - {y_{3k}})}^2}} }\end{array}} \right] + {\mathit{\boldsymbol{v}}_{13k}}=\\& {\mathit{\boldsymbol{H}}_{13k}}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{v}}_{13k}}=\\& \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{H}}_{1k}}} & {\bf{0}} & {{\mathit{\boldsymbol{H}}_{3k}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{X}}_{1k}}}\\{{\mathit{\boldsymbol{X}}_{2k}}}\\{{\mathit{\boldsymbol{X}}_{3k}}}\end{array}} \right] + {\mathit{\boldsymbol{v}}_{13k}}\text{。}\end{split}$ | (11) |
式中:
| ${\mathit{\boldsymbol{R}}_{{\rm{13k}}}} = E\left[ {{\mathit{\boldsymbol{v}}_{{\rm{13k}}}}\mathit{\boldsymbol{v}}_{13k}^{\rm T}} \right]\text{。}$ | (12) |
按照上述推导,多UUV协同定位系统状态空间模型为:
| $\left\{ {\begin{array}{*{20}{c}}\begin{array}{l}\!\!\!\!\!\!\!\!\!\!{X_{k + 1}} = \left[ {\begin{array}{*{20}{c}}{{X_{1k + 1}}}\\{{X_{2k + 1}}}\\{{X_{3k + 1}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{F_{1k}}}&{\bf{0}}&{\bf{0}}\\{\bf{0}}&{{F_{2k}}}&{\bf{0}}\\{\bf{0}}&{\bf{0}}&{{F_{3k}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{X_{1k}}}\\{{X_{2k}}}\\{{X_{3k}}}\end{array}} \right] + \\\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}{{G_{1k}}}&{\bf{0}}&{\bf{0}}\\{\bf{0}}&{{G_{2k}}}&{\bf{0}}\\{\bf{0}}&{\bf{0}}&{{G_{3k}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{w_{1k}}}\\{{w_{2k}}}\\{{w_{3k}}}\end{array}} \right]\text{,}\end{array}\\\!\!\!\!\!{{Z_k} \!\!=\!\! {{\bf{H}}_{13k}}{X_k} \!+\! {{\bf{v}}_{13k}} \!=\! \left[ {\begin{array}{*{20}{c}}{{{\bf{H}}_{1k}}}&\!\!\!\!\!\!{\bf{0}}&\!\!\!\!\!{{{\bf{H}}_{3k}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{X_{1k}}}\\{{X_{2k}}}\\{{X_{3k}}}\end{array}} \right] \!\!+\!\! {{\bf{v}}_{13k}}}\text{。}\!\!\!\!\end{array}} \right.$ | (13) |
|
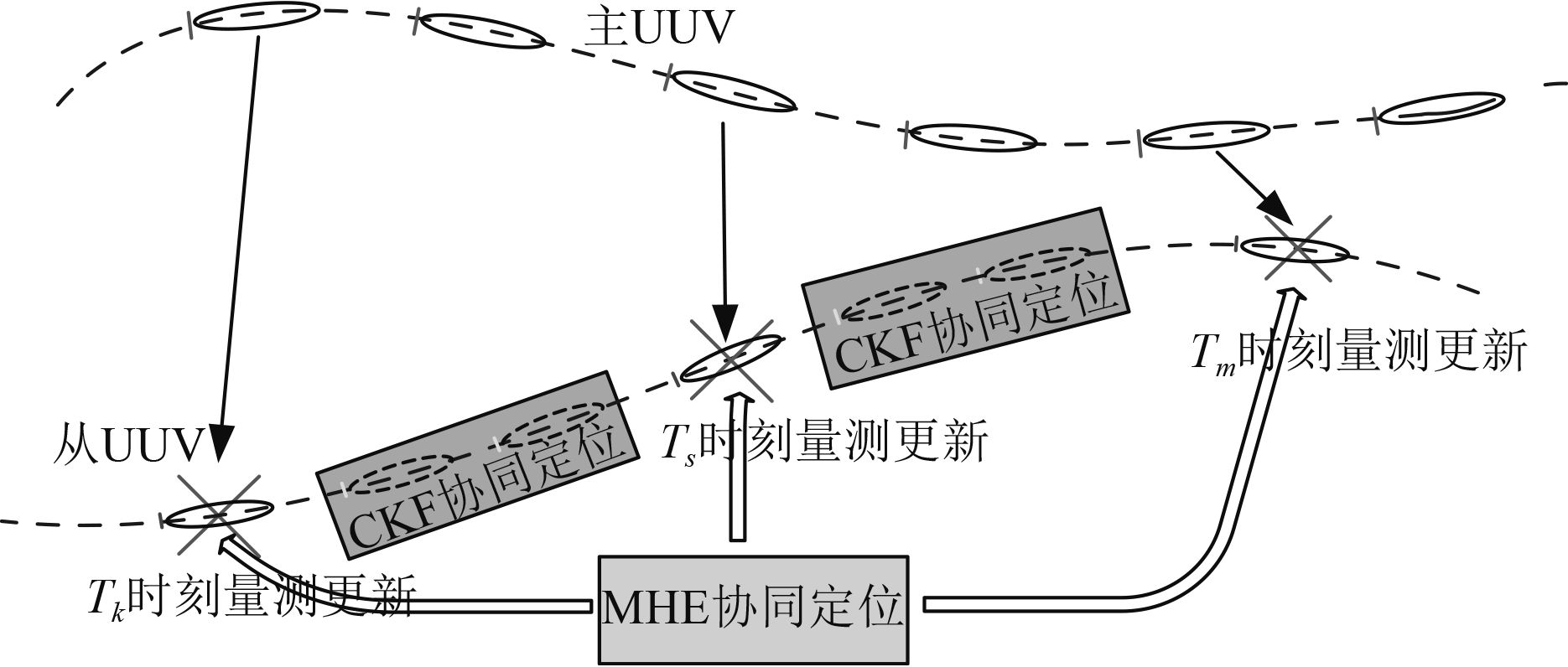
图 1 协同定位示意图 Fig. 1 Schematic diagram of cooperation localization |
如图1所示,在主从式多UUV协同定位系统中,若主UUV个数较少(为了节约成本,一般不超过2个),则无论多个主UUV如何轮替对从UUV进行协同定位,从UUV在2次信息交流之间必然有一段时间需要进行无量测信息更新的协同定位,如果主UUV个数极少同时从UUV个数较多(10个左右),那么航推时间会相应增长,这对于一般惯性导航定位的滤波周期(通常为毫秒级)而言比较大,为了更好地将2个不同阶段的协同定位结合起来,本文提出一种基于CKF的滚动时域方法,其基本思路是建立2种不同处理周期、不同处理模式的状态估计方法分别去完成无量测更新协同定位以及有量测更新协同定位,后一阶段计算的初始条件需要用到前一阶段的结果以及相对观测信息,然后将有量测更新协同定位的结果作为无量测更新协同定位的初始条件代入下一次定位循环。如图1所示,从UUV在2次协同定位之间需要进行一段时间的无量测更新协同定位,这阶段的定位精度会对协同定位精度产生较大影响,为了分析方便,我们假设主UUV1与从UUV2在tk时刻系统进行协同定位,为了更好地实现从UUV的无量测更新阶段自身定位,保证无量测更新阶段定位误差的精度,本文提出利用在无量测更新阶段采用CKF非线性滤波方法对协同定位问题进行处理。
2.1 无量测更新阶段CKF滤波假设k–1时刻状态估计协方差
| ${{\mathit{\boldsymbol{P}}}_{k - 1|k - 1}} = {{\mathit{\boldsymbol{S}}}_{k - 1|k - 1}}{\mathit{\boldsymbol{S}}}_{k - 1|k - 1}^{\rm T}\text{,}$ | (14) |
计算Cubature点
| ${{\mathit{\boldsymbol{X}}}_{i,k - 1|k - 1}} = {{\mathit{\boldsymbol{S}}}_{k - 1|k - 1}}{{\mathit{\boldsymbol{\xi }}}_i} + {{\hat{x}}_{k - 1|k - 1}}\text{,}$ | (15) |
其中n为UUV个数,
| $\left\{ \begin{array}{l}{{\mathit{\boldsymbol{\xi }}}_i} = \sqrt {\displaystyle\frac{m}{2}} {[1]_i}\text{,}\\{{\mathit{\boldsymbol{\omega }}}_i} = \frac{1}{m},i = 1,...m,m = 2n\text{。}\end{array} \right.$ | (16) |
通过2.1节定义的状态方程(7)传播Cubature点:
| ${\mathit{\boldsymbol{X}}}_{i,k|k - 1}^ * = f({{\mathit{\boldsymbol{X}}}_{i,k - 1|k - 1}}){\rm{ }}\text{,}$ | (17) |
估计k时刻的状态预测值:
| ${{\hat{x}}_{k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\mathit{\boldsymbol{X}}}_{i,k|k - 1}^ * } \text{,}$ | (18) |
估计k时刻的状态误差协方差预测值:
| ${{\mathit{\boldsymbol{P}}}_{k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\mathit{\boldsymbol{X}}}_{i,k|k - 1}^ * } {\mathit{\boldsymbol{X}}}_{i,k|k - 1}^{ * {\rm T}} - {{\hat{x}}_{k|k - 1}}{\hat{x}}_{k|k - 1}^{\rm T} + {{\mathit{\boldsymbol{Q}}}_{k - 1}}{\rm{ }}\text{,}$ | (19) |
通过Cholesky分解
| ${{\mathit{\boldsymbol{P}}}_{k|k - 1}} = {{\mathit{\boldsymbol{S}}}_{k|k - 1}}{\mathit{\boldsymbol{S}}}_{k|k - 1}^{\rm T}\text{,}$ | (20) |
计算Cubature点
| ${{\mathit{\boldsymbol{X}}}_{i,k|k - 1}} = {{\mathit{\boldsymbol{S}}}_{k|k - 1}}{{\mathit{\boldsymbol{\xi }}}_i} + {{\hat{x}}_{k|k - 1}}\text{,}$ | (21) |
通过2.2节定义的观测方程传播Cubature点:
| ${{\hat{z}}_{k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\mathit{\boldsymbol{Z}}}_{i,k|k - 1}}} \text{,}$ | (22) |
估计自相关协方差阵:
| ${{\mathit{\boldsymbol{P}}}_{zz,k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\mathit{\boldsymbol{Z}}}_{i,k|k - 1}}} {\mathit{\boldsymbol{Z}}}_{i,k|k - 1}^{\rm T} - {{\hat{z}}_{k|k - 1}}{\hat{z}}_{k|k - 1}^{\rm T} + {{\mathit{\boldsymbol{R}}}_k}\text{,}$ | (23) |
估计卡尔曼增益:
| ${{\mathit{\boldsymbol{W}}}_k} = {{\mathit{\boldsymbol{P}}}_{xz,k|k - 1}}{\mathit{\boldsymbol{P}}}_{zz,k|k - 1}^{ - 1}\text{,}$ | (24) |
k时刻状态估计值:
| ${{\hat{x}}_{k|k}} = {{\hat{x}}_{k|k - 1}} + {{\mathit{\boldsymbol{W}}}_k}({{\mathit{\boldsymbol{z}}}_k} - {{\hat{z}}_{k|k - 1}})\text{,}$ | (25) |
k时刻状态误差协方差估计值:
| ${{\mathit{\boldsymbol{P}}}_{k|k}} = {{\mathit{\boldsymbol{P}}}_{k|k - 1}} - {{\mathit{\boldsymbol{W}}}_k}{{\mathit{\boldsymbol{P}}}_{zz,k|k - 1}}{\mathit{\boldsymbol{W}}}_k^{\rm T}\text{。}$ | (26) |
如图1所示,假设tk、ts、tm时刻主UUV1与从UUV2存在水声通信,即量测信息实现更新,则在两相邻量测时刻之间,从UUV会进行基于UKF的无量测更新协同定位,假设
| $\mathop {\min }\limits_{\left\{ {{{\mathit{\boldsymbol{x}}}_i}} \right\}_{i = k}^s、\left\{ {{{\mathit{\boldsymbol{w}}}_j}} \right\}_{j = k}^{s - 1}} {\rm{ }}{{\mathit{\boldsymbol{J}}}_s} = \mathop {\min }\limits_{\left\{ {{{\mathit{\boldsymbol{x}}}_i}} \right\}_{i = k}^s、\left\{ {{{\mathit{\boldsymbol{w}}}_j}} \right\}_{j = k}^{s - 1}} {\rm{ }}\left( {\begin{array}{*{20}{c}}{\displaystyle\sum\limits_{i = k}^{s - 1} {\left\| {{{\mathit{\boldsymbol{w}}}_i}} \right\|_{{\mathit{\boldsymbol{Q}}}_i^{ - 1}}^2} }\\{ + \displaystyle\sum\limits_{i = k}^s {\left\| {{{\mathit{\boldsymbol{v}}}_i}} \right\|_{{\mathit{\boldsymbol{R}}}_i^{ - 1}}^2} }\\{ + {{\mathit{\boldsymbol{\Phi }}}_k}\left( {{{\mathit{\boldsymbol{x}}}_0}、\left\{ {{{\mathit{\boldsymbol{w}}}_i}} \right\}_{i = 0}^{k - 1}} \right)}\end{array}} \right)\text{。}$ | (27) |
式中:下标k代表tk时刻的量;下标s代表ts时刻的量;
| ${{\mathit{\boldsymbol{\varPhi }}}_k} = {\left( {{{\mathit{\boldsymbol{x}}}_k} - {{{\hat{x}}}_k}} \right)^{\rm T}}{\mathit{\boldsymbol{P}}}_k^{ - 1}\left( {{{\mathit{\boldsymbol{x}}}_k} - {{{\hat{x}}}_k}} \right) + {{\mathit{\boldsymbol{J}}}_k}*\text{。}$ | (28) |
其中:
为了分析影响多UUV协同定位误差的主要因素以及验证MHE方法对协同定位精度的改进,本文将利用Matlab软件编写相应算法程序对实验数据进行离线处理以验证算法的有效性。试验采用2个主UUV轮替对从UUV进行协同定位,在没有通信丢包情况下,每个主UUV与从UUV的通信周期为5 s,由于是两主UUV轮替与从UUV进行协同定位,因此在没有通信丢包情况下,从UUV2~3 s即会收到某个主UUV的相对定位信息。滤波中设定距离测量噪声方差为
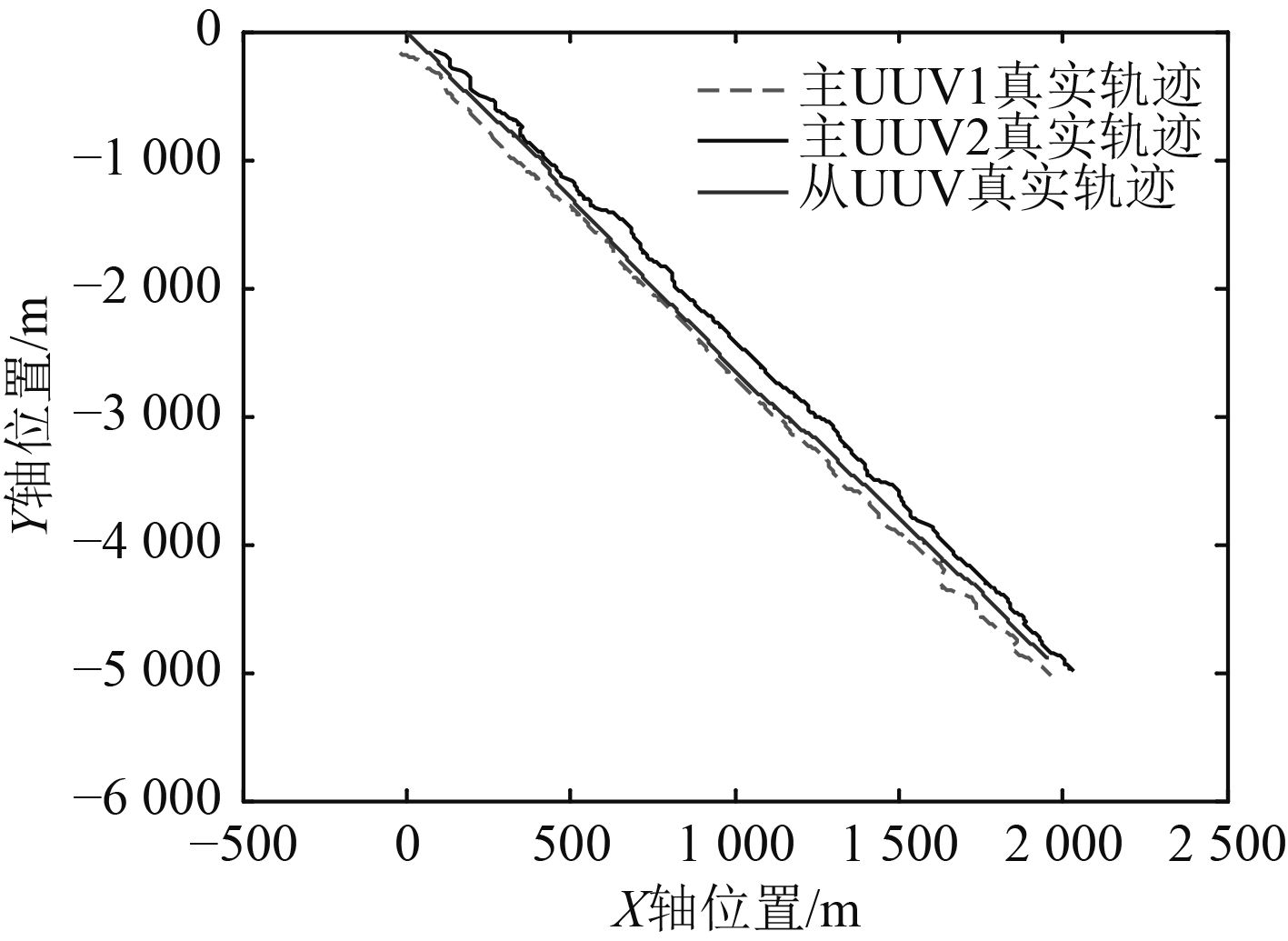
主、从UUV运动轨迹见图2,三UUV近似为直线运动,从UUV运动轨迹在两主UUV之间。
|
图 2 UUV运动轨迹 Fig. 2 The trajectories of UUVs |
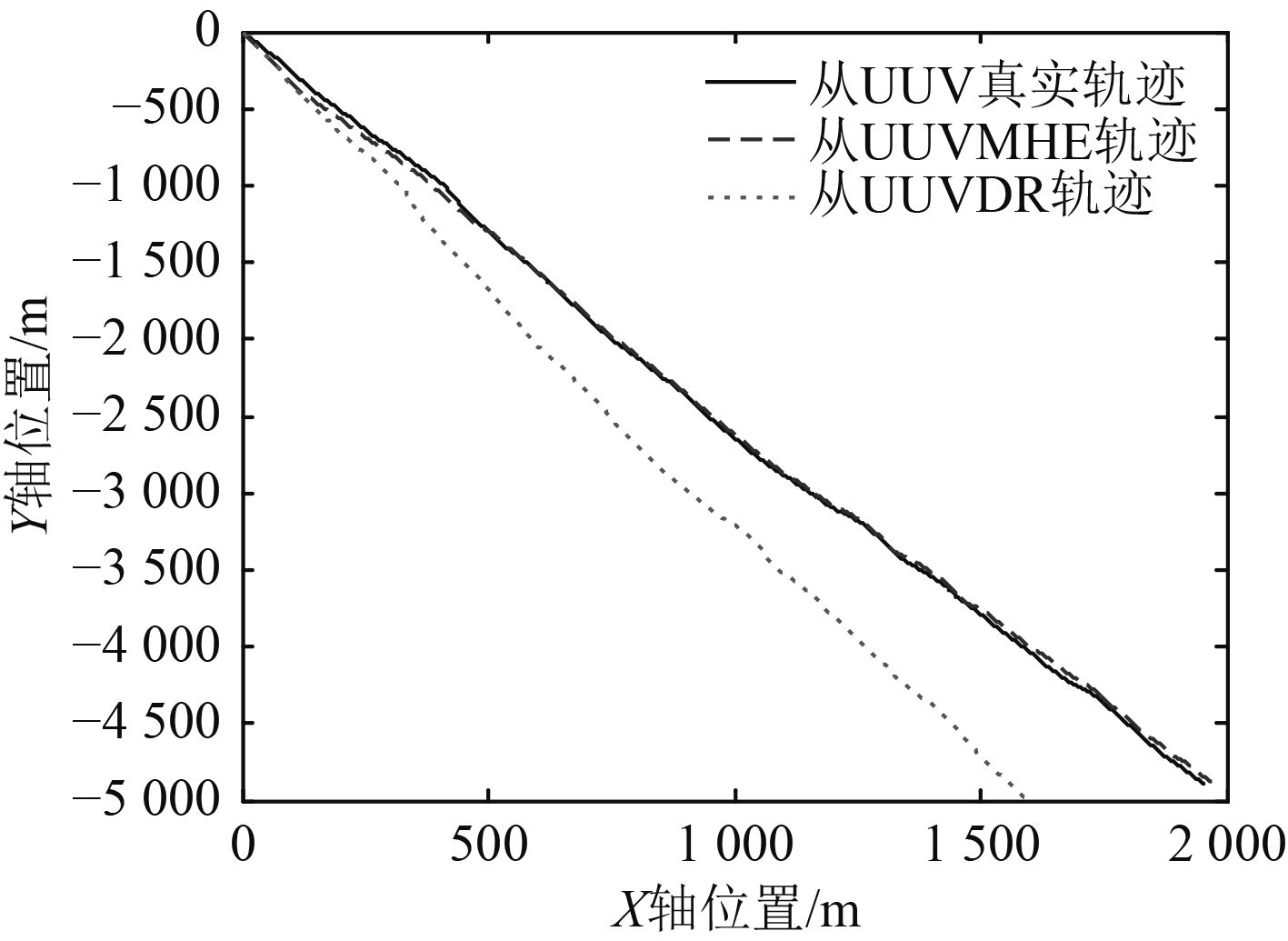
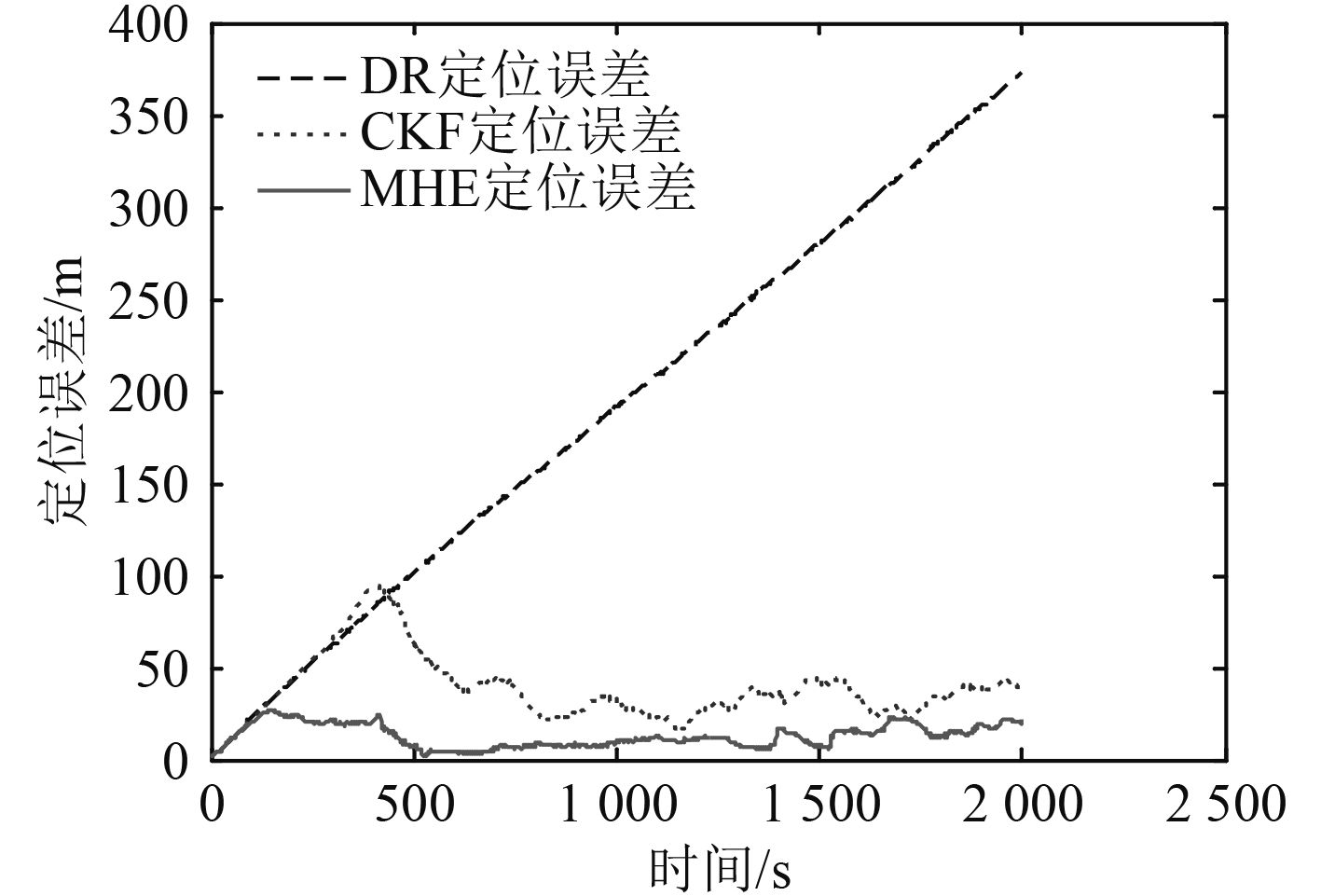
图3为从UUV导航轨迹,从图中可看出,从UUV利用MHE状态估计方法产生的协同导航轨迹与真实轨迹基本重合,而利用自身导航传感器进行的航推(DR)定位轨迹与真实轨迹相差较大,证明了基于MHE的协同定位方法的有效性,图4为具体的定位误差比较图,采用MHE方法比直接采用CKF方法定位协同精度要有所提升,证明了方法的可行性。
|
图 3 从UUV导航轨迹 Fig. 3 The navigation trajectories of slaver UUVs |
|
图 4 从UUV定位误差比较图 Fig. 4 Comparison chart of slaver UUVs’ localization errors |
本文在建立多UUV协同定位方案设计基础上,利用UUV运动学模型,建立多UUV协同定位状态空间非线性模型,在此基础上,提出利用MHE方法实现多UUV协同定位最优状态估计,通过试验验证,证明了基于MHE的多UUV协同定位方法的有效性。
| [1] | 许真珍, 封锡盛. 多UUV协作系统的研究现状与发展[J]. 机器人, 2007, 29 (2): 186–192. |
| [2] | BACCOU P, JOUVENCEL B, CREUZE V. Single beacon acoustic for AUV navigation[C]// International Coference on Advanced Robotics, Budapest ICAR, 2001:1253–1260. |
| [3] | 李闻白, 刘明雍, 张立川, 等. 单领航者相对位移测量的多自主水下航行器协同导航[J]. 兵工学报, 2011, 32 (8): 1002–1007. |
| [4] | BAHR A, WALTER M R, LEONARD J J. Consistent cooperative localization. in robotics and automation[C]// IEEE International Conference on Robotics and Automation (ICRA'09), 2009: 3415–3422. |
| [5] | BAHR A. Cooperative Localization for Autonomous Underwater Vehicles [D]. MIT, 2009. |
| [6] | AGUIARY A, ALMEIDAY J, BAYATY M, et al. Cooperative autonomous marine vehicle motion control in the scope of the EU GREX project: theory and practice[C]// Oceans 2009-Europe. IEEE, 2009: 1–10. |
| [7] | DIBA M. Strategies in tracking and localization of distributed underwater systems [D]. San Diego, University of California. 2010. |
| [8] | 张立川, 刘明雍, 徐德民, 等. 基于水声传播延迟的主从式多无人水下航行器协同导航定位研究[J]. 兵工学报, 2009, 30 (12): 1674–1678. DOI: 10.3321/j.issn:1000-1093.2009.12.020 |
| [9] | 穆华. 多运动平台协同导航的分散式算法研究[D]. 长沙: 国防科学技术大学, 2010 |
| [10] | C. Constraint state estimation for nonlinear discrete-time systems: Stability and moving horizon approximations[J]. IEEE Transactions on Automatic Control, 2003, 48 (2): 246–258. DOI: 10.1109/TAC.2002.808470 |
 2017, Vol. 39
2017, Vol. 39
