重于水型自治潜器(简称AUV)的局部路径规划是指在未知的水下环境中,潜水器根据传感器对环境的探测,自行规划得到一条无碰撞路径。AUV如何根据规划算法实时地推理出下一步的行进路线,是局部路径规划的关键。比较典型的方法有Khatib提出的人工势场法[1],但该算法易陷入局部最小点,存在目标不可达问题[2]。另一种方法是根据Zadeh在1965年提出的模糊集合理论发展而来的模糊路径规划方法,通过把人的经验归纳为模糊规则来控制AUV在水下未知环境中进行路径规划。目前,陈卫东[3]、付宜利[4]通过与传统规划方法的对比, 论证了模糊路径规划的有效性。孙兵[5]、杨敬辉[6]等学者使用智能算法对模糊控制器进行优化,获得了更好的路径规划效果。但是上述优化大多以优化路径为目标,未考虑系统的节能等因素,且应用对象很少是AUV。本文针对水下潜器的运动特性设计了模糊控制器,实现了AUV的局部路径规划。考虑到模糊控制器很大程度上依赖于专家经验,可能会造成能源的浪费,故将遗传算法应用于模糊控制器的优化设计,通过选择AUV的主要耗能装置螺旋桨的转速作为评价指标,实现了AUV局部路径规划时消耗更少的系统能源。该方法的有效性通过仿真得到验证。
1 模型 1.1 重于水型AUV模型重于水型AUV配置了机翼,不依靠浮力而是通过潜水器航行中获取的流体升力平衡其在水中的剩余重量。不需要安装庞大的浮力部件,其体积远小于常规的潜水器,能够在速度、成本、机动性等方面体现其优势。大范围巡航作业过程中使升力大致与AUV水中重量相等,并由操纵面对AUV姿态进行调整[7]。模型以上海交通大学水下工程研究所的“飞鱼”Ⅱ重于水型AUV为原型,其外形如图1所示。
|
图 1 “飞鱼”Ⅱ型AUV Fig. 1 Flying-fish Ⅱ AUV |
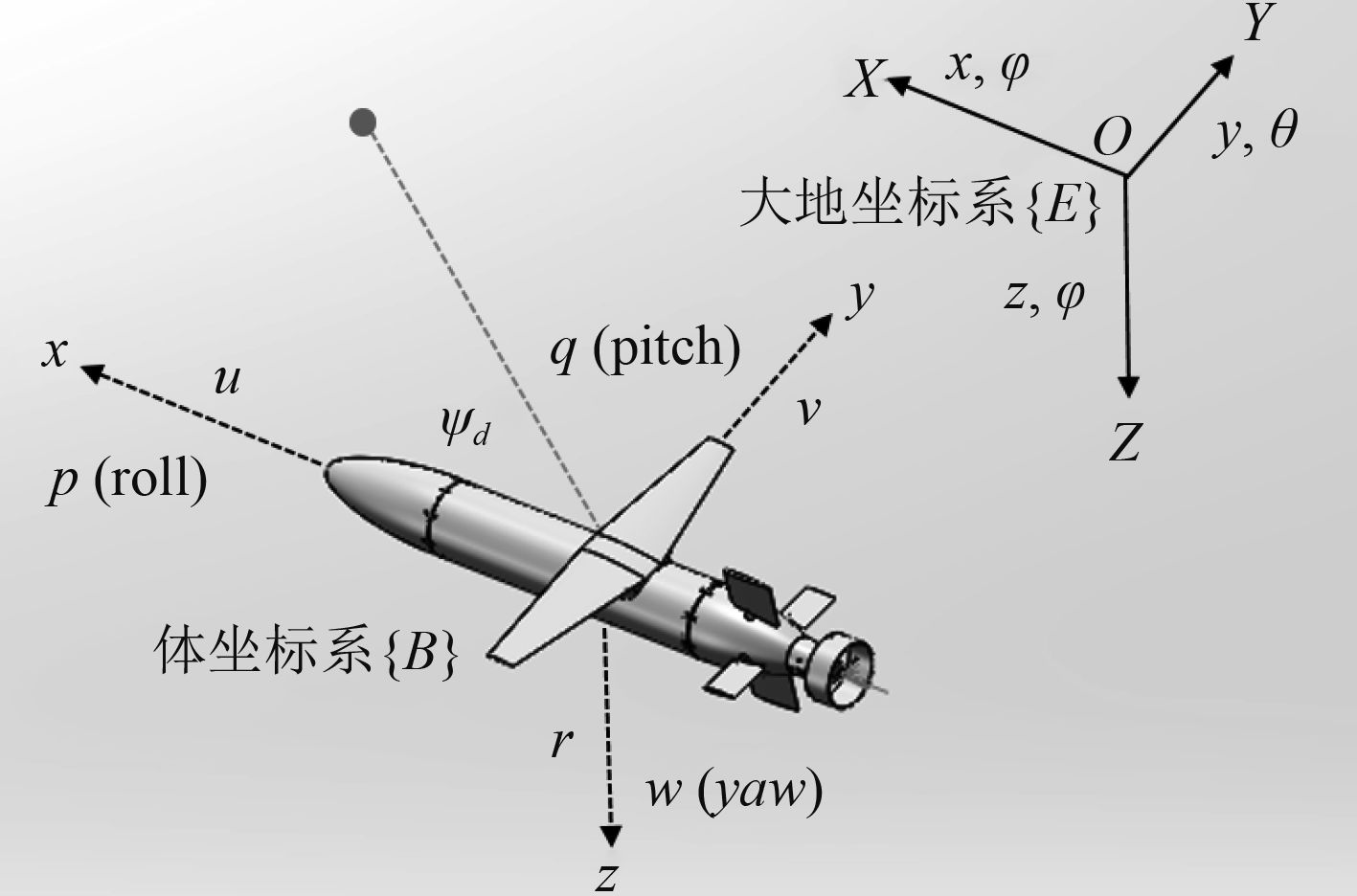
仿真环境的坐标系如图2所示,大地坐标系记为
|
图 2 坐标系 Fig. 2 Coordinate system |
潜水器的运动方程可以表示为非线性微分方程[8],见式(1)。
| ${\mathit{\boldsymbol{M}}}\dot v + {\mathit{\boldsymbol{C}}}(v)v + {\mathit{\boldsymbol{D}}}(v)v + g(\eta ) = \tau\text{,} $ | (1) |
其中:M为刚体质量和附加质量矩阵;C(v)为刚体转动惯量和科氏力矩阵;D(v)为线性和二次水动力项矩阵;g(η)为重力和浮力项;
η为大地坐标系下AUV的位置和欧拉角信息;ν为体坐标系中的(角)速度信息;τ为输入的力(矩)。其中,η和ν之间存在转换关系
| ${\mathit{\boldsymbol{J}}}(\eta ) = \left[ {\begin{array}{*{20}{c}}{{J_l}(\varphi ,\theta ,\psi )}&{{0_{3 \times 3}}}\\{{0_{3 \times 3}}}&{{J_a}(\varphi ,\theta ,\psi )}\end{array}} \right] \text{。}$ | (2) |
“飞鱼”Ⅱ型AUV在水中重力 P 大于浮力 B,且方向总是铅锤的,故在大地坐标系中分量为
| $g(\eta ) = \left[ {\begin{array}{*{20}{c}}{ - (P - B)\sin \theta }\\{(P - B)\cos \theta \sin \varphi }\\{\left( {P - B} \right)\cos \theta \cos \varphi }\\{ - {y_C}B\cos \theta \cos \varphi + {z_C}B\cos \theta \sin \varphi }\\{{z_C}B\sin \theta + {x_C}B\cos \theta \cos \varphi }\\{ - {x_C}B\cos \theta \sin \varphi - {y_C}B\sin \theta }\end{array}} \right] \text{。} $ | (3) |
“飞鱼”Ⅱ型的机翼布置于AUV重心正上方,在运动中将产生升力,在体坐标系中的分量表示为
| $L = \frac{1}{2}\rho {v^2}S{}_W{C_L} \text{,}$ | (4) |
| $\left\{ \begin{array}{l}{C_L} = {{\hat C}_{L,\alpha }}(\alpha - {\alpha _0}) + {C_{L,0}} \text{,} \\{{\hat C}_{L,\alpha }} = \frac{{{S_w}}}{{{l^2}}}{C_{L,\alpha }} \text{。} \end{array} \right.$ | (5) |
对式(1)线性化简和移项,得到重于水型AUV的空间运动状态方程,见式(6)。其中
| $\dot v = - {{\mathit{\boldsymbol{M}}}^{ - 1}}\tilde {\mathit{\boldsymbol{D}}}(v)v + {{\mathit{\boldsymbol{M}}}^{ - 1}}(\tau - g(\eta )) \text{。}$ | (6) |
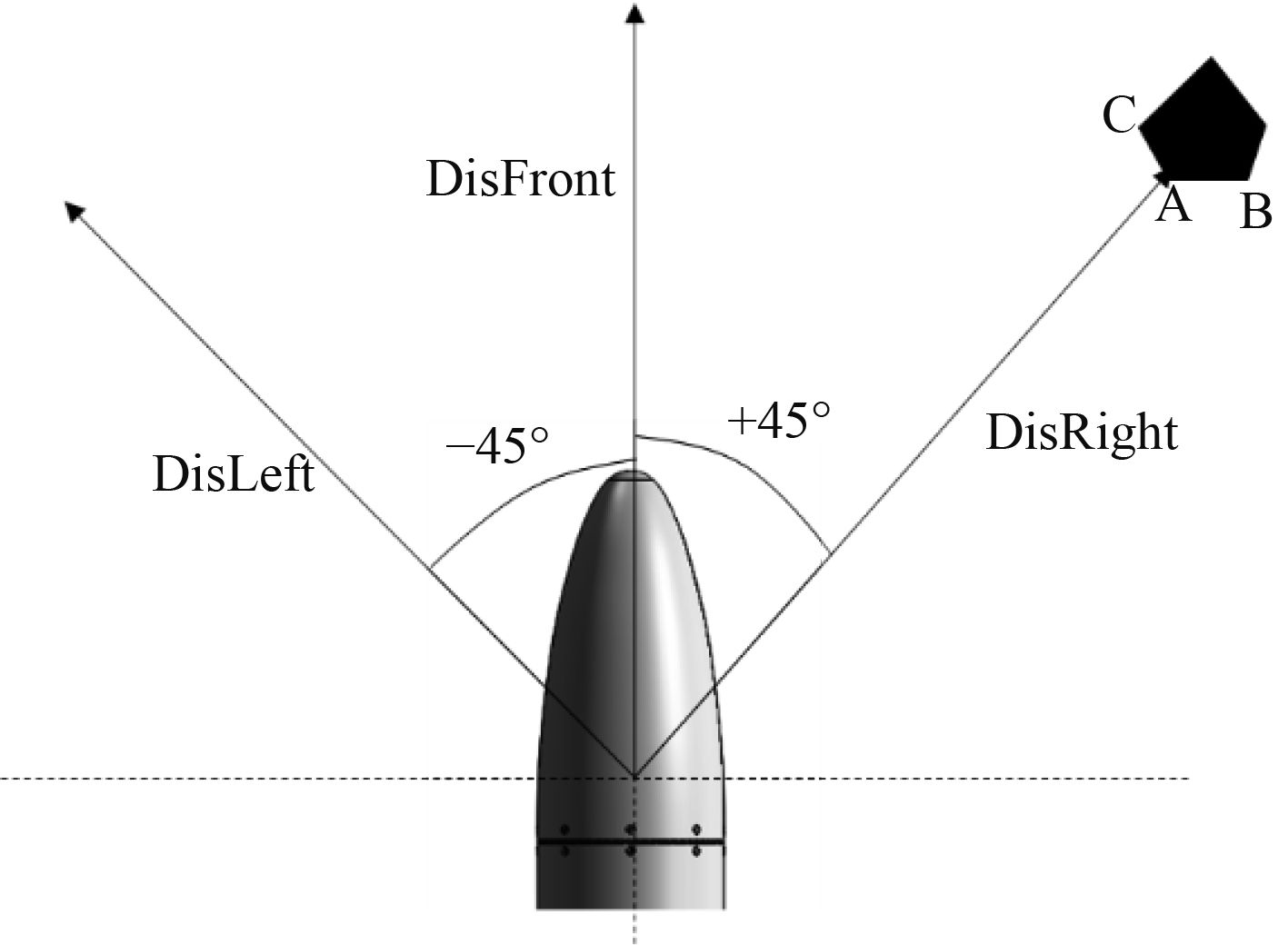
未知的水下环境中,AUV需要通过声呐获取周围障碍物的分布情况,并根据障碍物的距离推理出适当的转速与舵角,进行局部路径规划。仿真中依据实际声呐参数建立声呐模型,模拟声呐对未知水下障碍物的探测。重于水型AUV使用某型避障声呐,声呐水平开角范围
|
图 3 避障声呐 Fig. 3 Obstacle avoidance sonar |
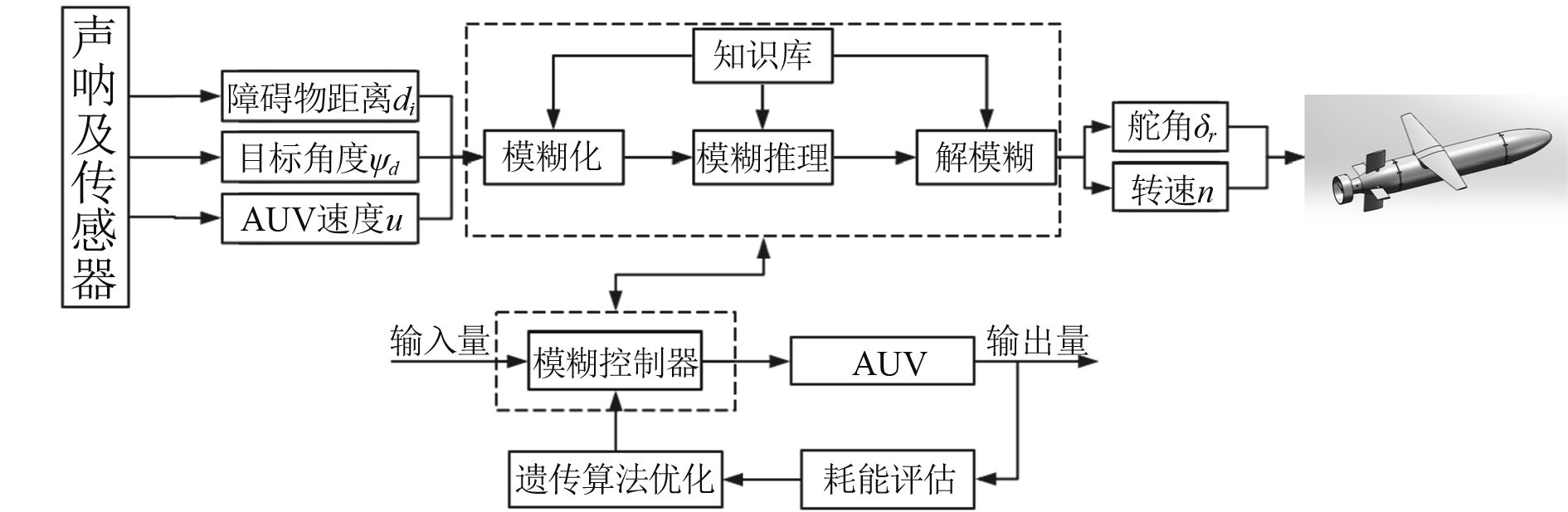
AUV在水下的低速运动可以解耦为水平面和垂直面2个平面空间的运动,本文设计的模糊控制器实现的是水平面内的局部路径规划,AUV的深度由单独的深度控制器控制,拟采用S面控制器[12]。模糊控制器的输出为垂直舵的舵角和螺旋桨转速。模糊控制器的主要结构包括:模糊化模块、知识库、模糊推理模块和清晰化模块4部分,如图4中虚线框部分。图4为遗传算法优化的模糊路径规划系统。
|
图 4 模糊路劲规划系统 Fig. 4 Fuzzy path planning system |
|
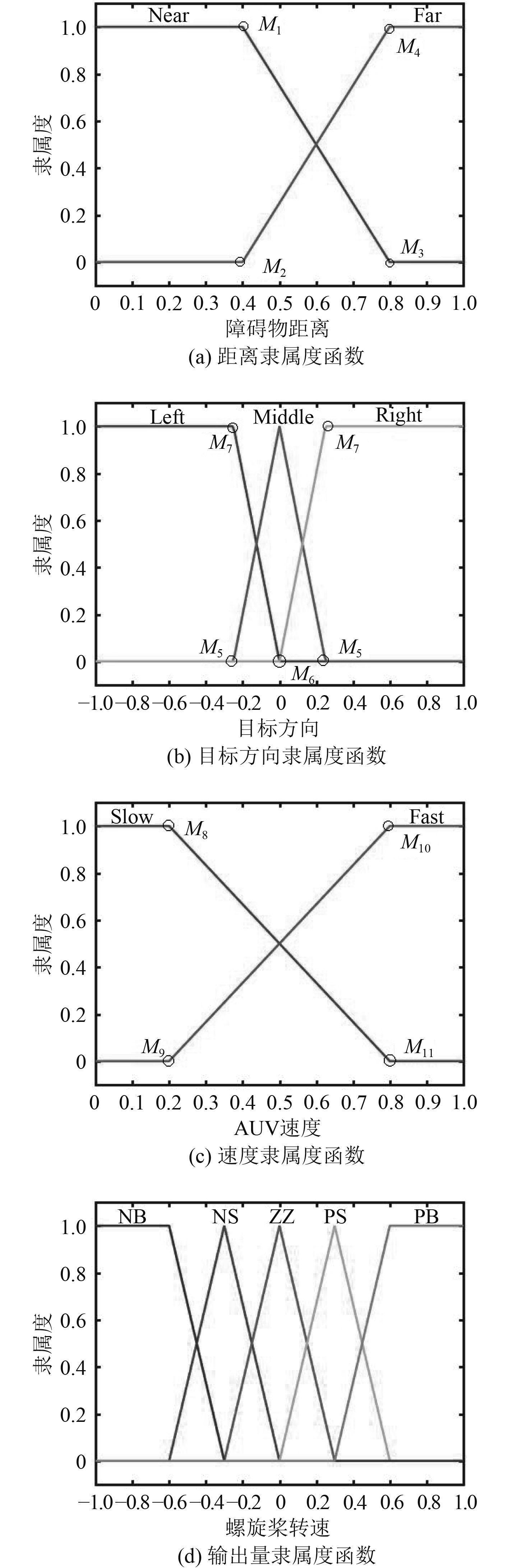
图 5 模糊隶属度函数 Fig. 5 Membership function |
模糊控制器5个输入量为:
1)声呐获取的3个方向的障碍物距离信息
2)目标方向(Direction)表示目标位置和体坐标原点连线与AUV首向的夹角
3)AUV当前的“速度(Speed)”包含{Slow,Fast}2个集合。
模糊控制器2个输出量为:
“舵角(Rudder)”和螺旋桨的“转速(RPM)”,为了实现对输出量较为精细地控制,舵角和转速分别划分为5个模糊集合,分别为{BRight, SRight, Middle, SLeft, BRight}和{NB, NS, ZZ, PS, PB}。
2.2 隶属度函数设计AUV具有转向半径较大和欠驱动等特点。所以,需要根据其特点专门设计隶属度函数和模糊规则库。设计如下:
1)语言变量“距离”的隶属度函数采用不对称的设计,形状为梯形,论域为[–1,1],如图5(a)所示,整体偏向右侧,即AUV更加倾向于将障碍物距离判断为Near,保证其与障碍物之间留有足够的安全距离。但是这样做也可能导致规划路径变长、能耗增加,因此后面将对隶属度函数进行优化。
2)目标方向隶属度函数为对称设计,障碍物在首向左侧为负,右侧为正,如图5(b)所示。
3)速度隶属度函数如图5(c)所示。
4)输出量舵角(Rudder)和转速(RPM)的隶属度函数形状一致,皆如图5(d)所示。
输入量隶属度函数图中
完成隶属度函数的设计后,根据经验定义模糊规则库,作为AUV路径规划的指导规则。该模糊控制器总共有5个输入,每个输入量包含的模糊集合数量分别为2,2,2,3,2,所以该模糊规则库共有2×2×2×3×2=48条规则,部分模糊规则见表1。
|
|
表 1 模糊规划规则表 Tab.1 Fuzzy control rules |
上面设计的隶属度函数很大程度上依赖于专家的经验知识[13],可能无法适应所有的水下障碍物环境,且浪费系统能源。对此本文采用遗传算法来优化隶属度函数的设计,进一步提高模糊路径规划的可靠性和能量利用率。
|
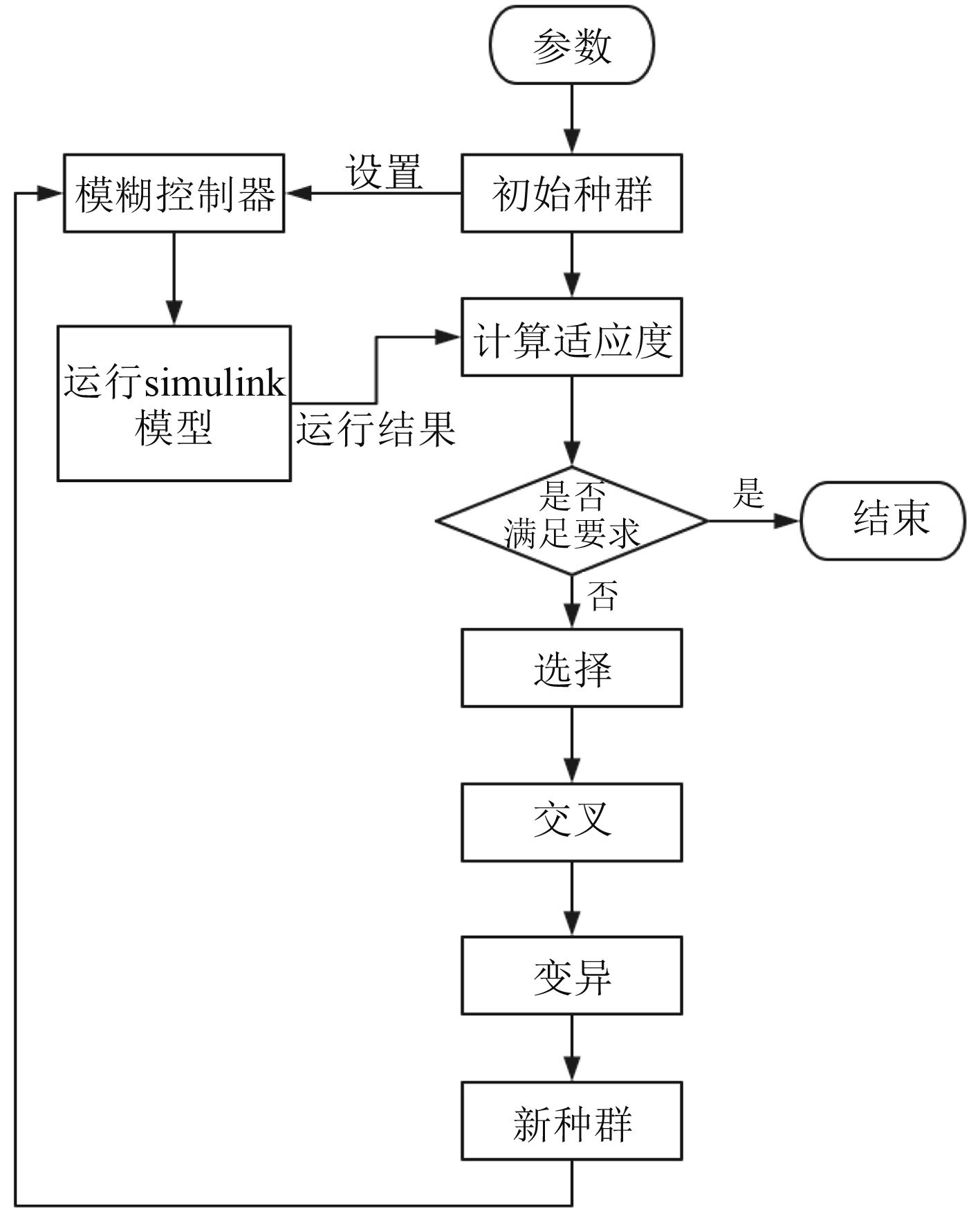
图 6 遗传算法流程图 Fig. 6 Genetic algorithm flowchart |
遗传算法优化的主要运行流程如图6所示:
1)初始种群生成。首先产生包含30个个体的“种群”,个体的基因选择为隶属度函数图5中标注拐点处的横坐标值,表示为向量
2)仿真测试。调用每个个体设置模糊控制器,控制AUV进行路径规划,并返回AUV的运行结果。
3)计算适应度。在单个个体控制AUV进行避障路劲规划后,选取推进器在运动期间的总旋转圈数(简称总转数)作为种群中每个个体的适应度评价指标,见式(7)。并线性地给每个个体分配适应度,见式(8)。总转数越低,适应度越大,即个体基因有更大概率遗传到下一代;反之就越小,更容易被淘汰(碰到障碍物的个体直接被淘汰)。
| ${\bar n_i} = \int_{{t_0} = 0}^t {n(t){\rm d}t} \text{,} (i = 1,2,...,30) \text{,}$ | (7) |
| $fitness(i) = ranking({\bar n_1},{\bar n_2},...,{\bar n_{30}}) \text{。}$ | (8) |
4)根据每个个体的总转数,计算种群的标准差
5)选择。根据每个个体的适应度,运用轮盘赌选择法对个体进行选择。
6)最后进行复制、变异和交叉操作,产生新种群。基因交叉的概率设置为80%,变异概率为8%。然后重复步骤 2 ~ 步骤 5。
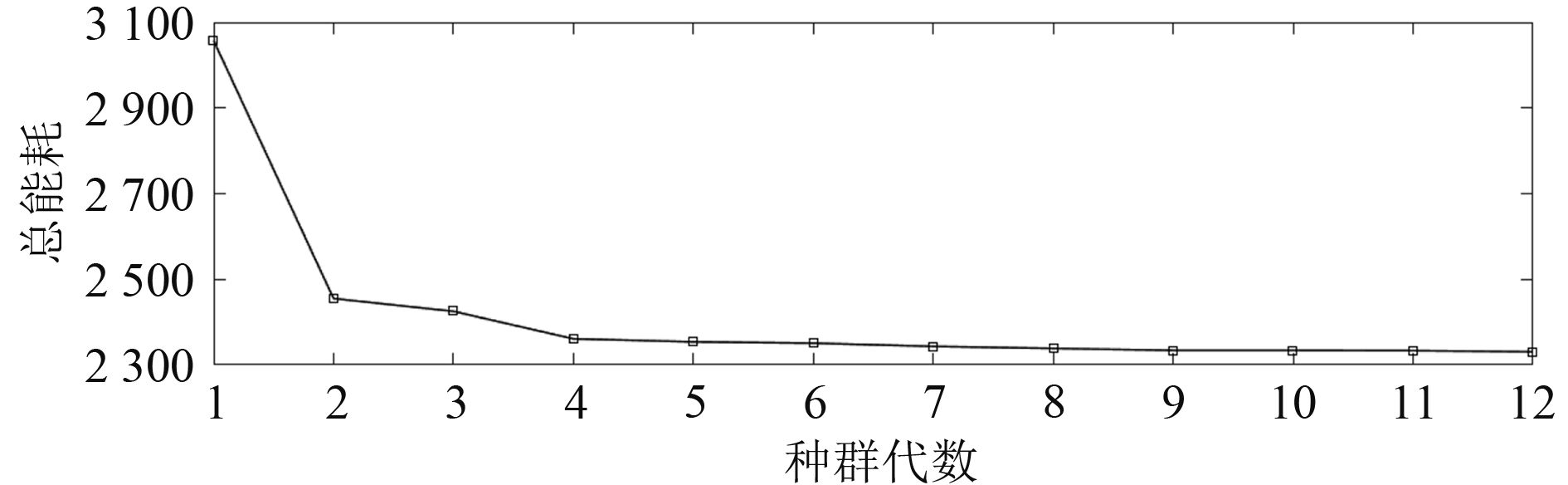
3 结果与分析为了加速优化过程,首先在简单障碍物环境中进行路径规划和遗传算法的优化。优化仿真中种群繁衍至第12代停止,每一代的总能耗(使用种群平均的总转数表示)如图7所示。可以看出,经过一代进化,由于初始种群中一些适应度很低的个体被淘汰,种群的总能耗已有了大幅降低;随后每代种群总能耗平稳收敛,直到满足种群差异性的要求,结束优化。末代种群中的最优个体总转数为
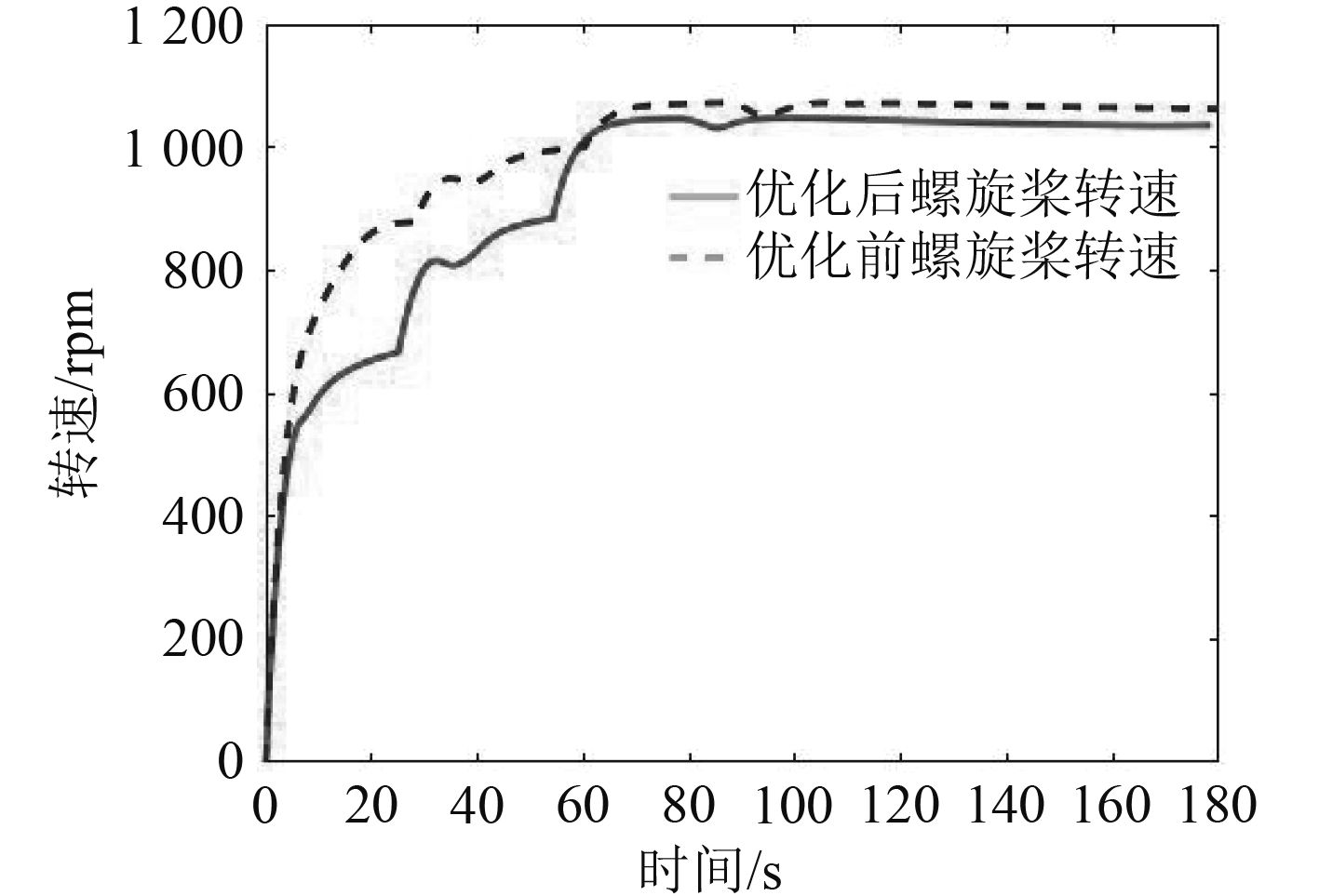
优化前,模糊控制器隶属度函数的定义如图5所示,其基因(拐点横坐标)为M=[0.4 0.4 0.8 0.8, 0.25 0 0.25, 0.2 0.2 0.8 0.8];优化后的基因为
|
图 7 各代总耗能 Fig. 7 Total energy consumption of each generation |
|
图 8 转速对比 Fig. 8 Comparison of rpm |
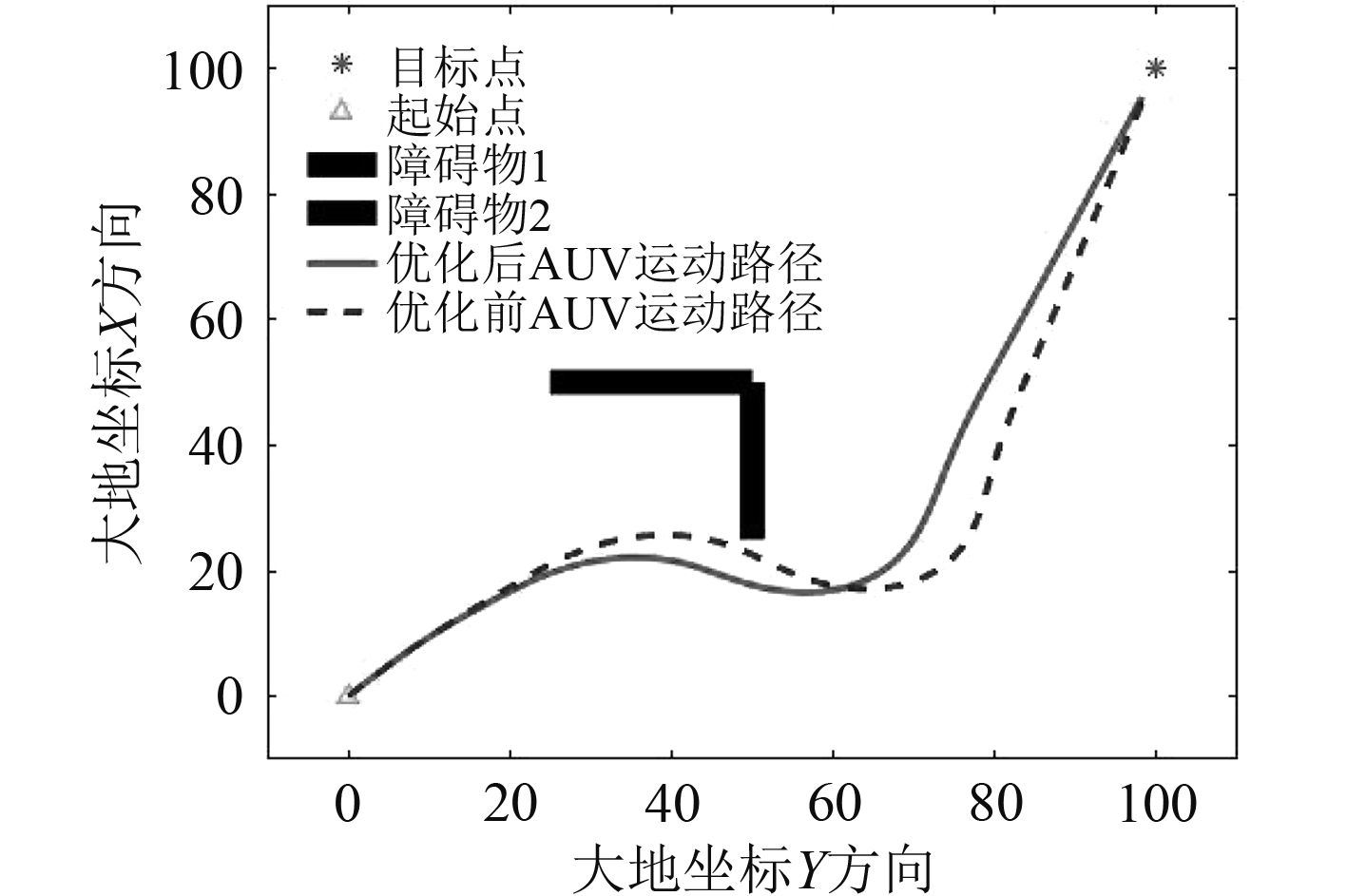
|
图 9 路径对比 Fig. 9 Comparison of route |
为了验证优化后模糊路径规划的可靠性和节能特性,本文设置了更加复杂的环境,检验AUV在不同环境中是否能达到快速、节能的目标。图10为复杂环境中AUV路径规划期间转速的对比,其具体性能比较见表2。可以看出避障机动期间(曲线凹陷部分),优化后的AUV转速更低。虽然时间有略微增加,但是总体来说总转数降幅更加明显。图11是优化前后AUV规划路径的对比。说明优化后的模糊控制器可以适应复杂的水下环境,并控制AUV更加节能地完成局部路径规划任务。
|
|
表 2 路径规划性能比较 Tab.2 Comparison of path planning performance |
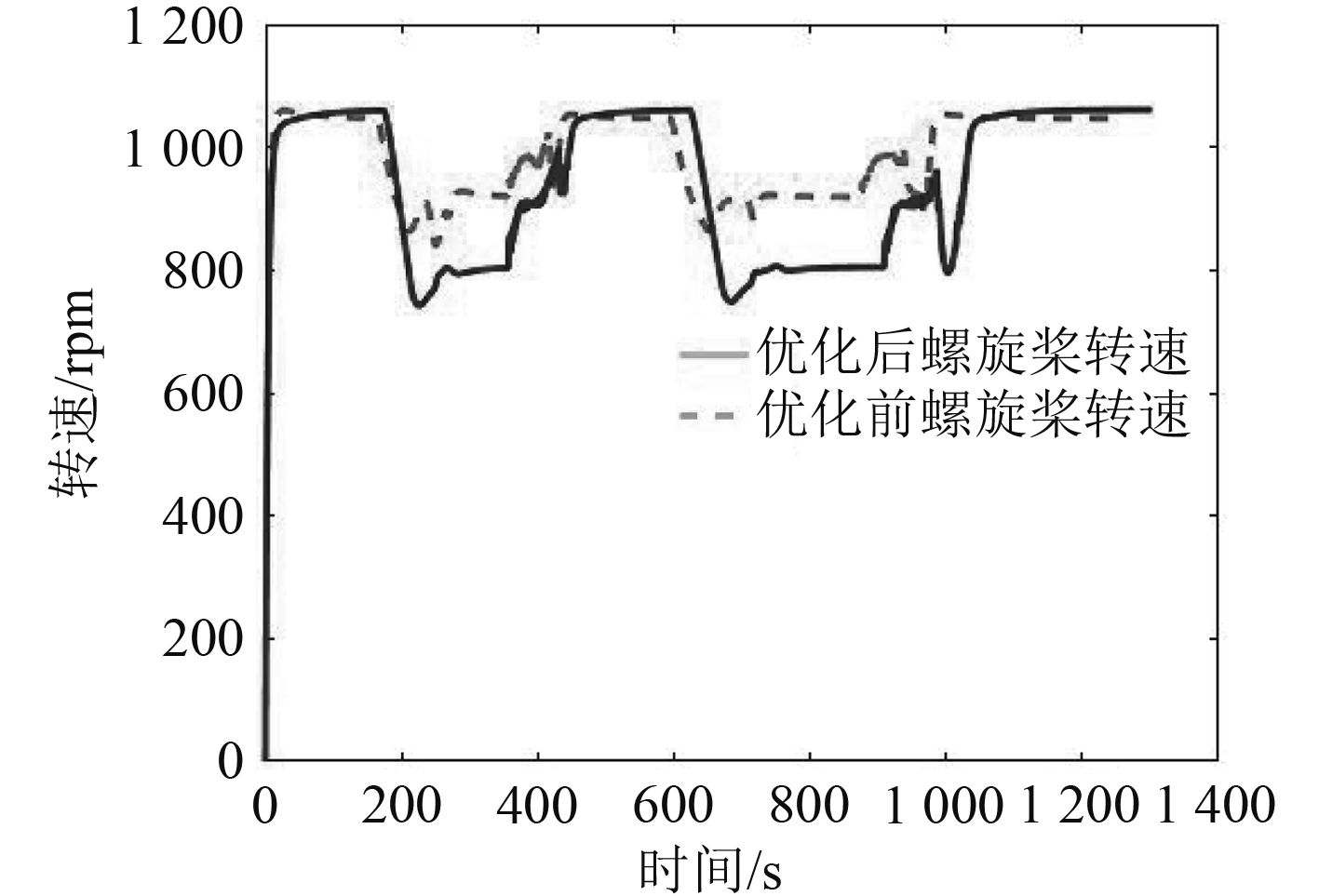
|
图 10 复杂环境转速对比 Fig. 10 Comparison of rpm in complex environment |
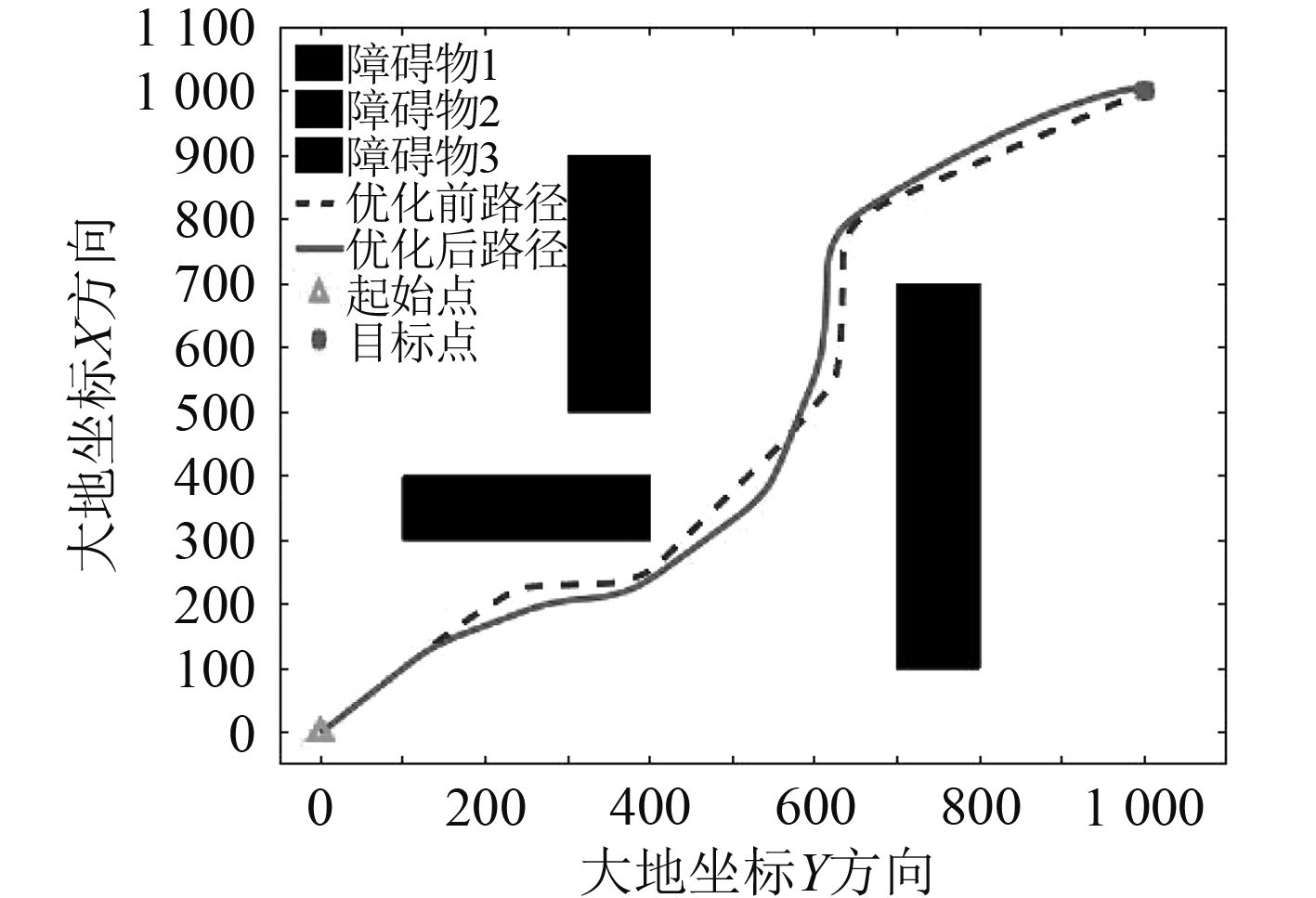
|
图 11 复杂环境路径对比 Fig. 11 Comparison of route in complex environment |
本文建立了重于水型AUV的动力学模型,为其设计了模糊控制器,并使用遗传算法对控制器进行优化。优化后的模糊控制器使重于水型AUV可以在未知水域中更加节能地完成路径规划任务,对于提高能量利用效率具有重要意义。模糊控制器输入输出量严格对应实际潜水器,可通过离散化的方式将控制器翻译为C语言,并移植到水下嵌入式平台上,对于实现重于水型AUV在水下环境中的局部路劲规划具有重要的应用价值。
| [1] | KHATIB O. Real time obstacle avoidance for manipulators and mobile robots[J]. International Journal of Robotics and Research, 1986, 5 (1): 90–98. DOI: 10.1177/027836498600500106 |
| [2] | LI Ying, HONG Sheng, HUANG Jun, et al. The new environment model building of penetration mission based on the artificial potencial field approach[C]. Proc of 2012 IEEE International Muti-Disciplinay Conference on Congnitive Methods in Situation Awareness and Decision Support, 2012: 121–124. |
| [3] | 陈卫东, 朱奇光. 基于模糊算法的移动机器人路径规划[J]. 电子学报, 2011 (04): 971–974+980. |
| [4] | 付宜利, 靳保, 王树国, 等. 未知环境下基于行为的机器人模糊路径规划方法[J]. 机械工程学报, 2006 (05): 120–125. DOI: 10.3321/j.issn:0577-6686.2006.05.023 |
| [5] | 孙兵, 朱大奇, 杨元元. 基于粒子群优化的自治水下机器人模糊路径规划[J]. 高技术通讯, 2013, 12 : 1284–1291. DOI: 10.3772/j.issn.1002-0470.2013.12.011 |
| [6] | 杨敬辉, 洪炳镕, 朴松昊. 基于遗传模糊算法的机器人局部避障规划[J]. 哈尔滨工业大学学报, 2004, 07 : 946–948. DOI: 10.3321/j.issn:0367-6234.2004.07.033 |
| [7] | 颜翚, 葛彤, 王彪. 一种新型重于水的自治式潜水器及其先进性分析[J]. 上海交通大学学报, 2012, 08 : 1173–1177. |
| [8] | M, et al. Modelling and simulation of a robust energy effcient AUV controller[J]. Mathematics and Computers in Simulation, 2016, 121 : 34–47. DOI: 10.1016/j.matcom.2015.08.021 |
| [9] | FOSSEN. guidance and control of ocean vehicles[M]. Norway, 1994. |
| [10] | 施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995. |
| [11] | 毛宇峰, 庞永杰, 李晔. 速度矢量坐标系下水下机器人动态避障方法[J]. 哈尔滨工程大学学报, 2010, 02 : 159–164. DOI: 10.3969/j.issn.1006-7043.2010.02.005 |
| [12] | 刘建成, 于华男, 徐玉如, 等. 水下机器人改进的S面控制方法[J]. 哈尔滨工程大学报, 2002, 23 (1): 33–36. |
| [13] | 孙增圻. 智能控制理论与技术[M]. 北京: 清华大学出版社, 1996. |
 2017, Vol. 39
2017, Vol. 39
