21世纪以来,海洋资源的开发和利用问题越来越引起人们的关注,随着技术的不断成熟,水下滑翔机作为一种新型的海洋勘测工具逐渐发展起来。水下滑翔机中的姿态调节单元能调整机体的俯仰角和偏转角,是AUV的重要运动功能单元,其设计的优劣直接影响AUV运动性能的好坏。传统的方式通过调整内部压载重块的位置,在浮力调节单元外皮囊体积变化和水平机翼的配合下,实现航行器转向运动。由于这种方法是间接通过改变重心来改变姿态的,这就导致控制过程中的不精确和不稳定性,尤其在受到外界干扰时,这种不稳定性会被放大,从而导致任务失败。针对水下滑翔机动力学的非线性、强耦合、模型参数复杂,因此设计了多桨驱动无舵水下滑翔机[1]。通过4个螺旋桨的互相协调配合,直接改变转速来改变运动姿态,在建立了运动模型基础上,结合PID算法,设计合理的PID控制器,用仿真来验证算法的稳定性和抗干扰能力,并通过试验来验证这种方法的有效性。
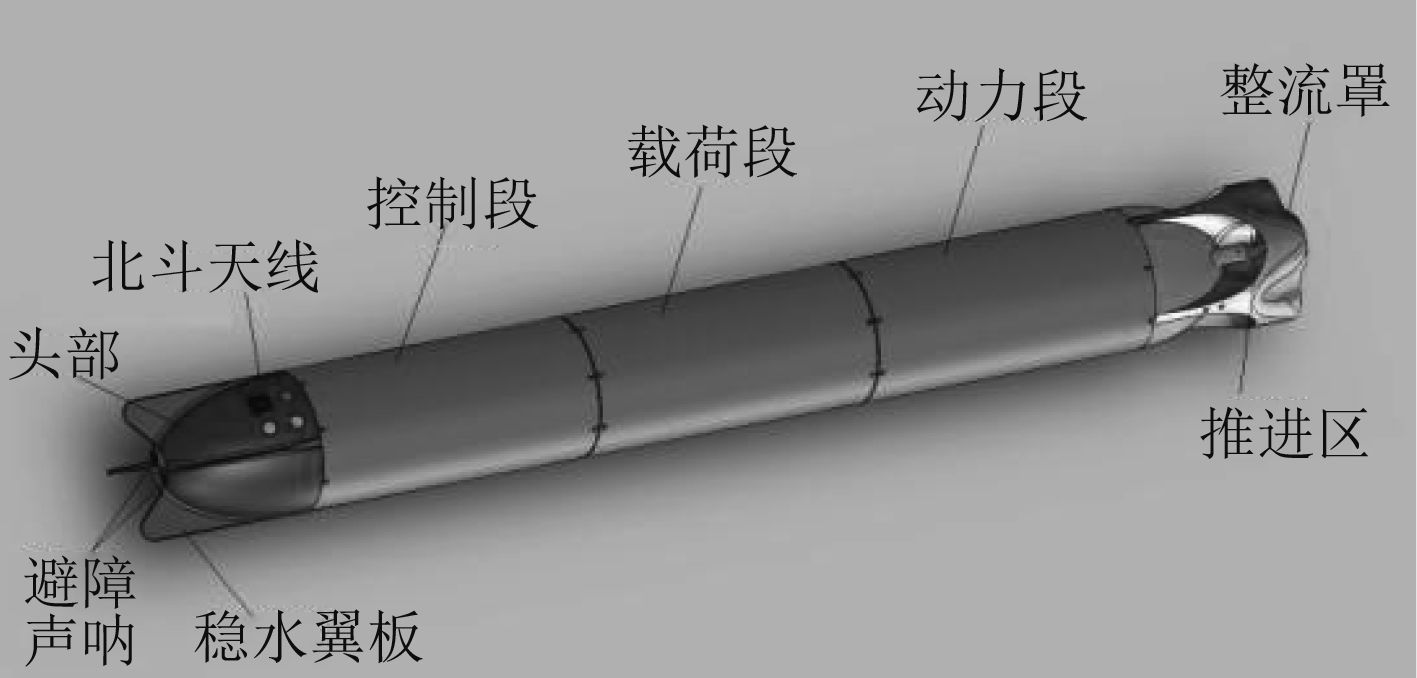
1 结构及其工作原理按照水下滑翔机所实现的功能来分,其结构主要可以分为:头部装置、控制段、载荷段、动力段、整流罩。具体结构如图 1所示。
|
图 1 滑翔机整体结构图 Fig. 1 Overall structure of the glider |
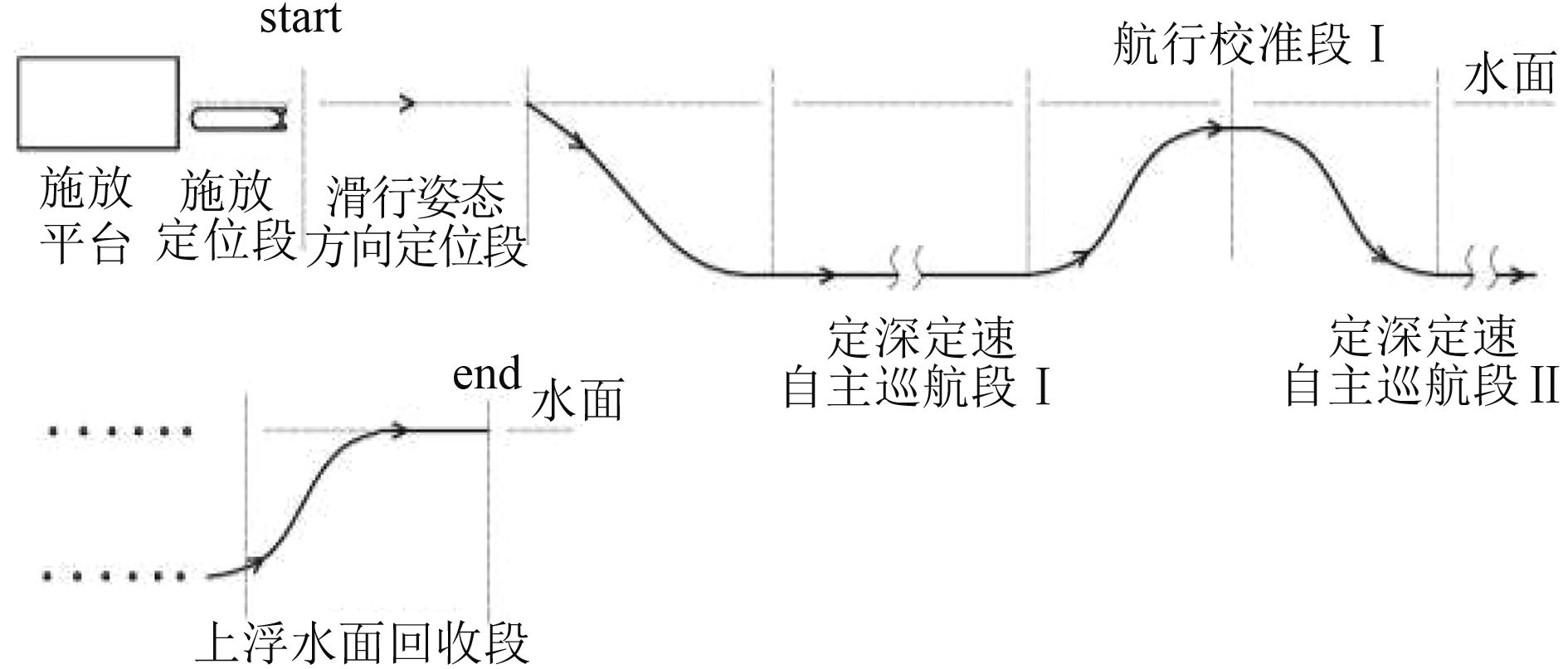
工作原理:水下滑翔机依靠电机驱动液压泵,调节内压水仓的体积,从而改变整个系统的总浮力, 使其上浮或者下潜,其姿态通过尾部的螺旋桨产生的推力来实现。它以中等航程、高稳定度姿态航行、定时间任务为目标。结构形式为,其装配小型化平衡用压水舱,其余空间大量列装高能电池,以自身携带的高能电池为动力,依托压水舱的作用,完成浮力变化,当浮力与重量相当时,即可进入运动模式,工作流程如图 2所示。
|
图 2 滑翔机运动示意图 Fig. 2 Glider motion diagram |
水下滑翔机是一个非线性、多变量、高度耦合的系统,所以在实现其功能的精确控制之前,首先必须对其进行力学和动力学上的分析,并且建立合适的动力学模型,最后根据其控制对象设计合理的控制器。
2.1 坐标系的选择和建立想要建立水下滑翔机模型,第1步的任务就是建立适当的坐标系,对于本设计,我们可以通过建立2个坐标系来解决,这2个坐标系分别为地面和载体坐标系体,都符合右手定则[2]。
2.1.1 地面坐标系地面坐标系(以下称为SE)的坐标原点选在滑翔机的入水处,EX为水平方向,EY轴垂直水面向下,EZ轴与EX EY轴垂直,其方向由右手定则确定。
2.1.2 载体坐标系为了方便分析,我们选取载体坐标系的原点在其浮心,Bx与滑翔机机身平行,方向水平向前,By与机身垂直,Bz轴分别于Bx By轴垂直。

|
图 3 滑翔机坐标系的建立 Fig. 3 The establishment of the glider coordinate system |
2个坐标系之间的向量变化需要通过旋转矩阵来变换,其变换矩阵为:
| $\begin{split}R_B^E = \left[ {\begin{array}{*{20}{l}}{\cos \psi \cos \theta }&{\sin \theta }\\{\sin \psi \sin \phi - \cos \psi \sin \theta \cos \varphi }&{\cos \theta \cos \varphi }\\{\cos \psi \sin \theta \sin \phi + \sin \psi \cos \varphi }&{ - \cos \theta \sin \varphi }\end{array}} \right.\\\left. {\begin{array}{*{20}{c}}{ - \sin \psi \cos \theta }\\{\sin \theta \sin \psi \cos \varphi + \cos \psi \sin \varphi }\\{\cos \psi \cos \varphi - \sin \psi \sin \theta \sin \varphi }\end{array}} \right]\text{,}\end{split}$ | (1) |
其中俯仰角为θ,横滚角为
螺旋桨在高转速运行时会出现反扭矩,并且其方向与本身旋转的方向相反,然而这种反方向的扭矩对整个系统的稳定性有很严重的影响。为了消除这种反扭矩,我们通常会采用尾桨或者与其共轴的反转螺旋桨来解决问题,但是对于本设计,由于其结构的原因,不需要再做一些附加的工具或者方法,完全可以通过合理4个螺旋桨的转向来消除[3]。如图 4所示,将4个螺旋桨按照旋转45°的“十”字方式来排列,逆时针对其进行编号,分别为1,2,3,4,这时只需要保持1号和3号螺旋桨逆时针旋转,而2号和4号螺旋桨顺时针旋转,2号和4号螺旋桨产生的反扭矩顺其自然的就会与1号和3号螺旋桨产生反扭矩抵消掉。
四螺旋桨的姿态控制主要包括俯仰角控制、横滚角控制、偏航角控制,通过调节各个螺旋桨的转速即可调节AUV的姿态。

|
图 4 螺旋桨旋转方向图 Fig. 4 Propeller rotation pattern |
对于AUV来讲,它的运动形式和飞机一样,具有六自由度,在空间中的包括3个平移和3个旋转运动。
2.3.1 平移运动方程设AUV的浮心在地面坐标系中的坐标为
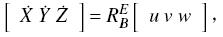
|
(2) |
| $\left\{ \begin{array}{l}\dot X = u\cos \theta \cos \psi + v\sin \psi \sin \phi - v\sin \theta \cos \psi \cos \phi + \\w\sin \psi \cos \phi + w\sin \theta \cos \psi \sin \phi \\\dot Y = u\sin \theta + v\cos \theta \cos \phi - w\cos \theta \sin \phi \\\dot Z = - u\cos \theta \sin \psi + v\cos \psi \sin \phi + v\sin \theta \sin \psi \cos \phi + \\w\cos \psi \cos \phi - w\sin \theta \sin \psi \sin \varphi \end{array} \right\}\text{。}$ | (3) |
根据之前所述,转动矢量
| ${\varOmega} = \left[ {\begin{array}{*{20}{c}}{\sin \theta }&0&1\\{\cos \theta \cos \phi }&{\sin \phi }&0\\{ - \cos \theta \sin \phi }&{\cos \phi }&0\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\dot \psi }\\{\dot \theta }\\{\dot \phi }\end{array}} \right]\text{。}$ | (4) |
如图 5所示,滑翔机在水下工作的过程中,由于重心和浮心不重合,将会产生一个扶正力矩,对滑翔机进行受力分析,包括浮力B,重力G,螺旋桨推力Ft,水动力FV,FI。

|
图 5 滑翔机受力分析图 Fig. 5 Glider force analysis chart |
在滑翔机刚放入水中时,由于它本身的重力等于浮力,并且方向相反,大小相等,所以垂直方向的合力为0。在建立载体坐标系的时候,选取浮心为原点,然而由于浮心与重心的位置并不重合,所以浮心和重心的位置矢量为
| ${F_G} = R_B^E\left[ {\begin{array}{*{20}{c}}0\\G\\0\end{array}} \right] = G\left[ {\begin{array}{*{20}{c}}{\sin \theta }\\{\cos \theta \cos \phi }\\{ - \cos \theta \sin \phi }\end{array}} \right]\text{,}$ | (5) |
| ${F_B} = R_B^E\left[ {\begin{array}{*{20}{c}}0\\{ - {B_{}}}\\0\end{array}} \right] = {B_{}}\left[ {\begin{array}{*{20}{c}}{ - \sin \theta }\\{ - \cos \theta \cos \phi }\\{\cos \theta \sin \phi }\end{array}} \right]\text{,}$ | (6) |
| $\begin{split}T{}_G = {r_G} \times {F_G} = G\left[ {\begin{array}{*{20}{c}}0\\{{y_G}}\\0\end{array}} \right] \times \left[ {\begin{array}{*{20}{c}}{\sin \theta }\\{\cos \theta \cos \phi }\\{ - \cos \theta \sin \phi }\end{array}} \right]=\\ G{y_G}\left[ {\begin{array}{*{20}{c}}{ - \cos \theta \sin \phi }\\0\\{ - \sin \theta }\end{array}} \right]\text{。}\end{split}$ | (7) |
根据螺旋桨环流理论的观点,在不可压缩的理想流体中,螺旋桨转动所产生的推力Ft和扭矩Tt可以用式(8)表示。
| $\left\{ \begin{array}{l}\begin{array}{*{20}{c}}\!\!\!\!\!\!\!\!{{F_t} = \rho Z\int_{{r_h}}^{_{{r_t}}} {\Gamma (r)({w_t}r - 0.5{u_t})(1 - \varepsilon tg{\beta _i}){\rm d}r} }\text{,}\\[5pt]\end{array}\\\!\!\!\!{T_t} = \rho Z\int_{{r_h}}^{{r_t}} {\Gamma (r)(V + 0.5{u_a})(1 + \varepsilon ctg{\beta _i})r{\rm d}r} \text{。}\end{array} \right.$ | (8) |
对于式(8),其中包含着对环量和诱导速度的计算,但是由于在实际工程中没有必要设计这么详细的计算,所以将其简化,故螺旋桨推力Ft和扭矩Tt在载体坐标系下可表示为式(9)。
| $\left\{ {\begin{array}{*{20}{l}}{{F_t} = (1 - t){K_T}\rho {n^2}d_\rho ^4}\text{,}\\{{T_t} = {K_Q}\rho {n^2}d_p^5}\text{。}\end{array}} \right.$ | (9) |
式中:KT为推力系数;t为推力减额系数;n为螺旋桨转速,r/s;dP为螺旋桨外径,m;KQ为力矩系数。Kt和KQ可根据螺旋桨模型敞水试验获得。
另外由于滑翔器配有4个螺旋桨,其按环形布置,如图 4所示。设4个推力器关于o点对称布置,这种布置方案的机动性能好。所以其空间总推力和总力矩的计算式为:
| $\left[ {\begin{array}{*{20}{c}}{{F_T}}\\{{T_T}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\displaystyle\sum\limits_{i = 1}^2 {{F_i}} }\\{\displaystyle\sum\limits_{i = 1}^2 {{T_i}} }\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{({F_1} + {F_2} + {F_3} + {F_4})\cos \alpha }\\{({F_1} - {F_2} - {F_3} + {F_4})\sin \alpha }\\0\\0\\0\\{c({F_1} - {F_2} + {F_3} - {F_4})\sin \alpha }\end{array}} \right]\text{。}$ | (10) |
分为粘性水动力和惯性水动力,在此不具体分析,见参考文献[4]。
粘性水动力和产生的转矩可表示为
惯性水动力和产生的转矩可表示为
根据前面的分析结果,将各个力和力矩结合起来,就可以得出滑翔器所受到的总外力和力矩,如下所示:
| $\begin{array}{l}F = \displaystyle\sum\limits_i {{F_i}} = {F_G} + {F_B} + {F_v} + {F_T} + {F_I}\text{,}\\T = \displaystyle\sum\limits_j {{T_j}} = {T_G} + {T_B} + {T_T} + {T_V} + {T_I}\text{。}\end{array}$ | (11) |
为使被研究的问题简化,由于滑翔机本身在工作中自身的变化不影响整个的运动过程,因此可以将滑翔机视作刚体,各个变量如表1所示。
|
|
表 1 变量定义 Tab.1 Variable definitions |
根据地面坐标系与本体坐标系之间的坐标转换关系,以及刚体的动量定理,最终得到了滑翔器的动量和角动量在本体坐标系下的表达形式:
| $\begin{array}{l}\dot P = P \times \Omega + F\text{,}\\\dot L = l \times \Omega + R_B^E\displaystyle\sum\limits_{i = 1} {({d_i} \times f{}_i} ) + T\text{。}\end{array}$ | (12) |
其中fi为滑翔机受到的外力在地面坐标系下的表达,di为fi的作用点到浮心得距离。
除此之外,根据刚体转动定律可以推出滑翔机对质心动量矩的另一种表示:
| ${L_B} = {{J}_C}\varOmega = {I_{Cx}}pi + {I_{Cy}}qj + {I_{Cx}}rk\text{,}$ | (13) |
其中
在一般情况下,由于水下环境复杂,可能存在着暗流、暗礁等,为了提高滑翔机稳定性,在对滑翔机的机械结构设计时,通常会故意将滑翔机的重心在铅垂方向上略低于浮心。根据运动学知识以及刚体转动定理最终得到了滑翔机的动力学模型。
| $\Bigg\{ {} \begin{array}{*{20}{c}}\!\!{m(\dot V + \dot \varOmega \times {r_G} + \varOmega \times V + ({r_G} \times \varOmega ) \times \varOmega ) = F}\text{,}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{J_C}\dot \varOmega + {J_C}\varOmega \times \varOmega = R_B^E\displaystyle\sum\limits_{i = 1} {({d_i} \times {f_i}) + T} }\text{。}\end{array}$ | (14) |
之后将滑翔机的运动方程即平移和旋转方程代入进一步可得滑翔机的空间运动方程和动力学方程在本体坐标系下的一般表达形式:
| $\begin{array}{c}\!\!\!\!\!\!\!\! \left\{ {\begin{array}{*{20}{l}}{\dot X = u\cos \theta \cos \psi \!\!+\!\! v\sin \psi \sin \phi \!-\! v\sin \theta \cos \psi \cos \phi }\text{,}\!\!\\{\dot Y = u\sin \theta + v\cos \theta \cos \phi - w\cos \theta \sin \phi }\text{,}\\{\dot Z = - u\cos \theta \sin \psi \!\!+\!\! v\cos \psi \sin \phi \!\!+\!\! v\sin \theta \sin \psi \cos \phi }\text{,}\!\!\!\\{\dot \psi = q\cos \phi /\cos \theta - r\sin \phi /\cos \theta }\text{,}\\{\dot \theta = q\sin \phi + r\cos \phi }\text{,}\\{\dot \phi = p - q\cos \phi \tan \theta + r\sin \phi \tan \theta +}\end{array}} \right.\\\begin{array}{*{20}{c}}{ w\sin \psi \cos \phi + w\sin \theta \cos \psi \sin \phi }+\\{ w\sin \psi \cos \phi + w\sin \theta \cos \psi \sin \phi }\text{。}\end{array}\end{array}\!\!\!\!\!\!\!\!$ | (15) |
| $\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{m\dot u - m{y_G} - mv\dot r + mwq + m{y_G}pq = }\\{m\dot v + \dot r - mwp + mur - m{y_G}({r^2} + {p^2}) = }\\{m\dot \omega - \dot q + m{y_G}\dot p - muq + mvp + m{y_G}rq = }\\{{J_{Bx}}\dot p \!+\! m{y_G}(vp \!+\! \dot w - uq) \!+\! ({J_{Bs}} \!-\! {J_{By}})qr \!+\! G{y_G}\cos \theta \sin \phi }=\\{ {J_{By}}\dot q + \dot w + ({J_{Bx}} - {J_{BG}})rp = (mg - b)\cos \theta \sin \phi }\\{{J_s}\dot r + \dot v + m{y_G}(wq + \dot u - vr) + ({J_{By}} - {J_{Bx}})pq - }\end{array}} \right.\\\begin{array}{*{20}{l}}{ {B_b}\sin \theta + (G - {B_0})\sin \theta + (1 - t){K_T}\rho {n^2}{d_p}^4}-\\{ {B_b}\cos \theta \cos \phi + (G - {B_0})\cos \theta \cos \phi }\\{{B_b}\cos \theta \sin \phi - (G - {B_0})\cos \theta \cos \phi }\\{{K_Q}\rho {n^2}{d_p}^5 + mg[(1-\cos \varphi )\cos \theta \sin \phi-\sin \varphi \cos \theta \cos \phi]}+\\{ mg\sin \varphi \sin \theta }\\{mg\cos \theta \cos \phi + G{y_G}\sin \theta }\text{。} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\, \end{array}\end{array}$ | (16) |
将滑翔机的各项参数代入式(15)和式(16)之后,经过计算可以得到稳态滑翔机稳态参数,以及该平衡点附近的小扰动线性系统。
3 PID控制器设计滑翔机PID控制示意图如图 6所示,其中θ,

|
图 6 控制系统框图 Fig. 6 Block diagram of the control system |
选取系统的状态向量和控制输入向量为
| $\begin{array}{l}x = {(u, v, w, p, q, r, \theta, \phi, \varphi )^{\rm T}}\text{,}\\u = ({u_1}, {u_2}, {u_3}, {u_4})\text{。}\end{array}$ | (17) |
对滑翔机在平衡态处线性化,得到小扰动线性化模型:
| $\Delta \dot x = A\Delta x + B\Delta u\text{,}$ | (18) |
式中:
实际过程控制中,PID控制器的数学模型为:
| $u(t) = {K_P}\left\{ {e(t) + 1/{T_i}\int_0^t {e(t){\rm d}(t) + {T_{d}}\frac{{{\rm d}[e(t)]}}{{{{\rm d}_t}}}} } \right\}\text{,}$ | (19) |
其中:Kp,
| ${n_r} = {K_{pr}}e + {K_{ir}}\int_{{t_0}}^t {e(\tau ){\rm d}\tau + {K_{{ d}r}}\dot e} \text{。}$ | (20) |
式中,r为螺旋桨编号。
4 Matlab/Simulink仿真根据PID系统的结构图,搭建Matlab simulink模型并仿真。
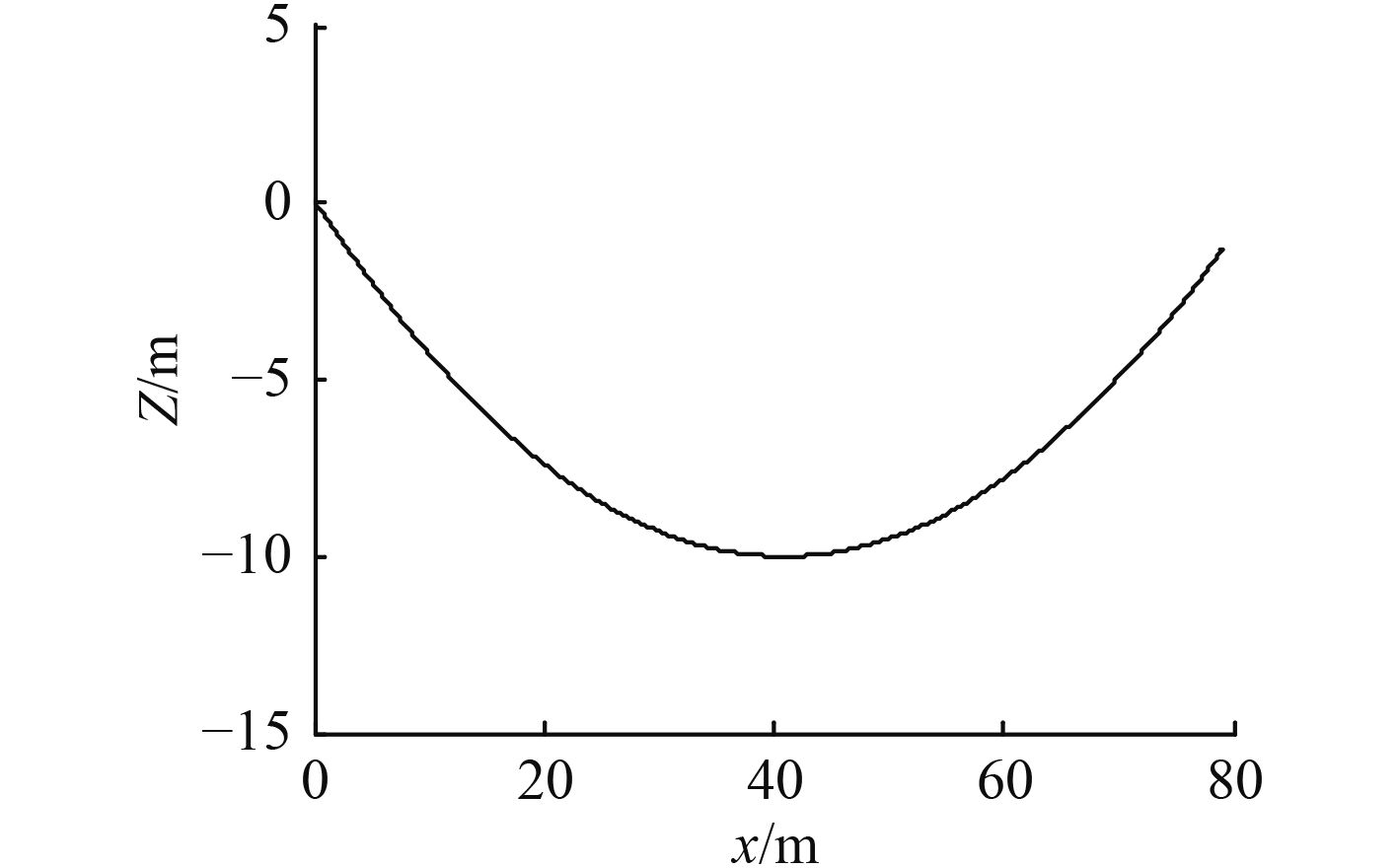
4.1 下潜与上浮过程仿真假设初始情况下,滑翔机浮力等于重力,并且以设定的速度匀速在水面直行,下潜程序启动,此时2,3电机为主转电机,1,4号电机为辅助电机,使滑翔机以–45°的滑翔角下潜,下潜至定深10 m时,开始上浮,电机的功能与下潜时相反,以+45°的仰角到达水面。滑翔轨迹如图所示。选取
|
图 7 航行轨迹图 Fig. 7 Sailing chart |
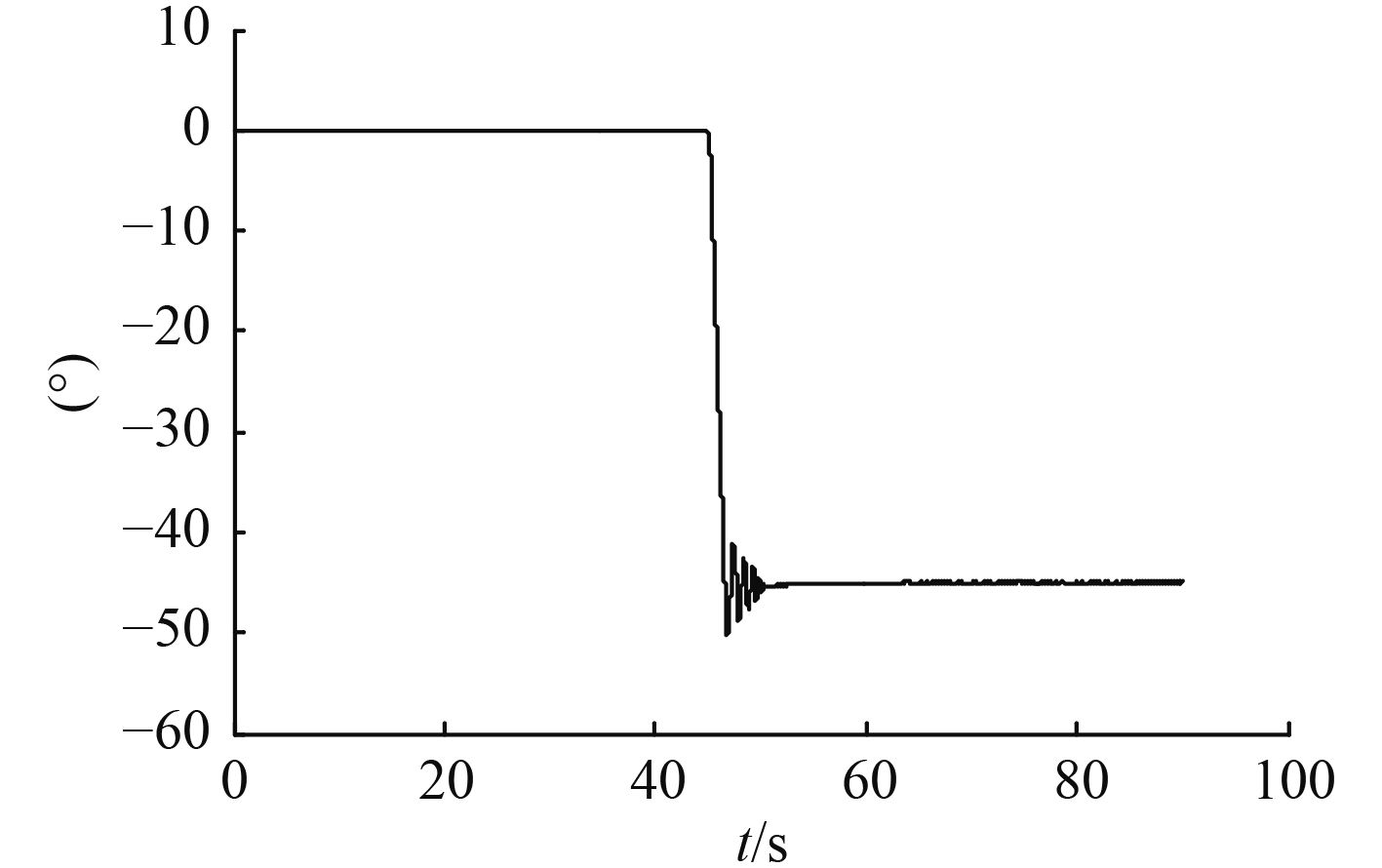
|
图 8 下潜时变化 Fig. 8 Changes when dive |

|
图 9 2,3号电机转速变化 Fig. 9 No.2.3 motor speed change |
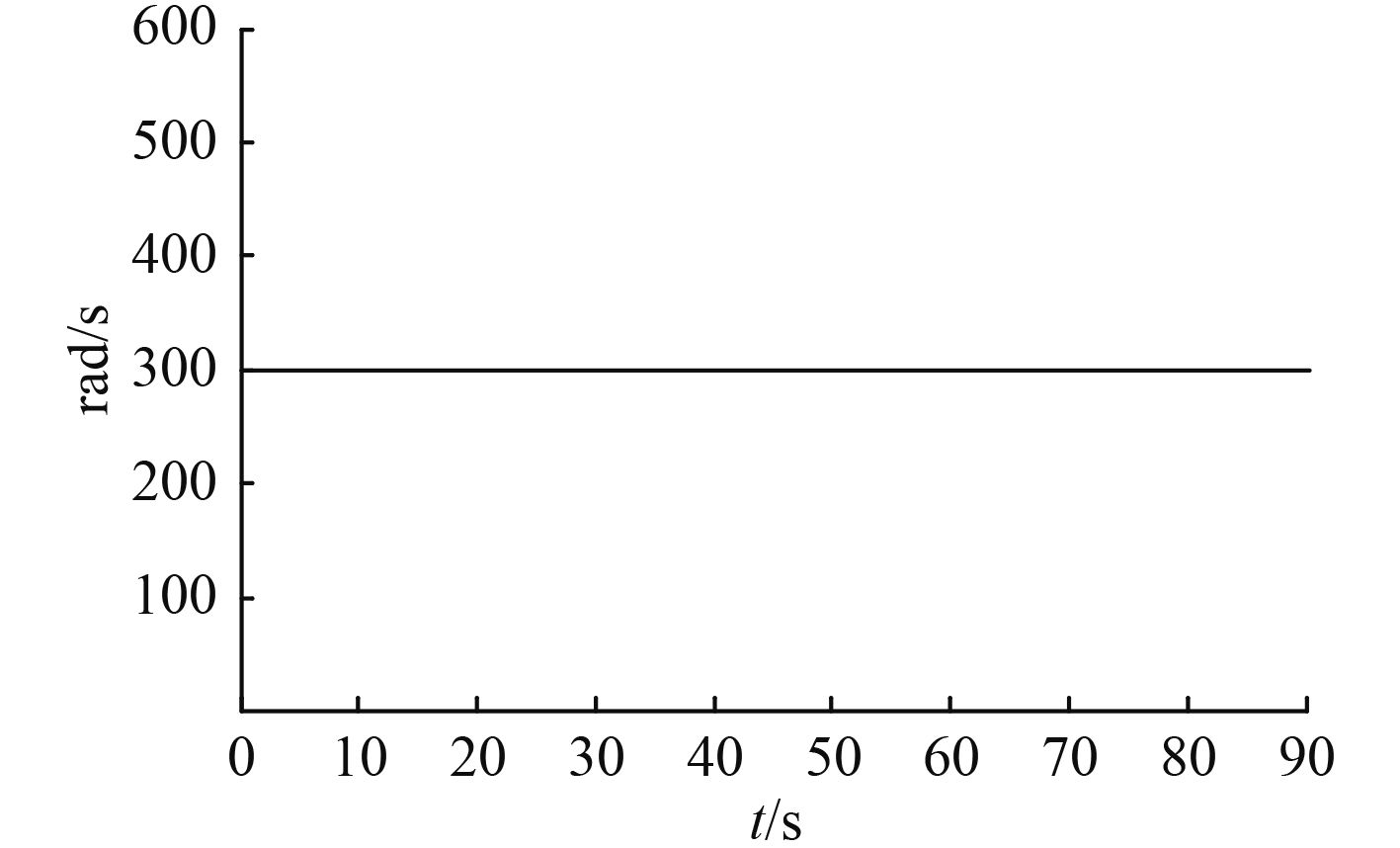
|
图 10 1,4号电机转速变化 Fig. 10 1,4 motor speed changes |
由图 8可以看出,在43 s时执行下潜程序,滑翔机以–45°开始下潜,下潜过程中,角度以及主转电机响应速度快,并且在到达设定值时,系统稳定性好。
4.2 偏转过程仿真滑翔机初始情况与4.1相同,当到达设定的偏转位置时,1,2号电机作为主转电机,3,4号为辅助电机,使滑翔机以给定偏航角进行转弯,此时希望转弯半径尽可能达到最小选取

|
图 11
转向时
|
由于在偏转过程中,主转电机与下潜过程中主转电机相似,在这里不重复表达。
仿真结果表明:PID参数的合理选取,使得系统超调量较小,稳态误差几乎为零,响应速度快,系统仿真验证了PID控制的有效性。
5 湖 试为了验证系统的可行性,首先选择在千岛湖进行湖试,主要目的是对系统的下潜和偏转的稳定性进行试验。试验的过程主要围绕选定的3个位于三角形顶点的GPS点进行,如图 12所示,试验路线由起点1到2 到3 再返回到1,1号点到2号点之间进行的为水面的直线运动,2号点到3号点进行完成了下潜,并做定深运动,3号到1号点进行上浮。整个过程的实际航线、偏转角度、速度以及下潜深度等由记录仪进行记录,在试验结束之后下载到电脑进行分析。
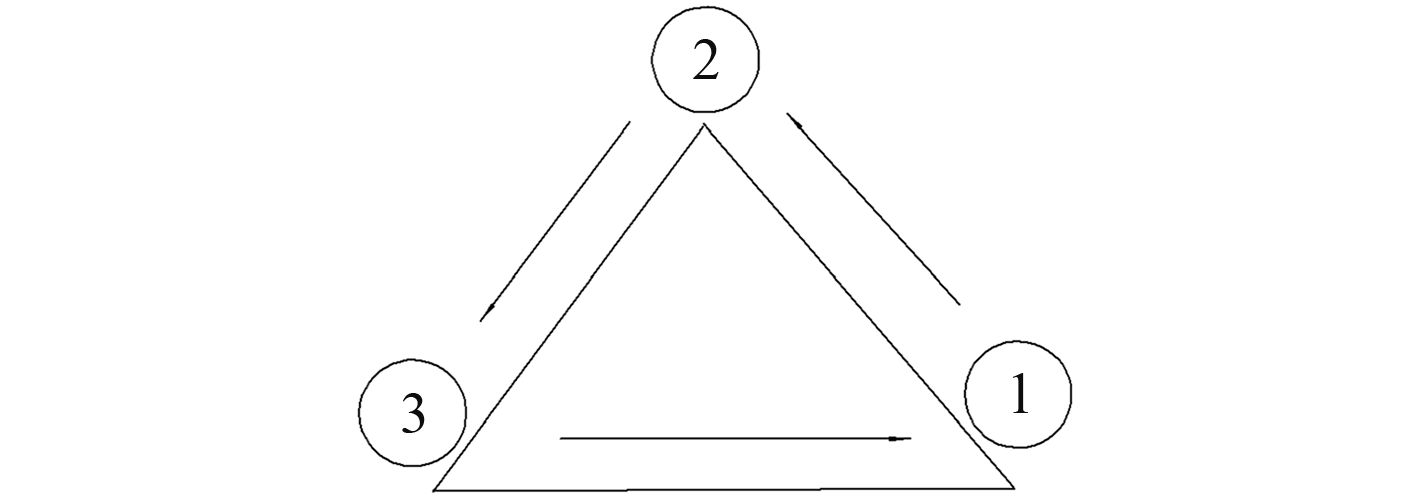
|
图 12 试验路线 Fig. 12 Test route |
如图 13所示,其中0~60 s,对应1号点到2号点的运动过程,为滑翔机下潜过程,由图可以看出,从响应开始到稳定整个俯仰角度的调节过程只需要3 s左右,超调量在5%左右。同样60~120 s和120~180 s分别对应2号点到3号点再到1号点的定深运动和上浮过程。从而可以得出调节时间较短,超调量较小,与仿真结果相符。
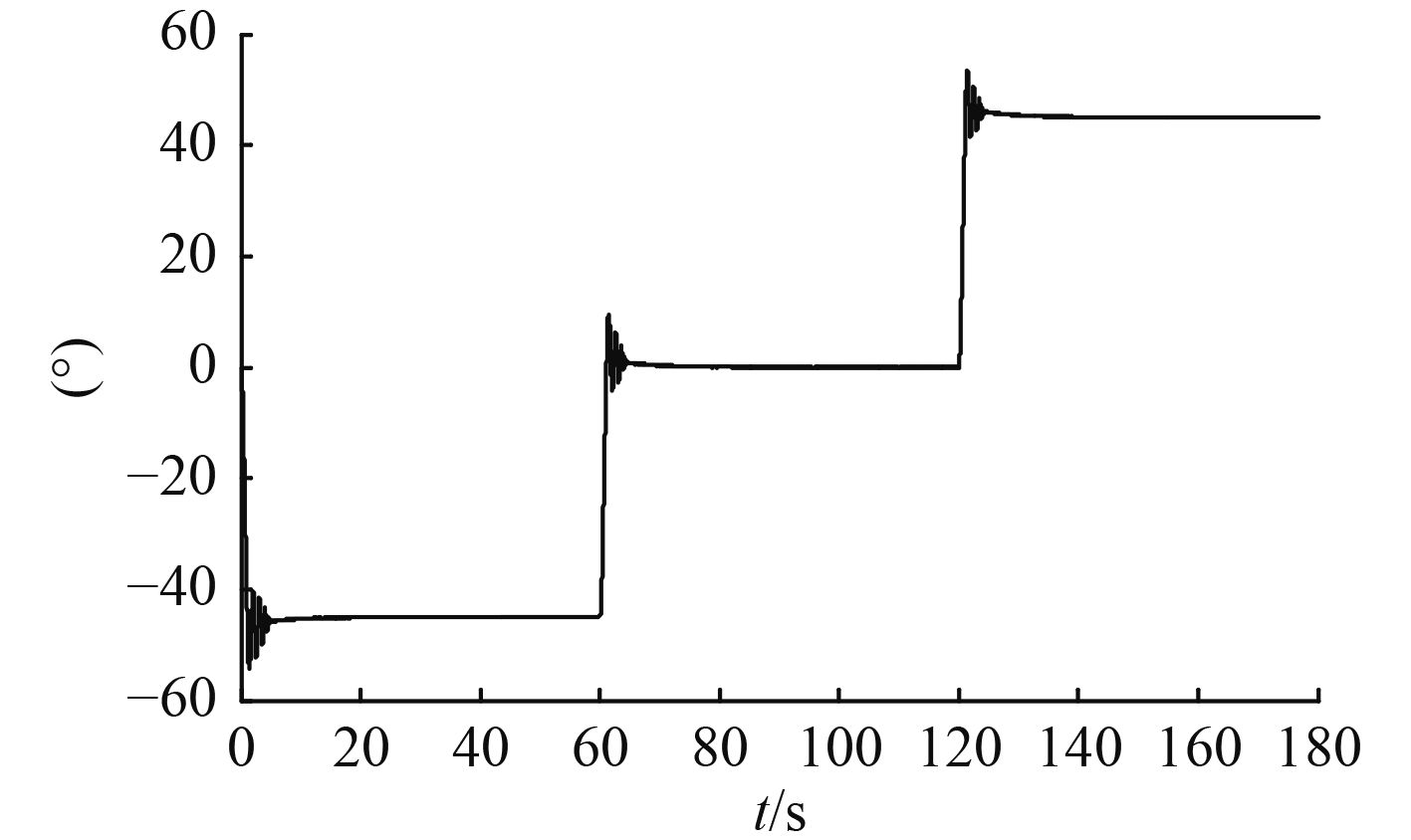
|
图 13 试验过程中θ变化 Fig. 13 θ change during the test |

|
图 14 试验现场 Fig. 14 Test site |
本设计摒弃了大部分滑翔机带舵的设计思路,整体类似于一个圆柱体,本身阻力很小,主要通过调节4个对称螺旋桨的转速来实现调姿。本文建立了滑翔机的动力学模型并且得到了其小扰动模型,在此基础上设计了合理的控制器,之后在Matlab/simulink上进行仿真,并将其结果与湖试结果对比,验证了PID控制器的可靠性。
| [1] | WANG S X, SUN X J, WU J G, et al. Motion characteristic analysis of a hybrid-driven underwater glider[C]// OCEANS 2010 IEEE-Sydney. IEEE, 2010: 1–9. |
| [2] | 王树新, 刘方, 邵帅, 等. 混合驱动水下滑翔机动力学建模与海试研究[J]. 机械工程学报, 2014, 50 (2): 16–17. |
| [3] | 杨庆华, 宋召青. 四旋翼飞行器的建模控制与仿真[J]. 海军工程学院学报, 2009, 24 (5): 485–502. |
| [4] | 王晓鸣. 混合驱动水下自航行器动力学行为与控制策略研究[D]. 天津: 天津大学. 2009: 20–25. |
| [5] | ROBERTS G N, SUTTON R. Further advances in unmanned marine vehicles[M]. Piscataway: IET, 2006: 33–35. |
| [6] | JOSHUA G G. Underwater gliders: dynamics, control and design[D]. New Jersey: Princeton University, 2005: 15–17. |
| [7] | SALIH. L, MODELLING and PID controller design for a quadrotor unmanned air vehicle[J]. IEEE AQTR, 2010, 39 (5): 697–699. |
| [8] | 陈宇航. 水下滑翔机建模与控制研究[R]. 西安: 西北工业大学, 2009. |
| [9] | 蒋新松, 封锡盛, 王棣棠. 水下机器人[M].沈阳: 辽宁科学技术出版社, 2000: 304–311. |
| [10] | 郭威, 崔胜国, 赵洋, 等. 一种遥控潜水器控制系统的研究与应用[J]. 机器人, 2008, 30 (5): 5–6. |
 2017, Vol. 39
2017, Vol. 39
