为降低劳动强度并减少人为事故,各国海军都将水下航行器操纵的自动控制与仿真研究放在重要位置。目前已经形成了较为通用的控制算法,PID控制是部分水下航行器自动舵采用的控制算法。经典的PID算法依赖于水下航行器运动数学模型,其控制效果受模型影响较大。一些大型的水下航行器由于惯性较大,同时耦合性、非线性及时变性较强,并且易受干扰,其运动过程难以用数学模型准确描述,一般的控制算法难以适应这种复杂的控制对象。
模糊控制是智能控制中发展较为成熟的一种方法。水下航行器的运动控制就是一个具有复杂特性的控制对象,一般常规控制方法的效果并不理想。作为智能控制的一种,模糊控制具有很多传统控制方法所没有的优点,它可以充分运用专家经验,对数学模型的精确性要求不是很高,具有较好的鲁棒性,在某些领域具有一定的优势。对于水下航行器来说,相较水面船舶而言增加了首部潜浮舵和尾部潜浮舵,以控制深度及纵倾。因此,深度和纵倾是其重要的控制参数。本文以模糊控制理论为基础,研究适用于水下航行器运动的模糊PID控制算法,并以深度和纵倾控制为例进行控制器设计及仿真研究。
1 模糊PID控制器将模糊控制与PID控制相结合,产生模糊参数自整定PID控制器,以模糊控制器在线调整PID控制器的参数,使其更加适应于时变性、非线性的复杂控制对象。
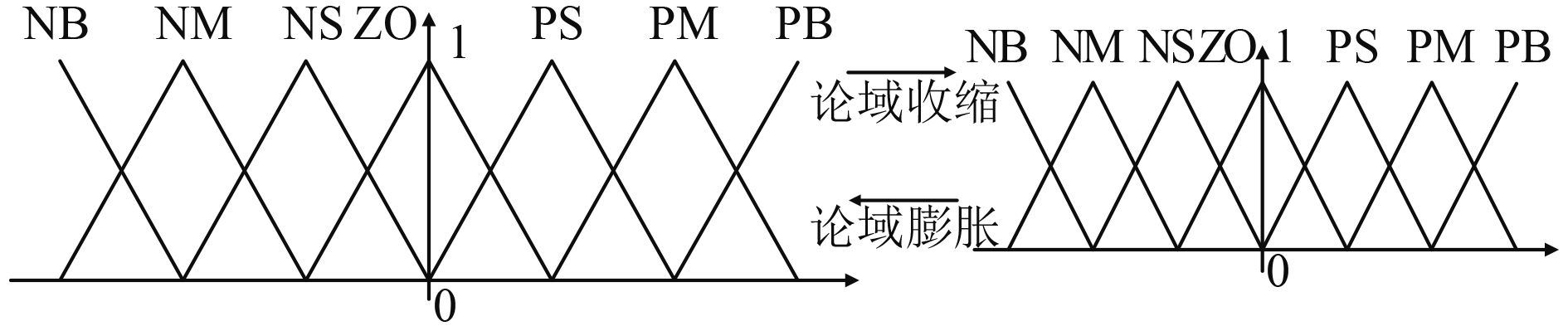
对于一般的模糊控制器,其论域一旦确定之后,就不再改变。在很多控制系统中,误差的变化范围很大,在初始阶段,误差的绝对值一般会较大,在接近于稳定时,误差的绝对值较小。这就给模糊控制器的设计带来了困难,为了充分包含误差的变化范围,将论域定的较大,而为了防止推理规则过于复杂,模糊集不能取得过密。这样一来,当误差的绝对值较小时,会使模糊控制器的灵敏度降低,并且会出现较大的控制盲区。变论域模糊控制将论域随着误差变化而伸缩,但是推理规则形式保持不变。误差减小时,论域收缩使模糊集加密,提高精度;误差增大时,论域膨胀使模糊集稀疏,提高运算速度。论域的膨胀与收缩如图1所示。
|
图 1 论域的收缩与膨胀 Fig. 1 Shrinking and expanding of the universe |
对于初始7个模糊集的模糊控制器,通过增加模糊集的方法和收缩论域的方法对其进行改进,2种方法的对比如表1所示。可以看出,增加模糊集的方法会使推理规则数急剧增加,灵敏度的变化幅度却较少;而收缩论域的方法却能保持推理规则数不变,灵敏度的变化可以根据实际情况设定。
|
|
表 1 改进方法的对比 Tab.1 Contrast of improved method |
一般情况下,论域
| $U\left( u \right) = \left[ { - \alpha \left( u \right)E,\alpha \left( u \right)E} \right]\text{。}$ | (1) |
伸缩因子应满足下列条件
1)
2)
3)α(u)在[0,E]上单调增;
4)
目前,较为常用的伸缩因子如式(2)所示
| $\alpha \left( u \right) = {\left| {\frac{u}{E}} \right|^\tau } + \delta ,\tau \in \left( {0,1} \right)\text{。}$ | (2) |
按照这种变论域的方法,在运算过程中的每一步都要重新确定论域,划分模糊集,而推理规则却只使用一条,下一步又要重新计算,造成了计算的复杂和不必要的浪费。本文参考变论域思想,结合具体被控对象的特点,提出分级变论域方法,即根据误差变化的范围由大到小设计3~4个论域。这样在误差变化过程中,逐渐进入较小论域,模糊集逐渐加密,控制精度逐渐提高,最终误差稳定在较小论域内,并能充分发挥其各条推理规则,既可以简化控制算法,又能得到较好的效果。论域变化规则见表2所示。
|
|
表 2 论域变化规则 Tab.2 Rule of shrinking and expanding of the universe |
水下航行器与水面船舶最大的区别在于其主要在水下活动,可以实施垂直面上的机动,与之相应的,水下航行器的首部潜浮舵和尾部潜浮舵(一般简称为首舵与尾舵),以实现对深度及纵倾的控制。一般情况下,水下航行器改变深度的手段主要有:压载水舱注排水、操首舵及尾舵。当航行器处于水面状态时,其下潜过程大致为:首先,向首组、尾组压载水舱注水,使水下航行器潜至半潜状态,然后向中组压载水舱注水,使其潜至潜望状态,然后操潜浮舵,使其潜至指令深度。水下航行器正常上浮过程与之相反,先通过操舵上浮至潜望深度,再吹除压载水,使其浮至水面。在应急情况下,可在某深度直接吹除压载水,使其产生较大正浮力,迅速上浮至水面。
在水下航行器潜浮机动中,在一定航速下辅之以一定的纵倾角,可以迅速潜浮至指令深度。为了保证航行器上设备或人员的正常工作,其潜浮过程中有一定的纵倾限制,在接近指令深度时,使纵倾逐渐减小至0。纵倾控制主要通过平衡调节水舱和尾舵。平衡调节水舱主要用于调节水下航行器静平衡,当水下航行器具有一定航速后,主要以尾舵控制纵倾。
2.2 水下航行器垂直面运动模型| $\left\{ \begin{aligned}m\left( {\dot w - uq} \right) = &\displaystyle\frac{1}{2}\rho {L^4}\left( {{{Z'}_{\dot q}}\dot q + {{Z'}_{\left. q \right|\left. q \right|}}\left. q \right|\left. q \right|} \right) +\displaystyle\frac{1}{2}\rho {L^3}\left( {{{Z'}_{\dot w}}\dot w }+\right. \\&\left.{{{Z'}_q}uq + {{Z'}_{\left. w \right|\left. q \right|}}\left. w \right|\left. q \right| + {{Z'}_{\left| q \right|{\delta _s}}}u\left| q \right|{\delta _s}} \right) + \displaystyle\frac{1}{2}\rho {L^2} \times \\& \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\left( {{{Z'}_{uu}}{u^2} + {{Z'}_w}uw +{{Z'}_{\left| w \right|}}u\left| w \right| + {{Z'}_{\left. w \right|\left. w \right|}}\left. w \right|\left. w \right| + {{Z'}_{ww}}{w^2}} \right)+\\ & \displaystyle\frac{1}{2}\rho {L^2}\left( {{{Z'}_{{\delta _s}}}{u^2}{\delta _s} + {{Z'}_{{\delta _b}}}{u^2}{\delta _b}} \right) + P\text{,}\\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{I_y}\dot q = \displaystyle\frac{1}{2}\rho {L^5}\left( {{{M'}_{\dot q}}\dot q + {{M'}_{\left. q \right|\left. q \right|}}\left. q \right|\left. q \right|} \right) + \displaystyle\frac{1}{2}\rho {L^4}\left( {{{M'}_{\dot w}}\dot w + {{M'}_q}uq +}\right.\\&\!\!\!\!\!\!\!\!\!\!\!\!\left.{{{M'}_{\left. w \right|\left. q \right|}}\left. w \right|\left. q \right| + {{M'}_{\left| q \right|{\delta _s}}}u\left| q \right|{\delta _s}} \right) +\displaystyle\frac{1}{2}\rho {L^3}\left( {{{M'}_{uu}}{u^2} +}\right.\\&\!\!\!\!\!\!\!\!\!\!\!\!\left.{{{M'}_w}uw + {{M'}_{\left| w \right|}}u\left| w \right| + {{M'}_{\left. w \right|\left. w \right|}}\left. w \right|\left. w \right|} \right.\left. { + {{M'}_{ww}}{w^2}} \right) +\\ &\!\!\!\!\!\!\!\!\!\!\!\!\displaystyle\frac{1}{2}\rho {L^3}\left( {{{M'}_{{\delta _{\rm{s}}}}}{u^2}{\delta _{\rm{s}}} +{{M'}_{{\delta _{\rm{b}}}}}{u^2}{\delta _{\rm{b}}}} \right) - mgh\sin \theta + Mp\text{,}\\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\dot \theta = q\text{,}\\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\dot \zeta = - u\sin \theta + w\cos \theta\text{。} \end{aligned} \right.$ | (3) |
式(3)中共有4个方程,第三、四方程形式较为简单,难点是对第一、二方程的求解。将其写为简捷形式
| $ {A}\left( {\begin{array}{*{20}{l}}{\dot w}\\{\dot q}\end{array}} \right) = \left( {\begin{array}{*{20}{l}}{{f_1}\left( {w,q,{\delta _s},{\delta _b}} \right)}\\{{f_2}\left( {w,q,{\delta _s},{\delta _b}} \right)}\end{array}} \right)\text{,}$ | (4) |
式中:
| $\begin{split}{f_1}&\left( {w,q,{\delta _s},{\delta _b}} \right) \!\!=\!\! \displaystyle\frac{1}{2}\rho {L^4}{{Z'}_{\left. q \right|\left. q \right|}}\left. q \right|\left. q \right|\! +\!\left( {\displaystyle\frac{1}{2}\rho {L^3}{{Z'}_q} \!+\! m} \right)uq +\!\!\!\\&\displaystyle\frac{1}{2}\rho {L^3}{{Z'}_{\left. w \right|\left. q \right|}}\left. w \right|\left. q \right|+\displaystyle\frac{1}{2}\rho {L^2}\left( {{{Z'}_{uu}}{u^2} }+\right.\\&\left.{{{Z'}_w}uw + {{Z'}_{\left| w \right|}}u\left| w \right| + {{Z'}_{\left. w \right|\left. w \right|}}\left. w \right|\left. w \right| + {{Z'}_{ww}}{w^2}} \right) + P\text{,}\end{split}$ |
| $\begin{split}{f_2}& \left( {w,q,{\delta _s},{\delta _b}} \right) =\displaystyle\frac{1}{2}\rho {L^5}\left( {{{M'}_{\left. q \right|\left. q \right|}}\left. q \right|\left. q \right|} \right) + \displaystyle\frac{1}{2}\rho {L^4}\left( {{{M'}_q}uq +}\right.\\&\left.{{{M'}_{\left. w \right|\left. q \right|}}\left. w \right|\left. q \right|} \right) + Mp+\displaystyle\frac{1}{2}\rho {L^3}\left( {{{M'}_{uu}}{u^2} + {{M'}_w}uw +}\right.\\ &\left.{{{M'}_{\left| w \right|}}u\left| w \right| + {{M'}_{\left. w \right|\left. w \right|}}\left. w \right|\left. w \right| + {{M'}_{ww}}{w^2}} \right) - mgh\sin \theta \text{。}\end{split}$ |
运用克莱姆法则,可求解出
| ${T_E}\dot \delta = {K_E}\left( {{\delta _e} - \delta } \right)\text{。}$ | (5) |
式(5)为首舵或尾舵的响应模型。其舵角及转舵速度的限制条件为:首舵
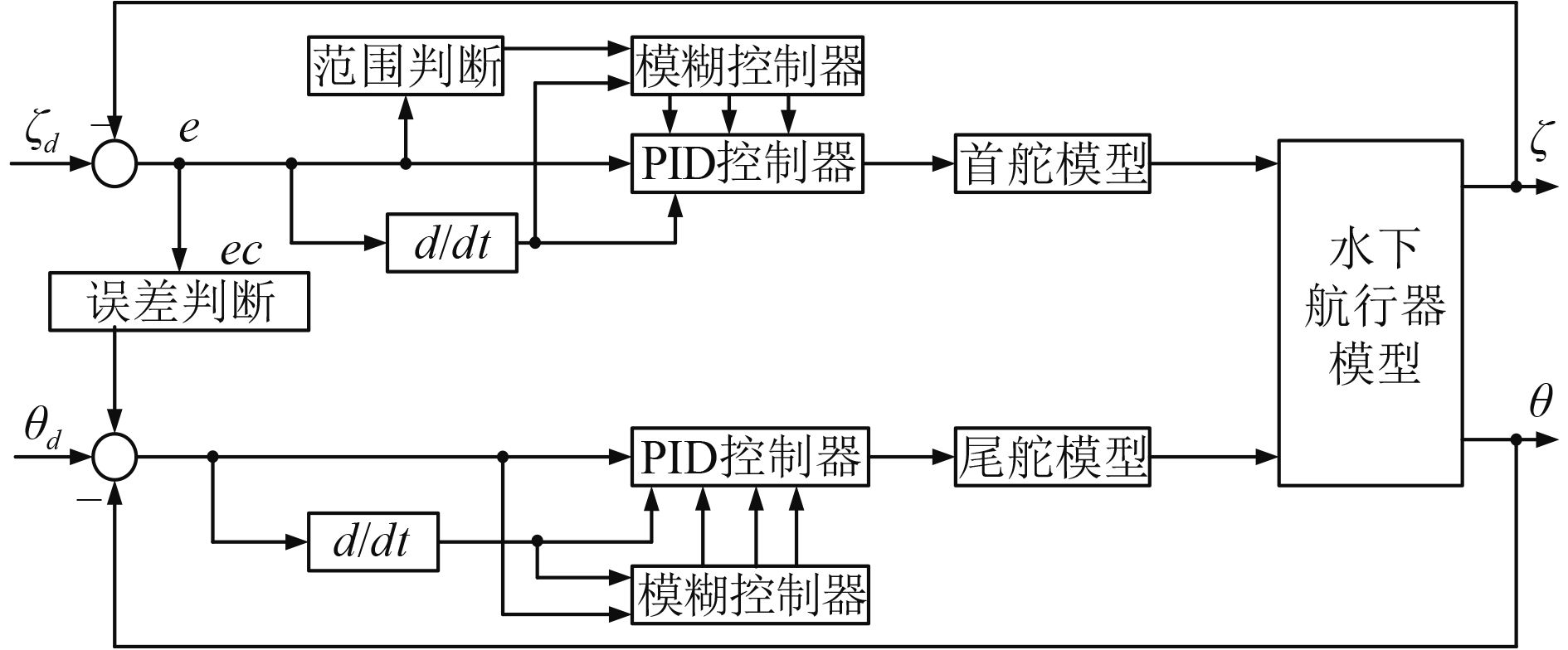
本文主要研究水下航行器在潜望深度与工作深度之间,通过操舵进行深度控制,因此,其深度误差eζ范围为[–240, 240] m。水下航行器水下深度机动,要操尾舵产生纵倾,在一定航速下潜浮,为防止出现过大超调,当实际深度与目标深度差20 m左右时,逐渐减小纵倾角至0°。在产生纵倾时为保证设备或人员的正常工作,一般纵倾角限制为|θ|≤10°。这样在深度误差eζ、深度误差变化率ecζ、纵倾误差eθ及纵倾误差变化率ecθ中,只有eζ的变化范围较大,需要进行分级变论域设计。设计论域为Uζ1=[–240, 240] m,Uζ2=[–180, 180] m,Uζ3=[–120, 120] m,Uζ4=[–60, 60] m,Uζ5=[–30, 30] m,即伸缩因子为α1=0.75,α2=0.5,α3=0.25,α4=0.125。深度论域等级的划分,是考虑水下航行器垂直面机动时经常使用的深度值来设计的。航行器水下机动,一般从压载水舱注满水以后开始,此时其深度约为10 m,而其经常活动的最大深度为250 m,对于250~300 m的极限深度只能在人为控制下有限次的达到。因此自动控制器设计中将深度误差最大范围定为Uζ1=[–240, 240] m;Uζ2,Uζ3及Uζ4根据不同深度机动范围设计,控制器根据深度误差选择论域范围进行运算;控制过程中,深度误差将逐渐变小,最终进入Uζ5=[–30, 30] m的论域内,较小的论域范围可以减小其稳态误差,提高其灵敏度。同样采用逆向方法将eζ在进入控制器前先除以伸缩因子。控制器的原理结构如图2所示。
|
图 2 深度纵倾控制器原理结构 Fig. 2 Configuration of depth and pith fuzzy PID controller |
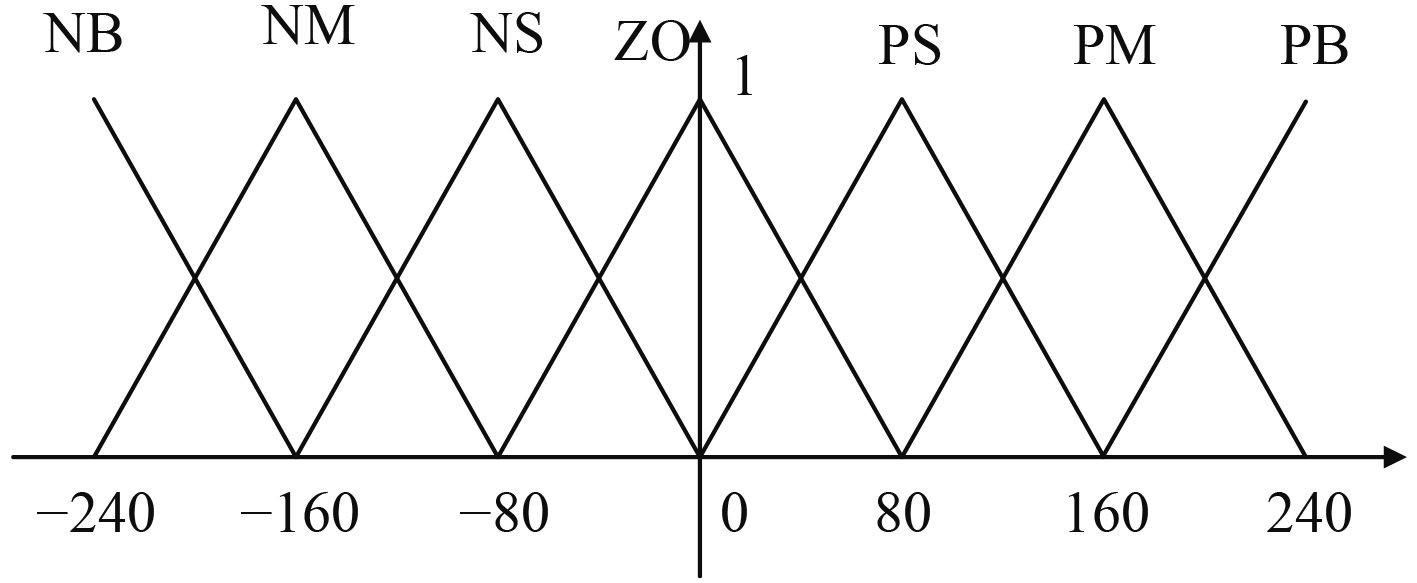
划分深度误差eζ的模糊集如图3所示,其他变量深度误差变化率ecζ、纵倾误差eθ及纵倾误差变化率ecθ模糊集的划分与之类似。PID三个参数比例系数kp、积分时间常数ki和微分时间常数kd的调整规则见表3~表5。
|
|
表 3 kp调整规则 Tab.3 Adjust rules of kp |
|
图 3 深度误差模糊集 Fig. 3 Fuzzy set of depth error |
|
|
表 4 ki调整规则 Tab.4 Adjust rules of ki |
|
|
表 5 kd调整规则 Tab.5 Adjust rules of kd |
在计算机上进行仿真试验,验证分级变论域模糊PID控制器的深度纵倾控制效果,同时与经典PID控制的效果进行对比。针对某型水下航行器初始条件设定为:初始航速u=6 kn;初始深度ζ0=10 m;初始纵倾θ=0°。
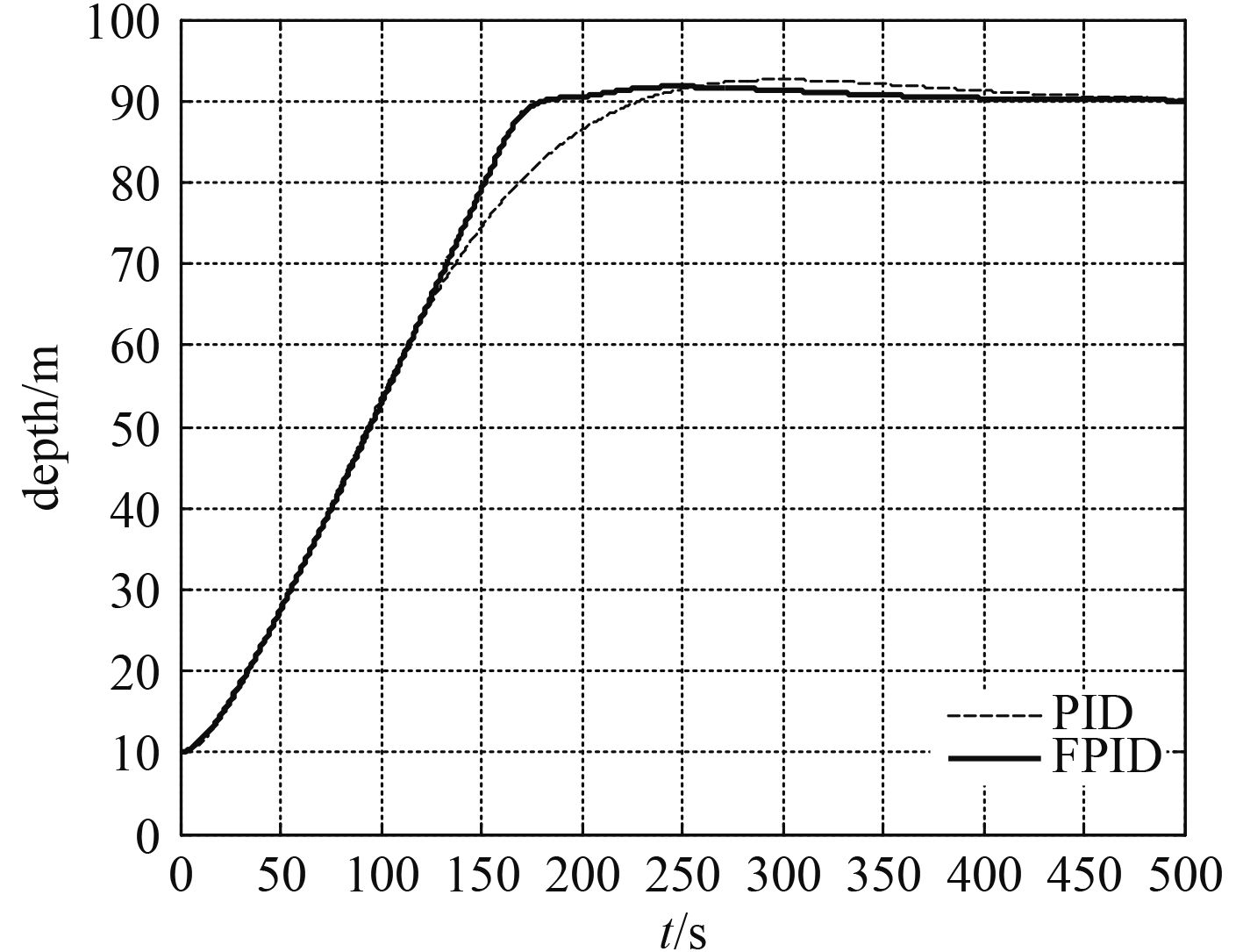
试验1中,目标深度为90 m,纵倾限制为–10°,结果如图4和图5所示。
|
图 4 目标深度90 m控制效果 Fig. 4 Control result of depth aim 90 m |
|
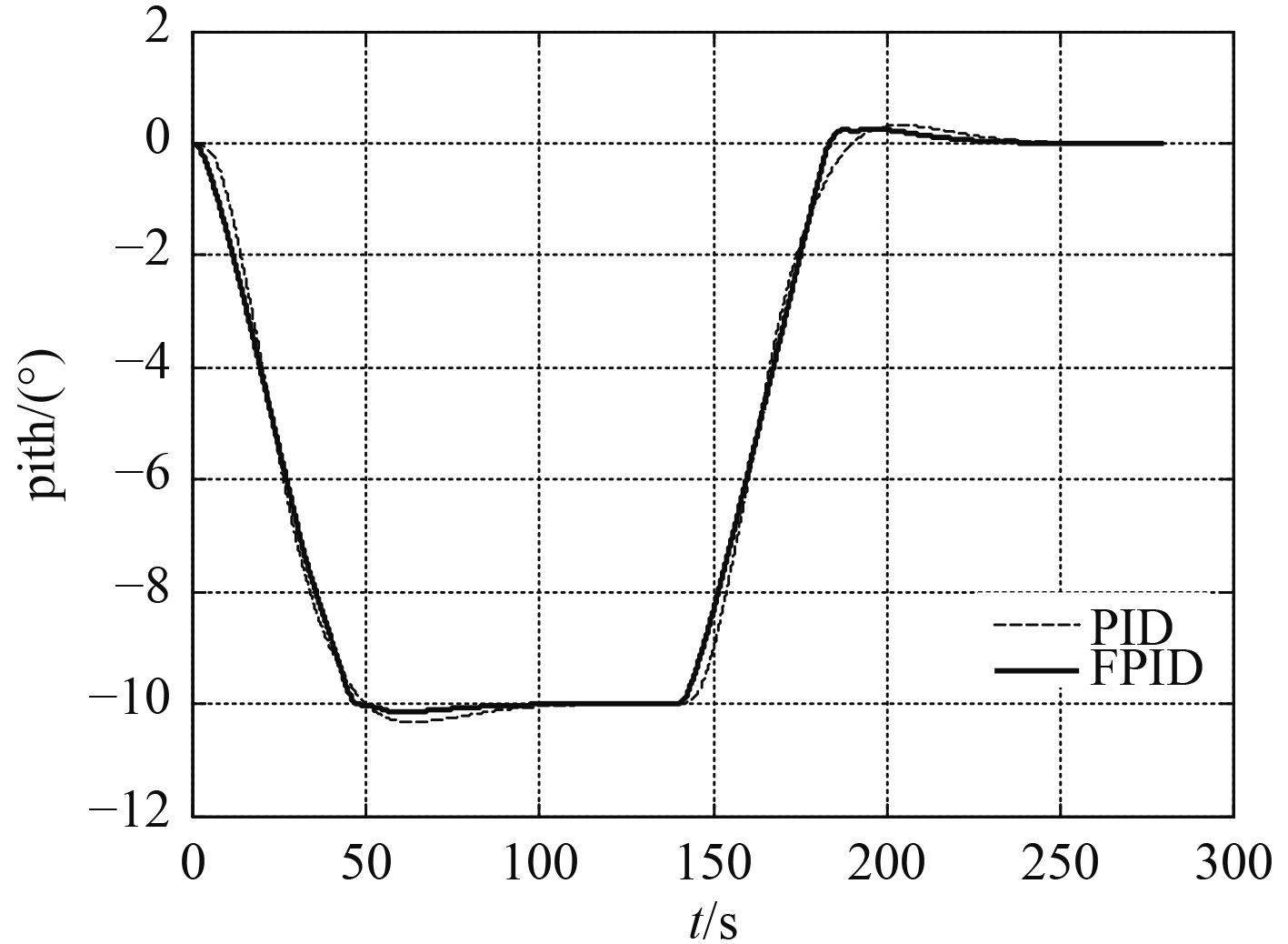
图 5 纵倾控制效果 Fig. 5 Result of pitch control |
从结果中可以发现在深度及纵倾控制中,与经典PID控制相比,模糊PID控制具有上升速度快,超调量小,过渡时间短等优点。
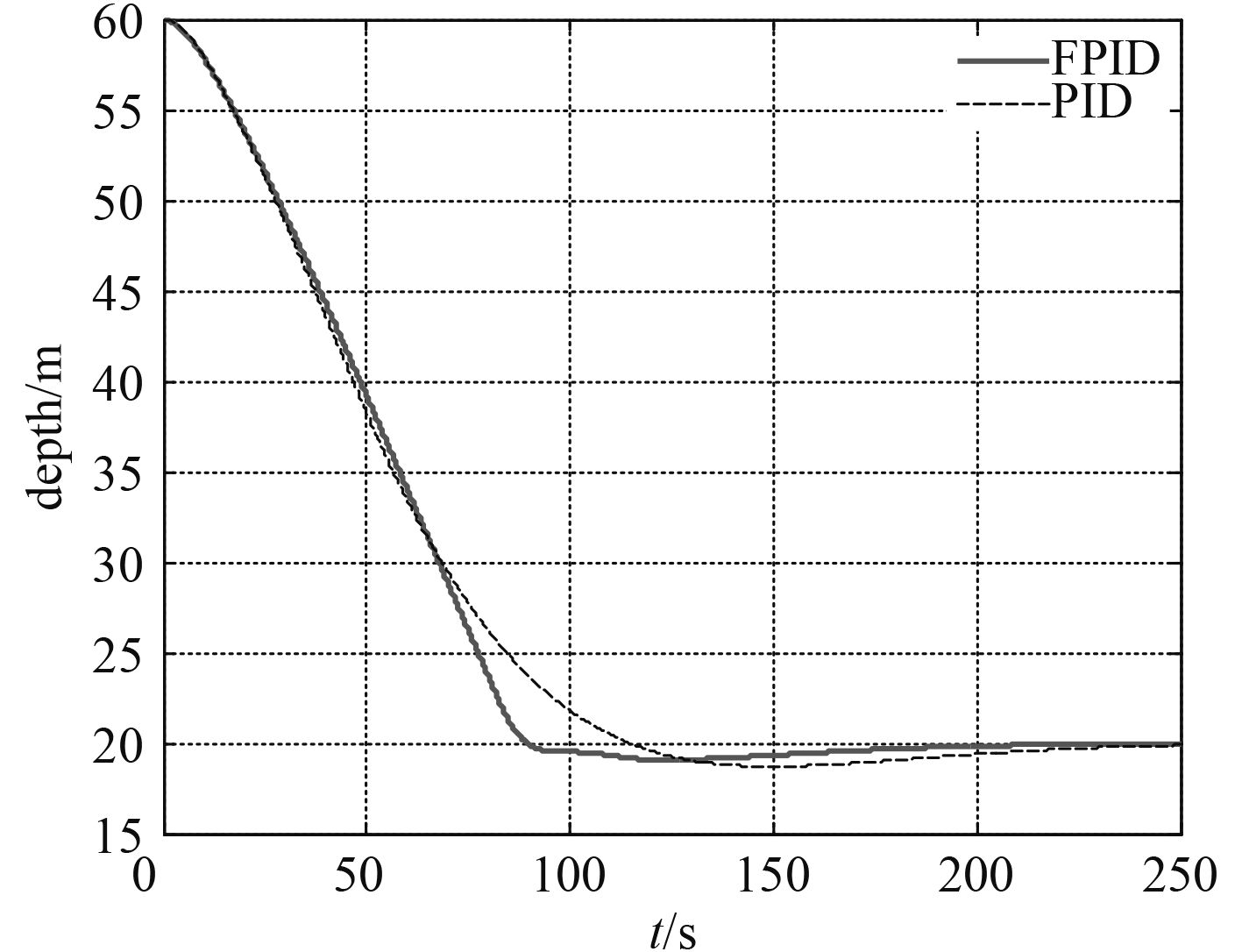
试验2改变设定条件以考察模糊PID控制的鲁棒性,其中初始深度ζ0=60 m;目标深度为20 m,控制器参数与试验1保持一致,结果如图6所示。可以发现模糊PID控制保持了试验1中的各项优点。
|
图 6 目标深度20 m控制效果 Fig. 6 Control result of depth aim 20 m |
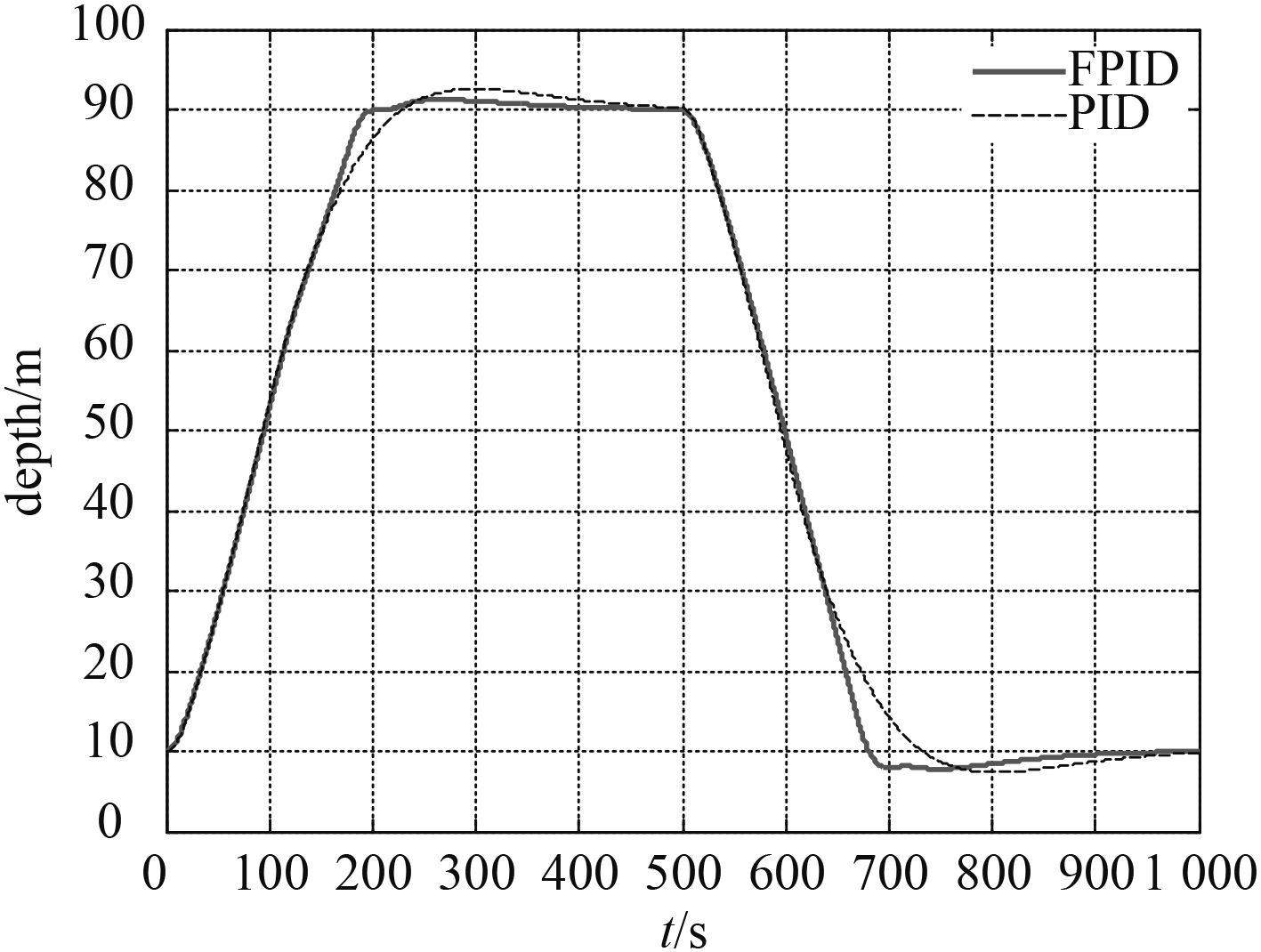
试验3考察模糊PID控制跟踪时变信号的能力,初始条件设置同于试验1,目标深度以90 m与10 m交替给出,结果如图7所示。可以发现,模糊PID控制能够较好地跟踪时变深度信号。
|
图 7 跟踪深度时变信号控制效果 Fig. 7 Control result of variable depth signal |
在深入研究模糊控制的数学基础上,分析了模糊控制中存在的控制盲区等问题,为消除控制盲区,分析了模糊控制与PID控制结合的方案。研究了现有的变论域模糊控制思想,并针对其运算量大、推理规则利用率低等缺点,提出了分级变论域的方法。对于某型水下航行器水平面及垂直面的一般正常机动,采用分级变论域的方法,分别设计相应的模糊PID控制器,并利用计算机进行仿真试验。结果表明,相较于传统PID控制,在水下航行器深度及纵倾控制中,模糊PID控制器具有速度快、超调小、稳定时间短以及鲁棒性好等特点,对于复杂非线性对象的控制器设计有着较好的借鉴意义。
| [1] | 熊瑛. 基于智能控制的水下航行器操纵运动仿真研究[D]. 武汉: 中国舰船研究院, 2011. |
| [2] | 李平. 非线性系统自适应模糊控制方法研究[D]. 沈阳: 东北大学, 2010. |
| [3] | 龙祖强. 变论域模糊控制器的若干重要问题研究[D]. 长沙: 中南大学, 2011. |
| [4] | 石辛民, 郝整清. 模糊控制及其MATLAB仿真[M]. 北京: 清华大学出版社, 北京交通大学出版社, 2008: 10–51. |
| [5] | 王先洲. 船舶及水下航行器操纵中的鲁棒控制研究[D]. 武汉: 华中科技大学, 2008. |
| [6] | Shun Hung Tsai, Tzuu Hseng S Li. Robust Fuzzy Control of a Class of Fuzzy Bilinear Systems with Time-delay[J]. Chaos Solitons and Fractals, 2009, 39 : 2028–2040. DOI: 10.1016/j.chaos.2007.06.057 |
| [7] | CHEN C S. Dynamic Structure Adaptive Neural Fuzzy Control for MIMO Uncertain Nonlinear Systems[J]. Information Sciences, 2009, 179 : 2676–2688. DOI: 10.1016/j.ins.2009.03.015 |
| [8] | 施生达. 水下航行器操纵性[M]. 北京: 国防工业出版社, 1995: 45–50. |
| [9] |
任洪亮, 边信黔. 基于模糊规则的多模型控制方法在AUV航向控制中的应用[J]. 自动化技术与应用, 2004, 23 (6): 1–4.
REN Hong-liang, BIAN Xin-qian. Fuzzy rule-based mulit-model control strategy and its application in AUV YAM control[J]. Techniques of Automation and Applications, 2004, 23 (6): 1–4. |
| [10] |
程启明. Fuzzy控制和PID控制集成的船舶操纵控制器研究[J]. 上海电力学院学报, 2001, 17 (4): 7–12.
CHENG Qi-ming. Integrated controllors of Fuzzy control and PID control for ship manoeuvring[J]. Journal of Shanghai University of Electric Power, 2001, 17 (4): 7–12. |
 2017, Vol. 39
2017, Vol. 39
