2. 上海交通大学 自动化系,上海 200240;
3. 上海交通大学 信息控制与信息处理教育部重点实验室,上海 200240
2. Department of Automation, Shanghai Jiaotong University, Shanghai 200240, China;
3. Key Lab of System Control and Information Processing, Shanghai Jiaotong University, Shanghai 200240, China
当今世界,人们把目光越来越多地投向蕴含丰富资源的海洋。大量的海洋探测工具被研发,尤其是水下自主航行器作为一种帮助人类探索、开发海洋的高度自主机器人受到了许多国家的重视[1 – 3]。
在国内,越来越多的高校与单位参与到了AUV的理论设计和实际研发当中,但是离产品化、模块化还有一定差距。本文以实验室与上海交通大学共同研制的ZY-1型自主水下航行器为研究对象,从推进装置设计和运动控制方法2个层面来介绍整个运动平台系统。之后通过实际的水下试验测评了航行器的运动控制性能。通过对试验结果数据进行分析,此AUV运行稳定,获得的性能参数满足此航行器的设计指标。
1 新型自主水下航行器上海交通大学与太原科技大学根据我国深海环境探测和水下侦察的需求,共同研发了新型AUV产品样机,如图1所示。此新型水下航行器主要面向高机动性与高度自主的应用需求,整体使用模块化设计,可灵活加减负载。同时为下一步的产品化打下坚实的基础。

|
图 1 新型自主水下机器人 Fig. 1 New type AUV |
当前,国内外的自主水下航行器主要是欠驱动类鱼雷形航行器,此类AUV适合水下机动,但因为其欠驱动的设计使得转弯半径较大[4],此外流线型航行器通常采用舵加桨驱动,使得其控制系统呈现非线性和强耦合的特性。因此,实验室自主研发出一种多推进器的新型自主水下航行器,AUV尾部4个螺旋桨以X形布置。无舵桨,减小运行阻力、转弯半径,通过对4个螺旋桨的分别控制,配合以后部导流罩的设计,实现水下航行器在水平面与垂直面上的灵活运动。
该新型AUV为类鱼雷流线外形,主要技术指标如下:重量:320 kg;长度:3.3 m;直径:323 mm;航速:3~5 kn;最大下潜深度:500 m;最大续航时间:24 h。
此新型AUV分为水下载体平台与水面命令软件系统2部分。水下载体平台用来实际完成探测采集任务,主要由控制系统、传感系统、导航系统构成。航行器后部推进器的布置方式为呈X形布置的四螺旋桨推进器,各自可依靠直流电机单独驱动,通过不同转速组合造成的推力差来实现运动平台的转首与俯仰控制,推进器反转可实现紧急制动。AUV安装有前视避障声呐,侧扫声呐与水速仪,可对水下地形进行精确观测,并采用锂电池组作为能源系统。水面命令软件系统由嵌入式控制器和信息处理软件组成,负责控制程序与任务程序的编写和下载,以及对水下数据的分析,是与AUV进行交互的平台。
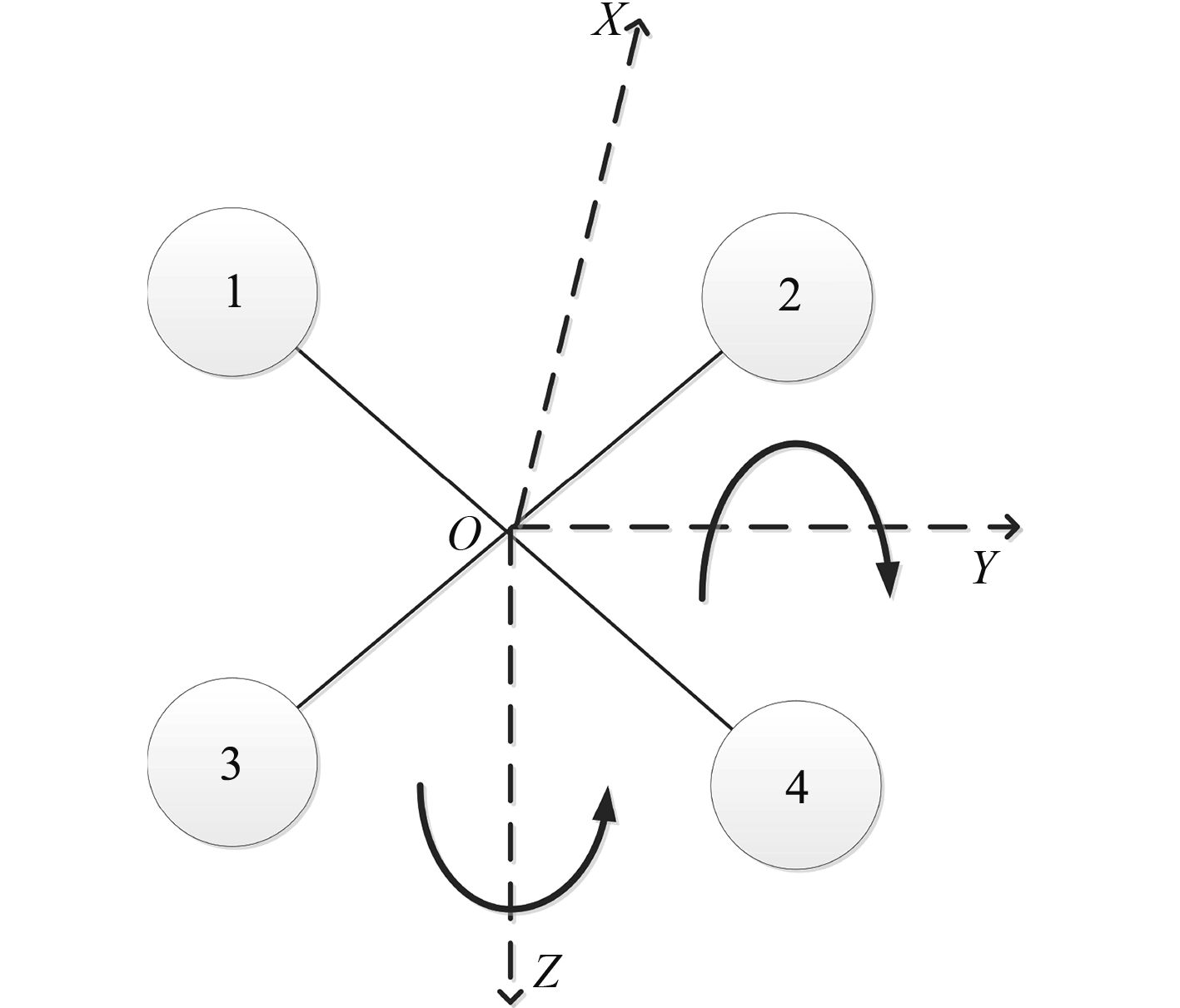
2 新型AUV运动控制 2.1 X形推进器推力分析图2所示为AUV在水下的载体坐标系,其在水下的运动方式为绕y轴的俯仰运动与绕z轴的转首运动。目前国内大多数AUV采用单推进器组合舵桨的方式进行运动控制,而此新型AUV的控制是由航行器后部4个呈X形分布的螺旋桨完成。为了研究其推进方式,首先需要对X形推进器的推力关系进行分析。
|
图 2 新型AUV尾部推进器示意图 Fig. 2 The tail propeller of new type AUV |
X型推进器控制方式有2种:一种是每个推进器单独控制;另一种是水平侧或者垂直侧的2个推进器联动。
首先定义如下规则:
1)4个螺旋桨有效面积相同且电机参数一致。编号1~4分别为左上、左下、右上、右下的螺旋桨。
2)图3中所示的螺旋桨1和4按逆时针转动,螺旋桨2和3按顺时针转动,各推进器的转动惯量大小相等,这就可以抵消机体的自旋,避免航体在水下造成横滚。δ1~δ4表示螺旋桨1~4的转速。
3)ψ表示首向角,θ表示俯仰角,φ表示横滚角。
Yx与Zx分别表示推进器部分在Oyz平面沿y轴和z轴受到的合力。当潜航器左转时,Yx>0;右转时,Yx<0;上升时,Zx>0;下降时,Zx<0,合力可由式(1)描述:
| $\left\{ \begin{array}{l}{Y_x} = {K_{yz}} \cdot \displaystyle\sum\limits_{i = 1}^4 {(\Delta _i^Y \cdot {\delta _i})} \text{,}\\{Z_x} = {K_{yz}} \cdot \displaystyle\sum\limits_{i = 1}^4 {(\Delta _i^Z \cdot {\delta _i})} \text{。}\end{array} \right.$ | (1) |
其中:Kyz为螺旋桨转速到静水推力的转换系数;
| $\left\{ \begin{array}{l}{Y_x} = {K_{yz}} \cdot ({\delta _1} + {\delta _2} - {\delta _3} - {\delta _4})\text{,}\\{Z_x} = {K_{yz}} \cdot ({\delta _1} - {\delta _2} + {\delta _3} - {\delta _4})\text{。}\end{array} \right.$ | (2) |
为了简化控制可以使用同侧螺旋桨联动的方式,设
| $\left\{ \begin{array}{l}{Y_x} = {K_{yz}}({\delta _{12}} - {\delta _{34}})\text{,}\\{Z_x} = {K_{yz}}({\delta _{13}} - {\delta _{24}})\text{。}\end{array} \right.$ | (3) |
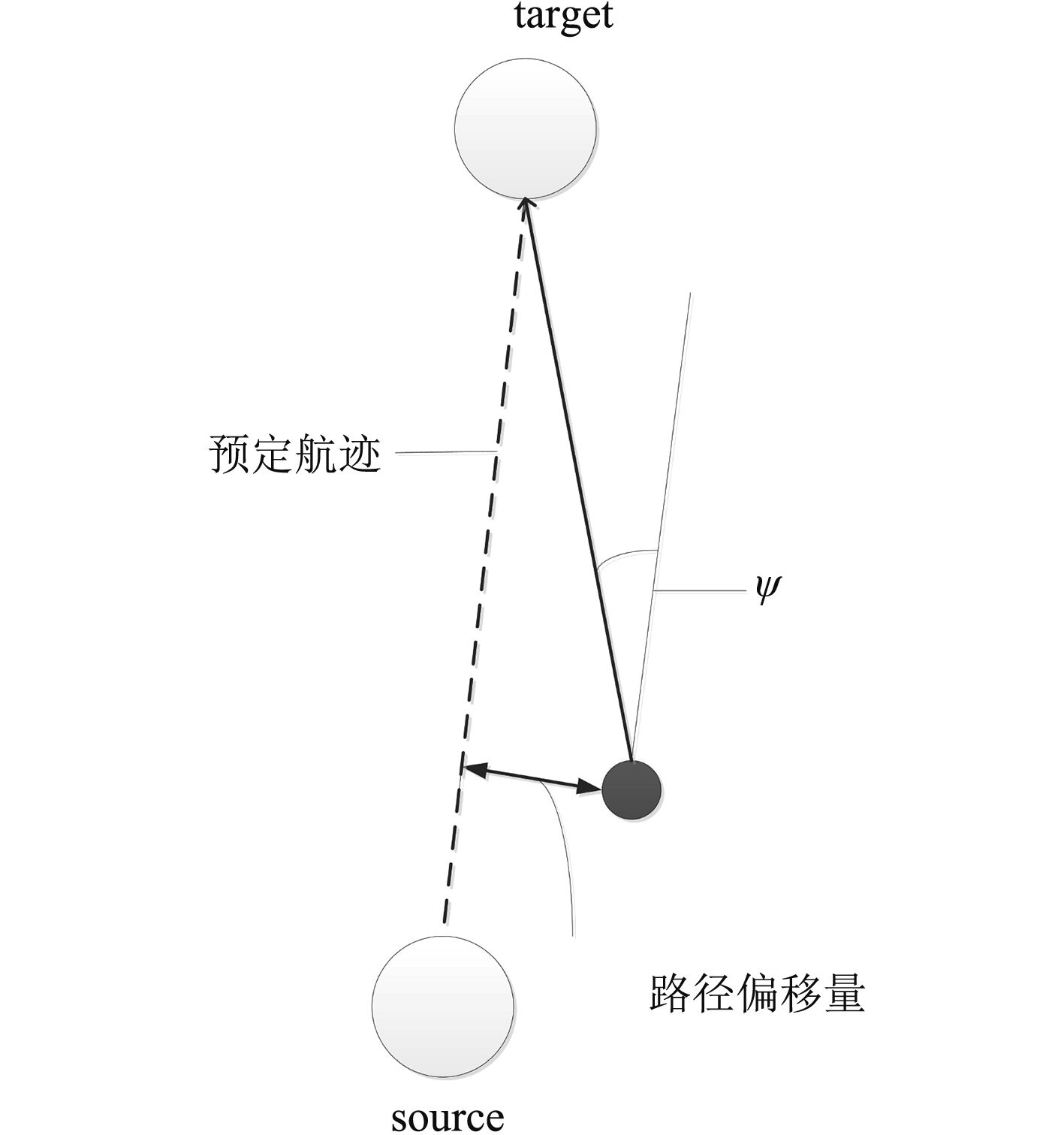
因为AUV在水下无法与陆地基站进行通信,2个坐标点之间的航行完全由AUV自主完成。基于上述原因,这里提出一种航向纠偏算法。AUV在水下的航行方向是通过电子罗盘指向下一目标坐标点[5]。通常在3级海况及以上,AUV会在海流的作用下偏离初始路径,这导致AUV在进行海底大尺度距离航行时,必须通过频繁的上浮水面来接收目标航点才可进行航向纠偏。为了加大其航行效率以及延长水下续航时间,在AUV的水平面航向控制中,将路径偏移量引入到航向控制回路中,通过自身实时调整航向角来减小路径偏移量[6],如图3所示。
|
图 3 AUV航向控制算法示意图 Fig. 3 The schematic diagram of AUV heading control algorithm |
AUV路径偏移量
| $\varepsilon (t) = {L_i} \times \sin \delta (t)\text{,}$ | (4) |
其中Li为AUV中心到下一路径点之间的距离:
| ${L_i} = \sqrt {{{(X_{wpt}^{}(i) - X(t))}^2} + {{({Y_{wpt}}(i) - Y(t))}^2}} \text{。}$ | (5) |
| $\delta (t) \!=\! \arctan \frac{{{Y_{wpt(i)}} - {Y_{wpt(i - 1)}}}}{{{X_{wpt(i)}} - {X_{wpt(i - 1)}}}} - \arctan \frac{{{Y_{wpt(i)}} - Y(t)}}{{{X_{wpt(i)}} - X(t)}}\text{。}$ | (6) |
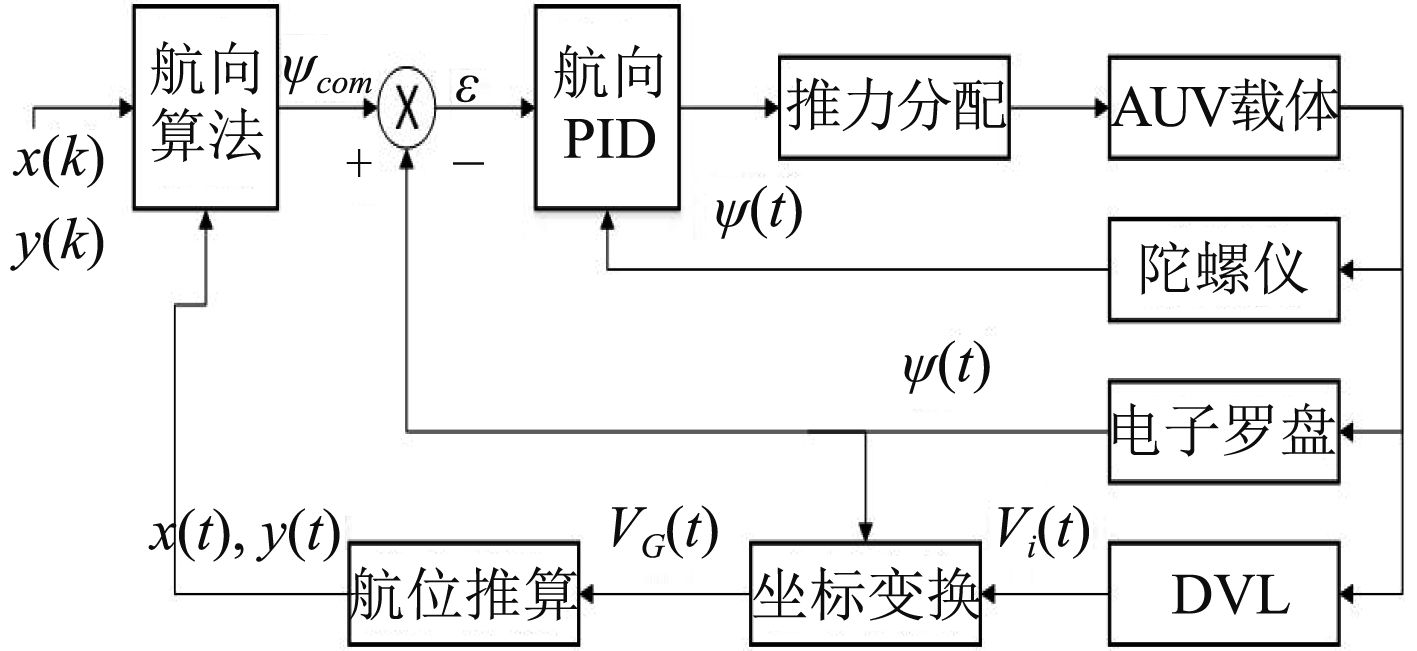
图4为AUV在水平面维度的控制环路,由航向PID内环控制和航迹PID外环控制构成。目标位置的经纬度数据作为系统输入,将陀螺仪的航向角速度数据用于PID微分计算[7],通过实现硬件微分有效提高控制精度。控制中的PID初始参数首先通过Matlab仿真确定,然后在搭建的实验平台上通过实际操作,获得各参数对运动控制的作用,反复整定,来获得最佳控制参数。
|
图 4 AUV航向控制环路图 Fig. 4 Horizontal control loop of the AUV |
其中多普勒计程仪DVL是用于测量AUV在航体坐标系下的三维运动速度向量
| ${V_G}(t) = {}_1^GR(t) \times {V_1}(t)\text{。}$ | (7) |
其中
| ${}_1^GR = \left[ \begin{array}{l}\sin \psi \cos {\theta _{}}\cos {\psi _{}}\sin \psi \sin \theta \\\cos \psi \cos {\theta _{}} - \sin {\psi _{}}\cos \psi \sin \theta \end{array} \right]\text{。}$ | (8) |
对
| $\hat p(t) = \hat p({t_0}) + \int_{t_0^{}}^t {{V_G}(\tau )} {\rm d}\tau \text{。}$ | (9) |
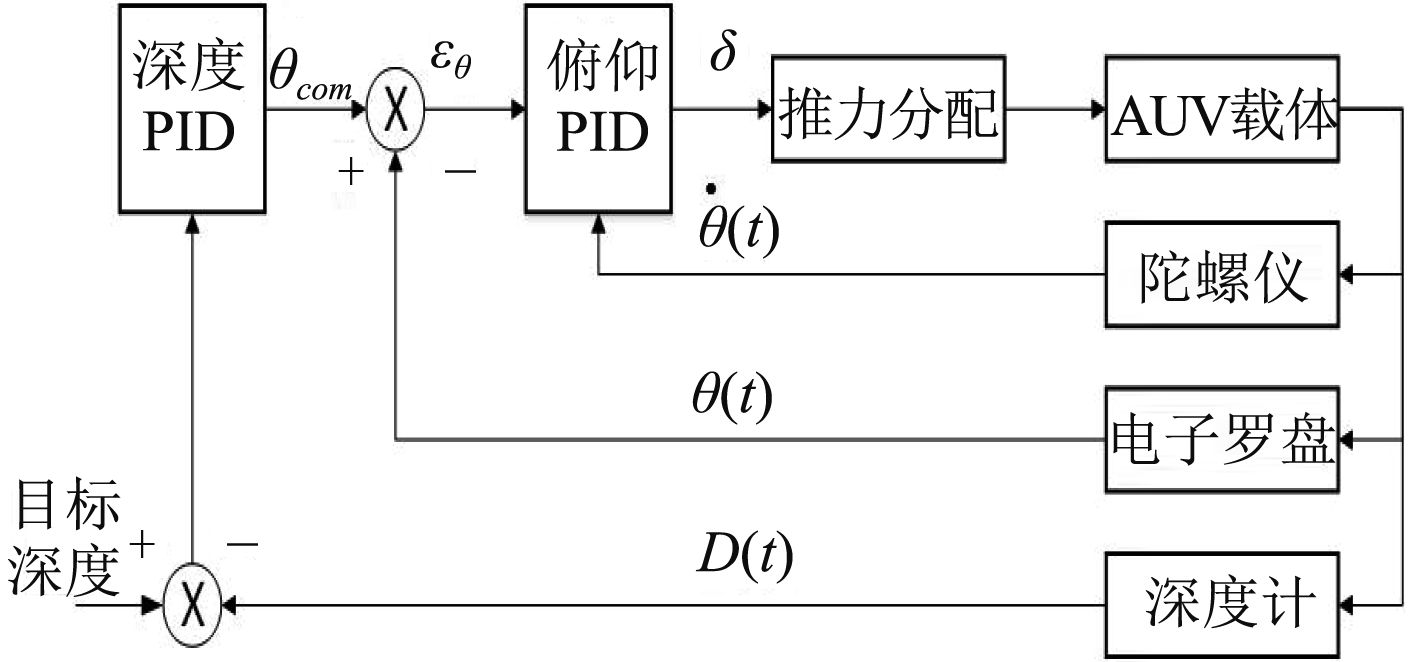
AUV在垂直面上的运动为自主定深下潜和上浮。由于AUV采用X形四螺旋桨的新型推进方式,所以其定深控制采用串级PID控制,外环为深度控制PID,内环为俯仰控制PID[8],整个系统控制环路如图5所示。
|
图 5 AUV垂直面控制环路 Fig. 5 Vertical control loop of the AUV |
首先通过增加上部2个螺旋桨的转速来克服AUV在水中的正向浮力,通过改变其转速可以有效地消除静差,所以深度PID闭环并没有使用积分项。其次AUV深度变化主要是由俯仰角变化引起,因此选择在俯仰PID控制中加入微分环节来抑制俯仰角的变化速率,来增加控制系统的稳定性[9]。内环俯仰PID的目的是快速对内环中的各种扰动做出反应。为了增加内环的调节效果,选择减弱其积分作用。综合以上分析,深度控制器使用比例控制,俯仰控制器使用比例和微分控制,控制律为式(14)。其中,
| $\delta (t) \!=\! {K_{{P_P}}} \times [{K_{{D_P}}} \times ({D_{com}} - D(t)) - \theta (t)] + {K_{{P_d}}} \times \dot \theta (t)\text{。}$ | (10) |
在实际的AUV控制系统中,对象往往很复杂,难以建立最为准确的模型。此时,可以根据之前研究建立的初步模型的响应函数来调整PID控制参数[10],然后在实验室搭建的实验平台上,可以试AUV模拟水平面与垂直面的运动。对AUV进行水平面转首和垂直面俯仰实验,根据实际实验结果对参数进行二次整定,参数整定如表1所示,YAW为水平面转首,PIT为垂直面俯仰。对AUV进行定深与定向角的测试,角度的变化可以实时地通过传感器发送到上位机软件上,通过观察试试变化曲线,对PID参数进行进一步调整。
|
|
表 1 参数整定 Tab.1 Optimization of control parameter |
为了验证控制系统的灵活性和可靠性,此新型AUV在上海交通大学拖曳水池进行多次试验,并在实验后将内部储存的传感器数据导出,并使用Matlab绘制曲线图。图6所示为AUV在3 kn航速下的水平面定航向曲线与垂直面定深曲线,其稳定航行后航向控制误差在±2°以内,深度控制误差在±0.3 m以内。

|
图 6 新型AUV定向与定深实验曲线 Fig. 6 The heading and depth curves of the AUV |
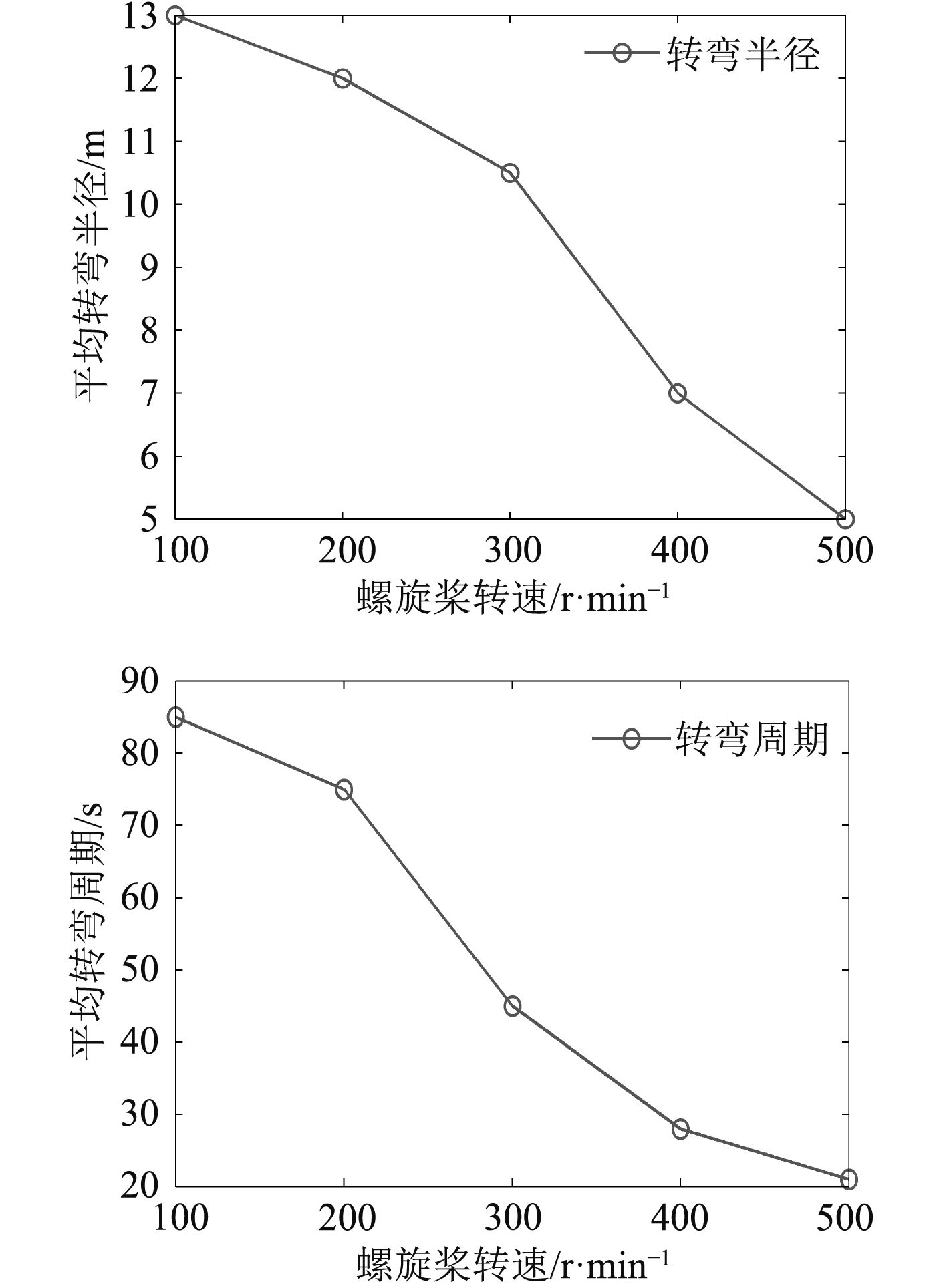
接着,为了测试新型推进器的机动性能,对不同螺旋桨转速下AUV的转弯半径与转弯周期进行测量。
|
图 7 新型AUV在不同推进器转速下的转弯半径与转弯周期 Fig. 7 Comparison of turning radius and turning period of the AUV under different conditions |
ZY-1型AUV于2017年3月在千岛湖实验湖区组织了规范化湖上实验,进一步验证了其运动控制系统的性能,图8所示为新型AUV正在进行湖上试验。

|
图 8 AUV在千岛湖试验区进行试验 Fig. 8 AUV was tested in the Thousand Island Lake Experimental Area |
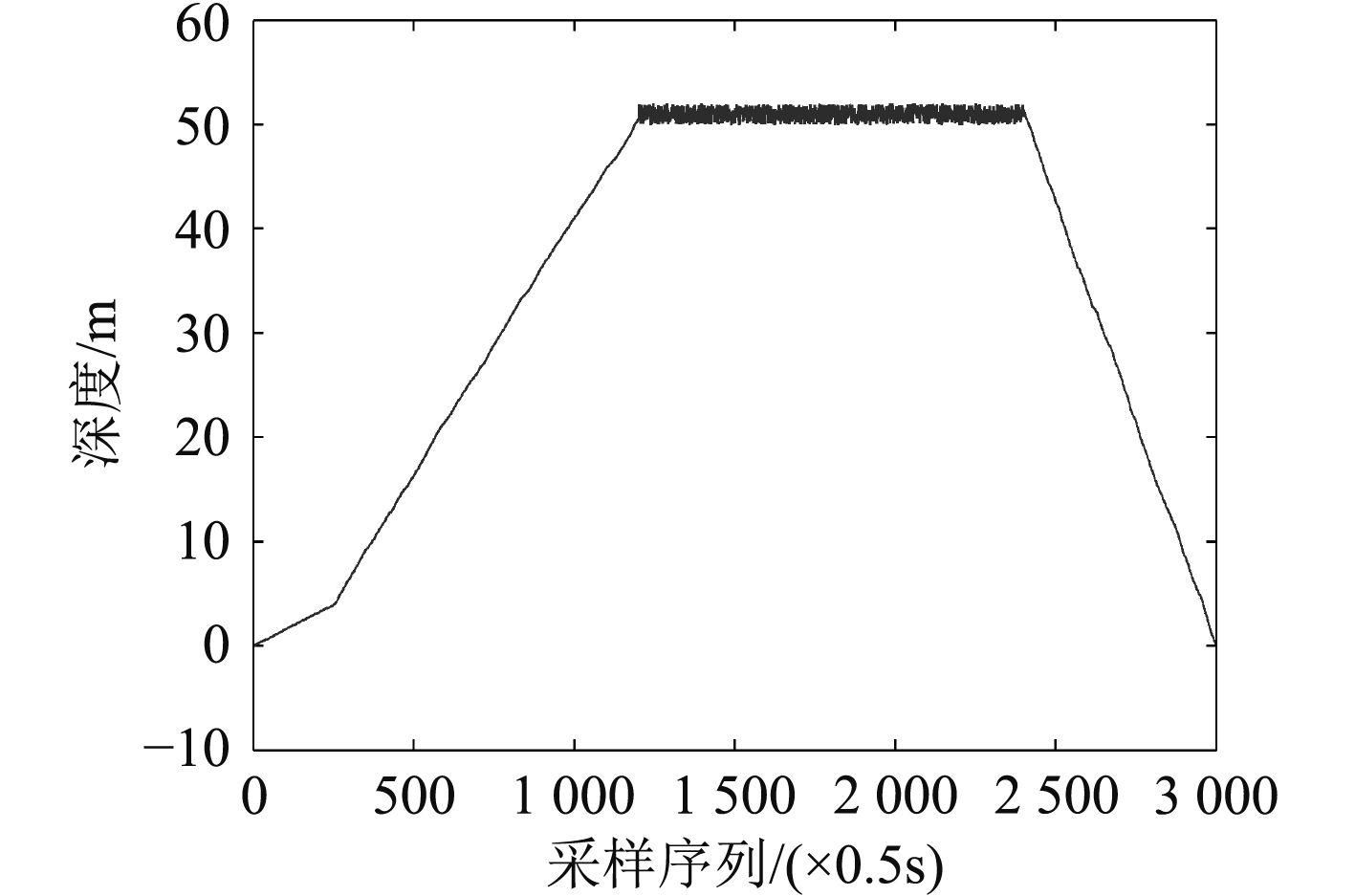
为了验证AUV在垂直面上的定深下潜性能,对其进行了50 m定深下潜试验,图9为实时深度曲线,从图中可见,下潜时间为50 min,最大下潜深度达到52 m,平均下潜速度约为0.25 m/s。上浮后对数据进行分析可知新型AUV下潜阶段俯仰角为–16°~–20°,稳定航行阶段俯仰角保持在3°左右,这是由于AUV需要固定的仰角使头部GPS露出水面,接收位置数据。
|
图 9 AUV下潜50 m深度变化曲线 Fig. 9 The depth curve of the AUV |
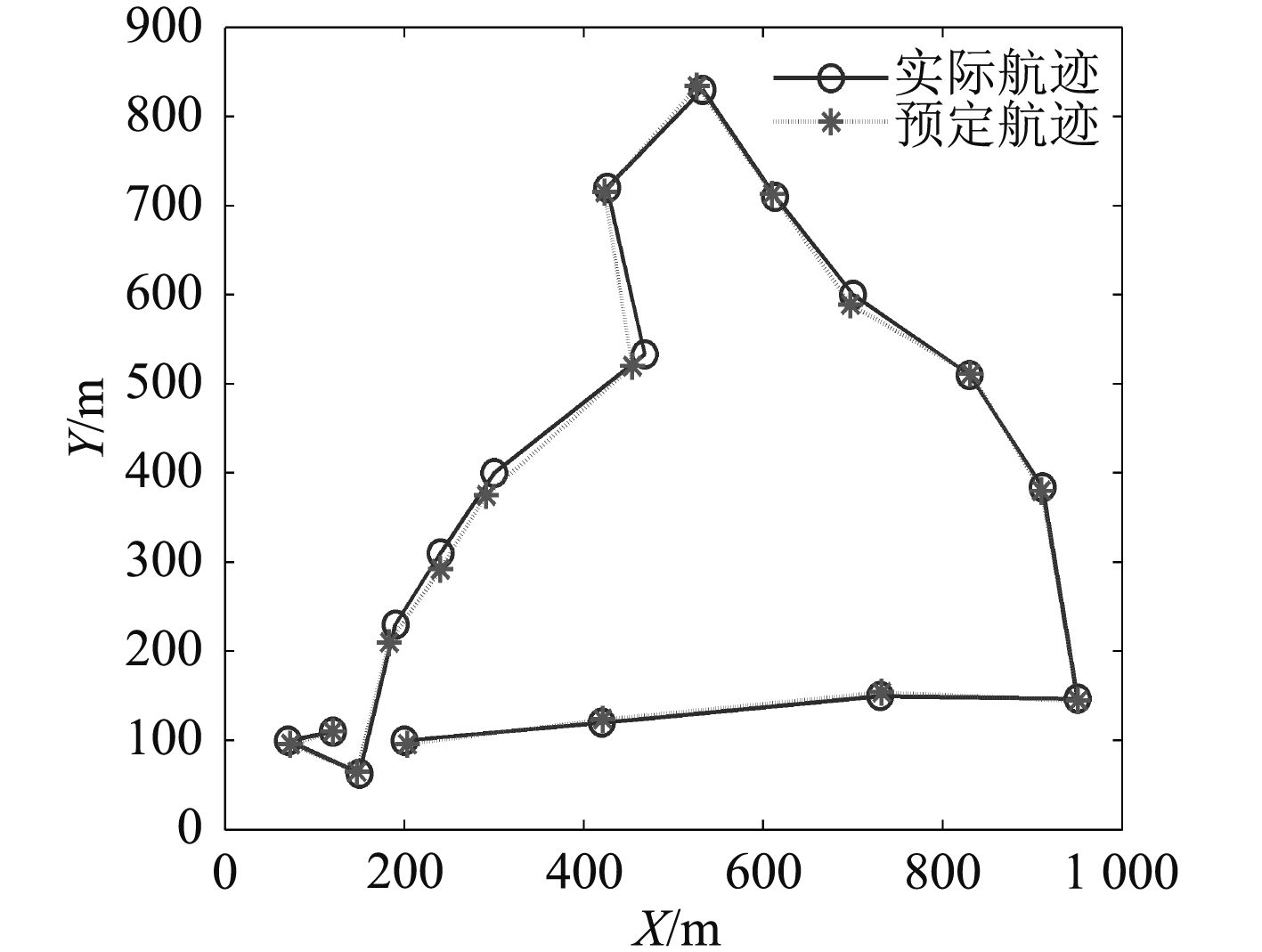
为了验证大尺度下AUV的航迹控制精度,新型AUV沿着实验湖区的水下边界航行。在此试验中,AUV能够稳定的跟踪预定航迹,连续在水下航行3 km。通过该试验验证了新型AUV在大尺度距离航行下跟踪预定航迹的能力和水平面维度控制系统的可靠性。
|
图 10 AUV航迹试验轨迹 Fig. 10 The horizontal trajectory of the AUV |
本文介绍了新型AUV的后置新型推进器及其控制系统,建立了X型推进器等效控制模型,接着提出了新型AUV在水平面与垂直面上的运动控制方法,并通过自建的实验平台对其进行了分析和研究。最后结合大量的现场试验数据对整个平台本身的运动控制性能进行评估与验证。此新型AUV具有易控制、模块化、低成本等特点,尤其在海洋环境监测与水下侦察等方面具有广泛的市场,其控制系统也将在未来的新型AUV产业化发展方向上发挥很大的作用。
| [1] | 张西勇, 王树宗, 李宗哲. 基于变结构的水下航行体航行姿态控制系统设计方法[J]. 兵工学报, 2013, 34 (3): 301–309. |
| [2] |
徐玉如, 李彭超. 水下机器人发展趋势[J]. 自然杂志, 2011, 33 (3): 125–132.
XU Y R, LI P C. Developing tendency of unmanned underwater vehicles[J]. Chinese Journal of Nature, 2011, 33 (3): 125–132. |
| [3] | 蒋新松, 封锡盛, 王棣棠. 水下机器人[M]. 沈阳: 辽宁科学技术出版社, 2000: 304–311. |
| [4] | KUKULYA A, PLUEDDEMANN A, AUSTIN T, et al. Under-ice operations with a REMUS-100 AUV in the Arctic[C]//IEEE/OES Autonomous Underwater Vehicles. Piscataway, USA: IEEE, 2010. doi: 10.1109/AUV.2010.5779661. |
| [5] | 张勋, 边信黔, 唐照东, 等. AUV均衡系统设计及垂直面运动控制研究[J]. 中国造船, 2012, 53 (1): 28–36. |
| [6] | 魏延辉, 田海宝, 杜振振, 等. 微小型自主式水下机器人系统设计及试验[J]. 哈尔滨工程大学学报, 2014, 35 (5): 566–570, 579. |
| [7] |
郭威, 崔胜国, 赵洋, 等. 一种遥控潜水器控制系统的研究与应用[J]. 机器人, 2008, 30 (5): 398–403.
GUO W, CUI S G, ZHAO Y, et al. Research and application of acontrol system for remotely operated vehicle[J]. Robot, 2008, 30 (5): 398–403. |
| [8] | ZENG J B, LI S, LI Y P, et al. Performance of the portable autonomous observation system[C]//OCEANS 2014. Piscataway, USA: IEEE, 2014. |
| [9] |
林俊兴, 戴余良, 张涛. X形舵和十字形舵操纵力等效关系的研究[J]. 舰船科学技术, 2004, 26 (5): 5–6, 13.
LIN J X, DAI Y L, ZHANG T. Study on the equivalent relationof the manipulative force between X sternplane and crucifor-m sternplane[J]. Ship Science and Technology, 2004, 26 (5): 5–6, 13. |
| [10] | 曹永辉, 石秀华, 许晖. 水下航行器水平面运动的滑模控制[J]. 弹箭与制导学报, 2005, 25 (SA): 337–338, 341. |
 2017, Vol. 39
2017, Vol. 39
