有缆水下航行器(Remote Operated Vehicle,ROV)耐压壳体材料大多采用铝合金、不锈钢、钛合金等金属材料,部分也使用玻璃纤维、碳纤维等非金属材料[1]。基于烷基苯溶液的特殊工作环境要求,一款专用ROV的壳体必须使用非金属材料——聚四氟乙烯。该ROV在工作时具有零浮力,任务结束或发生意外后,自身的安保系统必须产生足够的正浮力,保证航行器能够自动上浮。目前航行器各子系统配置完成后,其安保正浮力余量仅剩0.1 kg,不能满足安保要求,需要对ROV壳体进行优化,在满足外形尺寸限制的条件下,增大内部容积,减小壳体重量,增大安保系统的正浮力冗余。
1 水下航行器强度和稳定性模型ROV运动环境在直径36 m的盛满烷基苯溶液的球形罐体内,要求ROV外形限制在直径300 mm、高度500 mm的空间内,壳体使用非金属材料——聚四氟乙烯。ROV壳体受到的静态载荷主要有:液体的外压;壳体内部安装的推进装置、电池、电路板、配重等载荷的不均匀分布,在各载荷面处浮力和重力的差值产生的剪切与弯矩;在空气环境中吊装或者悬挂时受到的剪切与弯矩。以上各种载荷中,最大载荷是最大深度时所受液体的外压,因此本文中选取最深处环境液体压力
本文ROV壳体采用等间距矩形环肋加强圆柱壳体[2],圆柱壳体受到均匀侧向外压和轴向压力的联合作用,产生对称于轴线的变形,即在轴向(或纵向)产生均匀压缩及由肋骨支撑而引起的弯曲,在周向仅产生均匀压缩没有变形。本文在计算强度时采用相关的经验公式。
1)跨度终点处壳板的横向平均应力:
| $\sigma _2^0 = K_2^0{p_j}R/t \text{。}$ | (1) |
式中:pj为壳体计算压力,MPa;R为圆柱壳半径;cm;t为壳板厚度,cm。
2)肋骨处板壳的纵向相当应力:
| ${\sigma _{leg}}\left| {_{x = l/2} = (0.91{K_1} - 0.3{K_r}){P_j}R/t} \right. \text{。}$ | (2) |
3)肋骨上的应力:
| ${\sigma _r} = {K_r}{P_j}R/t \text{。}$ | (3) |
式(1)~式(3)中,系数
受外压的壳体与受内压的壳体不同,除了考虑强度之外,还要考虑其会由于丧失稳定性而导致壳体的破坏。承受均匀静水外压的加肋圆柱形的破坏防式一般可分为3种[3]:肋间壳体屈服、肋间壳板失稳、总体失稳。本文壳体稳定性从肋间壳板失稳和总体失稳的理论临界压力2个方面进行考虑。
1)肋间壳板稳定性
肋间壳板失稳时认为肋骨有足够的刚性,肋骨并没有失稳,壳体的理论临界压力可用式(4)计算:
| $\begin{split}p_{cr}^{\prime} & = \displaystyle\frac{E}{{{n_2} + 0.5{\alpha ^2} - 1}}\left[ {\displaystyle\frac{{{t^3}}}{{12(1 - {\mu ^2}){R^3}}}{{({n^2} + {\alpha ^2} - 1)}^2}} +\right.\\ & \left. { \displaystyle\frac{t}{R}\frac{{{\alpha ^4}}}{{{{({n^2} + {\alpha ^2})}^2}}}} \right] \text{。}\end{split}$ | (4) |
2)总体稳定性
通过弹性失稳理论用能量法可以推导出壳体整个舱段的理论临界压力为:
| ${(p_{cr}')_g} = \frac{E}{{1 + \displaystyle\frac{{\alpha _1^2}}{{2({n^2} - 1)}}}}\left[\frac{t}{R}\frac{{\alpha _1^4}}{{{{({n^2} + \alpha _1^2)}^2}({n^2} - 1)}} + \frac{{I({n^2} - 1)}}{{{R^3}l}}\right] \text{。}$ | (5) |
式中:
理论临界压力与实际情况存在不同程度上的不同,理论值一般偏高,因此需要对理论值进行修正:
| ${P_{cr}} = {\eta _1}{\eta _2}{P'_{cr}} \text{,}$ | (6) |
| ${({P_{cr}})_g} = {\eta _1}{\eta _2}{({P'_{cr}})_g} \text{。}$ | (7) |
式(6)和式(7)中,
水下航行器壳体优化目的是在满足结构和稳定性要求的前提下尽可能的增大壳体内部容积和减小壳体重量[4],以提高航行器的综合性能,本文ROV壳体优化主要是为了增大安保系统的浮力冗余。
1)设计变量
通过分析,壳板厚度、肋骨间距、肋骨截面参数和壳体外径的变化是影响壳体应力和稳定性的重要因素。在此,确定壳体结构设计变量有5个,即:壳体外径R、肋骨间距l、壳体厚度t和肋骨参数a,b,如图1所示。
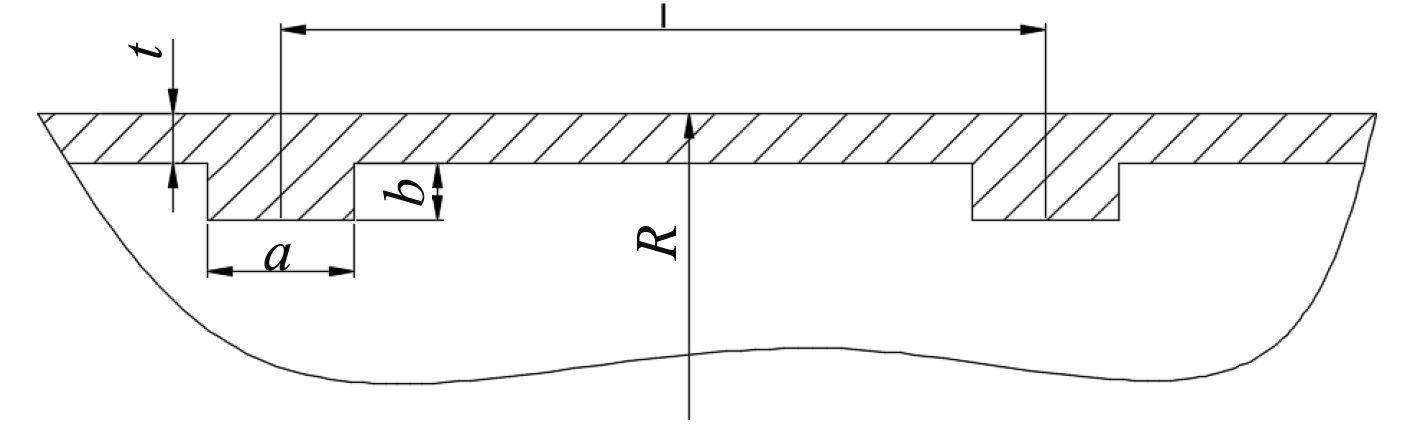
|
图 1 壳体中部矩形肋骨结构图 Fig. 1 Rectangular rib structure chart in the middle of the shell |
2)目标函数
本文以求得最大内部容积函数为目的,壳体内部容积的计算如下:
| $V = \pi {(R - t)^2} \cdot h - \pi [{(R - t)^2} - {(R - t - b)^2}] \cdot a \cdot (\left\lceil {\frac{h}{l}} \right\rceil + 1) \text{。}$ | (8) |
3)约束条件
壳体结构设计中,根据壳体强度及稳定性校核标准,壳体结构应力及稳定性必须满足一定要求。
在计算外力Pj的作用下,肋骨中间板壳的横向平均应力不得大于
| $\sigma _2^0 \leqslant 0.85{\sigma _s} \text{,}$ | (9) |
肋骨处壳板的纵向相当应力不超过屈服极限
| ${\sigma _{leg}}\left| {_{x = l/2}} \right. \leqslant {\sigma _s} \text{,}$ | (10) |
肋骨应力
| ${\sigma _r} \leqslant 0.55{\sigma _s} \text{,}$ | (11) |
壳板稳定性要求壳板的实际临界压力
| ${P_j} \leqslant {P_{cr}} \text{,}$ | (12) |
总体失稳的临界压力
| $\left( {1.1 \sim 1.3} \right){P_j} \leqslant {(P_{cr}^{})_g} \text{,}$ | (13) |
式(8)、式(10)、式(11)、式(12)和式(13)整理组成优化模型的非线性约束条件:
| ${N_{noli}} \leqslant 0 \text{,}$ |
壳体结构设计中,根据加工与设计要求设计,为了使整体结构更为合理,对变量设定上下界,使优化结果出现在设定区间内。优化参数的上下界设定为:
| $\begin{array}{l}{R_1} \leqslant R \leqslant {R_2} \text{,}\\{l_1} \leqslant l \leqslant {l_2} \text{,}\\{t_1} \leqslant t \leqslant {t_2} \text{,}\\{a_1} \leqslant a \leqslant {a_2} \text{,}\\{b_1} \leqslant b \leqslant {b_2} \text{,}\end{array}$ | (14) |
由上面3式,可将航行器壳体优化模型归纳为:
目标函数:
| $\text{约束条件}\left\{ \begin{array}{l}\text{非线性约束}:{N_{noli}} \leqslant 0 \text{,}\\\text{优化变量约束}:\left\{ \begin{array}{l}100 \leqslant R \leqslant 150 \text{,}\\100 \leqslant l \leqslant 300 \text{,}\\3 \leqslant t \leqslant 15 \text{,}\\3 \leqslant a \leqslant 50 \text{,}\\3 \leqslant b \leqslant 20 \text{。}\end{array} \right.\end{array} \right.$ | (15) |
ROV实际的外形相关尺寸作为优化初始值:
优化可以看作寻找函数最小值的过程,最小值又可以分成局域最小值和全域最小值点,优化模型为求解带约束多变量非线性目标函数的最小值[5]。使用全局搜索(globalsearch)方法在可行域内寻求最优解,先由分散搜索算法在可行域产生试验点测试集合,抽取部分试验点并结合局部优化工具(fmincon)计算出局部最优解,直至所有试验点被使用。最后将得到的所有局部最优解进行比较,得到可行域内的全局最优解。考虑到加工与加工误差,将优化后的参数进行整理:将肋骨的宽b取整,肋骨采用矩形肋骨,取其长宽比为2。最终优化与整理结果见表1。
|
|
表 1 优化前后设计变量与目标函数对比 Tab.1 Comparison of design variables and objective functions before and after optimization |
由表1可以得到优化后的参数值,与整理后的参数值,其中航行器在实际加工中应取整理后的值。
优化后体积变化:
| $\frac{{0.032\;4 - 0.029\;6}}{{0.029\;6}} \times 100\% = 9.46\% \text{,}$ | (16) |
优化后质量变化:
| $10.202\;7 - 5.878\;8 = 4.323\;9\; {\rm kg} \text{,}$ | (17) |
| $\frac{{4.323\;9}}{{10.202\;7}} \times 100\% = 42.38\% \text{。}$ | (18) |
经式(15)、式(16)和式(17)的计算,优化后壳体内部容积增加9.46%,质量减少4.323 9 kg,约为原质量的42.38%。由结果可得,此次优化主要体现在肋骨尺寸与壳体厚度的变化上,且在得到壳体最大内部容积的同时质量也相应地减小,解决了ROV上浮时正浮力不足的问题。
3 有限元分析根据上面的计算结果,采用solidworks软件对ROV壳体进行三维建模,导入Ansys中,进行结构静力学分析,得到壳体在载荷及约束条件下的应力结果;在静力学分析的基础上,进行BUCKING屈曲分析,得到壳体的临界失稳载荷[6]。有限元分析过程中划分的壳体单元数为92 923,节点数为30 406,模型约束为一端为固定约束,另一端只允许轴向移动[7]。根据ROV的工作环境,其最大工作深度为36 m,载荷的施加分为2部分,其一是外表面的压力载荷,其值为0.36 MPa;其二是轴向载荷,其值要通过压力转换计算而来,通过计算发现,轴向载荷为2.66 MPa。
从图2可以看出,36 m水深时此结构最大应力

|
图 2 壳体的Mises应力图 Fig. 2 Mises stress chart of the shell |
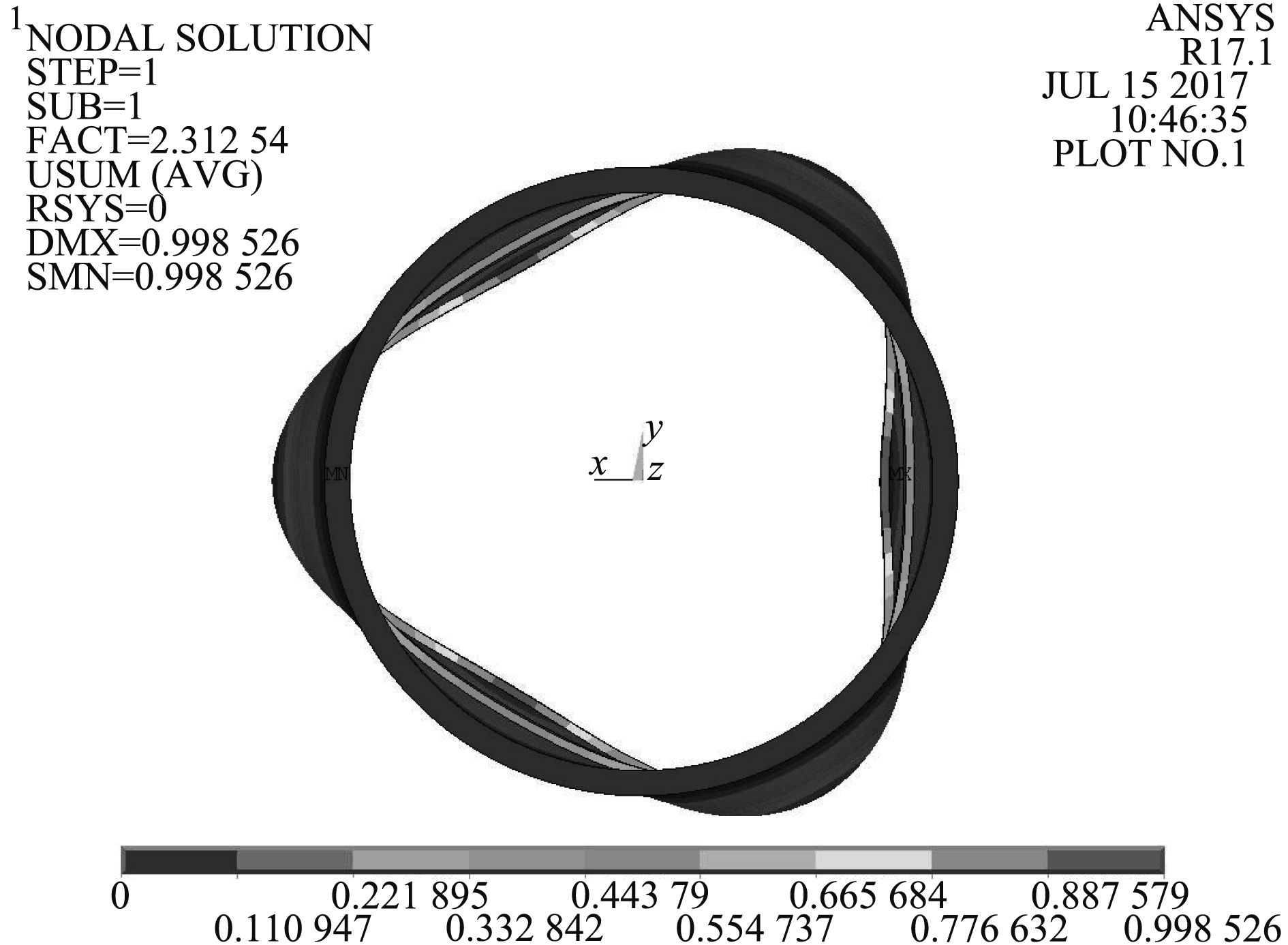
|
图 3 壳体稳定性分析图 Fig. 3 Stability analysis chart of shell |
本文根据某型特种ROV的浮力冗余要求,以ROV壳体最大内部容积为目标函数,建立了壳体优化设计模型。,使用全局搜索(globalsearch)方法并结合局部优化工具(fmincon)对ROV壳体进行优化设计,完成了基于聚四氟乙烯(PTFE)材料的ROV圆柱壳体结构的优化设计,并将优化后的模型利用Ansys进行强度和稳定性分析。结果表明,优化后的壳体满足强度、稳定性的要求, 优化后壳体内部容积增加9.46%,,质量减少4.3239 kg,约为原质量的42.38%,解决了ROV上浮时正浮力不足问题。
| [1] | 张铁栋. 潜水器设计原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2011: 80–92. |
| [2] | 吕春雷, 王晓天, 姚文. 多种型式肋骨加强的耐压圆柱壳体结构稳定性研究[J]. 船舶力学, 2006, 10 (5): 113–118. |
| [3] | 张宇文. 鱼雷总体设计方法[M]. 西安: 西北工业大学出版社, 1998: 123–130. |
| [4] | 胡培民, 石秀华, 余绍勇. 鱼雷壳体的参数化设计[J]. 舰船科学技术, 1999 (5): 26–28. |
| [5] | 付锦江, 颜昌翔, 刘伟. 椭圆弧柔性铰链刚度简化计算及优化设计[J]. 光学精密仪器, 2016, 24 (7): 1703–1710. |
| [6] | 鲁鹏, 耿文豹. 海洋探测型AUV壳体设计与强度校核[J]. 舰船科学技术, 2015, 37 (5): 119–121. |
| [7] | 张宗尧, 赵石军. 基于ANSYS的外压容器稳定性分析[J]. 设计与计算, 2010 (2): 21–23. |
 2017, Vol. 39
2017, Vol. 39
