随着水下武器装备的快速发展,如鱼雷、潜艇等,逐步向大深度、远航程这一更高目标迈进。在这个过程中,电动力推进系统尾轴动密封问题显得尤为突出,也对其提出了更为严格的要求。磁耦合传动装置作为将推进尾轴连接部位的动密封转化为静密封的装置,利用隔离罩内外永磁体之间的磁力耦合相互作用[1-2],来实现对转矩的无接触摩擦传递。磁耦合传动装置具有以下优势:1)转矩传递平稳,无接触,无摩擦;2)传递转矩过载时,自动保护停止工作;3)装置相对转动时,由于不存在直接接触,可保证密封可靠性[3]。鉴于磁耦合传动的以上优点,在水下特别是大深度工作时具有广阔的应用前景。
磁耦合传动装置工作转速低,传递功率大,工作时,由于气隙磁场的交变在钛合金隔离罩产生涡流损耗,涡流损耗长时积聚导致其发热严重产生形变。另一方面,温升过高也会使永磁体退磁,工作性能下降。所以,对磁耦合传动装置及隔离罩等主要部件的温度场进行详细分析对于提高整个传动装置的安全可靠性能有着十分重要的意义。
本文通过对某型磁耦合传动装置不同永磁体布置方式下的隔离罩涡流损耗进行计算,以减小隔离罩涡流损耗为目标,找到最优的永磁体布置方式,然后对最优方式下整个磁耦合传动装置,隔离罩、永磁体的瞬态温度场求解分析,从而为其热力学分析提供一定的依据。
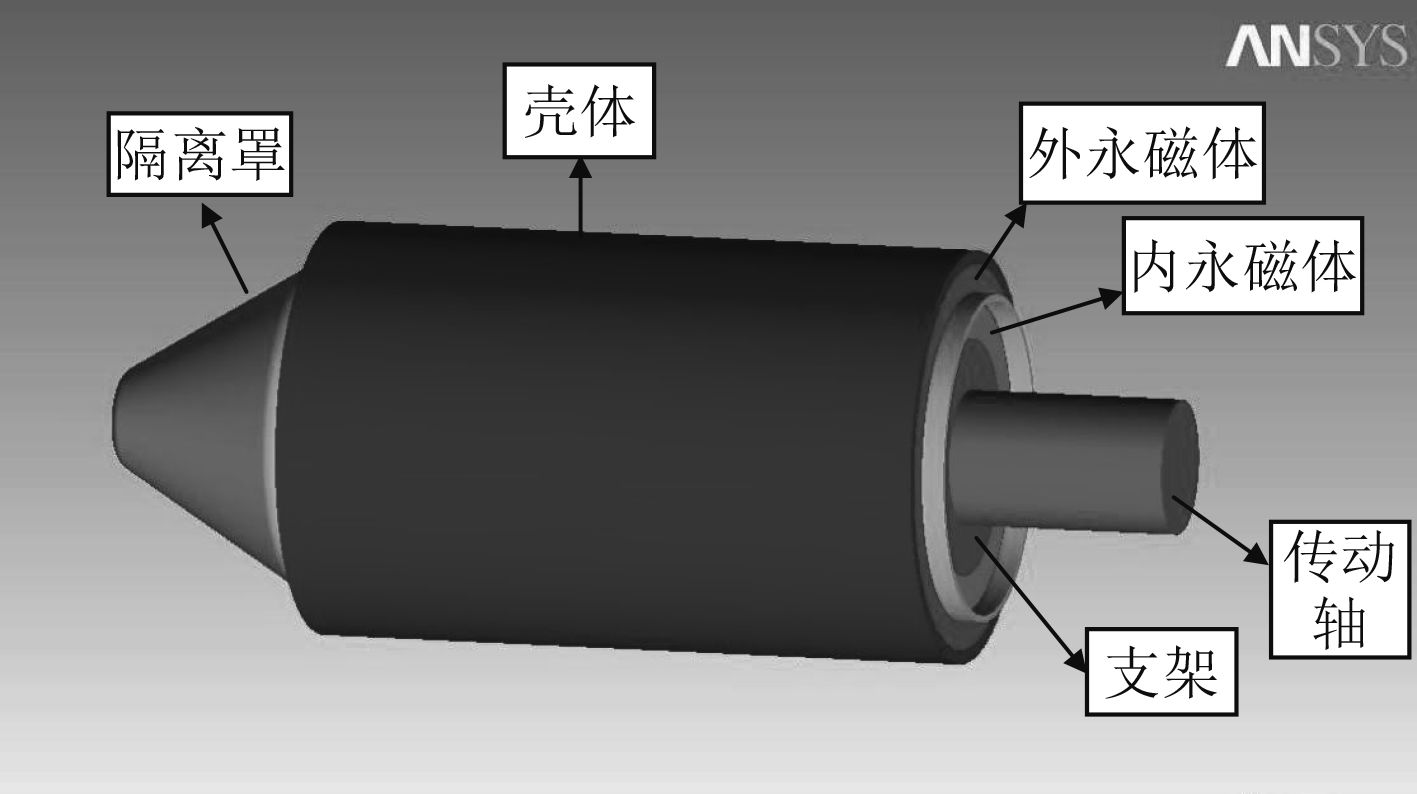
1 几何模型建立图1为该磁耦合传动装置的三维几何模型,由传动轴、支架、内永磁体、隔离罩、外永磁体、壳体等6部分组成,其各部分材料见表1。
|
图 1 磁耦合传动装置三维几何模型 Fig. 1 The 3D geometric model of magnetic coupling driving device |
|
|
表 1 磁耦合传动装置各部件材料 Tab.1 Each component material of magnetic coupling driving device |
在本磁耦合传动装置中,隔离罩涡流损耗作为整个装置的主要热源,从而影响其瞬态温度场分布。因此首先计算隔离罩在不同永磁体布置方式下的涡流损耗。
2.1 隔离罩涡流损耗理论由于隔离罩采用钛合金材料,根据电磁感应定律,气隙交变磁场在隔离罩内产生涡流,涡流会使隔离罩发热最终以热量的形式耗散出去,从而引起隔离罩、永磁体等温度升高,降低了传动效率[4-5]。设气隙磁密幅值为Bδ,则垂直于隔离罩表面感应的磁密Bγ为:
| ${{{B}}_{\rm{\gamma }}} = {{{B}}_{\rm{\delta }}} \times \sin {\rm{\gamma }}\text{。}$ | (1) |
式中:γ为内外转子间相位差。
根据麦克斯韦方程组有
| $\frac{{\partial {{{B}}_{\rm{\gamma }}}}}{{\partial {\rm{\beta }}}} = - \frac{1}{{{R}}} \times \frac{{\partial {{E}}}}{{\partial {\rm{\gamma }}}}\text{。}$ | (2) |
式中:β为隔离罩厚度;R为隔离罩半径。
将式(1)代入式(2)可得:
| $\frac{{{{\rm d}E}}}{{{\rm{d\gamma }}}} = - {{R}} \times \frac{{2{\rm{\pi f}}}}{{{P}}}{{{B}}_{\rm{\delta }}} \times {\rm{cos\gamma }}\text{。}$ | (3) |
式中:f为电频率;P为极对数。
式(3)两侧同时积分可得:
| $\int_0^{{{E}}(\gamma )} {dE = - R\frac{{2\pi f}}{P}{B_\sigma }} \int_0^\gamma {\cos } \gamma \times d\gamma \text{,}$ | (4) |
| ${{E}}\left( {\rm{\gamma }} \right) = - \frac{{2{{R\pi f}}}}{{{P}}}{{{B}}_{\rm{\delta }}}{\rm{sin\gamma }}\text{。}$ | (5) |
隔离罩感应电流密度:
| ${{J}} = - \frac{{2{{\pi Rf\sigma }}}}{{{P}}}{{{B}}_{\rm{\delta }}}{\rm{sin\gamma }}\text{。}$ | (6) |
式中:σ为隔离罩材料电导率。
对整个空间区域积分,隔离罩涡流损耗为:
| $\begin{split}{{{P}}_{{z}}} =& \int_0^L \int_0^{2 \pi} {\left[{{JR{\rm d}}\left( {{\rm{\beta \gamma }}} \right)} \right]^2}\frac{1}{{\rm{\sigma }}} \times \frac{{{{{\rm d}L}}}}{{{Rd}\left( {{\rm{\beta \gamma }}} \right)}} =\\&4{L}{{R}^3}{{\sigma \beta B}}_{\rm{\delta }}^2\frac{{{{\pi }^3}{{{f}}^3}}}{{{{P}^2}}}\text{。}\end{split}$ | (7) |
式中:L为隔离罩轴向长度。
由式(7)可以看出,减小材料的电导率或隔离罩轴向长度可减少隔离罩涡流损耗。此外,在保证传动扭矩要求的条件下,减小工作气隙磁密也可达到相同目的。增加极对数也可实现,前提是对成本进行控制。降低电频率f虽然可降低损耗,由于电频率f和转速成正比,与此同时也减小了磁耦合装置的工作转速[6]。
2.2 隔离罩2D和3D损耗模型有限元计算本文通过对永磁体轴向分段数的不同来间接改变隔离罩材料的电导率,从而使得涡流损耗发生变化,为最小涡流损耗时永磁体轴向布置方式的优化奠定基础。
通过对磁耦合装置建立2D和3D有限元模型,计算2D整体永磁体隔离罩涡流损耗;对3D模型永磁体在轴向上分为2段、3段、4段,相差一个极距时分别计算其隔离罩涡流损耗,如图2~图5所示。
|
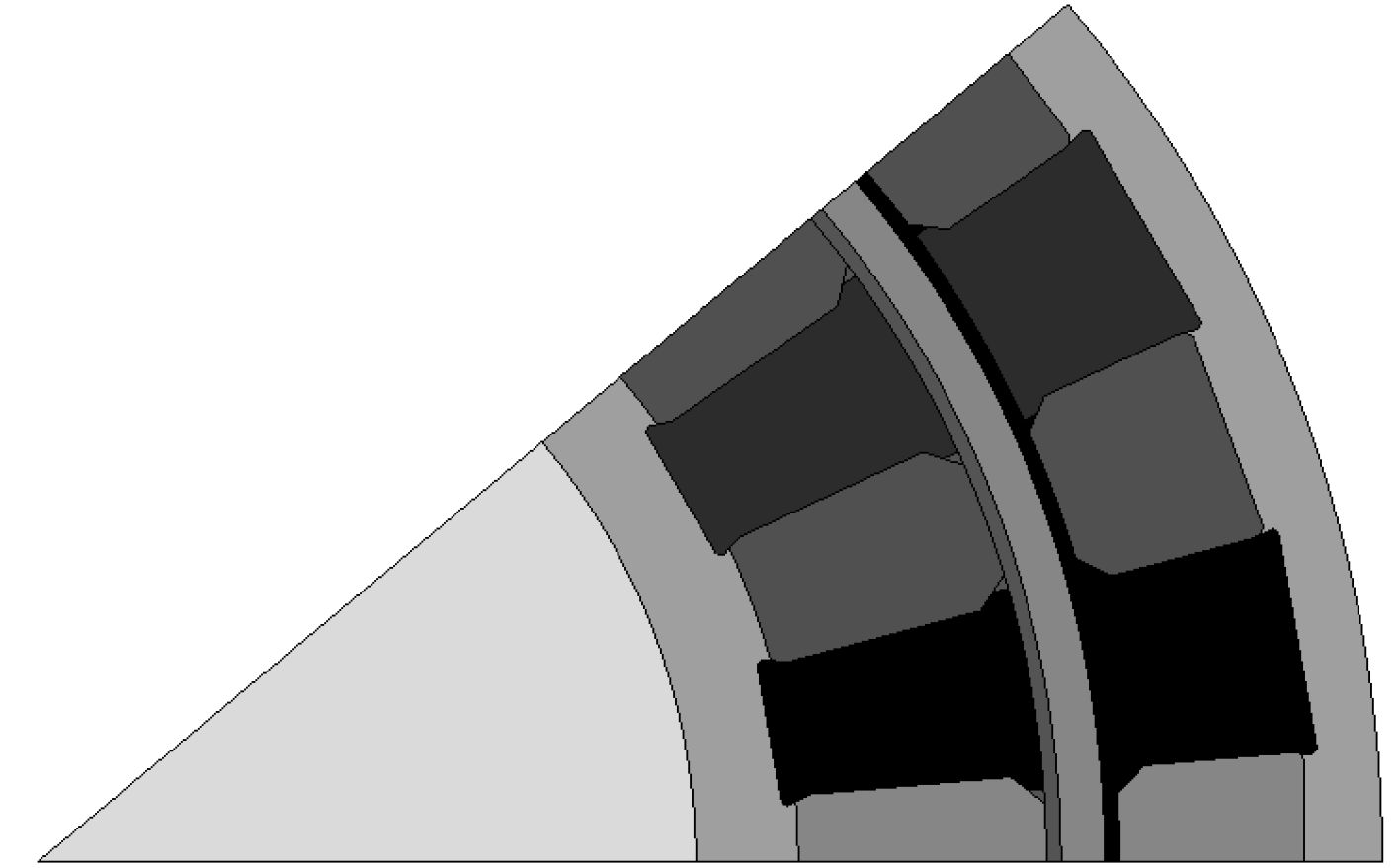
图 2 2D整体永磁体损耗模型 Fig. 2 The loss model of 2D permanent magnets |
|
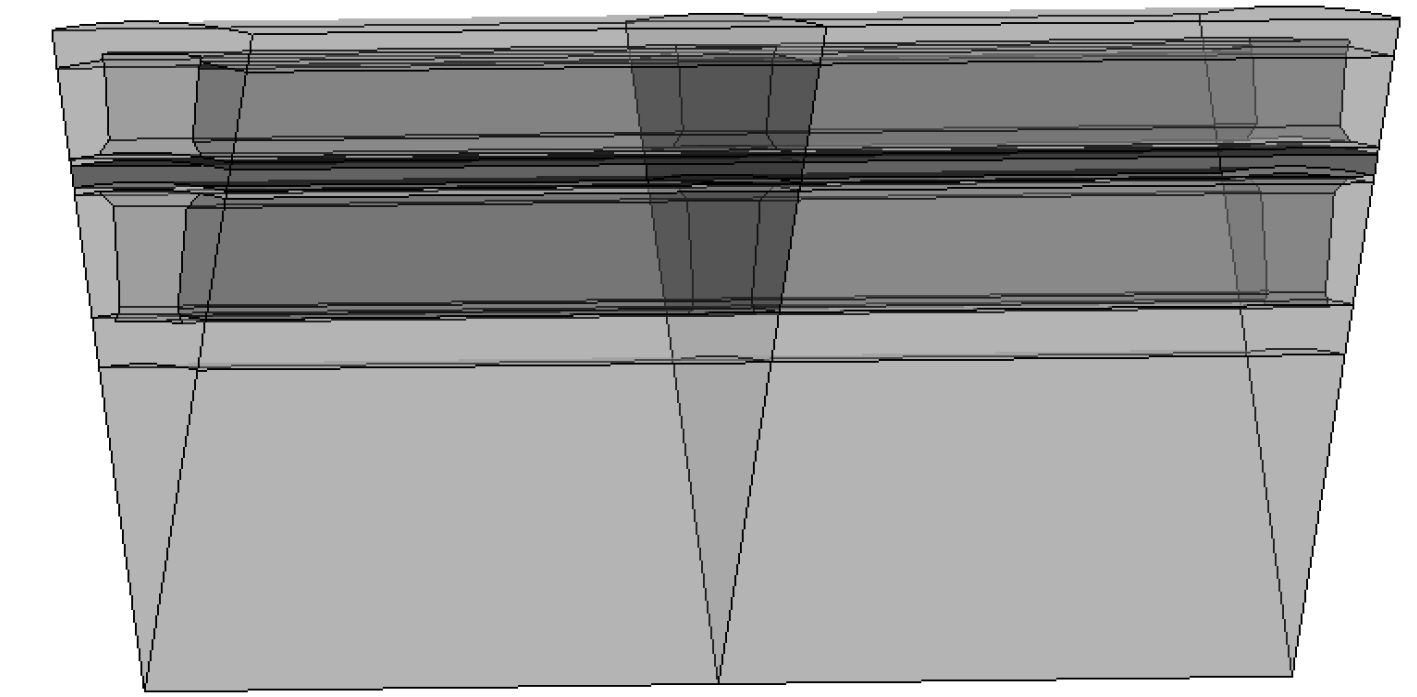
图 3 永磁体轴向2段3D模型 Fig. 3 The 3D model of axial two-segment permanent magnets |
|
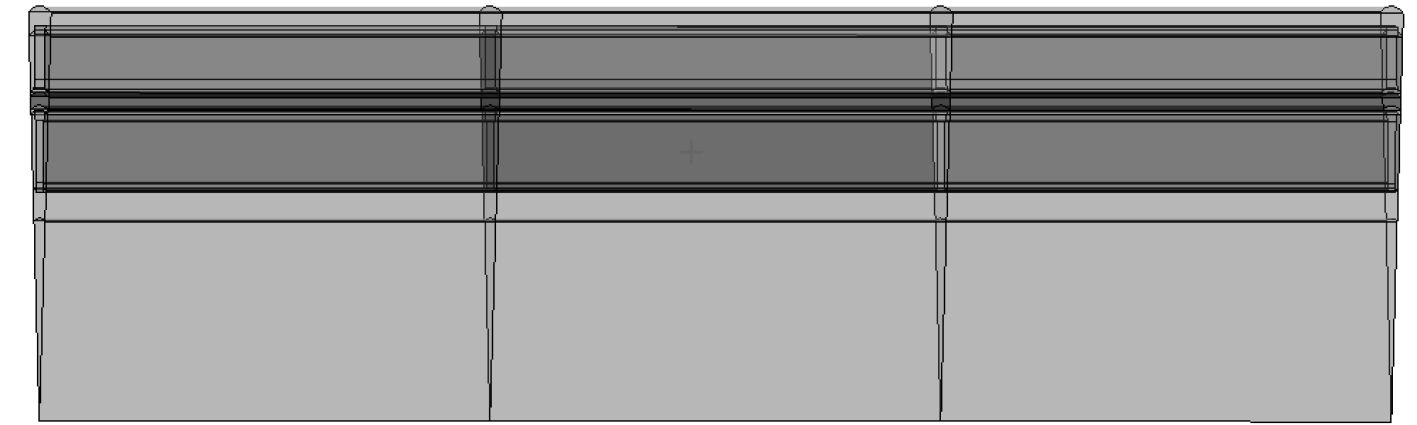
图 4 永磁体轴向3段3D模型 Fig. 4 The 3D model of axial three-segment permanent magnets |
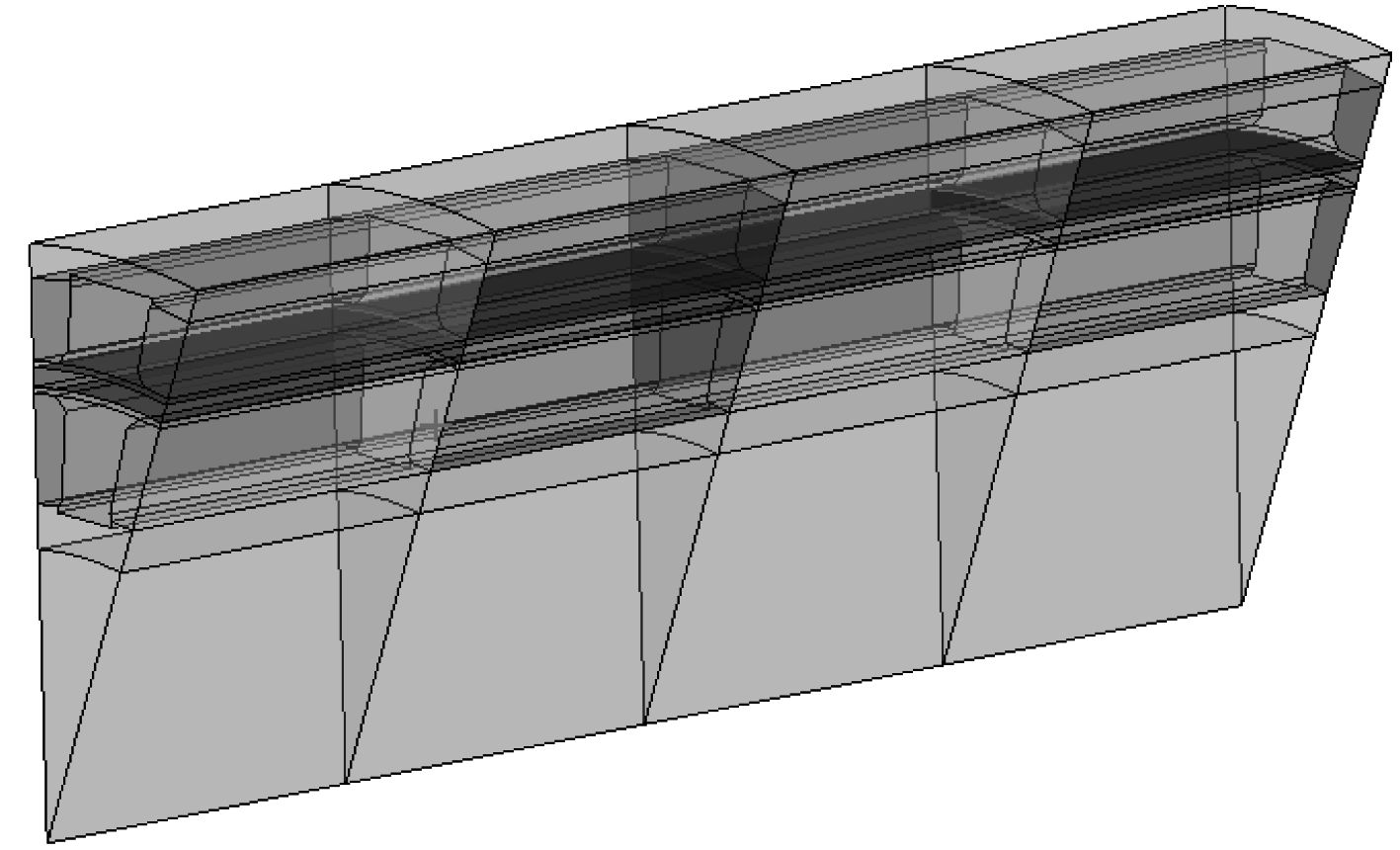
|
图 5 永磁体轴向4段3D模型 Fig. 5 The 3D model of axial four-segment permanent magnets |
计算不同模型下隔离罩涡流损耗,结果见表2。
|
|
表 2 磁耦合装置2D,3D不同模型下隔离罩涡流损耗 Tab.2 The isolation cover eddy current loss of the 2D, 3D of different model of magnetic coupling device |
根据表2结果可知,当永磁体轴向分4段时,其隔离罩涡流损耗最小,为1.890 kW。
3 温度场求解隔离罩涡流损耗作为磁耦合传动装置主要热源,将3D永磁体轴向分4段时的涡流损耗作为温度场求解热载荷,利用Fluent软件建立三维有限元模型对瞬态温度场进行求解,由于此装置为短时工作制,求解分析10 min时整个传动装置、隔离罩、永磁体等温度场分布。
3.1 传热学理论对于二维有内热源的非稳态导热问题,其导热微分方程[7]为:
| $\frac{\partial }{{\partial {{x}}}}\left( {{{k}}\frac{{\partial {{T}}}}{{\partial {{x}}}}} \right) + \frac{\partial }{{\partial {{y}}}}\left( {{{k}}\frac{{\partial {{T}}}}{{\partial {{y}}}}} \right) + {{\dot q}} = {{\rho }}{{{c}}_{{p}}}\frac{{\partial {{T}}}}{{\partial {{t}}}}\text{。}$ | (8) |
三维情况下有:
| $\frac{\partial }{{\partial {{x}}}}\left( {{{k}}\frac{{\partial {{T}}}}{{\partial {{x}}}}} \right) + \frac{\partial }{{\partial {{y}}}}\left( {{{k}}\frac{{\partial {{T}}}}{{\partial {{y}}}}} \right) + \frac{\partial }{{\partial {{z}}}}\left( {{{k}}\frac{{\partial {{T}}}}{{\partial {{z}}}}} \right) + {{\dot q}} = {{\rho }}{{{c}}_{{p}}}\frac{{\partial {{T}}}}{{\partial {{t}}}}$ | (9) |
式中:k为导热系数,W/(m·K),设导热介质为各向同性材料,所以x,y,z三个方向的热导率和传导的方向无关,从而有
初始条件为环境温度20 ℃,即293 K,由于工作环境为水下,且隔离罩热源相比于水要小的多,所以边界条件设为恒温边界条件,即293 K,本例中用1/10模型进行温度场求解分析,侧面为绝热边界条件,如图6所示。

|
图 6 温度场求解1/10模型 Fig. 6 The 1/10 model of temperature field solution |
在隔离罩损耗计算中,3D永磁体轴向分4段时涡流损耗为1.890 kW。本文磁耦合装置中,隔离罩发热源部分轴向长度为150 mm,直径为71.5 mm,厚度为1.5 mm,算得体积
| ${{\dot q}} = \frac{{P_Z}}{V}\text{。}$ | (10) |
经计算,源项在3D永磁体轴向分4段时的值为3.74×107 W/m3。
为了对隔离罩受热形变以及永磁体退磁温升进行分析,重点求解了整个传动装置,隔离罩及内外永磁体10 min时温度场分布,如图7~图10所示。
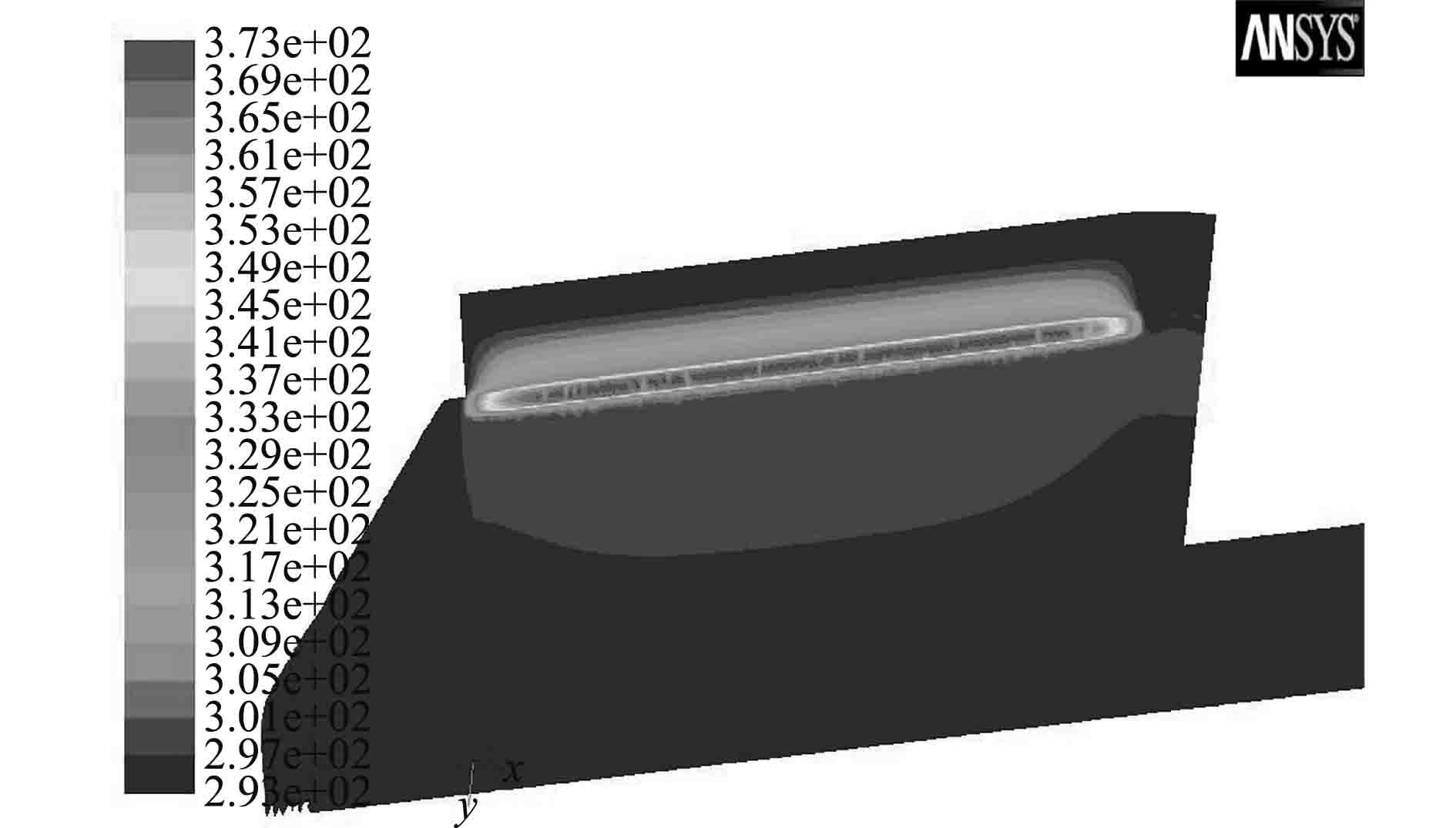
|
图 7 磁耦合传动装置10 min温度场 Fig. 7 The 10 minutes temperature field of magnetic coupling driving device |
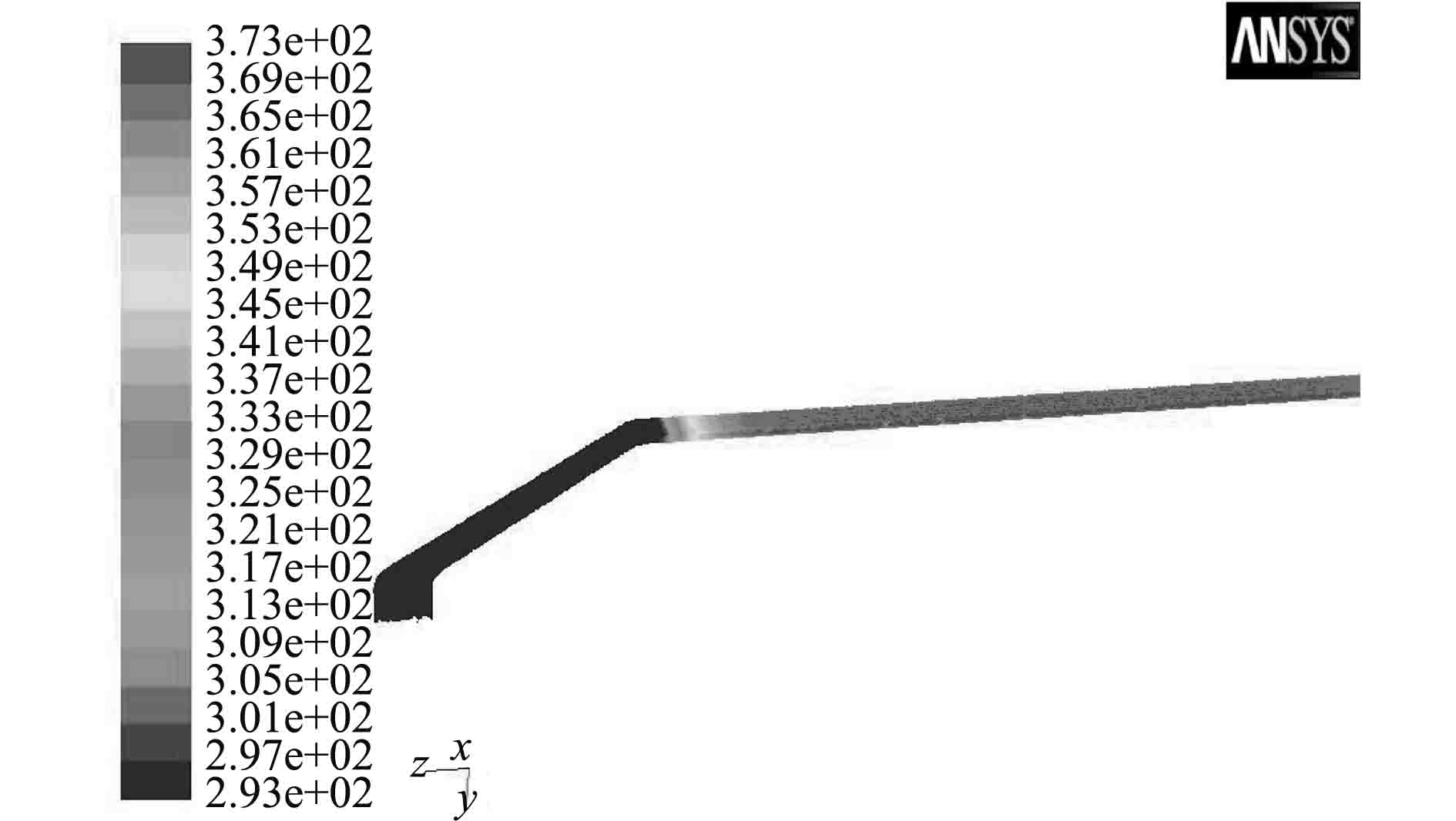
|
图 8 隔离罩10 min温度场 Fig. 8 The 10 minutes temperature field of isolation cover |

|
图 9 内永磁体10 min温度场 Fig. 9 The 10 minutes temperature field of internal peranment magnet |
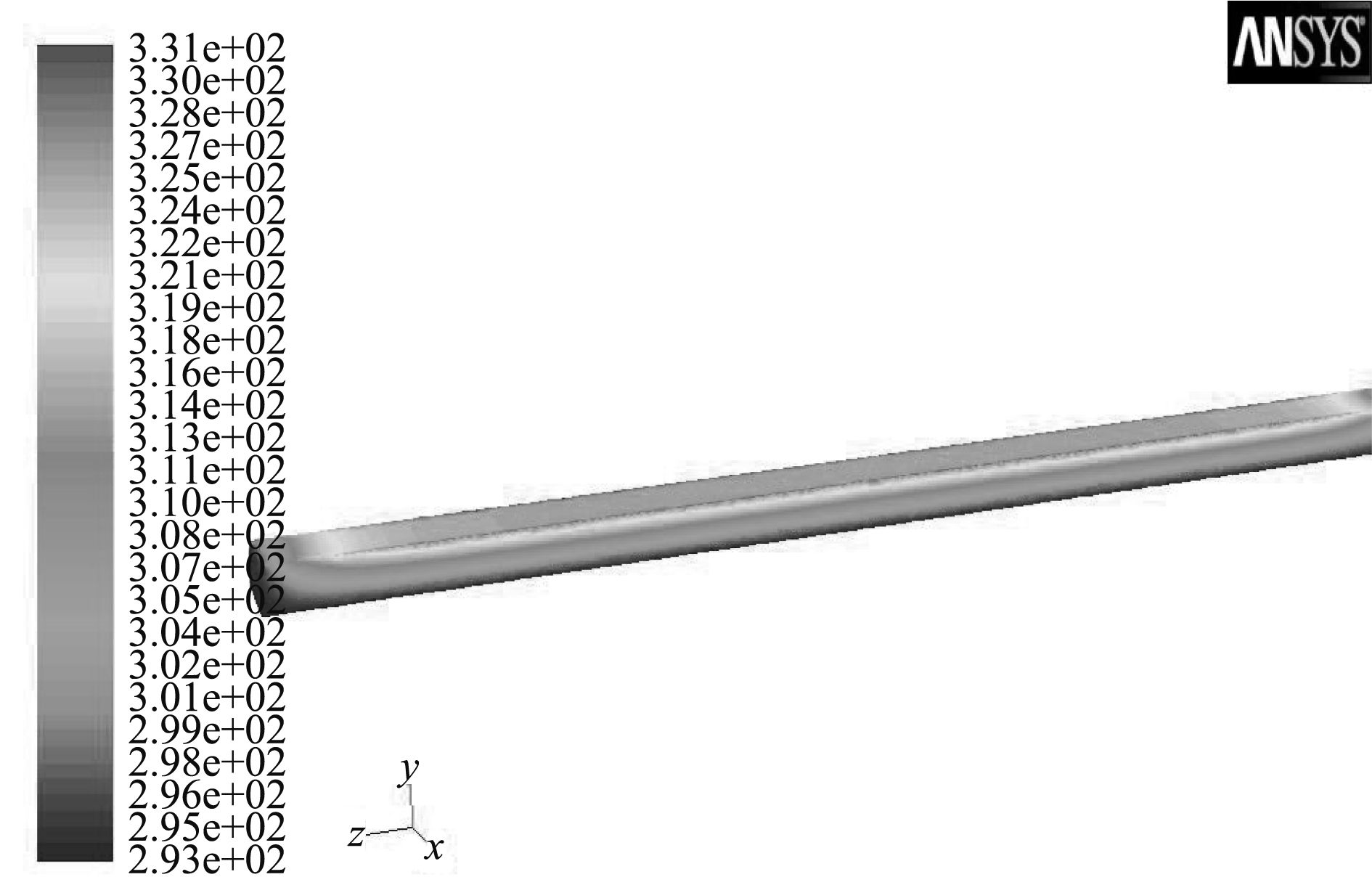
|
图 10 外永磁体10 min温度场 Fig. 10 The 10 minutes temperature field of external peranment magnet |
利用Fluent软件对磁耦合传动装置从开始运行到10 min时的瞬态温度场进行计算,钛合金隔离罩由于受气隙磁场的交变作用,切割磁力线产生涡流损耗,而涡流损耗的大小与隔离罩材料的电导率有很大关系。首先计算了不同永磁体布置方式下的隔离罩涡流损耗,对比得当永磁体轴向分4段时隔离罩涡流损耗最小,利用Fluent软件求解此布置方式下10 min时传动装置,隔离罩及内外永磁体瞬态温度场。
10 min时磁耦合装置最高温度出现在热源钛合金隔离罩中心处,373 K,对比初始环境温度293 K,温升为80 ℃;外磁体最高点温度58 ℃,远低于N38UH永磁体不退磁安全温度200 ℃。内永磁体温升仅为20 ℃。整个传动装置从温度云图来看,温度梯度基本呈径向变化,同一半径处轴向温度基本保持一致,装置外隔离罩圆锥部分由于浸水环境和内充空气,热阻大,导致温升不明显。支架和轴部分虽然热导率大,由于远离热源和工作时轴浸入液体的原因,温度没有显著变化。此工作时长下,钛合金隔离罩温升在合理范围内,材料强度不受影响。
4 结 语本文计算了2D和3D不同永磁体排布方式下隔离罩的涡流损耗,优化得出最小损耗时的永磁体布置方式。利用Fluent软件对此布置方式下磁耦合装置,隔离罩、内外永磁体工作10 min的瞬态温度场进行了分析求解。结果表明,装置短时工作时,永磁体轴向分4段时隔离罩涡流损耗最小,温度最高点出现在隔离罩中心处,温度梯度基本呈径向分布,在保证装置安全性能的前提下,各主要部件温升在合理范围内。本研究可为水下电动力推进装置中磁耦合传动温度场分析提供一定的热力学计算依据。
| [1] | 于雅莉, 赵波. 水下磁耦合器隔离套涡流损耗及系统传动效率分析[J]. 电工技术学报, 2014, 29 (1): 15–22. |
| [2] | 赵克中. 磁耦合传动装置的理论与设计[M]. 北京: 化学工业出版社, 2009. |
| [3] | 王小雷, 樊晓波. 鱼雷磁耦合传动金属隔离罩分析与优化设计[J]. 鱼雷技术, 2014, 22 (5): 347–351. |
| [4] | 王梦文. 磁力耦合器隔离套涡流场与温度场的数值计算[J]. 机电工程, 2010 (8): 40–47. |
| [5] | CHARLESS J M. Magnetic Coupling Protects Machinery[J]. Design New, 1999, 7 : 26–28. |
| [6] | SMITH A C, WILLIAMSON S, BENHAMA A, et al. Magnetic Drive Couplings[J]. IEEE-EMD Conference, 1998, 153 (2): 289–294. |
| [7] | (美)英克鲁佩勒(Incropera, F. P.)等著; 葛新石, 叶宏译. 传热和传质基本原理: 第六版[M]. 北京: 化学工业出版社, 2007. |
 2017, Vol. 39
2017, Vol. 39
