0 引　言

水下航行器是世界各国海军均争相发展的武器装备，在水声探测技术日益完善、水下对抗日趋激烈的形势下，安静型水下航行器已成为各国海军追逐的目标^[1]。水下航行器尾部的主要结构一般为推进器、推进轴系与壳体的组合。理论计算及实测都表明水下航行器尾部壳体的振动在多数情况下高于其他舱段。因此开展水下航行器推进器-轴系-壳体耦合系统声振问题研究具有重要意义。

目前国内主要针对潜艇开展了大量桨-轴-艇体结构耦合振动的相关研究。曹贻鹏^[2]与张文平^[3]建立了带有推进轴系的潜艇尾部有限元模型，用有限元/边界元的分析方法研究了轴系纵振对艇体尾部结构水下声辐射特性的影响，并分析了螺旋桨激励力的传递路径，提出纵振减振的几种控制措施。陈发祥等^[4]分析了螺旋桨激励下轴系-艇体耦合系统的低频声辐射特性。邹明松^{[5 – 7]}利用三维水弹性力学理论，采用计及自由液面效应的理想可压流体Green函数，构建了船舶三维声弹性理论，并在Abaqus软件的基础上开发了三维水弹性声学分析软件Thafts-acoustic。该软件已经应用于多型水面、水下船舶、潜艇的声学设计、声学性能评估以及振动噪声机理探索与分析，并通过正确性与实用性系列试验考核验证。吴仕昊^[8]采用有限元/边界元法对带有复杂轴系子系统的桨-轴-艇耦合结构进行仿真分析。研究了螺旋桨激励力经轴系激励艇体所引起的艇体振动声辐射特性。对于鱼雷、无人潜航器等尺度相对小的水下航行器，与潜艇、船舶等相比，在结构、尺寸、振源特性、振动与声辐射关心频段等均存在较大差异，在推进器-轴系-壳体系统声振问题方面，一些声振规律并不相同，而国内针对该类水下航行器尚缺乏直接针对性的研究工作。

因此本文主要针对鱼雷、无人潜航器等尺度相对较小的水下航行器，建立了典型推进器-轴系-壳体整体结构振动与声辐射分析模型，运用三维声弹性理论和三维水弹性声学分析软件Thafts-acoustic计算分析了推进器-轴系-壳体系统在螺旋桨等典型激励力作用下的振动与声辐射规律。

1 水中结构三维声弹性理论

水中结构在内外激励下做微幅振动和变形假定条件下，可将连续结构处理成具有有限个自由度离散的系统（采用有限元等数值方法得到），其动力学方程可表示为：

${{\mathit{\boldsymbol{M}}}_S}\ddot u(t)\ + {{\mathit{\boldsymbol{C}}}_S}\dot u(t)\ + {{\mathit{\boldsymbol{K}}}_S}(t)\ = \ F_e(t)\ + \ F_p(t)\ \text{，}$

(1)

其中： ${{\mathit{\boldsymbol{M}}}_S}$ ， ${{\mathit{\boldsymbol{C}}}_S}$ ， ${{\mathit{\boldsymbol{K}}}_S}$ 分别为空气中干结构的质量矩阵，阻尼矩阵和刚度矩阵； $\ \ddot u(t)\ $ ， $\ \dot u(t)\ $ 和 $\ u(t)\ $ 为结构离散节点的加速度，速度和位移列向量；t为时间； $\ {F_e}(t)\ $ 为等效到结构离散节点上的非声介质流场外激励力列向量，包括机械激励力或其他激励力； $\ F_p(t)\ $ 为由声介质流场作用于结构体的动态力列向量。

采用模态叠加法求解结构系统的动态响应，离散系统节点位移可以表示为：

${{{\mathit{\boldsymbol{U}}}(t) = {\mathit{\boldsymbol{D}}}{\rm q}(t) = }}\sum\limits_{{{r = 1}}}^{{m}} {{{{{\mathit{\boldsymbol{D}}}}}_{{r}}}} {q_r}(t) \text{，}$

(2)

其中： $D_r$ ，（ $r = 1,2,...,m$ ）为第r阶模态对应的振型位移列向量； $q(t)$ ， ${q_r}(t)$ 分别为广义主坐标列向量及第r阶干模态的主坐标分量。

假设弹性结构体周围为均匀可压、无粘的理想声介质，以及由结构振动诱导的声波场都是微幅线性的。在此假设下，总的流场速度势可表示为各阶声波辐射速度势的线性叠加：

$\varPhi {{(x,y,z,t) = }}\sum\limits_{{{r = 1}}}^{{m}} {{\phi _{{r}}}(x,y,z,t)} \text{，} $

(3)

其中， $(x,y,z,t)$ 为场点坐标。

声波速度势 $\phi $ 满足Helmholt方程：

${\nabla ^2}\phi - \frac{{{\partial ^2}\phi }}{{\partial {t^2}}} = 0 \text{，} $

(4)

每一阶干模态振型的流固耦合湿表面边界条件：

$\frac{{\partial {\varPhi _r}}}{{\partial \overrightarrow n }} = i\omega ({u_r}{n_x} + {v_r}{n_y} + {w_r}{n_z}) \text{，} $

(5)

式中：u_r，v_r，w_r为第r阶干模态位移； $\overrightarrow n $ 为流固湿表面单位法向量。

与自由液面边界条件对应的Green函数为：

${{G(P,Q) = }}\frac{{\rm{1}}}{{{\rm{4}}\pi {r_1}}}{e^{ - ik{r_1}}} - \frac{{\rm{1}}}{{{\rm{4}}\pi {r_2}}}{e^{ - ik{r_2}}} \text{，} $

(6)

式中： ${r_1} = \sqrt {{{(x - {x_0})}^2} + {{(y - {y_0})}^2} + {{(z - {z_0})}^2}} $ ； ${r_2} = \sqrt {{{(x - {x_0})}^2} + {{(y - {y_0})}^2} + {{(z + {z_0})}^2}} $ ；

$k = \omega /{c_0}$ 为流体中声波波数； $({x_0},{y_0},{z_0})$ 为源点在平衡坐标系中的坐标。

针对各阶干模态得到的对应的简单源边界积分方程：

$\phi (P) = \frac{1}{{4\pi }}\iint {\sigma (Q)} {{G(P,Q)d}}{{{S}}_{{Q}}} \text{，} $

(7)

式中： $\sigma (Q)$ 为结构体湿表面上的源强。

流场中的辐射波声压为：

$\begin{split}p(x,y,z,t) = & - \rho \sum\limits_{{{r = 1}}}^{{m}} {\frac{{\partial {\phi _{\rm{r}}}}}{{\partial {{t}}}}} = \\& - \rho \sum\limits_{{{r = 1}}}^{{m}} {(i\omega )\{ {{G(P,Q)d}}{{{S}}_{{Q}}}\} } \text{。}\end{split}$

(8)

振动加速度级的计算公式如下：

${L_a}(\omega ) = 20\lg \frac{{a(\omega )}}{{{a_0}}} \text{，} $

(9)

其中： $a(\omega )$ 为加速度谱值；基准值 ${a_0} = 1 \times {10^{ - 6}}({\rm m}/{{\rm s}^2}) \cdot {{\rm Hz}^{ - 1/2}}$

场点声压级的计算公式如下：

${L_p}(\omega ) = 20\lg \frac{{p(\overrightarrow r ,\omega )}}{{{p_0}}} \text{，} $

(10)

其中： $p(\overrightarrow r ,\omega )$ 为场点声压谱值； $\overrightarrow r $ 为场点坐标；基准值 ${p_0} = 1 \times {10^{ - 6}}{\rm Pa} \cdot {{\rm Hz}^{ - 1/2}}$ 。

由辐射声功率换算声源级的公式为：

${L_S}(\omega ) = 10\lg \frac{{P(\omega )}}{{{P_0}}} \text{。} $

(11)

其中： $P(\omega )$ 为浮体辐射的声功率量值；基准值 ${P_0} = 4\pi {p_0}^2/({\rho _0}{{\rm{c}}_0})$ 。

对于单位力扫频激励的情况，式（9）和式（10）中的振动加速度、声压均取有效值。

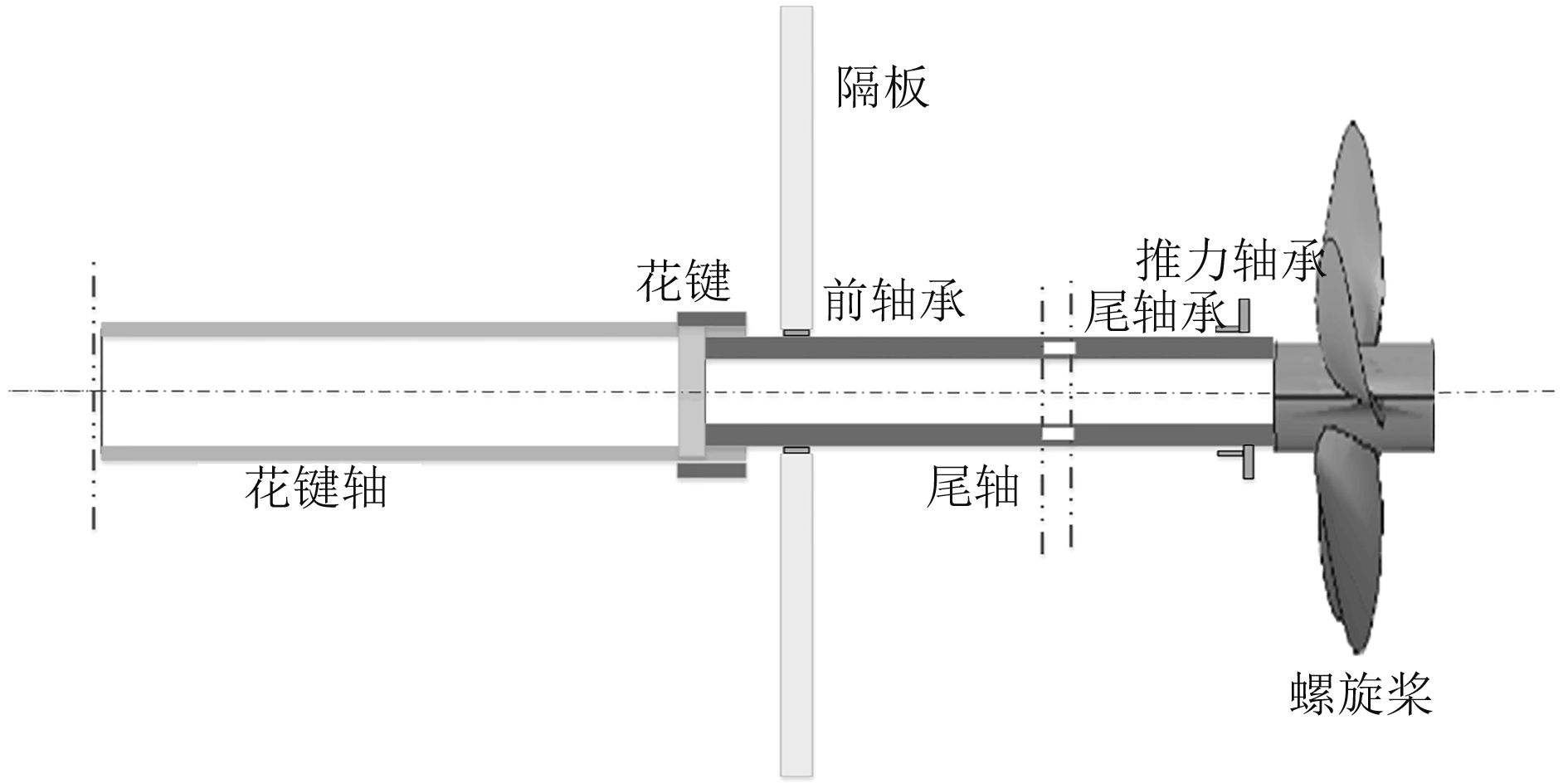
2 推进器-轴系-壳体系统振动与声辐射分析模型 2.1 推进器-轴系结构

典型的水下航行器推进轴系结构一般分2段，花键轴和尾轴。靠近发动机或电动机一端的花键轴通过弹性联轴器与动力输出轴相连，花键轴后段通过花键与尾轴相连，尾轴后端与推进器转子相连。这种短轴系在径向上一般有2处轴承支撑。前轴承通常用滚动轴承支撑在隔板上，后轴承通常为滑动轴承，推力轴承采用尾置式，推进器转子产生的推力通过推力轴承传递到尾部壳体^[11]。简化的推进器-轴系结构如图1所示。

2.2 推进器-轴系-壳体系统模型

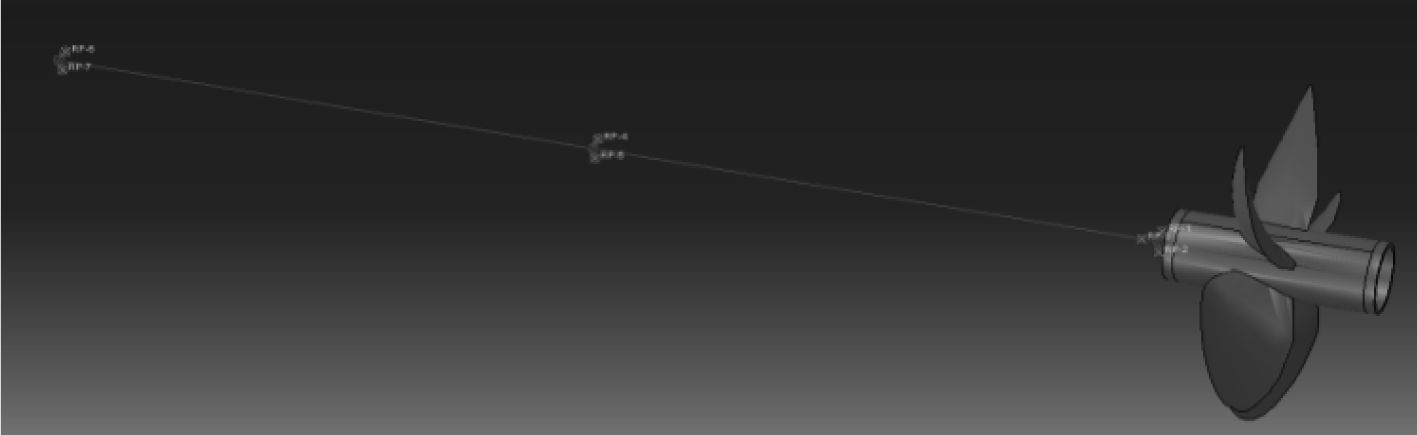
参照水下航行器基本的推进器-轴系结构和壳体结构在Abaqus中建立推进器-轴系-壳体系统模型。对推进器-轴系结构，花键轴前端与动力输出轴相连，这里只保留了花键轴及尾轴部分，将动力输出轴对花键轴前端的支撑作用等效为与2个水平和垂向的弹簧单元连接。花键采用等效轴段法处理，轴系采用1D梁单元模拟。将轴承与轴系的连接简化为弹簧弹性支撑，由于支撑轴承对轴系主要起到水平和垂向约束，所以将前支撑轴承模拟为水平和垂向弹簧，将尾后部支撑轴承与推力轴承对轴系的共同作用简化为水平、垂向和纵向的弹簧连接。螺旋桨选取的是5叶三维弹性桨, 用3D实体单元模拟，在螺旋桨桨毂内表面与轴建立约束关系。建立的推进器-轴系结构模型如图2所示。

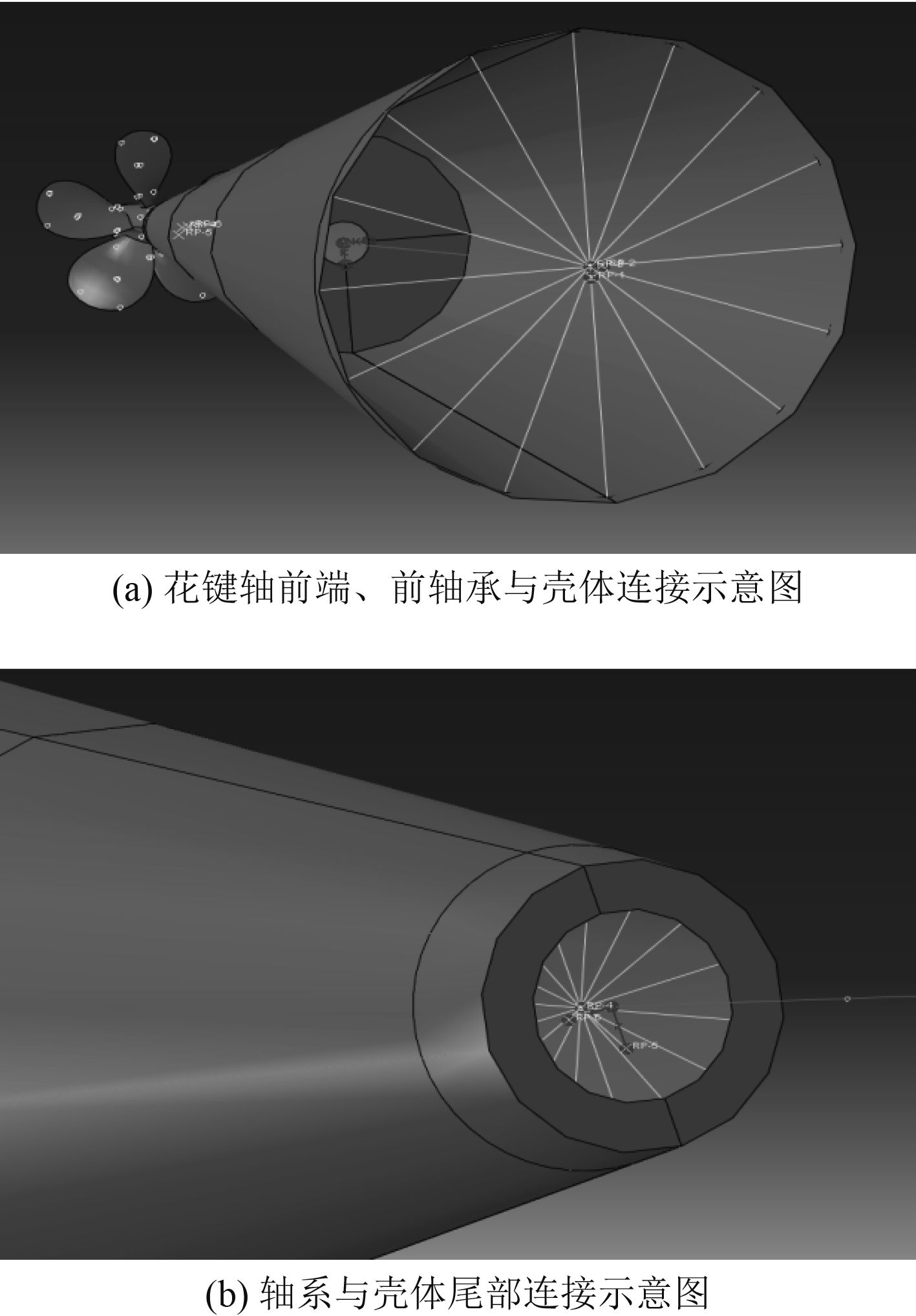
水下航行器通常为舱段结构，舱段之间为隔板，且壳体内部布置有环肋。不考虑内部质量的影响，在建立的推进器-轴系结构模型基础上，增加分舱段、含隔板和环肋的壳体结构。将轴系模型中简化轴承的弹簧一端与轴系在相应的轴承位置处相连，另一端与壳体结构在轴承相应位置处连接，模型的连接如图3所示。

建立完成的完整的推进器-轴系-壳体耦合系统模型如图4所示。为利用三维水弹性声学分析软件，还需建立壳体结构与流体接触的湿表面，以及螺旋桨与流体接触的湿表面。

3 推进器-轴系-壳体系统振动与声辐射特性分析 3.1 推进器-轴系-壳体系统振动特性分析

推进器-轴系-壳体系统通过轴系传递的主要激励力包括来自发动机的激励力和推进器的激励力。以花键轴前端横向激励、花键轴前端纵向激励、螺旋桨横向激励、螺旋桨纵向激励等4种典型激励工况为例，研究分析推进器-轴系-壳体系统的振动特性。在花键轴前端处施加横向非定常单位激励力与纵向非定常单位激励力，模拟来自发动机的激励，在三维弹性桨桨叶0.7R处施加横向非定常单位激励力与纵向非定常单位激励力，模拟推进器的激励力，激励频率均为1~600 Hz。激励力施加位置如图5所示。

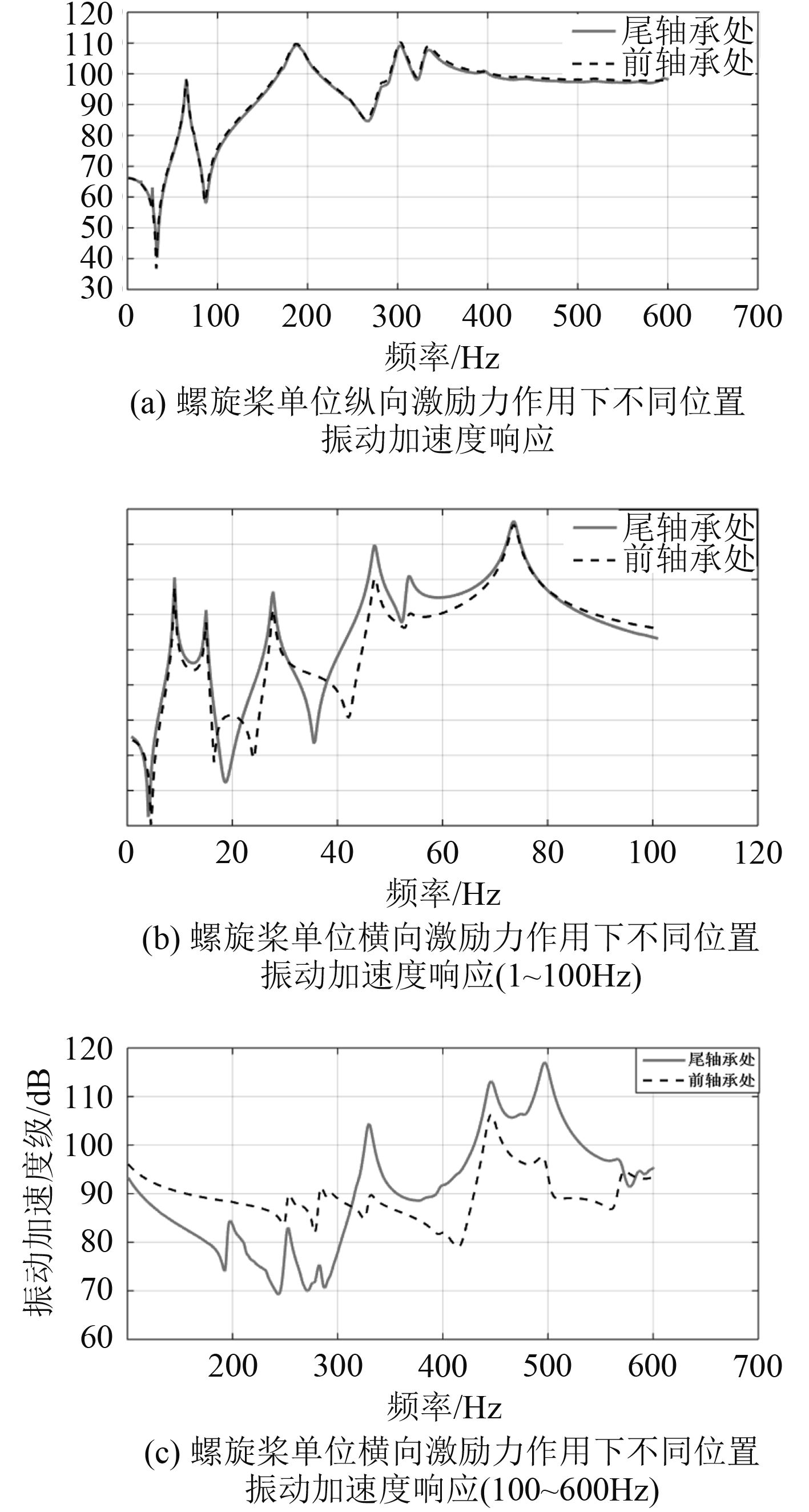
计算分析4种激励工况下在尾轴承和前轴承与壳体连接位置处的振动加速度响应，如图6所示。

由图6可以看出：

1）不论是来自螺旋桨，还是来自花键轴前端，在纵向非定常激励力作用下，尾轴承、前轴承与壳体连接处振动加速度响应曲线趋势一致，振动响应效果基本相同，但前轴承处振动加速度级略大。

2）螺旋桨横向激励力作用下，1~100 Hz的低频段内，在几个峰值频率处尾轴承处振动加速度响应均高于前轴承；100~300 Hz频段内，前轴承处的振动加速度响应整体高于尾轴承处；大于300 Hz, 尾轴承处的振动在几个峰值频率处，振动加速度响应均明显高于前轴承。推进器-轴系-壳体系统受花键轴前端横向非定常单位激励力的作用规律与之类似。

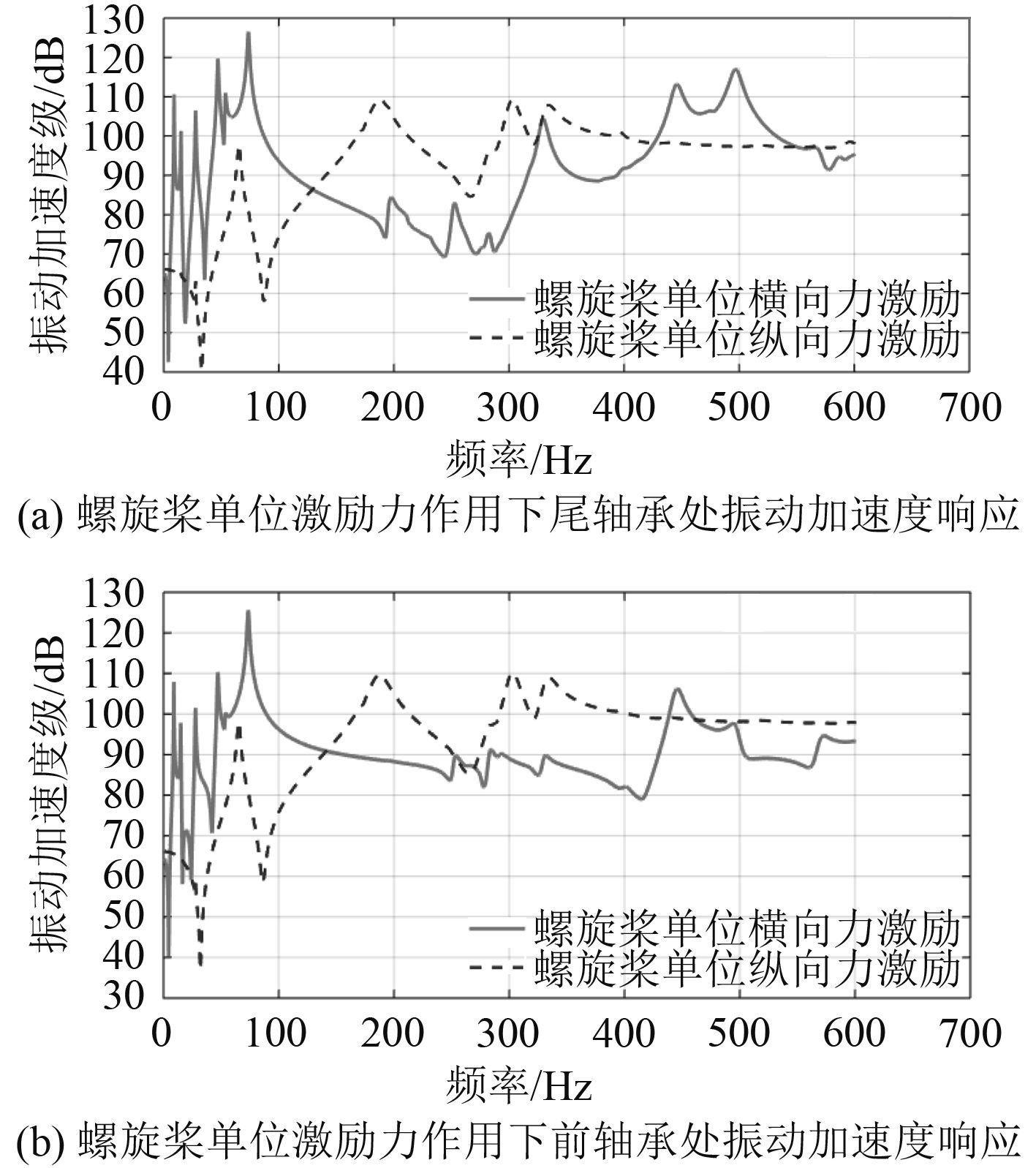
对比分析螺旋桨非定常单位激励力作用下在前轴承、尾轴承与壳体连接处的振动响应，结果如图7所示。

由图7可以看出，1~100 Hz低频段内，前轴承和尾轴承处受螺旋桨横向单位激励力作用产生的振动加速度响应均明显高于螺旋桨纵向单位激励力作用下的振动加速度响应；在140~440 Hz频段内，前轴承和尾轴承处受螺旋桨纵向单位激励力作用产生的振动响应明显高于横向单位激励力作用。

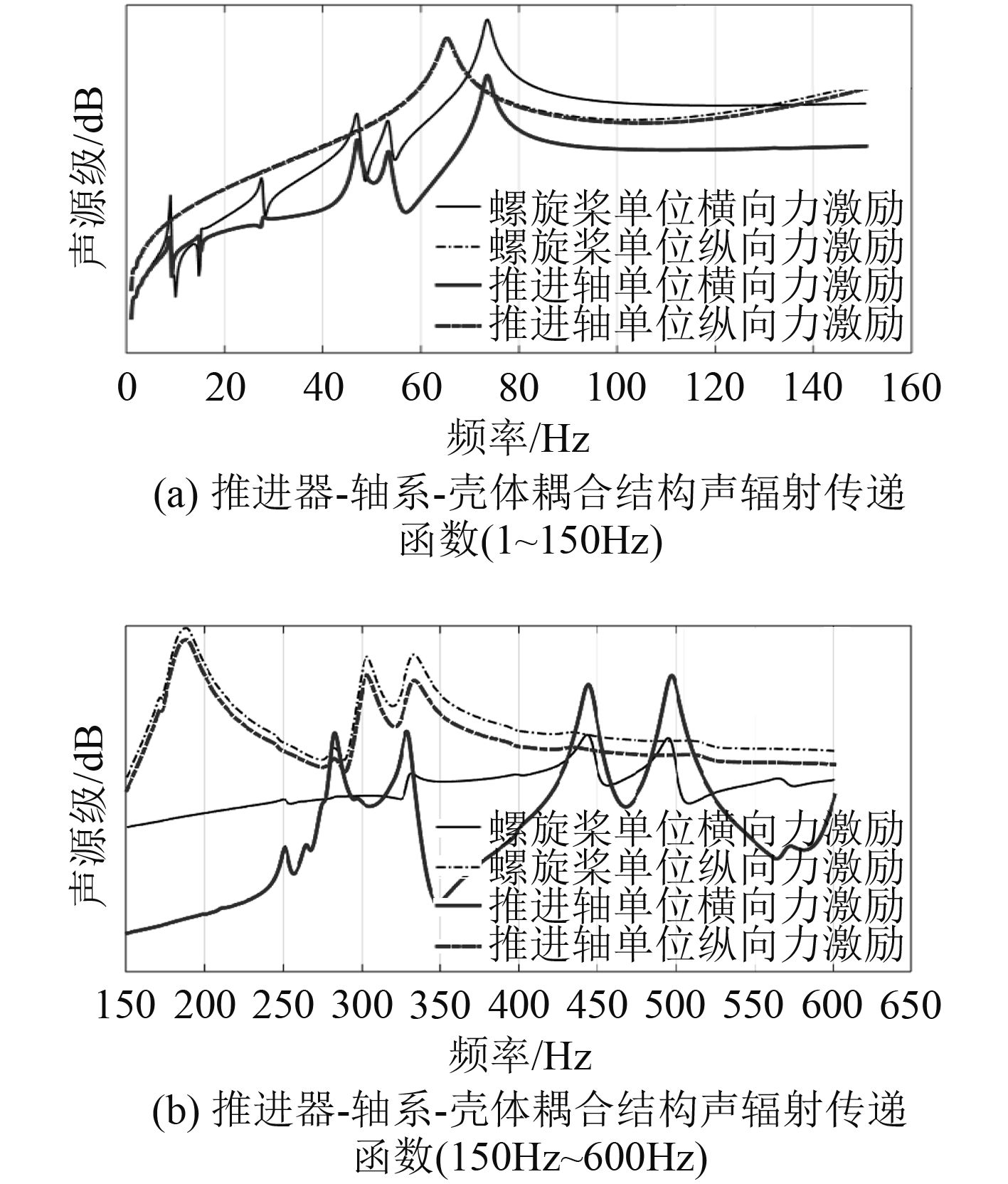
3.2 推进器-轴系-壳体系统声辐射特性分析

采用建立的推进器-轴系-壳体系统模型和三维声弹性计算方法，计算3.1节4种激励工况下推进器-轴系-壳体耦合结构声辐射传递函数，结果如图8所示。

图8给出了螺旋桨单位横向力、纵向力以及推进轴上单位横向力、纵向力激励下耦合结构的声辐射传递函数对比曲线。从图中可以看出：

1）在70 Hz以下的低频段以及140~500 Hz频段内螺旋桨纵向非定常单位激励力作用下耦合结构的声辐射明显大于横向激励力作用下的声辐射，这是由于耦合结构的纵向振动以及纵向模态辐射效率高造成的；在70~140 Hz频段内螺旋桨横向非定常单位激励力作用下耦合结构的声辐射明显大于纵向激励力下的声辐射，这是由于耦合结构的弯曲振动引起的。

2）在小于300 Hz的频段内，耦合结构受螺旋桨纵向非定常单位激励力与受轴上纵向非定常单位激励力作用引起的声辐射效果基本相同，随着激励频率的提高，声辐射传递函数曲线趋势仍然一致，但螺旋桨上单位纵向力激励高于轴上单位纵向力激励引起的声辐射。

3）在小于250 Hz的频段内，耦合结构受螺旋桨上横向非定常单位激励力引起的声辐射明显大于受轴上横向非定常单位激励力引起的声辐射，在高于250 Hz的频段内，耦合结构受轴上横向非定常单位激励力引起的声辐射起伏较大，在峰值频率处明显大于受螺旋桨上横向非定常单位激励力引起的声辐射。

3.3 典型激励工况振动声辐射声压指向性分析

利用三维声弹性计算方法计算4种激励工况下声辐射峰值频率处的辐射声压云图，结果如图9所示。由此可以分析耦合结构横向激励和纵向激励作用下水下声辐射亮点区域。

由图9可以看出，声辐射峰值频率处耦合结构受螺旋桨纵向激励时辐射声压主要集中在在头部和尾部的锥壳部分，受螺旋桨横向激励时辐射面在壳体两侧。在峰值频率处，受螺旋桨横向激励和纵向激励时都会导致头部有较强的辐射声压，说明这类水下航行器在受到尾部横向和纵向激励时，对头部均会有很大的影响，因此在对水下航行器的头部声学换能器进行声学设计时应给予重视。

4 结　语

本文针对尺度相对较小的水下航行器，运用三维声弹性理论，分析了推进器-轴系-壳体系统的振动与声辐射特性，主要得出以下结论：

1）不论是来自螺旋桨，还是来自花键轴前端轴上，在纵向非定常激励力作用下，尾轴承、前轴承与壳体连接处振动加速度响应曲线趋势均一致，振动响应效果基本相同，但前轴承处振动加速度级略大。

2）1~100 Hz低频段内，前轴承和尾轴承处受螺旋桨横向单位激励力作用产生的振动加速度响应均明显高于螺旋桨纵向单位激励力作用下的振动加速度响应；在140~440 Hz频段内，前轴承和尾轴承处受螺旋桨纵向单位激励力作用产生的振动响应明显高于横向单位激励力作用。

3）在中低频段内，推进器-轴系-壳体耦合结构受螺旋桨纵向非定常单位激励力与受花键轴前端纵向非定常单位激励力作用引起的声辐射效果基本相同，随着激励频率的提高，声辐射传递函数曲线趋势仍然一致但螺旋桨上单位纵向力激励高于轴上单位纵向力激励引起的声辐射。

4）声辐射传递函数峰值频率处，耦合结构受螺旋桨纵向激励时辐射声压主要集中在头部和尾部的锥壳部分，受螺旋桨横向激励时辐射面在壳体两侧。