水下机器人是海洋开发、水下探测中非常重要的工具,在进行水下作业过程中,海洋环境对水下机器人的影响至关重要。比如海水温度会影响探测设备的正常工作,盐度会对水下机器人系统造成严重的腐蚀,可见度则影响水下作业的精确度。在各类海洋环境因素中,对水下机器运动产生决定性影响的是海流[1]。目前海流对水下机器人运动规律影响的研究主要采用的是相对运动的方法,以计算域的运动来模拟水下机器人的运动[2],这种方式有失真实性。
本文以数值模拟的方法,采用动网格技术以六自由度运动方式(6DOF)来研究海流速度对水下机器人运动特性的影响。通过改变计算域速度入口的来流速度来模拟不同的海流速度[3],然后观察水下机器人系统在不同的海流速度下,受到恒定的力与力矩时的运动规律。首先根据所选的水下机器人系统几何要素构造三维几何模型[4],其次是构建结构网格与非结构网格混合计算域[5],以计算流体力学方法在整个计算域内求解其控制方程。以此对不同海流速度、不同受力情况下的水下机器人的运动特性进行模拟和观察。并从中分析、总结出某些一般性的结论。
1 数学模型及计算方法 1.1 控制方程与湍流模型计算中设定流体为不可压缩粘性流体,则水下机器人系统在运动过程中其周围流场的控制方程如下[6]:
连续性方程:
| $\frac{{\partial {u_x}}}{{\partial x}} + \frac{{\partial {u_y}}}{{\partial y}} + \frac{{\partial {u_z}}}{{\partial z}} = 0\text{,}$ | (1) |
动量方程:
| $\begin{aligned}\rho \left( {\frac{{\partial {{\rm{u}}_x}}}{{\partial t}} + {u_x}\frac{{\partial {{\rm{u}}_x}}}{{\partial x}} + {u_y}\frac{{\partial {{\rm{u}}_x}}}{{\partial y}} + {u_z}\frac{{\partial {{\rm{u}}_x}}}{{\partial z}}} \right) =\\- \frac{{\partial p}}{{\partial x}} + \nu \rho \left( {\frac{{{\partial ^2}{{\rm{u}}_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{{\rm{u}}_x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{{\rm{u}}_x}}}{{\partial {z^2}}}} \right)\text{,}\end{aligned}$ | (2) |
| $\begin{aligned}\rho \left( {\frac{{\partial {{\rm{u}}_y}}}{{\partial t}} + {u_x}\frac{{\partial {{\rm{u}}_y}}}{{\partial x}} + {u_y}\frac{{\partial {{\rm{u}}_y}}}{{\partial y}} + {u_z}\frac{{\partial {{\rm{u}}_y}}}{{\partial z}}} \right) =\\- \frac{{\partial p}}{{\partial y}} + \nu \rho \left( {\frac{{{\partial ^2}{{\rm{u}}_y}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{{\rm{u}}_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{{\rm{u}}_y}}}{{\partial {z^2}}}} \right)\text{,}\end{aligned}$ | (3) |
| $\begin{aligned}\rho \left( {\frac{{\partial {{\rm{u}}_{\rm{z}}}}}{{\partial t}} + {u_x}\frac{{\partial {{\rm{u}}_z}}}{{\partial x}} + {u_y}\frac{{\partial {{\rm{u}}_z}}}{{\partial y}} + {u_z}\frac{{\partial {{\rm{u}}_z}}}{{\partial z}}} \right) =\\- \frac{{\partial p}}{{\partial z}} + \nu \rho \left( {\frac{{{\partial ^2}{{\rm{u}}_z}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{{\rm{u}}_z}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{{\rm{u}}_z}}}{{\partial {z^2}}}} \right)\text{。}\end{aligned}$ | (4) |
式(1)~式(4)中,
流场中的流体湍流流动采用标准的RNG
| $\begin{split}& \frac{{\partial \rho k}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}(\rho {u_j}k) = - \frac{2}{3}\rho k\frac{{\partial {u_k}}}{{\partial {x_j}}} +\\ &\frac{\partial }{{\partial {x_j}}}(\frac{{{\mu _{eff}}}}{{{\sigma _k}}}\frac{{\partial k}}{{\partial {x_j}}}) + {G_k} - \rho \varepsilon \text{,}\end{split}$ | (5) |
| $\begin{array}{l}\displaystyle\frac{{\partial \rho \varepsilon }}{{\partial t}} + \displaystyle\frac{\partial }{{\partial {x_j}}}(\rho {u_j}\varepsilon ) = - [(\displaystyle\frac{2}{3}{C_{\varepsilon 1}} - {C_{\varepsilon 3}} + \displaystyle\frac{2}{3}{C_\mu }{C_\eta }\displaystyle\frac{{k\partial {u_k}}}{{\varepsilon \partial {x_k}}})\rho \varepsilon \displaystyle\frac{{\partial {u_k}}}{{\partial {x_k}}}\\ \quad\quad+ \displaystyle\frac{\partial }{{\partial {x_j}}}(\displaystyle\frac{{{\mu _{eff}}}}{{{\sigma _\varepsilon }}}\displaystyle\frac{{\partial \varepsilon }}{{\partial {x_j}}})] + \rho \displaystyle\frac{\varepsilon }{k}[({C_{\varepsilon 1}} - {C_\eta }){C_k} - {C_{\varepsilon 2}}\rho \varepsilon ]\text{,}\ \; \, \end{array}$ | (6) |
式中:
本文所采用的水下机器人主体是一水滴流线型柱体结构,主体总长L=510 mm,最大宽度B=320 mm,距首部约3/5L处,总高H=240 mm。左、右舷侧对称布置一导管螺旋桨,主要用于驱动主体转向的用途;尾部布置一导管螺旋桨,主要用于对主体产生向前或向后的推力[2]。为了能够使用6DOF模型进行数值模拟,在建模过程中采用细小的连接构件将整个水下机器人系统连接为一个整体。所构建的水下机器人系统三维几何模型如图1所示。
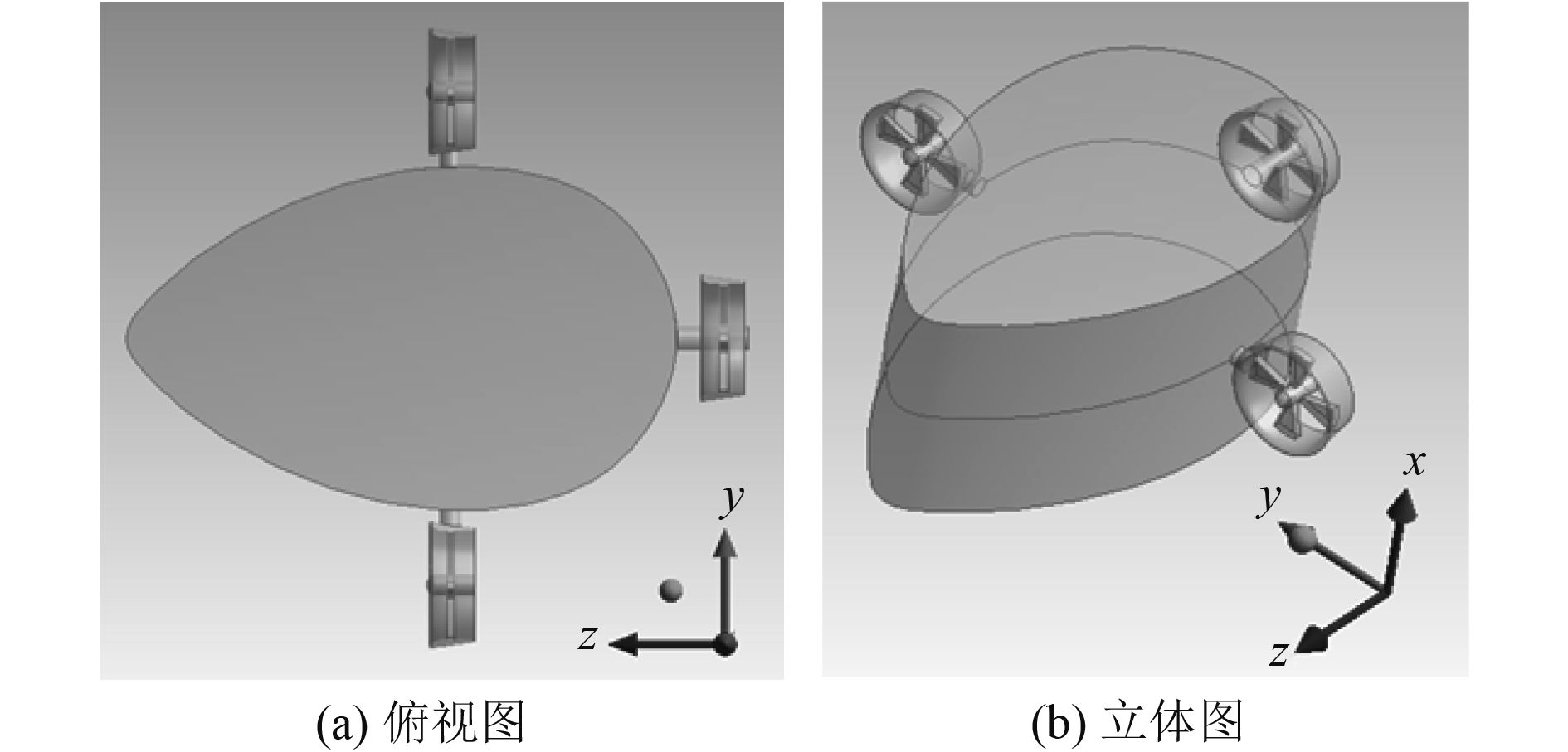
|
图 1 导管螺旋桨几何模型 Fig. 1 Geometric model of catheter propeller |
数值模拟的计算域、水下机器人系统几何模型位置如图2所示。水下机器人位于计算域的中央,非结构网格计算域Ⅰ为水下机器人的运动区域,结构网格计算域Ⅱ为外围计算域[8]。各计算域几何尺寸、网格数量、网格类型见于表1,计算域网格见于图3。
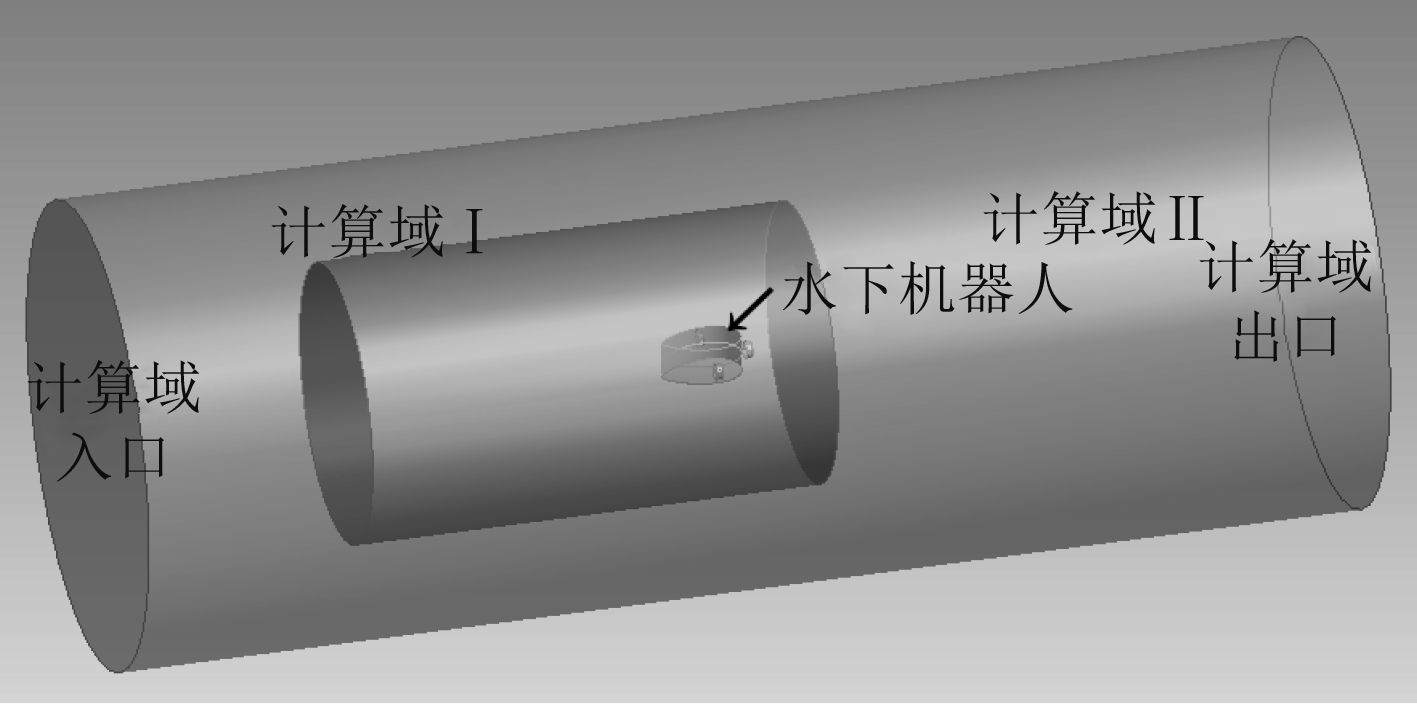
|
图 2 水下机器人系统计算域 Fig. 2 Computing domain of underwater robot system |
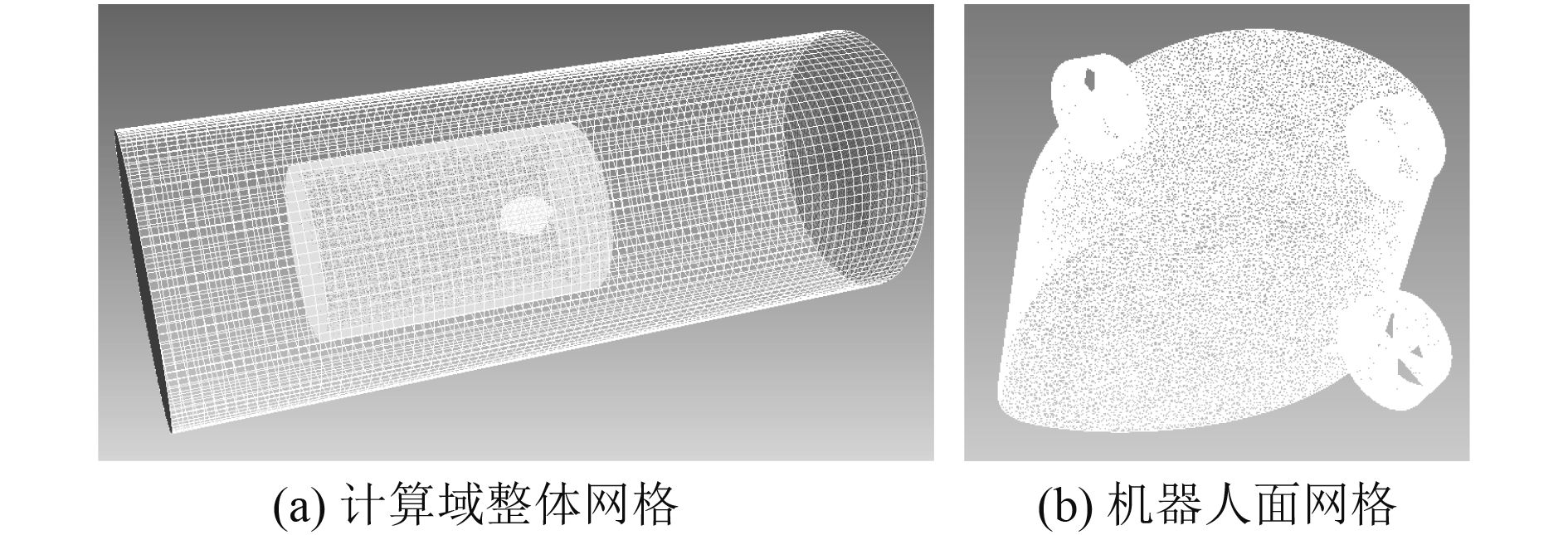
|
图 3 水下机器人系统计算域网格 Fig. 3 Computing domain grid of underwater robot system |
|
|
表 1 水下机器人系统计算域网格信息 Tab.1 Computing domain grid information of underwater robot system |
将一个整体计算域划分为结构网格计算域、非结构网格计算域2种不同类型的网格计算域,主要是为了能够让水下机器人实现多自由度运动的同时(水下机器人的运动不能超出计算域Ⅰ)[9],尽量减少网格数量,减少计算的时间成本,并且保证计算精度。
在进行数值计算时,首先要设定每一个计算域边界的边界条件以及水下机器人系统的表面条件。表2给出了文中各子计算域之间的边界条件类型。
|
|
表 2 水下机器人系统边界条件 Tab.2 Boundary conditions of underwater robot system |
区域Ⅰ与区域Ⅱ之间相互重合的面,是2个计算域之间的交界面。采用界面耦合技术(interface)处理可以使2个计算域流通,使之形成一个完整的计算域[2]。
1.4 网格更新方式本文的数值计算中,水下机器人系统的运动采用真实的机器人在流体中运动,利用动网格技术来实现[10]。这种技术主要采用网格拉伸、压缩、增加、减少网格或者通过网格的局部重构来实现计算域的改变。动网格更新方法主要有3种:光顺方法(Smoothing)、动态层方法(Layering)、及局部重构(Remeshing)[11]。本文采用的是弹簧光顺与局部重构相结合的网格更新方式。
1.5 6DOF计算方法Fluent中的6DOF计算模型用于计算刚体在流体作用下的运动参数(速度、角速度等)、运动轨迹(重心位置)。在该模型中,物体或边界的运动是由作用在其上的力、力矩以及其自身所受的重力、初始推力等外力的共同作用决定[11]。所以物体的运动与流场的计算相互耦合,这种运动我们称之为耦合运动。
在本文的计算中,通过UDF调用“DEFINE_SDOF_PROPERTIES”宏对水下机器人施加恒定的力与力矩,并在UDF里面释放水下机器人2个方向(Z轴方向和Y轴方向)的平动自由度与一个方向(绕X轴方向)的转动自由度,通过改变计算域速度入口的边界条件模拟不同的海流速度[11]。以此观察水下机器人在这样一种受力情况下,在不同海洋环境中的耦合运动规律。
2 数值模拟结果假定水下机器人所受浮力与重力时刻相等,即不考虑重力与浮力的影响。对于文中涉及的速度、力的方向,这里统一给出定义:如图1(b)所示,Z方向为前进方向,正值表示前进,负值表示后退;Y方向为左右方向,正值表示右方向,负值表示左方向。Z方向和Y方向的速度、力为正值表示方向与Z轴正方向、Y轴正方向一致,反之,则相反[12];
2.1 逆向来流、无转矩恒定推力作用假定水下机器人系统3个位置的螺旋桨发出的推力大小相等,恒为10 N,则水下机器人受到30 N的恒定推力作用,不受转矩。
图4给出了水下机器人在逆向海流速度为0,0.1 m/s,0.3 m/s,0.5 m/s时,受到Z轴正方向恒定为30 N推力作用下重心的运动轨迹曲线。横坐标表示Z方向,纵坐标表示Y方向。

|
图 4 逆向来流轨迹曲线 Fig. 4 Trajectory curve under reverse flow |
从图4中看到,水下机器人在受到恒定推力、零转矩作用时,在运动过程中受海流影响明显:在低流速时,水下机器人的运动轨迹接近为直线,左右摆动微小;随着海流速度的增加,左右摆动的幅度逐渐增加,而且增速越来越快;在运动一段距离后会出现明显的偏航,随着流速的增加,偏航的幅度也越来越大,且发生偏航时在Z方向的运动距离大幅度提前。
之所以会出现上述的运动规律,原因在于:水下机器人在水下运动过程中,是迎着来流(海流)运动,这种迎流运动会使水下机器人周围的流场发生剧烈变化,造成水下机器人表面左舷与右舷、首部与尾部出现流速差,流速不相等会导致压力分布不均匀,产生压力差。最终使得水下机器人的运动出现左右摇摆以及偏航。随着海流速度的增加,这种由于流场变化而导致的压力差会急剧增加,使得水下机器人的左右摇摆以及偏航更加剧烈。
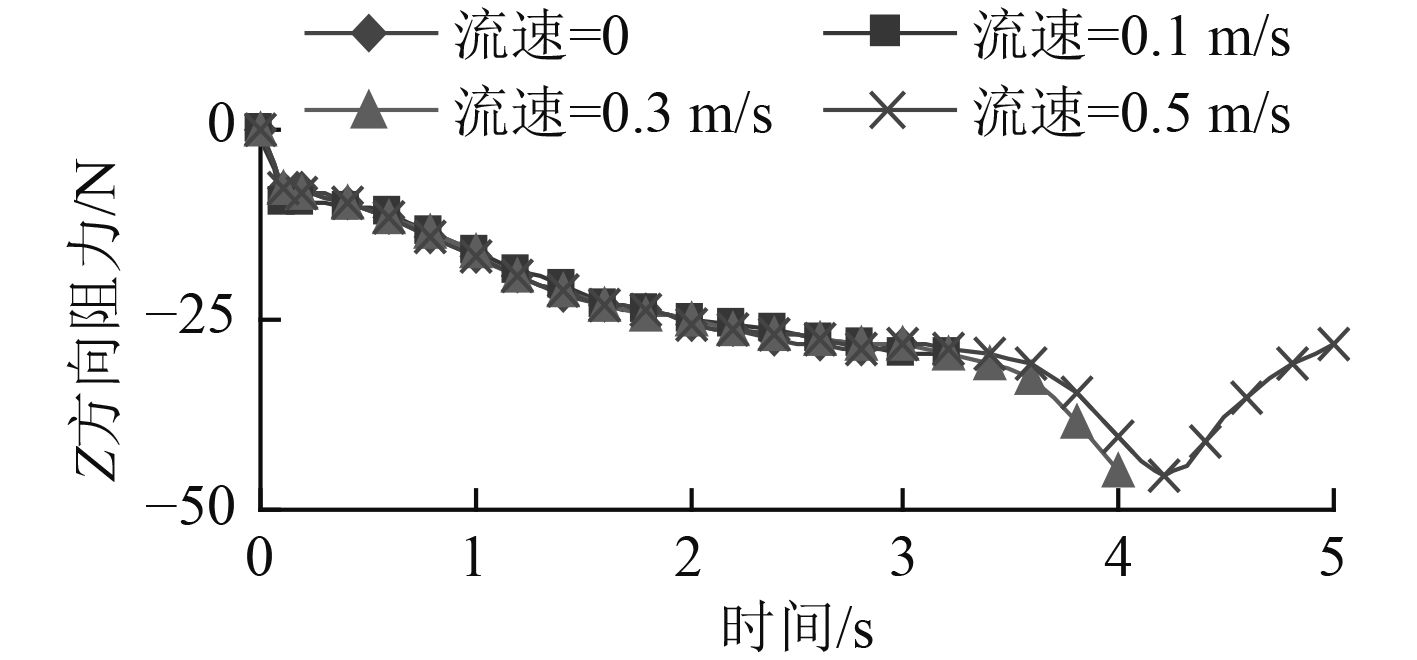
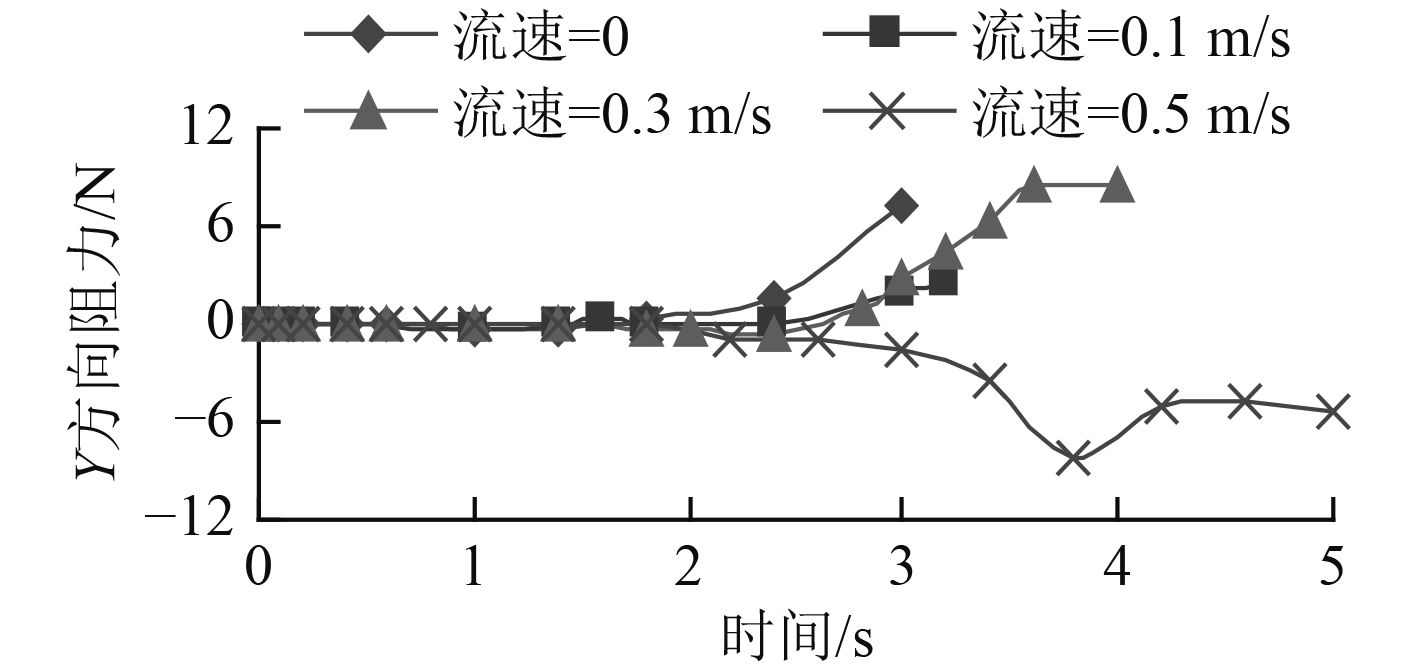
图5,图6,图7,图8分别给出了水下机器人Z方向速度,Y方向速度随时间变化曲线和Z方向阻力,Y方向阻力随时间变化曲线。
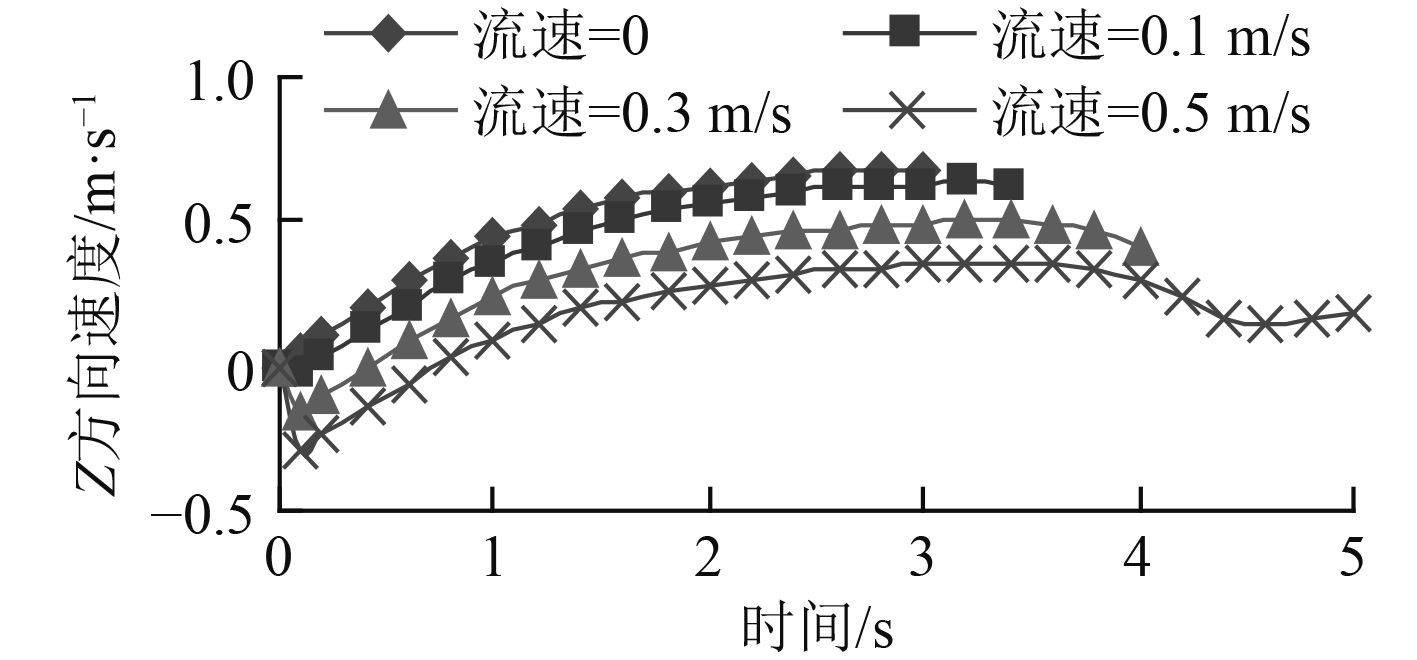
|
图 5 逆向来流Z方向速度曲线 Fig. 5 Z direction velocity curve under reverse flow |

|
图 6 逆向来流Y方向速度曲线 Fig. 6 Y direction velocity curve under reverse flow |
|
图 7 逆向来流Z方向阻力曲线 Fig. 7 Z direction resistance curve under reverse flow |
|
图 8 逆向来流Y方向阻力曲线 Fig. 8 Y direction resistance curve under reverse flow |
图7、图8为图5、图6速度曲线对应下的水下机器人流体阻力曲线。由于水下机器人是受恒定推力作用,因此,从图7、图8和图5、图6可以看到:阻力曲线与速度曲线完全对应,在速度曲线斜率变小(加速度变小)时,此时水下机器人受到的流体阻力变大,在恒定推力的作用下,必然会导致运动方向合外力的减小。根据牛顿第二定律,在质量不变时,合外力减小,加速度减小;而阻力减小时,则相反,加速度在增加。
从图4~图8中可以看到,水下机器人在受到恒定推力、零转矩作用,在不同的逆向海流速度下运动时,无论是位移轨迹曲线还是速度随时间的变化曲线都出现明显的不同:随着海流速度的增加,运动的不稳定性逐渐增加,而且增速越来越快。
2.2 顺向来流、无转矩恒定推力作用水下机器人在水下作业过程中,由于海洋环境的复杂性,所遭受到的海流既有逆流,也有顺流,还会有侧流的情况。作为对比,本节给出在顺向来流影响下,水下机器人系统的运动规律以及运动特性。
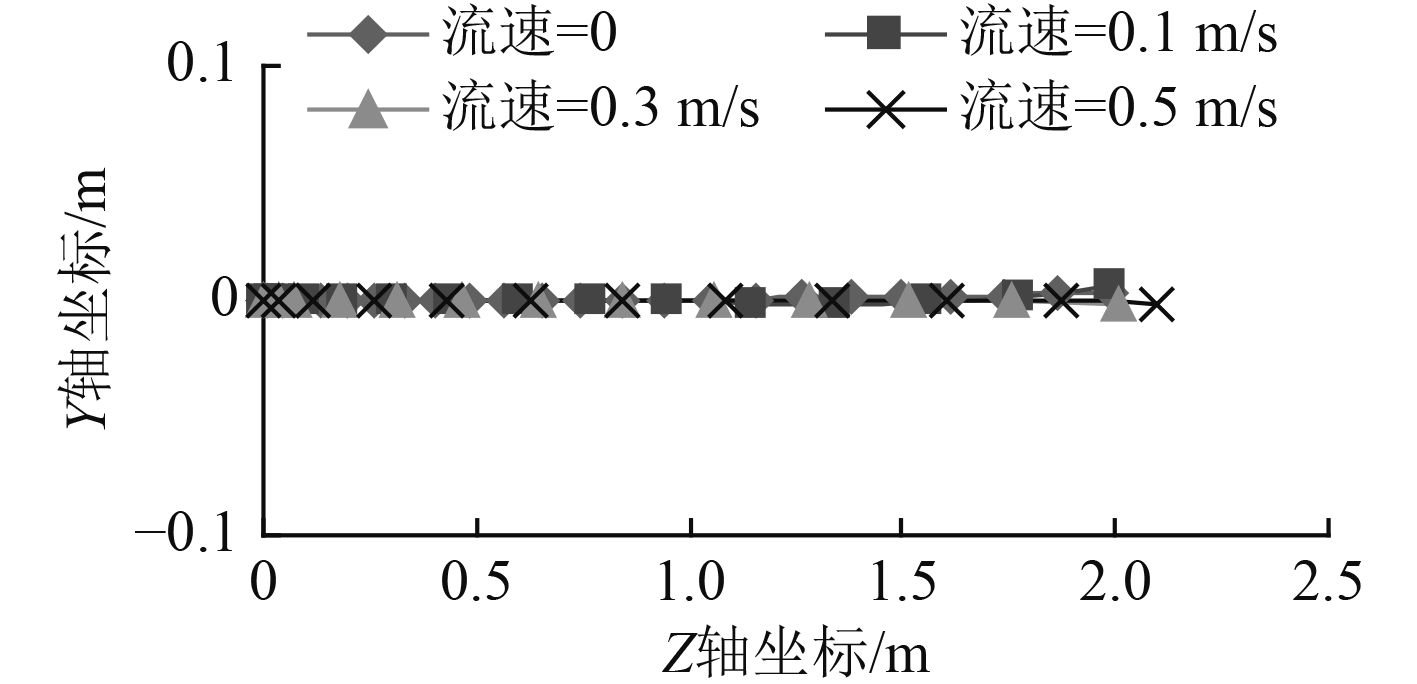
图9为水下机器人在顺向海流速度为0 m/s,0.1 m/s,0.3 m/s,0.5 m/s时,受到Z轴正方向恒定为30 N的推力作用下重心的运动轨迹曲线。
|
图 9 顺向来流轨迹曲线 Fig. 9 Trajectory curve under forward flow |
从图9中看到,在顺向来流时,无论来流速度多大,水下机器人的运动都呈现出明显的直线性,几乎不会出现左右方向的摆动,且这种运动规律一直延续到计算终止。只有在低速海流(流速小于0.1 m/s)时,才会在运动后期出现微小的偏航。作为对比,在图4中看到,逆向来流时,水下机器人的运动会有明显的左右摆动,且在运动后期出现较大的偏航。说明逆向来流时,水下机器人所处流场明显复杂于顺向来流。这种运动特性可以为选择水下机器人下水位置提供参考。
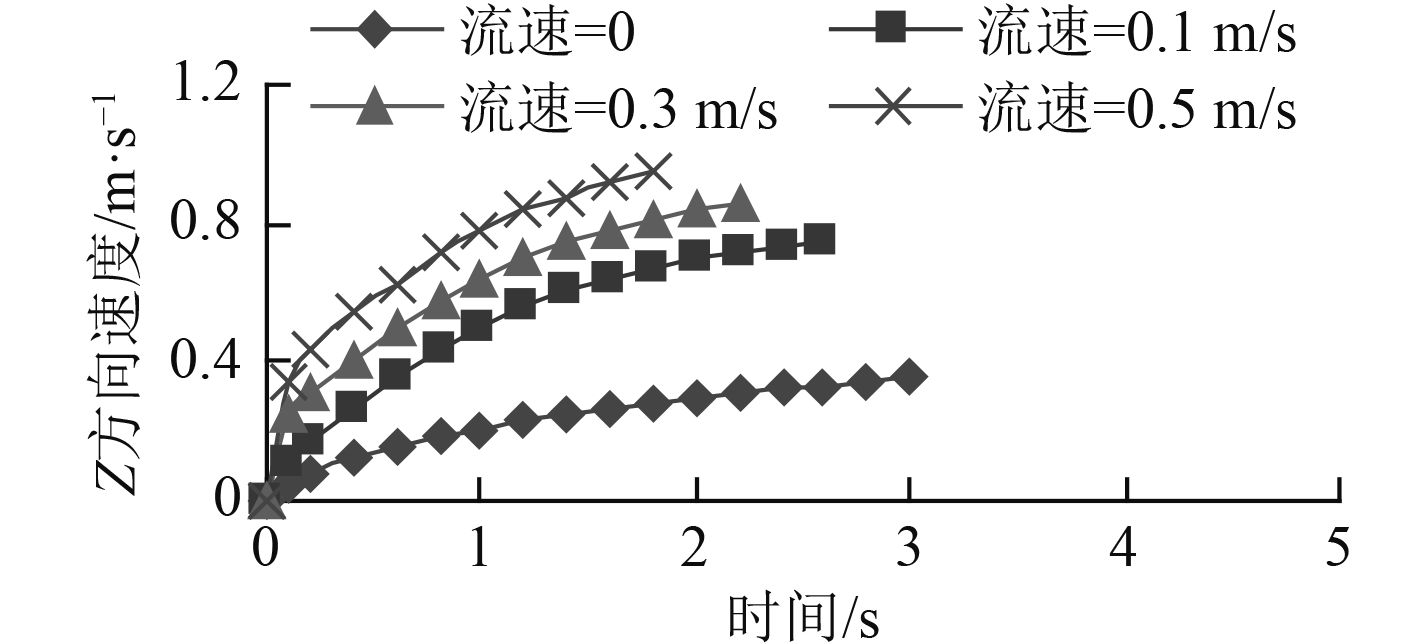
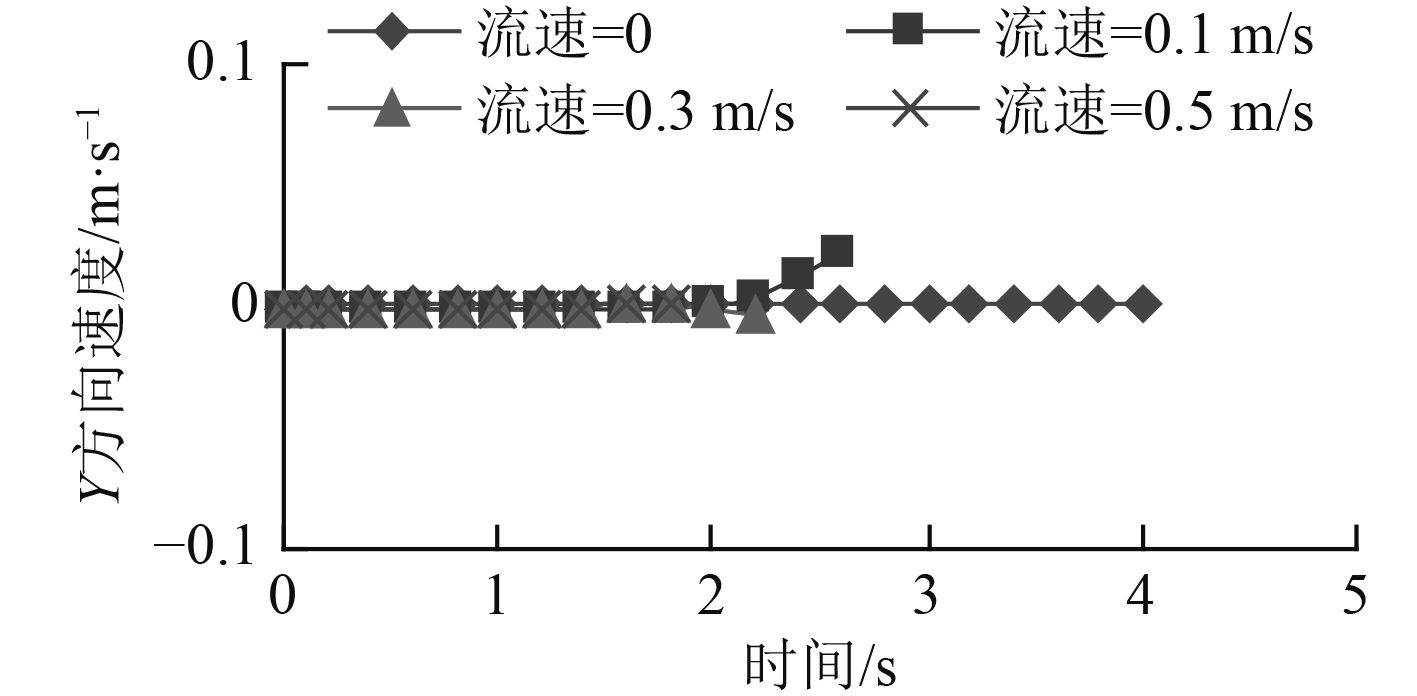
图10和图11分别为水下机器人在顺向海流速度为0 m/s,0.1 m/s,0.3 m/s,0.5 m/s时,受到Z轴正方向恒定为30 N的推力作用下,Z方向速度、Y方向速度随时间变化曲线。
从图10可以看到,在顺向海流影响下,水下机器人Z方向运动速度、Z方向加速度(速度曲线的斜率)都较逆向海流影响时(见图5)明显偏大,且随着海流速度的增加,速度与加速度都在增加。其原因在于:海流在顺向时,水下机器人会受到1个Z轴正方向的流体推力作用,相当于水下机器人在受到恒定30 N推力作用的同时,额外受到1个与推力方向相同的流体力作用。根据牛顿第二定律,在质量不变时,合外力越大,加速度越大。随着海流速度的增加,这种流体推力也在增加。
从图11中看到,在顺向海流影响下,水下机器人Y方向运动速度、Y方向加速度与逆向海流影响时(见图6)存在明显不同:在顺向海流时,速度曲线是一条无明显波动的直线,速度值一致为0,只有在低速海流时才会在运动后期出现速度为正值;而逆向海流时,速度曲线一致都表现出明显的波动性,且在运动后期会出现较大的速度正、负值。原因在于:顺向海流运动时,水下机器人对于流场的扰动较小,机器人两侧的水流流速均匀,使得两侧的压力分布一致,没有产生像逆向海流运动时明显的压力差。
|
图 10 顺向来流Z方向速度曲线 Fig. 10 Z direction velocity curve under forward flow |
|
图 11 顺向来流Y方向速度曲线 Fig. 11 Y direction velocity curve under forward flow |
从上述的对比分析可以看到:海流速度方向、速度大小对于水下机器人的运动稳定性至关重要,在条件允许情况下,尽量使水下机器人进行顺流运动。这不仅可以满足水下机器人所搭载设备的工作要求,从而保证工作精度、保证水下机器人的安全。还可以减少控制机构导管螺旋桨的操纵次数,节省能源。
2.3 逆向来流、恒定转矩变推力作用水下机器人在进行水下作业过程中,由于周围流场的变化,导管螺旋桨所发出的推力并不是一成不变的[13],即使是左右完全对称的螺旋桨也会产生不一样的推力,下面采用对比法来研究水下机器人在不同推力、恒定转矩作用下的运动规律,以及在不同的海流速度下水下机器人的运动情况。
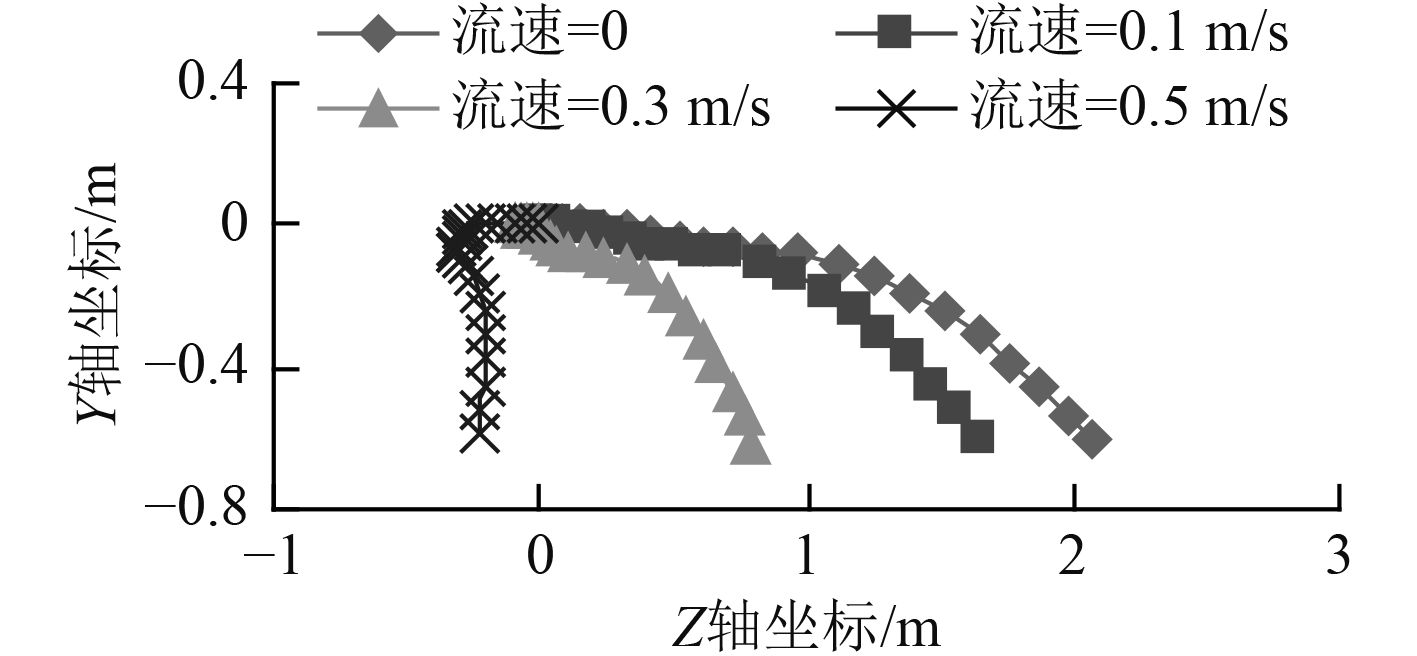
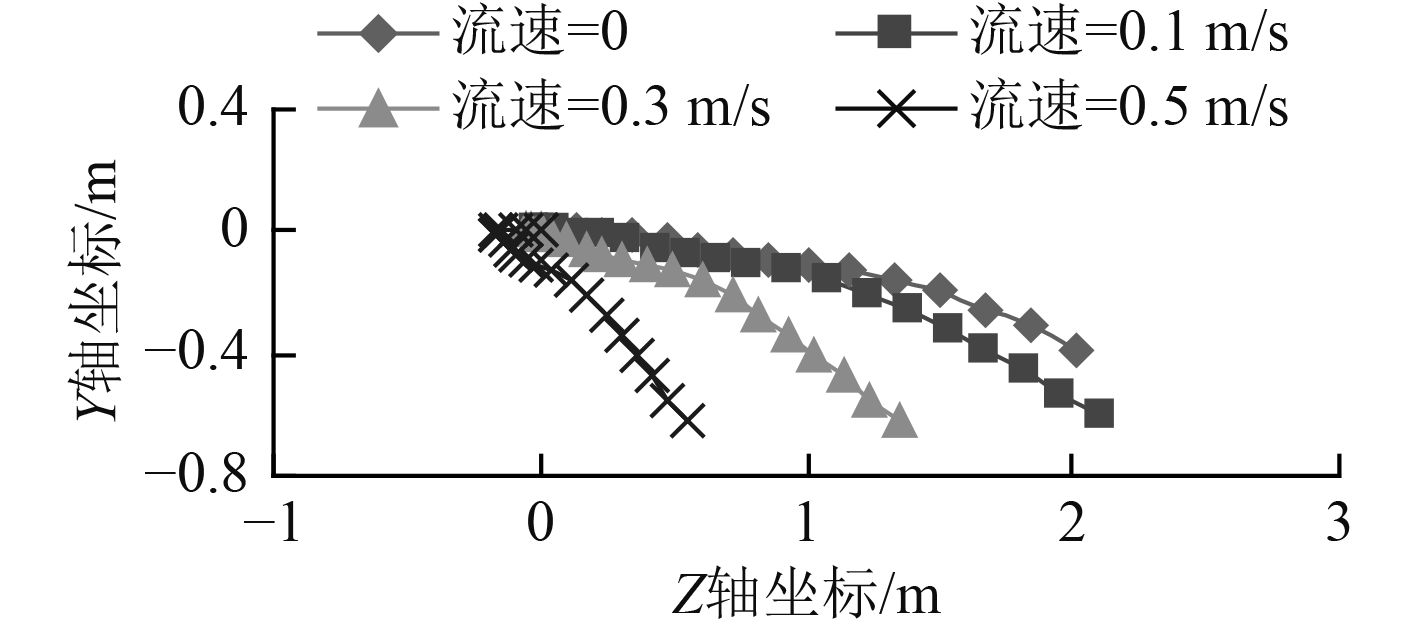
图12~图14分别给出了水下机器人在受到绕X轴1 N·m的恒定转矩,Z轴正方向20 N,30 N,40 N恒定推力作用时,不同逆向海流速度下的位移轨迹曲线。
从图12~图14中可以看到,水下机器人受到恒定转矩、不同推力作用时,其运动规律存在明显不同:在推力较小时,位移轨迹曲线都是明显的曲线,且弯曲程度非常明显,偏航程度随着运动的进行急剧增加;随着推力的增加,位移轨迹曲线的曲度逐渐减小,出现相同偏航距离(Y轴负方向运动距离)时Z轴正方向运动距离逐渐增加。这里以流速为0.3 m/s、Y轴负方向运动距离为0.5 m进行数据对比:推力为20 N时,Z轴正方向运动距离为0.732 m;推力为30 N时,Z轴正方向运动距离为1.181 m;推力为20 N时,Z轴正方向运动距离为1.422 m。
原因在于:水下机器人所受的转矩是绕X轴正方向,根据力矩的定义与右手螺旋定则,受此力矩,水下机器人的转动方向是逆时针,在转动的同时由于还受Z轴正方向的推力作用。因此,水下机器人的运动会出现往转动方向的偏航,也就是图中所示的往Y轴负方向的偏航。随着Z轴正方向推力的增加,水下机器人在Z轴正方向的运动加速度与速度都在增加。因此,在相同的时间内,在Z轴正方向的运动距离会增加,也就会使位移轨迹曲线的曲度逐渐减小。
在相同受力情况下,对不同海流速度的位移轨迹曲线进行对比发现:随着海流速度的增加,水下机器人位移轨迹曲线的曲度逐渐增加,而且增速越来越快。表现为:前进相同的距离,流速越大,偏航的距离越大。这里以推力为30 N、不同海流速度下的位移轨迹曲线(见图13)进行数据说明,Z轴正方向的位移为0.5 m:海流速度为0 m/s时,Y轴负方向的位移为0.041 m;海流速度为0.1 m/s时,Y轴负方向的位移为0.066 m;海流速度为0.3 m/s时,Y轴负方向的位移为0.135 m;海流速度为0.5 m/s时,Y轴负方向的位移为0.566 m;
原因在于:水下机器人受到恒定推力、恒定转矩作用而迎流运动时,会迫使水下机器人所处的流场环境发生改变,使得机器人两侧的流体流速不同,产生流速差,进而产生压力差;随着流速的增加,这种由流速差而产生的压力差急剧增加,使得水下机器人在前进相同的距离时的偏航距离更大。而且,由于迎流速度(流速)的增加,产生相同压力差的位置点会越靠近Z轴的零点,使得出现急剧偏航的位置点提前。
|
图 12 推力为20 N轨迹曲线 Fig. 12 Trajectory curve under thrust is 20 N |
|
图 13 推力为30 N轨迹曲线 Fig. 13 Trajectory curve under thrust is 30 N |

|
图 14 推力为40 N轨迹曲线 Fig. 14 Trajectory curve under thrust is 40 N |
将受到恒定为30 N推力、不受转矩作用的水下机器人位移轨迹曲线(见图4)与同样受到30 N恒定推力、绕X轴正方向1 N·m恒定转矩作用的位移轨迹曲线(见图13)进行对比可以发现:转矩对于水下机器人运动轨迹的影响至关重要;受转矩作用时,其轨迹曲线会出现明显的定向偏航,偏航方向与水下机器人的旋转方向符合右手螺旋定则,且随着海流速度的增加,这种偏航会越来越厉害。这对于水下机器人在水下作业过程中进行姿态控制具有重要的指导意义。
3 结 语1)基于动网格技术,采用弹簧光顺与局部网格重构的组合式网格更新方式,以六自由度(6DOF)运动方式来模拟水下机器人不同的受力情况、不同的海流速度下的运动行之有效,可以获得水下机器人的运动规律。
2)不同海流方向、不同海流速度大小、不同受力情况下,水下机器人的运动规律表现出明显的不同:随着海流速度的增加,水下机器人运动的不稳定性逐渐增加,在运动后期会出现明显的偏航,且发生偏航的距离点随着海流速度的增加而提前;随着推力的增加,位移轨迹曲线、速度曲线的曲度逐渐减小,逐渐由曲线过渡为直线;而且,随着运动时间的推进,水下机器人的运动趋向于平稳;顺向海流影响时,水下机器人运动稳定性明显高于逆向海流,相同推力下的运动速度、加速度都较逆向海流时大。
| [1] | 李慧, 赵琳, 毛英. 海况干扰下潜艇六自由度运动分析[J]. 哈尔滨工程大学学报, 2015, 31 (4): 1–7. |
| [2] |
吴家鸣, 邓威, 赖华威. 回转状态下导管螺旋桨水动力特性的数值模拟[J]. 华南理工大学学报: 自然科学版, 2010, 38 (7): 90–96.
WU Jia-ming, DENG Wei, LAI Hua-wei. Numerical simulation of hydrodynamic characteristics of ducted propeller in turning motion[J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38 (7): 90–96. |
| [3] |
吴家鸣, 叶志坚, 金晓东, 等. 水下潜器导管螺旋桨在转艏摆动中的推力特性分析[J]. 华南理工大学学报: 自然科学版, 2015, 43 (12): 141–148.
WU Jia-ming, YE Zhi-jian, JIN Xiao-dong, et al. Analysis of thrust characteristics of ducted propellers in underwater vehicle with yawing motion[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43 (12): 141–148. |
| [4] | 张宏伟, 王树新, 侯巍, 等. 螺旋桨三维建模方法研究[J]. 机床与液压, 2006 (5): 60–62. |
| [5] |
李迎华, 吴宝山, 张华. CFD动态网格技术在水下航行体非定常操纵运动预报中的应用研究[J]. 船舶力学, 2010, 14 (10): 1100–1108.
LI Ying-Hua, WU Bao-Shan, ZHANG Hua. Research on application of prediction for unsteady maneuvering motion of underwater vehicle by dynamic mesh technique in CFD[J]. Journal of Ship Mechanics, 2010, 14 (10): 1100–1108. DOI: 10.3969/j.issn.1007-7294.2010.10.004 |
| [6] | 王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 1–4. |
| [7] | 韩占忠, 王敏, 兰小平. FLUENT流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2004: 15. |
| [8] |
吴家鸣, 钟乐, 张恩伟, 等. 水下机器人进行逆向运动时导管螺旋桨推力特性的模拟[J]. 船舶工程, 2017, 39 (S1): 225–229.
WU Jia-ming, ZHONG Le, ZHANG En-we, et al. Study on hydrodynamics of underwater robot in reverse propeller and negative speed[J]. Ship Engineering, 2017, 39 (S1): 225–229. |
| [9] | ANTONELLI G. On the use of adaptive/integral actions for six-degrees-of- freedom control of autonomous underwater vehicles[J]. IEEE Journal of Oceanic Engineering, 2007, 32 (2): 300–312. DOI: 10.1109/JOE.2007.893685 |
| [10] | 张来平, 邓小光, 张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展, 2010, 40 (4): 424–447. DOI: 10.6052/1000-0992-2010-4-J2009-123 |
| [11] | 隋洪涛, 李鹏飞, 马世虎. 精通CFD动网格工程仿真与案例实战 [M]. 北京: 人民邮电出版社, 2013:5. |
| [12] | He ZHANG, Yu-ru XU, Hao-peng CAI. Using CFD Software to Calculate Hydrodynamic Coefficients[J]. Journal of Marine Science and Application, 2010 (9): 149–155. |
| [13] |
吴家鸣, 郁苗, 朱琳琳. 带缆遥控水下机器人水动力数学模型及其回转运动分析[J]. 船舶力学, 2011, 15 (8): 827–843.
WU Jia-ming, YU Miao, ZHU Lin-lin. A hydrodynamic model for a tethered underwater robot and dynamic analysis of the robot in turning motion[J]. Journal of Ship Mechanics, 2011, 15 (8): 827–843. |
 2017, Vol. 39
2017, Vol. 39
