测试性建模是进行测试性预计、测试点优化和诊断策略优化的重要工具,是开展产品测试性设计的基础[1 – 2] ,选择一个合适的建模与分析方法可大为提高测试性设计的效率和准确性[3]。随着计算机技术的发展,利用测试性建模与分析工具软件可快速、方便地建立产品的测试性模型,并对测试性设计进行有效的分析和指导[4 – 5]。
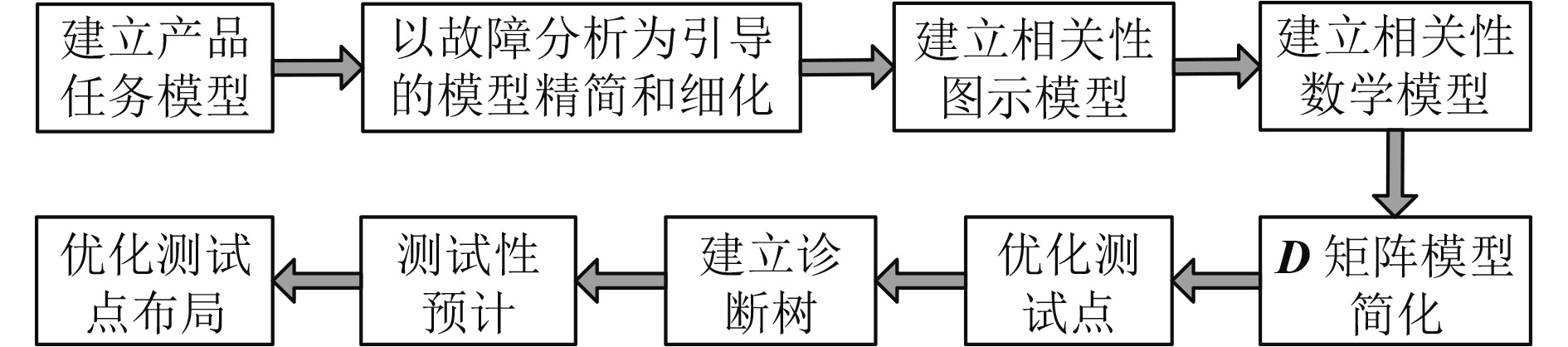
当前,测试性模型按照形式、用途和目的不同,有多种分类。其中,基于多信号流的相关性模型是进行测试性预计、测试性设计分析的主流模型[6 – 7]。相关性模型的概念最早由美国人De Paul提出[8],是一种以相关性推理为基础,按照故障如何被发现的过程来设计产品故障检测和隔离的分析方法[10 – 11],其工作流程如图1所示。经过数十年的发展,相关性模型已广泛应用于美、英、俄、德等国武器装备的测试性设计、诊断策略设计、可靠性维修性设计之中;同时国内学者也对其进行了大量的应用研究,并在不同装备的测试性设计中都取得了一定的成果[9]。
|
图 1 基于相关性模型的测试性建模与分析流程 Fig. 1 The process of test modeling and analysis based on relevant model |
本文在相关性模型的理论基础上提出一种舰船系统级产品的测试性建模与分析方法,并开展舰用燃气轮机滑油系统的测试性建模、诊断树建立、测试性预计以及诊断策略优化等应用研究,为舰船系统级产品的测试性建模与分析研究提供新的思路和手段。
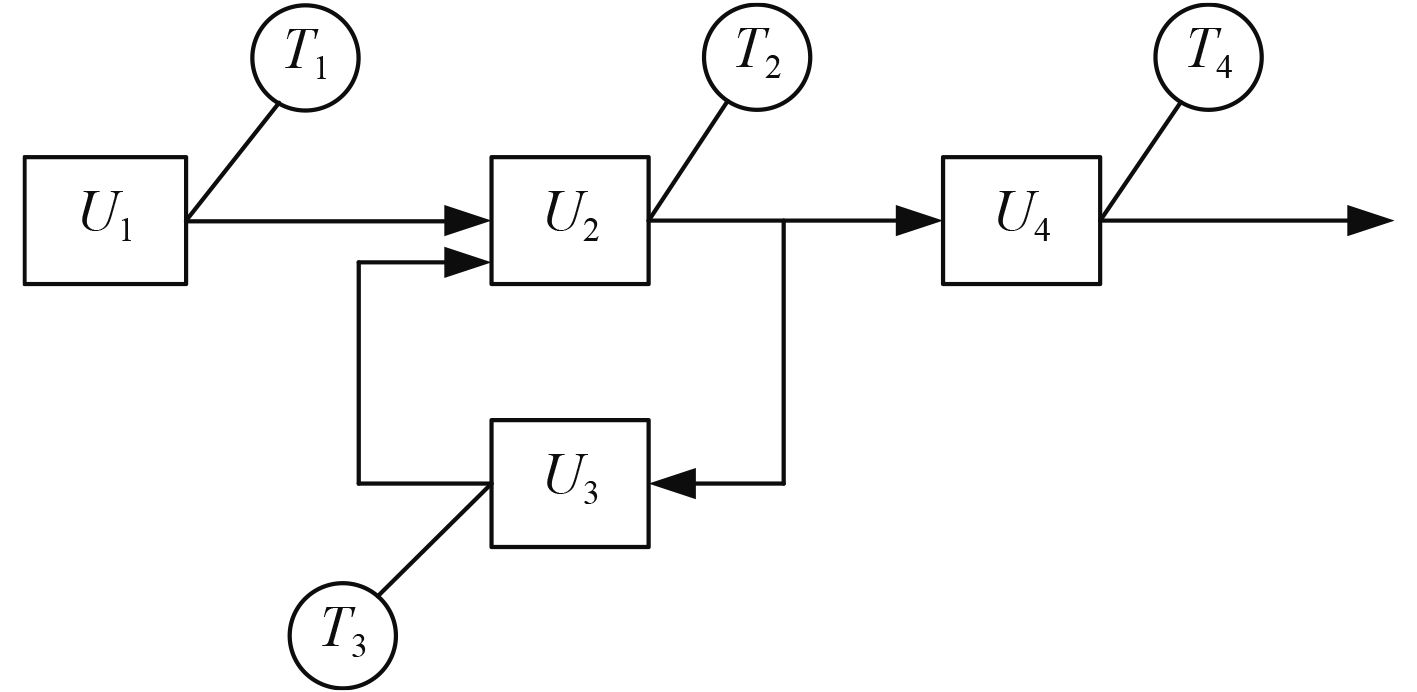
1 相关性建模理论相关性模型是在产品任务模型的基础上,清晰表明任务信息流方向和各功能部件相互连接关系,并以此表明各功能部件与各测试点关系的一种测试性模型[8],分为图示模型和数学模型2种,其中相关性图示模型的作用是用有向图的型式来表示测试与测试、测试与诊断结果之间的连接关系,如图2所示,其中方框代表测试单元(功能部件),圆圈代表测试点,箭头表明了功能信息的传递方向。
|
图 2 相关性图示模型举例 Fig. 2 Example of relevant graphical model |
数学模型的作用是在图示模型的基础上用矩阵形式来描述故障模式与测试之间的相关性,以分析出系统中哪些故障模式不可测、哪些故障模式冗余、哪些故障模式构成了模糊组,进而可建立系统故障诊断树和生成诊断策略。相关性数学模型可用下述矩阵来表示:
| ${{D}_{m \times n}} = \left[ {\begin{array}{*{20}{c}}{{d_{11}}} & {{d_{12}}} & \cdots & {{d_{1n}}}\\{{d_{21}}} & {{d_{22}}} & \cdots & {{d_{2n}}}\\ \vdots & \vdots & {} & \vdots \\{{d_{m1}}} & {{d_{m2}}} & \cdots & {{d_{mn}}}\end{array}} \right]\text{,}$ | (1) |
其中第i行矩阵:
| ${{F}_i} = [{d_{i1}}{d_{i2}} \cdots {d_{in}}]\text{,}$ | (2) |
表示系统中第i个故障模式在各个测试点上的反应信息,它表明了Fi和测试点Tj(j=1,2,…,n)的相关性。而第j列矩阵
| ${{T}_j} = {[{d_{1j}}{d_{2j}} \cdots {d_{mj}}]^{\rm T}}\text{,}$ | (3) |
表示了第j个测试点可测得的各组成单元故障模式信息。它表明了Tj与系统中各故障模式Fi(i=1,2,…,m)之间的相关性。其中,当Tj可测得Fi信息时(即Tj与Fi相关),dij = 1;当Tj不能测得Fi信息时(即Tj与Fi不相关),dij =0。
相关性数学模型也称产品D矩阵模型,采用直接分析法或一阶相关性列矢量法可将基于图2所示的信息流图示模型转化为式(4)所示的矩阵型式数学模型。
| $\begin{array}{*{20}{l}}{}\\{{{F}_1}}\\{{{F}_2}}\\{{{F}_3}}\\{{{F}_4}}\end{array}\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{{T}_1}} & {{{T}_2}} & {{{T}_3}} & {{{T}_4}}\end{array}}\\{\left[ {\begin{array}{*{20}{c}}1 & 1 & 1 & 1\\0 & 1 & 1 & 1\\0 & 1 & 1 & 1\\0 & 0 & 0 & 1\end{array}} \right]\text{。}}\end{array}$ | (4) |
燃气轮机滑油系统是舰船平台中一个典型二级子系统,其功能是向舰上使用的燃气轮机提供滑油,实现燃气轮机的独立运转。燃气轮机滑油系统由电动供油泵、电动回油泵、滑油冷却器、滑油加热循环柜、滑油滤器、滑油贮存柜和滑油手摇泵等设备组成,其工作原理为:燃气轮机发出起动指令后,与电动供油泵和电动回油泵同时起动,电动供油泵从滑油加热循环柜中吸取滑油,供燃气轮机使用。电动回油泵的回油经滑油滤器输送至滑油冷却器,经滑油冷却器冷却后再输送至滑油加热循环柜中供电动供油泵吸取滑油。其中,滑油加热循环柜具有加热功能,可保证燃气轮机起动所需的滑油温度;滑油贮油柜在必要时可利用重力向单台滑油加热循环柜中补充备用滑油;滑油手摇泵的作用是将滑油加热循环柜和备用滑油贮存柜内的底部残油排至废油舱。
根据上述燃气轮机滑油系统的系统组成和工作原理,可建立其典型任务模型如图3所示。

|
图 3 燃气轮机滑油系统典型任务模型 Fig. 3 The typical task model of warship gas turbine lube oil system |
故障模式、影响及危害性分析(FMECA)是测试性建模中进行产品任务模型精简和细化的有效途径,通过对产品各组成单元进行功能故障分析,可剔除重要程度相对较低的组成单元,并可对重要程度较高的组成单元或功能模式进行细化,以获得更加准确和高效的产品任务模型。
为建立合理准确的测试性模型,本文对燃气轮机滑油系统进行FMECA,可获得各组成设备的所有故障模式及其危害性指数如表1所示。
|
|
表 1 燃气轮机滑油系统故障模式及其危害性指数 Tab.1 The fault model and its hazard index |
根据相关性模型的建模原则,可将故障危害性程度较低的组成单元剔除,本研究选择将故障模式危害性指数大于19(即GJB/Z1391《故障模式、影响及危害性分析指南》中“危害性指数矩阵表”规定的危害程度最轻的故障模式)的功能部件剔除(若该部件有多个故障模式,则每个故障模式危害性指数均应大于19)。由表1可知,滑油手摇泵具有“残油泄漏F14”和“无法排除残油F15”2个故障模式,而这2个故障模式的危害性指数均为19,因而可在建立相关性模型时将该设备省略,以提高系统建模的效率和准确性。
2.3 建立相关性图示模型 2.3.1 初步设置测试点建立相关性图示模型之前,应预先设置各组成单元的初步测试点,以提供建模所需的测点检测信息。初步测点的设置原则应全面覆盖FMECA中的所有故障模式,但考虑到测试成本、可行性以及同型号产品的设计经验等,对于危害性程度较小或者测试成本较高的故障模式可暂不设测点,待完成测试性预计后再进行测试点布局优化。根据这一原则,系统中的滑油贮存柜故障模式对于整个系统的影响程度较小(危害性指数为18),且必要时才会对整个系统有所影响,因而可不对其设置初步测点;而对于电动供油泵、电动回油泵“振动过大”这一故障模式,由于其测试成本较高,也可不对其设置初步测点。
根据上述原则,对本文燃气轮机滑油系统设置的初步测点和测试内容如表2所示。
|
|
表 2 初设的燃气轮机滑油系统测试点 Tab.2 Initial set of test points |
相关性模型的建立可通过人工绘制图示模型和计算数学模型进行,但对于复杂的舰船系统设备,人工绘图和计算的工作量较大、差错率较高。而使用商业化的工具软件可以加速建模过程,同时简化测试性设计分析工作,极大提高了测试性建模与分析工作的效率和准确性[12 – 13]。
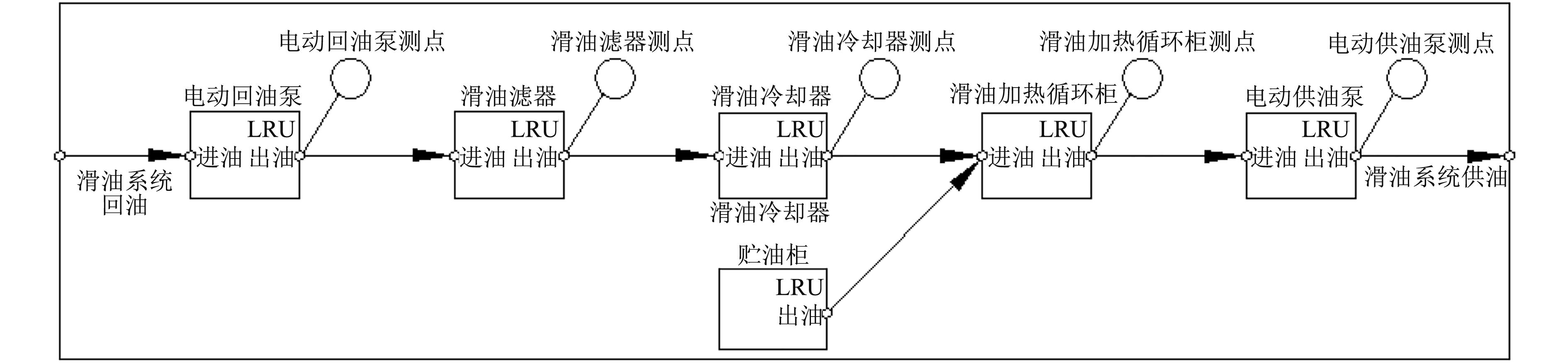
|
图 4 燃气轮机滑油系统相关性图示模型 Fig. 4 The relevant diagram model |
本文选择TesLab-Designer作为建立相关性模型的工具软件,开展相关的测试性建模与分析研究。TesLab-Designer是一款基于相关性建模理论开发的测试性建模与模型管理分析软件,可通过输入产品的结构组成、任务流向、测点关系等信息,利用多信号流建模技术自动建立复杂产品的相关性模型,并可通过内部迭代运算完成D矩阵模型简化、测试点选择优化等繁琐计算过程,从而快速生成诊断树和诊断策略,完成测试性预计和测试点布局优化等工作,极大提高了测试性建模的效率和准确性。
根据精简后的燃气轮机滑油系统典型任务模型以及表2所示的初设测点布局,利用TesLab-Designer软件平台,输入各设备的连接关系和信息流方向,可建立燃气轮机滑油系统基于任务的相关性图示模型如图4所示。
2.4 建立相关性数学模型根据上述燃气轮机滑油系统的相关性图示模型,TesLab-Designer软件可通过一阶相关性列矢量法,自动求解得到其相关性数学模型(D矩阵模型),如表3所示,其中测试点可检测该故障用“1”表示,无法检测该故障用“0”表示。
|
|
表 3 燃气轮机滑油系统的相关性数学模型 Tab.3 The relevant mathematical model |
由于TesLab-Designer软件平台可通过内部迭代运算完成D矩阵模型简化和优化测试点等繁琐计算过程,即将冗余的测试和模糊组合并,并完成检测用测试点选择和隔离用测试点选择等工作,因此可在表3所示D矩阵模型基础上,利用下行法分割矩阵(具体计算方法见作者在文献[14]中所阐述),进行6次分割后,即可生成燃气轮机滑油系统的诊断树如图5所示。在该诊断树表中,选择滑油冷却器压力测点为第1个隔离用测试点,若该点测试的滑油冷却器输出压力正常,则说明系统故障发生在其后端设备中或者在系统供油温度方面;若滑油冷却器输出压力不正常,则说明系统故障发生在其前段设备中。接着选择滑油加热循环柜测点为第2个隔离用测试点、电动回油泵测点为第3个隔离用测试点等,最多经过3级检测可最终隔离出是哪个设备(或模糊组)的故障。若所有测试点的检测结果均为正常,则说明系统无故障发生或发生了当前无可检测的故障模式。
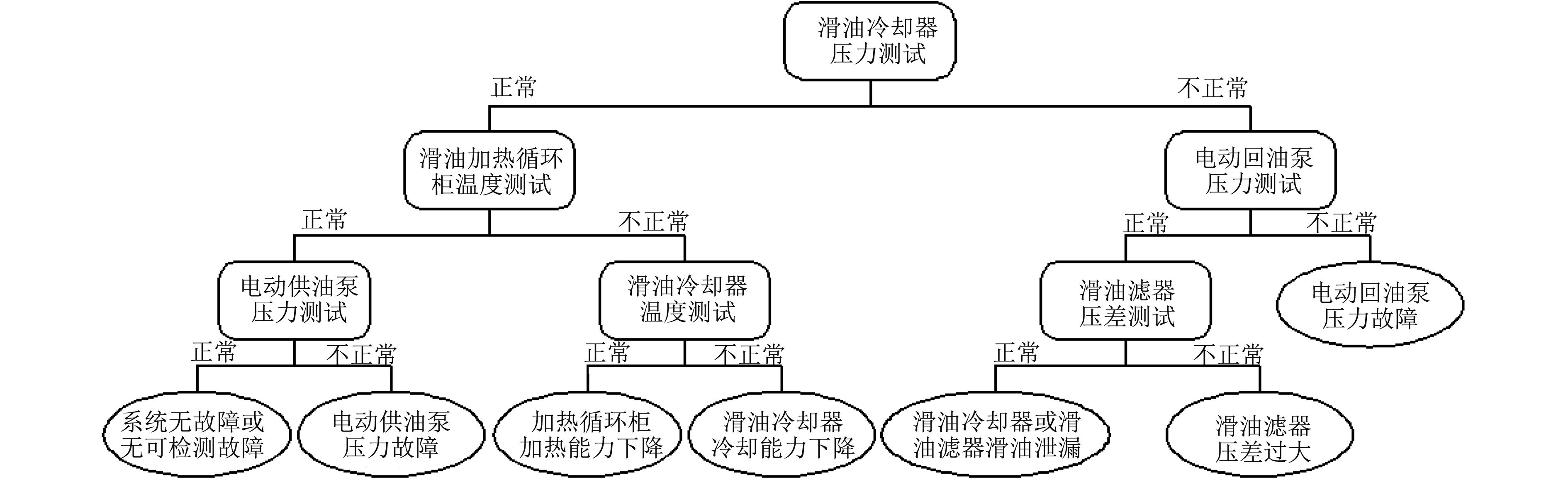
|
图 5 燃气轮机滑油系统诊断树 Fig. 5 The fault diagnosis tree |
诊断树可用于确定产品的诊断策略,也可用于预计产品的故障检测率(FDR)和故障隔离率(FIR)等测试性指标,其计算公式如下:
| ${\gamma _{{}_{FD}}} = \frac{{{U_{FD}}}}{{{U_T}}} \times 100\%\text{,}$ | (5) |
| ${\gamma _{{}_{FI}}} = \frac{{{U_{FI}}}}{{{U_{FD}}}} \times 100\% \text{。}$ | (6) |
式中:γFD为预计的产品故障检测率;γFI为预计的系统故障检测率;UFD为测试点能够检测到的系统故障模式数量;UFI为测试点能够正确隔离出的故障模式(或模糊组)数量;UT为系统故障模式总数。
对燃气轮机滑油系统FMECA结果、相关性数学模型以及诊断树进行分析,可得到本系统测试方案中的UT、UFD、UFI如表4所示。
|
|
表 4 燃气轮机滑油系统的故障模式检测情况 Tab.4 The detection condition of fault model |
燃气轮机滑油系统的故障模式总数UT为15,能够检测到的故障模式数量UFD为9,能够正确隔离出的故障模式(或模糊组)数量UFI为6,因而可预计出其故障检测率FDR、故障隔离率FIR为:
| ${\gamma _{FD{\text{燃滑}}}} = \frac{{{U_{FD}}}}{{{U_T}}} \times 100\% = \frac{9}{{15}} \times 100\% = 60\% \text{,}$ | (7) |
| ${\gamma _{FI{\text{燃滑}}}}{\rm{ = }}\frac{{{U_{FI}}}}{{{U_{FD}}}} \times 100\% {\rm{ = }}\frac{6}{9} \times 100\% = 66.7\% \text{。}$ | (8) |
测试性预计是产品诊断策略优化的依据,根据上述测试性预计结果可知,燃气轮机滑油系统的FDR、FIR指标均相对较低,可通过增加UFD和UFI数量的方式进行提高,具体建议如下:
根据FMECA和诊断树,系统中无法检测的故障模式、故障模式模糊组以及未使用的测试分别如表5~表7所示。
|
|
表 5 无法检测的故障模式 Tab.5 The fault model of failed to detect |
|
|
表 6 故障模式模糊组 Tab.6 The detectable fault fuzzy set |
|
|
表 7 未使用的测试 Tab.7 The unused test points |
由表5可知,在初设测点的基础上,增设电动供油泵、电动回油泵振动测试,可检测其“振动过大”的故障模式;增设滑油贮油柜流量测试,可检测“加热循环柜滑油泄漏”的故障模式;增设滑油贮油柜压力测试,可检测“滑油贮油柜无油”的故障模式;增设滑油手摇泵压力测试,可检测其“残油泄露”和“无法排除残油”的故障模式,从而增加可UFD的数量,提高系统的FDR。
由表6可知,在初设测点的基础上,在电动供油泵和电动回油泵周围设置油液探测器,可分辨其是否发生滑油泄漏还是无法供油;在滑油滤器设置压力测试,可分辨是滑油滤器还是滤清器发生泄漏,从而增加可UFI的数量,提高系统的FIR。
此外,由表7可知,由于滑油贮油柜可自动调节加热循环柜的滑油输出压力,加热循环柜的压力测试功能无法起到监测作用,因而可在初设测点的基础上剔除该测试功能,以提高系统测试效率、降低测试成本。
4 结 语测试性建模与分析是开展产品测试性设计的基础。本文在相关性建模的理论基础上,提出了一种开展舰船系统级产品的测试性建模与分析的方法,通过建立产品任务模型、相关性图示模型等求解产品的相关性数学模型,进而建立产品诊断树和进行测试性预计,并为优化产品诊断策略提供建议。同时,选取舰用燃气轮机滑油系统为对象,建立其典型任务模型,并在此基础上进行测试性建模、诊断树建立、测试性预计以及诊断策略优化等,举例结果表明该方法具有直观、高效的建模与分析功能,适用于装备测试性建模与分析工作,为舰船系统级产品的测试性建模、分析和诊断策略研究提供了新思路和手段。
| [1] | YANG S M, QIU J, LIU G J, et al. A hierarchical model-based approach to testability modeling and analysis for PHM of aerospace systems[J]. Journal of Aerospace Engineering, 2014, 27 (1): 131–139. DOI: 10.1061/(ASCE)AS.1943-5525.0000203 |
| [2] | TAN X D, QIU J, LIU G J, et al. Fault evolution testability modeling and analysis for centrifugal pumps [C]// Proceedings of Prognostics and System Health Management Conference (PHM-2014 Human). IEEE, Zhangjiajie, 2014: 469–473. |
| [3] |
刘刚, 黎放, 胡斌. 基于相关性模型的舰船装备测试性分析与建模[J]. 海军工程大学学报, 2012, 24 (4): 46–51.
LIU Gang, LI Fang, HU Bin. Test and modeling of vessel equipment based on relevant model[J]. Journal of Naval University of Engineering, 2012, 24 (4): 46–51. DOI: 10.7495/j.issn.1009-3486.2012.04.010 |
| [4] |
闵荫庭, 江露, 刘莉. 测试性建模以及测试性验证试验应用[J]. 航空电子技术, 2016, 47 (1): 41–51.
MIN Tingyin, JIANG Lu, LIU Li. Application of testability modeling and testability verification test[J]. Avionics Technology, 2016, 47 (1): 41–51. |
| [5] |
马春江, 侯轶宸. 基于模型的测试性设计分析方法讨论[J]. 电子技术与软件工程, 2015, 19 : 88–89.
MA Chunjiang, Hou Yichen. Discussion on the method of testability design analysis based on model[J]. Electronic Technology & Software Engineering, 2015, 19 : 88–89. |
| [6] | LIANG H, LIU X B, ZHANG X X. Information collecting of PHM and task-based test modeling of warship product [C]//Proceedings of the 5th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems, IEEE, Shenyang, 2015: 1752–1756. |
| [7] |
谭晓栋, 罗建禄, 李庆, 等. 机械系统的故障演化测试性建模及预计[J]. 浙江大学学报(工学版), 2016, 50 (3): 442–459.
TAN Xiaodong, LUO Jianlu, LI Qing, et al. Fault evolution testability modeling and prediction for mechanical systems[J]. Journal of Zhejiang University (Engineering Science), 2016, 50 (3): 442–459. |
| [8] | JULIE M, MILER M D, CARLOS E. Diagnostic performance of coronary angiography by 64-row CT[J]. Autotestcon, 2009, 27 (11): 1143–1156. |
| [9] |
翟助群, 许正, 刘刚. 复杂可修系统任务测试性建模[J]. 兵工自动化, 2016, 35 (1): 37–41.
ZHAI Zhuqun, XU Zheng, LIU Gang. Modeling of testability based on complex repairable system[J]. Ordnance Industry Automation, 2016, 35 (1): 37–41. |
| [10] |
石君友, 龚晶晶, 徐庆波. 考虑多故障的测试性建模改进方法[J]. 北京航空航天大学学报, 2010, 36 (3): 270–273.
SHI Junyou, GONG Jingjing, XU Qingbo. Improvement method for testability modeling with multiple faults[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36 (3): 270–273. |
| [11] | 石君友, 田仲, 候文魁, 等. 测试性设计分析与验证[M]. 北京: 国防工业出版社, 2011. |
| [12] |
张勇, 邱静, 刘冠军. 测试性模型对比及展望[J]. 测试技术学报, 2011, 25 (6): 504–514.
ZHANG Yong, QIU Jing, LIU Guanjun. Comparison and prospect of testability models[J]. Journal of Test and Measurement Technology, 2011, 25 (6): 504–514. |
| [13] | SHEPPARD J W, SIMPSON W R. A mathematical model for integrated diagnostics[J]. Design & Test of Computers, 2007, 8 (4): 25–38. |
| [14] |
刘晓白, 梁鸿. 基于任务的舰船装备测试性建模与分析研究[J]. 舰船科学技术, 2016, 38 (11): 156–160.
LIU Xiaobai, LIANG Hong. Research on task-based test modeling and analyzing of warship equipment[J]. Ship Science and Technology, 2016, 38 (11): 156–160. |
 2017, Vol. 39
2017, Vol. 39
