2. 华中科技大学 机械科学与工程学院,湖北 武汉 430074
2. School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
近年来,随着我国经济的快速发展,对石油等资源的需求大幅增长[1],密集的海上石油运输使船舶溢油事故的风险日益增加[2]。例如,近年来“蓬莱19-3”油田溢油事故,美国墨西哥湾和大连新港“7.16”原油泄露[3–5]等事故不仅对海洋生态环境造成重大污染,更对渔业、水产养殖业、旅游业、酒店业等造成重大经济损失。严重的溢油事故给我们敲响了警钟,水上溢油应急系统已经受到世界各国的关注。作为溢油应急系统中不可或缺的组成部分,溢油回收船可在最短时间内迅速赶到溢油污染事故现场,进行不同粘度和不同厚度的溢油回收和储存。作为溢油回收船的重要组成部分,溢油回收装置的设计将直接影响溢油回收船的回收功能。
目前,国外溢油回收装置的主要类型有美国Slickbar和Marco溢油回收装置、芬兰劳模(Lamor)溢油回收装置(见图1)、挪威法兰克蒙(Framo)溢油回收装置(见图2)、英国维克马(Vikoma)溢油回收装置(见图3)和荷兰Vos溢油回收装置(见图4)等[4, 6]。国内的溢油回收装置与国外发达国家相比还有很大差距,目前国内的溢油回收装置主要有青岛光明溢油回收装置、青岛华海溢油回收装置。

|
图 1 Lamor侧挂式 Fig. 1 Lamor side hanging type |

|
图 2 Framo堰式 Fig. 2 Framo weir type |

|
图 3 Vikoma Lp3000 Fig. 3 Vikoma Lp3000 |

|
图 4 Vos船携式 Fig. 4 Vos ship carrying type |
随着计算机技术的快速发展和普及,依托理论力学、数学、计算机技术的结构有限元分析技术得到了巨大发展,有限元分析技术成为了一种丰富多彩、应用广泛且实用高效的数值分析方法,其实用性、方便性、有效性得到了广泛认可。近年来,在船舶领域的有限元虚拟仿真技术成为了广泛研究的热点[7]。
利用虚拟仿真技术对溢油回收船溢油回收装置进行结构性能仿真与优化对溢油回收装置的结构性能、寿命和可靠性提升等具有极其重要的意义。因此本文拟对某溢油回收船溢油回收装置的结构性能进行仿真与优化,以实现仿真驱动设计,从而对溢油回收装置的设计提供指导。
1 虚拟仿真技术与结构优化设计方法 1.1 虚拟仿真技术有限元分析是一种高效的数值分析方法,在虚拟仿真方面得到了快速发展,它是利用数学近似方法对真实物理系统(模型和载荷工况)进行模拟,还利用有限数量且简单而又相互作用的元素(即单元)去逼近无限未知量的真实系统。在进行结构有限元分析时,首先需要创建结构的有限元模型,包括模型网格离散、材料属性定义、载荷和边界约束施加,然后可对有限元模型进行强度、刚度、模态等结构特性仿真分析。在此基础上,按照优化算法在设计域内进行优化求解,最终得到满足迭代终止条件的最优结构设计方案。因此,有限元分析是结构性能仿真与优化的基础。
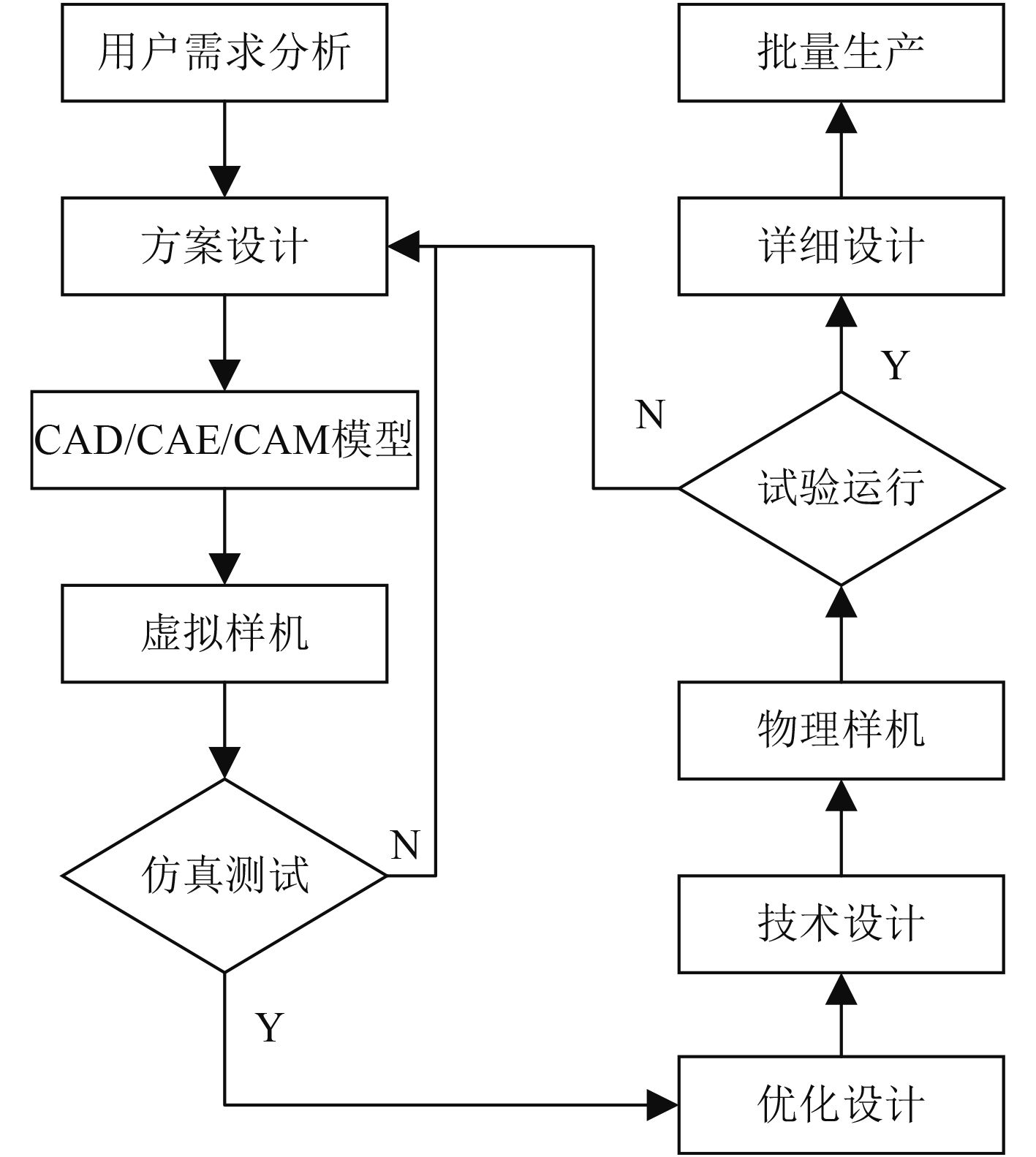
虚拟仿真是实现结构性能仿真与优化的主要手段,利用虚拟仿真技术指导船舶设计可以提高船舶设计质量,降低研发成本,加快研发周期。相比传统的设计理念,虚拟仿真技术能够在产品概念设计阶段对产品性能进行评估,图5列出了基于虚拟仿真的产品设计流程。
|
图 5 虚拟仿真设计流程图 Fig. 5 Flowchart of the virtual simulation design |
如今,虚拟仿真技术已经应用在船舶建造前期论证评估、船舶建造设计方案评估、船舶生产方案比较和船舶建造过程等各个阶段[8 – 10]。挪威UD公司在所有新船型初步设计时,都会建立船的三维模型,并在虚拟环境下对整船布置、设备布局、外观等进行综合评价和仿真[10]。
1.2 结构优化设计方法结构优化经历了截面尺寸优化、形状优化和拓扑优化3个阶段[11]。截面尺寸优化以结构的尺寸大小为设计变量,其最优解的搜索过程并不改变结构的拓扑形式,因此很难实现对原结构的较大优化。形状优化比尺寸优化有效,以控制结构形状的某些边界控制点的几何信息为设计变量,通过调整结构的内外边界以达到节省材料的目的。结构拓扑优化又称为结构布局优化,其目的是在限定的结构设计空间中,基于给定的结构边界条件和负载条件,通过一定的优化方法,寻找满足设计约束的最优拓扑结构,包括结构构件的连接方式,结构内孔洞的有无、位置和数量等[11–13]。经过近30年发展,常用的拓扑优化方法主要有均匀化方法、变密度法、水平集法以及渐进结构优化法,其中较为成熟的变密度法已广泛应用于热传导、减震降噪、柔顺机构等的拓扑优化设计中。
基于变密度法的结构拓扑优化的主要求解思路是将寻求最优拓扑结构问题转化为在给定的设计空间中寻求最优的材料分布问题[14]。因此连续体结构的拓扑优化过程本质上就是有效材料的保留和无效材料的删除过程。
变密度法的基本思想是人为假定一种工程中并不存在的密度可变材料单元,依据离散化的拓扑优化建模思想,这种材料单元的密度设置为[0, 1]之间的连续变量。与此同时,还需人为设定材料单元的密度与材料物理属性间的一种插值函数关系,从而使材料的这种物理属性可以以材料单元密度函数的形式表达,目前运用较多的插值模型有SIMP插值模型[15]和RAMP插值模型[16]。本文采用效果较好的SIMP插值模型。
在SIMP材料插值模型中,人工材料单元的密度表示为:
| $\varphi ({x_i}) = {x_i}^P{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i} \in [{x_{\min }},1]{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,3...,n\text{。}$ | (1) |
假设材料各向同性,材料的泊松比取值为与材料密度无关的常量,建立人工材料单元密度与材料弹性模量间的关系:
| $\begin{split}E({x_i}) = &{E_{\rm {min}}} + \varphi ({x_i})(E - {E_{\rm {min}}}){\kern 1pt} {\kern 1pt} {\kern 1pt} = {E_{\rm {min}}}{\rm{ + }}{\kern 1pt} \Delta E{x_i}^P{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \\{\rm{ }}{\kern 1pt} \Delta E = & E - {E_{\rm {min}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm {i}} = 1,2,3...,n\text{。}\end{split}$ | (2) |
为了保证数值计算的稳定性,通常取
基于SIMP材料插值模型,强度或刚度约束下的结构体积最小化拓扑优化问题可描述为:
| $\begin{array}{l}Find:\;\;\;\;\;\;\;X = {\left\{ {{x_1},{x_2},...,{x_n}} \right\}^{\rm T}} \in \Omega \text{,}\\Minimize:\;\;\sum\limits_{i = 1}^n {{x_i}} {v_i}\text{,}\\Subject{\kern 1pt} {\kern 1pt} to:\;\;{\sigma _i} \leqslant {\sigma _l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if{\kern 1pt} {\kern 1pt} {x_i} > 0\text{,}\\{\kern 1pt} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{F}} = \mathit{\boldsymbol{KU}}\text{,}\\{\kern 1pt} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < {x_{min}} \leqslant {x_i} \leqslant 1{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,3,...,n)\text{。}\end{array}$ | (3) |
其中:xi为材料单元的相对密度,作为整个优化模型的设计变量;n为设计域内单元总数;K, U和F分别为结构总体刚度矩阵、位移向量和外力向量;ui为材料单元位移列向量;k0为材料密度为“1”的单元刚度矩阵;vi为材料单元相对体积;V为设计域总体积;f为给定的体积率;xmin为最小材料单元密度,通常取为0.01,以避免有限元计算过程中刚度矩阵的奇异。
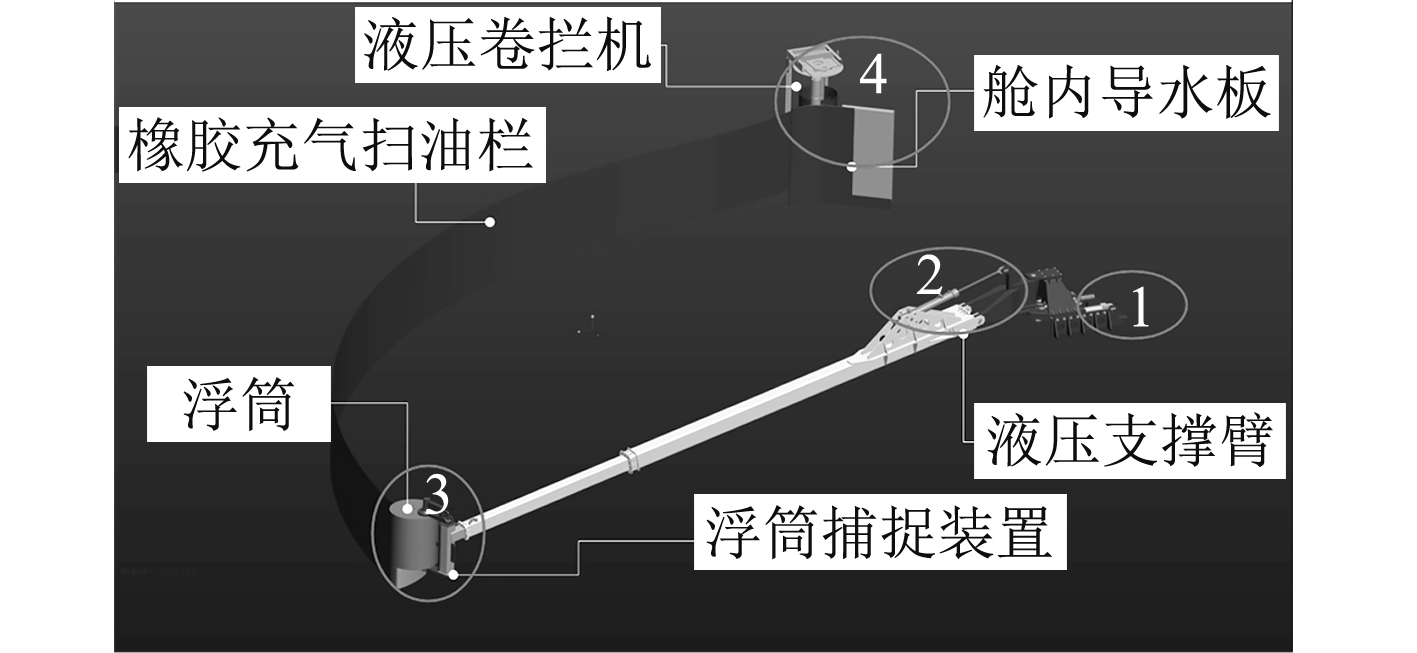
2 溢油回收装置有限元模型建立图6为某溢油回收装置示意图,从图中可以看出溢油回收装置主要由导水板、扫油栏、支撑臂和浮筒捕捉装置等结构组成。根据实际工作环境,以1~5级海况、4kn航速为背景对溢油回收装置的液压支撑臂及其支撑装置、浮筒捕捉装置进行有限元建模、仿真分析和优化设计。
|
图 6 溢油回收装置示意图 Fig. 6 Schematic diagram of spilled oil recovery equipment |
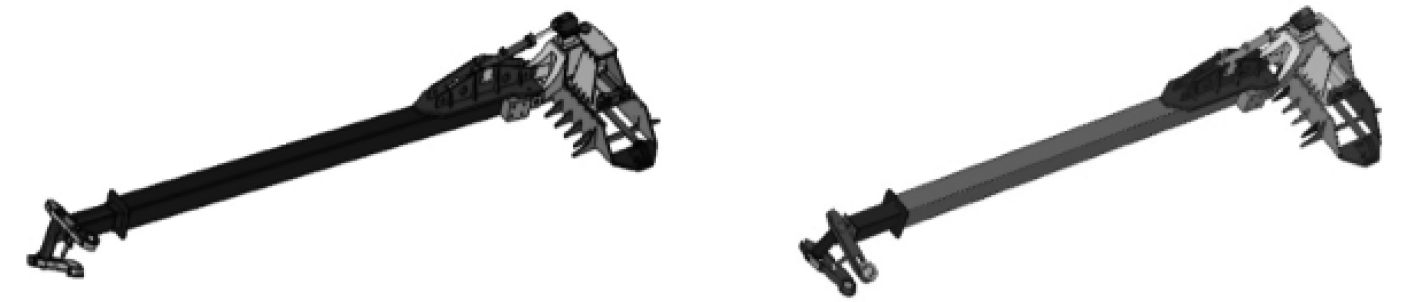
溢油回收装置由于其功能特殊性和设计复杂性,拥有大量的传动零部件,具有相当复杂的装配关系和结构特征,在构建有限元网格模型进行仿真分析前,需要开展重复实体、重复曲面和非关键性特征的消除等高强度的几何清理操作。以图6中溢油回收装置为例,执行几何清理操作后,特征零配件总数由167降低为54,能有效满足可持续的高效网格划分要求。几何清理前后溢油回收装置CAD模型的对比如图7所示。
|
图 7 几何清理前后模型对比 Fig. 7 Comparison of the initial model and the model after geometric cleaning |
有限元分析中最为关键的一步是划分实体网格(即将连续的实体离散化),网格质量好坏将影响计算精度,质量太差的网格甚至会中止计算。直观上看,网格各边或各个内角相差不大、网格面不过分扭曲、边节点位于边界等分点附近的网格质量较好。
本文对所选取的溢油回收装置进行网格划分,最终生成的网格模型如图8所示,经过Hypermesh检测,能达到有限元分析所需计算精度和效率的网格质量要求。

|
图 8 局部网格划分放大图 Fig. 8 Amplification of local grids |
根据溢油回收船溢油回收装置的实际工作环境,以1~5级海况为背景,5级为极限海况,对航速为4kn运行条件下的装置进行仿真分析。先确定具体载荷,然后在建好的有限元模型上,根据不同的海况,施加对应的载荷和边界约束条件,以准确模拟溢流回收装置的工作环境。
3 仿真分析与拓扑优化设计 3.1 溢油回收装置仿真分析 3.1.1 静力学分析在有限元模型正确建立、载荷和边界条件正确施加、连接关系正确模拟的情况下,对溢油回收装置进行结构性能仿真分析。利用Hyperworks强大的求解器Optistruct,对回收装置进行静力学结构性能仿真,求得回收装置不同工况下的应力和位移分布云图,从而对整体结构进行性能评价。
根据上述工况和约束条件,得到5种工况下溢油回收装置的最大位移、最大应变和最大应力(见表1)。图9给出了工况5条件下溢油回收装置的位移、应变和应力云图。

|
图 9 工况5对应的位移、应变、应力云图 Fig. 9 Cloud of displacement, strain and stress under working condition 5 |
|
|
表 1 5种不同工况下仿真分析结果 Tab.1 Simulation analysis results under five working conditions |
由于所选取的溢油回收装置其液压支撑臂为细长杆结构(长达10 m),且主要承受轴向力,由于外部风浪情况复杂,随机扰动概率较高且多变,为了对溢油回收装置进行失稳性研究,需要对其进行屈曲分析,从而找到结构的屈曲因子,得到结构的失稳临界载荷。
选择工况5(极端工况)进行分析,分析结果如图10和图11所示。由计算结果可以看出,屈曲频率(特征值)为3.02 Hz,即屈曲因子或安全系数为3.02,结构的临界屈曲载荷为3倍的结构载荷,结构的第1阶屈曲模态完全满足设计要求。

|
图 10 屈曲因子 Fig. 10 Buckling factor |

|
图 11 结构变形图 Fig. 11 Structural deformation diagram |
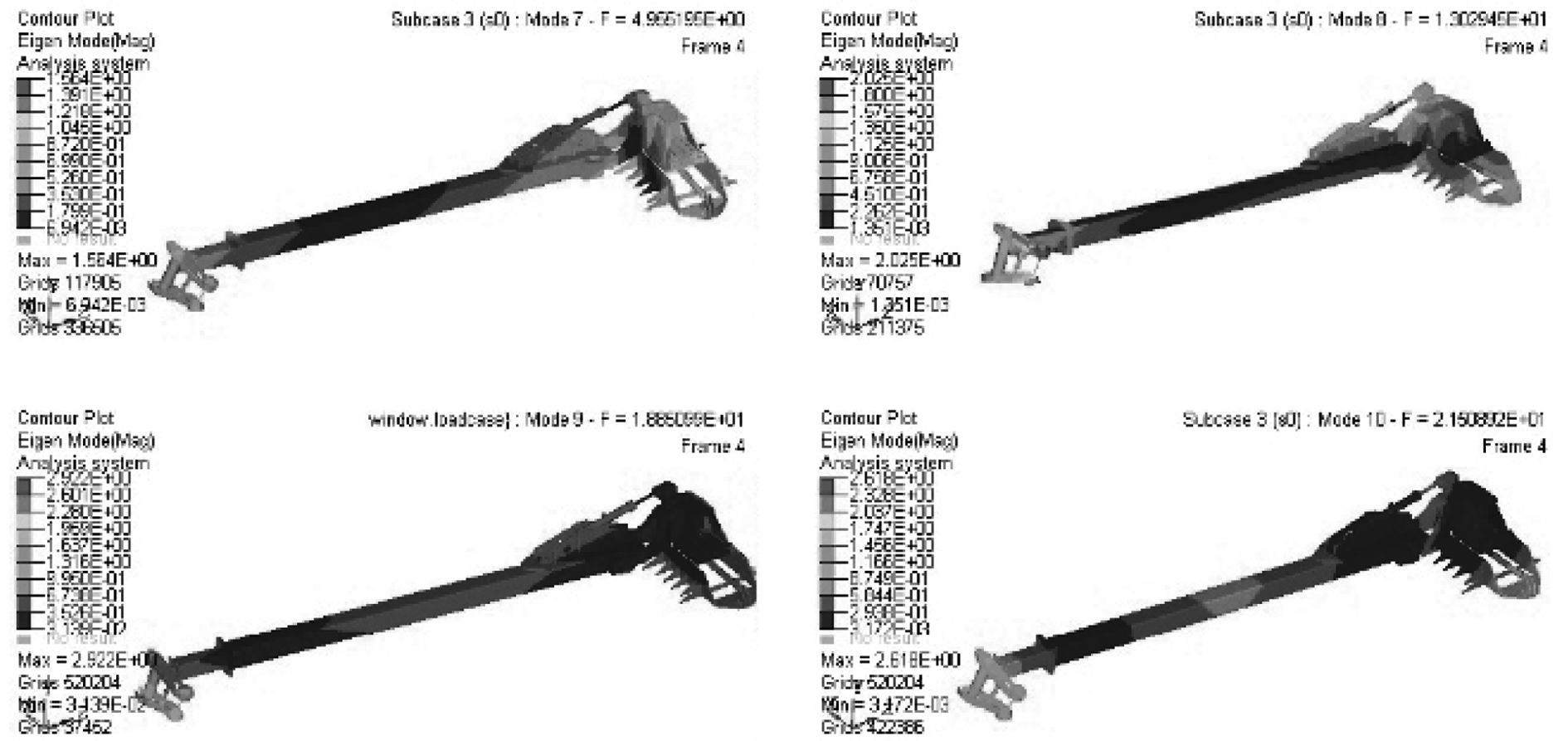
为了对溢油回收装置进行振动预测,本文基于动力学方法对溢油回收装置进行自由模态分析,得到了回收装置的结构固有频率和对应模态振型仿真分析结果,如图12所示。
|
图 12 前4阶模态振型 Fig. 12 The first fourth-order modal vibration mode |
由以上云图分析可以得到,溢油回收装置的结构固有频率(1阶频率)为F7=4.955 Hz,由于1阶模态值约为5 Hz,因此很容易受外环境低频振动的影响而发生共振,主要发生在液压臂和支撑结构连接部分的扭转振动。
3.1.4 瞬态动力学响应分析瞬态响应分析属于时域分析,其计算结构在随时变化载荷作用下的响应。使用有限元方法计算瞬态响应实际上是在指定的时间点上计算结构的响应,从而得到结构关心点的输出响应。
由于溢油回收装置的浮筒捕捉结构在水浪作用下会产生一个类似正弦的结构力,本分析将针对工况3(水浪一般情况)开展瞬态响应分析。载荷简化形式为F=F0sinwt,加入结构阻尼0.2后,对关心点的位移响应进行仿真,分析结果如图13和图14所示,最大位移为3.75 mm,能满足实际工况要求。

|
图 13 动态响应点位置 Fig. 13 Location of dynamic response point |
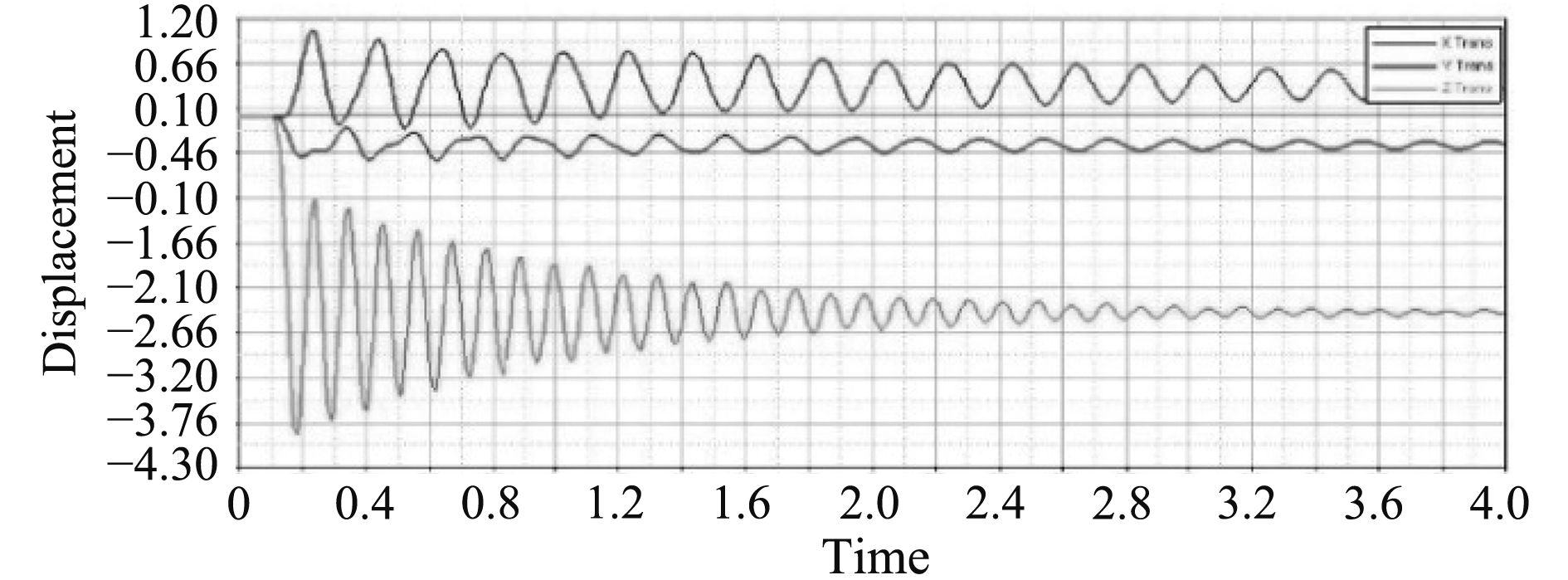
|
图 14 位移响应 Fig. 14 Displacement response |
对溢油回收装置结构进行上述仿真分析后,发现回收装置在刚度和强度方面有较大的改善余量,因此为了充分利用材料性能,在满足结构刚度和强度性能的前提下,对其进行拓扑优化,以寻求最佳的材料布局,从而实现溢油回收装置结构轻量化[17, 18]。
根据仿真结果,以结构体积分数最小化(减重)为目标函数,约束强度(200 MPa)和刚度(对静力学分析中最大点约束位移为11 mm),选取极限工况5对溢油回收装置进行拓扑优化。

|
图 15 初始密度云图 Fig. 15 Initial density cloud |

|
图 16 优化后密度云图 Fig. 16 Optimized density cloud |
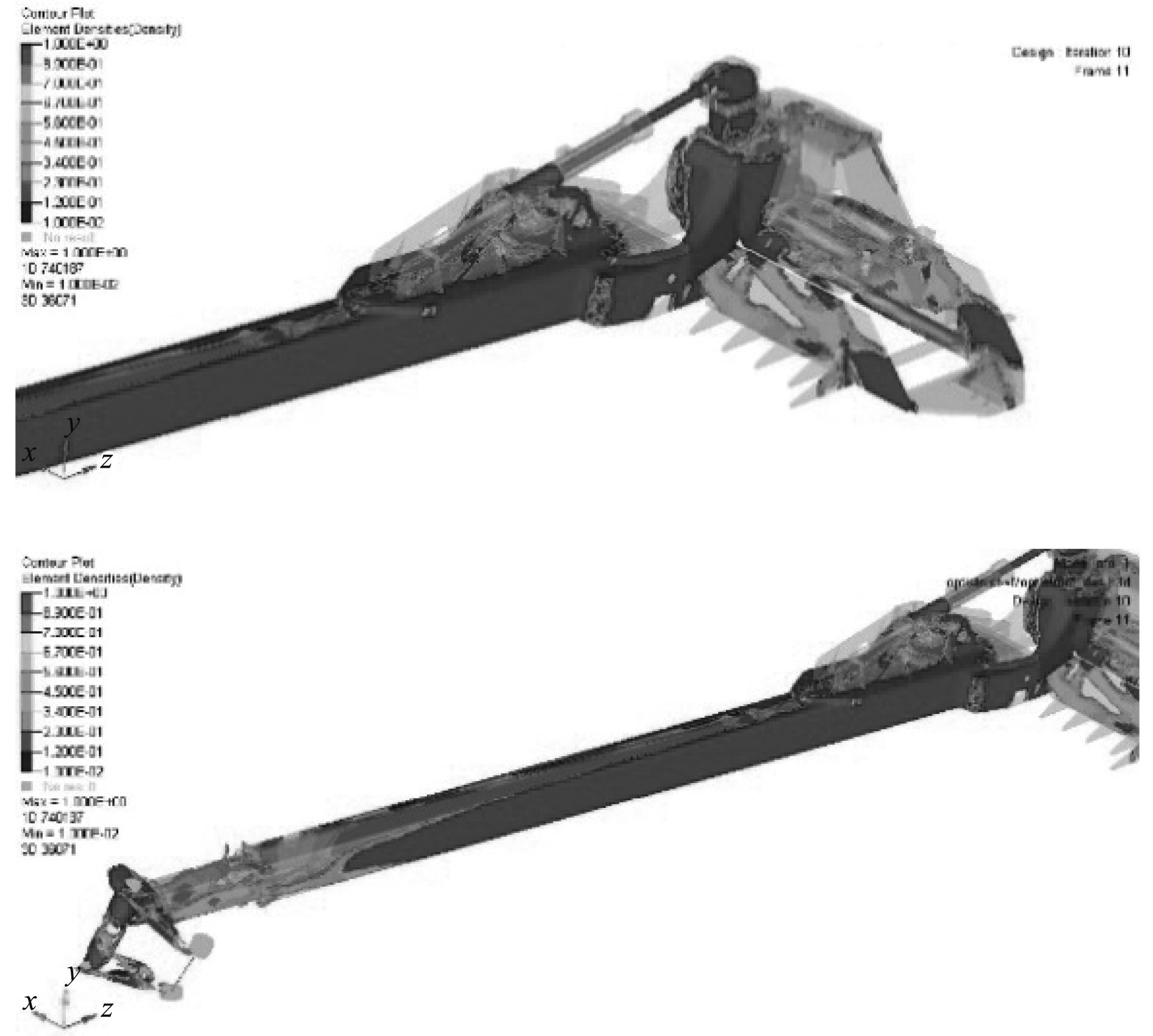
|
图 17 优化后局部放大云图 Fig. 17 Local amplification cloud of the optimized equipment |
经过优化迭代收敛,优化前后相对密度云图如图15~图17所示,最终溢油回收装置的体积分数减少35%(减重1.4 t),且对于液压悬支撑臂和支撑座均需要利用加强筋进行重新布局和优化,迭代收敛后的最大位移为10.3 mm(优化前18.125 mm,提升43%),刚度明显提升,上述结果表明拓扑优化技术对于溢油回收装置的减重和性能提升具有重要作用。
4 结 语随着现代设计方法的不断发展,虚拟仿真技术在航空航天、舰船等领域的应用越来越多。利用仿真驱动设计技术可以实现由面向功能的结构设计向面向性能的结构设计转变。
本文在探讨了基于虚拟仿真技术的结构性能评估和优化设计方法的基础上,以某溢油回收船溢油回收装置的结构性能仿真和轻量化设计为例,详细介绍了虚拟仿真技术在船舶设计中的应用,对溢油回收船溢油回收装置的设计具有非常重要的指导意义。
| [1] | 封培元, 史琪琪, 王磊. 多功能海上溢油处理装置设计[J]. 船舶工程, 2009 (31): 131–134. |
| [2] | 邹云飞, 谢琛, 张德文. 溢油应急设备库现状及发展前景综述[J]. 环境工程, 2012 (30): 427–429. |
| [3] | 孙江, 王海涛. 我国海洋环境风险防范制度完善研究——蓬莱溢油事故之应对及反思[C]// 2012年全国环境资源法学研讨会, 成都, 2012: 77–89. |
| [4] | 丛岩. 国内溢油回收船现状及溢油回收装置选型研究[J]. 船舶工程, 2015, 37 (5): 1–6. |
| [5] | 邹云飞, 张德文, 张鹏. 溢油回收船的现状及发展趋势[J]. 中国水运, 2015, 15 (5): 23–29. |
| [6] | 张同戌, 张德文, 任良成. 国内外船携式溢油回收系统比较[J]. 中国水运, 2009, 9 (2): 10–14. |
| [7] | 冯伯威, 李俊华, 汪玉, 等. 虚拟仿真技术在船舰研制评估中的应用研究[J]. 船舶, 2005 (5): 54–57. |
| [8] | MCLEAN C, SHAO G. Simulation of shipbuliding operations[C]// Processing of the 2001 Winter Simulation Conference. Washington, DC: IEEE, 2001: 870–876. |
| [9] | KIM H T, LEE J G, LEE S S. A simulation based shipbuilding system for evaluation of validity in design and manufacturing[C]// Processing of IEEE international Conference on System, Man and Cybernetics. Washington, DC: IEEE, 2003: 522–529. |
| [10] | 余建星, 张长林, 张裕芳, 等. 虚拟现实技术及其对船舶制造业的影响[J]. 船舶工程, 2003, 25 (3): 1–3. |
| [11] | BENDSOE M P, KIKUCHI N. Generating optimal topologies in structure design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 71 (2): 197–224. |
| [12] | FUKUSHIMA J. Shape and topology optimization of a car body with multiple loading conditions[J]. SAE Technical Paper Series, 1992, 920777 : 1–3. |
| [13] | VOLKSWAGEN A G. Topology optimization of an engine mount bracket using Altair OptiStuct[C]//. Volkswagen A.G, 2003. |
| [14] | BENDSOE M P, SIGMUND O. Topology optimization: Theory, methods and applications[C]//. New York: Springer, 2003. |
| [15] | RIETZ A. Sufficiency of a finite exponent in SIMP (Power law) method[J]. Structure and Multidiscipline Optimization, 2001, 21 : 159–163. DOI: 10.1007/s001580050180 |
| [16] | STOPLE M. An alternative interpolation scheme for minimum compliance topology optimization[J]. Structural and Multidiscipline Optimization, 2001, 22 : 116–124. DOI: 10.1007/s001580100129 |
| [17] | 王碧玲, 刘本刚, 许世娇, 等. 虚拟仿真技术在飞机轻量化设计中的应用[J]. 航空制造技术, 2015 (17): 32–36. |
| [18] | MAYER R R. The application of topological optimization techniques to nonlinear structural problems using variable material densities[J]. Optimization Industry, 1999 (2): 243–251. |
 2017, Vol. 39
2017, Vol. 39
