2. 海军装备研究院,北京 100036;
3. 中国舰船研究设计中心,湖北 武汉 430064
2. Naval Academy of Armament, Beijing 100036, China;
3. China Ship Development and Design Center, Wuhan 430064, China
随着海洋资源开发和国防事业的发展,各类海上结构物的需求越来越大,发展越来越迅速,已经成为世界各国发展的新热点。因此,对于海洋结构物的运动特性进行研究就显得十分必要。
理论研究方面,来自MIT的Johansson[1]建立了一种非线性的有限元模型,在仅有锚链的一端被迫运动情况下,对模型锚链的动力响应进行数值分析,并在Newmark工作的基础之上,提出一种新方法用于耦合运动方程的数值积分。史琪琪等[2]运用波浪交互理论,在不同间距下,对一个箱型多浮体系统的水动力问题进行求解。范菊等[3]应用频域方法,在由波频运动引起低频率慢荡阻力的条件下,探究了锚泊线所引起的相关的力。刘应中等[4]针对风浪流联合作用下的海上系泊系统,应用准定常的时域方法,分析其运动及动力特征,应用准静态方法得到每一时间步的系泊力。
数值仿真方面,冷述栋等[5]探究了浮筒单点系泊系统的形态,结果表明锚链的结构和布置方式有一定影响。李威等[6]针对单点系泊的FPSO船体模型,对系泊系统响应进行数值仿真分析,得出性能更为优良的系泊系统参数。童波等[7]对悬链式深水平台进行研究,考虑缆绳长度、布置角度等因素对系泊系统的影响。刘建成等[8]利用设计谱理论和经验公式等得到了各种外界载荷,设计了一种简易单点系泊系统,并论证了系统在理论上的可行性和经济性。刘元丹等[9]研究了旁靠系统的水动力响应,计算两旁靠船舶所受到的波浪载荷,与不考虑耦合作用的计算结果进行对比,并分析了不同旁靠间距对水动力性能的影响。付强等[10]针对LNG运输船旁靠FLNG进行卸载作业时的情况进行研究,考虑连接缆和防碰垫受力情况及斜浪对系统的影响。徐乔威等[11]研究了FPSO旁靠系泊系统的屏蔽效应,在频域下研究了阻尼和船体响应RAO的特性,以及两船间距因素的影响。
前述的各项理论研究及仿真研究中,主要对简易的系泊系统进行相应的研究,对实际应用的旁靠系泊系统研究较少,且缺乏完整性和系统性。旁靠补给方式是一种相对较新颖的补给方式。尤其对于军船,常规的补给方式只能进行小型物资的补给,大型物资的补给必须返回港口码头进行,旁靠补给对于军船的大型物资补给方面有很大的优势。
本文建立了相对完整的旁靠补给系泊系统,包含作业船舶、浮箱、各类缆索和护舷等部件,考虑结构间相互耦合作用,可以施加任意大小和方向的风浪流载荷。针对旁靠补给系泊系统,在频域和时域的特性进行较深入的研究,在频域重点关注结构的水动力特性,在时域重点关注目标船与补给船间的相对位移响应及缆索张力最大值,以验证系统的稳定性和可靠性。
1 系泊系统设置 1.1 不同系泊方式的比较本文建立了旁靠补给系泊系统,目标船通过1根缆绳系泊到海底,补给船与目标船平行排列,两船通过缆绳连接;两船间设置2个浮箱防止两船相撞,且浮箱两面均布置有护舷缓冲碰撞力。船体具体参数设置见表1。
整体系泊系统示意图见图1,两船之间共设置8条缆绳,自船首至船尾依次编号为1~8号,目标船与海底之间缆绳编号为9号。
|
|
表 1 船体参数 Tab.1 Parameters of ships |
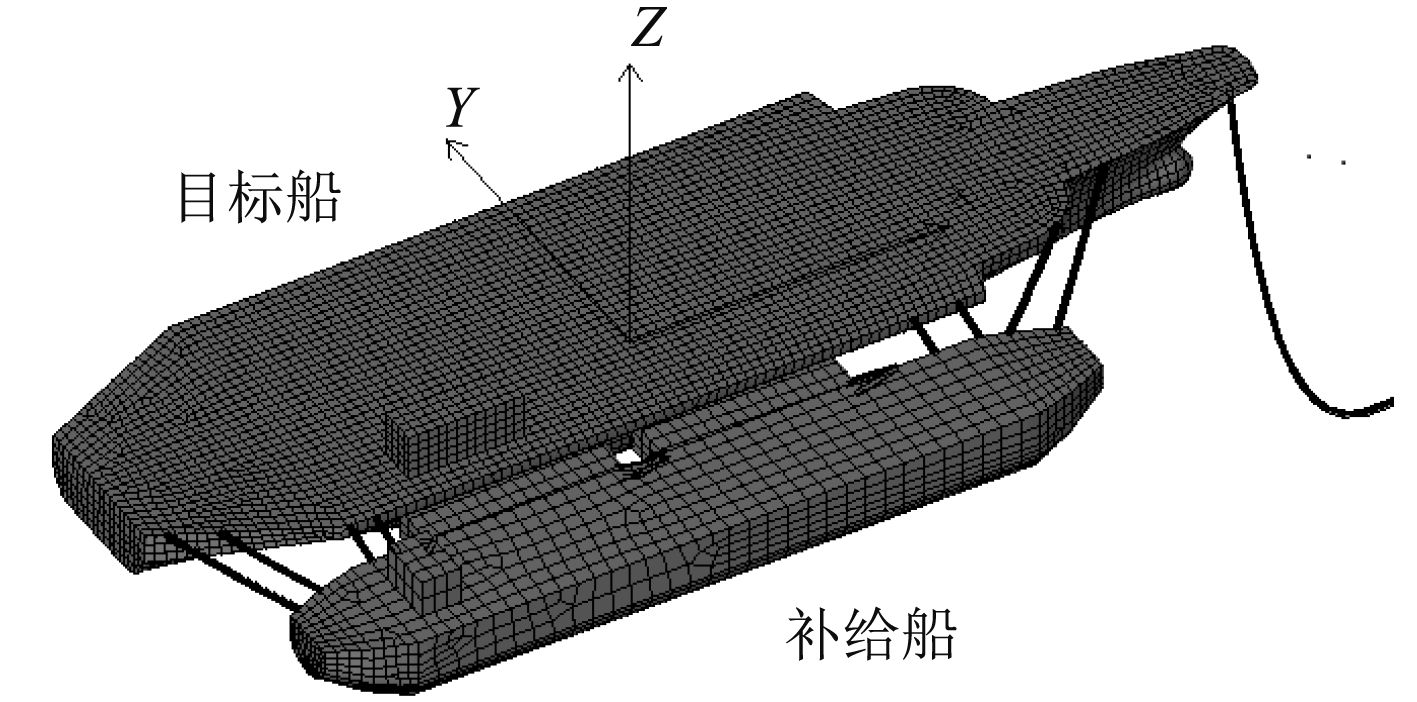
|
图 1 系泊系统模型 Fig. 1 Model of mooring system |
在计算程序中,设定X轴正方向为0°,沿X轴逆时针方向旋转为正。水深为100 m,风速为10.7 m/s,方向为190°;流速为1.8 m/s,方向为170°;波高为2.5 m,波周期为10 s,波浪方向为180°。
2 计算分析本节分别在频域和时域内,对系泊系统的动力响应进行分析计算,以得到系统的运动特性,并得到更加优化的系泊系统参数设置。由于本系统属于单点系泊系统,最终系统都会处于迎浪状态,此时的浪向为180°。
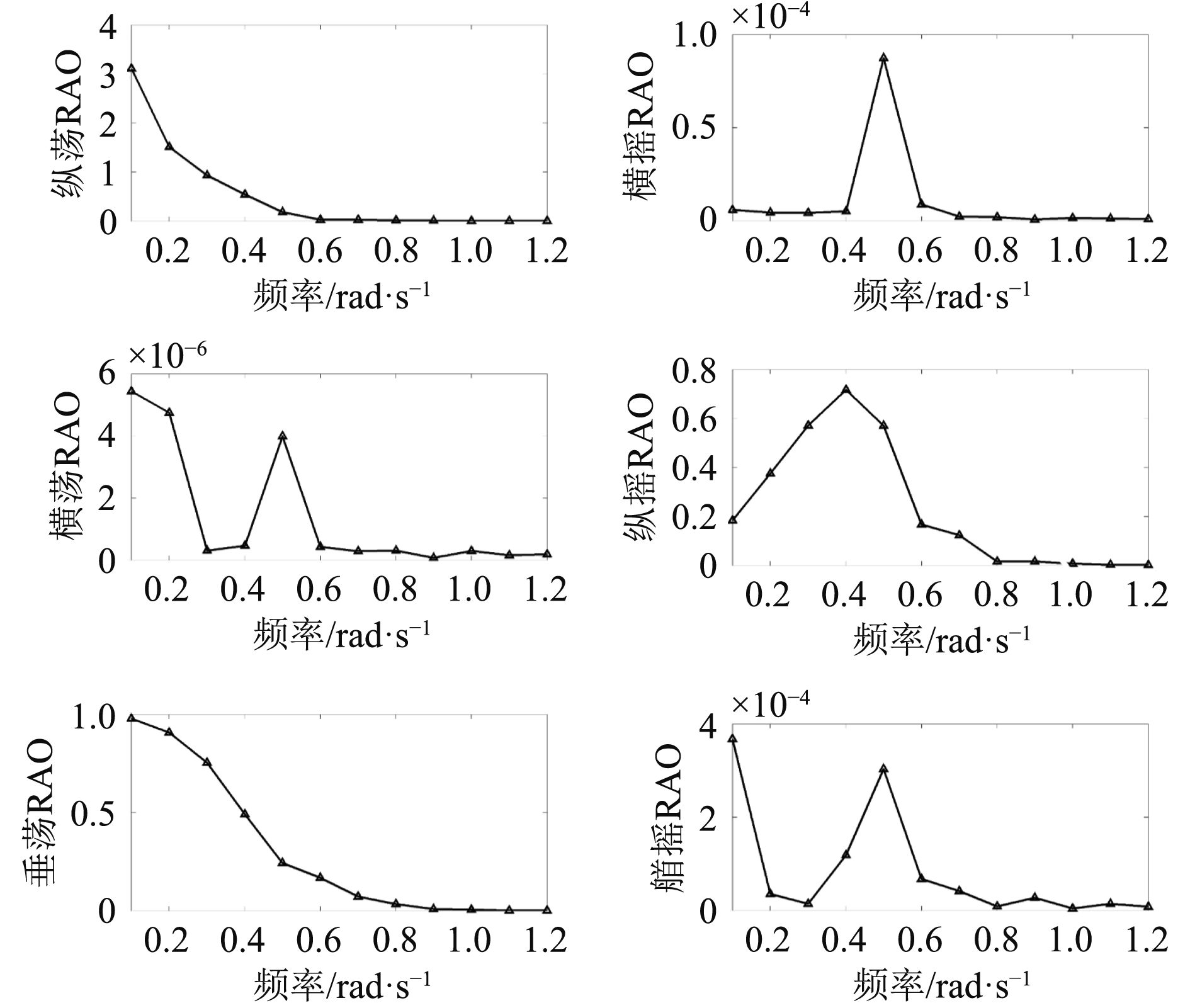
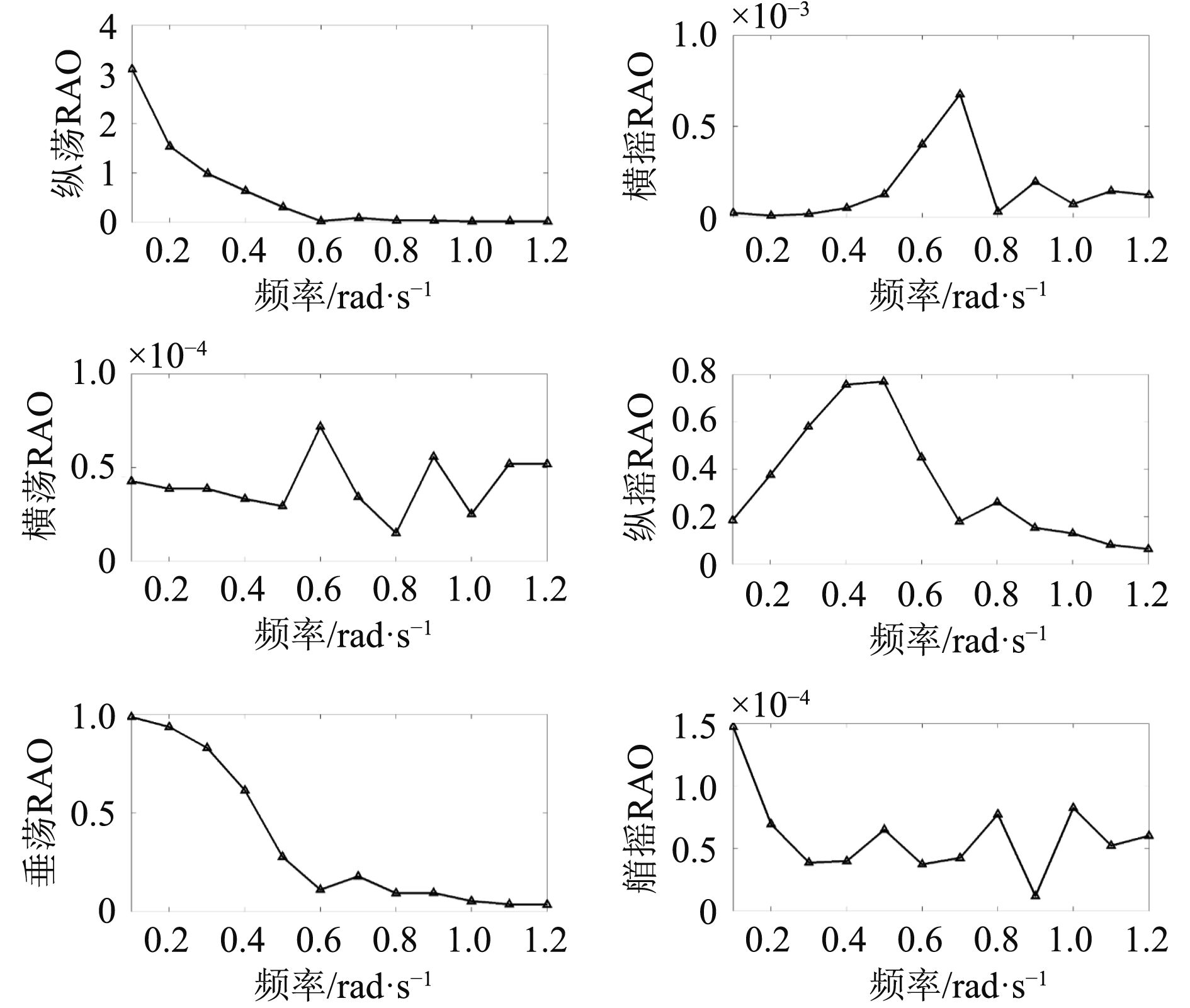
2.1 频域分析在对系统的动力特性进行频域分析时,需要引入RAO(幅值响应算子)的概念。RAO相当于将波浪载荷转换为结构物运动响应的传递函数,它描述了结构物在6个自由度下的运动特性。在180°浪向下,目标船和补给船的六自由度RAO曲线如图2和图3所示。
|
图 2 目标船RAO曲线 Fig. 2 Rao curves in of target ship |
|
图 3 补给船六自度RAO曲线 Fig. 3 Rao curves in of supply ship |
由图可知,对于目标船,纵荡、垂荡和纵摇的量级远大于其他3个自由度,说明180°的波浪主要影响船体的纵荡、垂荡和纵摇运动;纵荡和垂荡RAO随着频率的增大逐渐减小,而其他4个自由度RAO都有峰值出现,峰值出现的范围在0.4~0.6 rad/s,之后RAO值会随着频率的增大逐渐减小。
对于补给船,纵荡、垂荡和纵摇的量级远大于其他3个自由度,说明180°的波浪主要影响船体的纵荡、垂荡和纵摇运动;纵荡和垂荡RAO随着频率的增大逐渐减小,而其他4个自由度RAO在0.4 rad/s之后都有峰值出现。
由此可知,应尽量避免频率范围在0.4~0.6 rad/s的波浪。
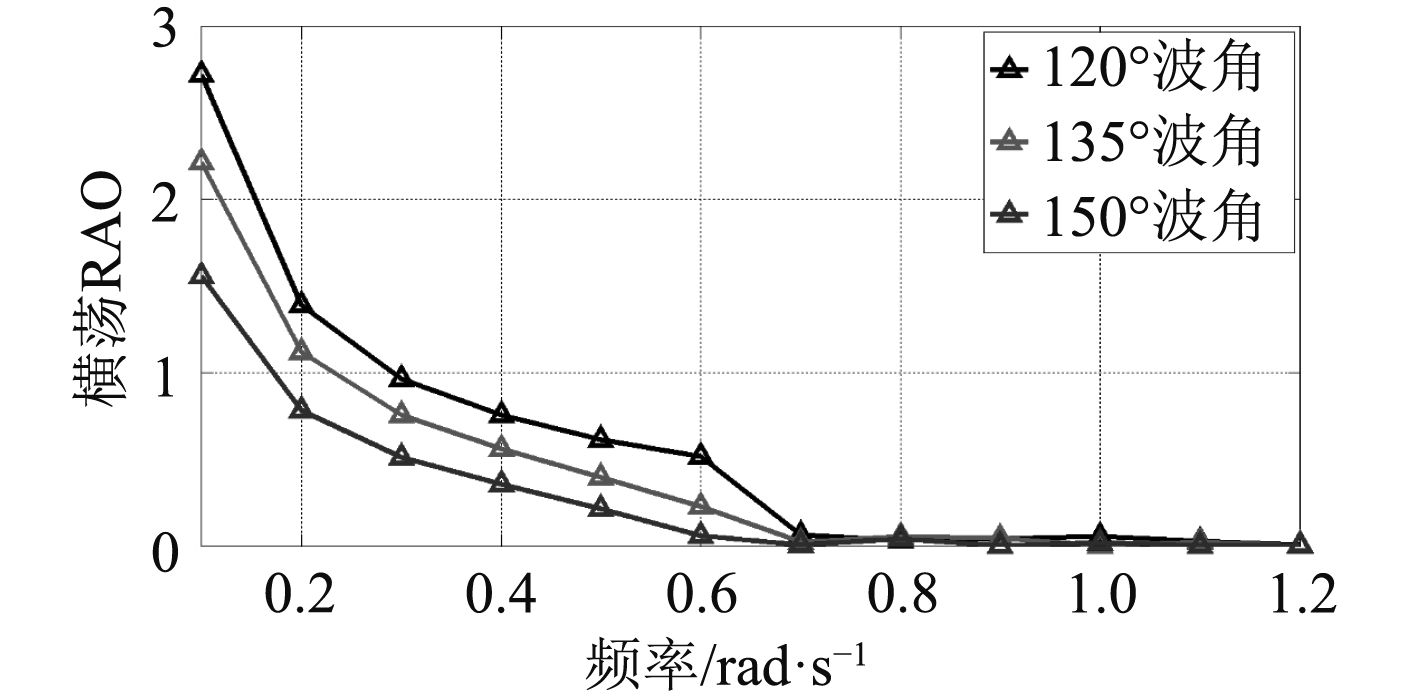
为了研究不同角度的波浪对与船体的运动响应的影响,选取120°、135°和150°的波浪进行研究,考察其对横荡运动的影响,如图4和图5所示。

|
图 4 目标船不同角度下横荡RAO比较曲线 Fig. 4 Rao curves in different angles of target ship |
|
图 5 补给船不同角度下横荡RAO比较曲线 Fig. 5 Rao curves in different angles of supply ship |
由图可知,对于目标船和补给船,不同角度的波浪对与船体的运动响应有不同的影响,在本例中,对于横荡运动,频率小于0.6 rad/s时,120°波浪对运动响应的影响要大于135°和150°波浪。扩展到所有的浪向,以及其对全部6个不同自由度的研究,就可以得出系统结构的运动响应特性。
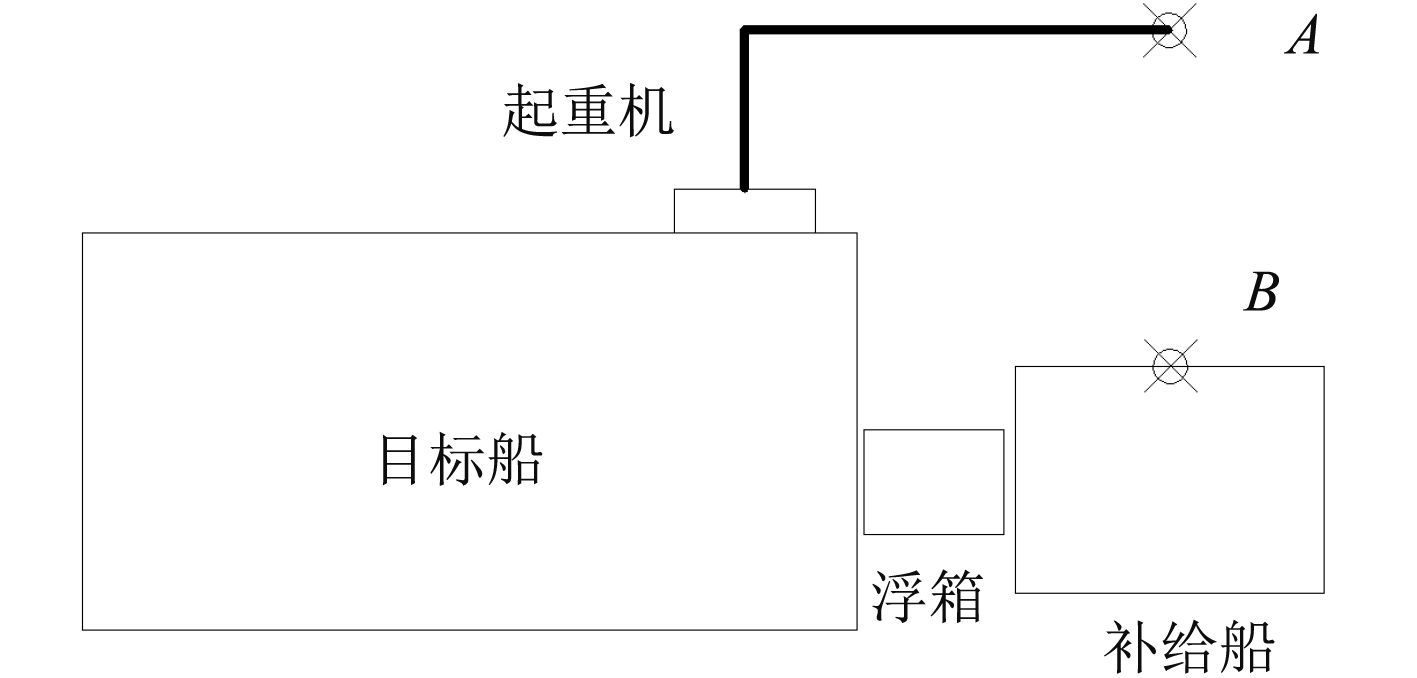
2.2 时域分析在旁靠补给系泊系统中,在目标船上设置有起重机,货物由起重机从补给船运送到目标船上,由于两船在外界载荷的作用下具有相对运动,对货物的安全起吊产生严重影响。为了消除这种影响,起重机上安装波浪补偿装置,可以对两船之间的相对线性运动进行补偿,包括相对位移补偿和相对速度补偿。
本文的旁靠补给系统中,货物的起吊点B位于补给船甲板的中部,起重机的工作点A位于起吊点的正上方,工作示意图如图6所示。
|
图 6 旁靠补给系泊系统工作示意图 Fig. 6 Diagram of supply mooring system |
在时域计算中,可以得到系统中结构的运动响应和缆绳的张力最大值,为了更真实地模拟现实中作业情况,本文中的位移响应和张力最大值均取自系统运动稳定的阶段。对于旁靠补给方式,最重要的是保证其实施的可靠性,即要使两船之间的相对位移和相对速度尽可能小,才可以保障补给的安全进行。其次,为使系泊系统性能达到最优,缆绳的张力最大值应尽量小且分布均匀。
2.2.1 两船间缆绳刚度设置不同类型和材质的缆绳具有不同的刚度(EA),选取不同的两船间缆绳刚度(Line1~8),时域仿真的结果如表2和表3所示(表格中,Lx为纵向相对位移,Ly为横向位移,Lz为垂向位移,Vx为纵向相对速度,Vy为横向相对速度,Vz为垂向相对速度)。
|
|
表 2 不同刚度下相对位移 Tab.2 Relative displacement in different stiffness |
|
|
表 3 不同刚度下缆绳张力最大值 Tab.3 Max tension of cables in different stiffness |
由表4可知,缆绳刚度为4×106时,两船相对位移明显大于其他2种刚度的情况,3种刚度下两船相对速度相差不大;由表5可知,缆绳刚度为1.6×107时,缆绳的张力最大值较大幅度的高于刚度为8×106时;综合位移和张力最大值数据,两船间缆绳刚度为8×106时为最优情况。
|
|
表 4 不同刚度下相对位移 Tab.4 Relative displacement in different stiffness |
|
|
表 5 不同刚度下缆绳张力最大值 Tab.5 Max tension of cables in different stiffness |
不同类型锚链具有不同的刚度(EA),选取不同的海底锚链刚度(Line9),时域仿真的结果如表6和表7所示(表格中,Lx为纵向相对位移,Ly为横向位移,Lz为垂向位移,Vx为纵向相对速度,Vy为横向相对速度,Vz为垂向相对速度)。
由表6可知,海底缆绳刚度为8×108时,大部分相对位移明显小于其他2种刚度的情况;由表7可知,缆绳刚度越小,缆绳的张力最大值越小;综合位移和张力最大值情况,海底缆绳刚度为8×108时为最优情况。
2.2.3 海底系泊点位置设置对于系泊系统来说,海底系泊点位置的选择是一个重要的因素,不同系泊点位置决定了海底锚链(Line9)的长度,不同的锚链长度决定了不同的系统平衡位置。本文中选择了4种不同的系泊点位置,研究其影响。字母L代表海底锚链(Line9)两端之间的水平距离,具体结果如表8和表9所示(表中Lx为纵向相对位移,Ly为横向位移,Lz为垂向位移,Vx为纵向相对速度,Vy为横向相对速度,Vz为垂向相对速度)。
|
|
表 6 不同位置下相对位移 Tab.6 Relative displacement in different stiffness |
|
|
表 7 不同位置下缆绳张力最大值 Tab.7 Max tension of cables in different stiffness |
由表8可知,当L等于500 m时,两船相对位移值均小于其他3种情况,对于两船的相对速度,4种情况的差别很小;由表9可知,4种情况下两船间缆绳张力最大值差别较小,而对于海底锚链,L越大时,锚链的张力最大值越小,但是L为500 m和800 m时,张力最大值的差别不大;因此综合位移和张力最大值情况,当L为500 m时为最优情况。
2.2.4 两船间缆绳长度设置分析上述算例(方案1)中两船缆绳的张力最大值分布,可以发现缆绳中的张力分布较不均匀,Line1,Line2,Line5和Line6承受了大部分的张力,为了探究使两船间缆绳中张力分布更加均匀的方法,改变缆绳的长度来进行调节。具体的方式是适当的增加Line1、Line2、Line5和Line6这4根缆绳的长度,适当的减小其他4根缆绳的长度,缆绳长度的改变量均小于缆绳原长的5%。通过不断地改变各条缆绳的长度,并根据缆绳张力最大值的分布情况反复的进行调整,得出1套比较理想的缆绳长度数据(方案2),具体的计算结果如表10和表11所示(表格中,Lx为纵向相对位移,Ly为横向位移,Lz为垂向位移,Vx为纵向相对速度,Vy为横向相对速度,Vz为垂向相对速度)。
|
|
表 8 不同缆绳长度下相对位移 Tab.8 Relative displacement in different stiffness |
|
|
表 9 不同缆绳长度下缆绳张力最大值 Tab.9 Max tension of cables in different stiffness |
由表中数据可知,通过不断地调节缆绳长度,可以使两船间缆绳张力最大值分布变得更加均匀;对于两船的相对位移和相对速度,方案1和方案2相差极小,说明缆绳长度的调整可以使缆绳张力最大值分布更加合理,但对相对位移和相对速度的影响较小。
2.2.5 两船间缆绳布置为了探究两船间缆绳的布置方式对系泊系统性能的影响,且考虑到原先的布置方案中张力最大值的分布不均匀的特征(方案1),改变Line3,Line4,Line7和Line8的布置位置,即把这4根缆绳在目标船上的系泊点位置向船首方向移动一段距离(方案2),使缆绳的方向更加平行于浪向(180°)。而目前可用的波浪补偿起重机,相对位移补偿能力大致为1.2 m,相对速度补偿能力大致为1 m/s。具体的计算结果如表10和表11所示(表中Lx为纵向相对位移,Ly为横向位移,Lz为垂向位移,Vx为纵向相对速度,Vy为横向相对速度,Vz为垂向相对速度)。
|
|
表 10 不同缆绳布置方式下相对位移 Tab.10 Relative displacement in different stiffness |
|
|
表 11 不同缆绳布置方式下缆绳张力最大值 Tab.11 Max tension of cables in different stiffness |
由上面表格数据可知,改变缆绳的布置方式后,张力最大值在缆绳中的分布变得更加均匀,说明当缆绳的方向越接近浪向,承受的张力最大值会越大;方案2与方案1相比两船的相对位移和相对速度略微变大,但差别较小,在垂向位移和垂向速度上还略有减小,且2种方案都在补偿能力范围之内。因此,在实际操作中,要综合考虑缆绳的布置方式对张力和相对位移响应的影响,选取最合适的布置方式。
3 结 语根据上面的分析结果,可以得到如下结论:
1)对于目标船和补给船,180°的波浪主要影响船体的纵荡、垂荡和纵摇运动,对其他3个自由度的运动影响较小;
2)纵荡和垂荡RAO随着频率的增大而减小,而横荡、横摇、纵摇和首摇RAO都有峰值出现,对其中受影响最大的纵摇运动,峰值出现在0.4~0.6 rad/s,因此系泊系统应该尽量避免这个频率范围的外界载荷,包括环境载荷和船用机械产生的载荷等;
3)两船间缆绳刚度、海底锚链刚度和海底系泊点位置都对系泊系统性能有较大的影响,在旁靠补给的目的下,两船间的相对位移和相对速度是主要的考察指标,兼顾缆绳的张力最大值分布,通过比较分析,可以得出最优的参数值;
4)调节两船间的缆绳长度,可以使两船间缆绳张力最大值分布变得更加均匀,但对两船的相对位移和相对速度无明显改善;改变缆绳的布置方式,使小张力的缆绳方向越接近浪向,承受的张力最大值会越大,因此可以使张力最大值在缆绳中的分布变得更加均匀,同时两船的相对位移和相对速度会略有增加,因此在工程实践中,需要根据补偿能力进行适当的取舍。
本文对旁靠补给方式进行了较深入的研究,通过对系泊系统的各种参数进行对比分析,可以得出一个较为优良的旁靠系泊方案,保障旁靠补给的安全进行。本文研究可以为工程实践提供一定的指导意义,在实践中根据具体情况选择恰当的参数确定系泊方案,可以最大程度地提高系统的作业性能。
| [1] | PER I. JOHANSSON. A finite element model for dynamic analysis of mooring cables[R]. USA: Massachusetts Institute of Technology, 1976. |
| [2] |
史琪琪, 柏木正, 杨建民. 三维多浮体水动力学问题中波浪交互理论的参数应用特性探究分析[J]. 科技通报, 2012, 07 : 1–7+13.
SHI Qiqi, BO Muzheng, YANG Jianmin. Research on Application Characteristics of Parameters in Wave-interaction Theory when Solving Hydrodynamic Problems of 3-D Multiple Floating Bodies[J]. BULLETIN OF SCIENCE AND TECHNOLOGY, 2012, 07 : 1–7+13. DOI: 10.3969/j.issn.1001-7119.2012.01.001 |
| [3] |
范菊. 锚泊线的动力分析[J]. 中国造船, 1999, 01 : 13–20.
FAN Ju, et al. THE ANALYSIS OF MOORING LINE DYNAMICS[J]. SHIPBUILDING OF CHINA, 1999, 01 : 13–20. |
| [4] |
刘应中, 等. 系泊系统动力分析的时域方法[J]. 上海交通大学学报, 1997, 11 : 9–14.
LIU Yingzhong, et al. A Time Domain Computation Method for Dynamic Behavior of Mooring System[J]. JOURAL OF SHANGHAI JIAOTONG UNIVERSITY, 1997, 11 : 9–14. DOI: 10.3321/j.issn:1006-2467.1997.07.003 |
| [5] | 冷述栋. CALM系泊系统动力响应分析[D]. 大连: 大连理工大学, 2013. |
| [6] |
李威, 纪仁超. FPSO单点系泊系统性能仿真分析[J]. 计算力学学报(增刊), 2015, 32 : 128–133.
LI Wei, JI Renchao. Simulation Analysis of FPSO single point mooring system[J]. Chinese Journal of Computational Mechanics (Supplement), 2015, 32 : 128–133. |
| [7] |
童波, 杨建民, 李欣. 深水半潜平台悬链线式系泊系统耦合动力分析[J]. 中国海洋平台, 2008, 06 : 1–7.
TONG Bo, YANG Jianmin, LI Xin. Deepwater semi-submersible platform catenary mooring system coupling dynamic analysis[J]. China ocean platform, 2008, 06 : 1–7. DOI: 10.3969/j.issn.1001-4500.2008.01.001 |
| [8] |
刘建成, 等. 一种简易单点系泊系统的可行性研究[J]. 上海交通大学学报, 2000, 01 : 132–136.
LIU Jiancheng, et al. Feasibility study on simply equipped single point mooring system[J]. JOURAL OF SHANGHAI JIAOTONG UNIVERSITY, 2000, 01 : 132–136. DOI: 10.3321/j.issn:1006-2467.2000.01.030 |
| [9] |
刘元丹, 等. 基于AQWA的旁靠油轮水动力相互作用研究[J]. 舰船科学技技术, 2012, 05 : 13–15+17+22.
LIU Yuandan, et al. Analysis of hydrodynamic interaction between side by side mooring tankers[J]. SHIP SCIENCE AND TECHNOLOGY, 2012, 05 : 13–15+17+22. |
| [10] |
付强. 旁靠系泊油船水动力相互作用分析[J]. 船海工程, 2012, 04 : 16–20.
FU Qiang, et al. Analysis of Hydrodynamic Interaction between Side-by-side Mooring Tankers[J]. SHIP & OCEAN ENGINEERING, 2012, 04 : 16–20. DOI: 10.3963/j.issn.1671-7953.2012.03.006 |
| [11] |
徐乔威. LNG运输船旁靠FLNG卸载作业时的水动力性能试验[J]. 中国海上油气, 2015, 02 : 112–119+126.
XU Qiaowei, et al. Hydrodynamic of an FLANG system in side-by-side offloading operation with a LNG carrier[J]. CHINA OFFSHORE OIL AND GAS, 2015, 02 : 112–119+126. |
 2017, Vol. 39
2017, Vol. 39
