2. 江苏科技大学 机械与动力工程学院,江苏 镇江,212003
2. School of Mechanical and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China
在“一带一路”到“海洋强国”的背景下,造船技术及海工装备制造技术已经成为国家海洋发展战略中的关键支撑技术。然而,由于风、浪、流的作用,海上作业十分困难,船舶甲板及海工作业平台表现为横摇、纵摇、首摇、横荡、纵荡、垂荡的6个自由度的不规则运动(见图1),给海上作业带来了很大挑战。例如,舰船海上航行补给作业的大横摇严重影响补给装置的可靠性,铺管船的沉管导架的扭转问题、医疗舰的手术甲板平台的不规则运动等严重影响海上作业精度。因此,研制一种波浪补偿装置,通过主动的运动补偿来抵消6个自由度的不规则运动已经成为当下迫切需要解决的难点问题之一[1–2]。
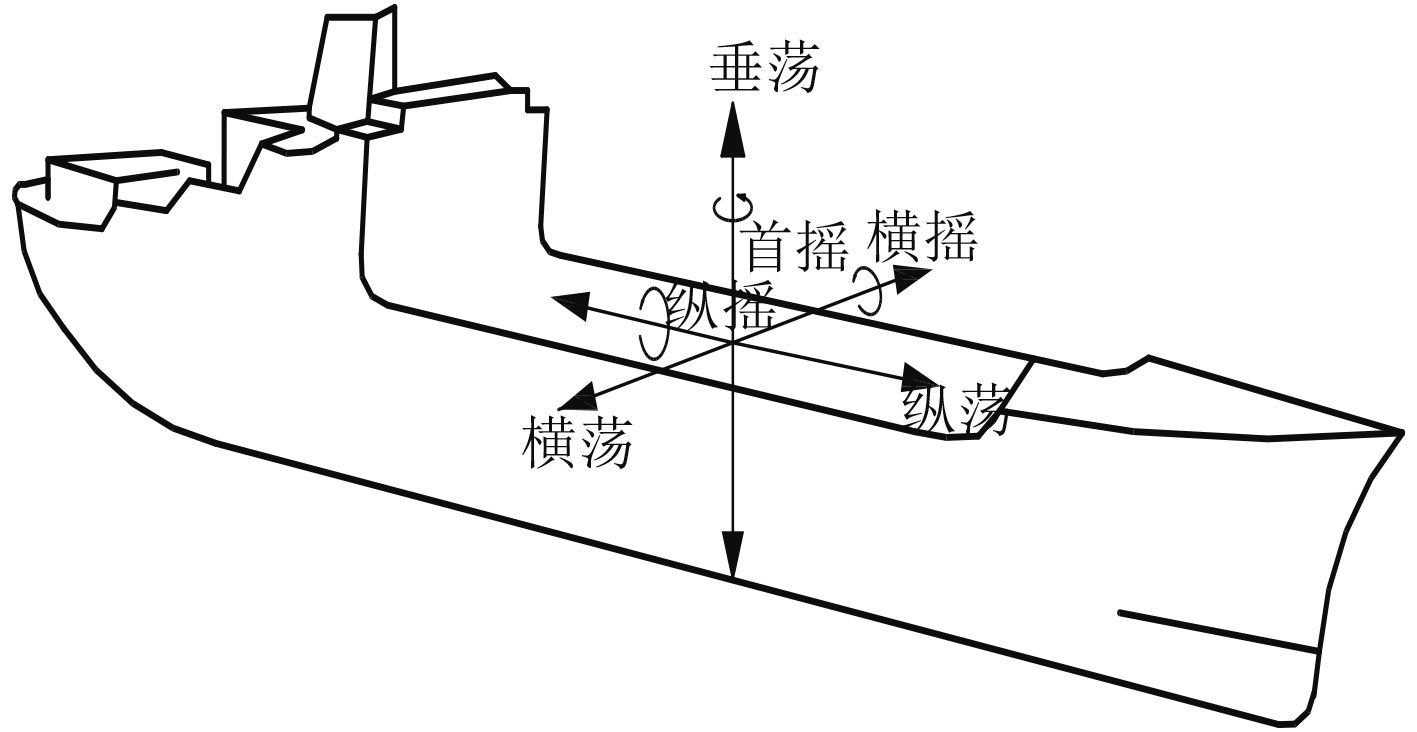
|
图 1 船舶六自由度运动 Fig. 1 Ship 6-DOF motion |
船舶6个自由的不规则运动中,横荡、纵荡、首摇可以借助船舶动力定位系统或者锚泊技术实现补偿,对于横摇、纵摇、垂荡很难借助船舶自身实现补偿。目前,研究最前沿的为荷兰barge master公司设计的1套三自由度波浪补偿控制平台(见图2),其通过液压缸的垂直升降和位置移动来实现位移补偿[3]。

|
图 2 波浪补偿平台结构装置 Fig. 2 The structure of waving compensation device |
本文以某型号风力发电船为例,在海况等级为6级、义波高为5.7时,运用Matlab对船舶的横摇、纵摇角度以及垂荡高度进行仿真,并以此为约束条件,对波浪补偿装置平台的结构进行优化设计。以波浪补偿装置平台的可控性能和平台机构尺寸作为目标函数进行加权优,并采用遗传算法,对平台进行结构参数化设计。
1 6级海况下船舶响应 1.1 波浪特性分析海面上的风浪具有不规则性和随机性,通常对波形长峰不规则波的描述,定义波浪为二因次,其数学表达式写成:
| $\zeta (t) = \sum\limits_{i = 1}^\infty {{\xi _a}\cos ({k_i}\xi \cos \mu + {k_i}\eta \sin \mu - {\omega _i}t + {\varepsilon _i})} \text{。}$ | (1) |
我国海洋部门提出的东海区域谱密度公式为:
| ${S_\zeta }(\omega ) = \frac{{0.74}}{{{\omega ^5}}}\exp ( - \frac{{96.2}}{{{U^2}{\omega ^2}}})\text{,}$ | (2) |
式中:U为风速,m/s。在该密度公式中,风速和义波高之间的关系为:
| $U = 6.28\sqrt {{{\bar \zeta }_{\omega /3}}}\text{。} $ | (3) |
根据谱密度公式绘制出海况等级为6级、义波高为5.7波谱密度,如图3所示。
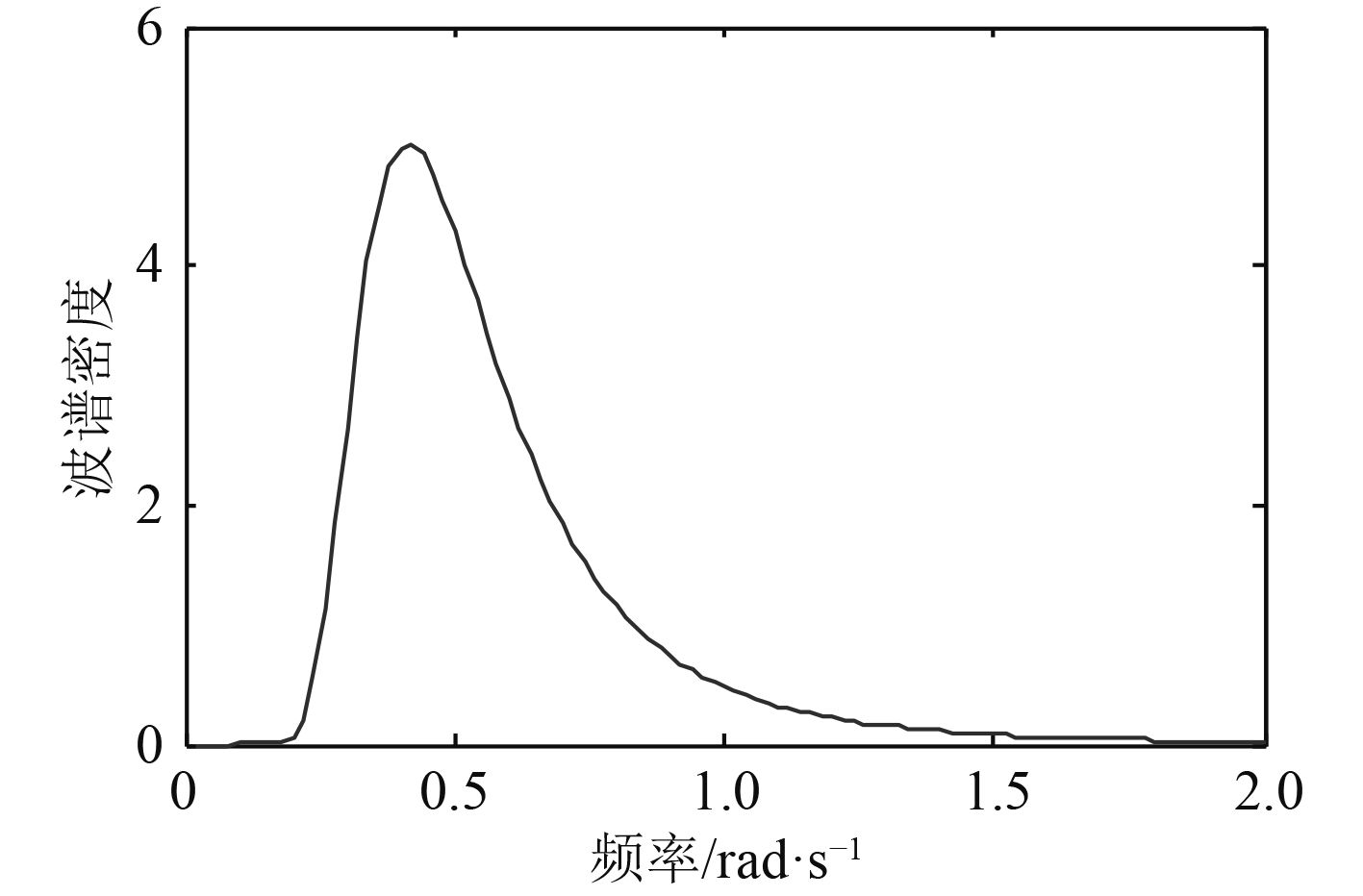
|
图 3 义波高为5.7时波谱密度 Fig. 3 The spectral density at significant wave height 5.7 |
根据风浪谱密度图,当频率确定时,就可以得到一个与之对应的密度值,如果波浪频率范围定义为
|
|
表 1 不同频率对应波浪振幅 Tab.1 Wave amplitude at different frequencies |
运用Matlab绘制出航向角为90°、海况等级为6级、义波高为5.7的波倾角曲线,如图4所示。

|
图 4 遭遇角为90°时波倾角仿真曲线 Fig. 4 Wave slope simulation curve at 90° encounter angle |
研究船舶在不规则波中运动时,为方便建立船舶运动数学模型,假定船舶是线性定常系统且假定充分成长的随机波浪是平稳随机过程,根据船舶水动力理论[4 – 5],船舶在规则波浪中的横摇、纵摇与升沉分别为式(4)~式(6)。
横摇运动方程:
| ${I_{x1}}\ddot \varphi + 2{N_\varphi }\dot \varphi + Dh\varphi = Dh{\alpha _m}\text{,}$ | (4) |
式中:
纵摇运动方程:
| $\ddot \theta + 2{v_{\theta \theta }}\dot \theta + {n_\theta }^2\theta = \frac{{\overline {{F_{\theta \theta }}} }}{{{J_{\theta \theta }} + {\lambda _{\theta \theta }}}}\sin (\omega t + {\xi _{\theta \zeta }})\text{,}$ | (5) |
式中:θ为船舶纵摇角;
类似于横摇运动,规则波中升沉运动方程可写成:
| $\ddot z + 2{v_{zz}}\dot z + {n_z}^2z = \frac{{\overline {{F_{zz}}} }}{{\displaystyle\frac{D}{g} + {\lambda _{zz}}}}\cos (\omega t + {\xi _{z\zeta }})\text{。}$ | (6) |
式中:Z为升沉运动位移;
对式(6)分别进行拉氏变换后与波倾角求卷积得到近似船舶的横摇、纵摇和升沉运动方程。运用Matlab进行仿真,得到船舶在义波高为5.7下的横摇、纵摇和升沉运动曲线如图5~图7所示。
|
|
表 2 某型号海上风电安装船部分参数 Tab.2 Some parameters of a certain type of wind farm installation vessel |

|
图 5 6级海况下船舶横摇运动 Fig. 5 The ship’s roll motion at six level of sea state |
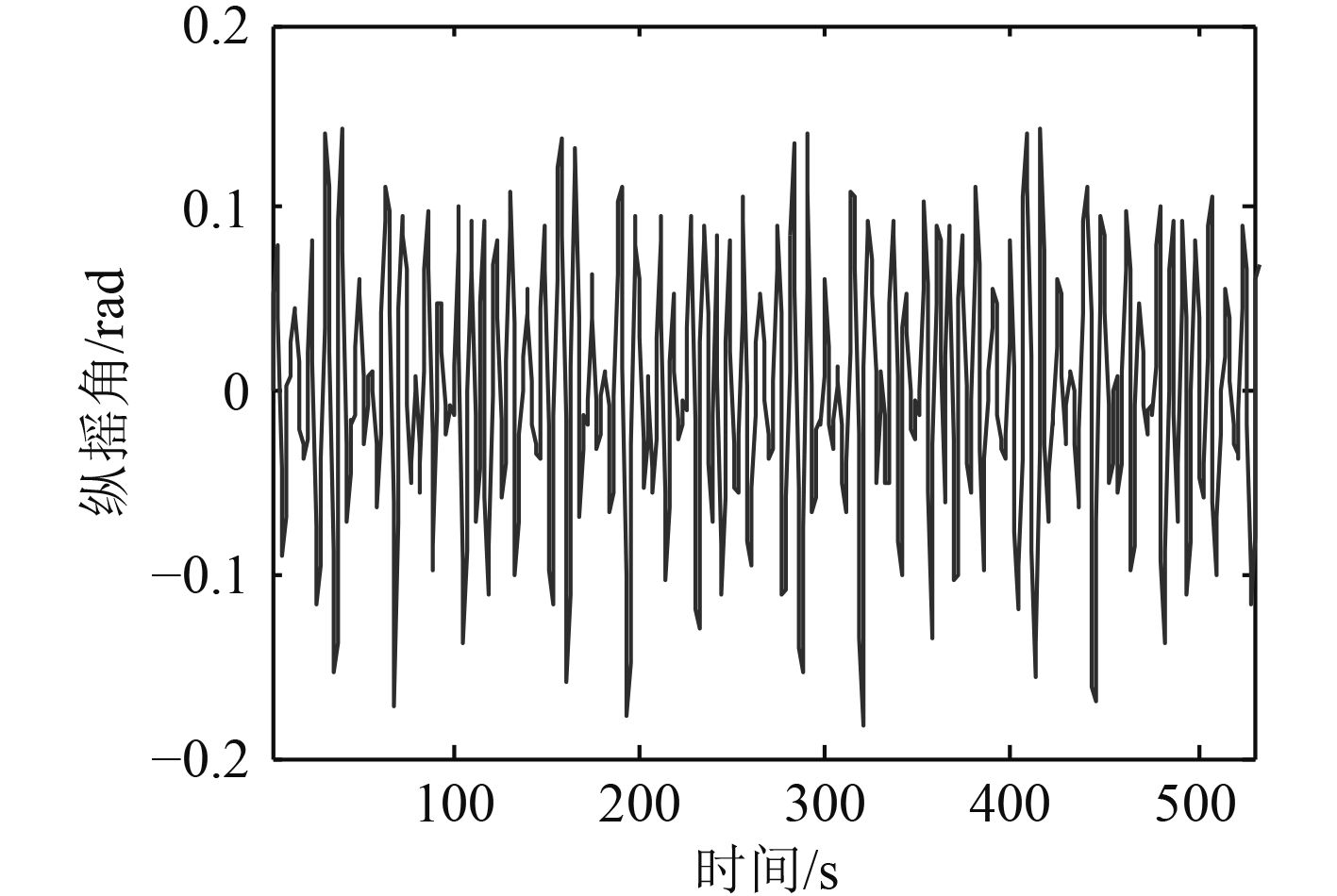
|
图 6 6级海况下船舶纵摇运动 Fig. 6 The ship’s pitching motion at six level of sea state |
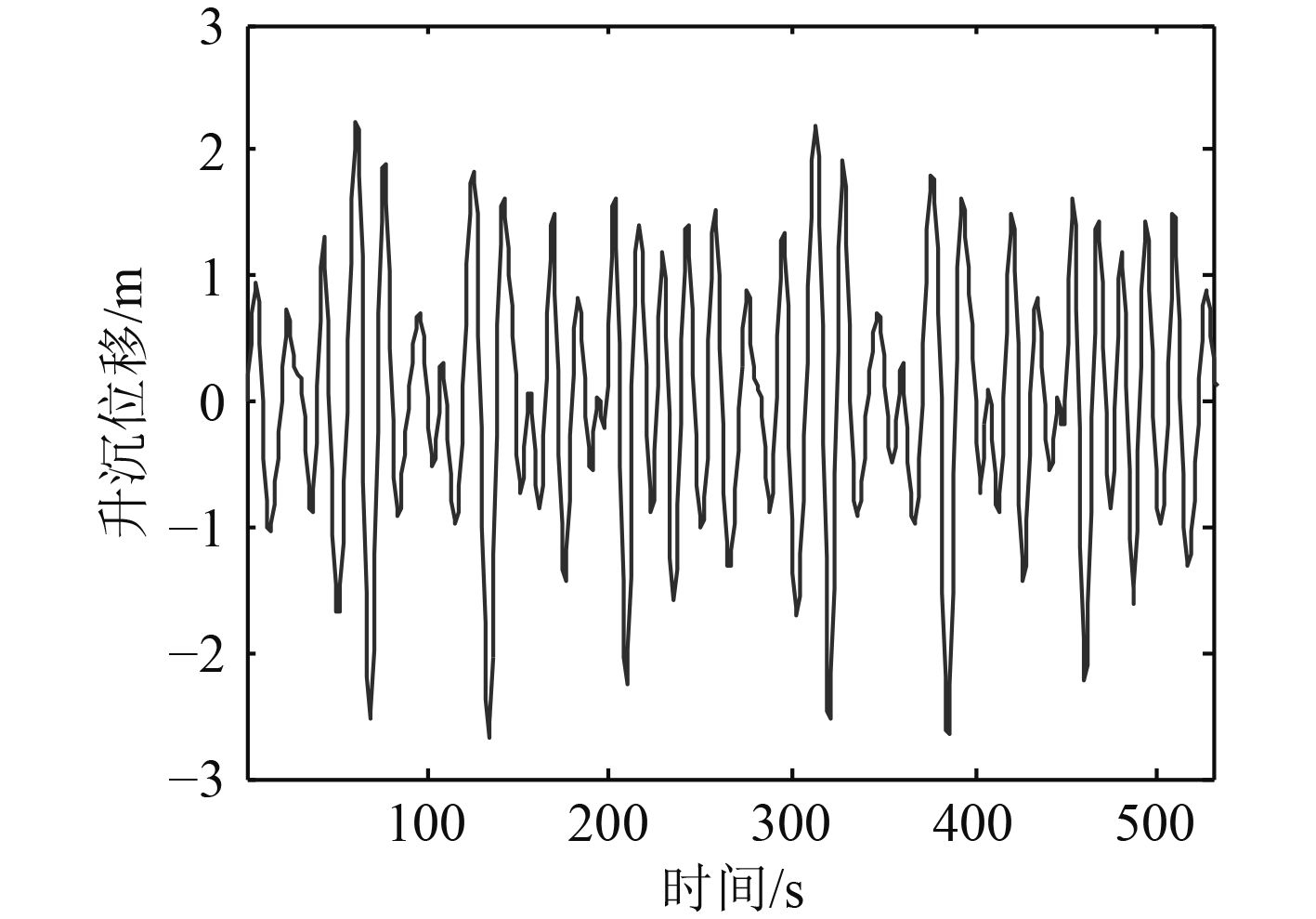
|
图 7 6级海况下船舶升沉运动 Fig. 7 The ship’s pitching motion at six level of sea state |
根据上述仿真结果,利用Matlab模拟仿真出风力发电船在海况等级为6级、义波高为5.7海浪下的运动,这为设计波浪补偿平台的设计提供数据参考。通过Matlab对坐标获取,整理得到船舶运动数据如表3所示。
|
|
表 3 海上风电安装船运动数据 Tab.3 The motion data about wind farm installation vessel |
波浪补偿装置平台是一种安装在船舶甲板与浮式起重机之间的装置平台,通过平台的三自由度运动特性对船舶的横摇、纵摇和升沉运动实时反向补偿。评价平台性能的指标主要分为平台结构的小型化和平台具有良好的可控性两方面。
基于这一想法提出以平台的运动空间和平台结构尺寸为目标函数,进行加权最优[6]。波浪补偿装置平台的工作特性受机构的设计尺寸影响较大,本文补偿平台的结构参数主要包括:上平台铰链点组成的等边三角形变长d、下平台铰链点组成的等边三角形变长D、液压缸的行程L。因此机构的优化设计变量可以简化为:
|
|
表 4 平台机构参数设计范围 Tab.4 Design parameter range of the platform |
平台的运动范围约束:最大横摇角度
平台机构目标函数如下:
| $f(x) = {c_1}\eta (x) + {c_2}m(x)\text{,}$ | (7) |
| $\eta (x) = \iiint\limits_w {\frac{1}{{k(J)}}{\rm d}w} /\iiint\limits_w {{\rm d}w} \text{,}$ | (8) |
| $k(J) = \left\| J \right\| \circ \left\| {{J^{ - 1}}} \right\|\text{。}$ | (9) |
式中:c1,c2均为加权系数,根据平台实际情况选取;n(x)为平台的全域条件数,本文主要设计3个性能指标,分别为:机构动力学性能、刚度性能能、机构速度性能。
m(x)为平台整体机构尺寸的衡量标准;w为平台的运动区域;k(J)为机构局部条件数;J为平台的雅克比矩阵。
3 优化过程及分析 3.1 平台结构优化根据数学模型,得知平台优化问题属于多变量非线性有约束的优化。本文采用遗传算法进行优化。遗传算法是一种借鉴生物进化规律演化而来的随机优化搜索方法。该种算法直接对结构对象操作,具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。算法的实现过程参考文献[7 – 8]。
采用Matlab自带的GA工具箱进行优化设计[9],步骤及参数设定如下:①编码长度e=15;②初始群体总数为50;③迭代次数为50;④适应度值评估坚检测;⑤变异率Pm=0.01;⑥中止。式中的加权系数分别为
根据图8仿真结果得知机构在38代时开始收敛,最终得到机构综合优化性能的指标值为
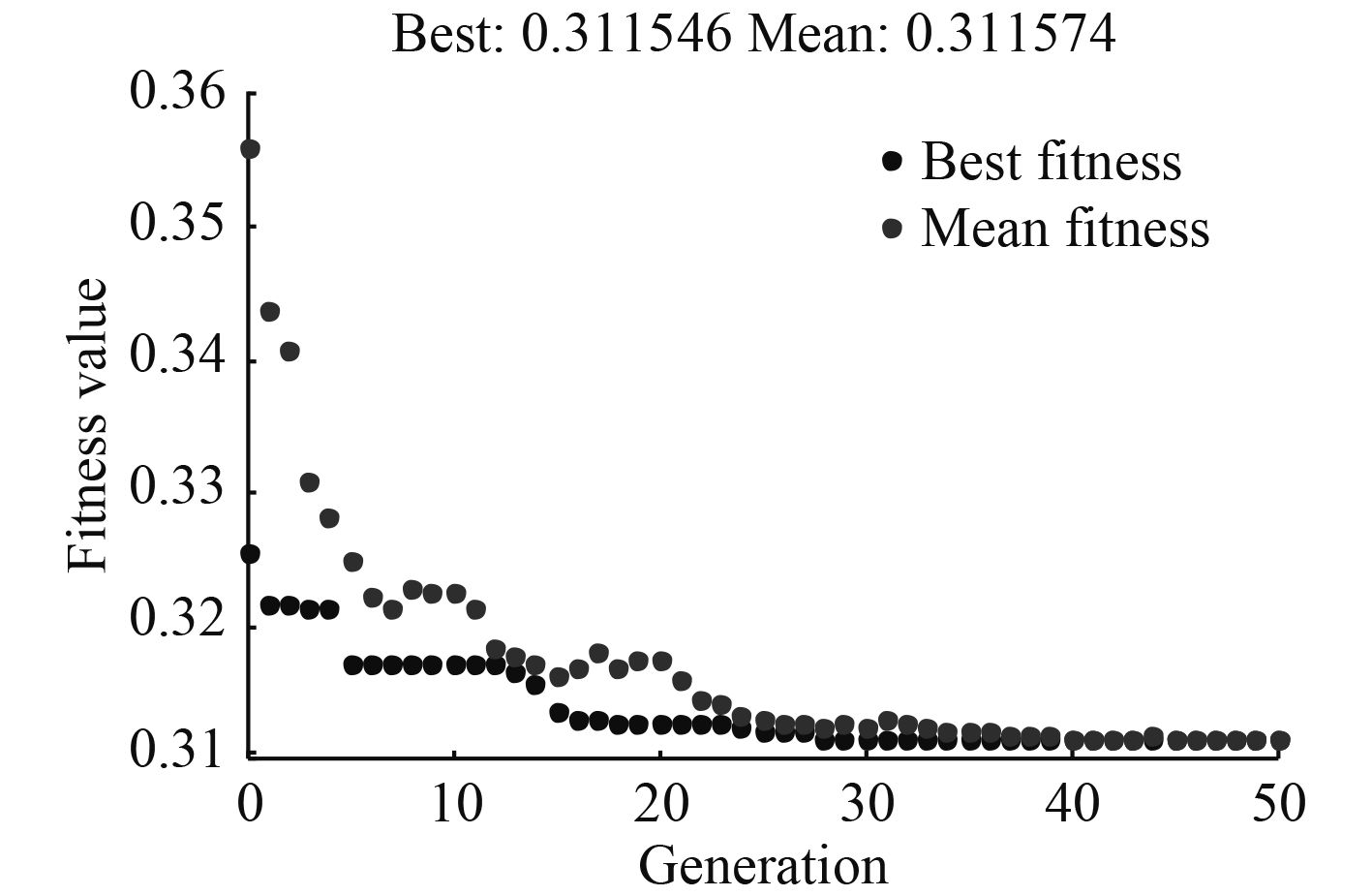
|
图 8 机构综合性能优化结果 Fig. 8 Optimization results about mechanism comprehensive performance |
|
|
表 5 机构参数优化结果 Tab.5 Optimization results of mechanism parameters |
|
|
表 6 平台运动范围 Tab.6 Motion range of the platform |
以平台最终的优化结果为设计平台的参考依据,对补偿装置平台的摆放方式以及个性化设计具有指导意义。因此,为了充分分析平台的运动角度范围与各机构之间的关系,分别设定部分参数机构为常量,剩余参数为变量,求出平台性能优良的解集合。
根据补偿平台在Solidworks中的motion模块仿真得知,液压缸行程长度一定时,平台的升降高度、纵摇角度和横摇角度与上平台铰链点距离d、下平台铰链点距离D距离有关。设定液压缸的行程L=2.89,机构参数d、D与机构性能之间的函数关系如图9所示,机构性能f(x)遗传优化的结果存在于深色区域内,因此该区域满足平台的运动范围。根据图9可以得知,d在[3.51,3.69]、D在[3.87,3.98]区域内平台具有更好的综合性能[10]。
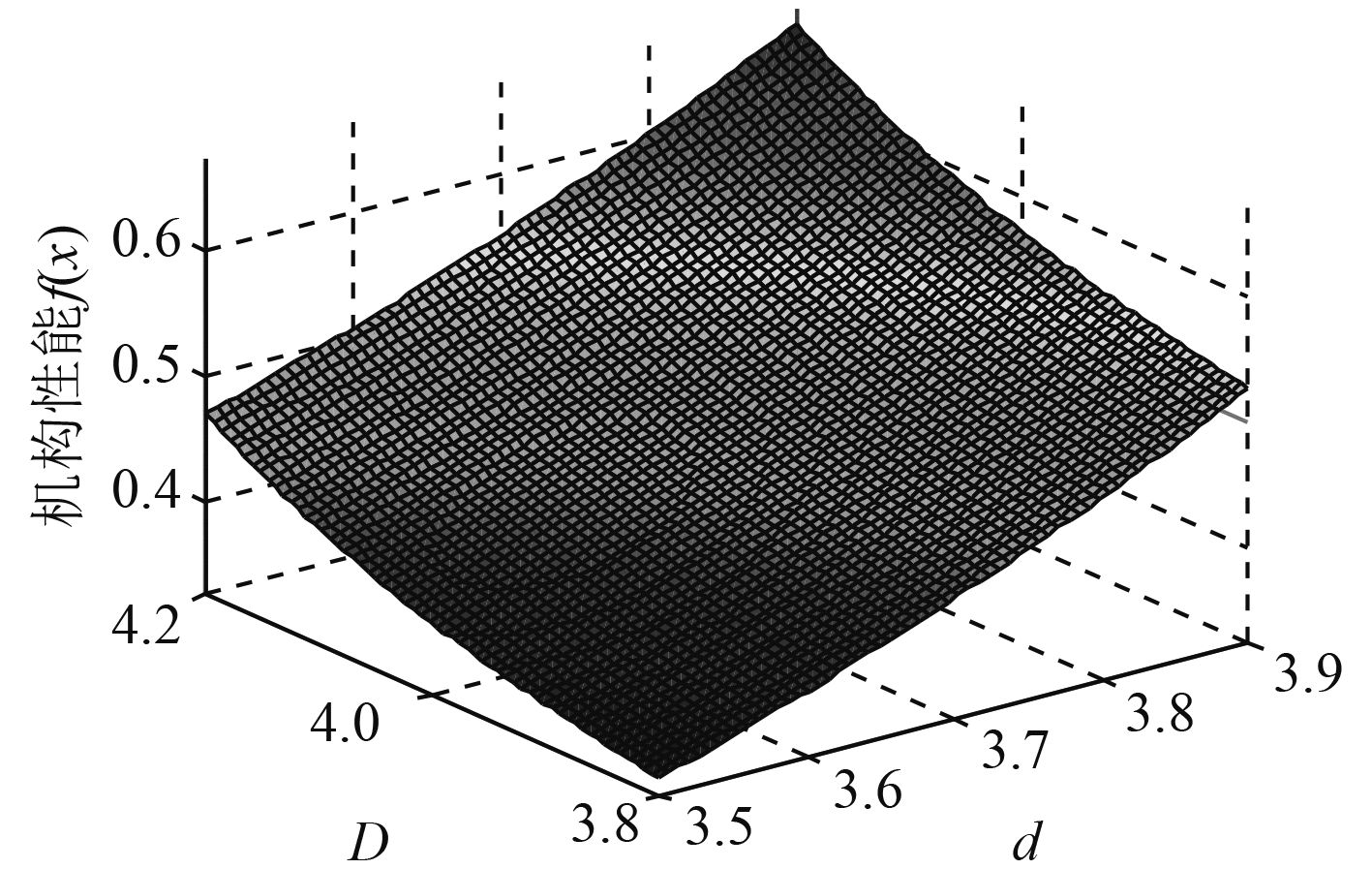
|
图 9 机构性能与参数d、D之间函数关系 Fig. 9 The function relation between mechanism and parameter D,d |
给定约束条件,设定d=3.62 m,D=3.91 m,以平台的液压缸高度L为目标函数,建立L与f(x)之间函数关系。优化结果如图10所示,随着液压缸行程变长,波浪补偿装置平台的结构性能呈下降趋势。所以选取液压缸行程时,应遵循保证机构性能的前提下,选择最短行程。
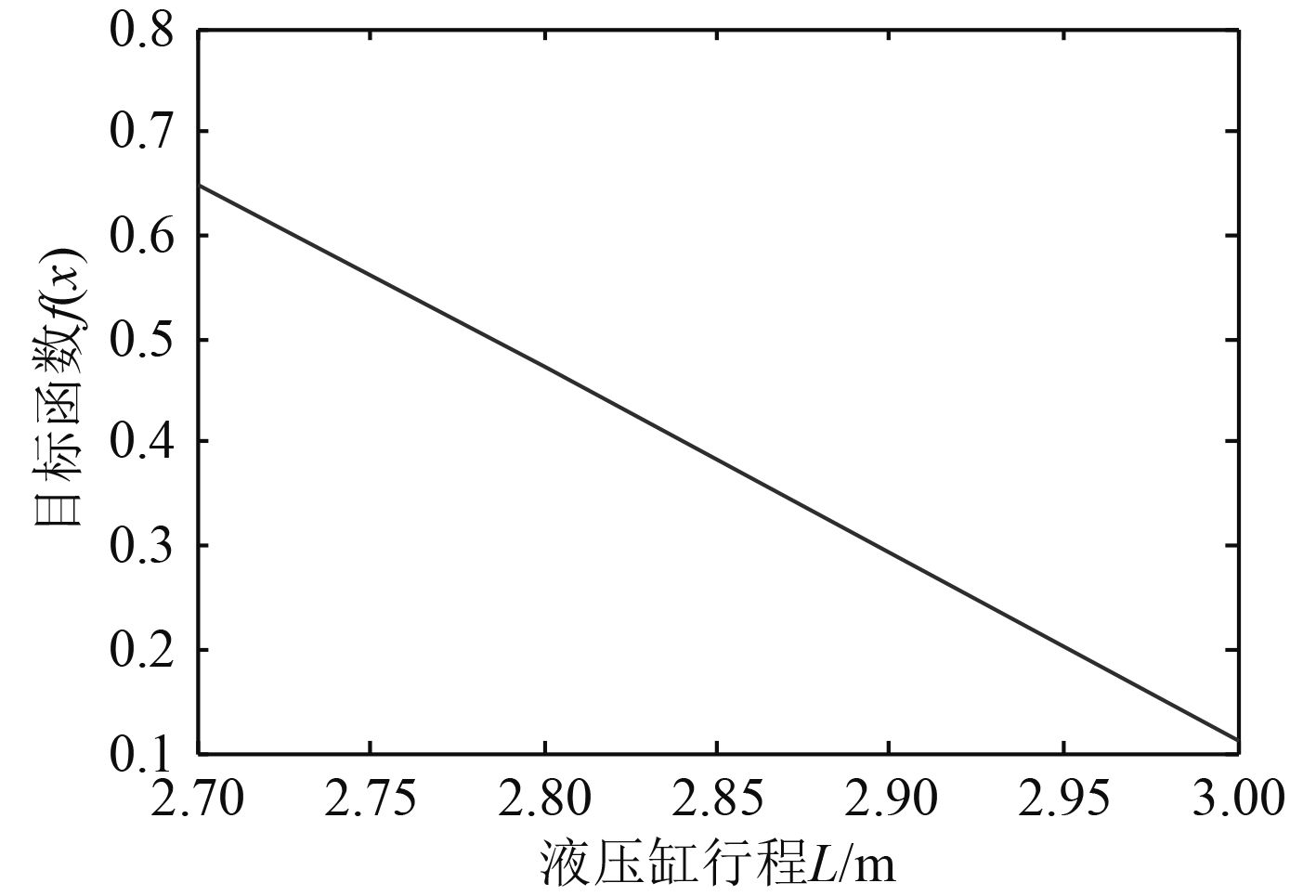
|
图 10 机构性能随液压缸行程变化曲线 Fig. 10 The changing curve between mechanism performance and the stroke of hydraulic cylinder |
1)本文以某型号风电安装船为研究对象,利用Matlab软件计算得到了我国东海区域6级海况、义波高为5.7的船舶横摇
2)以平台运动范围约束波浪补偿装置平台的运动空间,建立平台的优化模型,采用遗传算法对平台机构进行优化,得到性能最优时平台的机构的尺寸,分别为d=3.68 m、D=3.83 m、L=2.89 m。
3)设定参数L为常量,机构尺寸d、D为变量建立与平台综合性能f(x)之间的函数变量关系,得到当L为2.89时,参数d在[3.51,3.69]、D在[3.87,3.98]区域内平台具有更好的综合性能;当平台性能得到满足,参数d,D为已知,液压缸行程L选取最短。
| [1] |
张昊, 王辉, 何宁. 海洋工程大型起重设备及其关键技术研究[J]. 海洋工程, 2009, 27 (4): 130–139.
ZHANG Hao, WANG Hui, HE Ning. Analysis of the key technology of the offshore engineering lift system and the crane[J]. The Ocean Engineering, 2009, 27 (4): 130–139. |
| [2] |
高磊, 唐国元, 黄道敏, 邓智勇, 等. 并联式主被动升沉补偿系统的非线性分析与仿真[J]. 舰船科学技术, 2015, 37 (10): 72–75.
GAO Lei, TANG Guo-yuan, HUANG Dao-min, DENG Zhi-yong, et al. The nonlinear research and simulation of active-passive heave compensation system based on parallel cylinders[J]. Ship Science Technology, 2015, 37 (10): 72–75. DOI: 10.3404/j.issn.1672-7649.2015.10.015 |
| [3] |
陆会胜. 船舶动力定位系统的使用[J]. 航海技术, 2006 (5): 31–33.
LU Hui Sheng. The use of ship dynamic positioning system[J]. Marine Technology, 2006 (5): 31–33. |
| [4] |
詹金林, 卢晓平, 李光磊. 三体船操纵性水动力的势流理论计算[J]. 哈尔滨工程大学学报, 2012, 33 (5): 642–647.
ZHAN Jinlin, LU Xiaoping, LI Guanglei. Calculation of trimaran’s maneuverability hydrodynamics by the potential flow theory[J]. Journal of Harbin Engineering University, 2012, 33 (5): 642–647. |
| [5] |
任爱娣, 张得伟, 余鹏. 基于AMESim的被动式作动筒张力器仿真研究[J]. 舰船科学技术, 2015 (4): 88–91.
REN Ai-di, ZHANG De-wei, YU Peng. The simulation research of passive ramtensioner base on the AMESim[J]. Ship Science Technology, 2015 (4): 88–91. |
| [6] |
郭晓松, 唐圣金, 周召发, 等. 重心法中的非线性加权系数研究[J]. 激光与红外, 2010, 40 (1): 109–111.
GUO Xiaosong, TANG Shengjin, ZHOU Zhaofa. Study on optimal nonlinear weighting coefficient of barycenter algorithm[J]. Laser And Infrared, 2010, 40 (1): 109–111. |
| [7] | CAI Z, SI S, SUN S, et al. Optimization of linear consecutive-k-out-of-n, system with a Birnbaum importance-based genetic algorithm[J]. Reliability Engineering & System Safety, 2016, 152 : 248–258. |
| [8] |
孙全颖, 王艺霖, 杜须韦. 遗传算法在机械优化设计中的应用研究[J]. 哈尔滨理工大学学报, 2015, 20 (4): 46–50.
SUN Q Quanying, WANG Yilin, DU Xunwei. Application and research of genetic algorithm in mechanical optimization[J]. Journal of Harbin University of Science and Technology, 2015, 20 (4): 46–50. |
| [9] | 张晋西, 蔡维, 谭芬. SolidWorks Motion机械运动仿真实例教程[M]. 北京: 清华大学出版社, 2013: 45–53. |
| [10] | 高飞. Matlab智能算法超级学习手册[M]. 北京: 人民邮电出版社, 2014: 349–366. |
 2017, Vol. 39
2017, Vol. 39
