舰船长期浸泡于海水中,其自腐蚀作用及腐蚀防护措施均会导致产生静电场。舰船静电场量级较大,通过特征明显,易被作为水雷等武器的触发信号[1],因而受到研究人员的广泛关注。
近年来,海洋环境中舰船腐蚀相关电场特征分析问题,日益成为舰船隐身领域颇为关心的课题。文献[2]通过解析方法对舰船及其物理缩比模型的外加电流阴极保护系统产生的水下电势特征的相似性进行理论分析。文献[3]基于物理缩比模型试验研究了船舶轴频电场的传播特征。文献[4]基于有限元模型分析了舰船在周围海水中形成的静电场的分布状况。文献[5]采用COMSOL多物理场仿真软件分析了舰船水下电势分布,并基于静电场隐身目的开展了外加电流阴极保护优化设计工作。文献[6]采用边界元方法对安装了外加电流阴极保护系统船舶的水下静电场进行仿真建模,并分别对平时和战时2种情况下船舶外加电流阴极保护系统的电流输出进行优化,以实现船舶的静电场隐身。文献[7–8]采用空气-海水-海床3层模型对静态电偶极子在海水中产生的标量电位及静态电场分布特征进行了数值计算和分析,在此基础上提出了基于点电源的船舶静电场深度换算方法,可较好地用于船舶静电场反演及换算。文献[9]采用直流水平电偶极子理论研究并分析了海水中舰船在界面处产生的电磁场。文献[10]研究并给出了舰船电场海上测量方法及传感器布设原则。上述电场数值仿真及试验相关的研究成果对舰船水下电场分布特性分析具有重要的参考意义。
本文基于船模水下电场测量试验方法,研究了模拟海水环境中舰船物理缩比模型的腐蚀相关静电场的分布特性,通过对比分析考察了不同辅助阳极位置及输出电流强度情形下的静电场特征,为实现舰船电场隐身设计提供技术支撑。
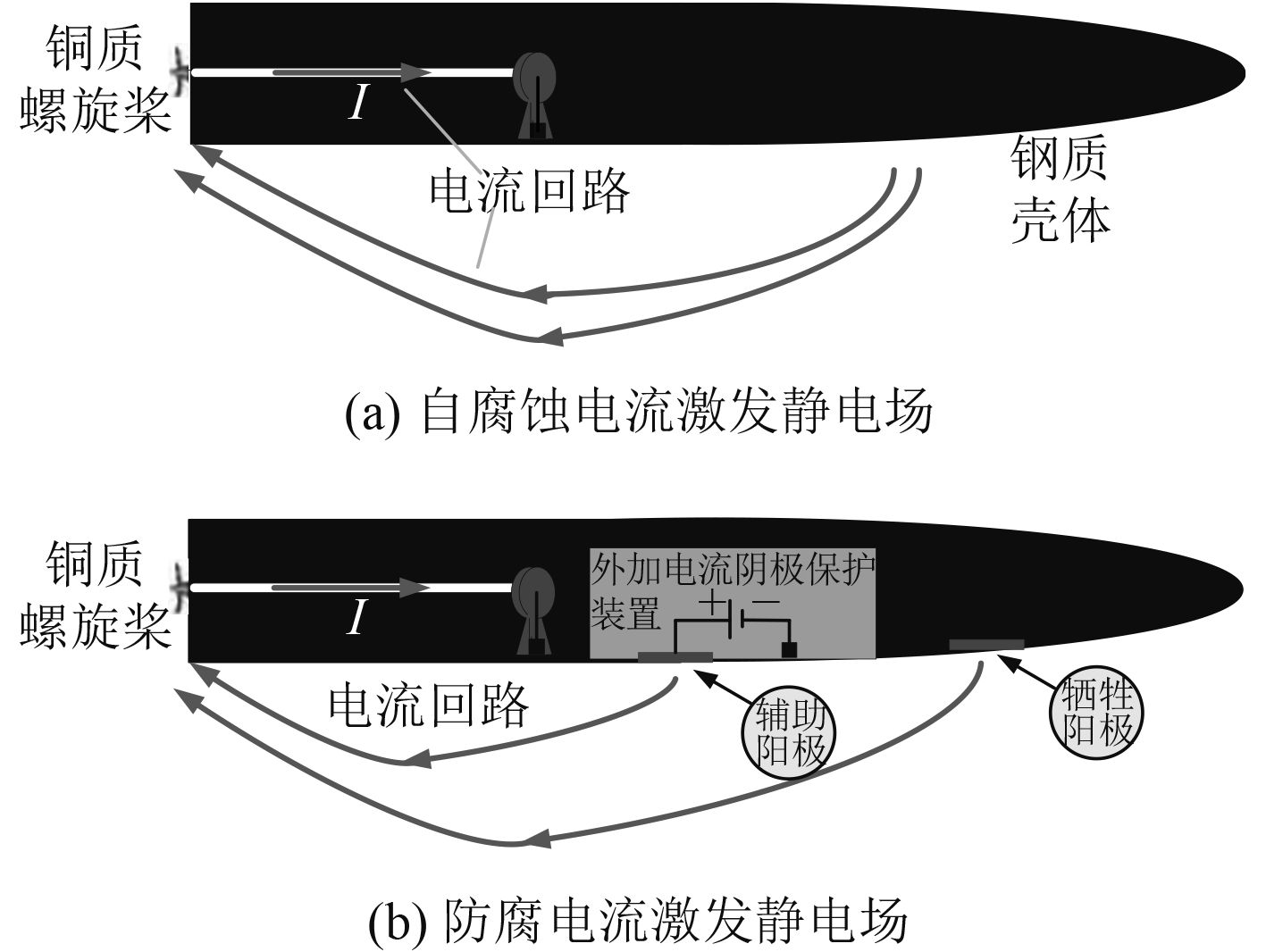
1 舰船静电场产生原理及分析方法舰船激发水下静电场的原理如图1所示。该静电场信号主要来源于两方面:一方面,由于船体、螺旋桨等主要组成部件由不同的材料建造而成,其自腐蚀电位的不同会导致产生自腐蚀电流;另一方面,为了对舰船进行腐蚀防护,往往采用了牺牲阳极阴极保护和外加电流阴极保护系统,会在舰船周围海水中产生防腐电流。
|
图 1 舰船静电场产生原理 Fig. 1 Principle of static electric field produced by ship |
该腐蚀/防腐电流经海水-螺旋桨-轴回到船体,形成电流回路,其中的直流电流会激发静电场信号,并按一定的衰减规律在舰船周围水下形成特定的电场分布。
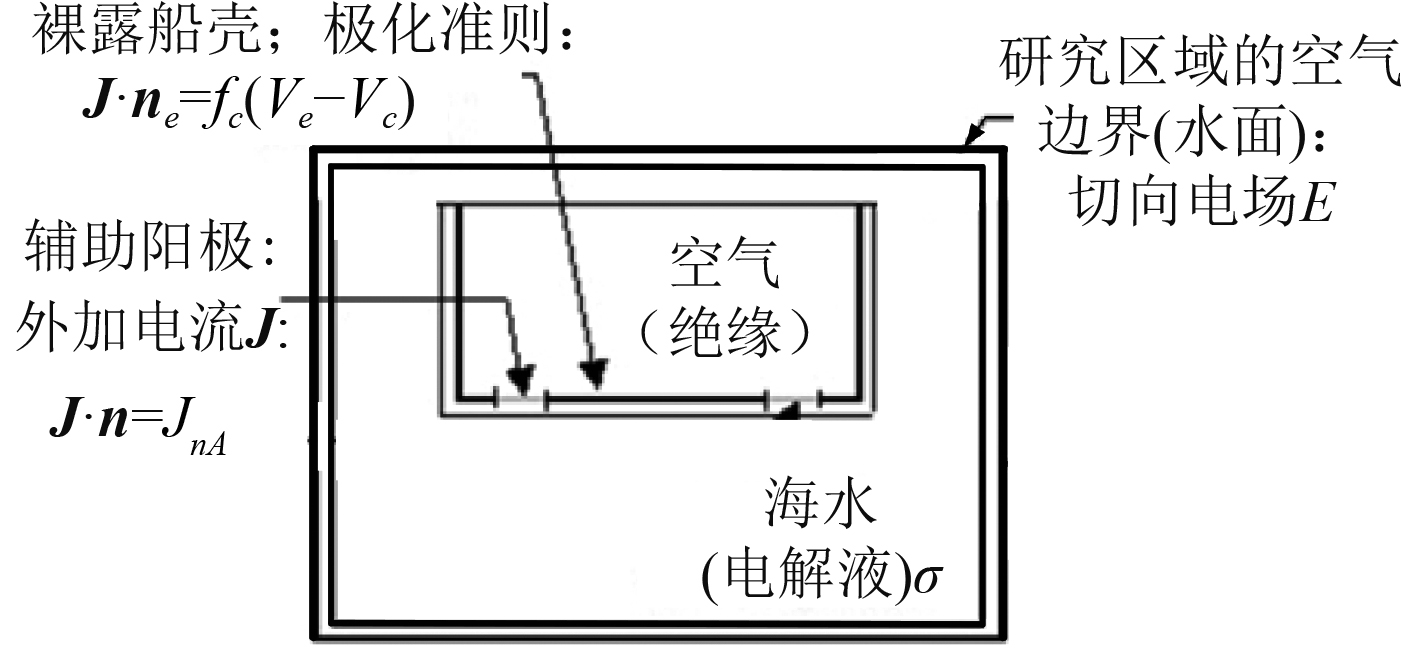
舰船腐蚀相关静电场的等效模型如图2所示,该静电场问题满足如下标量电势方程。
|
图 2 舰船腐蚀相关静电场的物理模型 Fig. 2 Equivalent model of ship’s corrosion related static electric field |
| $\nabla \cdot \sigma \,\nabla V = 0\text{,}$ | (1) |
且满足如下边界条件:
1)海水与空气边界处,电势V满足:
| $\frac{{\partial V}}{{\partial n}} = 0\text{,}$ | (2) |
2)辅助阳极处外加电流源I,其表面电流密度J满足:
| $\int {\int {_{{\Omega _{\,bc}}}} \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{J}} {\rm d}{\Omega _{\,bc}}} = I\text{,}$ | (3) |
3)船体与海水介质接触表面上,电势满足混合边界条件:
| $V + \alpha \frac{{\partial V}}{{\partial n}} = \beta \text{。}$ | (4) |
其中:σ为海水电导率;系数α和β对应船体材料在海水电解液中的电化学极化特性。
一般而言,由于海上实船测量试验成本高、周期长,且易受环境条件限制,难以获取较为完备的数据,因此,舰船静电场特征分析主要通过数值仿真、物理缩比模型试验2种途径来实现。
有限元/边界元、电偶极子等数值仿真方法,较好地模拟了海水电解液、组成船体的不同金属表面极化特性以及阴极保护环境,在一定程度上可以有效获取舰船静电场特征。但需要说明的是,数值仿真方法受限于船体内部桨-轴等复杂结构难以模拟,以及船体材料极化曲线试验数据不易获取等因素,而相比之下,物理缩比模型试验方法则克服了这些缺点,效果更直观,数据更稳定,对于舰船电场特征分析及隐身技术研究领域起到愈来愈重要的辅助作用。
2 舰船物理缩比模型静电场测量为了掌握舰船静电场特征,需通过水下电场试验系统,进行模拟海水环境中舰船物理缩比模型的腐蚀相关静电场测量,其原理如图3所示。

|
图 3 舰船物理缩比模型腐蚀相关静电场测量原理 Fig. 3 Measure principle of corrosion related static electric field produced by ship’s physical scale model |
舰船物理缩比模型静电场测量的具体过程为:在水槽底部适当位置布设三分量银/氯化银电场测量传感器,用于接收水下电场原始信号;在试验水槽中制备模拟海水,通过调整含盐度实现所需的海水电导率;将船模固定安装于拖动台架上,调整横向位置和垂向吃水深度,试验过程中通过步进电机拖动船模在水中沿纵向缓慢匀速地移动,同时控制船模的桨-轴结构匀速旋转,模拟实船航行工况;将辅助阳极和参比电极以左右舷对称方式成对布置在船模表面相应位置,通过参比电极接收船体表面水下电势信号,作为控制指令信号控制恒电位仪,通过辅助阳极实时输出保护电流,使船体处于阴极保护状态;拖动船模的同时,同步进行水下电场信号测量分析。
3 舰船物理缩比模型静电场特性以某型船物理缩比模型为例,船模长约3 m,在水下0.2 m匀速直航,在船首部、中部偏后、尾部表面水线下分别布置3对辅助阳极,阳极编号如图3所示,参比电极布置于2号辅助阳极和3号辅助阳极之间。模拟海水电导率为0.72 S/m,分析不同阳极输出情形对应船模静电场特征。
考察辅助阳极全关(自腐蚀)、仅辅助阳极1工作、仅辅助阳极2工作、仅辅助阳极3工作4种情形,对应的船模正下方0.5 m、纵向距离–2.5~2.5 m处的水下静电场各分量的通过特性曲线如图4所示。

|
图 4 辅助阳极不同工作状态对应船模水下静电场分布 Fig. 4 Distribution of static electric field produced by ship’s physical scale model, with different work state of anodes |
分析结果可知,辅助阳极位置对船模下方静电场分布特征产生较大影响。船模水下静电场x分量峰值强度最大,z分量次之,y分量幅度接近0,这是由于测量线对应船模纵向中轴线正下方,对称布置于左右两舷的辅助阳极输出电流在测量线上产生的静电场y分量相互抵消导致的。
当辅助阳极全都不工作时,船模处于自腐蚀状态,钢制船体与铜质螺旋桨形成电解偶,船体为阳极,桨为阴极,靠近尾部桨附近的静电场形成阴极峰值,静电场曲线中间的过零点位于阳极的等效中心附近。
仅辅助阳极1工作时,船体和桨都作为阴极,因此,静电场曲线在纵向距离–150~50 cm这个较宽的区间范围均形成阴极峰,过零点位于辅助阳极1所在位置附近。仅辅助阳极2工作时,船体尾部和桨都作为阴极,静电场曲线在纵向距离–150~–100 cm区间范围均形成阴极峰,过零点位于辅助阳极2所在位置附近。
仅辅助阳极3工作时,船体尾部和桨都作为阴极,静电场曲线在纵向距离–200~–130 cm区间范围均形成阴极峰,过零点位于辅助阳极3所在位置附近。但由于此时辅助阳极位置与桨非常接近,且参比电位未达到金属保护电位,因此船体发生一定程度的腐蚀,船体与铜质螺旋桨形成自腐蚀电解偶,船体为阳极,桨为阴极,静电场曲线在纵向距离–120~–60 cm区间范围均形成阴极峰,在辅助阳极所在位置向船体首部方向一定距离处形成静电场曲线的第2个过零点。
4种情形下船模静电场强度峰峰值如表1所示。
|
|
表 1 船模正下方静电场峰峰值(单位 mV/m) Tab.1 Underwater static electric field peak-peak values of ship’s scale model |
根据表1可以看出,辅助阳极的布放位置对船体下方静电场强度产生较大影响。辅助阳极全都不工作,船模自腐蚀情形对应的静电场峰峰值并不是最小的,将辅助阳极布置于3号阳极所处位置,并调节参比电位至–0.7 V,对应的静电场x分量强度峰峰值以及z分量强度峰峰值分别比自腐蚀情形减小了43.2%和44.6%。该特征对基于静电场特征控制的舰船隐身设计至关重要。
4 结 语舰船静电场特性分析方面的现有研究,大都是基于有限元、边界元、电偶极子等数学模型仿真手段,在一定程度上模拟了海水电解液、组成船体的不同金属表面极化特性以及阴极保护环境。但由于船体内部桨-轴等复杂结构难以通过软件或理论公式模拟,且船体材料极化曲线试验数据不易获取,因而具有一定的局限性。本文基于物理缩比模型试验方法,首次针对舰船的大尺寸缩比模型,直接模拟真实的阴极保护环境和舰船内部构造,得到的静电场数据更贴近实际工况,提出的试验分析方法及得出的结论对于舰船电场特征预报及隐身技术研究具有重要指导意义。对不同辅助阳极位置及输出电流强度情形静电场特征进行分析,试验结果表明,舰船静电场与辅助阳极布放位置及输出电流关系密切,经过优化的辅助阳极布置可以在较大程度上降低舰船静电场强度。可以考虑将船体周围水下电流密度或静电场强度作为优化目标,通过优化算法对阳极数量及布设位置进行合理的优化设计,通过物理缩比模型试验对优化结果进行修正,实现舰船静电场特征的有效控制。
| [1] |
张华, 王向军, 单潮龙, 等. 基于目标静电场的水中兵器制导方法研究[J]. 电子学报, 2013, 23 (3): 470–474.
ZHANG H, WANG X J, SHAN C L, et al. Research of Guidance Method Based on the Electrostatic Field of Target for Underwater Weapon[J]. Acta Electronica Sinica, 2013, 23 (3): 470–474. |
| [2] | DITCHFIELD R W, McGRATH J N, TIGHE-FORD D J. Theoretical validation of the physical scale modelling of the electrical potential characteristics of marine impressed current cathodic protection[J]. Journal of Applied Electrochemistry, 1995 (25): 54–60. |
| [3] |
梁成浩, 于楠, 黄乃宝, 等. 船舶缩比模型轴频电场的传播特征[J]. 大连海事大学学报, 2008, 34 (1): 116–121.
LIANG C H, YU N, HUANG N B, et al. Transmission characteristic of shaft-frequency electric field based on ship’s physical scale model[J]. Journal of Dalian Maritime University, 2008, 34 (1): 116–121. |
| [4] |
卞强, 张民, 柳懿, 等. 一种基于ANSYS 的舰船静电场分析方法[J]. 海军工程大学学报, 2010, 22 (6): 65–69.
BIAN Q, ZHANG M, LIU Y, et al. An analytic method of ship static electric field[J]. Journal of Naval University of Engineering, 2010, 22 (6): 65–69. |
| [5] | DAVID S, JENS D, ANDREAS R, et al. Numerical analysis of propeller-induced low-frequency modulations in under electric potential signatures of naval vessels in the context of corrosion protection systems[C]//Proceedings of the 2011 COMSOL Conference in Stuttgart, 2011. |
| [6] |
李俊, 包中华, 龚沈光, 等. 优化ICCP 系统的船舶静电场隐身研究[J]. 海军工程大学学报, 2011, 23 (1): 67–72.
LI J, BAO Z H, GONG S G, et al. Optimization of ICCP systems to minimize static electric signatures for stealth vessels[J]. Journal of Naval University of Engineering, 2011, 23 (1): 67–72. |
| [7] |
陈聪, 龚沈光, 李定国. 基于混合模型的舰船腐蚀相关静态电、磁场[J]. 哈尔滨工业大学学报, 2010, 42 (3): 495–499.
CHEN C, GONG S G, LI D G. Corrosion related static electric and magnetic field of ships based on mixed modeling[J]. Journal of Harbin Institute of Technology, 2010, 42 (3): 495–499. DOI: 10.11918/j.issn.0367-6234.2010.03.034 |
| [8] |
姜润翔, 胡英娣, 龚沈光. 基于点电源的船舶静态电场深度换算方法研究[J]. 电波科学学报, 2014, 29 (4): 685–693.
JIANG R X, HU Y D, GONG S G. Depth conversion of the vessel static electric field based on point charge source[J]. Chinese Journal of Radio Science, 2014, 29 (4): 685–693. |
| [9] |
王西乾, 韩逍菲, 彭怀云, 等. 海水中的直流水平电偶极子在界面处产生的电磁场[J]. 电波科学学报, 2014, 29 (6): 1030–1035.
WANG X Q, HAN X F, PENG H Y, et al. Electromagnetic fields generated by a horizontal static electro dipole beneath the sea surface[J]. Chinese Journal of Radio Science, 2014, 29 (6): 1030–1035. |
| [10] |
胡英娣, 龚沈光, 陈聪. 舰船电场测量站测量阵列布设原则[J]. 西南交通大学学报, 2013, 48 (1): 135–140.
HU Y D, GONG S G, CHEN C. Layout scheme of measuring array in ship’s electric field measuring station[J]. Journal of Southwest Jiaotong University, 2013, 48 (1): 135–140. |
 2017, Vol. 39
2017, Vol. 39
