随着潜艇消声降噪技术的广泛应用,传统声学方法探测潜艇已经不能满足现代潜艇探测的要求,这就促进了非声探测潜艇技术的发展。由于潜艇运动产生的内波信号,可作为鱼雷跟踪与制导的目标特征信号;探潜与潜艇隐身的博弈,对认识潜航体在分层流体中激发内波的目标特征提出了更高的要求。
对于潜航体在分层流中激发的内波,现有文献已经从流体力学理论、数值模拟以及实验等诸多方面开展了大量的研究工作。近年来,梁川[1]、魏岗[2]以及李万鹏[3]分别从不同的方面研究了内波的特征,内波实验研究通常采用盐度分层或温度分层构造所需的密度剖面[4],相应的测量方法有电导率探头、温度探头,用于测量探头位置的内波信号(波幅、脉动频谱等);激光PIV技术原则上可以测量一个截面内的速度场,从而获得内波在该截面上产生的流场结构,但实际上由于内波流场速度通常极为缓慢,以及分层流体中布放长时间稳定的示踪粒子存在较大困难,使得激光PIV技术在内波微弱流场测量中的应用受到很大的限制,周文进[5]运用表面PIV技术研究了潜体在分层流体中运动激发内波传递到流体表面的特征;数值纹影技术是一种非接触式光学测量,可以方便地得到内波场的全场信息,对于内波场的整体特征有很好的展示。1998年Dalziel[6]等最初运用数值纹影技术研究二维内波场;Stuart B Dalziel[7]等于2007年利用数值纹影技术进行内孤立波的实验研究;中国海洋大学内波研究室与清华大学精密仪器系合作研制成功一种大型立式纹影仪[4]。
对于潜航体激发的三维内波场,以电导率探头为代表的局部定量测量与以数值纹影为代表的半定量全局观测,目前处于各有优缺点、互为补充的状态。从军事应用的角度来看,潜航体激发的三维内波场的水平分布是重要的目标特征,所以本文作者在水平数值纹影技术的基础上,发展了垂直数值纹影技术,实验观测了潜航体在线性分层流体中运动产生的类Kelvin波[8],研究了波长和张角随无纲量常数弗罗德数的变化规律、还就带指挥塔附体与不带指挥塔拖曳潜航体在分层流体中运动激发的三维内波开展了对比试验研究。本文介绍利用垂向数值纹影技术测量潜航体三维内波目标特征的实验结果。
1 实验设备与分层剖面 1.1 实验水槽实验水槽安装在面积约50 m2的房间内,室温约为20 ℃,实验时关闭门窗减小空气流动;水槽用不锈钢架和透明的钢化玻璃制成,水槽长度L=2 400 mm,水槽深度H=800 mm,水槽宽度W=800 mm;利用架设在水槽上方的一面倾斜45°的镜子,实现从水平方向拍摄获取垂向观测图像。与实验相关的几何参数:相机距镜子的距离为L1,镜子据水面的距离为L2,水深为L3,模型中心距离水底的距离为L4,水槽底部距点阵的距离为L5。
1.2 实验模型拖曳模型为基洛级潜艇模型,模型头部为半椭球形,尾部为细长流线锥形。该模型的缩比为1:350,模型主体参数为:模型长度Lm=200 mm,模型最大直径Dm=30 mm;指挥塔参数为:指挥塔的高度Th=13 mm,指挥塔的长度Tc=41 mm,指挥塔的最大宽度Tk=5 mm,指挥塔头部距模型首端距离Td=62 mm。为做对比实验,部分实验将模型指挥塔去掉,只留下模型主体部分。
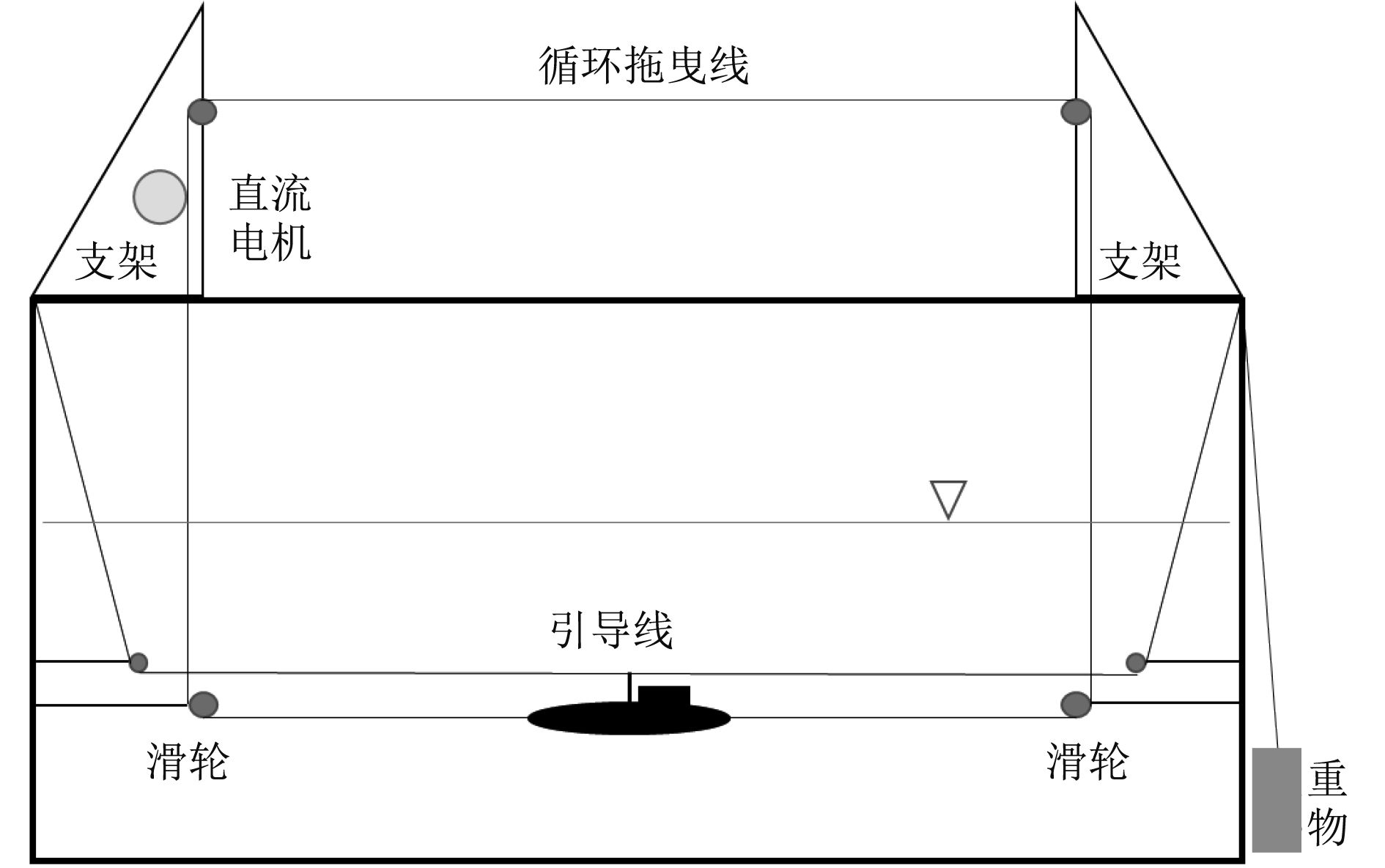
1.3 模型拖曳系统模型拖曳系统(见图1)由微型减速电机驱动,电机额定电压为12 V。直流电源输出电压在3~20 V可调,控制精度为±0.01 V。在此电压区间内,测得电压和拖曳速度成线性关系。
为了增加拖曳过程中模型的稳定性,在模型控制塔上设置1根带圆孔的引导杆,并且在拖曳线上方设置1根与模型运动方向平行且穿过导引杆圆孔的引导线,引导线一端固定在水槽壁上,另一端悬挂一重物,产生恒定的张力,使引导线拉直,起到稳定模型的作用。实验时,模型距水槽底面高度L4=270 mm。若无特殊说明,文中模型距水面(或底面)距离均指模型中心(即拖曳线)距水面(或水底)距离。
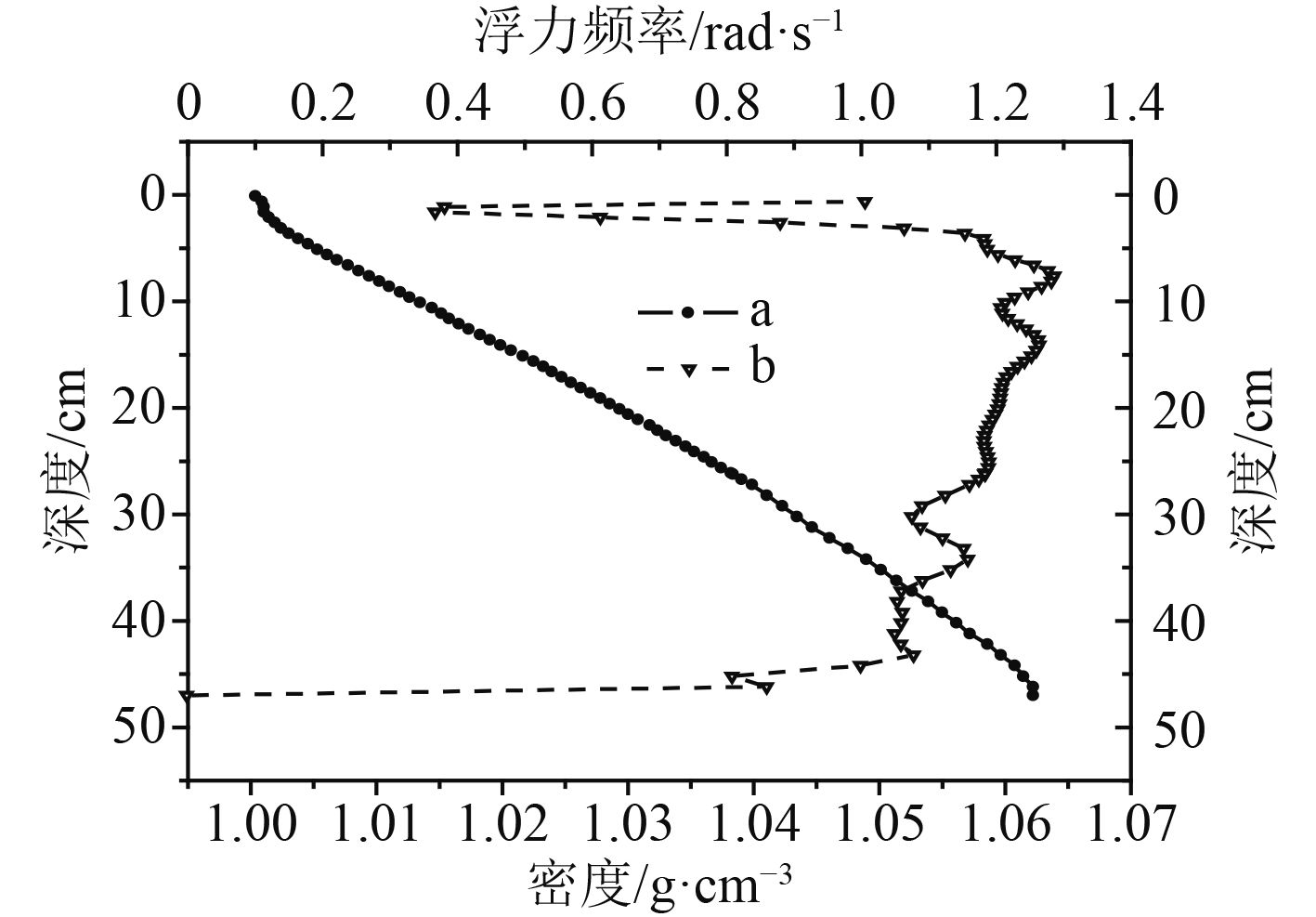
1.4 分层流密度剖面为得到线性密度分层,本文采用多ρ层等密度差分层技术[9],先往水槽中注入一层淡水(厚度为2 cm),再利用自制的碟形出阀贴近水槽底板,依次水平喷注盐水,其盐度逐步线性递增(每层的厚度相同),由于扩散效应,原阶梯形密度分布1–2天之后就会变成较为理想的密度线性分层剖面。本实验每层盐水厚度为2 cm,每层盐水的密度差为0.002 9 g/cm3,共24层,运用电导率仪及玻璃密度计得到的实际密度分层剖面如图2曲线a所示,图2曲线b是相应的浮力频率曲线。可见除了表面及底部较薄层之外,在整个水体的大部分区域内分层流体的密度呈线性变化,其浮频率近似为常数,约为N=1.2左右。
|
图 1 分层流水槽潜航体拖曳系统 Fig. 1 Submerged tank trailer system with layered sink |
|
图 2 分层流密度剖面及浮频率曲线 Fig. 2 Density profile and floating frequency curve |
由几何光学原理可知,当光束穿越不同密度
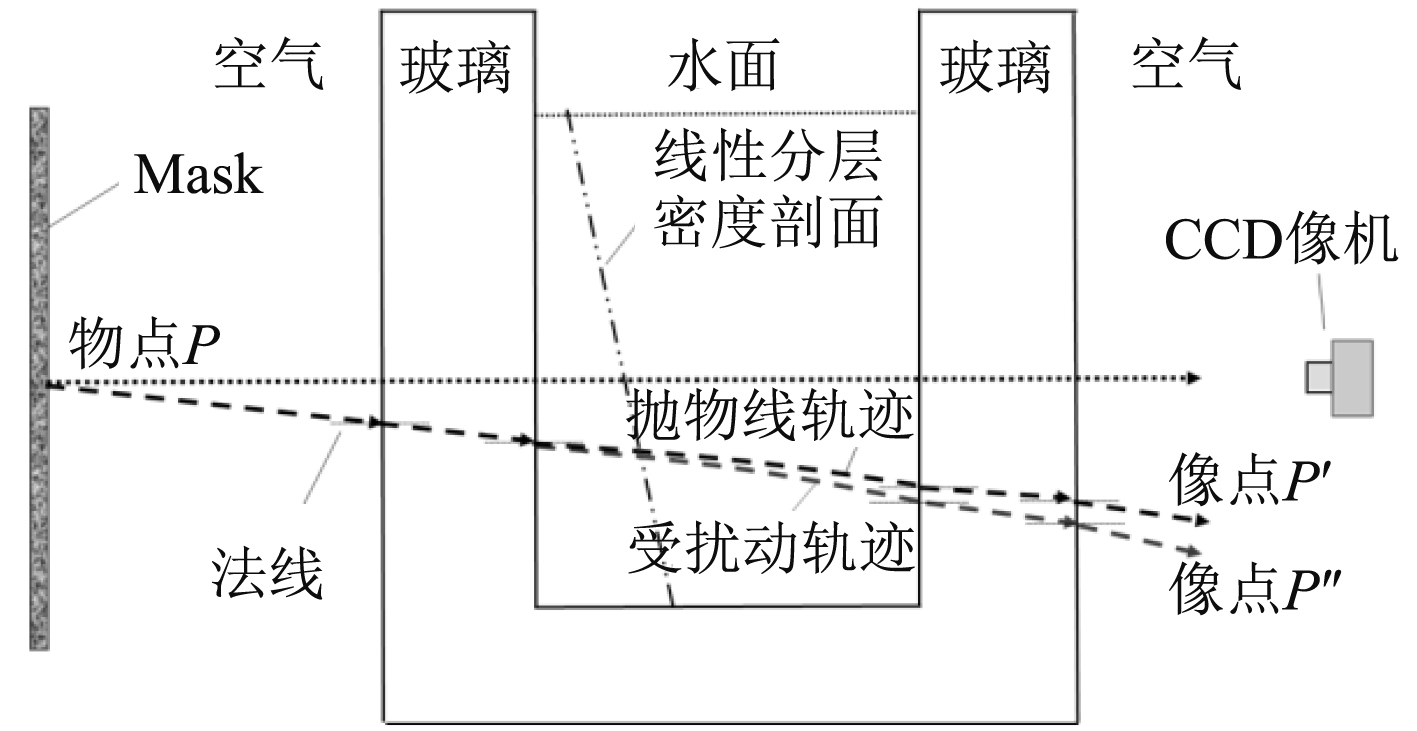
分层流内波场是现代数值纹影技术的重要应用领域,对于二维内波场,J. Fluid Mech[11]建立了水平数值纹影测量的理论及实验方法,理论推导了“表观位移”与介质密度变化的定量关系,并成功运用于振动圆柱体激发的二维内波场的水平数值纹影观测。图3是水平数值纹影成像光线轨迹的示意图,理论分析表明对于水平数值纹影观测系统,当光束水平穿越稳定分层流水槽的二维内波场时,光束的轨迹近似为抛物线,这是运用数值纹影技术对二维内波场进行定量观测的数学基础。对于拖曳球体激发的三维内波场,目前水平数值纹影只能得到“表观位移”与密度扰动场沿水平展向的“宽度平均”的关系[11],因而还是一种半定量的测量。尽管如此,由水平数值纹影图像相关计算得到的“表观位移场”还是为研究者提供了潜航体三维内波场的许多重要信息。
|
图 3 水平数值纹影仪光路原理图 Fig. 3 Level NSS optical schematic |
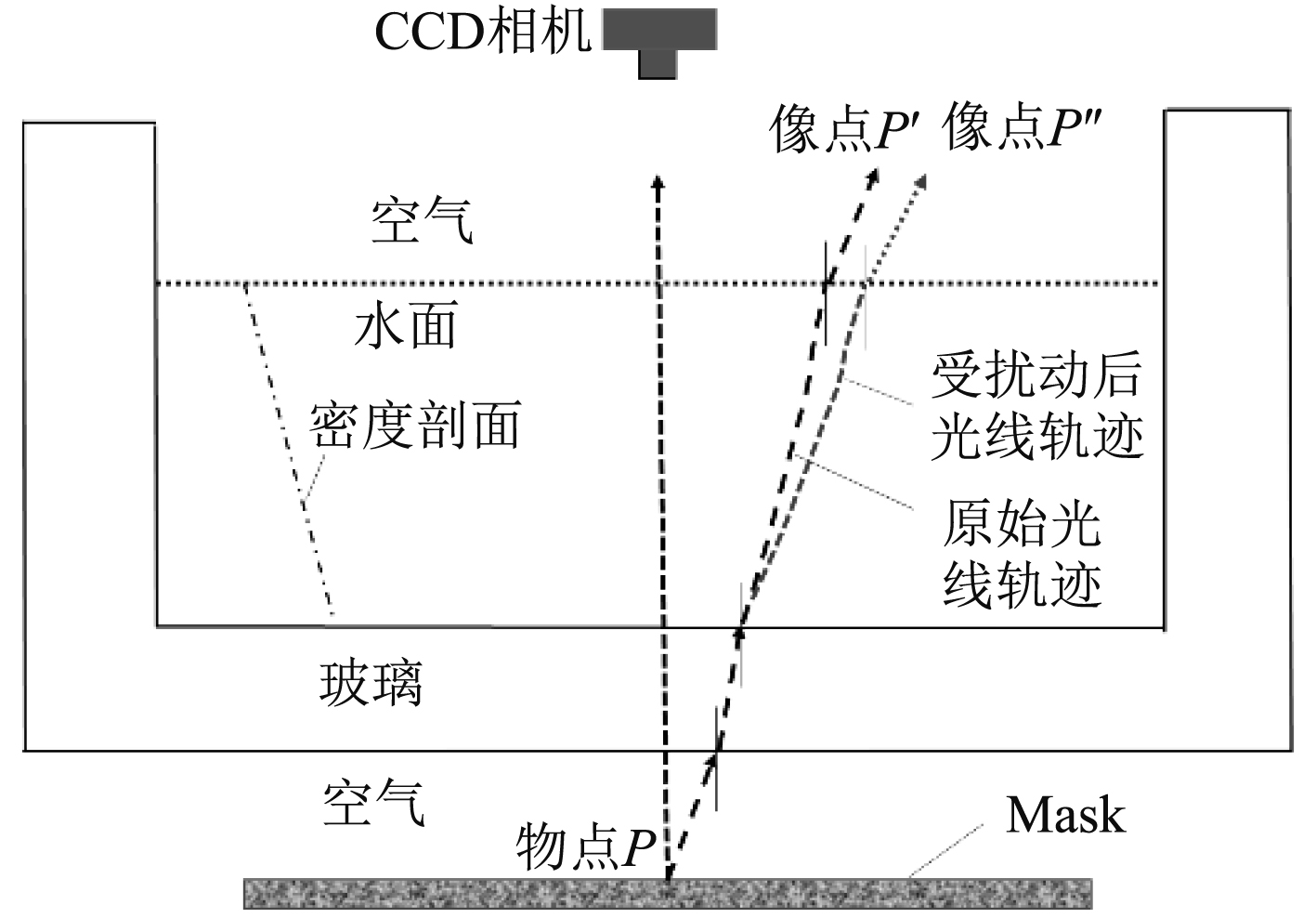
如果将水平方向观测改为垂直方向观测,原则上就成为“垂向数值纹影”,这里存在一个重要的差别就是:垂向光束在分层水体中的轨迹一般不再是抛物线,因为垂向光束在各处的偏转程度(曲线斜率)与分层流的密度剖面
|
图 4 垂向数值纹影光路原理图 Fig. 4 Vertical NSS optical schematic |
本文设计的垂向数值纹影拍摄系统,采用1台CCD摄像机通过一面45°反射镜实现垂直向下观测位于水槽下方的随机点阵图像(Mask)。CCD摄像机的分辨率为1 920×1 080像素,拍摄速度为24帧/s。为了消除表面兴波对垂向数值纹影(NSS_V)观测的影响,可以在水面上悬置一透明平板(有机玻璃)。实验所用随机点阵图(Mask)的灰度值在0~225随机分布,随机点的线度影响数值纹影仪的空间分辨率,通常以随机点在CCD图像上的大小约为3×3个像素为宜;系统采用2台白炽幻灯机作光源分别从左右2个方向照亮随机点阵图(Mask),并尽可能减少背景杂散光的影响。
3 实验结果分析潜航体分层流实验的无量纲参数为弗罗德数
为直观地展示内波场的时空分布特征,本文采用伪彩图表示潜航体内波产生的数值纹影“表观位移场”。伪彩图的坐标为计算表观位移场的图像相关区域的个数,其空间尺度的大小由CCD摄像范围决定,本文采用模型的尺寸对伪彩图的坐标进行标定。对于给定像素的数码相机,图像相关计算区域的像素越少,显示分辨率越大;伪彩图的色彩表示光束的表观位移量,伪彩图颜色的深浅代表表观位移的强弱,参见相应的色标图。
内弗罗德数

|
图 5 拖曳潜艇模型激发三维内波的垂向数值纹影y方向表观位移伪彩图(带指挥塔模型,模型深度200 mm,拖曳速度42 mm/s,Fr=1.0,Re=1 260) Fig. 5 3D Internal wave y direction data pseudo-color map with dragging submarine by vertical NSS (With the command tower model,H=200 mm,U=42 mm/s,Fr=1.0,Re=1 260) |
由图5可见,线性分层流体中内波波系表现为典型的类Kilven水面波系,V字型张角与模型运动方向相同,开口与模型运动方向相反。试验结果表明,弗罗德数较低,雷诺数也较低时,湍流尾迹效应不明显时,拖曳潜航体激发的机制主要是其体积效应,在随体运动参照系中类Kilven V型内波具有较好的定常性。在地面参照系中观察,V型内波的张角随时间演化逐渐变小;在随体运动参照系中则表现为:在模型运动的下游距离越远,V型内波的张角越小。图6是V型内波的张角随无量纲距离(L/D)的变化曲线。

|
图 6 V型内波张角随无纲量距离(L/D)变化曲线 Fig. 6 The curve of the angle varies with L/D |
实验表明三维内波场的V型张角随着弗罗德数变化而变化。由于三维内波场的V型波峰线的张角随时间与空间位置而变化,本文就表观位移场y方向伪彩图中模型下游第2个V型波测量其张角,得到张角与弗罗德数的关系如图7所示。

|
图 7 V型内波张角随弗罗德数变化曲线 Fig. 7 Internal wave angle with Fr change curve |
为减小测量误差,采用多次测量求平均的方法,图7 给出了同一弗罗德数之下张角测量的上下界。测量结果表明:在弗罗德数为0.6~2.5的范围内,内波半角的大小整体变化趋势为随着弗罗德数的增加而减小;在弗罗德数为0.7~1.0范围内,攻度与弗罗德数呈近似线性相关,其拟合公式为
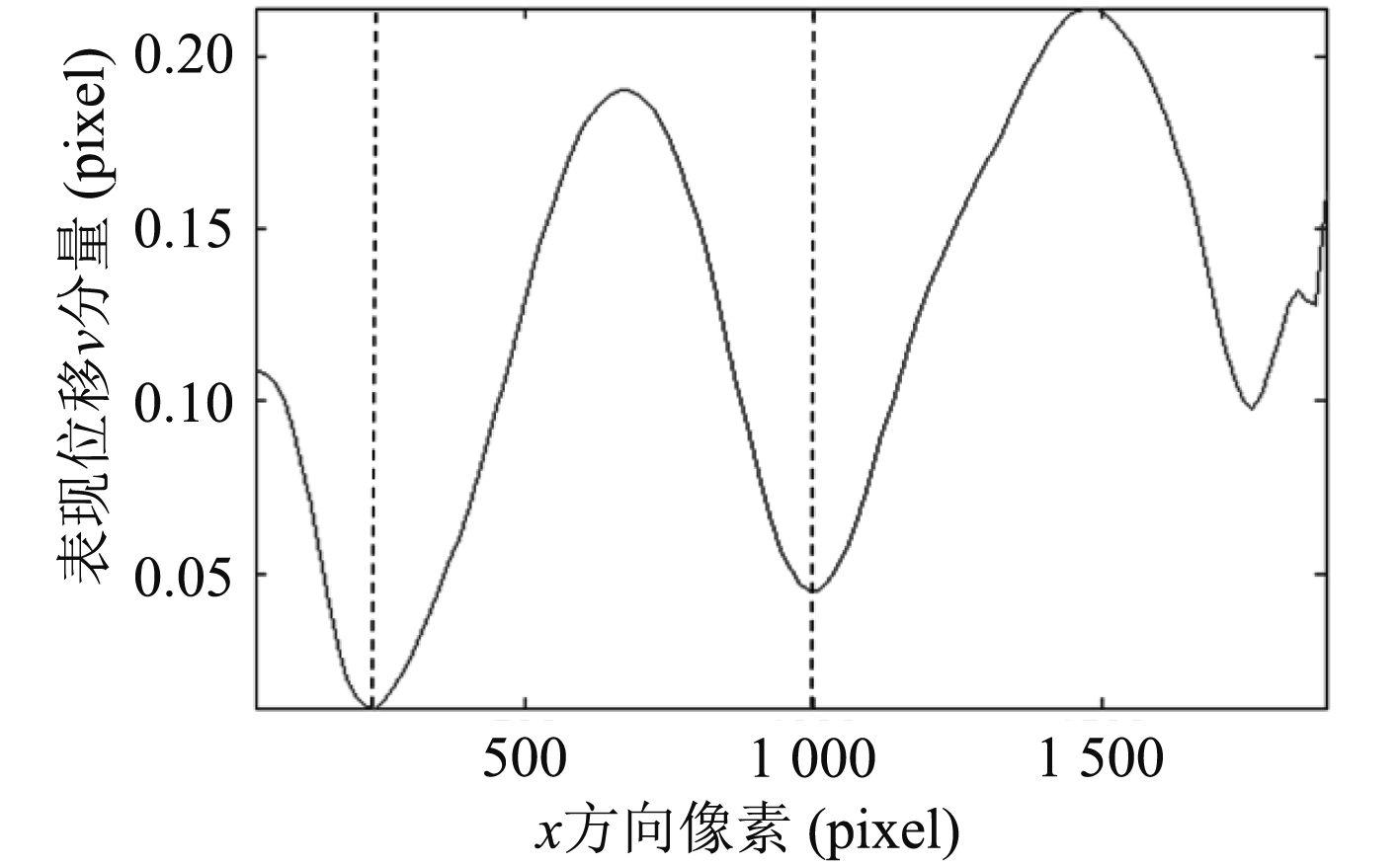
波长是同一波射线上相位差为2π的两点之间的距离,对于单色简谐波波长的测量比较容易,但是对于潜航体激发的三维内波场,要从实验上测量其波长却不是一件容易的事。本文采用垂向数值纹影方法,将三维内波场的“垂向投影”用视频直观地呈现出来,潜航体激发内波的类开尔文V型特征及其波峰线的演变过程得到清晰的展示。然而即使如此,由于内波场特殊的色散性、群速度与相速度的不同向等特性,导致内波的波长是时间与空间的函数
|
图 8 沿Ny=50提取的数据经低通滤波后的曲线 Fig. 8 The data extracted along Ny=50 are then low-pass filtered |
|
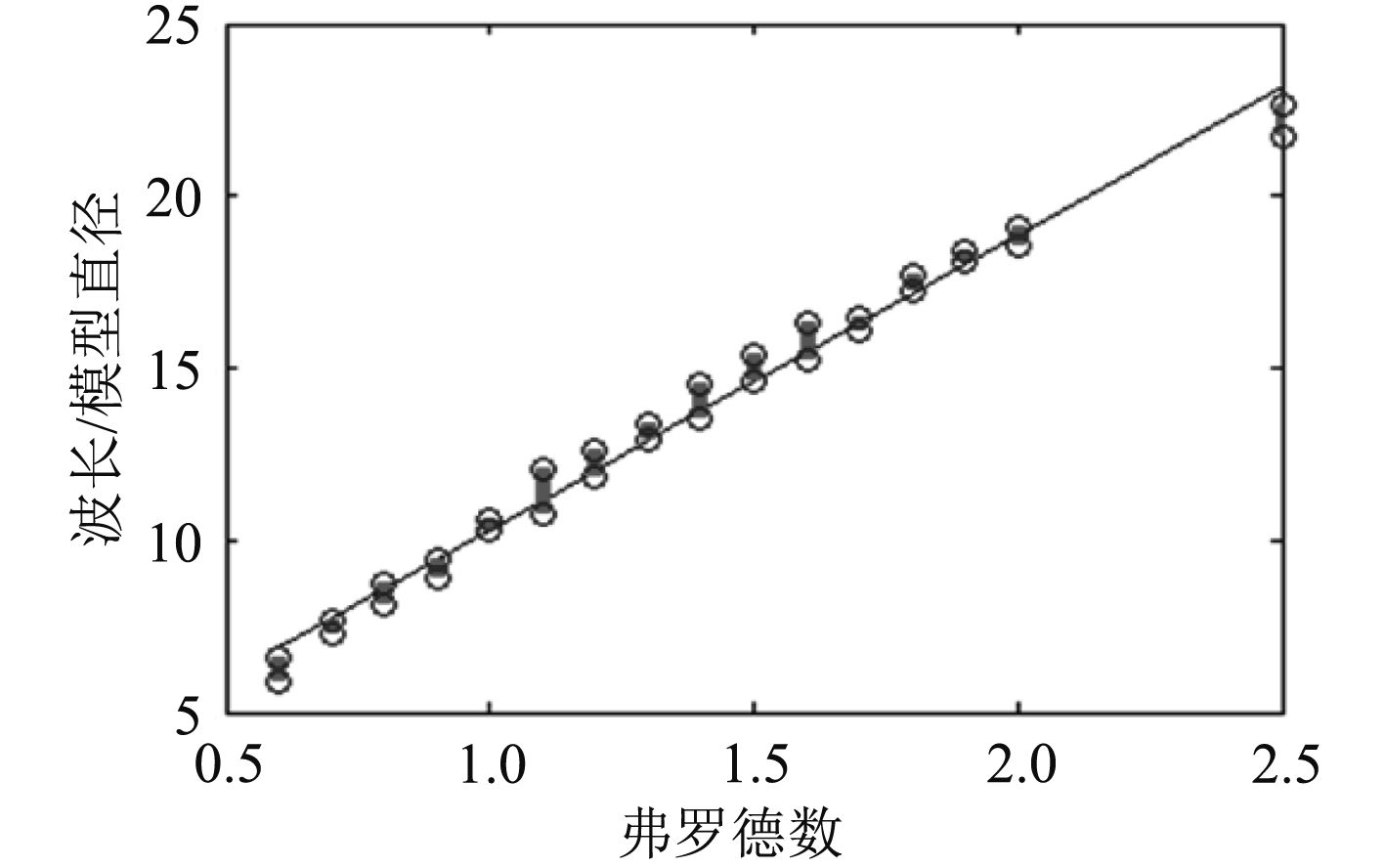
图 9 内波波长随弗罗德数变化曲线 Fig. 9 Internal wave wavelength with Froude number change curve |
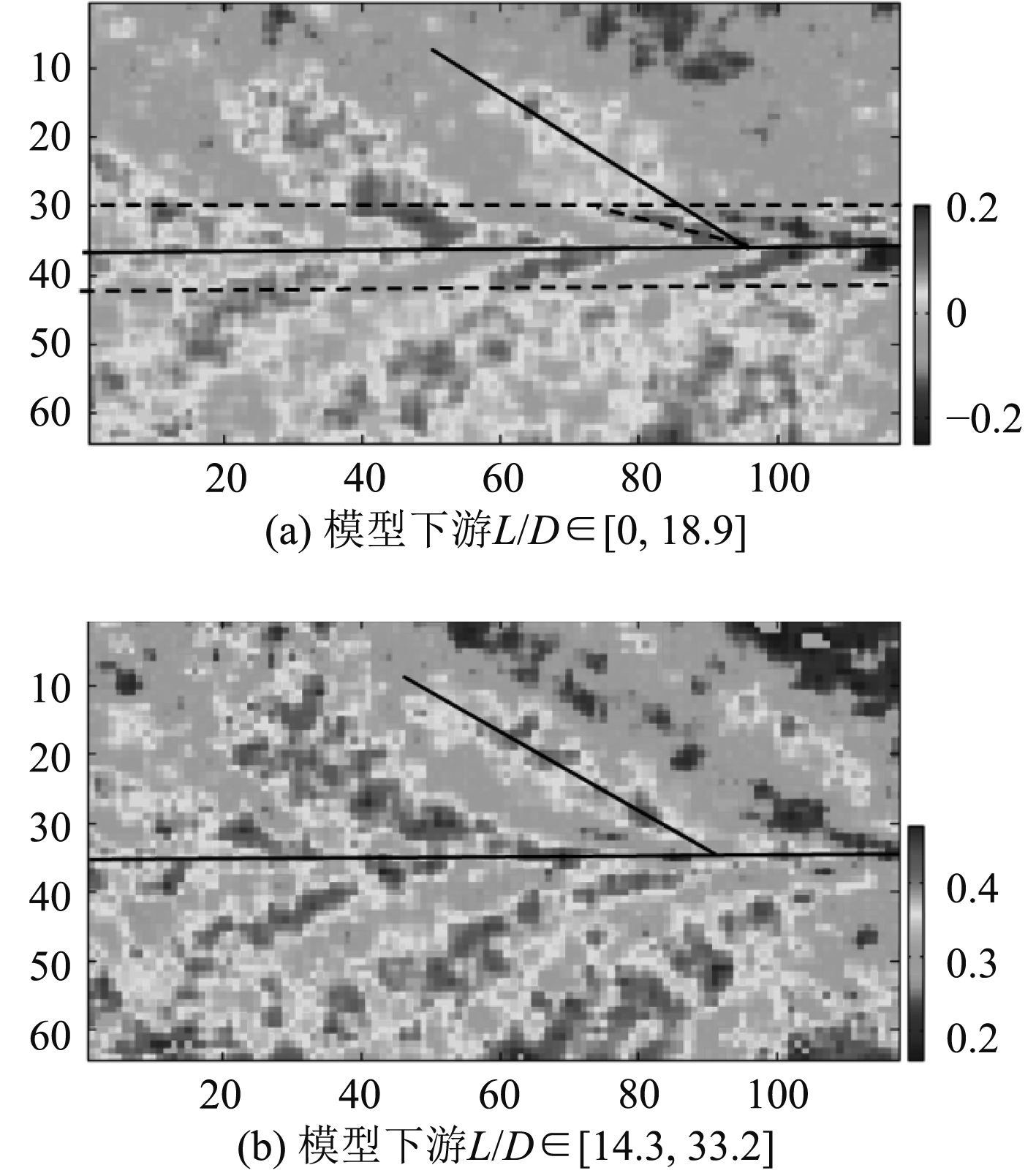
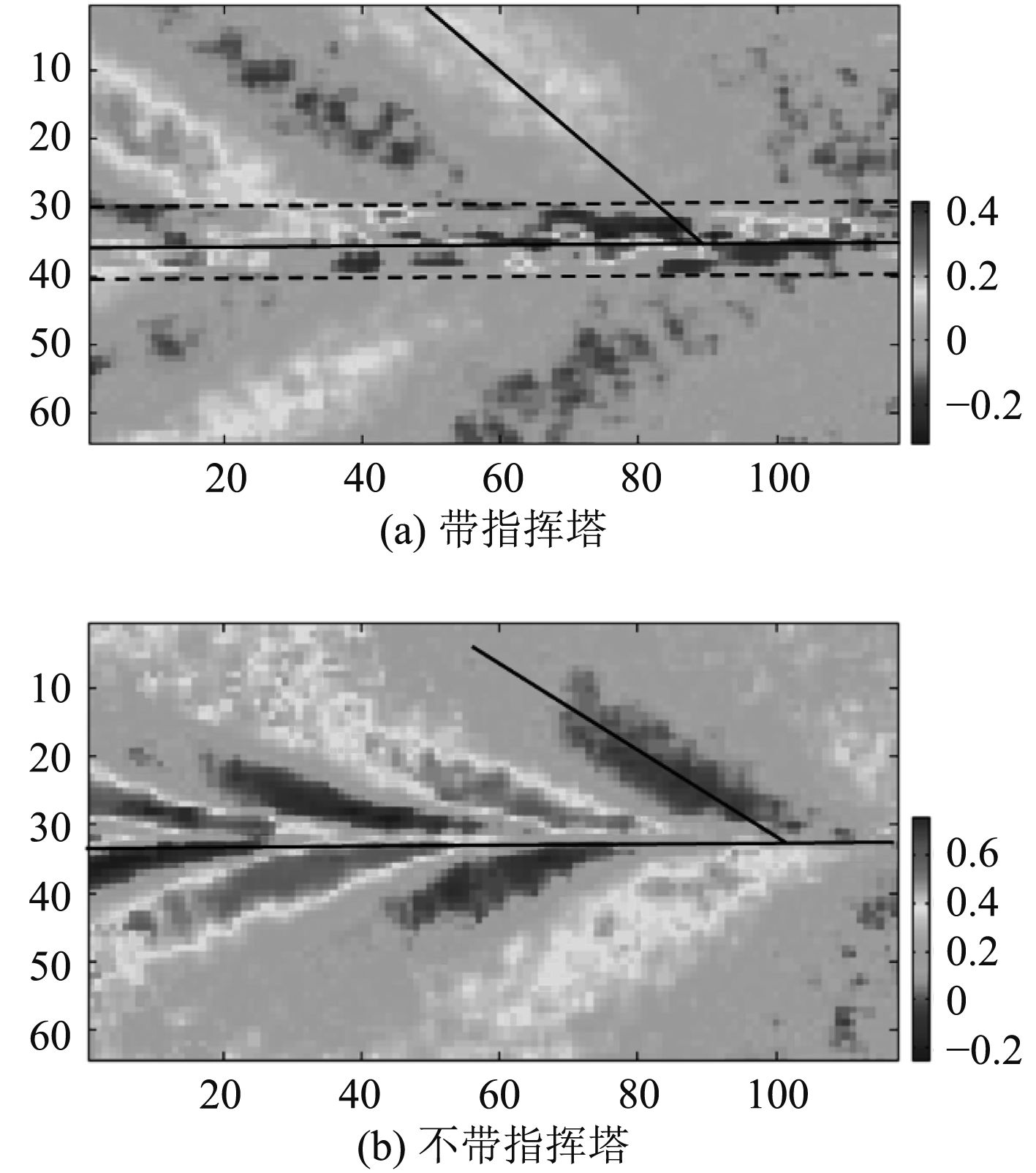
除了定常体积效应之外,潜航体的非定常尾流场对分层流的扰动也是激发内波的扰动源。潜艇的指挥塔向水面方向突出与艇体构成垂直的角区,这样的角区会形成所谓马蹄窝形复杂流场[13],必将影响潜艇尾迹流场乃至内波尾迹目标特性。为了观测指挥塔突出物对细长体模型激发内波尾迹的影响,本文开展了无附体潜艇模型与带指挥塔潜艇模型的对比实验。实验结果表明当拖曳速度较低时,带指挥塔潜艇模型的角区流动湍流度较低,内波尾迹形态表现为艇体的体积效应与指挥塔的体积效应两部分的叠加,图10(a)是带指挥塔模型的垂向数值纹影图(Fr=0.6,Re=756),指挥塔体积效应激发的内波表现为张角较小的窄V型,由于指挥塔的体积较小,窄V型内波的存续时间较艇体激发内波的要短,图10(b)显示在L/D∈[14.3,33.2]处窄V型内波已不明显;当拖曳速度提高,指挥塔角区湍流度增大,指挥塔的体积效应被湍流尾迹效应替代,图11(a)是带指挥塔模型的垂向数值纹影图(Fr=1.0,Re=1260),图11(b)是相同条件下去掉指挥塔后的对比实验结果(Fr=1.0,Re=1 260),可见在没有指挥塔角区复杂流场扰动的情况下,细长艇体激发内波的扰动源主要是其体积效应。
|
图 10 带指挥塔模型低速拖曳时垂向数值纹影表观位移矢量y方向数据伪彩图(U=25.2 mm/s,Fr=0.6,Re=756,h=200 mm) Fig. 10 Y direction data pseudo-color map with low velocity towing in the towing tower model (U=25.2 mm/s,Fr=0.6,Re=756,h=200 mm) |
|
图 11 带指挥塔与不带模型的对比实验,垂向数值纹影表观位移矢量y方向数据伪彩图(U=42 mm/s,Fr=1.0,Re=1260,h=200 mm) Fig. 11 A comparative experiment with a control tower and without this (U=42 mm/s,Fr=1.0,Re=1260,h=200 mm) |
在图13(a)中存在2个波系,图中虚线范围内有一个限制在尾迹区较小范围内的窄V型波系,当拖曳速度增加时,窄V型波系便转变为湍流尾迹(见图11(a));当去掉指挥塔后,这个湍流尾迹不复存在(见图11(b))。这一事实表明指挥塔体积效应激发的定常内波只是在航速较低时存在,随着速度的提高,受指挥塔与模型主体间的角区复杂流动的影响,窄V型波系便变成混乱的类湍流尾迹。值得注意的是这个湍流尾迹区比艇体体积效应激发内部的影响区域要窄的多。
4 结 语本文利用垂向数值纹影技术系统地研究了弗罗德数Fr与雷诺数Re对线性分层环境中潜航体激发三维内波场的影响,模型实验弗罗德数:Fr∈[0.6,2.5],雷诺数:Re∈[756,3 150],并且就带指挥塔与不带指挥塔模型激发的内波场开展了对比试验研究,得出如下结论:
1)利用垂向数值纹影技术可以观测潜航体模型在线性分层流体中运动所激发的内波,其特征为典型的类Kelvin波系,即内波波峰线构成V字形结构,V型内波的张角随时间(或空间位置离模型的距离)而逐渐减小。
2)在给定空间位置,V型内波的张角随着弗罗德数的增加而减小.在弗罗德数Fr∈[0.7,1.0]范围内,V型内波的张角与弗罗德数近似线性相关,半攻度拟合公式为
3)内波沿运动方向的相关波长(即波峰线在x方向上的间距)
4)带附体潜航体激发的内波呈现出2个波系,其中张角较大的V型波系由艇体体积效应激发,而限制在尾迹区较小范围内张角较小的V型波系(低速拖曳时)由指挥塔的体积效应激发,由于指挥塔与艇体间复杂的角区湍流涡系的干扰作用,随着速度的增大,窄V型内波波系便不复存在,在垂向数值纹影图像中变成非定常湍流尾迹。
| [1] |
梁川, 洪方文, 姚志崇. 有限深分层流体中运动物体尾流生成内波的一种移动脉动源方法[J]. 水动力学研究与进展, 2015, 30 (1): 9–17.
LIANG Chuan, HONG Fang-wen, YAO Zhi-chong. Atranslating and pulsating source method for internal waves generated by the wake of a body moving in a stratified fluid of finite depth[J]. Chinese Journal of Hydro-dynamics, 2015, 30 (1): 9–17. |
| [2] |
魏岗, 吴宁, 徐小辉, 等. 线性密度分层流体中半球体运动生成内波的实验研究[J]. 物理学报, 2011, 60 (4): 0447041–0447047.
WEI Gang, WU Ning, XU Xiao-Hui, et al. Experiments on the generation of internal waves by a hemispheroid in a linearly stratified fluid[J]. Acta Phys. Sin, 2011, 60 (4): 0447041–0447047. |
| [3] |
李万鹏, 魏岗, 杜辉, 等. 分层流体中螺旋桨效应激发内波的实验分析[J]. 解放军理工大学学报: 自然科学版, 2014, 15 (6): 556–582.
LI Wanpeng, WEI Gang, DU Hui, et al. Experimental study on internal wave generated by apropeller in a stratified fluid[J]. Journal of PLA University of Science and Technology(Natural Science Edition), 2014, 15 (6): 556–582. |
| [4] |
徐肇廷, 于佳, 王伯雄. 光学在内波实验研究中的应用[J]. 中国海洋大学学报(自然科学版), 2007, 6 (6): 861–867.
XU Zhao-Ting, YU Jia1, WANG Bo-Xiong. Application of Optics to Internal Wave Experimental Research[J]. Periodical of Ocean University of China (natural science), 2007, 6 (6): 861–867. |
| [5] |
周文进, 蒋小勤, 王建中, 等. 表面PIV在潜航体兴波伴流场测量中的应用[J]. 舰船科学技术, 2016, 38 (6): 75–80.
ZHOU Wen-jin, JIANG Xiao-qin, WANG Jian-zhong, et al. The Application of Surface PIV in Measurement of Wave Wake of Underwater Moving Body[J]. Ship science and technology, 2016, 38 (6): 75–80. |
| [6] | S. Whole-field density measurements by’synthetic schlieren’[J]. Experiments in Fluids, 2000, 28 (4): 322–335. DOI: 10.1007/s003480050391 |
| [7] | STUART B D, MAGDA C, SVEEN J K, et al. Simultaneous synthetic schlieren and PIV measurements for internal solitary waves[J], Meas. Sci. Technol. 2007: 18: 533–547. http://iopscience.iop.org/article/10.1088/0957-0233/18/3/001 |
| [8] | WEHAUSEN J V, LAITONE E V. Surface wave[M]. Berlin; Handbuch der Physik 9, 1960. |
| [9] | Wu J. Mixed Region Collapse With Internal Wave Generation In A Density-Stratified Medium[J]. Journal of Fluid Mechanics, 1969, 35 (3): 531–544. DOI: 10.1017/S0022112069001261 |
| [10] |
冯天植, 刘成民, 赵润祥, 等. 纹影技术述评[J]. 弹道学报, 1994, 2 : 89–96.
FENG Tianzhi, LIN Chengmin, ZHAO Runxiang, et al. Schlieren methods: A review of techniques[J]. Journal of Ballistics, 1994, 2 : 89–96. |
| [11] | MAXWORTHYT. On the formation of non-linear internal waves from the gravitational collapse of mixed regions in two andthree dimensions[J]. Journal of Fluid Mechanics, 1980. 96(1): 47–64. http://adsabs.harvard.edu/abs/1980JFM....96...47M |
| [12] |
赵先奇, 尤云祥, 等. 分层流体中细长体生成内波的实验研究[J]. 上海交通大学学报, 2009, 8 .
ZHAO Xian-qi, YOU Yun-xiang, et al. Experimental Study on the Generation of Internal Wavesby a Slender Body in Stratified Fluid[J]. Journal of Shanghai Jiaotong University, 2009, 8 . DOI: 10.3321/j.issn:1006-2467.2009.01.035 |
| [13] |
张华, 吕志咏, 孙盛. 应用PIV对角区非定常马蹄涡结构的实验研究[J]. 力学学报, 2008, 40 (2): 171–178.
ZHANG Hua, LU Zhiyong, SUN Shengdong. The experimental study on unsteady horseshoe vortex structure in juncture flow PIV[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40 (2): 171–178. DOI: 10.6052/0459-1879-2008-2-2007-246 |
 2017, Vol. 39
2017, Vol. 39
