2. 海军装备部,北京 100071
2. Department of Navy Armament, Beijing 100071, China
叶片是压气机的重要组成部分之一,在压气机工作过程中起着转换不同形式能量的作用,是压气机的关键部位,其强度直接影响压气机的性能和可靠性[1, 2]。国内外的军用和民航航空发动机以及燃气轮机在运行中,几乎都发生过叶片故障方面的问题,对发动机的使用安全影响很大,是叶片强度技术问题中比较突出的问题。压气机叶片在工作时,环境比较恶劣,除了需要承受非定常气动力、离心力的作用,还受变工况、固定约束力和振动等因素的影响。在这种复杂的情况下,叶片必须具有较高的强度,否则燃气轮机难以正常工作。它的结构设计强度,对压气机的寿命、可靠性、耐久度有重要影响[3]。
孙涛[4]对变厚度叶片对离心压缩机结构强度和性能影响进行分析,马辉[5]采用变厚度壳单元模拟叶片的固有频率和振动响应。张震宇[6]对采用TC4钛合金作为压气机叶片的超高周疲劳失效机制及强度-寿命预测方法进行研究。此外,早在20世纪70年代,蒙先信等已对压气机叶片的强度和振动进行了相关计算;近期,古成中等[7]采用UG软件针对燃气轮机叶片进行精确建模,为结构强度、温度场等有限元分析提供基础;付雷等[8]研究了毫米级微型燃气轮机系统的设计原则;丁彦闯等[9]对压气机叶片结构–振动关系进行了一体化系统研究。国外Geng等[10]和Yamazaki等[11]的研究中也着重分析了叶片厚度与强度的关系。
目前改变叶片厚度对叶片强度影响的研究不是很丰富,而叶片自身强度也不是很高,受交变载荷等因素影响容易产生疲劳裂纹,在一定的条件下,裂纹继续扩展,直至剩余的承力面积不足以承受离心力造成的应力时,叶片将折断,后果是对整个叶轮机械构成损害,危害巨大。
本文在分析影响压气机叶片强度因素的基础上,分别从理论规律和数值分析的角度分析压气机叶片的应力及变形,并进行静力学分析,得到叶片厚度对叶片强度的影响规律,对提高叶片强度,进而为增强压气机的可靠性、经济性、寿命等具有重要意义。
1 压气机叶片强度影响因素分析 1.1 载荷分析对于压气机叶片来说,主要受4个力的作用:离心力、气动力、重力和叶片根部的固定力,这4个力的剧烈变化必然会直接影响到叶片的强度。
当压气机出现喘振等不正常工作运行因素时都会对叶片造成损伤或毁坏,影响叶片的强度,以及叶片厚度、材料,材料的密度,泊松比[7]等都会关系到叶片强度的改变。随着压比和转速的升高对叶片的强度也同样构成影响。在高温高压的情况下,以及腐蚀、振动、氧化的作用下,叶片的强度也会发生变化。还有在叶片的高速运转过程中,叶片承受着比较高的气动力、离心力、热应力等负荷的作用,这些力会围绕在叶片周边进而形成激振力,而且呈周期性变化。当这种激振力频率也就是外力频率与叶片的固有频率相等或者相近时,叶片就会产生共振,发生形变,甚至损坏,容易发生故障。下面对这些影响因素进行分析:
1)离心力作用将会使压气机叶片产生沿着内径方向的拉应力,而对于扭转叶片,则同时生成扭转应力,而当积叠线不与径向线重合时会生成弯曲应力。在设计转子动叶片时,恰恰是利用这一特性,通过抵消气动和离心弯曲应力来达到减小叶片所受应力的目的。
2)气动载荷[8]是所有叶片都要承受的气动力作用。气动力是表面分布压力,作用在叶片表面,它沿叶宽以及叶高方向的分布不平均。工作中,压气机叶片承受着气体流动所产生的气动力和扭矩、弯矩以及轴向力载荷。气动力不仅会使叶片承受弯曲应力,还有扭转应力。
3)在压气机正常工作时,压气机叶片的温度变化不是很大,叶片所受的热应力也很小,一般叶片自身的热应力可以不计入载荷。
4)压气机中激振力的形式多样,对于叶片,具有特定变化规律的激振力是主要影响其强度的力。具有特定周期规律的激振力包含叶片旋转失速造成的激振力、机械激振力和气体尾流激振力。激振力多数直接作用在叶片上,使叶片强迫生成振动,危害很大。
5)叶片振动的参数由振型、振幅、振动频率等组成。材料属性、几何特征以及边界条件决定振动频率的大小,其中包含静频以及动频。由于叶片是弹性体元件,具有无限多个振动形态。在振动应力接近一定数值并且经过一定时间后,叶片就会生成裂纹,叶片强度丧失。
1.2 固有频率分析叶片固有频率的影响因素主要有:
1)离心力的影响
离心力拥有使叶片趋向平衡位置的作用,等于加大了叶片的弹性恢复力,加强了叶片的刚度,增大了叶片的频率。转速越快,离心力就越大,频率升高的越多。离心力对叶片的弯曲振动频率有比较大的影响,对低阶频率有更明显的影响。
2)叶片扭角的影响
压气机叶片为了达到气动性能的要求,沿叶高会有比较大的扭角,存在扭角叶片的弯曲振动频率低于没有扭角的叶片的弯曲振动频率,通常要低5%~20%。
3)叶片根部连接情况的影响
在分析叶片的振动时,通常将叶片的根部视为固定支撑。然而实际中,榫头和榫槽间有一定大小的间隙,当转速不是很高时,离心力也比较小,所以只能视为半固定支撑状态,只有当转速比较高时,在比较大的离心力的作用下,才可以彻底清除间隙,成为理论方面的“完全固定支撑”情况。所以,叶片的实际频率要低于理论固定支撑模型的频率。
2 厚度对叶片强度影响的理论分析
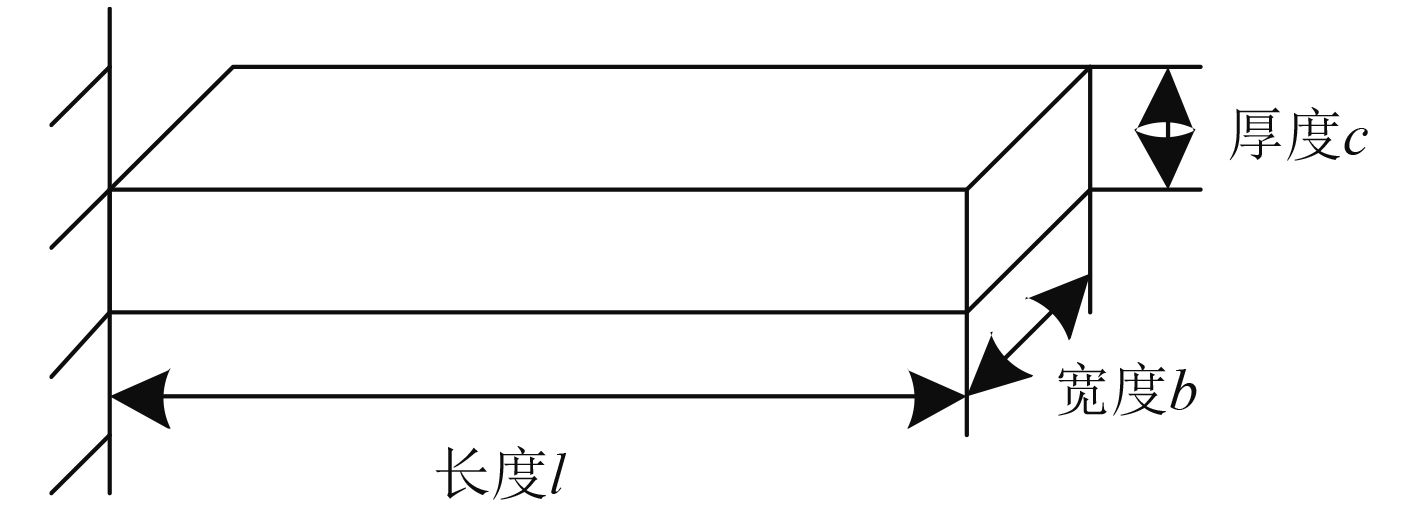
|
图 1 压气机叶片等效图(悬臂梁) Fig. 1 Compressor balde equivalent figure of cantilever beam |
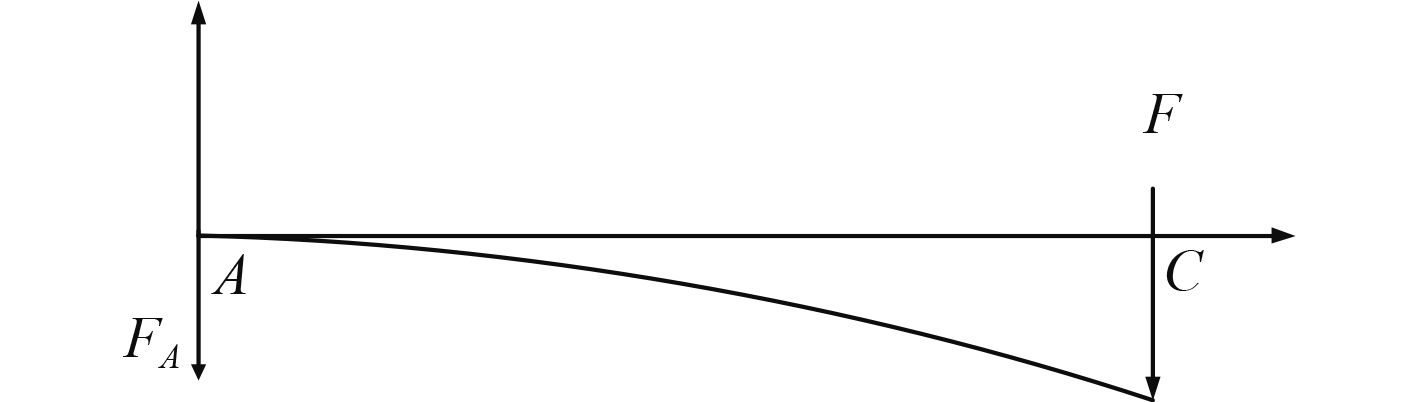
|
图 2 压气机叶片力学模型 Fig. 2 Statics model of compressor blade |
悬臂梁的挠度曲线
| $w = \sqrt {\frac{{{{\int_0^l {EI\left( {\displaystyle\frac{{{{\rm d}^2}y}}{{{\rm d}{x^2}}}} \right)} }^2}{\rm d}x}}{{\rho \int_0^l {A{y^2}} {\rm d}x}}} = \sqrt {\frac{{140EI}}{{11\rho A{l^4}}}} \text{,}$ | (1) |
将A=bc,
| $w = \frac{c}{{{l^2}}}\sqrt {\frac{{35E}}{{33\rho }}}\text{。} $ | (2) |
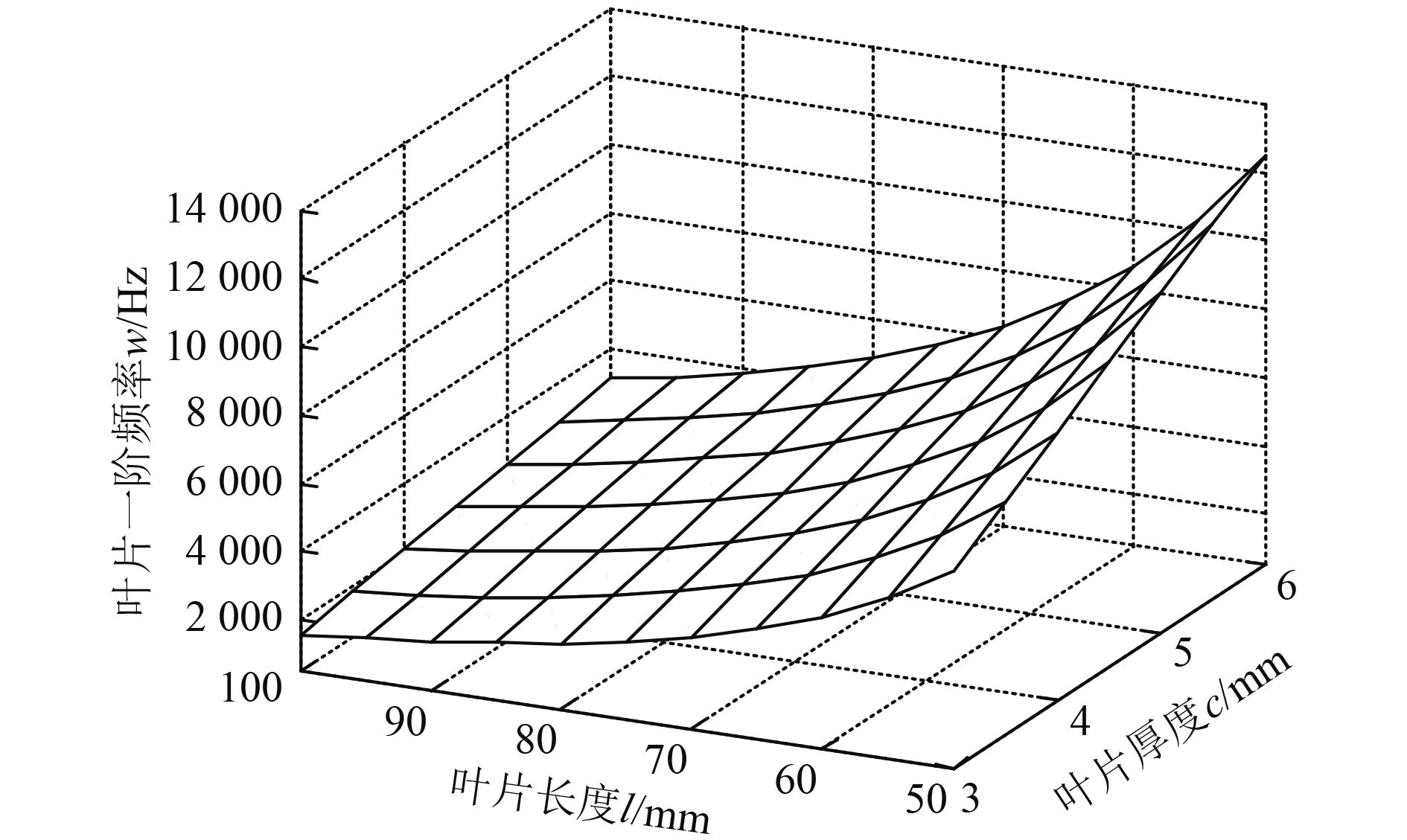
|
图 3 不同叶形几何参数下叶片的1阶频率变化规律图 Fig. 3 The variance of the first-order frequency for the different blade with various geometric parameters |
本文数值分析采用自由网格划分,将要素尺寸定为3 mm之后进行网格划分。网格节点数为25 328,网格单元数为4 221。划分网格图,如图4所示。
3.2 计算设置叶片的材料特性:弹性模量为200 000 MPa,泊松比为0.3,密度为7.85 g/cm3。因为叶片与榫头一体,故当省略榫头单独分析叶片时,叶片与榫头的连接处表面被固定约束。压气机运行时,离心力、重力以及气动力是叶片最主要的应力,忽略气动力。只考虑离心力、重力和固定约束力。在惯性载荷项中,设置叶片的正常工作转速为8 000 r/min。
3.3 厚度影响规律及分析本文共对9组不同厚度的叶片进行分析,厚度分别为3 mm,5 mm,6 mm,7 mm,9 mm,11 mm,12 mm,13 mm,14 mm,编号为a~i。其中c=3 mm在静力学分析时所得应力分布云图,如图5所示。

|
图 4 网格图 Fig. 4 Grid figure under the various parameters |

|
图 5 3 mm厚叶片的应力分布云图 Fig. 5 Stress distribution for a compressor blade of 3mm |
以最开始的原型叶片c为分析分隔点把9种不同厚度的叶片分成2组,即组1:叶片c~a,组2:叶片c~i,通过比较分析最大等效应力值以及它的位置,进行结果分析。表格1列出了叶片的最大等效应力值。对于组1,叶片厚度从初始厚度到厚度逐渐变小这一过程,最大等效应力值呈现逐渐减小的趋势。并且3种不同厚度叶片的最大等效应力均位于叶根固定约束处。通过仿真分析得知,叶片a比叶片c的最大等效应力增加了1.1%。因此,对于初始厚度的叶片,如果减小叶片的厚度,就会降低叶片的结构强度。一般,叶片厚度的增加会提高叶片的强度,组1数据证明这个理论正确。但是,影响叶片强度的因素还有很多,叶片的厚度增减势必会引起叶片自身重力的变化、叶片所受的离心力以及压气机的气动布局的变化,这方面的变化及其影响在组2体现的最明显。对于本文所研究的9种变厚度的叶片,最大等效应力值的变化趋势并不完全是按照线性变化的。对于组2中的叶片c~i,依照叶片由c到i的顺序分析,即叶片厚度从初始厚度到厚度逐渐变大这一过程,最大等效应力值的变化具有一定规律性。以叶片c的应力值作为参考点,随着叶片厚度的增加,在c–d–e、g–h–i过程中最大等效应力呈现增加趋势,但是在e–f–g过程中最大等效应力呈现下降趋势。并且,叶片a~i的最大应力都位于叶根固定约束处,随着叶片厚度的增加,叶片的重力以及其所受的离心力增大,叶片承受的最大应力出现浮动变化,因此,随着叶片厚度的增加,最大等效应力值按照先增加后下降再增加的规律变化。由表格可知,叶片g与叶片c相比较,最大等效应力值减小了0.2%,适当增加叶片的厚度对提高叶片的结构强度非常有利,组1的分析判断结果和增加叶片厚度会显著提高叶片的结构强度相符合,这说明过分减小叶片的厚度会对叶片的结构强度产生不利影响。而组2的数据分析表明,增加叶片的厚度并不一定会增强叶片的强度,最大等效应力值按照先增加后下降再增加的规律进行变化。但是,当叶片的厚度增加到一定的合适的数值时,就能够提高叶片的结构强度。在这次分析中叶片g的最大等效应力值最小,可以得出12 mm厚度的叶片在这9组不同厚度的叶片中,强度最佳,是本文得到的最好方案与优化方案。
|
|
表 1 叶片的最大应力值 Tab.1 The maximum stress value for the compressor blade |
本文对8 000 r/min的优化叶片g进行模态分析,其中叶片c的前6阶振形图、最大应力云图如图6~图17所示。

|
图 6 第1阶振形图 Fig. 6 The first-order vibration illustration |

|
图 7 第2阶振形图 Fig. 7 The second-order vibration illustration |

|
图 8 第3阶振形图 Fig. 8 The third-order vibration illustration |

|
图 9 第4阶振形图 Fig. 9 The fourth-order vibration illustration |
|
图 10 第5阶振形图 Fig. 10 The ffifth-order vibration illustration |
|
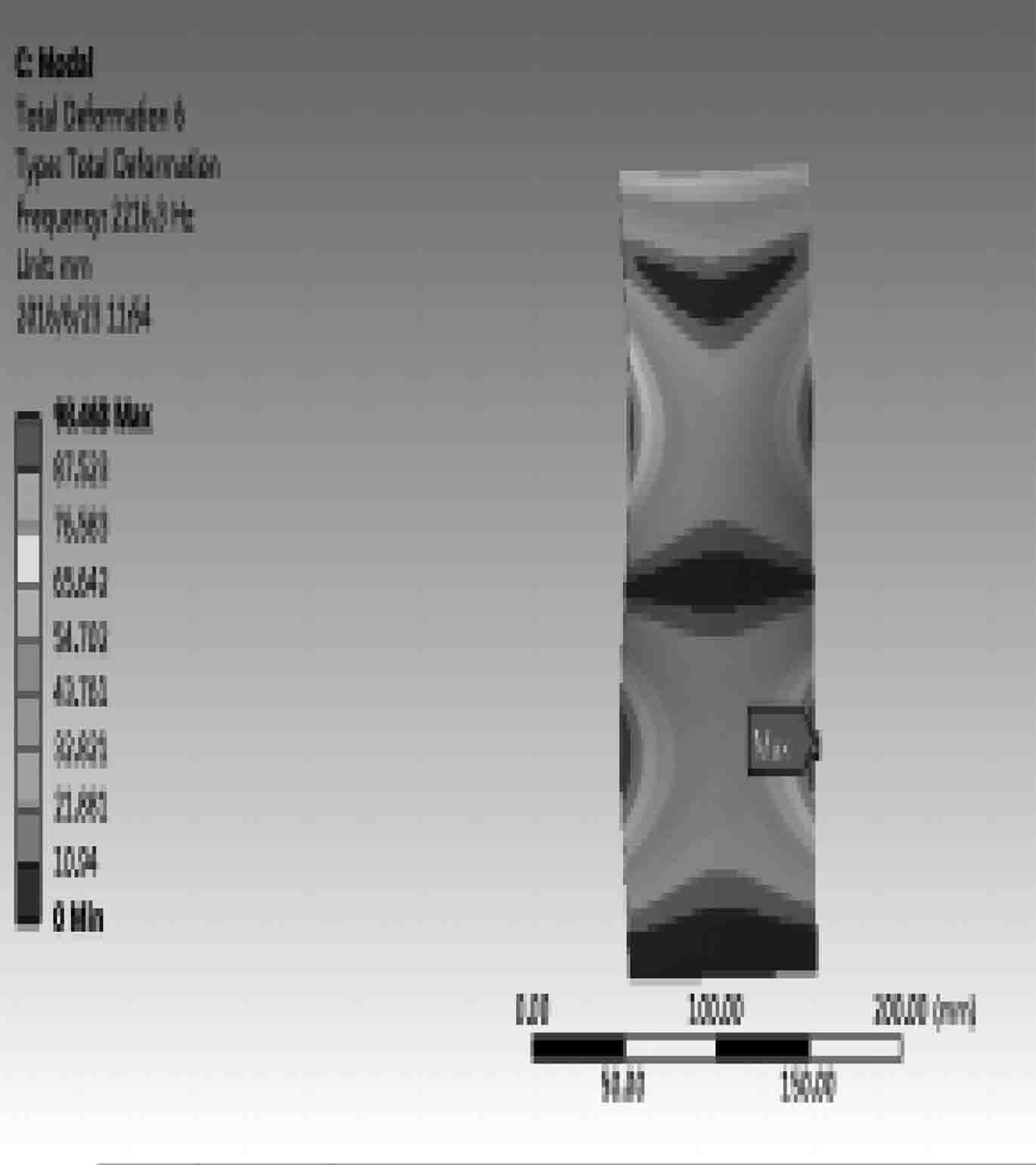
图 11 第6阶振形图 Fig. 11 The sixth-order vibration illustration |

|
图 12 第1阶振动应力分布云图 Fig. 12 The first-order vibration-stress illustration |
|
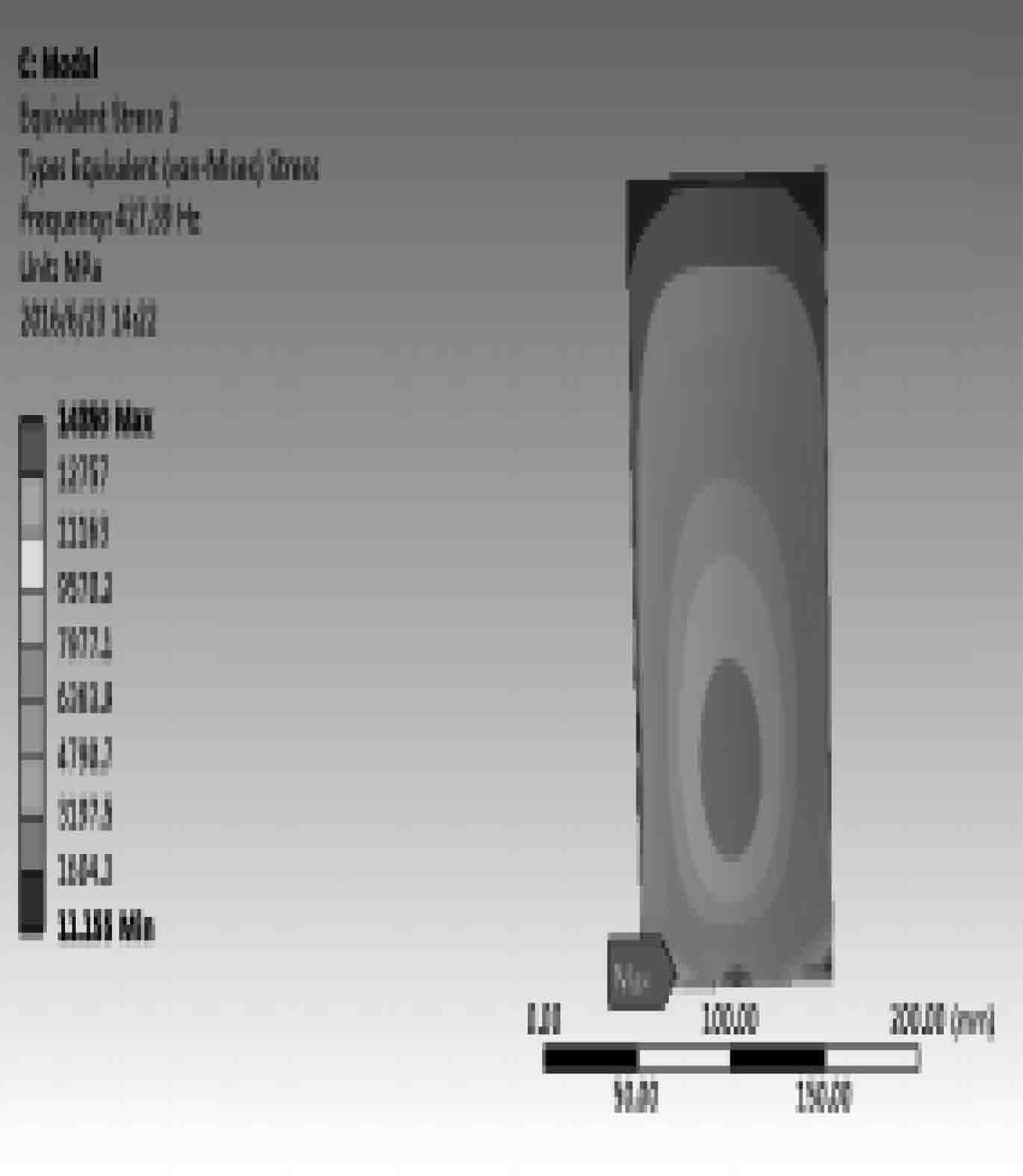
图 13 第2阶振动应力分布云图 Fig. 13 The second-order vibration-stress illustration |

|
图 14 第3阶振动应力分布云图 Fig. 14 The third-order vibration-stress illustration |

|
图 15 第4阶振动应力分布云图 Fig. 15 The fourth-order vibration-stress illustration |

|
图 16 第5阶振动应力分布云图 Fig. 16 The fifth-order vibration-stress illustration |

|
图 17 第6阶振动应力分布云图 Fig. 17 The sixth-order vibration-stress illustration |
通过叶片g前6阶的振形图和振动应力分布云图以及最大及较大振动应力区域的比较,发现无论是振动的幅度、形变的大小还是应力值的比较情况来看,叶片g都优于叶片c。
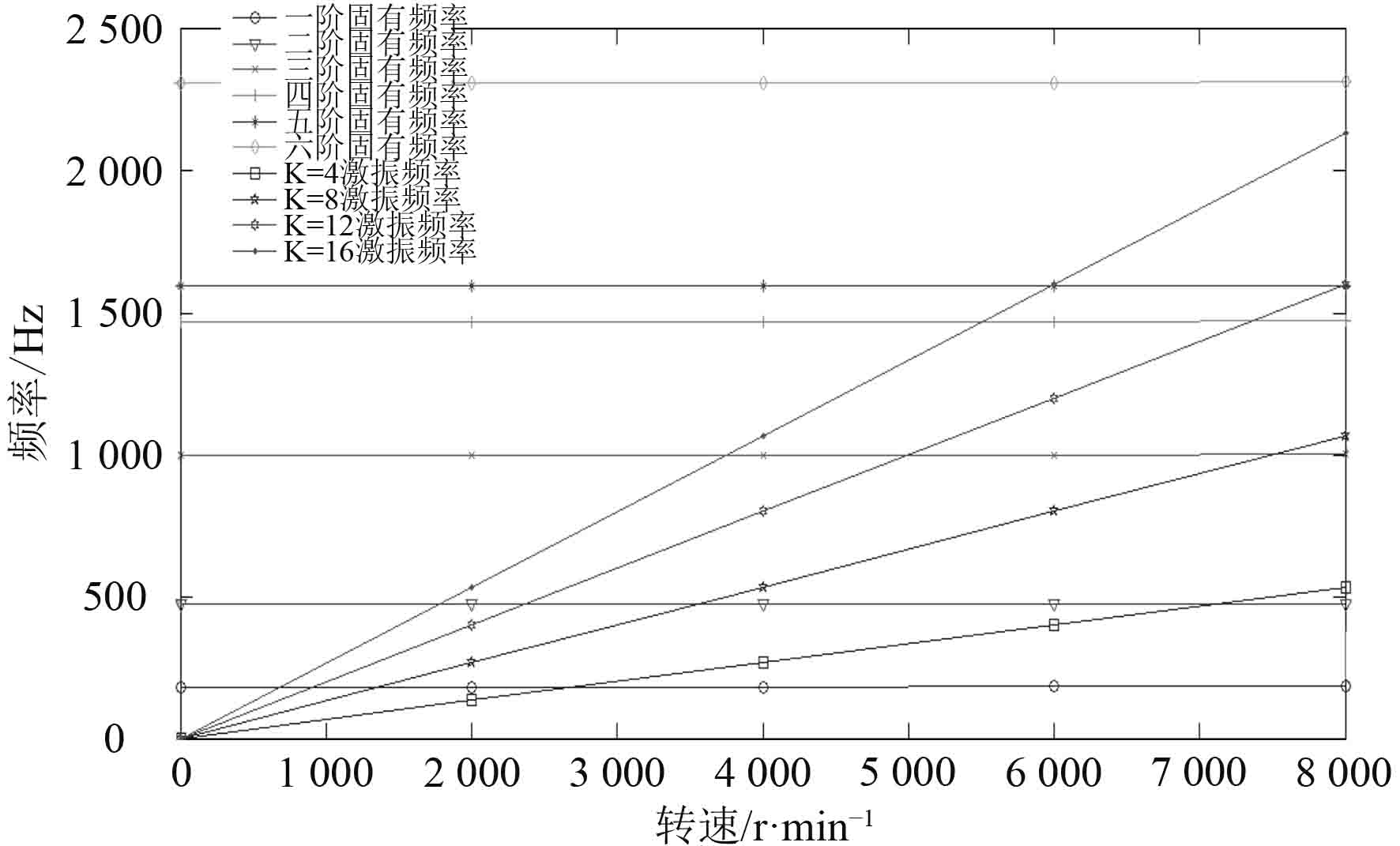
本文对初始厚度叶片在不同转速下模态分析的结果中,选取前6阶的固有频率进行分析、汇总并制作表2。以K=8为例,激振频率曲线与1阶固有频率曲线、2阶固有频率曲线和3阶固有频率曲线分别相交,相交时的转速大约为1 450 r/min,3 700 r/min和7 354 r/min。说明当转速接近或等于这些转速时,外力频率会接近或等于1阶、2阶和3阶的固有频率,引起共振。
|
|
表 2 各转速运转时的前6阶固有频率 Tab.2 The inherent frequency of the first six order under various rotate speed |
|
图 18 坎贝尔共振分析图 Fig. 18 Campbell diagram with sympathetic vibration |
本文对压气机叶片,利用结构有限元软件中的静力学分析得到不同叶片厚度对其最大应力的影响规律,从结构强度的角度来增加叶片结构可靠性,随着叶片厚度的增加,叶片的最等效应力值按照先增加后下降再增加的规律变化,存在最优厚度。对叶片进行模态分析,得到前6阶固有频率、振形图以及最大应力云图,得到叶片最大及较大振动应力区域,最后绘制坎贝尔图,得出共振点的分布情况,为避免发生共振提供理论依据。
| [1] | 李其汉, 王延荣. 航空发动机结构强度设计问题[M]. 上海: 上海交通大学出版社, 2014. |
| [2] | 李娜. 涡轮增压器压气机叶片静态和动态特性研究及优化设计[D]. 大连: 大连交通大学, 2007. |
| [3] | 曲文浩. 航空发动机压气机叶片的静力学及模态分析[D]. 沈阳: 东北大学, 2012. |
| [4] | 孙涛, 王毅, 王晓放, 等. 变厚度叶片对离心压缩机结构强度和性能影响[J]. 大连理工大学学报, 2012, 52 (1): 29–34. DOI: 10.7511/dllgxb201201006 |
| [5] | 马辉, 能海强, 吕颂, 等. 变厚度壳单元的旋转叶片振动响应分析[J]. 机械设计与制造, 2013 (11): 109–112. DOI: 10.3969/j.issn.1001-3997.2013.11.033 |
| [6] | 张震宇. 压气机叶片TC4钛合金超高周疲劳失效机制及强度-寿命预测方法[D]. 北京: 北京理工大学, 2015. |
| [7] | 古成中, 吴新跃. 燃气轮机叶片实体建模[J]. 船海工程, 2006, 35 (3): 69–72. |
| [8] | 付雷, 丰镇平. 毫米级微型燃气轮机系统设计原则与可实现循环分析[J]. 西安交通大学学报, 2011, 45 (5): 42–46. DOI: 10.7652/xjtuxb201105008 |
| [9] | 蒙先信, 段虞荣, 李佩仙. 涡轮增压器压气机导风轮叶片的强度和振动计算[J]. 重庆大学学报(自然科学版), 1978 (1): 155–157. |
| [10] | GENG S J, CHEN N X, ZHANG H W, et al. An improvement on the Efficiency of a Single Rotor Transonic Compressor by Reducing the Shock Wave Strength on the Blade Suction Surfaces[J]. Proceedings of the Institute of Mechanical Engineering, 2012, 21 (2): 127–135. |
| [11] | YAMAZAKI Y, SHIN I, YOSHIDA K T. Evaluation of Interfacial Strength by an Instrumented Indentation Method and its Application to an Actual TBC Vane[J]. Proceedings of the Institute of Mechanical Engineering, 2011, 24 (2): 109–117. |
 2017, Vol. 39
2017, Vol. 39
