我国海域辽阔,海洋资源丰富。近年来,随着海洋能开发逐渐向远岸深海方向发展,漂浮式海洋能装置得到广泛应用。漂浮式海洋平台运动响应的耦合预报问题成为制约该类装置设计、开发和工程应用的关键,是目前漂浮式海洋能装置研究的热点[1 – 3]。
针对漂浮式海洋平台运动响应耦合预报问题,王兴刚[4]在确定平台与系缆全耦合计算的初值时,运用了非线性有限元法来计算系泊缆索在浮体处于静平衡状态时的系泊缆索张力。单鹏昊[5]应用有限元法完成了深海平台系泊缆索的动力响应分析。并用自主开发的计算程序,对规则波作用下深海浮式平台运动和缆索张力的瞬态及稳态响应的特性进行分析。而特别针对海洋能系统的运动响应耦合预报问题,叶小嵘[6]以5 MW风机Spar平台为研究对象,分别进行浮式平台水动力性能预报和风机受力性能预报,实现了半耦合计算分析。赵玉娜[7]同样以Spar风机平台为研究对象,在计算过程中进行了平台运动分析和系缆分析之间的实时反馈,实现了全耦合预报。其系缆系统采用的是准静态的计算方法。张楠针[8]对“150 kW漂浮式潮流能电站”,使用了船舶与海洋工程通用软件MOSES,在未考虑潮流能机载荷的情况下对3套不同系泊方案进行分析和比较,得出最优的方案。
本文针对漂浮式海洋能装置,基于间接时域法,建立浮式平台时域运动方程,基于悬链线理论和全矢量形式的三维集中质量法,建立系统运动方程,并使用自行开发的计算程序对以上方程进行求解,计算核心主要使用C++语言生成。再以系缆和浮式平台的受力和位移作为2个运动方程的交互输入与输出,建立浮式平台与系泊系统的全耦合计算方法,并对简化的浮式海洋平台进行计算,分析载体平台的运动响应和系缆受力情况。
1 载体平台运动计算 1.1 频域计算载体平台是漂浮式海洋能系统的基础装置,为了简化问题,本文以圆柱型载体平台为例,首先建立直角坐标系和柱坐标系,如图1所示。直角坐标系的z轴竖直向上,xOy平面位于未扰动的静水平面上,柱坐标系的原点与直角坐标系原点重合,z轴与直角坐标系的z轴重合,x方向θ角为0。圆柱型平台直径为a,吃水为b,轴线位于z轴上。水深为h。

|
图 1 圆柱型平台坐标系及流域划分示意图 Fig. 1 Cylindrical platform coordinate system and flow field division |
在柱坐标系中,流场任意一点的速度势表示为
| $\varPhi (r,\theta ,z,t) = {\mathop{\rm Re}\nolimits} \left\{ {\phi (r,\theta ,z){e^{ - i\omega t}}} \right\}\text{。}$ | (1) |
流场中任意一点的动压力为
| $P = - \rho \frac{{\partial \Phi }}{{\partial t}}\text{,}$ | (2) |
载体平台所受x方向载荷
| ${F_x} = - \int_0^{2π } {\int_{ - b}^0 {P(a,\theta ,z,t)a\cos \theta {\rm{d}}z{\rm{d}}\theta } } \text{,}$ | (3) |
z方向载荷
| ${F_z} = \int_0^{2π } {\int_0^a {P(r,\theta , - b,t)r{\rm{d}}r{\rm{d}}\theta } }\text{,}$ | (4) |
以z轴与海底相交点为参考点,载体平台所受力矩
| ${M_s} = - \int_0^{2π } {\int_{ - b}^0 {(z + h)P(a,\theta ,z,t)a\cos \theta {\rm{d}}z{\rm{d}}\theta } } \text{,}$ | (5) |
相对于z轴,载体平台受到的力矩
| ${M_b} = \int_0^{2π } {\int_0^a {P(r,\theta , - b,t){r^2}{\rm{d}}r{\rm{d}}\theta } } \text{。}$ | (6) |
当入射波符合微幅波假定时,流场中速度势可以看作4个部分的线性叠加:
| $\phi = {\phi _d} + {\hat \xi _1}{\phi _1} + {\hat \xi _3}{\phi _3} + a{\hat \xi _5}{\phi _5}\text{,}$ | (7) |
其中ϕd为绕射势,即当假定载体平台固定时流场的速度势,ϕ1,ϕ2,ϕ3分别为载体平台做第1,第3和第5自由度(纵荡、垂荡、纵摇)方向上单位运动产生的辐射势。
根据式(7),将速度势求解分为绕射问题和辐射问题,对辐射势求解便得到了所需的水动力系数用于间接时域法计算。
1.2 间接时域法载体平台频域运动方程表示为
| $\begin{split}& \displaystyle\sum\limits_{j = 1}^6 {\left\{ {{M_{ij}} \!\cdot\! {{\ddot x}_j} \!+\! {A_{ij}} \!\cdot\! {{\ddot x}_j}\left( {\omega ,t} \right) \!+\! {B_{ij}} \!\cdot\! {{\dot x}_j}\left( {\omega ,t} \right) + {C_{ij}} \!\cdot\! {x_j}\left( {\omega ,t} \right)} \right\}} =\\& {F_{wai}}\cos \left( {\omega t + {\varepsilon _{wi}}\left( \omega \right)} \right)\text{,}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(8)\end{split}$ |
载体平台时域运动方程为
| $\begin{split}& \displaystyle\sum\limits_{j = 1}^6 {\left\{ {\left( {{M_{ij}} + {m_{ij}}} \right) \cdot {{\ddot x}_j}\left( t \right) + \int_{ - \infty }^t {{{\dot x}_j}\left( \tau \right){K_{ij}}\left( {t - \tau } \right){\rm{d}}\tau }} \right\}} +\\ & {C_{ij}}{x_j}\left( t \right) = X{}_i\left( t \right)\text{,}\end{split}$ | (9) |
其中Xi(t)为第i个自由度上的外力或外力矩。对式(9)进行积分变换,得到
| $\begin{split}& \displaystyle\sum\limits_{j = 1}^6 {\left\{ {\left( {{M_{ij}} + {m_{ij}}} \right) \cdot {{\ddot x}_j}\left( t \right) + \int_0^{ + \infty } {{{\dot x}_j}\left( {t - \tau } \right){K_{ij}}\left( \tau \right){\rm{d}}\tau }} \right\}} + \\&{C_{ij}}{x_j}\left( t \right) = X{}_i\left( t \right)\text{。}\end{split}$ | (10) |
其中Xi(t)为第i个自由度上的外力或外力矩,包括波浪载荷、风载荷、流载荷和轮机载荷。Kij称为延迟函数(Retardation Function),表示当前的单位速度对未来的影响。
为了得到附加质量mij和延迟函数Kij,直接方法是求解速度势ψj和χj,而求解速度势的过程比较复杂。间接时域的方法不直接求解运动过程中的速度势,而是通过已知的频域运动方程的系数,得到时域运动方程的系数。
只考虑线性运动的条件下,水动力系数C33、C35、C44、C53、C55由载体平台在水线面以下的几何形状和载体平台的质量分布决定,Cij其他项为0,且时域运动方程和频域运动方程的Cij相等。
经推导可知
| ${A_{ij}}\left( \omega \right){\rm{ = }}{m_{ij}} - \frac{1}{\omega }\int_0^{ + \infty } {{K_{ij}}\left( \tau \right)\sin \left( {\omega \tau } \right){\rm{d}}\tau } \text{,}$ | (11) |
| ${B_{ij}}\left( \omega \right){\rm{ = }}\int_0^{ + \infty } {{K_{ij}}\left( \tau \right)} \cos \left( {\omega \tau } \right){\rm{d}}\tau \text{,}$ | (12) |
由式(11)可知
| ${m_{ij}}{\rm{ = }}{A_{ij}}\left( { + \infty } \right)\text{,}$ | (13) |
由式(12)可知,Bij和Mij是傅里叶变换和逆变换的关系,则
| ${K_{ij}}\left( \tau \right){\rm{ = }}\frac{2}{π }\int_0^{ + \infty } {{B_{ij}}\left( \omega \right)} \cos \left( {\omega \tau } \right){\rm{d}}\omega \text{。}$ | (14) |
当水动力系数Aij和Bij已知的情况下,通过式(13)和式(14)得到mij和Kij,从而实现频域运动方程的求解。
通过数值运算求解,得到的Bij(ω)是有限长离散序列,则需要对式(14)做适当处理[9]。已经得到B关于ω的有限长离散序列
| ${\rm{DFT: }}X\left[ k \right] = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]} \cdot \exp \left( { - {\rm{j}} \cdot 2\pi \cdot \frac{k}{N}n} \right)\text{,}$ | (15) |
即
| $X\left[ k \right] = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]} \cdot \cos \left( {2π \cdot \frac{k}{N}n} \right) - {\rm{j}} \cdot \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]} \cdot \sin \left( {2\pi \cdot \frac{k}{N}n} \right)\text{。}$ | (16) |
设B[n]经离散傅里叶变换后得到的序列为X[k],对比式(14)和式(16)可知以下转换关系:
| $K\left[ k \right] = \frac{2}{π }{\mathop{\rm Re}\nolimits} \left\{ {X\left[ k \right]} \right\}\Delta \omega \text{,}$ | (17) |
其中K[k]的采样间隔为
| $\Delta t{\rm{ = }}\frac{{2π }}{{\Delta \omega }} \cdot \frac{1}{N}\text{。}$ | (18) |
根据离散傅里叶变换结果的对称性,只取K[k]序列的前一半作为延迟函数。
2 系泊分析系泊系统是漂浮式海洋能装置的重要组成部分,系缆张力是载体平台在横荡、纵荡、首摇3个自由度上回复力的重要来源。系缆有多种形式,本文以锚链为例,分别给出系缆静态和动态分析方法。
2.1 静力分析锚链的静力分析可以为锚链动态的计算提供初始位移和张力值。根据悬链线理论,可以快速估计给定长度锚链顶端水平张力、竖直张力与泊距之间的关系。对一段锚链a-b进行受力分析,如图2所示。

|
图 2 a-b段锚链受力分析 Fig. 2 a-b segment anchor force analysis |
静力分析的悬链线方程为:
| $z = \frac{{{T_h}}}{w}\left[ {\cosh \left( {\frac{w}{{{T_{\rm{h}}}}}x} \right) - 1} \right]\text{,}$ | (19) |
| $s = \frac{{{T_h}}}{w}{\rm{sinh}}\left( {\frac{w}{{{T_{\rm{h}}}}}x} \right)\text{。}$ | (20) |
式中,z和x分别为垂向和水平坐标,s为锚链长度,Th为锚链顶端的水平张力,锚链微元外力包括重力和浮力,二者合成湿重w。
2.2 动力分析本文采用集中质量法对锚链进行动力分析。分析时将锚链中心线视作空间中的任意一条连续曲线,曲线上任意一点的位置由直角坐标系
xj为第j个集中质量点的位移,
| ${\mathit{\boldsymbol{x}}_j}{\rm{ = }}\left[ {\begin{array}{*{20}{c}}{{x_j}}\\{{y_j}}\\{{z_j}}\end{array}} \right]\text{。}$ | (21) |
编号为j的质量点和编号为j+1的质量之间,为编号为j的弹簧,弹簧初始长度为Lj,当弹簧有线性相对伸长量εj时,
| ${\varepsilon _j} = \frac{{{T_j}}}{{{E_j}{A_j}}}\text{,}$ | (22) |
其中Ej为杨氏模量,Aj为横截面积。
定义编号为j+1的质量点与编号为j的质量点之间的弹簧的张力的矢量式
| ${\mathit{\boldsymbol{T}}_j}{\rm{ = }}{T_j}\frac{{{\mathit{\boldsymbol{x}}_{j + 1}} - {\mathit{\boldsymbol{x}}_j}}}{{\left| {{\mathit{\boldsymbol{x}}_{j + 1}} - {\mathit{\boldsymbol{x}}_j}} \right|}}\text{。}$ | (23) |
则对于编号为j的集中质量点,其运动方程为:
| ${\mathit{\boldsymbol{M}}_j}{\ddot{x}_j} = {\mathit{\boldsymbol{G}}_j} + {\mathit{\boldsymbol{B}}_j} + {\mathit{\boldsymbol{H}}_j} + {\mathit{\boldsymbol{K}}_j} + {\mathit{\boldsymbol{T}}_j} - {\mathit{\boldsymbol{T}}_{j - 1}}\text{,}$ | (24) |
其中:Mj为质量矩阵;Gj为集中质量点受到的重力;Bj为浮力;Vj是编号为j的集中质量点的体积;Kj为海底对集中质量点的作用力,作用于靠近海底的集中质量点。Hj为分段在水中运动时受到的流体阻力,分段可看作长径比很大的小尺度构件,单位长度受到的流体动力使用Morrison公式计算:
| $\mathit{\boldsymbol{H}} = \frac{1}{2}\rho D\left( {{C_{dn}}\left| {{\mathit{\boldsymbol{v}}_n}} \right|{\mathit{\boldsymbol{v}}_n} + {\rm{π }}{C_{dt}}\left| {{\mathit{\boldsymbol{v}}_t}} \right|{\mathit{\boldsymbol{v}}_t}} \right) + \frac{{\rm{π }}}{4}\rho {D^2}\left( {{C_{an}}{\mathit{\boldsymbol{a}}_n}} \right)\text{,}$ | (25) |
其中:v为集中质量点的速度;a为集中质量点的加速度;vt为切向速度;vc和vw分别为流的速度和波的速度;vn为法向速度;at为切向加速度;an为法向加速度。
3 耦合计算方法本文所采用的运动响应耦合计算方法,并非将载体平台运动方程和系缆运动方程分别独立求解的“半耦合”的方法,而是将平台时域运动方程和系缆运动方程同时数值求解并考虑平台和系泊系统相互影响的“全耦合”方法。该方法同步进行2个数值求解过程,求解过程中每个时间步上进行载体平台和系缆的位移和受力数据的交互。此外,在考虑海洋能发电系统的载荷对平台影响时,可以根据已知的时变载荷方程,在每个计算步开始时输入一个水轮机或风机载荷值。
3.1 坐标变换在进行耦合计算时,需要建立2个坐标系:固定坐标系和运动坐标系。其中,固定坐标系即大地坐标系,运动坐标系则固结于载体平台上,随载体平台一起进行6个自由度运动。
由于外力直接作用于运动坐标系上,而讨论载体平台的运动却是在固定坐标系中,所以计算时需要将运动坐标系中的坐标点和空间矢量变换到固定坐标系中去。
3.2 耦合计算流程耦合计算的流程包括参数的输入、数据预处理、程序计算、数据输出等几个步骤。
1)输入参数包括平台参数、锚链参数、波浪参数和其他外力参数等。平台参数包括平台的几何参数、质量、转动惯量等。锚链参数包括锚链顶端的位置(导缆孔位置),锚链的总长、刚度、直径等。其他外力参数包括水轮机或风机的时变载荷方程,亦或是定常载荷值(本次研究中只是设立接口,暂不考虑转子系统的载荷影响)。
2)数据预处理指的是根据输入参数,处理成为计算中实际需要的数据。包括由输入的平台参数,经频域计算程序处理为平台的附加质量系数和阻尼系数。以及由锚链锚点参数,经锚链静态分析程序计算出锚链各个节点的数据。
3)程序计算的过程中,在各个时间步,锚链将张力数据传递给平台,平台按照锚链当前张力运动一个时间步之后,将位移传递给锚链,锚链再根据位移计算张力,如此往复迭代计算。
4)数据输出部分,程序会将载体平台位移和锚链顶端张力的计算结果输出到文件。
4 平台与系泊系统耦合运动计算分析本文仅对简单形式的载体平台和系泊系统进行耦合计算分析。其中平台继续选用圆柱型平台,系泊系统为4锚链对称布置。
4.1 载体平台参数载体平台选择圆柱型平台,参数如表1所示。
|
|
表 1 载体平台主尺度 Tab.1 Carrier platform main dimensions |
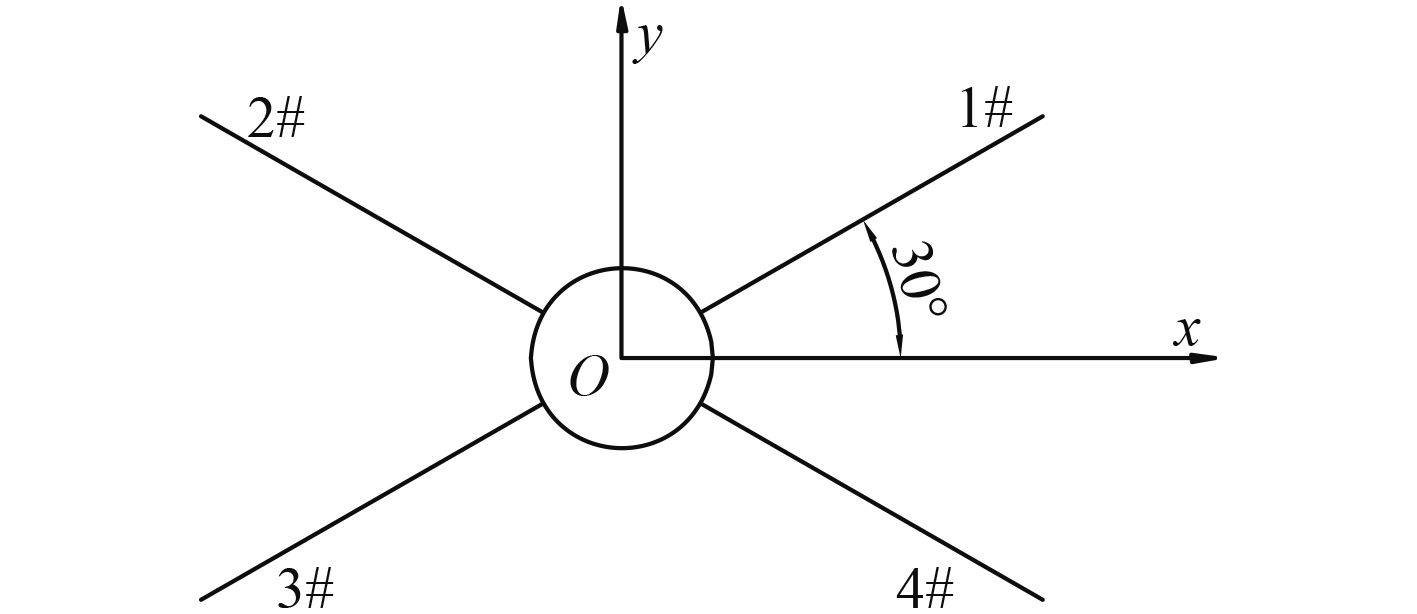
耦合计算采用的锚系布置方式如图3所示,任意2条相邻锚链均关于x轴或y轴对称。表2给出了所选用1#锚泊参数,其中点的坐标相对于固定坐标系。
|
图 3 锚系布置示意图 Fig. 3 Schematic diagram of mooring layout |
|
|
表 2 1#锚链参数 Tab.2 1# anchor chain parameters |
由于第1节中计算载体平台水动力系数时,选择的波浪圆频率从0.1开始,至4.0结束,中间每个间隔0.1,因此在耦合计算分析时选取的波浪圆频率从已经算过的波浪频率中选取,波高为2.0 m,浪向0°。
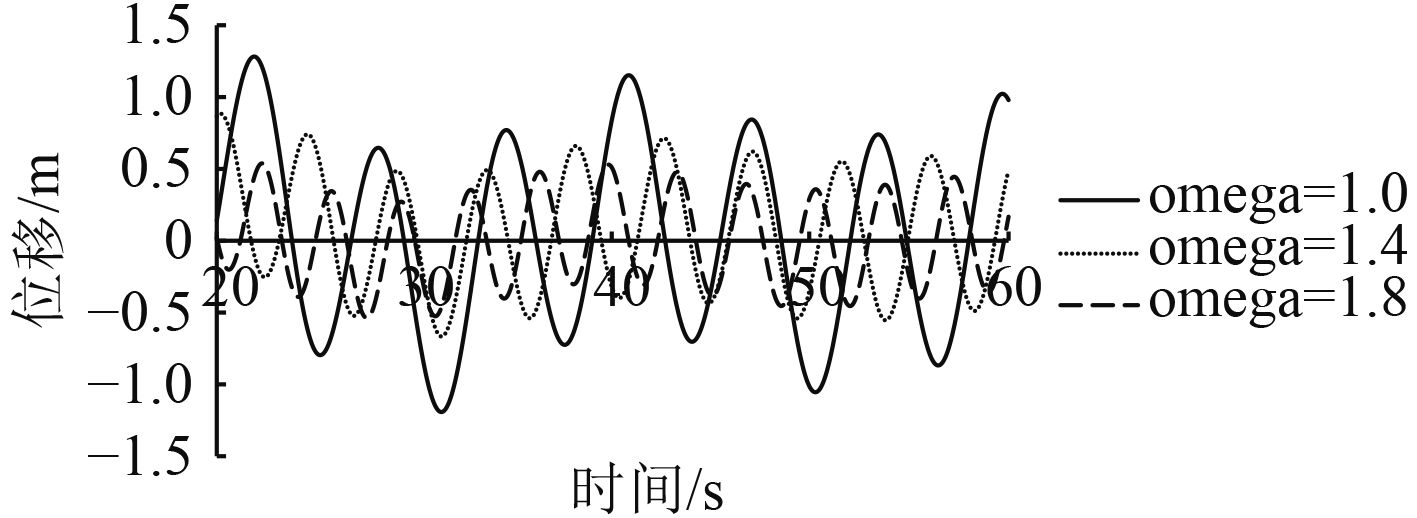
4.4 载体平台运动响应分析载体平台运动响应分析主要考察不同波浪频率下载体平台运动幅值。图4~图6分别给出了不同频率下(图中仅显示1.0,1.4,1.8三个频率)纵荡、垂荡、纵摇时历曲线。
|
图 4 不同波浪频率下纵荡时历曲线 Fig. 4 Surging curves at different wave frequencies in time domain |
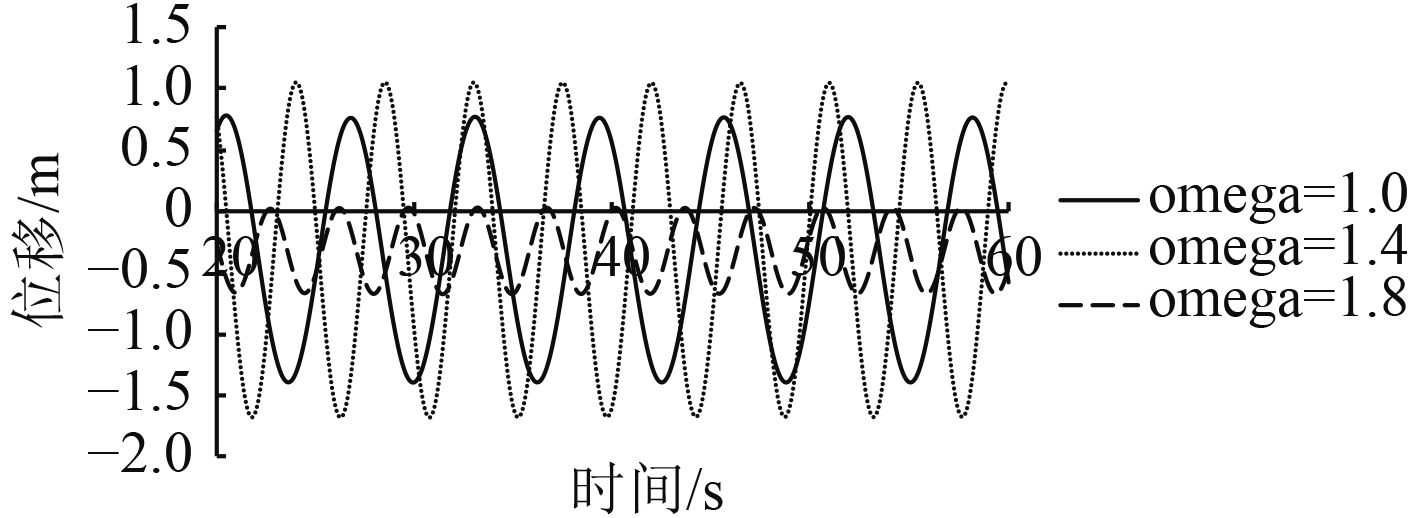
|
图 5 不同波浪频率下垂荡时历曲线 Fig. 5 Heaving curves at different wave frequencies in time domain |
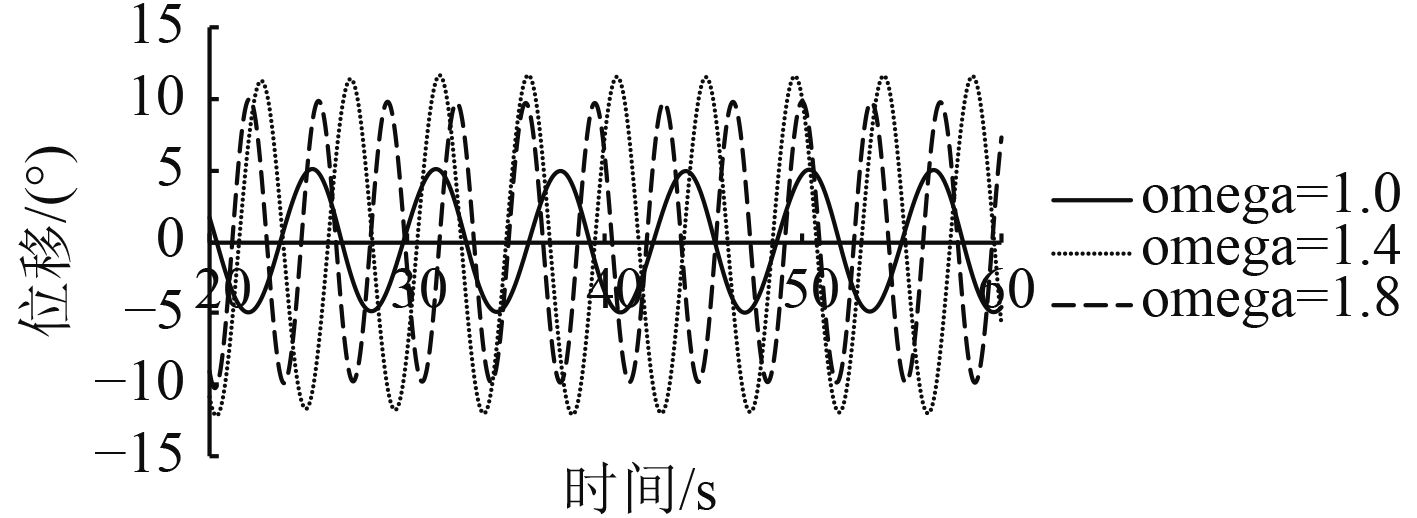
|
图 6 不同波浪频率下纵摇时历曲线 Fig. 6 Pitching curve at different wave frequencies |
将不同频率下时历曲线的最大幅值进行统计,形成以下统计结果。
|
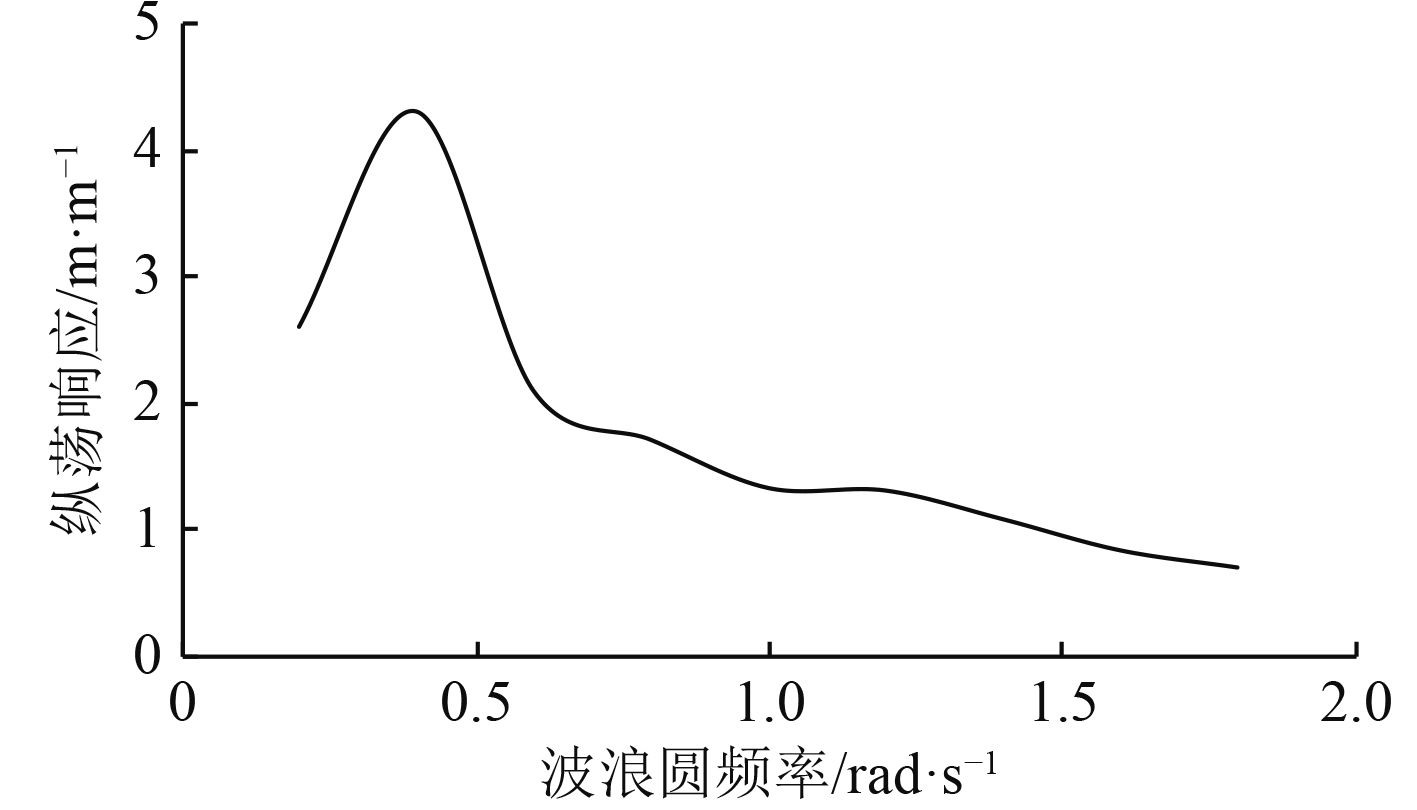
图 7 纵荡响应曲线 Fig. 7 Surging response curve |
|
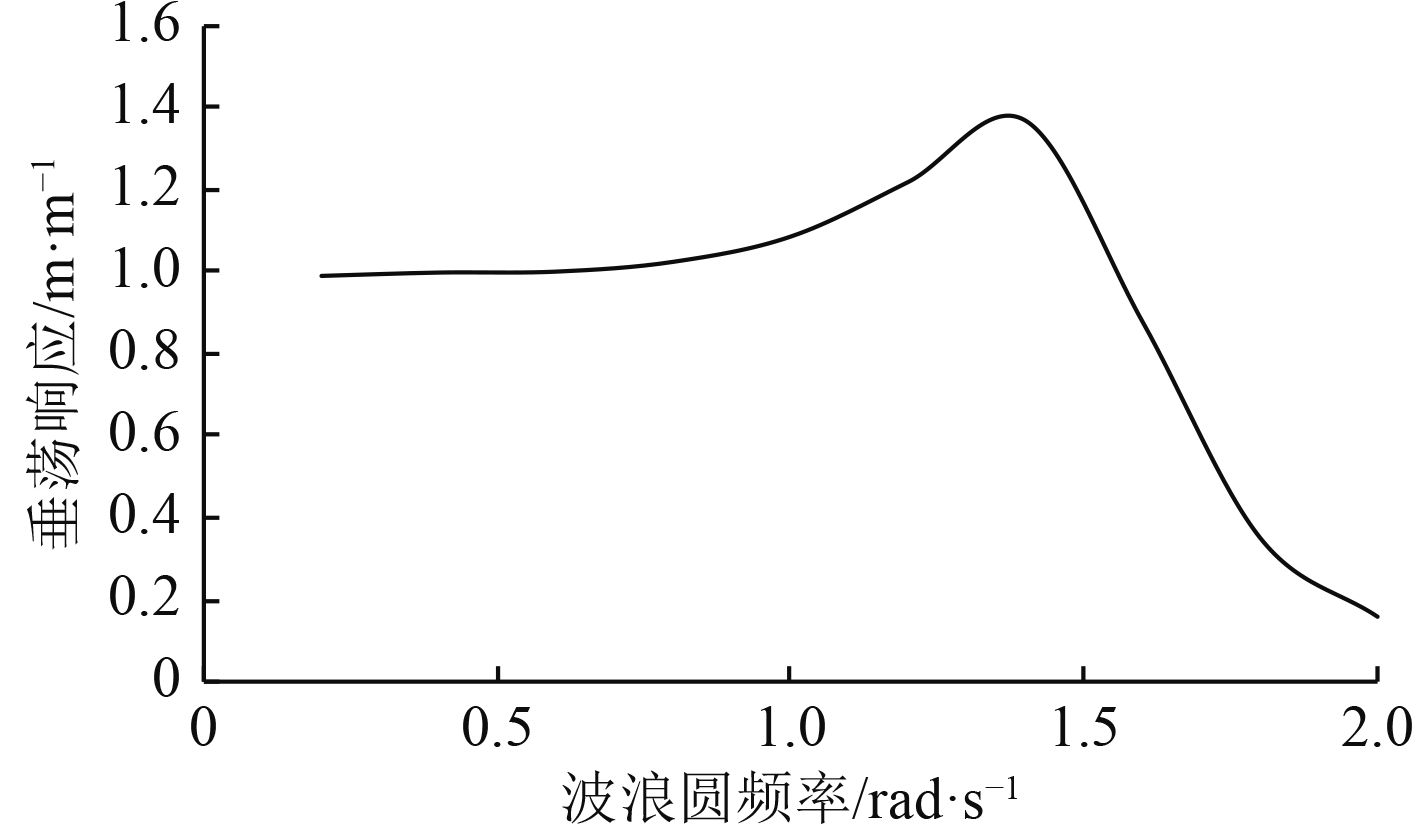
图 8 垂荡响应曲线 Fig. 8 Heaving response curve |
|
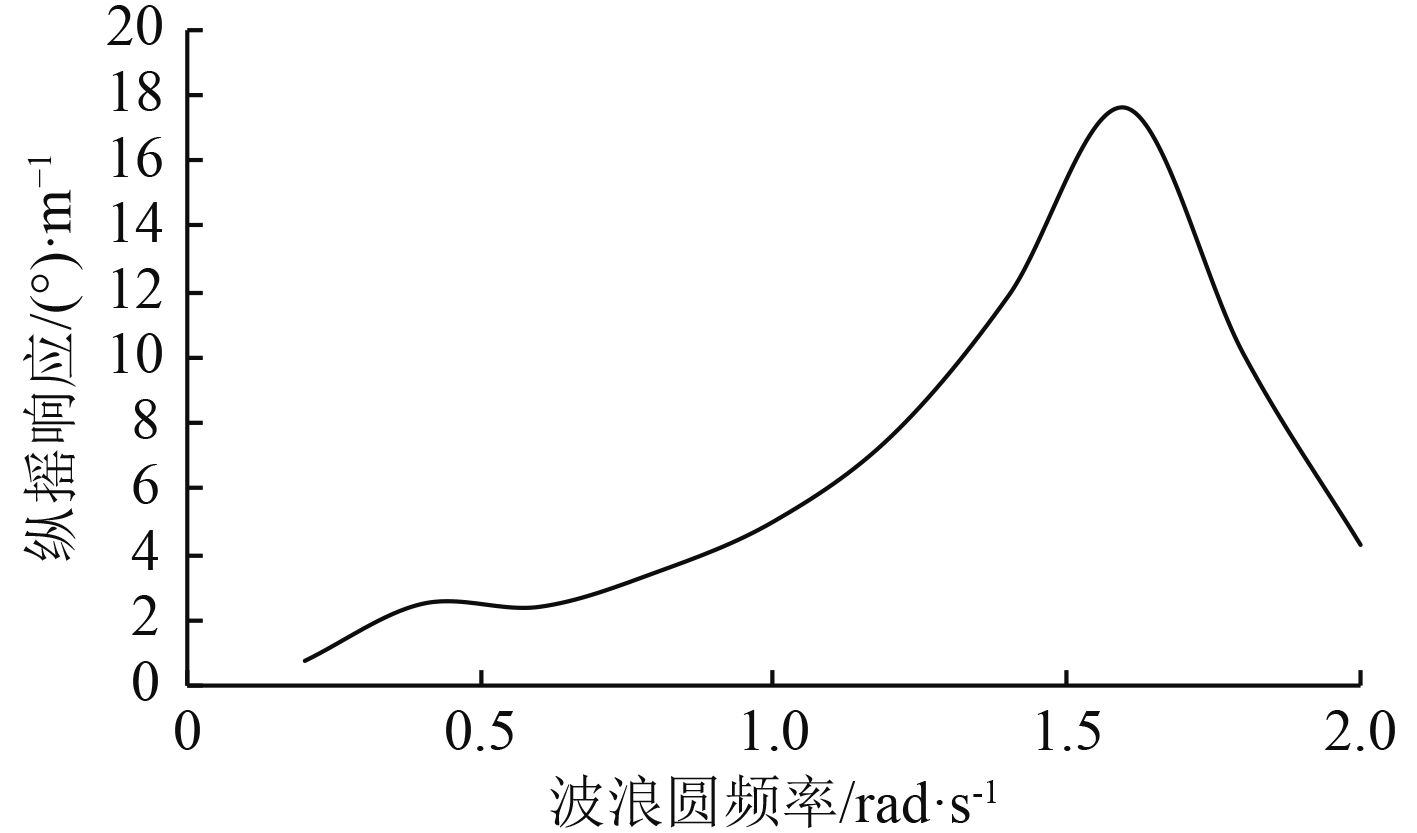
图 9 纵摇响应曲线 Fig. 9 Pitching response curve |
由频域曲线可知,当波浪频率为0.25时,纵荡响应幅值约为2,随着波浪频率的增大,纵荡响应幅值开始迅速上升,当波浪频率为0.4时达到峰值约4.4,后缓慢下降,可见纵荡运动的共振频率在0.4左右。垂荡响应幅值在波浪频率小于0.6时都接近于1,随着波浪频率的增大,垂荡响应幅值从1开始缓慢上升,当波浪频率为固有频率时达到峰值约1.4,后迅速下降,波浪频率为2时垂荡响应幅值为0.2,可见垂荡运动的共振频率约为1.4。纵摇响应曲线的变化趋势与垂荡响应曲线较为相似,当波浪频率小于0.25时,纵摇响应幅值约为1,随着频率增大,响应迅速增大,频率约为1.65时响应幅值达到峰值约18,后迅速下降,波浪频率为2时响应幅值约为4,可见纵摇运动的共振频率约为1.65。
4.5 系缆受力分析系缆受力分析主要考察不同波浪频率下系缆张力幅值的变化。根据载体平台的对称性和锚系布置的对称性,1#锚链张力与4#锚链相同,2#锚链张力与3#锚链张力相同。以下仅对1#锚链张力和2#锚链张力进行分析。
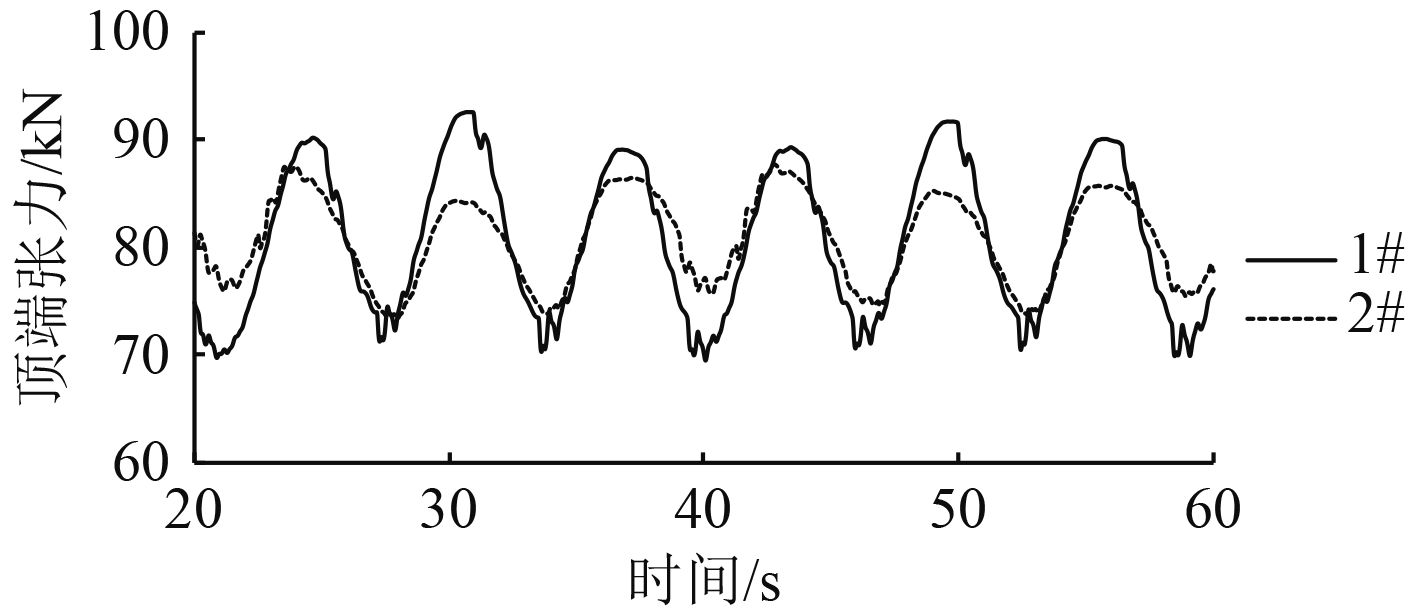
图10~图12分别给出了不同频率下(仅取1.0,1.4,1.8三个频率)锚链顶端张力的时历曲线。
|
图 10 波浪圆频率为1.0时的锚链顶端张力时历曲线 Fig. 10 Tension curve in time domain on the top of the anchor when wave circle frequency is 1.0 rad/s |
|
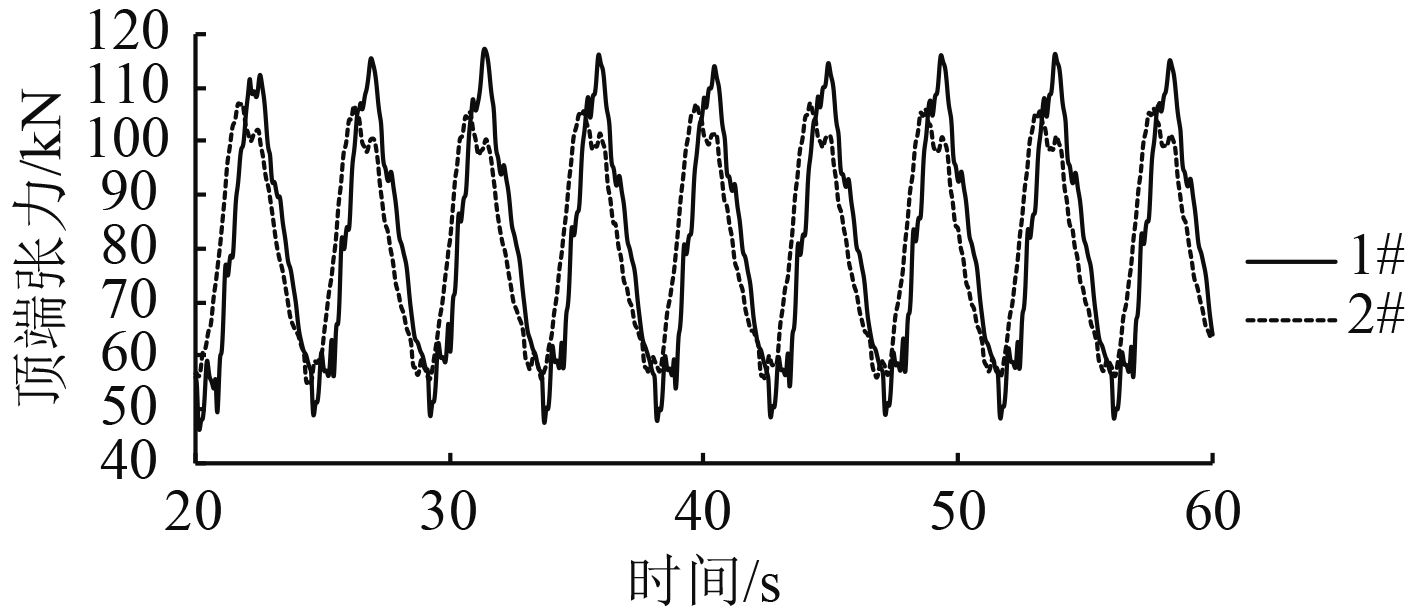
图 11 波浪圆频率为1.4时的锚链顶端张力时历曲线 Fig. 11 Tension curve in time domain on the top of the anchor when wave circle frequency is 1.4 rad/s |

|
图 12 波浪圆频率为1.8时的锚链顶端张力时历曲线 Fig. 12 Tension curve in time domain on the top of the anchor when wave circle frequency is 1.8 rad/s |
将不同波浪圆频率下锚链顶端张力的最大幅值进行统计,得出以下统计结果。

|
图 13 1#锚链顶端张力幅值响应曲线 Fig. 13 Tension amplitude response curve on the top of 1# anchor |

|
图 14 2#锚链顶端张力幅值响应曲线 Fig. 14 Tension amplitude response curve on the top of 2# anchor |
当波浪频率为0.2时,1#锚链的顶端张力约为95 kN,随着波浪频率不断增加,张力先迅速上升,在波浪频率约为0.45时达到第1个峰值约114 kN,后迅速下降,在波浪频率在0.6至1的区间内张力稳定在95 kN左右,后张力再次上升,当波浪频率为1.5时达到第2个峰值约122 kN,后再次下降。2#锚链的顶端张力在波浪频率为0.2时,约为100 kN,随着波浪频率不断增加,张力先迅速上升,在波浪频率约为0.45时达到第1个峰值约112 kN,后迅速下降,在波浪频率约0.6时为84 kN,后张力再次上升,当波浪频率为1.6时达到第2个峰值约120 kN,后再次下降。由频域曲线可以看出,1#锚链和2#锚链的张力变化趋势大致相同,张力幅值响应曲线在低频和高频处各有1个峰值,1#锚链和2#锚链较低的共振频率均在0.45左右,1#锚链较高的共振频率约为1.5,2#较高的共振频率约为1.6。
5 结 语本文总结了漂浮式海洋平台耦合运动的研究方法和经验,在此基础上分别研究了载体平台与系泊系统的计算理论,提出了耦合运动的计算方法并进行了相关计算程序的设计。通过对简化的圆柱形浮式平台进行计算分析,得出了以下结论:载体平台的纵荡、垂荡和纵摇运动均在0~2的波浪圆频域内有且仅有一个共振频率,相同频率的规则波作用下,纵荡运动比垂荡运动更加剧烈;系泊锚链的张力在0到2的波浪圆频域内有高低2个共振频率,且1#锚链与2#锚链的顶端张力随频率变化的趋势大致相同。
本文只是针对规则波环境下浮式圆柱形载体平台和系泊系统的运动响应耦合分析,没有考虑转子系统的载荷输入,以此为基础,后续可以开展不规则波环境下,考虑转子系统载荷影响的各类浮式载体平台和系泊系统的运动响应耦合分析。
| [1] | 裴丽. 海上风能与波浪能综合研究利用[D]. 天津: 天津大学, 2012. |
| [2] | 张庆丰, Crooks R. 迈向环境可持续的未来: 中华人民共和国国家环境分析[M]. 北京: 中国财政经济出版社, 2013. |
| [3] | 赵宗慈, 周天军. 法国外长谈2015巴黎气候大会的4个目标[J]. 气候变化研究进展, 2015 (03): 204–204. |
| [4] | 王兴刚. 深海浮式结构物与系泊缆索的耦合动力分析[D]. 大连: 大连理工大学, 2011. |
| [5] | 单鹏昊. 深海浮式平台及其系泊缆索的时域耦合分析[D]. 哈尔滨: 哈尔滨工程大学, 2012. |
| [6] | 叶小嵘. 海上浮式风力机系统环境载荷及耦合运动性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2013 |
| [7] | 赵玉娜. Spar型海上浮式风力系统运动耦合计算方法及性能研究[D]. 哈尔滨: 哈尔滨工程大学硕士学位论文, 2014. |
| [8] | 张楠. 漂浮式潮流电站叶轮与锚泊系统设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. |
| [9] | FALTINSEN O. Sea loads on ships and offshore structures[M]. Cambridge: Cambridge University Press, 1990. |
| [10] | JAIN R K. A simple method of calculating the equivalent stiffnesses in mooring cables[J]. Applied Ocean Research, 1980, 2 (3): 139–142. DOI: 10.1016/0141-1187(80)90006-1 |
 2017, Vol. 39
2017, Vol. 39
