0 引 言

在人工通气超空泡的研究中已经发现重力（或浮力）和攻角对空泡的形态有很大影响。其中重力对水平超空泡的影响可分为2个方面：一是导致空泡中轴线向上弯曲，即空泡尾部上浮；二是导致空泡横截面的底部形成一个向空泡内部的凸起。在一定条件下，即当空泡速度不大以至于重力影响较大时，向内凸起的空泡底部就有可能与空泡顶部壁面相交，将空泡横截面分为两部分，从而产生特有的双涡管外形。本文只考虑重力对空泡中轴线的偏移影响，利用小扰动方法可以估算重力影响下空泡轴线向上弯曲程度^[1]，而Logvinovich^{[2, 3]}则基于动量定理给出了一个工程上足够好用的简洁公式。类似的，攻角对空泡中轴线的偏移影响也很大，其原因是攻角改变了流动的对称性，使得空泡中轴线发生向上或向下弯曲，这取决于攻角的正负。由于攻角导致的升力与空泡尾流的动量变化率相等、方向相反，因此攻角对空泡中轴线偏移大小的影响也可以利用动量定理进行计算，可参考文献[2, 3]中Logvinovich给出的一个简化公式。

但是上述对空泡变形的研究都是针对无后体的空泡，而对有后体的空泡，即航行体上的局部空泡的变形研究则比较少。顾久渊^[4]为了估算带攻角航行体的空泡外形，给每一个空泡截面赋予一个在截面平面内的水平平移速度，并假设这个水平平移速度等于空化器穿越此截面平面的水平速度分量；程少华等^[5]也采用类似方法计算了空泡迎背水面的空泡长度，取得了很好效果。本文则将这种方法和攻角及重力导致的空泡变形结合起来，并以圆柱体上的局部空泡为例，建立小攻角条件下局部空泡变形的估算方法。

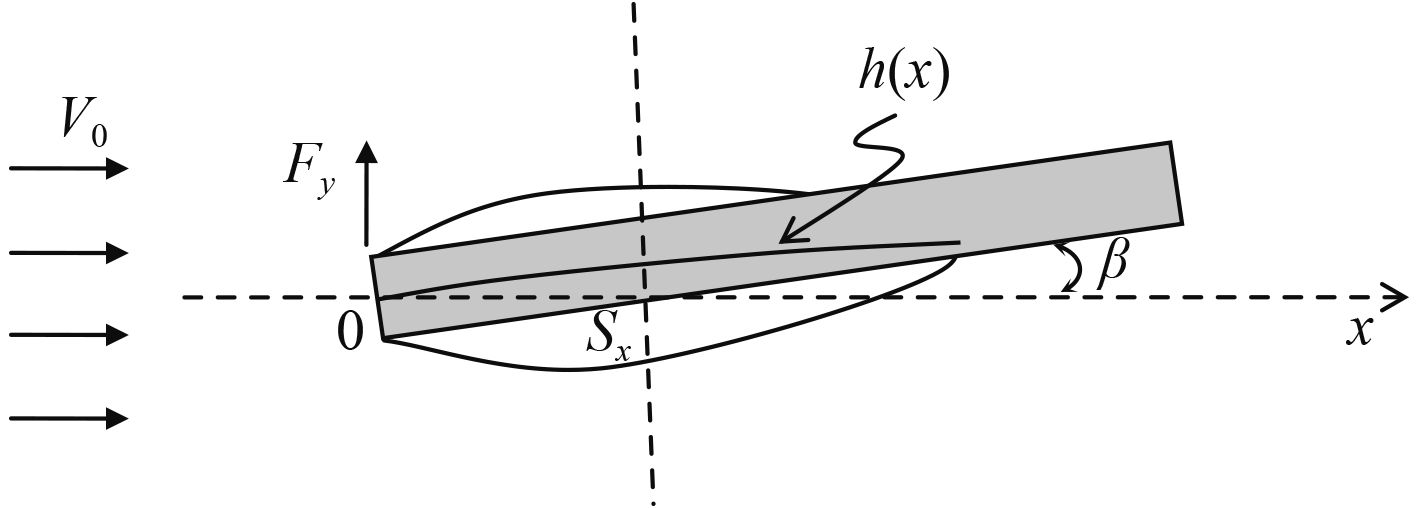
1 定常空泡受重力和攻角影响的理论模型

设无界重力流场中的航行体是一个足够长的圆柱体外形，航行体高速运动时头部产生空泡，空泡压力为p_c，空泡尾部闭合在航行体上，见图1，其中航行体的半径为R₀，速度为V₀，攻角为β，在定常条件下，以上参数都是常数。在来流作用下，由于攻角存在，因此航行体的头部会产生一个升力F_y，同时空泡由于攻角和重力的共同影响发生变形，在航行体的上表面（迎水面）和下表面（背水面）的闭合位置并不相同，2个位置之间的距离差反映了空泡变形的程度。这个空泡闭合位置的距离差直接影响到航行体的水动力大小，因此对这个距离差的计算是估算水动力大小的一个重要参数。

对于定常空泡，可以将坐标系建立在航行体上，坐标原点在航行体头部的中心点o，x轴平行与来流速度方向，y轴垂直向上。如果从航行体坐标系中观察相对流动，则航行体保持静止，无限远来流速度为V₀，S_x为在x坐标的空泡截面面积，见图1，同时假设流场是无旋、无粘理想流体。

当空泡截面S_x不在空泡闭合位置时，可认为空泡截面S_x并不受空泡闭合位置的流动影响，因此这个截面的空泡变形相当于无后体超空泡的变形。在文献[2]中，Logvinovich在假设空泡截面保持为圆形，即 ${S_x} = π R_x^2$ 的条件下，分别给出了超空泡在攻角和重力影响下，空泡截面中心偏离中轴线高度 $h\left( x \right)$ 的一阶估计式：

$h = \frac{{ - {F_y}}}{{π V_0^2\rho }}\int_0^x {\frac{{{\rm d}x}}{{R_x^2}}}{\text{，}} $

(1)

$h = \frac{g}{{V_0^2R_x^2}}\int_0^x {R_x^2{\rm d}x} = \frac{{\rho gQ\left( x \right)}}{{\rho V_0^2π R_x^2}}{\text{。}}$

(2)

上述式（1）表示攻角产生的升力F_y对空泡中轴线偏离高度 $h\left( x \right)$ 的贡献大小，式（2）表示浮力 $\rho gQ\left( x \right)$ 对空泡中轴线偏离高度 $h\left( x \right)$ 的贡献大小，其中 $Q\left( x \right)$ 是航行体头部的空化位置到空泡截面 ${S_x}$ 之间的空泡体积。

在文献[2]中，攻角和重力对空泡变形的影响分开考虑，但是很容易看出，如果航行体既有攻角，又考虑重力影响，则空泡中轴线的偏离应该同时受到两者的作用，因此完整的空泡中轴线偏离高度 $h\left( x \right)$ 的表达式可以很容易证明是式（1）和式（2）的叠加。

$h = \frac{g}{{V_0^2R_x^2}}\int_0^x {R_x^2{\rm d}x} + \frac{{ - {F_y}}}{{π V_0^2\rho }}\int_0^x {\frac{{{\rm d}x}}{{R_x^2}}} {\text{。}}$

(3)

其中的未知量是空泡截面半径 ${R_x}$ ，Logvinovich在文献[2]中建议空泡截面半径 $R_x^{}$ 用定常空泡的以下近似式估计

$R_x^{} = {R_k}\sqrt {1 - \left( {1 - \frac{{R_0^2}}{{R_k^2}}} \right){{\left| {1 - \frac{x}{{{L_k}}}} \right|}^{\frac{2}{\chi }}}} {\text{。}}$

(4)

其中 ${R_k}$ 为空泡中间位置的最大空泡截面半径， ${L_k}$ 为空泡半长，对于圆盘空化器，系数χ≈0.85。由于R_k和L_k很容易从实验图像中获得，因此式（4）适合作为空泡实验中的空泡表达式，但是在空泡工程计算中，R_k和L_k也是未知量，因此式（4）并不适用。

在空泡工程计算方法中，Logvinovich在文献[2]中提出的空泡截面独立膨胀原理得到实验证实并被广泛应用。因此对于细长体空泡，采用空泡截面独立膨胀原理来计算空泡大小可行，下面是Vasin^[6]基于空泡截面独立膨胀原理给出的空泡动力学方程在定常空泡状态下的表达式

$\frac{{{{\rm d}^2}{S_x}}}{{{\rm d}{x^2}}}V_0^2 = - k\frac{{p - {p_c}}}{\rho }{\text{，}}$

(5)

其中 ${S_0} = π R_0^2$ 是航行体头部发生空化部分的截面积，且

${S'_0} = \frac{{{\rm d}{S_0}}}{{{\rm d}x}} = \frac{{2π {C_x}{R_0}}}{a},k = \frac{{4π {C_x}}}{{{a^2}}}{\text{。}}$

(6)

这里a是一常数，对于半径为R₀的圆盘空化器，

$a = \frac{{\sigma {L_k}}}{{{R_0}}} \approx A\sqrt {{C_x}} ,A = \sqrt {\ln \frac{1}{\sigma }}{\text{。}} $

(7)

其中C_x为空化器阻力系数，L_k为空泡半长， $\sigma = \displaystyle\frac{{p - {p_c}}}{{1/2 \cdot \rho V_0^2}}$ 是空泡的空化数。

如果根据微分方程（5）求出R_x，再将其代入式（3），即可求出空泡截面中心的偏离高度 $h\left( x \right)$ 。

当空泡压力为常数时，由式（5）可得到：

${S_x} = {S_0} + {S'_0}x - k\frac{{p - {p_c}}}{\rho }\frac{{{x^2}}}{{2V_0^2}}{\text{。}}$

(8)

将式（6）代入式（8）整理得到

${S_x} = {S_0} + \frac{{2π {C_x}{R_0}}}{a}x - \frac{{π {C_x}\sigma }}{{{a^2}}}{x^2}{\text{。}}$

(9)

定义付汝德数 ${F_r} = \displaystyle\frac{{V_0^{}}}{{\sqrt {g{R_0}} }}$ ，升力系数 ${C_y} = \displaystyle\frac{{{F_y}}}{{1/2 \cdot \rho V_0^2{S_0}}}$ ， $\bar x = \displaystyle\frac{x}{{{R_0}}}$ ， $\bar h = \displaystyle\frac{h}{{{R_0}}}$ ，并将式（9）代入式（3）得到无量纲形式

$\bar h = \int\limits_0^{\bar x} {\left[ {\displaystyle\frac{{ - \frac{1}{2}{C_y} + \displaystyle\frac{{\bar x}}{{F_r^2}}\left( {1 + \displaystyle\frac{{{C_x}}}{a}\bar x - \displaystyle\frac{{{C_x}\sigma }}{{3{a^2}}}{{\bar x}^2}} \right)}}{{\left( {1 + \displaystyle\frac{{2{C_x}}}{a}\bar x - \displaystyle\frac{{{C_x}\sigma }}{{{a^2}}}{{\bar x}^2}} \right)}}} \right]} {\rm d}\bar x{\text{。}}$

(10)

已知对于小攻角，航行体头部的升力系数和阻力系数满足关系式

${C_x} = {C_{x0}}{\cos ^2}\beta ,{C_y} = {C_{x0}}\sin \beta \cos \beta ,\frac{{{C_y}}}{{{C_x}}} = \sin \beta{\text{。}} $

(11)

其中 ${C_{x0}}$ 是0攻角阻力系数。将式（11）代入式（10）得到

$\bar h = \int\limits_0^{\bar x} {\left[ {\displaystyle\frac{{ - \frac{1}{2}\sin \beta + \displaystyle\frac{{\bar x}}{{F_r^2}}\left( {\displaystyle\frac{1}{{{C_x}}} + \displaystyle\frac{1}{a}\bar x - \displaystyle\frac{\sigma }{{3{a^2}}}{{\bar x}^2}} \right)}}{{\left( {\displaystyle\frac{1}{{{C_x}}} + \displaystyle\frac{2}{a}\bar x - \displaystyle\frac{\sigma }{{{a^2}}}{{\bar x}^2}} \right)}}} \right]} {\rm d}\bar x{\text{。}}$

(12)

2 特殊解

在2种情形下重力对空泡偏移的影响可忽略：一是航行体速度较大，即 ${F_r} \to \infty $ ；二是航行体速度垂直于水面方向运动。由于在工程上这2种情形经常遇到，因此下面给出不考虑重力影响的解。

在上述2种情形下，方程（12）中与重力有关项可忽略，即式（12）可简化为

$\bar h = - \frac{1}{2}\sin \beta \int\limits_0^{\bar x} {\frac{{{\rm d}\bar x}}{{\frac{1}{{{C_x}}} + \frac{2}{a}\bar x - \frac{\sigma }{{{a^2}}}{{\bar x}^2}}}}{\text{。}} $

(13)

直接积分得到解析解

$\bar h = \frac{{\sin \beta }}{4}\frac{a}{{\sqrt {1 + \sigma /{C_x}} }}\ln \left( {\frac{{\bar x\left( {1 - \sqrt {1 + \sigma /{C_x}} } \right) + a/{C_x}}}{{\bar x\left( {1 + \sqrt {1 + \sigma /{C_x}} } \right) + a/{C_x}}}} \right){\text{。}}$

(14)

由于空泡独立膨胀原理在空泡的“1/3”位置后较为准确，因此公式（14）的应用范围应该取 $x \in \left[ {3{R_0},{L_c}} \right]$ ，或者 $\bar x \in \left[ {3,{L_c}/{R_0}} \right]$ 。

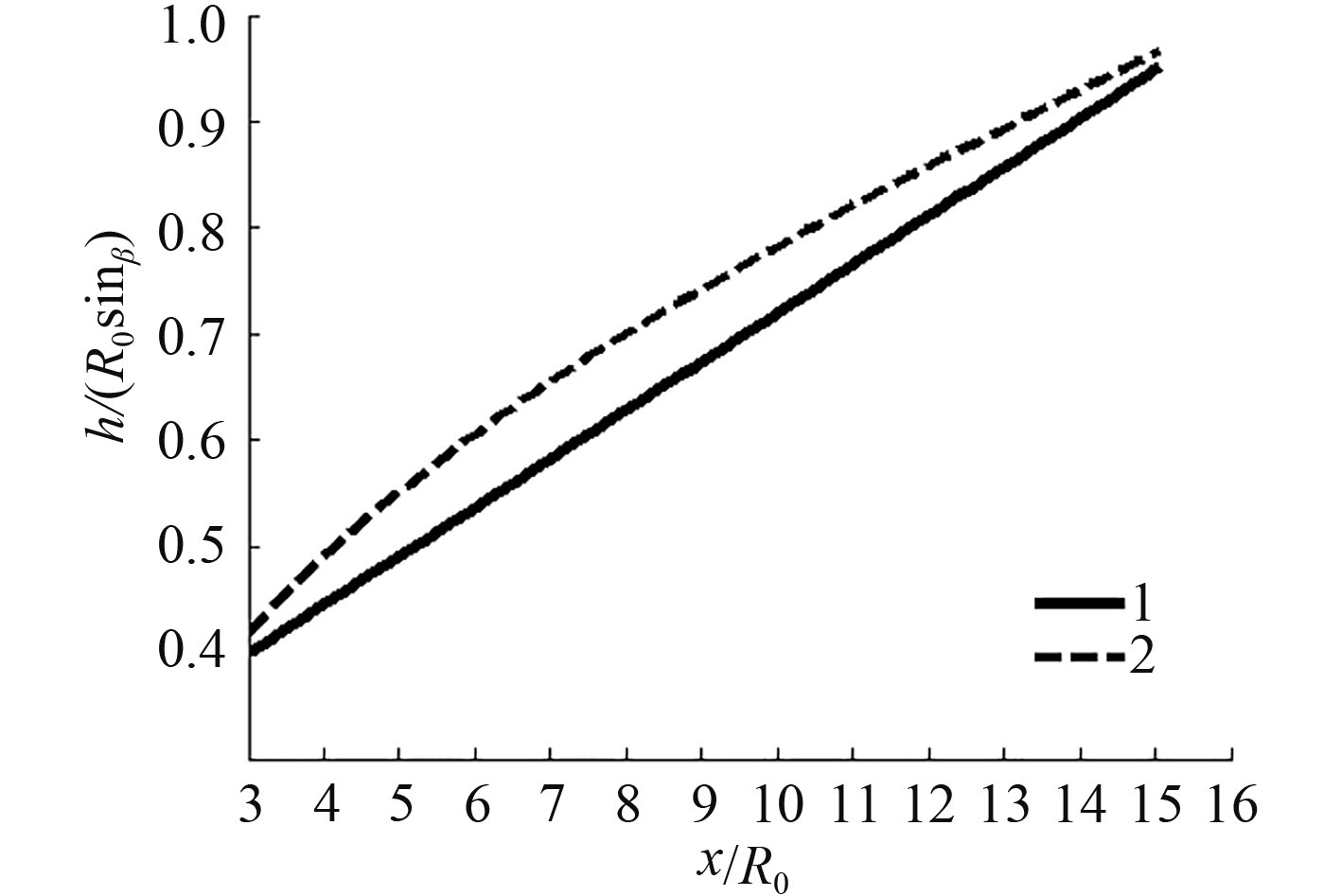
公式（14）的准确性可以通过与文献[2, 3]中利用小扰动方法得到的另一个计算公式

$\bar h = - {C_y}\left( {0.46 - \sigma + \bar x\frac{{2{R_0}}}{{{L_c}}}} \right){\text{。}}$

(15)

进行比较而得到。其中半径R₀与空泡半长L_k的比 ${R_0}/{L_k}$ 可由 ${R_0}/{L_k} = \sigma /a$ 估算。

取 $\sigma = 0.08$ ， ${C_{x0}} = 0.827$ ， $\beta = {33.5^o}$ ，由2个公式计算的结果见图2。由于文献[3]中的小扰动公式（15）与试验结果进行过对比，因此，如果公式（14）与小扰动公式（15）相吻合，则说明公式（14）也与试验结果相吻合。

从图2可看出，如果注意到小扰动公式（15）也是对具有一定离散度的实验数据的一个近似估计式，则可以认为公式（14）与公式（15）计算结果吻合的较好，这表明本文利用空泡独立膨胀原理计算空泡截面的偏移在工程上合理。

3 迎背水面空泡外形的计算

参考图1可看出，对于定常空泡，公式（14）或（15）都可给出空泡中心的位置。很容易看出，如果空泡截面都是圆形，则迎水面空泡外形的方程为

$\bar y = \bar h\left( {\bar x} \right) + {\bar R_x}\left( {\bar x} \right){\text{，}}$

(16)

类似的，背水面空泡外形的方程为

$\bar y = \bar h\left( {\bar x} \right) - {\bar R_x}\left( {\bar x} \right){\text{。}}$

(17)

其中 $\bar h\left( {\bar x} \right)$ 由公式（14）或（15）计算， ${\bar R_x}\left( {\bar x} \right)$ 由公式（9）计算，式（9）的无量纲形式为

$\bar R_x^2 = \frac{{{S_x}}}{{{S_0}}} = 1 + \frac{{2{C_x}}}{a}\bar x - \frac{{{C_x}\sigma }}{{{a^2}}}{\bar x^2}{\text{。}}$

(18)

将式（18）和式（14）代入式（16）和式（17）即可得到迎背空泡外形计算公式。由于公式表达式较复杂，因此直接用公式计算空泡外形比较繁琐，但是在计算机仿真中很容易实现。

4 迎背水面空泡长度差的计算

利用空泡外形公式（16）和式（17）以及航行体的外形还可以计算出迎背空泡长度差。从图1可看出，当迎水面空泡与航行体上表面相交时，可确定出航行体迎水面的空泡长度；类似的，当背水面空泡外形与航行体下表面相交时可确定空泡背水面的长度。

这里的航行体取圆柱体，见图1，因此航行体上表面的外形方程为直线方程

$\bar y = {\rm tg}\beta \cdot \bar x + \frac{1}{{\cos \beta }}{\text{。}}$

(19)

其中 $\bar x = x/{R_0}$ ， $\bar y = y/{R_0}$ 。

根据迎水面空泡外形方程（16）和航行体上表面外形方程（19）可确定迎水面空泡与航行体上表面的交点位置 $\bar x$ ，即 $\bar x$ 应满足方程

$ {\rm tg}\beta \cdot \bar x + \frac{1}{{\cos \beta }} = \bar h\left( {\bar x} \right) + {\bar R_x}\left( {\bar x} \right){\text{。}}$

(20)

为了简化计算，这里将式（15）和式（18）代入式（20），得到

$\begin{split}{\rm tg}\beta \cdot \bar x + \frac{1}{{\cos \beta }} = & - {C_x}tg\beta \left( {0.46 - \sigma + \bar x\sigma /a} \right) + \\ & \sqrt {1 + \frac{{2{C_x}}}{a}\bar x - \frac{{{C_x}\sigma }}{{{a^2}}}{{\bar x}^2}} {\text{。}}\end{split}$

(21)

类似的，由式（17）可以得到背水面空泡与航行体下表面相交的交点位置 ${\bar x_1}$ 所应满足的方程

$\begin{split}{\rm tg}\beta \cdot {\bar x_1} - \frac{1}{{\cos \beta }} =& - {C_x} {\rm tg}\beta \left( {0.46 - \sigma + {{\bar x}_1}\sigma /a} \right) - \\ &\sqrt {1 + \frac{{2{C_x}}}{a}{{\bar x}_1} - \frac{{{C_x}\sigma }}{{{a^2}}}{{\bar x}_1}^2}{\text{。}}\end{split}$

(22)

很容易看出，式（21）和式（22）都是一个二次多项式方程，可以直接求出 $\bar x$ 和 ${\bar x_1}$ 的解析解。空泡长度差 $\Delta \bar x$ 则为

$\Delta \bar x = {\bar x_1} - \bar x{\text{。}}$

(23)

虽然式（21）和式（22）都容易求解，但是其表达式过于繁琐，因此本文在这里省略其表达式。

应注意到如果在式（20）中去掉空泡中轴线的偏移项 $\bar h\left( {\bar x} \right)$ ，即有

$ {\rm tg}\beta \cdot \bar x + \frac{1}{{\cos \beta }} = {\bar R_x}\left( {\bar x} \right){\text{。}}$

(24)

则式（24）与文献[4–5]顾久渊、程少华等所采用的方法完全一样。但是对比式（24）和式（20）可看出，本文方法不仅考虑了航行体外形对空泡长度差的影响，还考虑了攻角通过改变流场的对称性而导致的空泡偏移对空泡长度差的影响。

5 结 语

航行体上非对称空泡外形对水动力有重要影响，因此建立快速估算非对称空泡外形的方法有重要意义。本文基于空泡截面独立膨胀原理，给出了攻角和重力使空泡发生变形的计算公式，并将其计入到空泡迎背水面外形的计算模型中，建立了可同时考虑攻角、重力及航行体几何外形的迎背空泡长度差的计算方法。