1. 海军驻431厂军事代表室,辽宁 葫芦岛 125004;
2. 武汉第二船舶设计研究所,湖北 武汉 430205;
3. 武汉大学,湖北 武汉 430072
收稿日期: 2017-04-06.
作者简介: 张卫东(1971 – ),男,高级工程师,研究方向为船舶辅机
Numerical investigation on hydraulic transient process of conveying water by compressed gas
1. The Navy Representative Department Resident in No. 431 Plant, Huludao 125004, China;
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China;
3. Wuhan University, Wuhan 430072, China
0 引 言 传统的流体输送方式除利用泵增压输送外,利用压缩空气增压移水在航空、船舶、化工等领域也广泛运用。其输水管路简单,只需要提供压缩气源即可完成输水。然而在气动移水过程中,阀门的启闭往往会诱发剧烈的水锤。作为一种非定常流动现场,水锤的出现会对系统管路造成较大的冲击,甚至破坏相关管道设备[1 – 4]。目前针对泵供水系统管路水锤的研究较多[5 – 8],然而针对气动供水方式下的水锤研究较少。与泵移水不同,气源在水箱内的压力并不稳定,气动移水在关阀过程中系统管路更易诱发剧烈的压力脉动。特别是在高速移水过程中,关阀引起的水锤对系统存在巨大的危害,需要引起重视。
本文针对典型的舰船上水箱间的气动移水过程,采用商业软件PIPENET对移水工程中阀门的瞬态启停过程进行仿真计算。气动移水系统由供水水箱、受水水箱、管道和控制阀门组成,受水舱气体压力始终为0 MPa(标准大气压相对值),供水舱内有高压气体,在压差的作用下实现供水舱向受水舱的移水,并随着移水过程气压不断降低。当满足移水要求的数量后,关闭管路系统上的控制阀门。通过对气动移水系统过渡过程仿真,得到水锤发生的位置规律及其压力变化特点,计算分析水舱供气压力、系统流速、关阀时间、阀门特性和控制阀位置对于水锤的影响并总结规律,然后根据此规律提出初步的水锤抑制方案。
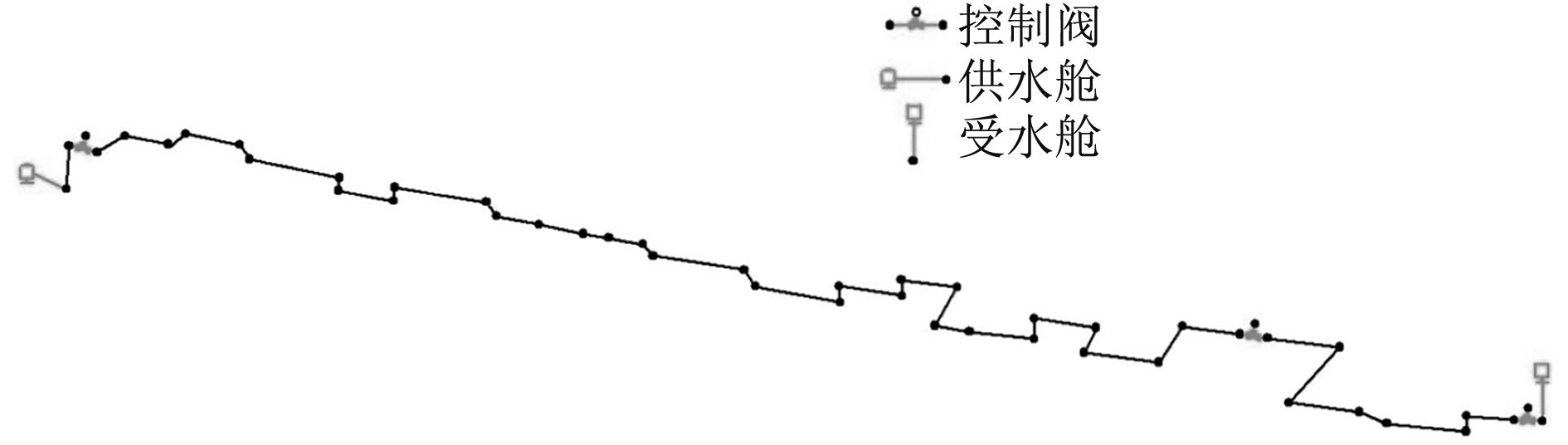
1 系统组成 图1所示为气动移水系统图,其主要部件包括:1号和2号水箱(互为供水水箱和受水水箱)、3个控制阀门(阀门1、阀门2、阀门3)、供气阀1和供气阀2、排气阀1和排气阀2等部件。
气动移水系统管路全长115 m,采用钢管布置,钢管规格为Φ108×5。阀门1和阀门2置于水箱出口处,阀门3布置于距离2号水箱约99 m处。水箱为圆柱型,体积60 m3,直径为4.37 m,高4 m。
系统运行时供水水箱排气阀关闭,供气阀开启接通气源水舱增压,而排水水舱供气阀关闭,排气阀打开接通大气。待供水水箱充压达到指定值时,关闭供气阀,开启控制阀。此时,供水水箱内介质在气压的作用下排向受水水箱,进而实现水箱间的移水。当移水达到指定量时,关闭控制阀,停止移水。
2 数值仿真方法 本次采用商业软件PIPENET对船舶泵阀系统的水力过渡过程进行计算分析。PIPENET系列软件已在国际范围内广泛的运用于石油化工、造船、工业循环水以及跨流域输送等行业,具备强大的工程管网系统的数值计算、模拟仿真和系统优化等功能。
2.1 水锤计算的特征线法 泵站水锤的计算是对整个水泵抽水装置进行计算分析,包括管道内点及与管道连接的泵装置中的各部分(边界点)。在水锤计算中,对于管道系统内点的计算是求解水锤基本方程,即由运动方程和连续性方程组成的双曲型偏微分方程组。为了实现计算机的编程计算,需采用特征线方法将该偏微分方程组离散化,为此,先沿特征线方向将它转换为水锤全微分方程:
|
${C_ + }:\left\{ \begin{array}{l}\displaystyle\frac{g}{a}\frac{{{\rm d}H}}{{{\rm d}t}} + \frac{{{\rm d}V}}{{{\rm d}t}} + \frac{{fv\left| v \right|}}{{2D}} = 0\text{,}\\\displaystyle\frac{{{\rm d}x}}{{{\rm d}t}} = + a\text{,}\end{array} \right.$
|
(1) |
|
${C_ - }:\left\{ \begin{array}{l} - \displaystyle\frac{g}{a}\frac{{{\rm d}H}}{{{\rm d}t}} + \frac{{{\rm d}V}}{{{\rm d}t}} + \frac{{fv\left| v \right|}}{{2D}} = 0\text{,}\\\displaystyle\frac{{{\rm d}x}}{{{\rm d}t}} = - a\text{。}\end{array} \right.$
|
(2) |
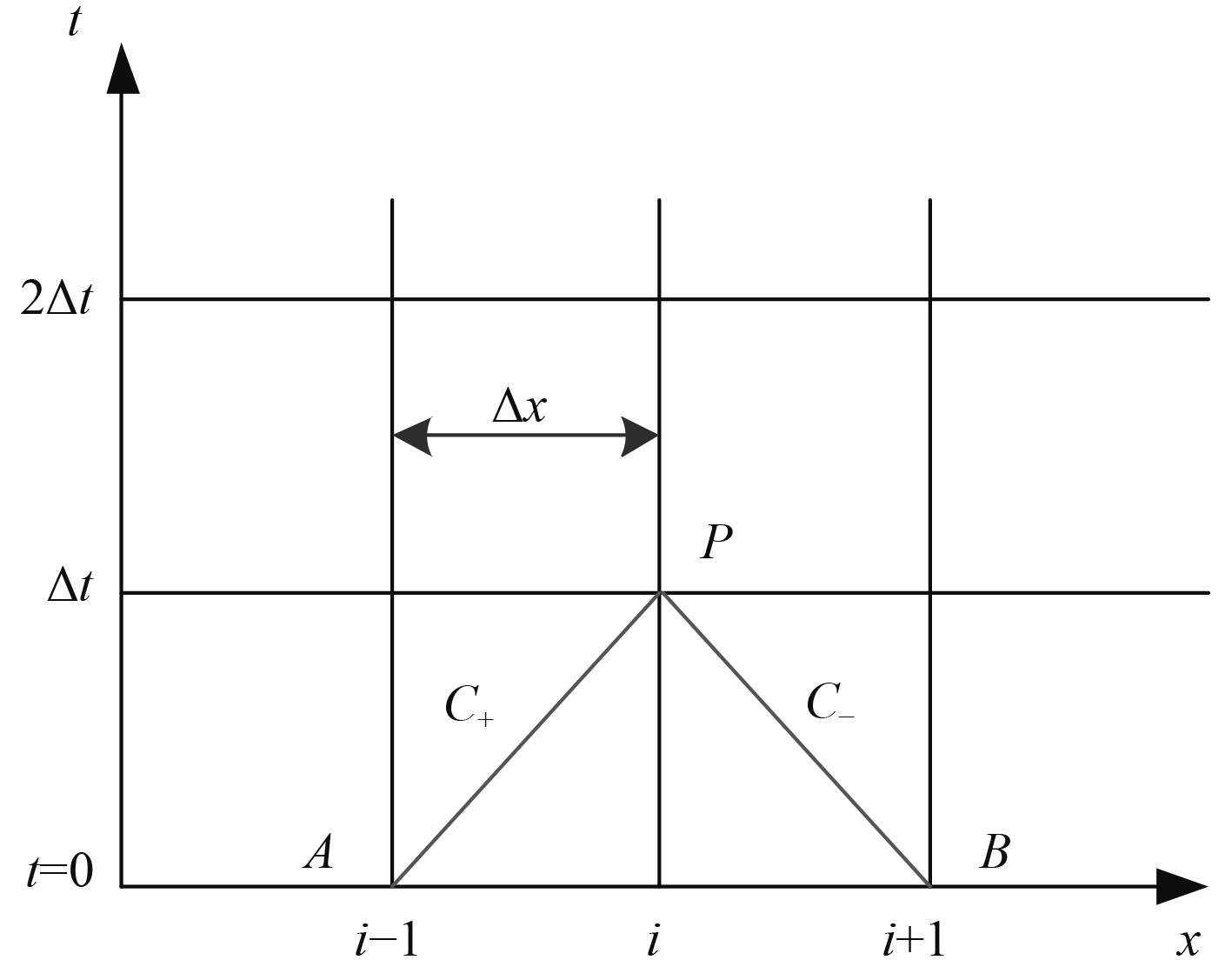
由式(1)和式(2)进行有限差分近似,可以得到对应于图2所示的水锤离散特征线方程。
|
${H_p} - {H_A} + \frac{a}{{gA}}\left( {{Q_p} - {Q_A}} \right) + \frac{{f\Delta x}}{{2gD{A^2}}}{Q_A}\left| {{Q_A}} \right| = 0\text{,}$
|
(3) |
|
${H_p} - {H_B} - \frac{a}{{gA}}\left( {{Q_p} - {Q_B}} \right) - \frac{{f\Delta x}}{{2gD{A^2}}}{Q_B}\left| {{Q_B}} \right| = 0\text{,}$
|
(4) |
解上述方程可得:
|
${C^ + }:{H_p} = {H_A} - B\left( {{Q_p} - {Q_A}} \right) - R{Q_A}\left| {{Q_A}} \right|\text{,}$
|
(5) |
|
${C^ - }:{H_p} = {H_B} + B\left( {{Q_p} - {Q_B}} \right) + R{Q_B}\left| {{Q_B}} \right|\text{。}$
|
(6) |
式中:
|
$B = \frac{a}{{gA}}\text{,}$
|
(7) |
|
$R = \frac{{f\Delta x}}{{2gD{A^2}}}\text{,}$
|
(8) |
|
${C_p} = {H_A} + B{Q_A} - R{Q_A}\left| {{Q_A}} \right|\text{,}$
|
(9) |
|
${C_M} = {H_B} - B{Q_B} + R{Q_B}\left| {{Q_B}} \right|\text{。}$
|
(10) |
2.2 仿真模型及工况 图3所示为PIPENET仿真模型示意图,左端为供水水箱,右端为受水水箱,从供水水箱至受水水箱,沿程布置3个控制阀,分别对应图1中阀1、阀3和阀2。供水水箱对应图1中1号水箱,受水水箱对应图1中2号水箱。仿真过程中主要对3个阀门的关闭时间以及水箱供气压力2个变量进行控制。供气压力分别设定为0.1 MPa、0.3 MPa、0.5 MPa和0.7 MPa,关阀时间分别设定为0.5 s、1.5 s、2.5 s、3.5 s、5.0 s。
3 计算结果与分析 3.1 不同阀门操作时间系统水锤对比 在气动移水管路上的阀门突然关闭,无论是阀前还是阀后都会诱发不同程度的冲击。图4所示为阀门3关闭过程中管道压力线。由图可知,阀前整体冲击压力要高于阀后,且越靠近阀门,管道在关阀过程中的最高压力也越大。与此相反,阀后的冲击相对较小,但最小压力则更低。图5~图7所示为阀门3关闭过程中阀前阀后的瞬时压力以及系统瞬时流量随时间的关系(供气压力0.7 MPa,t=0 s时开始关阀,t=3.5 s时阀门关闭)。关阀过程中系统流量变化相对平稳,但出现剧烈的压力波动。由图可知在阀门关闭过程中由于水击波的传递,阀前出现瞬时的压力冲击达110.46 m,在阀门关闭后,阀前也产生了连续的压力冲击,幅值高达80 m。由于阀后管路较短,故阀后压力冲击频率较高幅值较小,且压力波动衰减较快。
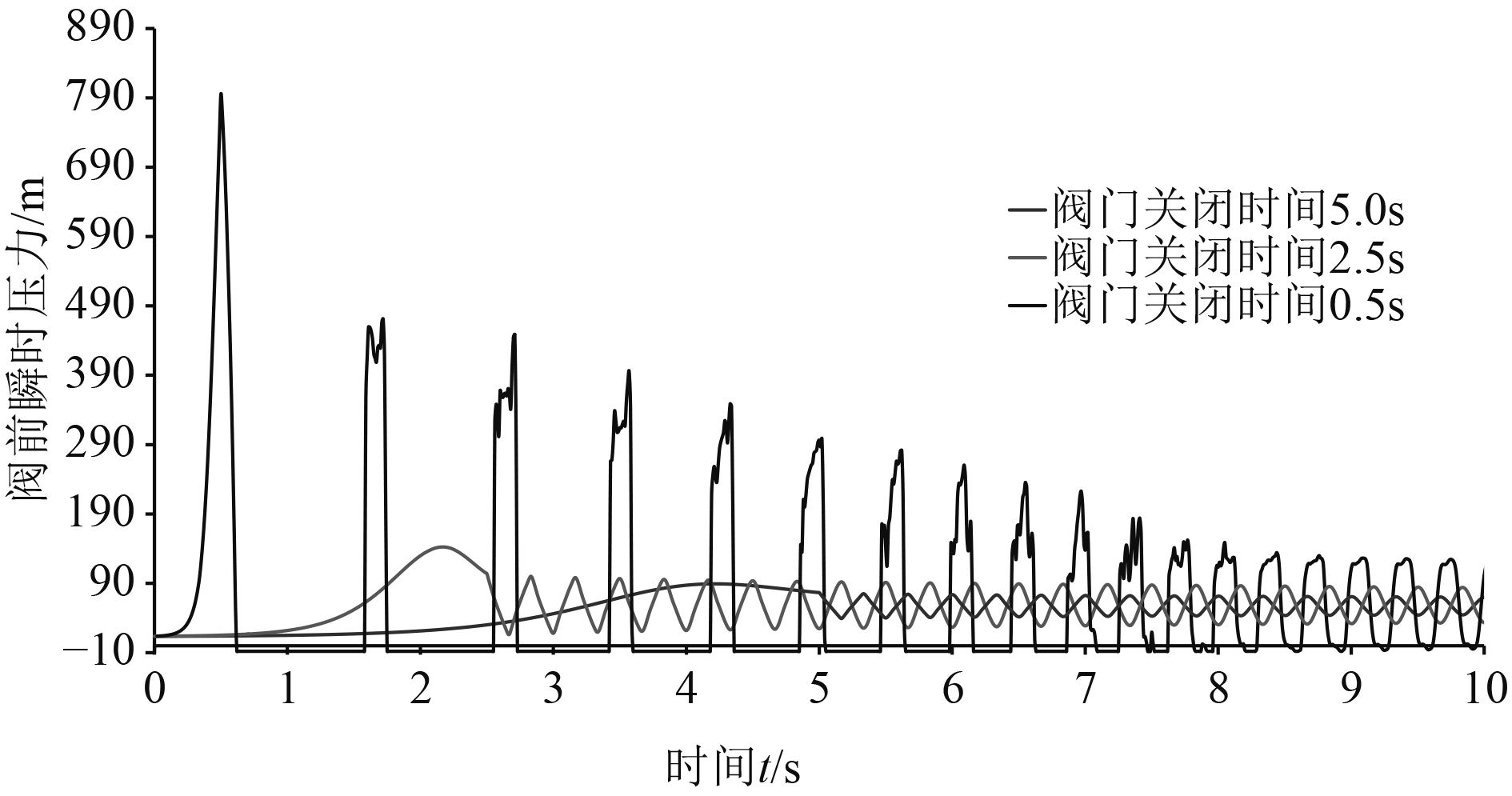
图8所示为不同关阀时间阀前压力随时间变化曲线(操作阀门3,供气压力0.7 MPa)。由图可知,随着关阀时间从5 s减少至0.5 s,阀前最大冲击压力由89.29 m增加至795 m,且阀前伴随空化现象。由图可知在关阀时间5.0 s和2.5 s时,阀前最大压力出现在阀门关闭前,可见阀门处的水锤压强受到降压顺行波影响开始减小。关阀时间0.5 s时,水锤最大冲击压力出现阀门关闭时,此时系统出现直接水锤,冲击压力达到最大。
表1所示为不同关阀时间下系统过渡特性对比表。当关阀时间控制在1.5 s时,阀前水锤引起的最大冲击压力可降低至231.8 m。然而此时阀后仍然存在较大的冲击压力,且伴随空化现象产生。当阀门关闭时间增长至3.5 s时,阀后最大冲击压力降低至15.1 s,且空化现象消失。可见增长关阀时间,可有效降低阀前和阀后的水锤冲击压力,并防止阀后空化现象的产生。
表 1(Tab. 1)

表 1 不同关阀时间下系统过渡特性对比表(操作阀门3)
Tab. 1 Comparisons of the system transient characteristics under different operating time
| 开/关中间阀时间/s |
供气压力/MPa |
阀前最大压力/m |
阀后最小压力 |
阀后最大压力/m |
系统最大流量/m3·s-1 |
| 0.5 |
0.7 |
795 |
空化 |
834.5 |
0.067 |
| 1.5 |
0.7 |
231.8 |
空化 |
518.13 |
0.067 |
| 2.5 |
0.7 |
142.41 |
空化 |
15.2 |
0.067 |
| 3.5 |
0.7 |
110.46 |
–4.36 |
15.1 |
0.067 |
| 5.0 |
0.7 |
89.25 |
–1.31 |
15.1 |
0.067 |
|
表 1 不同关阀时间下系统过渡特性对比表(操作阀门3)
Tab.1 Comparisons of the system transient characteristics under different operating time
|
3.2 不同供气压力下系统水锤对比 供气压力对系统水锤的相关动态特性也存在较大影响。图9所示为不同供气压力下阀门3关闭过程中阀前压力随时间的变化曲线(关阀时间2.5 s)。随着供气压力的降低,阀前关阀水锤最大冲击压力不断降低,水锤冲击波的振幅也有明显衰减。当供气压力为0.7 MPa时,阀前最大冲击压力可达142.4 m,然而当供气压力降低至0.1 MPa时,关阀过程中,阀前甚至因水锤波的传递出现了空化现象。表2所示为不同供气压力下系统过度特性对比表。当供气压力为0.7 MPa和0.1 MPa时,阀后都出现了空化现象,但供气压力为0.5 MPa和0.3 MPa时,阀后空化现象消失。由此可见,阀前压力过高或过低都会诱发系统管网的空化现象,实际操作中应根据具体使用工况,确定供气压力。
表 2(Tab. 2)

表 2 不同供气压力下系统过度特性对比表
Tab. 2 Comparisons of the system transient characteristics under different air pressrue
| 供气压力/MPa |
开/关中间阀时间/s |
阀前最大压力/m |
阀后最小压力/m |
阀后最大压力/m |
系统最大流量/m3·s-1 |
| 0.7 |
2.5 |
142.4 |
空化 |
15.2 |
0.067 |
| 0.5 |
2.5 |
118 |
–7.6 |
11.6 |
0.057 |
| 0.3 |
2.5 |
90.3 |
–6.7 |
8.15 |
0.043 |
| 0.1 |
2.5 |
50.1 |
空化 |
5.6 |
0.023 |
|
表 2 不同供气压力下系统过度特性对比表
Tab.2 Comparisons of the system transient characteristics under different air pressrue
|
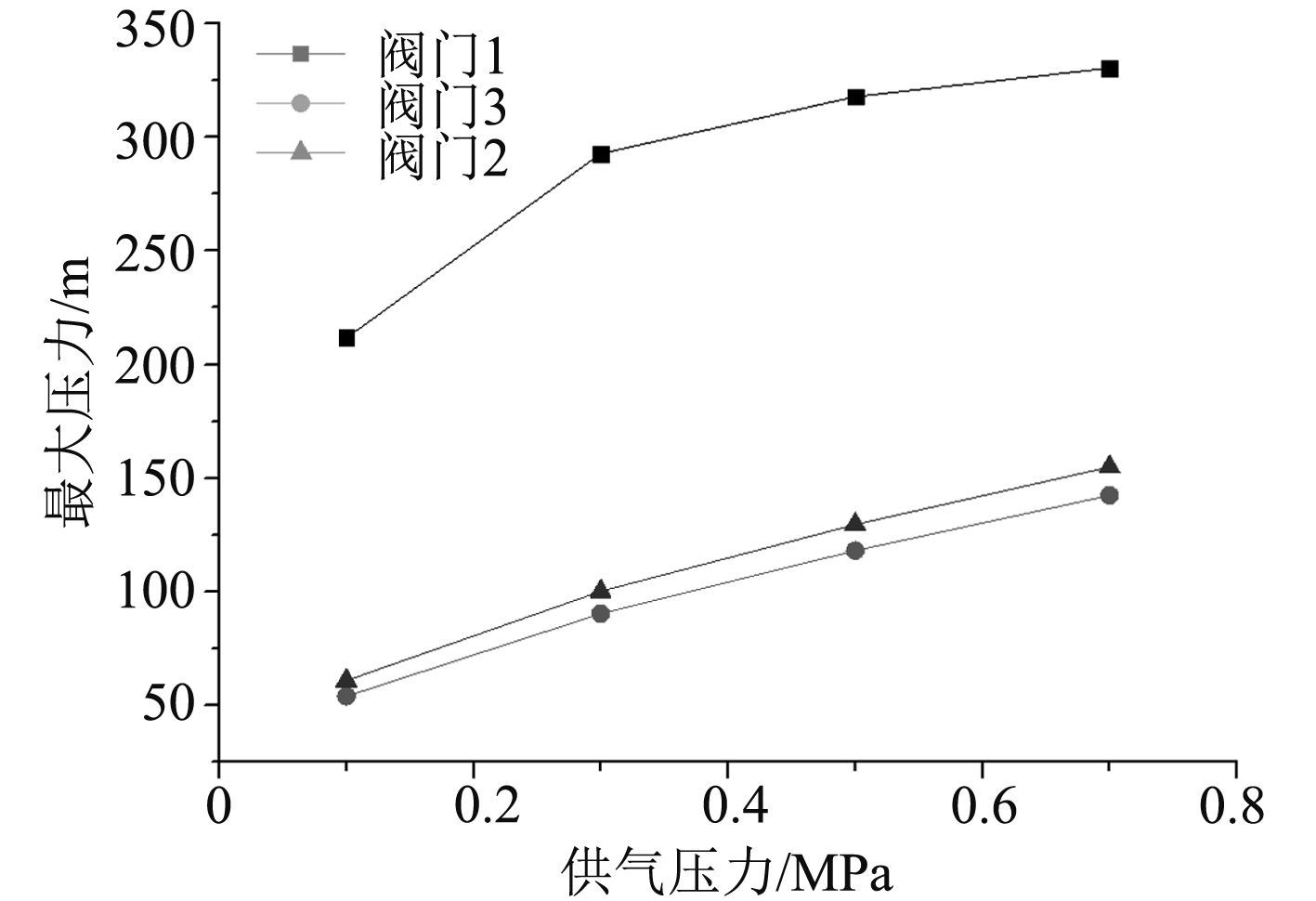
3.3 不同位置阀门关闭系统水锤对比 在1号水箱向2号水箱供水过程中,操作不同的阀门对系统的水锤冲击压力也存在较大影响。图10和图11分别比较了关阀时间为1.5 s和2.5 s时,系统最大压力(包括阀前压力和阀后压力)随供气压力的变化曲线。由图可知,操作阀门1系统产生的最大压力在不同供气压力下都要高于操作阀门2。可见在气动供水过程中,选择关闭靠近供水水箱的阀门(阀门1)时,系统水锤最大冲击压力高于受水水箱处阀门(阀门2)。此时最高压力主要是由于阀后的负压水锤引起。当操作阀门为位于中间位置的阀门3时,关阀时间对系统最大冲击压力有明显的影响。在关阀时间为1.5 s时,系统最大冲击压力随供气压力增加明显增大。在供气压力为0.1 MPa时,阀门3和阀门2关闭引起的冲击压力幅值相当,且最大压力都发生在阀前。然而,当供气压力增大至0.3 MPa以上时,阀门3关闭引起的最大冲击压力明显增大,且主要发生在阀后。当关阀时间增加至2.5 s时,阀门3关闭引起的系统最大水锤冲击压力则明显降低,甚至低于阀门2关闭引起的最大压力,且最大压力主要发生在阀前。
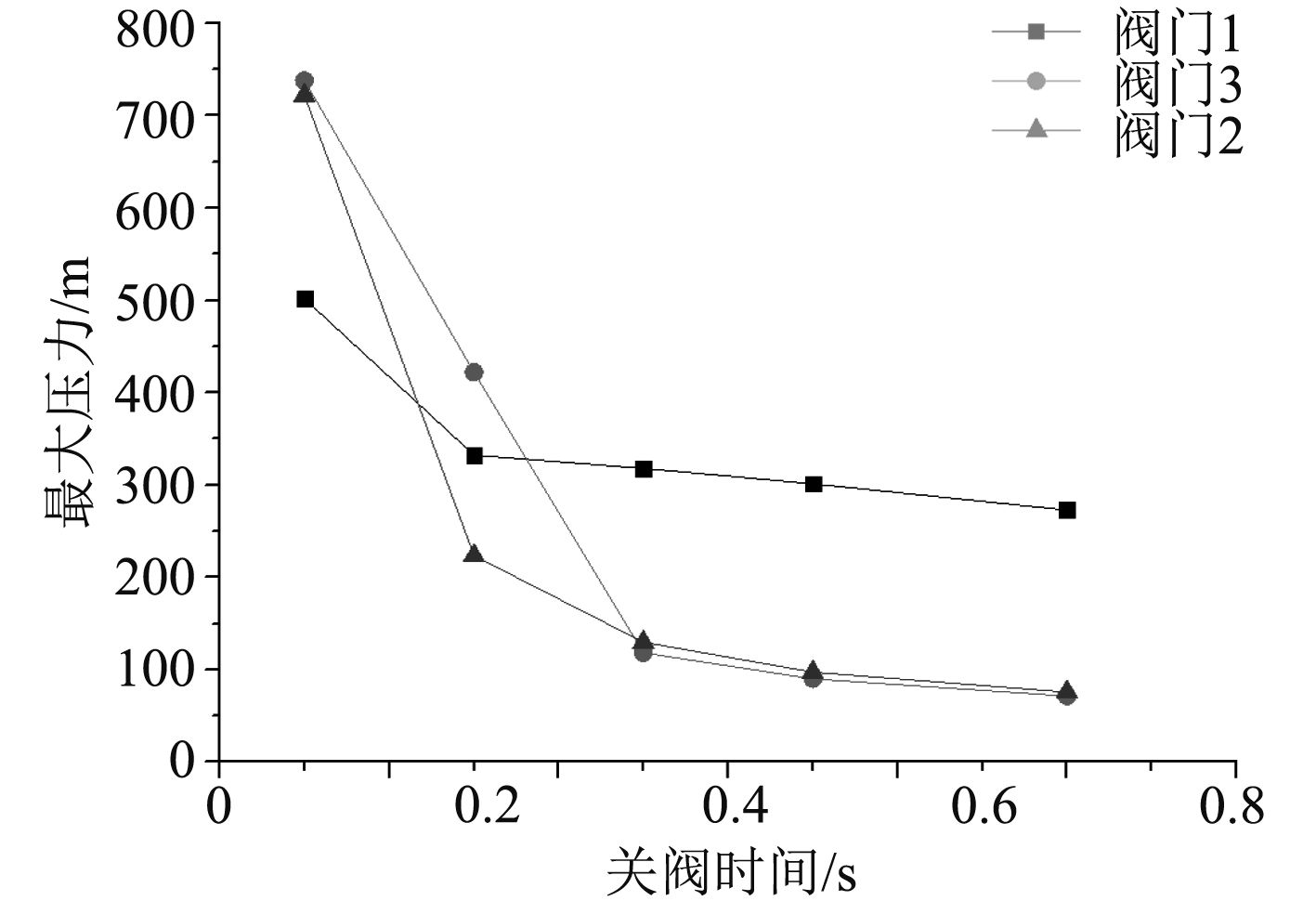
图12和图13进一步比较了供气压力为0.7 MPa和0.5 MPa时,系统最大压力(包括阀前压力和阀后压力)随供气关阀时间的变化曲线。当关阀时间为0.5 s时,关闭靠近受水水箱的阀门(阀门2)时,系统水锤最大冲击压力更大。可见在气动供水过程中,当关阀时间极短系统发生直接水锤时,阀门2相对阀门1关闭引起的水锤冲击更为剧烈。然而当关阀时间增加至1.5 s以上时,关闭靠近受水水舱阀门(阀门2)时,系统最大水锤冲击压力相对较小。此外,当关阀时间继续增加,阀门3和阀门2关闭时系统最大压力相当。虽然如此,阀门3引起的最大压力主要发生在阀后,而阀门2引起的最大压力主要发生在阀前。
4 结 语 本文通过商用软件PIPENET对气动移水阀门启闭的瞬态水锤进行了仿真计算,详细比较了阀门启停时间、供气压力、操作阀门位置对系统供水过程中水锤的影响,根据结论提出了相应的改进措施,具体结论如下:
1)延长阀门关闭时间及降低供气压力可有效抑制阀前和阀后的水锤最大冲击压力;
2)操作阀门的位置对水锤冲击压力有较大影响,靠近供水水箱的阀门关闭时阀前冲击压力较小,而阀后冲击压力较大且伴随严重的汽蚀。选择关闭靠近受水水箱的控制阀,虽然阀前冲击压力有所提高,但阀后冲击压力明显降低,且汽蚀现象也可得到有效控制;
3)在适当延长开阀时间的基础上,选择关闭靠近受水水箱或中间位置的控制阀都可有效抑制水锤。








 2017, Vol. 39
2017, Vol. 39
